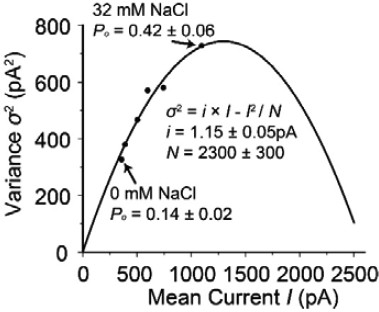
Cooperative regulation by G proteins and Na+ of neuronal GIRK2 K+ channels
- Howard Hughes Medical Institute, Rockefeller University, United States
- Harvard Medical School, United States
Figures
Figure 1 with 2 supplements
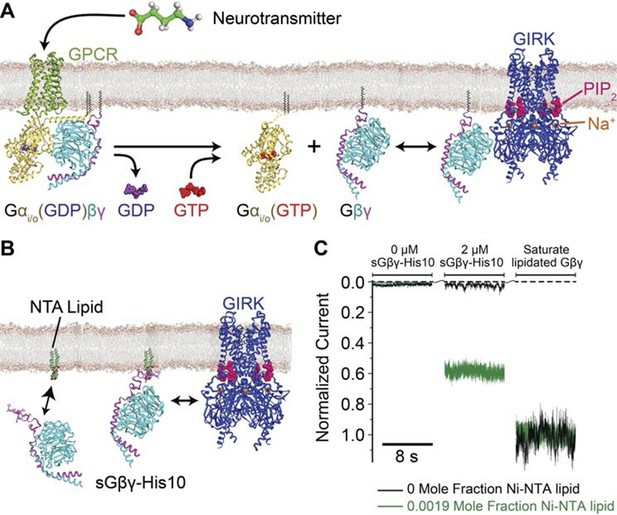
Membrane anchored Gβγ binds to GIRK and activates the channel.
(A) Inhibitory neurotransmitters activate Gi/o G protein coupled receptors (GPCRs) in neuron membranes. The GPCRs facilitate the exchange of GDP to GTP on the G protein hetero-trimer, releasing the Gαi/o subunit and Gβγ subunit. The membrane-anchored Gβγ subunit binds to and activates GIRK. (B) NTA lipid (head group modified with a Ni2+ chelator NTA, DOGS-NTA) is used to anchor non-lipid modified and His-tagged Gβγ (sGβγ-His10) onto the lipid membranes. 2 μM of sGβγ-His10 was used to fully saturate all NTA lipid on the membrane. The sGβγ-His10 density on the membrane can be controlled by the NTA lipid mole fraction. 32 μM C8-PIP2 was included on the same side as sGβγ-His10. (C) Membrane-bound sGβγ-His10 activates GIRK to different levels depending on the NTA lipid mole fraction. Lipid modified Gβγ is used to fully activate GIRK at the end of each experiment. GIRK currents corresponding to different NTA lipid mole fractions are normalized to the fully activated value. A detailed description of the experiment is shown in Figure 1—figure supplement 1. Example current traces of activation by sGβγ-His10 and lipid modified Gβγ in liposomes are shown in Figure 1—figure supplement 2.
Figure 1—figure supplement 1
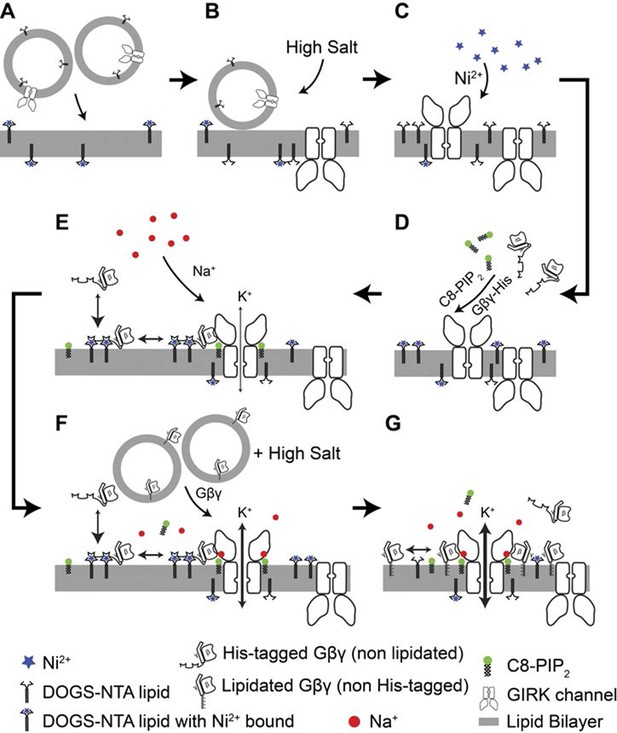
Details of the planar bilayer experiment.
To control Gβγ density in the membrane (A) GIRK2 channel proteoliposomes containing the corresponding mole fraction of DOGS-NTA-Ni2+ lipid were fused into planar lipid bilayers containing the same density of DOGS-NTA-Ni2+ lipid. (B) A high concentration KCl solution (1 M) was applied at the membrane to facilitate complete fusion of proteoliposomes attached to the membrane. (C) 1 mM NiSO4 was applied at the membrane to ensure that all NTA groups were charged with Ni2+. (D) sGβγ-His10 and C8-PIP2 were added to the top side of the membrane. GIRK2 channels with the cytoplasmic side facing the top side began to open. (E) A Na+ titration was then performed by stepwise addition of NaCl up to 32 mM final concentration. (F) After the Na+ titration, proteoliposomes of lipid modified Gβγ was fused to the membrane to maximize GIRK activation. (G) Maximum current of for each membrane is used for normalization of currents recorded in the same membrane.
Figure 1—figure supplement 2
Example traces of GIRK2 activation by sGβγ-His10 and lipid modified Gβγ in proteoliposomes.
Solution contains 10 mM potassium phosphate at pH 8.2 with 150 mM KCl on both sides of the membrane. 2 nM NiSO4, 2 mM MgCl2 and 32 μM C8-PIP2 were also included on the cytosolic side of the channel. Membrane voltage was held at -50 mV. (A) 0.03 mol fraction of Ni-NTA lipid was included in the lipid bilayer. 2 μM of sGβγ-His10 was applied to the membrane at the time indicated by the arrow. The activation by sGβγ-His10 generally takes a few seconds to a few tens of seconds to reach equilibrium. After reaching equilibrium, the current is stable for many minutes. (B) Application of Gβγ in proteoliposome vesicles activates GIRK with a slower apparent kinetics. ~700 mM KCl was included in the vesicles to facilitate fusion with the membrane. The decrease in current immediately after application of the high salt vesicles is due to the change in local electro-chemical gradient of K+ near the membrane. Mixing restores the ionic conditions. To ensure saturation of Gβγ binding on the channel, Gβγ vesicles were applied several times until the current (after mixing) no long increases. With good membranes, after saturation is reached, the current is stable for minutes. Voltage families were recorded during the breaks indicated by '/ /' which take around 1 min each.
Figure 2 with 1 supplement
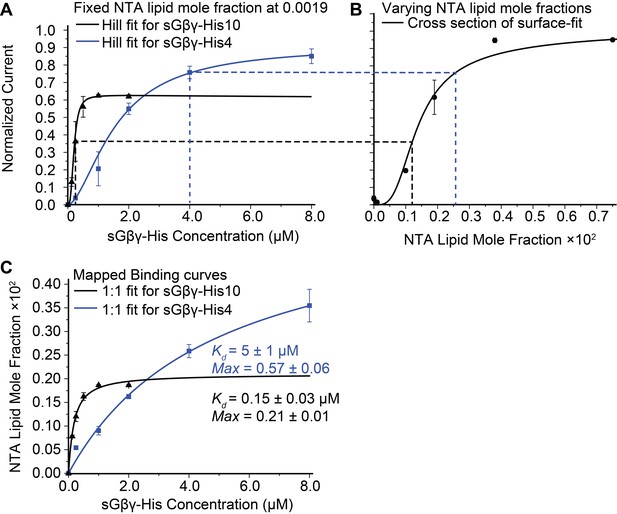
Calibration of sGβγ-His10 binding to NTA lipid.
(A) Titration of GIRK activity by sGβγ-His10 (black) or sGβγ-His4 (blue) to lipid membranes containing a fixed 0.0019 mol fraction of NTA lipid (n = 3–5 membranes, mean ± SEM). Solid lines are fits to the Hill equation: Current = Max × [Gβγ]n/ (Kdn + [Gβγ]n) with Kd = 200 ± 15 nM, n = 2.9 ± 0.4 (black, sGβγ-His10) and Kd = 1.6 ± 0.1 μM, n = 1.7 ± 0.05 (blue, sGβγ-His4). Solutions contained 150 mM KCl on both sides of the membrane and 32 mM NaCl on the inside where sGβγ-His was applied. (B) Titration of GIRK activity as a function of NTA lipid mole fraction in the presence of 2 μM sGβγ-His10 in solution. The solid line corresponds to a model (Figure 3—figure supplement 1). (C) Mapping of the NTA lipid concentration in panel (B) to the solution sGβγ-His concentration in panel (A) through GIRK activity. The curves are rectangular hyperbolas (Hill equation with n = 1) with Kd = 0.15 ± 0.03 μM (black) and Kd = 5.0 ± 1.0 μM (blue). A similar affinity (Kd = 0.09 ± 0.02 μM) was obtained for fluorescently labeled sGβγ-His10 adsorption to giant unilamellar vesicles (GUVs) containing 0.03 mol fraction of NTA lipid (Figure 2—figure supplement 1).
Figure 2—figure supplement 1
Binding of fluorescently labeled sGβγ-His10 to GUVs containing 0.03 mol fraction of NTA lipid.
(A) Typical confocal fluorescence images of the GUV equator planes. The corresponding concentration of sGβγ-His10 is indicated above each image. The first image from the right on the bottom row shows regions used for intensity quantification. The area between the yellow dashed concentric circles are used for calculating GUV fluorescence intensity, while the region inside the red dashed circle is treated as background. (B) Fitting of the dependency of GUV fluorescence intensity (n = 5–7 GUVs, Mean ± SEM) on sGβγ-His10-AF488 concentration to a simple 1:1 binding model. The apparent dissociation constant is around 90 nM.
Figure 3 with 2 supplements
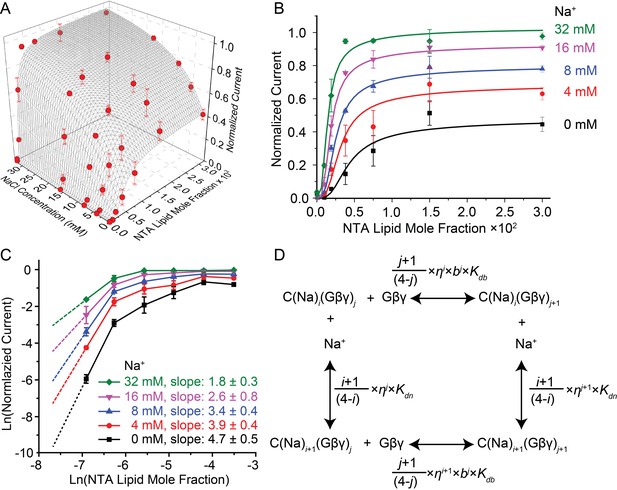
GIRK activity as a function of Gβγ and Na+ concentration.
2 μM sGβγ-His10 was included in the solution on the intracellular side of GIRK. (A) Normalized GIRK current (red spheres, mean ± SEM, n = 3–5 membranes) is graphed as a function of Gβγ and Na+ concentration. Surface mesh shows predictions of a model for ligand activation (Figure 3—figure supplement 1). (B) Data points in (A) are graphed as a family of curves (surface intersections) corresponding to each Na+ concentration. (C) Log-log plot of normalized current against NTA lipid mole fraction. Data points corresponding to 0.0001 NTA lipid mole fraction were excluded because the current levels (<0.02 normalized current) were much smaller than background noise. Other data points are connected with solid lines. Dashed lines show the slope of the line connecting the first two graphed data points. (D) A schematic of the ligand activation model fit to the data. i and j are integers between 0 and 4. The fitted parameters are: equilibrium dissociation constant for the first Na+ to bind in the absence of Gβγ, Kdn = 60 ± 20 mM, equilibrium dissociation constant for the first Gβγ in the absence of Na+, Kdb = 0.019 ± 0.007, cooperativity factor for each successive Gβγ binding b = 0.30 ± 0.06, cross-cooperativity factor between Gβγ and Na+ binding η = 0.63 ± 0.04 and an activity term θ as described in Figure 3—figure supplement 1. A comparison of fits to the data using cooperative and non cooperative models is shown in Figure 3—figure supplement 2.
Figure 3—figure supplement 1
Modeling of Na+ and Gβγ binding equilibrium with the GIRK2 tetramer.
GIRK binding with 0 to 4 Na+ and/or Gβγ is modeled with a system containing all 25 possible binding states. Symbols represent the following. C: GIRK tetramer with no ligand bound; C(Na+)i: channel with i Na+ bound; C(Gβγ)j: channel with j Gβγ bound; Kdn: equilibrium dissociation constant of Na+ with ligand-free channel; Kdb: equilibrium dissociation constant of Gβγ with ligand-free channel; n: cooperativity factor for each successive Na+ binding; b: cooperativity factor for each successive Gβγ binding; η: cross cooperativity between Gβγ and Na+ binding. Experimentally measurable GIRK activity is the sum of the activities of all species described in this model: GIRK Activity = ∑i,j (ci,j × θi,j) where ci,j is the population of GIRK with i Na+ and j Gβγ bound and θi,j is the activity of the corresponding species. Since the Na+ titration to GIRK with saturated Gβγ follows a simple 1:1 binding isotherm (rectangular hyperbola), we assumed the cooperativity factor n for Na+ binding to be 1 and that the channel activity increases proportionally with the number of occupied Na+ sites (θi,j = θ0,j + i × (θ4,j - θ0,j) / 4). Reasonable fitting was achieved only when opening was associated with 4 Gβγ bound (θi,j = 0 when j ≠ 4). Under these assumptions, parameters for the best fit are: Kdn = 60 ± 20 mM, Kdb = 0.019 ± 0.007, b = 0.30 ± 0.06, η = 0.63 ± 0.04, θ0,4 = 0.49 ± 0.04 and θ4,4 = 1.19 ± 0.05.
Figure 3—figure supplement 2
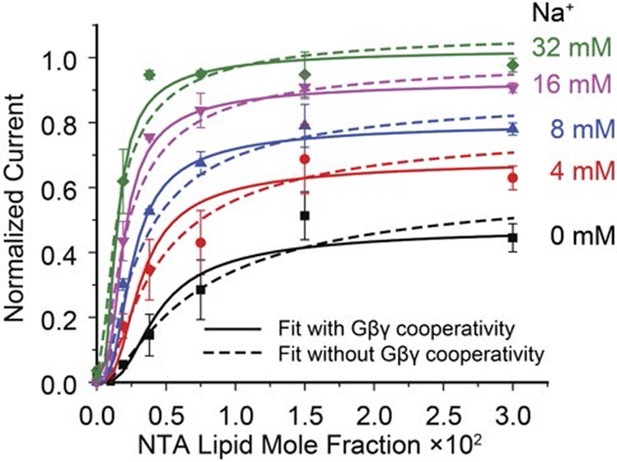
Comparison of fitted model allowing or not allowing cooperativity in Gβγ binding.
Solid lines represent surface intersections at various Na+ concentrations (color coded as shown in the figure) of the model allowing cooperativity of Gβγ binding (the same fit as in Figure 3A and Figure 3—figure supplement 1.). The scaled residual sum of squares is 0.064. Dashed lines represent the same intersections of the model fit assuming that Gβγ binding is not cooperative (b = 1). Corresponding parameter values for this non cooperative case are: Kdn = 110 ± 60 mM, Kdb = 0.0016 ± 0.0003, η = 0.62 ± 0.06, θ0,4 = 0.49 ± 0.04 and θ4,4 = 1.22 ± 0.08. The scaled residual sum of squares is 0.126.
Figure 4
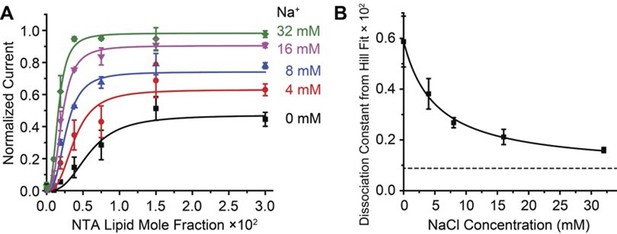
Na+ concentration regulates Gβγ affinity.
2 μM sGβγ-His10 was included in the solution on the intracellular side of GIRK. (A) Normalized current values from Figure 3A are fit to the Hill equation: Current = Max × [NTA-lipid mole fraction]n / (Kdn + [NTA-lipid mole fraction]n) with a Hill coefficient (n) of 2.8 ± 0.2 for all curves and equilibrium dissociation constant (Kd × 102) for Gβγ binding 0.6 ± 0.2, 0.38 ± 0.06, 0.27 ± 0.02, 0.21 ± 0.03 and 0.16 ± 0.01 for Na+ concentrations 0 mM, 4 mM, 8 mM, 16 mM and 32 mM, respectively. (B) Gβγ Kd values from fits in (A) are plotted as function of Na+ concentration. The curve is the rectangular hyperbola Kd = Kdmax + (Kdmin - Kdmax) × [Na+] / (Kd-Na+ + [Na+]), where Kd-Na+ = 5.1 ± 0.9 mM is the apparent Na+ dissociation constant as estimated through its effect on the affinity of Gβγ.
Figure 5
Structural basis for cooperativity in Gβγ activation of GIRK.
(A) Top view of the atomic structure of GIRK2 in complex with Gβγ, Na+ and PIP2 (PDB ID: 4KFM). Four Gβγ, Na+ and PIP2 molcules bind to one GIRK2 homo-tetramer, associated with rotation of the cytoplasmic domain with respect to the transmembrane as the channel opens. (B) Gβγ binding favors the cytoplasmic-domain-rotated, open conformation of the channel. The rigid body rotation of the cytoplasmic domain is associated with increased affinity of four Gβγ binding sites simultaneously, giving rise to strong positive cooperativity.
Figure 6
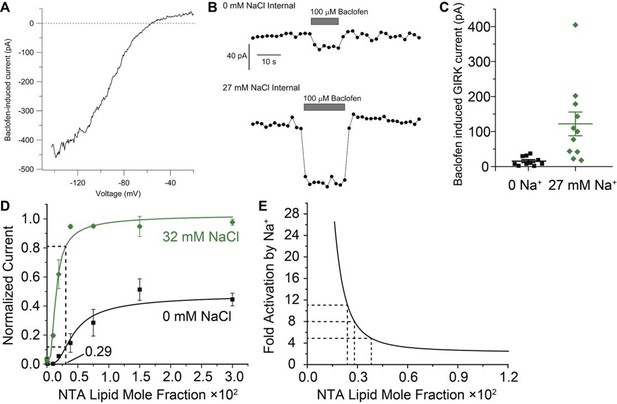
Estimation of Gβγ membrane density generated during GABAB receptor activation in mouse dopamine neurons.
(A) Current-voltage relationship for current induced by 100 μM baclofen in a dissociated dopamine neuron from the mouse substantia nigra pars compacta recorded with an external solution containing 16 mM K+ and an internal solution containing 126 mM K+ and 27 mM Na+. (B) Time-course of baclofen-induced current in two neurons recorded with an internal solution containing 0 mM Na+ (top) or 27 mM Na+ (bottom). The same scale is used for both recordings. Current was measured as the average current between -142 mV and -147 mV evoked by voltage ramps (1 mV/ms) from +8 to -147 mV delivered from a steady holding potential of -92 mV every 2 s. (C) Collected values for baclofen-induced GIRK current (mean ± SEM) in dopamine neurons equilibrated with 0 mM (n = 10) and 27 mM (n = 11) intracellular Na+. (D) Data and curves from Figure 3B are used to estimate the concentration of Gβγ required to yield the 8-fold amplification of GIRK current observed in (C). (E) A Na+ amplification curve is defined as the green curve (32 mM Na+, which is near 27 mM) divided by the black curve (0 mM Na+) in (D). Amplification is a steep function of Gβγ concentration near the stimulated levels of Gβγ in dopamine neurons.
Author Response Image 1
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Cooperative regulation by G proteins and Na+ of neuronal GIRK2 K+ channels
eLife 5:e15751.
https://doi.org/10.7554/eLife.15751
