Neural pattern change during encoding of a narrative predicts retrospective duration estimates
- Princeton University, United States
- University of California, Berkeley, United States
- University of Toronto, Canada
- Queen's University, Canada
Figures
Figure 1
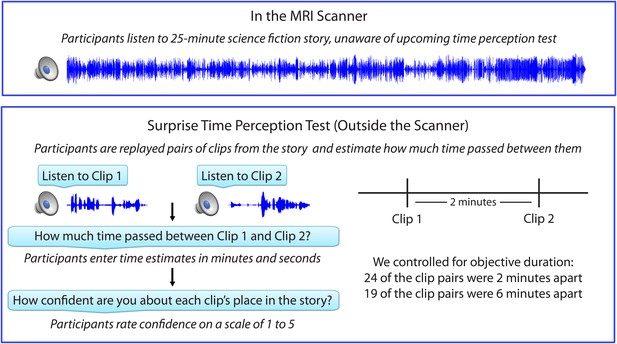
Experimental design.
https://doi.org/10.7554/eLife.16070.004
Figure 2 with 1 supplement
Mean duration estimates for all intervals (A) and confident intervals (B) as a function of their actual duration.
Each blue circle represents the mean duration estimate for an individual participant within a given interval duration (2 or 6 min). The blue bar heights represent the global means for 2 and 6-min intervals across intervals and participants.
-
Figure 2—source data 1
Duration estimates and confidence ratings for all participants and intervals.
To generate the plot in Figure 2, duration estimates for an objective duration (2 or 6 min) were first averaged within participants, for all intervals (Figure 2A) and for confident intervals only (Figure 2B). The global means (represented by the heights of the blue bars) were then obtained by averaging again across participants. Confidence ratings in this table are binary: 1 reflects a high-confidence interval and 0 reflects a low-confidence interval (see Removing low-confidence intervals in Materials and methods).
- https://doi.org/10.7554/eLife.16070.006
Figure 2—figure supplement 1
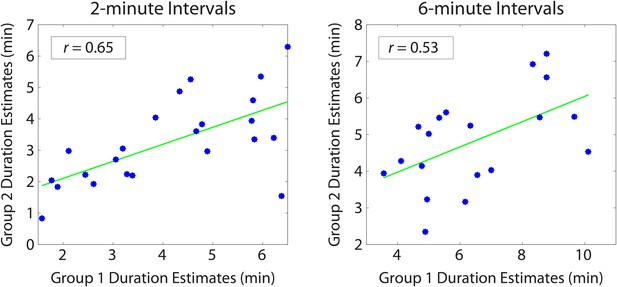
Reliability of duration estimates across participants.
Between-group correlations were obtained by splitting the participants randomly into two equal groups and averaging the duration estimates for each interval (across participants) within a group. Each dot in the scatterplot represents a particular temporal interval; its x and y coordinates indicate the mean estimated duration of that interval for Group 1 and Group 2 participants, respectively. We repeated this procedure 1000 times to ensure that we sampled a variety of group splits. The average correlation between the two groups was 0.64 (SD=0.09) for 2-min intervals and 0.54 (SD=0.15) for 6-min intervals. The above plot shows the grouping that was most representative of the mean.
Figure 3
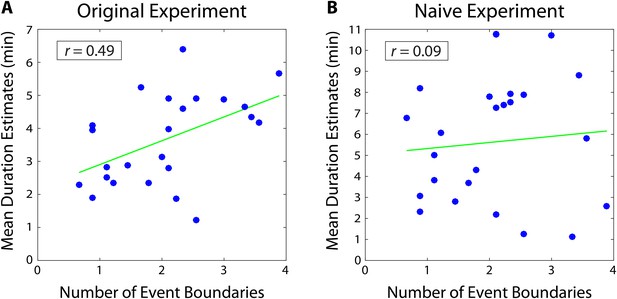
Mean duration estimates for 2-minute intervals as a function of the number of event boundaries in each interval.
The number of event boundaries in an interval predicted retrospective duration estimates in our original experiment (A), but did not significantly predict duration estimates of naïve participants (B) who had never heard the story. This suggests that the number of contextual changes between two clips influenced temporal distance judgments significantly more when the content of the story between the two clips could be recalled.
-
Figure 3—source data 1
Mean number of event boundaries and mean duration estimates from both original and naïve participants.
Intervals appear in chronological order and the 'position in story' indicates the middle time point between the two clips delimiting the interval. Mean duration estimates were obtained by averaging the duration estimates for a specific interval across participants. The mean number of event boundaries in an interval was obtained by averaging data from a separate group of participants who pressed the spacebar every time a boundary was occurring.
- https://doi.org/10.7554/eLife.16070.009
-
Figure 3—source data 2
Duration estimates from the naïve experiment, including both 2 and 6-min intervals.
As above, Intervals appear in chronological order and the 'position in story' indicates the middle time point between the two clips delimiting the interval.
- https://doi.org/10.7554/eLife.16070.010
Figure 4 with 1 supplement
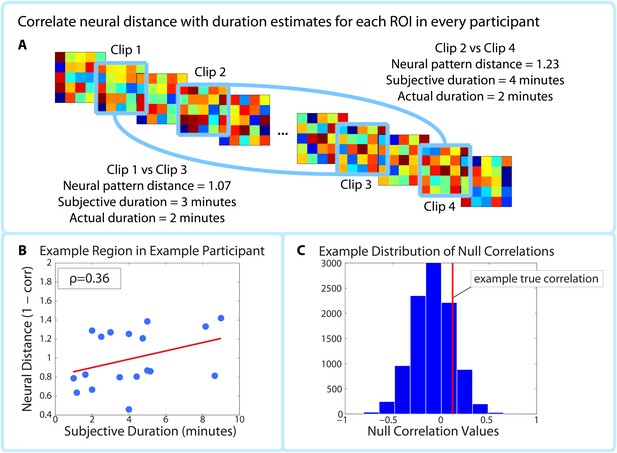
Correlating pattern distance with duration estimates within participants.
For each ROI in each participant, the pattern distance between each pair of clips at encoding was correlated with the participant’s retrospective duration estimate (A–B). The top panel (A) shows two example intervals. The neural distance (1-Pearson’s r) between clips 2 and 4 (second interval) is greater than the neural distance between clips 1 and 3 (first interval), as is the subjective duration estimate. (B) shows the correlation between neural distance and duration estimates in a hypothetical region and participant. (C) We used a permutation test to generate 10,000 surrogate pattern distance vectors (see Figure 4—figure supplement 1), which we then used to obtain a distribution of null correlations between neural distances and duration estimates. For each ROI in each participant, we calculated the z-scored correlation value, which reflects the strength of the empirical correlation relative to the distribution of null correlations. For each ROI, we performed a random effects t-test to assess whether the z-score was reliably positive across participants. P-values from this t-test were then subjected to multiple comparisons correction using False Discovery Rate (FDR).
Figure 4—figure supplement 1
Permutation test assessing the temporal specificity of correlations between pattern change and behavior.
This procedure is described in the Materials and methods (see Statistical analysis of correlations between pattern change and behavior). (A,B) The time course of pattern change is constructed using the distance (1 - Pearson’s r) between each pattern and the pattern 80 TRs (2 min) after it. As in the main analysis, we averaged over the 5 consecutive TRs surrounding each pattern (for simplicity, this is not shown in the above figure). (C) 10,000 surrogate pattern distance time courses are generated by randomizing the phases of the original time course, thus conserving the amplitude of each frequency component. (D) Surrogate pattern distances are correlated with time estimates, generating 10,000 null correlations. A Z-value for each ROI / searchlight in each participant is computed to compare the strength of the empirical correlation with the distribution of null correlations. The p-value for a given ROI is obtained using a right-tailed t-test on the Z-values across participants.
Figure 5 with 1 supplement
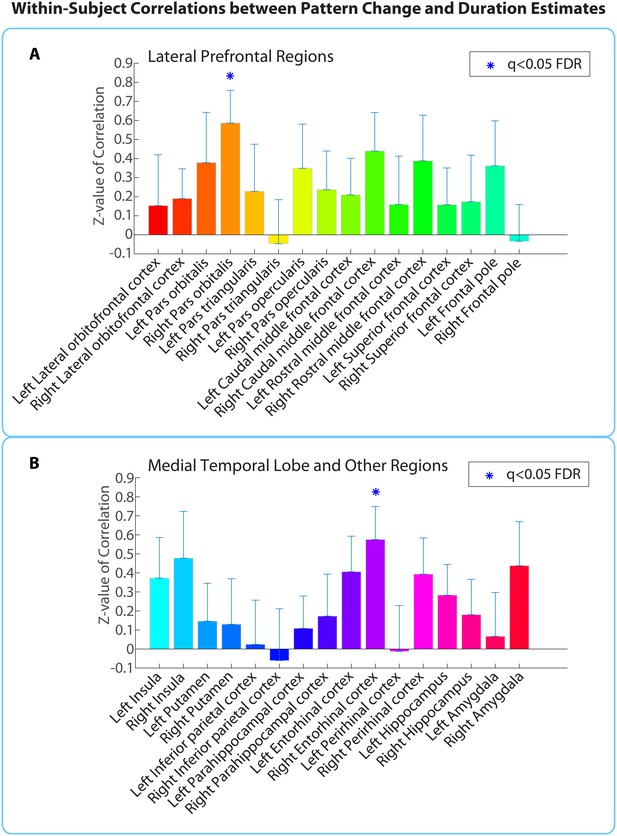
Within-participant ROI analysis: mean Z-values (across all 18 participants) of correlations between pattern distance and duration estimates for the 16 a priori ROIs.
Z-values were obtained from the phase randomization procedure and reflect the strength of the empirical correlation relative to the distribution of null correlations. Error bars represent standard errors of the mean. The blue dots over the right entorhinal cortex and right pars orbitalis indicate that these ROIs survived FDR correction at q<0.05.
-
Figure 5—source data 1
Within-participant analysis Z-values and Pearson’s r values for all participants and grey matter regions derived from FreeSurfer segmentation and the probabilistic MTL atlas.
Excel sheet 1 contains the Z-values for each participant and region, reflecting the strength of the empirical correlation between pattern distance and duration estimates relative to the distribution of null correlations. NaNs signify that a participant had fewer than 10 voxels in a given brain region, most likely due to signal dropout (this was only an issue for the frontal pole). The bar plots in Figure 5 were generated by plotting the mean Z-value (and standard error of the mean) across participants for each of the a priori ROIs. Excel sheet 2: T-values were obtained from a right-tailed t-test verifying whether the Z-values for a region were reliably positive across participants. The p-values from this t-test were then subjected to multiple comparisons correction using FDR. The three regions in bold survived whole-brain FDR correction at q<0.1 and are shown in Figure 5—figure supplement 1. Excel sheet 3 contains the Fisher-transformed Pearson’s r values for each participant and region.
- https://doi.org/10.7554/eLife.16070.014
Figure 5—figure supplement 1
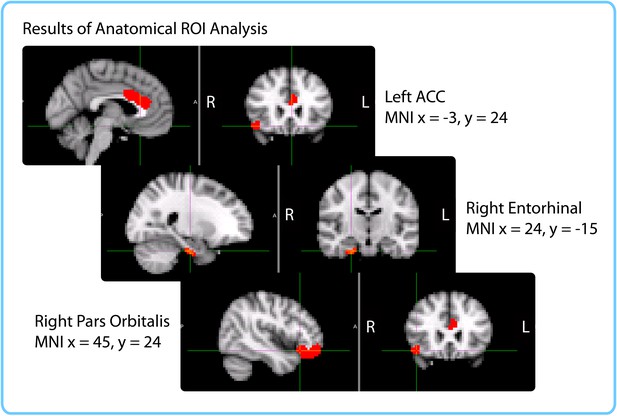
Anatomical ROIs that showed a significant correlation between pattern change and duration estimates within participants, after whole-brain FDR correction.
In red are regions with q<0.1: the right entorhinal cortex, right pars orbitalis and left caudal ACC. This analysis was performed in native space on participant-specific ROIs. ROIs were transformed from native functional space to MNI space for display purposes.
Figure 6
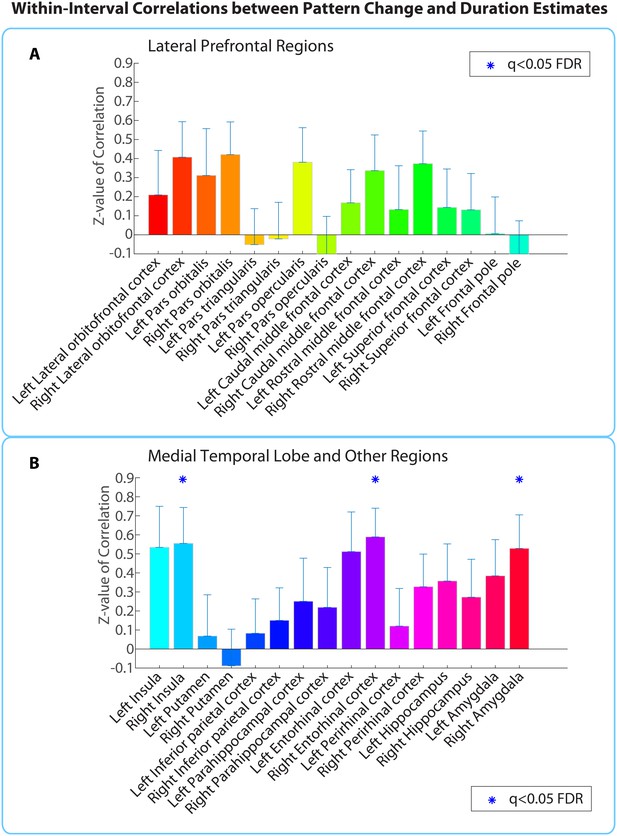
Within-interval ROI analysis: mean Z-values (across all 2-min intervals) of correlations between pattern distance and duration estimates for the 16 a priori ROIs.
Error bars represent standard errors of the mean. Correlations between pattern change and duration estimates were performed across participants, separately for each interval.
-
Figure 6—source data 1
Within-interval analysis Z-values and Pearson’s r values for all intervals and regions in the FreeSurfer and MTL atlases.
NaNs for a given interval and region indicate that there were not enough participants who rated that interval as confident and who had at least 10 voxels in the specific region to calculate a correlation (this was only an issue for the frontal pole). The bar plots in Figure 6 were generated by plotting the mean Z-value (and standard error of the mean) across intervals for each of the a priori ROIs. The t-values were obtained from a right-tailed t-test on the Z-values for each region. The p-values from this t-test were then subjected to multiple comparisons correction using FDR.
- https://doi.org/10.7554/eLife.16070.017
Figure 7
Parameter estimates and 95% confidence intervals for the fixed effect of neural pattern distance on duration estimates.
We also included the right amygdala and right superior temporal cortex in the figure, because their confidence intervals did not include 0 when a slightly less conservative fitting procedure was used (see Figure 7—source data 1 and Materials and methods).
-
Figure 7—source data 1
Parameter estimates (betas) and 95% confidence intervals for the fixed effects of neural pattern distance on duration estimates for all 84 anatomical regions.
Parameter estimates are provided for four variants of the mixed-effects ROI analysis: 1) full model (with naïve estimates) using the Chung et al., 2015 blme fitting procedure and Box-Cox transform of duration estimates (see Materials and methods), 2) model without naïve estimates, using the Chung et al., 2015 blme fitting procedure and Box-Cox transform of duration estimates, 3) full model (with naïve estimates) using the Bates et al., 2015 lme4 fitting procedure and Box-Cox transform of duration estimates, and 4) full model (with naïve estimates) using the Chung et al., 2015 blme fitting procedure, but without any transform of duration estimates. The first analysis variant, which is the most conservative, is the one reported in the Results and plotted in Figure 7.
- https://doi.org/10.7554/eLife.16070.019
Figure 8
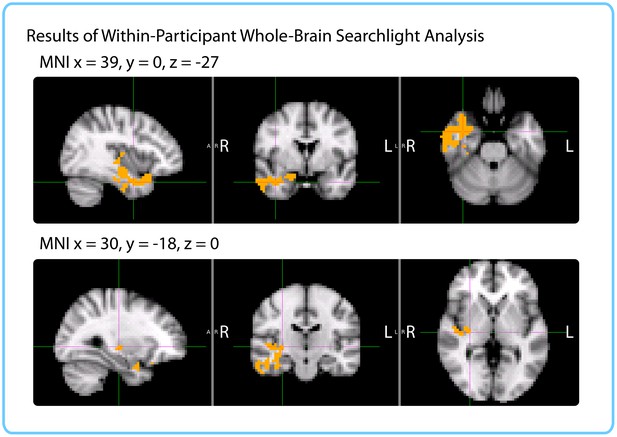
Results of within-participant whole-brain searchlight.
Voxels in orange represent centers of searchlights that exhibited significant correlations between pattern change and duration estimates within participants across intervals (p<0.05, FWE). The significant cluster had peak MNI coordinates (in mm): x = 45.6, y = -5.53, z = -21.7.
Figure 9
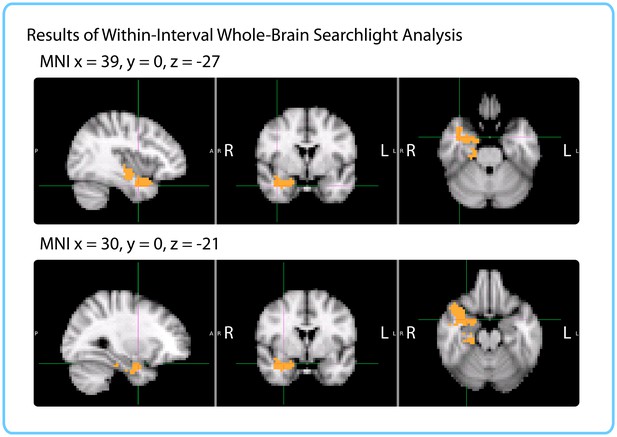
Results of within-interval whole-brain searchlight.
Voxels in orange represent centers of searchlights that exhibited significant correlations between pattern change and duration estimates across participants (p<0.05, FWE). The significant cluster had center of gravity MNI coordinates (in mm): x = 32.1, y = −10.2, z = −18.7.
Figure 10
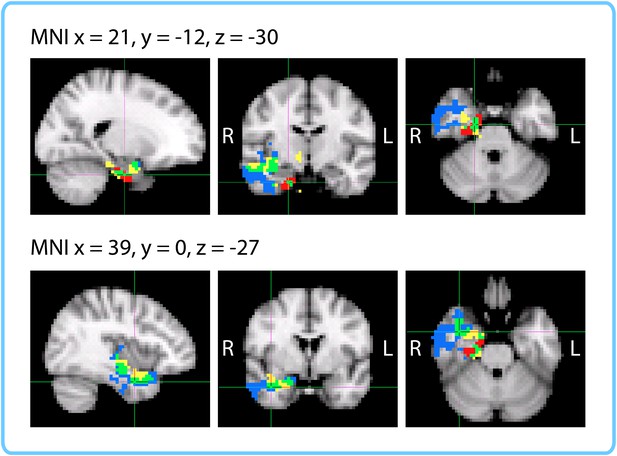
Comparison of ROI and Searchlight results.
The within-participant searchlight cluster (p<0.05, FWE) is displayed in blue; the within-interval searchlight cluster (p<0.05, FWE) is displayed in yellow; voxels that overlap between the searchlights are shown in green. The right entorhinal cortex (q<0.05 FDR in both ROI analyses) is displayed in red; voxels that overlap between the within-interval searchlight and the right entorhinal ROI are shown in green.
Figure 11
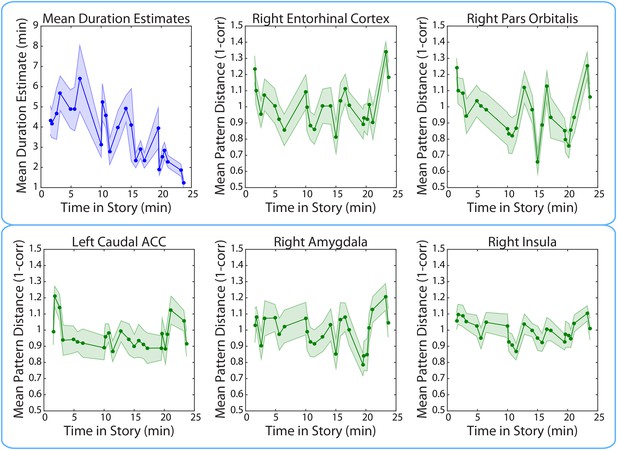
Mean duration estimates and pattern distances (across participants) for all 2-minute intervals as a function of the interval’s position in the story.
The middle time point of each 2-min interval (half-way between the two clips delimiting it) was chosen as the x-coordinate.
-
Figure 11—source data 1
Duration estimates and pattern distances in all FreeSurfer and MTL ROIs for each 2-minute interval in every participant.
Data prior to high-pass filtering and after high-pass filtering (cut-off = 480 s) are provided. The unfiltered neural pattern distances tend to increase with time in story, even in the CSF and white matter. To generate the plots in Figure 11, duration estimates and pattern distances were averaged across participants for each interval and plotted as a function of the interval’s position in the story. The interval’s position in the story (in minutes) was set as the middle time point between the two clips delimiting it.
- https://doi.org/10.7554/eLife.16070.025
Figure 12
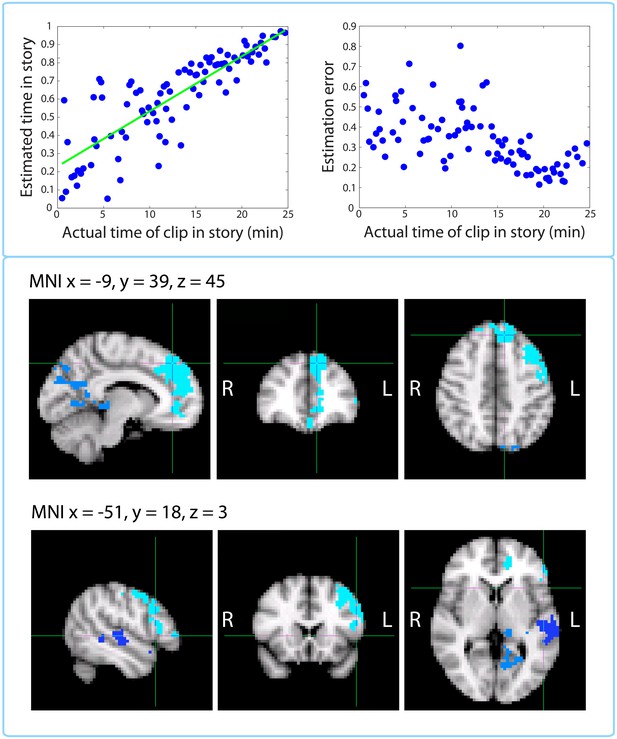
Replication of Jenkins and Ranganath (2010): activity at encoding predicts accuracy of temporal context memory.
Top left panel: Timeline estimates for a representative participant. The estimated temporal position of each clip is plotted against its actual position in the story. Top right panel: Group-averaged residual error for each clip plotted against its time in the story. Our behavioral results mimic those of Figure 2 in Jenkins and Ranganath (2010) showing that accuracy increases for clips that occurred later in the story. Bottom panels: Clusters that showed a significant correlation between activity at encoding and subsequent accuracy at placing a clip on the timeline of the story. The prefrontal cluster in light blue was significant (p=0.008, FWE), while the medial parietal cluster (p=0.058, FWE) and the lateral temporal cluster in dark blue (p=0.098, FWE) were trending.
Figure 13
Mean inter-subject correlations (ISCs) for 6 representative brain regions as a function of the high-pass filter cut-off.
Shaded error bars represent standard errors of the mean (across participants). Top panel (A) shows the mean ISCs after the residualization procedure has been applied (see Residualization of non-neuronal signal sources). The 480 s cut-off was the gentlest filter for which all of the grey matter regions listed above showed ISC values significantly above those in the CSF. Bottom panel (B) shows the mean ISCs prior to the residualization procedure. Without residualization, the ISCs of some grey matter regions never rise significantly above those in the white matter and CSF. Note that without high-pass filtering ('none') or residualization, all brain regions displayed spuriously high ISCs.
Author response image 1
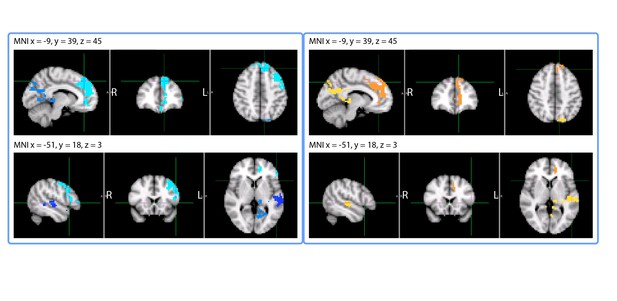
Clusters whose activity at encoding correlated with subsequent accuracy at placing clips on the timeline of the story.
The left panel (in blue) shows the results of the Pearson’s correlation between accuracy on a clip and the encoding activity for that clip. The right panel (red-yellow) shows the results of the contrast between activity for Hits (bottom 1/3 of residual error) and activity for Misses (top 1/3 of residual error) when placing the clip on the timeline of the story.
Tables
Table 1
Speed of pattern change in the right entorhinal cortex and left caudal ACC relative to the rest of the brain. Full-Width Half-Maximum (FWHM) values reflect how slowly patterns of activity (multivariate) or individual voxels (univariate) change over time. The Multivariate (-ROI size) column reflects the slowness of pattern change when controlling for the effect of ROI size.
| Multivariate | Multivariate (-ROI size) | Univariate | ||||
|---|---|---|---|---|---|---|
| Region | FWHM (TRs) | Ranking | FWHM (TRs) | Ranking | FWHM (TRs) | Ranking |
| Right entorhinal | M=18.9, SD=13.8 | 3rd | M=1.2, SD=1.9 | 4th | M=23, SD=15.6 | 1st |
| Left caudal ACC | M=8.3, SD=1.8 | 66th | M=-0.5, SD=0.5 | 67th | M=9.2, SD=3.8 | 46th |
| Right transverse temporal cortex | M=7.3, SD=1.2 | 80th | M=-0.8, SD=0.5 | 83rd | M=7.9, SD=1.2 | 68th |
| Right banks of superior temporal sulcus | M=9.0, SD=2.1 | 48th | M=-0.3, SD=0.4 | 49th | M=8.8, SD=1.7 | 61st |
| Right superior temporal cortex | M=11.0, SD=3.1 | 28th | M=0.4, SD=0.6 | 18th | M=10.3, SD=2.4 | 34th |
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Neural pattern change during encoding of a narrative predicts retrospective duration estimates
eLife 5:e16070.
https://doi.org/10.7554/eLife.16070
