Stacking the odds for Golgi cisternal maturation

Article
Figures and data
Abstract
Introduction
Results
Discussion
Materials and methods
References
Decision letter
Author response
Article and author information
Metrics

Abstract

What is the minimal set of cell-biological ingredients needed to generate a Golgi apparatus? The compositions of eukaryotic organelles arise through a process of molecular exchange via vesicle traffic. Here we statistically sample tens of thousands of homeostatic vesicle traffic networks generated by realistic molecular rules governing vesicle budding and fusion. Remarkably, the plurality of these networks contain chains of compartments that undergo creation, compositional maturation, and dissipation, coupled by molecular recycling along retrograde vesicles. This motif precisely matches the cisternal maturation model of the Golgi, which was developed to explain many observed aspects of the eukaryotic secretory pathway. In our analysis cisternal maturation is a robust consequence of vesicle traffic homeostasis, independent of the underlying details of molecular interactions or spatial stacking. This architecture may have been exapted rather than selected for its role in the secretion of large cargo.

https://doi.org/10.7554/eLife.16231.001

Introduction

The cisternal maturation model is a hypothesis about how the Golgi apparatus works (Emr et al., 2009; Luini, 2011; Glick and Luini, 2011). It posits that secretory cargo travel in cisternal compartments that slowly mature from the cis-Golgi to the trans-Golgi composition. This is driven by three processes. (1) New cis-cisternae are created by the homotypic fusion of ER-derived COPII vesicles at the ER-Golgi intermediate compartment (ERGIC) (Nakano and Luini, 2010). (2) Old trans-cisternae dissipate by the vesiculation of the trans-Golgi network (TGN) into Golgi-to-surface carriers (Bard and Malhotra, 2006; De Matteis and Luini, 2008). (3) Golgi-resident proteins are recycled along retrograde vesicles, including COPI vesicles, moving from older to younger cisternae (Papanikou et al., 2015). Similar processes govern the maturation of endosomes in the endocytic pathway (Rink et al., 2005; Poteryaev et al., 2010; Huotari and Helenius, 2011).

Cisternal maturation allows cells to process and secrete large cargo (Nakano and Luini, 2010). However, large secretory cargo would be impossible without a fully developed cisternal maturation mechanism in the first place. Exaptation can resolve this evolutionary Catch-22 paradox: if a complex trait arose in stages through neutral or non-adaptive processes, it could later be co-opted for new cellular functions (Lynch, 2007a). Such a mechanism explains the origins of complex eukaryotic features such as splicing, transcriptional feedback loops, and multi-subunit protein complexes (Lynch and Conery, 2003; Lynch, 2007b; Fernández and Lynch, 2011). Here we extend this idea beyond genomes, transcriptomes and proteomes, to eukaryotic membrane organization: we demonstrate that cisternal maturation is a near-inevitable consequence of the basic processes of vesicle traffic and cellular homeostasis, prior to any selection for function. The architecture of the Golgi could therefore have arisen non-adaptively, enabling the subsequent development of large-cargo secretion. Our results refute the Catch-22 and provide a strong evolutionary foundation for the cisternal maturation model, reinforcing the wealth of cell-biological evidence in its favor across multiple cellular contexts (Bonfanti et al., 1998; Losev et al., 2006; Matsuura-Tokita et al., 2006).

Results

From molecular rules to vesicle traffic

We set out to understand how molecular specificity and molecular exchange combined to determine the structure of a vesicle traffic network. Endomembrane vesicles and compartments are dynamically generated and maintained through specific molecular interactions (Munro, 2004). Coats and adaptors drive vesicle cargo loading and budding (Bonifacino and Lippincott-Schwartz, 2003; Robinson, 2004; Traub, 2009). Tethers and SNAREs regulate vesicle transport and fusion (Yu and Hughson, 2010; Jahn and Scheller, 2006; Wickner and Schekman, 2008). GTPases of the Arf and Rab families coordinate these events via regulatory cascades (D'Souza-Schorey and Chavrier, 2006; Stenmark, 2009). Vesicle exchange necessarily causes changes to source and target compartments, whose compositions are determined as an outcome of molecular gain and loss. This feedback underpins the complexity of vesicle traffic networks.

Previous mathematical analyses of vesicle traffic have used stochastic frameworks or continuous differential equations, and included such details as compartment size, location and chemical composition (Heinrich and Rapoport, 2005; Binder et al., 2009; Dmitrieff and Sens, 2011; Dmitrieff et al., 2013; Ramadas and Thattai, 2013). These approaches require a large number of quantitative kinetic parameters to analyze even simple systems with a few molecules and compartments, and are not suited to explore cell-wide vesicle traffic networks. Here we are primarily interested in cell-wide homeostatic network topologies. We have previously shown (Ramadas and Thattai, 2013) that topological features of a vesicle traffic network – the number of compartments and their connectivity – are robustly determined by qualitative molecular specificity rather than quantitative kinetics. We therefore formalize the properties of vesicle traffic using a Boolean framework (Mani and Thattai, 2016): we approximate molecular specificities and compartment compositions by a series of 1 s and 0 s (Materials and methods: The Boolean vesicle traffic model). We assume the cytoplasm is well mixed, and do not consider spatial organization; we are agnostic to the relative amounts of molecules on each vesicle, the size of vesicles and compartments, and the quantitative kinetic flux of vesicles between compartments. Boolean models have been successfully applied to transcriptional and signaling networks (Kauffman et al., 2003; Li et al., 2004; Chaves et al., 2005); but have not previously been used to study vesicle traffic. Our Boolean approach allows us to efficiently sample a large space of cell-biological rules, and produces results that are qualitatively similar to more detailed microscopic vesicle traffic models (Figure 1G,H; Box 1).

Figure 1 with 1 supplement see all

Download asset Open asset

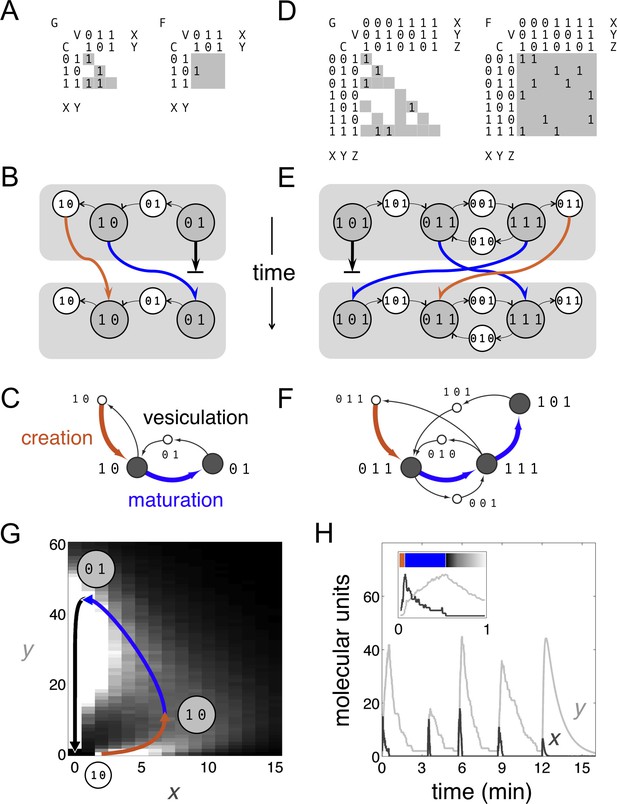
Boolean dynamics of compartments and vesicles: examples of maturation chains.

(A,B,C) A system with $N = 2$ molecular labels X and Y. (D,E,F) A system with $N = 3$ molecular labels *X, Y* and Z. (A,D) Left: the $C \times V$ budding matrix $G : G_{i j}$ = 1 means compartment type i (row) buds out vesicle type j (column). Vesicle compositions are subsets of source compartment compositions, so only some entries of $G$ can be non-zero (gray shading). Right: the $C \times V$ fusion matrix $F : F_{i j}$ = 1 means vesicle type j (column) can fuse with compartment type i (row). Any entry of $F$ can be non-zero (gray shading). (B,E) At each timepoint compartments (gray circles) accept (through fusion) or give away (through budding) vesicles (white circles). Gray rectangles show the state of the cell at successive timepoints, moving from top to bottom. Compartments can undergo maturation (blue arrows) or vesiculate by giving up all their cargo (thick black arrows); orphan vesicles can undergo homotypic fusion to generate new compartments (brown arrows). From the first to the second timepoint, individual compartments change composition but the full set of compartments is constant: the system has reached homeostasis. (C,F) Another representation of the homeostatic networks from Figure 1B,E, mapping out a cell in compositional space. Circles represent compartments (gray) or vesicles (white); each distinct circle represents a distinct compositional type. Thin black arrows show vesicles moving between compartments at one timepoint. Brown arrows followed by blue arrows show the creation and maturation of compartments, flowing from one timepoint to the next. (G,H) Results of a stochastic simulation of vesicle traffic for a system with two molecular labels X and Y (Box, Equation 1). The cell contains many vesicles and compartments, and reaches an equilibrium in which the vesicle pools and the number of compartments of each compositional type are approximately constant. Parameters: ${x_{t o t}, y_{t o t}}$ = {250 units, 5000 units}; {*A, B, C, D*} = {1000 units min⁻¹, 10 min⁻¹, 5 min⁻¹, 1 min⁻¹}; time-averaged vesicle pools $\bar{n_{X}} = 0.457$ , $\bar{n_{Y}} = 10.6$ . Timescales are chosen to qualitatively match real maturation dynamics (Losev et al., 2006). (G) The heatmap shows the equilibrium distribution of compartment compositions. Individual compartments change composition over time: the curve shows the deterministic limit-cycle solution to Equation 2, with different phases corresponding to creation (brown), maturation (blue), and vesiculation (black). Extrema of this curve correspond to the Boolean compartment compositions in Figure 1C. (H) Compositions of individual compartments over time for the full stochastic simulation (X in dark gray, Y in light gray). Compositions cycle periodically; each cycle is independent of the previous one, since new compartments are nucleated by fresh homotypic fusion events. The final cycle shows the deterministic limit-cycle solution to Equation 2 for comparison. The inset expands the first minute, with X and Y levels scaled against their maximum values so creation, maturation and vesiculation can be clearly observed. Figure 1—figure supplement 1 shows how non-vesicular transport can be included in this framework.

https://doi.org/10.7554/eLife.16231.002

Box 1

Stochastic, continuous, and Boolean models of cisternal maturation.

It is interesting to see how our Boolean model is related to more microscopic vesicle traffic models (Figure 1). Consider a system with two types of molecules X and Y, transported on distinct types of vesicles. We assume a well-mixed cytoplasm containing many compartments and vesicles. Each vesicle contains a fixed amount of each molecule, providing a measurement unit; anything larger than a vesicle is a compartment. We assume X vesicles can fuse to one another and, much less efficiently, to compartments; Y vesicles can fuse only to compartments; and compartments cannot fuse to one another. Let $n (x, y)$ be the number of compartments with x units of X and y units of Y. The number of free vesicles of each type is: $n_{X} \equiv n (1, 0)$ , $n_{Y} \equiv n (0, 1)$ . The total amount of each molecule remains constant, given by $x_{t o t} = \sum_{x, y} n (x, y) x$ , $y_{t o t} = \sum_{x, y} n (x, y) y$ . The allowed reactions are:

\begin{array}{l} T w o X v e s i c l e s f u s e h o m o t y p i c a l l y t o c r e a t e a c o m p a r t m e n t : \\ n_{X} ↓_{2}, n (2, 0) ↑^{1} r a t e A n_{X} (n_{X} - 1) \\ A c o m p a r t m e n t b u d s a n X o r Y v e s i c l e : \\ n_{X} ↑^{1} n (x, y) ↓_{1}, n (x - 1, y) ↑^{1} r a t e B x n (x, y) \\ n_{Y} ↑^{1} n (x, y) ↓_{1}, n (x, y - 1) ↑^{1} r a t e D y n (x, y) \\ A c o m p a r t m e n t f u s e s t o a n X o r Y v e s i c l e : \\ n_{X} ↓_{1} n (x, y) ↓_{1}, n (x + 1, y) ↑^{1} r a t e A \frac{x^{2}}{{(x + y)}^{2}} n_{X} n (x, y) \\ n_{Y} ↓_{1} n (x, y) ↓_{1}, n (x, y + 1) ↑^{1} r a t e C x n_{Y} n (x, y) \end{array}

Here, up/down arrows indicate increases/decreases in number, and rates correspond to reaction probabilities per unit time. Each term arises as follows: X or Y vesicles bud in proportion to the amount of X or Y on each compartment ( $B x$ , $D y$ terms). X promotes fusion of vesicles to compartments, cooperatively for X vesicles ( $A x^{2}$ term) and linearly for Y vesicles ( $C x$ term). The rate of fusion of X vesicles decreases sharply as the size of the compartment increases ( ${(x + y)}^{- 2}$ term); when a compartment is identical to an X vesicle this reduces to the homotypic fusion rate constant A. The parameters have the following dimensions: $n (x, y)$ , $n_{X}$ and $n_{Y}$ are pure numbers of compartments and vesicles in the cell; x and y are measured in units corresponding to the amount of X or Y on a single transport vesicle; A has dimensions of molecular units per unit time; B, C, and D have dimensions of inverse time. The value $D^{- 1}$ is the approximate time a compartment takes to fully vesiculate.

We simulate this stochastic system using Gillespie’s algorithm (Gillespie, 2007). From arbitrary initial conditions the system reaches a homeostatic state in which the free vesicle pools and the number of compartments of any given composition are nearly constant (Figure 1G). However, individual compartment compositions vary over time. In the mean-field limit each compartment approximately obeys a continuous deterministic version of Equation 1, where $\bar{n_{X}}$ and $\bar{n_{Y}}$ are time-averaged values:

\begin{array}{ll} \frac{d x}{d t} = & A \bar{n_{X}} \frac{x^{2}}{{(x + y)}^{2}} - B x \\ \frac{d y}{d t} = & C \bar{n_{Y}} x - D y \end{array}

By linear stability analysis, under the following parametric condition this system has no stable fixed point:

\frac{B}{B + D} \frac{C \bar{n_{Y}}}{C \bar{n_{Y}} + D} > \frac{1}{2}

Roughly, X vesicles must bud rapidly and Y vesicles must fuse rapidly. Compartment compositions then approach a limit-cycle trajectory (Figure 1G,H): nucleated by homotypic fusion of X vesicles (brown); maturing by budding X vesicles and fusing with Y vesicles (blue); and finally vesiculating into Y vesicles (black). These dynamics are similar to live-cell observations of cisternal maturation (Losev et al., 2006). Figure 1A shows the budding and fusion matrices corresponding to the Boolean version of Equation 1. The resulting Boolean homeostatic state (Figure 1B,C) displays the same qualitative features as the stochastic and continuous models (Figure 1G,H). These examples all describe the maturation chain, at different levels of abstraction.

https://doi.org/10.7554/eLife.16231.004

We consider a cell to be a collection of compositionally distinct membrane-bound compartments exchanging vesicles. Suppose there are N types of membrane-associated, transmembrane or lumenal molecules that determine the properties of compartments and vesicles. We refer to these as active molecular labels: they influence budding and fusion, and can be used to define the identity of compartments. The Boolean composition of a compartment or vesicle is given by a binary vector of length N: each element of the vector is 1 or 0 depending on whether that molecular label is present in high or low amounts. The state of a cell at any timepoint is specified by giving the list of compartments of various compositions it contains. A stream of vesicles bud out of source compartments and fuse into target compartments, as specified by budding and fusion matrices (Figure 1A,D). Over a timescale of minutes this flux depletes the source compartment and enriches the target compartment in the molecular labels carried by the vesicles. Compartment compositions are updated from one timepoint to the next by mass balance, applied to each molecular label (blue arrows, Figure 1B,E): if it’s coming but not going, you eventually gain it; if it’s going but not coming, you eventually lose it. Apart from homotypic vesicle fusion (brown arrows, Figure 1B,E) which we discuss below, this is the sum total of our model.

Though we refer to vesicle transport throughout the text, our Boolean framework can also accommodate non-vesicular pathways. Some types of molecular labels can exchange between compartments only via transport vesicles. These include most lipids, and transmembrane proteins such as receptors and SNAREs. Others can travel from one compartment to another via the cytoplasm, either directly or on non-vesicle carriers. These include some types of lipids via carrier proteins, as well as the Arf- and Rab-family GTPases which switch between soluble and membrane-associated forms (Stenmark, 2009). If we explicitly assign a label to membrane lipids, any pathway carrying a single non-membrane molecular label can optionally be interpreted as direct cytoplasmic transport. Such an approach can be used, for example, to model Rab conversion during endosomal maturation (Rink et al., 2005) (Figure 1—figure supplement 1).

Orphan vesicles and homotypic fusion

We assume a clear hierarchy of membrane-bound structures: compartments are large, transport vesicles are small. The behavior of vesicles and compartments depends on their compositions, but can also depend on their size, for example through the influence of curvature or membrane tension. Suppose the fusion matrix specifies that vesicles of composition A fuse to compartments of composition B. This does not automatically imply that two vesicles of compositions A and B, or two compartments of compositions A and B, must fuse to one another. Here we explicitly assume that compartments cannot fuse heterotypically to one another, and that transport vesicles cannot fuse heterotypically to one another. However, compartments (Stenmark, 2009) and transport vesicles (Nakano and Luini, 2010) are known to fuse homotypically in certain situations. Homotypic compartment fusion, if it does occur, has no influence on our Boolean dynamics; in contrast, homotypic vesicle fusion has a key role to play. The dynamics often generate orphan vesicles that find no target compartment. Left unchecked these would leak out of the system, preventing homeostasis. Here we focus on homeostatic states in which a small specific subset of orphan vesicles can undergo homotypic fusion and nucleate new compartments, as seen in real cells (Nakano and Luini, 2010). Such vesicles would have to fuse much more efficiently to one another than to compartments of the same composition, perhaps mediated by size-dependent effects (brown arrows, Figure 1; Box 1).

The following algorithm efficiently generates all homeostatic states with these properties (Figure 1B,E; Materials and methods: The Boolean vesicle traffic model). Starting from some initial condition, we run Boolean updates. If at any point we encounter a homeostatic state with no orphans, we stop. If we encounter a state with orphan vesicles, we check what happens if specifically those vesicles could homotypically fuse to nucleate compartments. If this produces a homeostatic state, we stop. If not, we use the resulting state as our initial condition. We nullify assumptions about homotypic vesicle fusion, and repeat the process. In practice we find that a small dose of homotypic fusion is often sufficient to achieve homeostasis: over 80% of our homeostatic networks require two or fewer types of homotypically fusing vesicles.

Statistical cell biology and non-adaptive evolution

In the most basic maturation chain, a compartment created by homotypic vesicle fusion matures into one or more successive compositional types, coupled with retrograde transport of cargo (brown creation arrow followed by blue maturation arrows, Figure 1C,F; Box 1). Multiple maturation chains could exist as an interlinked part of a larger vesicle traffic network (Figure 2C). If we precisely set the elements of the budding and fusion matrices by hand, we can ensure that vesicles of the right composition bud and fuse between the right compartments so as to generate maturation chains (as with the examples in Figure 1). But what if the elements of these matrices are set at random? What is the likelihood that complex structures such as maturation chains would then arise?

Figure 2 with 2 supplements see all

Download asset Open asset

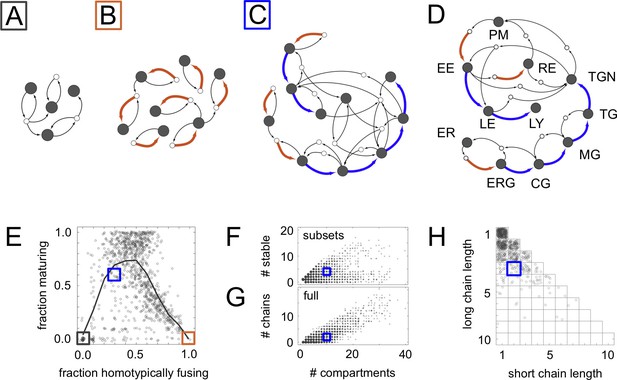
Homeostatic vesicle traffic networks.

These data relate to the 14,809 homeostatic networks for $N = 7$ molecular label types. (A–C) Examples of homeostatic networks (compartment and vesicle compositions are omitted for clarity) for budding and fusion rules generated using different parameter values ${N, A, f, g}$ (Materials and methods: Sampling homeostatic vesicle traffic networks). (A) {7, 1, 0.35, 0.35}, gray square icon. This is a transport-balanced network with no homotypic fusion or maturation. (B) {7, 4, 0.025, 0.75}, brown square icon. This is a network with high homotypic fusion but no maturation, and is broken into many disconnected subsets. (C) {7, 2, 0.1, 0.7}, blue square icon. This network has low homotypic fusion and high maturation, similar to a real eukaryotic cell. (D) Schematic vesicle traffic system of a eukaryotic cell. ER: endoplasmic reticulum. ERG: ER-Golgi intermediate compartment. CG: *cis*-Golgi. MG: medial-Golgi. TG: *trans*-Golgi. TGN: *trans*-Golgi network. PM: plasma membrane. EE: early endosome. LE: late endosome. LY: lysosome. RE: recycling endosome. (E) For each network in our dataset with ten or more compartments, we show the fraction of compartments undergoing maturation (outgoing blue arrow) vs. the fraction of compartments created by homotypic vesicle fusion (incoming brown arrow). The gray curve shows a moving average of the data. The colored squares show the position of the three networks in Figure 2A–C. Maturation is most likely at low-to-moderate rates of homotypic fusion. (F) The number of stable compartments vs. the total number of compartments for all the connected subsets in our dataset. The ER and plasma membrane are examples of stable compartments in real cells. (G) The number of maturation chains vs. the total number of compartments for all the networks in our dataset. (H) Chain lengths for all 841 networks in our dataset with precisely two maturation chains. In (E–H) we plot values with a random additive noise so the density of points can be observed. The blue square icon shows the properties of the cell-like network from Figure 2C. Figure 2—figure supplements 1,2 explore further properties of these homeostatic networks.

https://doi.org/10.7554/eLife.16231.005

This question is relevant because existing genetic variation constrains the directions in which natural selection can operate. It is therefore important to identify structures that arise in vesicle traffic systems prior to any selection for function. Inspired by statistical physics, we do a form of statistical cell biology: we make as few assumptions as possible, and thus sample a diverse ensemble of vesicle traffic systems. Just as polling a representative subset of likely voters provides information on election outcomes, statistically sampling a representative subset of budding and fusion rules reveals properties intrinsic to vesicle traffic. This represents a neutral null hypothesis: if a structure of interest occurs frequently in this sample without any fine tuning, it is consistent with a non-adaptive evolutionary origin.

Sampling homeostatic vesicle traffic networks

To systematically explore diverse behaviors, we sorted vesicle traffic systems according to the number of molecular labels, the number of adaptor/coatomer types, and how permissive vesicles were in selecting cargo and fusion targets (Figure 2—figure supplement 1; Materials and methods: Sampling homeostatic vesicle traffic networks). These parameters capture genetically-encoded properties such as the number, and the degree of interaction specificity, of cargo, adaptors, Arf and Rab GTPases, and SNAREs.

For each set of parameter values, we generated random instances of budding and fusion matrices (placed 1 s and 0 s at random positions). Given a budding and a fusion matrix, an arbitrary collection of compartments is almost certainly unstable: compartment compositions will update through molecular exchange, until finally the system settles into an unvarying homeostatic state (Figure 1B,E; Figure 2A–C). Different initial conditions lead to different homeostatic states. Each such state will typically contain only a small subset of all possible compartment compositions, and therefore depend only on a small number of elements of the full budding and fusion matrices. A homeostatic state represents a very special collection of compartments: either individual compartments in this set equalize gain and loss via vesicles – the balanced vesicular transport condition – or else different compartment types must interconvert between one another – the compartmental maturation condition.

Within a homeostatic state, compartments could segregate into subsets connected within themselves but disconnected from one another (Figure 2—figure supplement 2A). Most trivially, each compartment could be completely disconnected from all the others. In total we collected 63,897 homeostatic networks (35,838 non-trivial) for $N = 4, 5, 6, 7$ molecular label types. We found that network properties depended only weakly on $N$ (Figure 2—figure supplement 1A,B) so we focus the rest of the discussion on the 14,809 homeostatic networks (8614 non-trivial) obtained for $N = 7$ label types. For this number of molecular labels, there are $2^{7} - 1 = 127$ possible compartment or vesicle compositions, so the budding and fusion matrices contain thousands of elements (Figure 2—figure supplement 2F,G).

Among the networks generated by this procedure, 90% had 8 or fewer compartments and 11 or fewer vesicle types (Figure 2—figure supplement 2B,C). The compartments showed a bimodal distribution of compositional complexity, with an excess of compartments having very many or very few molecular labels (Figure 2—figure supplement 2D, top). In contrast, vesicles tended to be compositionally simple (Figure 2—figure supplement 2D, bottom). Molecular loss was offset by molecular gain at each stable compartment on fast timescales. However, compartment groups sometimes collectively received molecules that remained trapped within the group. Such molecular sinks create a need for compensatory synthesis elsewhere on slower timescales. We found that larger networks required synthesis of more types of molecular components (Figure 2—figure supplement 2E,H).

Cell-like networks and vesicle traffic motifs

A significant fraction of our homeostatic networks bore a striking resemblance to real eukaryotic vesicle traffic networks (Figure 2). In particular, they contained maturation chains. In terms of the number of compartments, number of chains, and chain lengths, the real eukaryotic traffic network (Figure 2D) appeared to be a typical example of a homeostatic network generated by our procedure (Figure 2C,E–H). Cell-like networks containing maturation chains were most likely to occur at low-to-moderate rates of homotypic vesicle fusion (Figure 2E): at very low rates all networks were of the transport balance type (Figure 2A); at very high rates they broke into many disconnected vesiculating subsets (Figure 2B). Nearly half the non-trivial homeostatic networks (4024/8614) contained a maturation chain of length one or more.

Unexpectedly, we found that the lengths of maturation chains were geometrically distributed (Figure 3C). Such distributions typically arise for processes in which each step is random and independent, for example counting the number of heads before hitting the first tail in a series of coin flips. This suggests that vesicle traffic networks might usefully be described by the random graph generation approaches that have provided insights into the structure of metabolic, neural, and ecological networks (Albert and Barabási, 2002) (Materials and methods: Randomly shuffled vesicle traffic networks).

Figure 3 with 1 supplement see all

Download asset Open asset

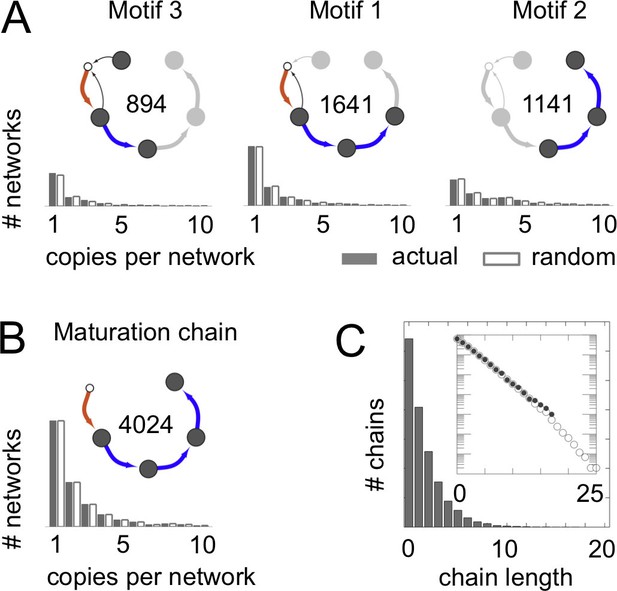
Frequent vesicle traffic motifs.

These data relate to the 14,809 homeostatic networks for $N = 7$ molecular label types. (A,B) Insets indicate the number of homeostatic networks that contain at least one copy of the motif. Histograms show the number of repeated copies of each motif per network, in actual (gray bars) or randomized (white bars) networks (Materials and methods: Vesicle traffic motifs; Materials and methods: Randomly shuffled vesicle traffic networks). (A) The three most frequent connected three-compartment motifs. (B) The maturation chain. (C) Histogram of maturation chain lengths. We consider any compartment with an incoming brown arrow as the start of a chain, and define length as the number of subsequent blue arrows. Inset: the same data in a log-linear plot. Both the real (grey dots) and randomized (white dots) networks show a geometric distribution of chain lengths. Figure 3—figure supplement 1 shows the frequency of the top 100 most common motifs.

https://doi.org/10.7554/eLife.16231.008

We wondered whether the networks lacking maturation chains were characterized by other distinct features. To quantify this, we did an unbiased search for highly represented network motifs (Milo et al., 2002) (Figure 3; Figure 3—figure supplement 1; Materials and methods: Vesicle traffic motifs). There are 43,700 ways in which three compartments can be connected to one another to form a motif. Strikingly, the three most frequent three-compartment motifs (Figure 3A) were all sub-graphs of the maturation chain, and eight of the ten most frequent motifs themselves contained maturation chains (Figure 3—figure supplement 1). In contrast, the 4590 non-trivial networks with no maturation chains showed no clear pattern: they were characterized by about 50 different motifs, no single one of which was found in more than 500 networks (Figure 3—figure supplement 1). The 15th most common three-compartment motif, occurring in 344 networks, is the maturation cycle (Figure 3—figure supplement 1). This corresponds to a compartment whose composition oscillates periodically. Cycles of various periods occurred in about a quarter (2407/8614) of all homeostatic networks. Out of 3173 non-trivial networks with no homotypic fusion, over a third contained cycles of maturing compartments (1053/3173).

Retrograde vesicles emerge spontaneously, driving cisternal maturation

What is the fate of a compartment that is created by homotypic vesicle fusion (Figure 4A)? It can proceed through steps of maturation, and finally end up as either a compartment of fixed composition, or one whose composition oscillates over time. Most maturation chains (72%) terminated at fixed compartments; terminal oscillating compartments were uncommon (Figure 4B). The majority (61%) of such fixed terminal compartments gave up all their cargo as vesicles at the next timepoint, and thus dissipated. When we examined the flow of molecules and vesicles within maturation chains (Figure 4C), we found a striking and unexpected feature: younger compartments were disproportionately likely to receive retrograde vesicles directly from their older successors, over eight times more often than expected by chance (Figure 4C, right panel). Individual molecules treadmilled in place within a chain, hopping to younger compartments via retrograde vesicles, driving their conversion to the older composition. The first compartment of a maturation chain tended to be compositionally simpler than its successors (at least in terms of the active labels considered here) due to the treadmilling molecules present on the latter.

Figure 4 with 1 supplement see all

Download asset Open asset

Anatomy of a cisternal maturation chain.

(A) A compartment created at the first timepoint (source, thick brown arrow) matures at each successive timepoint (inlet, thick blue arrows). This process can terminate at a compartment with fixed composition, or one with an oscillating composition (cycle of thick blue arrows). Vesicles move molecules between compartments. We classify vesicles as anterograde (thin light brown arrows), retrograde (thin dark brown arrows) and other (thin black arrows). Some vesicles are inbound or outbound from other parts of the network. (B) Properties of the terminal compartment of a maturation chain. There are 10,172 homotypically fusing sources in our dataset that have at least one maturation step, of which just 2899 terminate in a cycle. The remaining 7273 sources terminate at 4588 fixed compartments (the reduction in number is because maturation chains can converge). Finally, 2820 of these 4588 compartments dissipate at the next timestep, giving up all their cargo as vesicles. (C) Fraction of compartment pairs A,B with a B-to-A vesicle. Each dot in each panel represents values for a single network; we show data only for networks that have ten or more maturation edges. The x-axis is the vesicle fraction $f_{a l l}$ for all compartment pairs A,B in the network. The y-axis is the vesicle fraction $f_{s u b s e t}$ for the subset of compartment pairs A,B in the network where A sends a vesicle to B (left), B matures to A (middle), or A matures to B (right). For the left and middle panels, the chance of finding a B to A vesicle for the corresponding subset of pairs is the same as the chance between all pairs in a network. For the right panel, the chance of finding a B to A vesicle when A matures to B (median 0.75) is eight fold more than the chance across all pairs (median 0.09). For example, suppose a network with 10 compartments has $10 \times 9 = 90$ compartment pairs A,B. Suppose for 8 of these pairs we know that A matures to B. Now we count vesicles. We find that 8/90 = 0.09 of all pairs and 6/8 = 0.75 of the maturing pairs have a vesicle going from B to A. This corresponds to a network with an x-value of 0.09 and a y-value of 0.75: there are many more retrograde vesicles between maturing compartments than expected by chance. That is, a younger compartment in a maturation chain almost certainly receives a retrograde vesicle from its immediate older successor. Figure 4—figure supplement 1 explores the optimal spatial distribution of compartments in a maturation chain.

https://doi.org/10.7554/eLife.16231.010

Distilling these observations, here is our central result: across 8614 non-trivial homeostatic networks, we find 3111 maturation chains which precisely match all three diagnostic features of the cisternal maturation model (Figures 1,4). (1) The first compartment is created by homotypic vesicle fusion and then matures via one or more steps. (2) The terminal compartment dissipates by vesiculation. (3) Younger compartments receive retrograde vesicles directly from their older successors.

Discussion

We have answered the question posed at the outset: even when elements of the budding and fusion matrices are set at random, the stringent requirements of homeostasis drive cells toward highly structured compartment compositions, among which cisternal maturation chains frequently occur. The basic, well-established dynamics of vesicle traffic – in which the specificity of vesicle formation and fusion is locally regulated through molecular interactions – are sufficient to generate a Golgi-like structure without fine tuning. We emphasize that our results pertain to cell-wide vesicle traffic rather than narrowly to the Golgi apparatus, and have implications for maturation dynamics observed in other secretory and endocytic systems (Mani and Thattai, 2016). Almost all networks with maturation chains also contained stable compartments with balanced vesicular transport: these structures co-exist, they not mutually exclusive. Classic models of membrane traffic focus on the generation of stable compartments out of the dynamic process of vesicle exchange (Heinrich and Rapoport, 2005). The few that consider maturation introduce it by hand, and study subsequent features of protein transport (Glick et al., 1997; Weiss and Nilsson, 2000; Dmitrieff et al., 2013; Ispolatov and Müsch, 2013). In contrast, maturation is not built into our framework, it emerges spontaneously. When a basic model is sufficient to generate cisternal maturation, the burden of proof is on complex models to justify additional ingredients.

Our strongest result is the emergence of retrograde vesicles between maturing cisternae in the absence of a spatial coordinate. All earlier mathematical analyses explicitly or implicitly assumed that maturation was driven by retrograde vesicles moving between spatially neighboring compartments (Glick et al., 1997; Weiss and Nilsson, 2000; Dmitrieff et al., 2013; Ispolatov and Müsch, 2013). However, un-stacked Golgi are widespread (Mowbrey and Dacks, 2009); and do have retrograde vesicles (Papanikou et al., 2015). This is consistent with our results: it shows that spatial organization is not a pre-requisite for maturation, and supports the idea of a well-mixed cytoplasm.

A eukaryotic cell is an object distributed in both chemical and physical space (Misteli, 2001). The connectivity of a vesicle traffic network is primarily determined by molecular chemical specificity, while the locations of compartments are determined by complex and largely unknown biophysical mechanisms (Yadav and Linstedt, 2011). The spatial organization of a cell clearly impacts all aspects of its activity, including vesicle traffic. To add a physical dimension to our analysis, we explored the hypothesis that a cell is like an efficient city-wide logistics system: one in which no part of a city is too far from a warehouse, and warehouses with more traffic between them are placed closer to one another (Taniguchi et al., 1999). For each network in our dataset, we ran an optimization algorithm to distribute compartments uniformly across a cell while minimizing the distance travelled by vesicles between compartments (Materials and methods: Spatial optimization). Remarkably, maturation chains in such optimized networks immediately organized into spatially contiguous stacks: each compartment was adjacent in space to the type of compartment it matures to in time (Figure 4—figure supplement 1). This was mainly due to the excess of retrograde vesicles within maturation chains, though most vesicles still traveled long distances. The stacked morphology of the Golgi apparatus in many eukaryotes is thus consistent with the expectations of efficient traffic. Experiments with repositioned organelles might be used to test these ideas further (van Bergeijk et al., 2015). However, hypotheses about function and efficiency are much more difficult to prove than those about molecular mechanism. Our main result is based only on the latter: as vesicle traffic networks evolve, cisternal maturation is easily discoverable by mutation, prior to any selection. For the Golgi apparatus, form might have preceded function.

Materials and methods

The Boolean vesicle traffic model

Request a detailed protocol

We assume N types of active molecular labels, and A types of cytoplasmic adaptor/coatomer complexes. Compartments (C) and vesicles (V) are both collections of molecular labels, represented by binary row vectors of length N. Each element of such a vector is 1 or 0, indicating whether a certain label type is present in high or low amounts, loosely referred to as presence or absence. For example, for N = 3 the row vector [101] indicates that only the first and third label types are present on the corresponding compartment or vesicle. There are $C = 2^{N} - 1$ and $V = 2^{N} - 1$ possible non-zero types of compartments and vesicles, respectively. Vesicles with a single non-zero label may optionally be interpreted as membrane-associated molecules capable of cytoplasmic non-vesicular transport (Figure 1—figure supplement 1). Since our model is deterministic, a set of compartments of the same composition present at the same time will all have the same dynamics. It is therefore sufficient to keep track of whether some compartment of a given composition is present or absent. Each of the $\sim 2^{N}$ possible compartments could be present or absent at any timepoint, so the cell itself could be in one of $\sim 2^{2^{N}}$ possible states.

Let $i = 1, \dots, C$ index the possible compartment composition vectors, and $j = 1, \dots, V$ index the possible vesicle composition vectors. We use a convention in which vectors are sorted according to the standard binary ordering. Thus the row vector $c (i)$ or $v (j)$ has entries corresponding to the digits of the binary number $i$ or $j$ . For example, for N = 3 the compartment composition corresponding to the index i = 5 is the row vector $c (5) = [101]$ . If $n = 1, \dots, N$ runs over the label types, $c_{n} (i)$ or $v_{n} (j)$ represents the nth component of the compartment or vesicle row vector.

The dynamics are entirely specified by two matrices (Figure 1A,D): the $C \times V$ budding matrix G, and the $C \times V$ fusion matrix F. If a budding element $G_{i j} = 1$ , compartment type i generates vesicle type j. Since any vesicle vector must be a subset of the source compartment vector, the set of allowed non-zero elements of G has the form of a Sierpinski triangle. Each row of G can have at most A non-zero elements, since this is the number of distinct adaptor/coatomer complexes. If a fusion element $F_{i j} = 1$ , vesicle type j fuses into compartment type i, as long as the latter is present at that timepoint. Any element of F can be non-zero. Under these row-column conventions the product ${(G F')}_{i_{1} i_{2}}$ (mnemonic buddinG x Fusion’) represents the compartment-to-compartment matrix whose entries give the number of distinct vesicle types coupling any source compartment ( $i_{1}$ ) with any target compartment ( $i_{2}$ ).

At any timepoint t, let the sorted set of distinct compartments be $I^{t} \equiv {i_{1}^{t}, i_{2}^{t}, \dots}$ , where $i_{1}^{t} < i_{2}^{t} < \dots \leq C$ . The budding matrix G then specifies the sorted set of distinct vesicles being generated at that timepoint $J^{t} \equiv {j_{1}^{t}, j_{2}^{t}, \dots}$ , where $j_{1}^{t} < j_{2}^{t} < \dots \leq V$ . That is, $J^{t} = {j | \exists i \in I^{t} s . t . G_{i j} = 1}$ . For any compartment of interest $i \in I^{t}$ we can use G to find the vesicles $J (i \to) \subset J^{t}$ budding out of it, and use F to find the vesicles $J (i \leftarrow) \subset J^{t}$ fusing into it: $J (i \to) = {j \in J^{t} | G_{i j} = 1}$ and $J (i \leftarrow) = {j \in J^{t} | F_{i j} = 1}$ . Note that $J^{t} = \cup_{i} J (i \to)$ but $J^{t} \supset \cup_{i} J (i \leftarrow)$ since some orphan vesicles might not have targets at that timepoint.

Compartments change composition discretely and synchronously, using a binary version of mass balance (Figure 1B,E). Consider the kth entry in the sorted list of compartments present at timepoint t: it has index $i_{k}^{t} \in I^{t}$ . The shorthands

\begin{array}{ll} v_{n} (i_{k}^{t} \to) = & O R {v_{n} (j) | j \in J (i_{k}^{t} \to)} \\ v_{n} (i_{k}^{t} \leftarrow) = & O R {v_{n} (j) | j \in J (i_{k}^{t} \leftarrow)} \end{array}

represent the bitwise OR of the vesicle row vectors in these sets, effectively collapsing them into a single outgoing and a single incoming vesicle row vector for the kth compartment. The composition of this compartment updates according to the following Boolean expression:

c_{n} (i_{k}^{t + 1}) \equiv c_{n}^{t + 1} = v_{n} (i_{k}^{t} \leftarrow) \lor [\neg v_{n} (i_{k}^{t} \to) \land c_{n} (i_{k}^{t})]

where the leftmost relationship defines the index $i_{k}^{t + 1}$ as the binary number whose digits are given by the row vector $c_{n}^{t + 1}$ . Put simply, a compartment will gain a molecular label type if it is fusing in and not budding out, and will lose a molecular label type if it is budding out and not fusing in. For all other cases compartment composition does not change.

If at any timepoint some orphan vesicle type does not fuse to any of the available compartments, this cannot represent a homeostatic state. We then check what happens if each orphan type is separately allowed to undergo homotypic fusion to create a compartment (brown arrows, Figure 1B,E). In this way we generate a new set of compartments

I^{t + 1} = \underset{c r e a t e d c o m p a r t m e n t s}{\underset{⏟}{{j \in J^{t} | j \notin \cup_{k} J (i_{k}^{t} \leftarrow)}}} \cup \underset{m a t u r i n g c o m p a r t m e n t s}{\underset{⏟}{{i_{1}^{t + 1}, i_{2}^{t + 1}, \dots}}}

where any duplicates are removed and the indices are sorted. Any compartment which vesiculates by losing all its molecules updates to the zero compartment $c (0) = [000 \dots]$ and is not included in this set. The number of distinct compartments could increase through creation. It could decrease if any compartment loses all its molecules, or if two compartments at timepoint t update to the same composition at timepoint t+1. If the new updated state is identical to the previous one, this indicates we have found a homeostatic state, and we stop the updates. Otherwise, we nullify assumptions about homotypic vesicle fusion, and repeat the updates. Homeostatic states generated in this way contain compartments identical in composition to each orphan vesicle. Since orphans do not fuse to any existing compartment according to the fusion matrix, they necessarily cannot fuse heterotypically to one another.

Sampling homeostatic vesicle traffic networks

Request a detailed protocol

We sample a large number of budding and fusion matrices and examine the traffic networks that result. We generate these matrices using four parameters (Figure 2—figure supplement 1): N is the number of distinct molecular label types; A is the number of adaptor/coatomer complexes. The continuous parameter $g \in [0, 1]$ sets the propensity of molecular cargo loading (higher values of g mean vesicles have more 1 s). The continuous parameter $f \in [0, 1]$ sets the propensity of fusion (higher values of f mean the fusion matrix has more 1 s). All these parameters are ultimately genetically determined: N and A represent the number of protein types involved, while g and f summarize their interaction properties. For example, g depends on cargo-adaptor specificity, and f depends on SNARE-SNARE specificity. Our search is unbiased in the sense that we sample uniformly over these parameters.

We generate G and F as follows. Let $X \sim B e r (p)$ be a Bernoulli random variable, so $℘ (X = 1) = p$ , $℘ (X = 0) = 1 - p$ . For every possible compartment i we define A vesicle row vectors of length N, one for each possible adaptor/coatomer: $v_{n}^{a} (i \to) = c_{n} (i) ∙ X$ , where $X ~ B e r (g)$ and $a = 1, \dots, A$ . That is, each vesicle typically loads a fraction g of the cargo types on source compartments. The budding matrix is then given by $G_{i j} = 1 \Leftrightarrow \exists a s . t . v (j) = v^{a} (i \to)$ . Each row of G can have anywhere from 0 to A non-zero entries, since not all vesicles budding from each compartment are distinct, and the zero vesicle $v (0) = [000 \dots]$ is ignored. The fusion matrix is given by $F_{i j} = X$ , $X ~ B e r (f)$ . That is, each vesicle typically fuses to a fraction f of all compartment types. Once G and F are constructed, they remain constant throughout the dynamics.

We scan parameter values $N \in {4, 5, 6, 7}$ , $A \in {1, 2, 3, 4, 5}$ , $g, f \in {0.05, 0.10, \dots, 0.90, 0.95}$ , and additionally $f \in {0.025, 0.075, 1}$ , giving 8360 distinct combinations (Figure 2—figure supplement 1). For each parameter combination we sample ten F, G rules as described above. For each rule we start with a random initial condition $I^{t = 0} = {i_{1}^{0}, i_{2}^{0}, \dots}$ generated by uniformly sampling between 1 and $2^{N} - 1$ initial compartments, each of which can uniformly take any of the $2^{N} - 1$ possible Boolean indices. We use the prescription described in Equation 6 to update the system in discrete timesteps starting from the initial condition. Since this is a deterministic dynamical system over a discrete state space, once sufficient time has elapsed all trajectories will converge onto one or more periodic orbits: a set of states which form a cycle under updates. Each rule will in general have many periodic orbits as attractors, and different initial conditions can converge to different orbits. For each initial condition, we run the system for 1024 timesteps or until it reaches a periodic orbit. A period-1 orbit, which updates to itself, is particularly relevant: it is a homeostatic state (Figure 1B,E). We store all such homeostatic vesicle traffic networks for further analysis. A trivial state is one in which no compartment connects to any other. In our simulations for $N = 7$ , 98% of initial conditions reached an orbit within 1024 steps, of which 72% were homeostatic states. In total we found 17,458, 16,248, 15,382, and 14,809 homeostatic states (of which 9456, 8990, 8778, and 8614 were non-trivial) for $N = 4, 5, 6, 7$ , respectively.

Vesicle traffic motifs

Request a detailed protocol

In a homeostatic steady state, the full set of compartments remains constant, though individual compartments can interconvert between one another. We can represent each steady state as a graph (Figure 1C,F), where nodes ${i_{1}, i_{2}, \dots}$ are compartments, and there are three types of edges: vesicle edges, creation edges, and maturation edges. Vesicle edges (black) go from source to target compartments: $i_{1} \to i_{2}$ wherever ${(G F')}_{i_{1} i_{2}} = 1$ . Creation edges (brown) connect source compartments to newly created compartments generated by homotypic fusion of orphan vesicles (Equation 6): $i \to j$ for each vesicle such that $j \in J (i \to)$ , $j \notin \cup_{k} J (i_{k}^{t} \leftarrow)$ . Maturation edges (blue) connect compartment compositions at two successive timepoints (Equation 5): $i_{k}^{t} \to i_{k}^{t + 1}$ , unless the compartment is in transport balance such that $i_{k}^{t} = i_{k}^{t + 1}$ . A compartment is considered to be involved in a maturation step if it has an outgoing maturation edge. Considering only creation and maturation edges, there are 43,700 distinct connected three-compartment motifs. A maturation chain starts at a compartment with an incoming creation edge, and proceeds via maturation edges, stopping at a compartment with no outgoing maturation edge. If a compartment encountered earlier in the chain is repeated, this indicates a cycle so the chain is terminated before the repeat, and the cycle is stored for further analysis (Figure 4A,B).

Randomly shuffled vesicle traffic networks

Request a detailed protocol

One way to generate a random graph is to preserve the number and properties of individual nodes, but otherwise connect them at random (Albert and Barabási, 2002). For each homeostatic network in our dataset, we break the network into individual compartments, then reconnect them as follows. We remove all vesicle edges. We then randomly swap remaining edge targets, allowing only swaps between maturation edges or between creation edges. We reject the swap if: a self edge is lost; a self edge is created; or multiple edges of the same type arise between the same source and target nodes. This procedure preserves all individual node properties: self edges, and the separate indegrees and outdegrees of creation and maturation edges. We generate 1000 randomly shuffled networks for each original network. We find that these shuffled networks have precisely the same distribution of motif frequencies and maturation chain lengths as the original networks (Figure 3A,BC). This supports the idea that a random graph generation approach might capture relevant features of vesicle traffic networks.

Spatial optimization

Request a detailed protocol

We want to distribute the compartments of a vesicle traffic network in such a way that all parts of a cell are close to at least one compartment, while the distance travelled by vesicles between compartments is minimized (Figure 4—figure supplement 1). Let $r_{i}$ give the vector position of each compartment i, so pairwise distances between compartments are $s_{i j} = | r_{i} - r_{j} |$ . Define an energy function:

E = \sum_{i, j} \frac{1}{s_{i j}} + (a_{0} + a_{i j}) s_{i j}^{2}

where $a_{i j} = 1$ if a vesicle goes from compartment i to compartment j, and $a_{0} = 0.1$ sets a baseline value. By varying compartment positions to minimize this function, we achieve the desired optimal configuration. Intuitively: compartments act as repelling charges and spread out as uniformly as possible, while vesicle fluxes act as attractive springs and try to be as short as possible. Starting from random initial conditions, we numerically determined the optimal minimum energy compartment positions in two dimensions.

References

1. Albert R
2. Barabási A-L
(2002) Statistical mechanics of complex networks
Reviews of Modern Physics 74:47–97.
https://doi.org/10.1103/RevModPhys.74.47
- Google Scholar
1. Bard F
2. Malhotra V
(2006) The formation of TGN-to-plasma-membrane transport carriers
Annual Review of Cell and Developmental Biology 22:439–455.
https://doi.org/10.1146/annurev.cellbio.21.012704.133126
- Google Scholar
(2009) A conceptual mathematical model of the dynamic self-organisation of distinct cellular organelles
PLoS ONE 4:e8295.
https://doi.org/10.1371/journal.pone.0008295
- Google Scholar
(1998) Procollagen traverses the Golgi stack without leaving the lumen of cisternae: evidence for cisternal maturation
Cell 95:993–1003.
https://doi.org/10.1016/s0092-8674(00)81723-7
- Google Scholar
1. Bonifacino JS
2. Lippincott-Schwartz J
(2003) Coat proteins: shaping membrane transport
Nature Reviews Molecular Cell Biology 4:409–414.
https://doi.org/10.1038/nrm1099
- Google Scholar
(2005) Robustness and fragility of Boolean models for genetic regulatory networks
Journal of Theoretical Biology 235:431–449.
https://doi.org/10.1016/j.jtbi.2005.01.023
- Google Scholar
1. D'Souza-Schorey C
2. Chavrier P
(2006) ARF proteins: roles in membrane traffic and beyond
Nature Reviews Molecular Cell Biology 7:347–358.
https://doi.org/10.1038/nrm1910
- Google Scholar
1. De Matteis MA
2. Luini A
(2008) Exiting the Golgi complex
Nature Reviews Molecular Cell Biology 9:273–284.
https://doi.org/10.1038/nrm2378
- Google Scholar
1. Dmitrieff S
2. Rao M
3. Sens P
(2013) Quantitative analysis of intra-Golgi transport shows intercisternal exchange for all cargo
Proceedings of the National Academy of Sciences 110:15692–15697.
https://doi.org/10.1073/pnas.1303358110
- Google Scholar
1. Dmitrieff S
2. Sens P
(2011) Cooperative protein transport in cellular organelles
Physical Review E 83:041923.
https://doi.org/10.1103/PhysRevE.83.041923
- Google Scholar
1. Emr S
2. Glick BS
3. Linstedt AD
4. Lippincott-Schwartz J
5. Luini A
6. Malhotra V
7. Marsh BJ
8. Nakano A
9. Pfeffer SR
10. Rabouille C
11. Rothman JE
12. Warren G
13. Wieland FT
(2009) Journeys through the Golgi--taking stock in a new era
The Journal of Cell Biology 187:449–453.
https://doi.org/10.1083/jcb.200909011
- Google Scholar
1. Fernández A
2. Lynch M
(2011) Non-adaptive origins of interactome complexity
Nature 474:502–505.
https://doi.org/10.1038/nature09992
- Google Scholar
1. Gillespie DT
(2007) Stochastic simulation of chemical kinetics
Annual Review of Physical Chemistry 58:35–55.
https://doi.org/10.1146/annurev.physchem.58.032806.104637
- Google Scholar
(1997) A cisternal maturation mechanism can explain the asymmetry of the Golgi stack
FEBS Letters 414:177–181.
https://doi.org/10.1016/s0014-5793(97)00984-8
- Google Scholar
1. Glick BS
2. Luini A
(2011) Models for Golgi traffic: a critical assessment
Cold Spring Harbor Perspectives in Biology 3:a005215.
https://doi.org/10.1101/cshperspect.a005215
- Google Scholar
1. Heinrich R
2. Rapoport TA
(2005) Generation of nonidentical compartments in vesicular transport systems
The Journal of Cell Biology 168:271–280.
https://doi.org/10.1083/jcb.200409087
- Google Scholar
1. Huotari J
2. Helenius A
(2011) Endosome maturation
The EMBO Journal 30:3481–3500.
https://doi.org/10.1038/emboj.2011.286
- Google Scholar
1. Ispolatov I
2. Müsch A
(2013) A model for the self-organization of vesicular flux and protein distributions in the Golgi apparatus
PLoS Computational Biology 9:e1003125.
https://doi.org/10.1371/journal.pcbi.1003125
- Google Scholar
1. Jahn R
2. Scheller RH
(2006) SNAREs--engines for membrane fusion
Nature Reviews Molecular Cell Biology 7:631–643.
https://doi.org/10.1038/nrm2002
- Google Scholar
(2003) Random Boolean network models and the yeast transcriptional network
Proceedings of the National Academy of Sciences 100:14796–14799.
https://doi.org/10.1073/pnas.2036429100
- Google Scholar
1. Li F
2. Long T
3. Lu Y
4. Ouyang Q
5. Tang C
(2004) The yeast cell-cycle network is robustly designed
Proceedings of the National Academy of Sciences 101:4781–4786.
https://doi.org/10.1073/pnas.0305937101
- Google Scholar
1. Losev E
2. Reinke CA
3. Jellen J
4. Strongin DE
5. Bevis BJ
6. Glick BS
(2006) Golgi maturation visualized in living yeast
Nature 441:1002–1006.
https://doi.org/10.1038/nature04717
- Google Scholar
1. Luini A
(2011) A brief history of the cisternal progression-maturation model
Cellular Logistics 1:6–11.
https://doi.org/10.4161/cl.1.1.14693
- Google Scholar
1. Lynch M
2. Conery JS
(2003) The origins of genome complexity
Science 302:1401–1404.
https://doi.org/10.1126/science.1089370
- Google Scholar
1. Lynch M
(2007) The frailty of adaptive hypotheses for the origins of organismal complexity
Proceedings of the National Academy of Sciences 104:8597–8604.
https://doi.org/10.1073/pnas.0702207104
- Google Scholar
1. Lynch M
(2007) The evolution of genetic networks by non-adaptive processes
Nature Reviews Genetics 8:803–813.
https://doi.org/10.1038/nrg2192
- Google Scholar
1. Mani S
2. Thattai M
(2016) Wine glasses and hourglasses: Non-adaptive complexity of vesicle traffic in microbial eukaryotes
Molecular and Biochemical Parasitology S0166-6851(16)30023-8.
https://doi.org/10.1016/j.molbiopara.2016.03.006
- Google Scholar
(2006) Live imaging of yeast Golgi cisternal maturation
Nature 441:1007–1010.
https://doi.org/10.1038/nature04737
- Google Scholar
1. Milo R
2. Shen-Orr S
3. Itzkovitz S
4. Kashtan N
5. Chklovskii D
6. Alon U
(2002) Network motifs: simple building blocks of complex networks
Science 298:824–827.
https://doi.org/10.1126/science.298.5594.824
- Google Scholar
1. Misteli T
(2001) The concept of self-organization in cellular architecture
The Journal of Cell Biology 155:181–186.
https://doi.org/10.1083/jcb.200108110
- Google Scholar
1. Mowbrey K
2. Dacks JB
(2009) Evolution and diversity of the Golgi body
FEBS Letters 583:3738–3745.
https://doi.org/10.1016/j.febslet.2009.10.025
- Google Scholar
1. Munro S
(2004) Organelle identity and the organization of membrane traffic
Nature Cell Biology 6:469–472.
https://doi.org/10.1038/ncb0604-469
- Google Scholar
1. Nakano A
2. Luini A
(2010) Passage through the Golgi
Current Opinion in Cell Biology 22:471–478.
https://doi.org/10.1016/j.ceb.2010.05.003
- Google Scholar
1. Papanikou E
2. Day KJ
3. Austin J
4. Glick BS
(2015) COPI selectively drives maturation of the early Golgi
eLife 4:e13232.
https://doi.org/10.7554/eLife.13232
- Google Scholar
1. Poteryaev D
2. Datta S
3. Ackema K
4. Zerial M
5. Spang A
(2010) Identification of the switch in early-to-late endosome transition
Cell 141:497–508.
https://doi.org/10.1016/j.cell.2010.03.011
- Google Scholar
1. Ramadas R
2. Thattai M
(2013) New organelles by gene duplication in a biophysical model of eukaryote endomembrane evolution
Biophysical Journal 104:2553–2563.
https://doi.org/10.1016/j.bpj.2013.03.066
- Google Scholar
1. Rink J
2. Ghigo E
3. Kalaidzidis Y
4. Zerial M
(2005) Rab conversion as a mechanism of progression from early to late endosomes
Cell 122:735–749.
https://doi.org/10.1016/j.cell.2005.06.043
- Google Scholar
1. Robinson MS
(2004) Adaptable adaptors for coated vesicles
Trends in Cell Biology 14:167–174.
https://doi.org/10.1016/j.tcb.2004.02.002
- Google Scholar
1. Stenmark H
(2009) Rab GTPases as coordinators of vesicle traffic
Nature Reviews Molecular Cell Biology 10:513–525.
https://doi.org/10.1038/nrm2728
- Google Scholar
(1999) Optimal size and location planning of public logistics terminals
Transportation Research Part E: Logistics and Transportation Review 35:207–222.
https://doi.org/10.1016/S1366-5545(99)00009-5
- Google Scholar
1. Traub LM
(2009) Tickets to ride: selecting cargo for clathrin-regulated internalization
Nature Reviews Molecular Cell Biology 10:583–596.
https://doi.org/10.1038/nrm2751
- Google Scholar
(2015) Optogenetic control of organelle transport and positioning
Nature 518:111–114.
https://doi.org/10.1038/nature14128
- Google Scholar
1. Weiss M
2. Nilsson T
(2000) Protein sorting in the Golgi apparatus: a consequence of maturation and triggered sorting
FEBS Letters 486:2–9.
https://doi.org/10.1016/S0014-5793(00)02155-4
- Google Scholar
1. Wickner W
2. Schekman R
(2008) Membrane fusion
Nature Structural & Molecular Biology 15:658–664.
https://doi.org/10.1038/nsmb.1451
- Google Scholar
1. Yadav S
2. Linstedt AD
(2011) Golgi positioning
Cold Spring Harbor Perspectives in Biology 3:a005322.
https://doi.org/10.1101/cshperspect.a005322
- Google Scholar
1. Yu IM
2. Hughson FM
(2010) Tethering factors as organizers of intracellular vesicular traffic
Annual Review of Cell and Developmental Biology 26:137–156.
https://doi.org/10.1146/annurev.cellbio.042308.113327
- Google Scholar

Decision letter

Benjamin S Glick

Reviewing Editor; The University of Chicago, United States

In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.

Thank you for submitting your article "Stacking the odds for Golgi cisternal maturation" for consideration by eLife. Your article has been reviewed by three peer reviewers, one of whom, Benjamin Glick, also guest edited the paper, and the evaluation has been overseen by Randy Schekman as the Senior Editor. The following individuals involved in review of your submission have agreed to reveal their identity: Alberto Luini (Reviewer #2).

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Summary:

This paper explores the dynamic organization of the Golgi by a theoretical modeling of Boolean networks. The simplicity of the approach enables the authors to perform an unbiased survey of a large number of possible vesicle trafficking scenarios. A surprising and striking result is that many of the networks display the properties of compartmental maturation. Thus, the evolution of Golgi maturation can be viewed as a natural outcome of the intrinsic properties of vesicle trafficking systems. According to this view, the transport of large secretory cargo molecules was probably an adaptation that took advantage of an existing process.

Essential revisions:

The reviewers and reviewing editor had an interesting discussion about your paper. Multiple concerns were raised, and initially it seemed likely that the decision would be to decline the submission. In the end, we agreed that the story is interesting enough to merit a request for resubmission after major revisions. There is no guarantee that the revised version will pass muster, so you will need to decide whether the effort is worthwhile.

There is general agreement that the idea of approaching this problem with Boolean networks is creative and novel, and that the results are an important step forward if the approach is sound. But the following issues need to be addressed.

1) Your model assumes that compartment identity is determined by transmembrane and luminal components, which are necessarily exchanged by means of transport vesicles. But in reality, components recruited from the cytosol, such as GTPases and adaptors/coats and phosphoinositide modifying enzymes, play an important and perhaps central role in defining compartment identity. In some cases, Rab cascades are thought to regulate compartmental maturation. While your model necessarily is necessarily a simplified representation of reality, overlooking this fundamental property of the endomembrane system seems hard to justify.

2) The focus of your analysis is on the subset of networks that include maturation chains. But the majority of the networks do not show maturation. The neglect of those other outcomes is surprising. For example, how often is the traditional vesicle shuttle model replicated? What can be learned from analyzing the full set of networks?

3) The assumption that vesicles unable to find a target undergo homotypic fusion is troubling. This process may reflect the actual behavior of some vesicle types in cells, but why is homotypic fusion the default assumption? Does this feature predispose the model to generate maturing networks? Why wouldn't orphan vesicles fuse heterotypically, like other vesicles do?

4) The treatment of spatiotemporal aspects of membrane traffic raised two issues:

The description of virtual stacking (Figure 4) is not at all compelling. What is the justification for modeling vesicle fluxes as attractive springs while modeling compartments as repelling charges? That representation does not seem to correspond to any realistic picture of membrane traffic. This part of the story weakens the paper, and should probably be omitted unless it can be revised in a way that makes sense.

One of the reviewers was quite troubled by the lack of spatiotemporal parameters in your model (transport coefficients, distances, compartment sizes, etc). The other two reviewers were of the opinion that the cytoplasm is well mixed, so it is reasonable to assume that vesicles will reach any potential destination. But to convince the skeptical reviewer and other readers, you should explain why spatiotemporal parameters can be ignored for the purposes of your simulation. In particular, the markers used in your simulation reach a steady-state homeostatic distribution, but is it automatically true that all of the other components, such as lipids, will also undergo balanced flows in a given network? Does your model require the unrealistic assumption that every compartment generates the same number and size of vesicles per unit time? Is it obvious that movement between compartment is fast relative to formation and fusion of vesicles, so that spatial aspects can be neglected?

5) In general, the descriptions and discussion need to be expanded significantly to address the questions that will be raised by cell biologists. Perhaps it would be useful to rewrite the paper with input from a cell/membrane biologist. Here are examples of issues that should be addressed:

The introduction is too generic. It does not even mention the Boolean modeling approach, and does not describe either the power and limitations of this approach or the reasons for choosing it to address this particular topic.

The difference between actual and randomized networks in Figure 2A–C is confusing, and the significance of Figure 2D,E is hard to understand. Similarly, in Figure 3, what is the difference between special pairs and random pairs? The parameters and assumptions should be clearly described in terms that will make sense to cell biologists.

The phenomenon of compartments becoming richer in compositional complexity over time has not been described experimentally, and doesn't seem to make biological sense. Can you comment on this discrepancy?

Regarding the maturation chains, one reviewer wrote: "However, these striking observations are not clearly interpretable. The authors should provide much more detail on the characteristics of these chains, on the dynamics of their development, and on the number of the chains that possess these particularly complex features. They should also describe the networks that do not contain maturation chains, which actually represent the majority of the outcomes. They should discuss which parameters lead to realistic maturation chains, and which preclude maturation. What is interesting to me is not the fact that they observe maturation as this outcome is expected, but the fact that the maturation networks are so complex and so similar to the real ones, and so frequent. Again they should thoroughly describe the maturation chains, the alternative outcomes and the conditions where they obtain. Without this description we cannot judge the value of the simulations."

Do the authors wish to argue that their simulations reflect a potentially simpler situation early in evolution, and are therefore not constrained to incorporate features of currently existing trafficking systems? If so, they should make this point explicitly.

[Editors' note: further revisions were requested prior to acceptance, as described below.]

Thank you for resubmitting your work entitled "Stacking the odds for Golgi cisternal maturation" for further consideration at eLife. Your revised article has been favorably evaluated by Randy Schekman (Senior editor) and three reviewers, one of whom is a member of our Board of Reviewing Editors.

The manuscript has been improved but there are some remaining issues that need to be addressed before acceptance, as outlined below:

Once again the reviewers had an extended discussion of your manuscript. As before, one of the reviewers remains deeply concerned about the lack of spatiotemporal parameters in the simulations, while the other two reviewers feel that your approach makes sense and yields intriguing insights. After judging these arguments, I am prepared to accept your manuscript if you can address the following remaining issues either by revising the paper or by explaining why a revision is not warranted.

1) Even though the basic patterns of compartmental formation and communication can be described by the Boolean network approach, spatiotemporal parameters are clearly important in real cells to ensure that the membrane traffic machinery is efficient enough to support life. This point should be given further emphasis.

More generally, you should discuss the limitations of the described approach. Does the model make testable, falsifiable predictions? I suspect that this one can be addressed by the presentation. For example, if you predicted that maturation chains could have evolved without specific selection for the transport of large cargo, then the modeling matches this prediction. But are other aspects of membrane traffic not captured by your simple model?

2) The authors should discuss how to arrive at the Boolean network approach from a set of (partial) differential equations (similar to Heinrich/Rapoport's model or starting from overdamped Fokker-Planck equations). In particular: Which rates and transport coefficients are considered large or limiting w.r.t others, i.e. which quasi-equilibria are used for setting up the model from more fundamental approaches?

3) The biological meanings of the propensity parameters for budding and fusion are still unclear. Please provide an explanation. For example, does propensity to fuse reflect the spatial proximity of vesicle donor and acceptor compartments?

4) The assumption that orphan vesicles fuse homotypically continues to be troubling. You may not have fully understood the concern raised during the initial submission, so let's try again.

Vesicles are normally expected to fuse heterotypically. If a vesicle fails to find a target compartment, why should it then fuse homotypically? Why couldn't a vesicle of one type fuse heterotypically with a vesicle of another type? A priori, such heterotypic vesicle fusion may be more likely than homotypic vesicle fusion given that vesicles normally undergo heterotypic fusion with a target compartment.

The concern is that if homotypic vesicle fusion is programmed into the model as the default fallback option, then the model may be biased toward compartment formation and subsequent maturation.

5) Designating a GTPase that cycles through the cytoplasm as being formally equivalent to a vesicle is confusing. If your formalism treats a vesicle and a reversibly associating peripheral membrane protein as being equivalent, you should consider a term other than "vesicle". Maybe "carrier" would be more generic, and "membrane traffic" could be used rather than "vesicle traffic"?

6) At least some lipids can actually move via nonvesicular as well as vesicular pathways. The discussion of lipids may now be overly complex. The bottom line is that some components can only exchange between compartments via membrane vesicles (e.g., transmembrane proteins), some components could exchange either in vesicles or through the cytoplasm (e.g., certain lipids), and some components probably exchange only through the cytoplasm (e.g., certain GTPases).

7) Relevant to #7 above: does the model take into account the fact that the various components traveling from one particular compartment to another could travel at different times and at different rates? Maybe this point is implicit in the model, but it's hard to tell.

8) I didn't understand the discussion in the Results section about large global structures and shuffling the edges of a network. Is this issue important? If so, it should be explained better. If not, it should be omitted.

[Editors' note: further revisions were requested prior to acceptance, as described below.]

The manuscript has been improved but there are some remaining issues that need to be addressed before acceptance, as outlined below:

This manuscript has been extensively revised and extended, and is now a substantial contribution that will stimulate thinking in the field. I see no benefit in putting it through another round of review because the key concerns have been addressed. But I will ask the authors to address a few very minor comments about the new "Orphan vesicles and homotypic fusion" section.

1) In cells, many compartments fuse homotypically. For clarity, you should state the assumption that compartments cannot fuse heterotypically with one another.

2) The first paragraph in this section is now perhaps more complex than necessary, and is a bit confusing as a result. For example, I have trouble figuring out what this sentence means: "This is rare: in almost all instances we explored, at least some fusion products of orphans were themselves orphans; in the majority of instances even the initial orphans could not fuse with one-another."

3) "one another" is two words.

Please make these changes and submit a final version.

https://doi.org/10.7554/eLife.16231.012

Author response

Our Boolean framework in fact does incorporate cytoplasmic molecules such as Rab GTPases. For brevity we did not focus on this aspect in the original submission, and apologize for giving the impression that we have ignored these key components. To explicitly keep track of such players we can interpret any “vesicles” with only a single nonzero molecular component as a single molecule type moving directly through the cytoplasm. We must then add an explicit label to track the flow of membrane lipids on true vesicles. This is of course optional and a matter of interpretation, since in any case we have only considered a subset of all possible molecules in a vesicle traffic system. It would be interesting to ask what proportion of the molecules of a traffic network are transmembrane type (SNARE-like) and what proportion are membrane-associated (Rab-like). This type of analysis can be done within our framework, and would indeed be interesting to do, but takes us beyond the subject of this submission.

Figure 1—figure supplement 1 discusses an example explicitly including Rab GTPases and their regulators. The text has also been modified to emphasize these non-vesicular transport pathways:

Third paragraph of Results section: “N types of membrane-associated, transmembrane or lumenal molecules”

Sixth paragraph of Results section: “Among active labels the Arf- and Rab-family GTPases […] explicitly assigning a label to membrane lipids.”

Sixth paragraph of Results section: “Though GTPases diversified early in eukaryote evolution […] we do not explicitly distinguish between the Rab- centric and SNARE-centric views.”

First paragraph of Methods section: “Vesicles with a single non-zero label may optionally be interpreted as membrane- associated molecules capable of cytoplasmic non-vesicular transport (Figure 1—figure supplement 1).”

We had analyzed the full set of networks in the original submission, but had only emphasized the key point that cisternal maturation is the single most common type of motif. In this revision we provide much more extensive discussion of the properties of all networks beyond cisternal maturation, and also carry out new analysis. Note that we now discuss all types of networks, including the traditional transport balanced version, as shown in Figures 2B,F. Apart from this we provide several additions.

First, we explain our sampling procedure more carefully (“Sampling homeostatic vesicle traffic networks”). To generate diverse networks, we actually sample by sweeping over parameters corresponding to the number of molecular labels, the number of adaptor/coatomer types, and how permissive vesicles were in selecting cargo and fusion targets. For each parameter combination we get different types of networks, as discussed in Figure 2—figure supplement 1. We can explore how various network properties depend on one another, as we do in Figure 2F–I, and Figure 2—figure supplement 2A–E.

Second, we explicitly separate out the “trivial” networks. In about half our sampled data, the networks end up in a state where each compartment is completely disconnected from all the others. In real cells this would probably correspond to a completely inactive, perhaps dead, cell. Out of 14,809 homeostatic networks, only 8,614 are non-trivial. It is only among the latter that we should look for any structure at all.

Third, we emphasize that our search for network motifs is completely unbiased. In the original submission we had only discussed the three most frequent motifs (present Figure 3).

We now also discuss all 43,700 potential motifs, and the occurrence of the 100 most frequent motifs (Figure 3—figure supplement 1). The main lesson here is the following: there is indeed a great diversity in the structures that we find among our tens of thousands of networks. But half the non-trivial networks (4,024/8,614) contain a maturation chain. The other half contain hundreds of diverse motifs, each occurring infrequently; no single motif is prominent. To emphasize this, in the abstract we now describe the maturation chain as occurring in “the plurality” of traffic networks (borrowing from the political term in which the single largest party wins the vote).

Finally, we emphasize the following: we are not claiming that all vesicle traffic networks contain maturation chains. We did not put this into our framework by hand, and so we naturally see a lot of diversity. However, the maturation chain does occur in about half of all non-trivial networks. This makes it easily “discoverable” by neutral evolutionary search. In the discussion we make the point that even structures that seem likely in complex systems typically require fine-tuning of parameters, whereas cisternal maturation spontaneously arises in half the non-trivial networks.

Figure 2B,C,F discuss the properties of different types of networks in our dataset, and show the parameter ranges where cisternal maturation is likely to occur. Figure 3—figure supplement 1 shows the top 10 network motifs. The text has been modified as follows, discussing the properties of all our networks in more detail:

Abstract: “the plurality of networks contain chains of compartments…

Results section, subsection “Sampling homeostatic vesicle traffic networks”: To systematically explore diverse behaviors […] sampled uniformly over these parameters.”

Results section, subsection “Sampling homeostatic vesicle traffic networks”: “90% had 8 or fewer compartments […]”

Results section, subsection “Cell-like networks and vesicle traffic motifs”: “Cell-like networks are most likely to contain maturation chains at low-to-moderate […]”

Results section, subsection “Cell-like networks and vesicle traffic motifs”: “Nearly half the non-trivial homeostatic networks (4,024/8,614) contained a maturation chain of length one or more. We wondered whether the other half were characterized by other distinct features […]”

Figure 3—figure supplement 1 figure legend: “The 15th most common three-compartment motif, occurring in 344 networks, is the maturation cycle (Figure 3—figure supplement 1). This corresponds to a compartment whose composition oscillates periodically. Cycles of various periods occur in about a quarter (2,407/8,614) of all homeostatic networks.”

Results section, subsection “Cell-like networks and vesicle traffic motifs”: “We next checked if our networks contained any large global structures, beyond the scale of local motifs […]”

First paragraph of Discussion section: “For comparison consider a biological system described by ten parameters” “[…] most types of structures are rare and require fine-tuning of parameters.”

We apologize for not discussing this point in detail in the original submission. The key restrictive assumption we have made is that heterotypic vesicle fusion does not occur. Our Boolean framework can accommodate heterotypic fusion, and it would be interesting to explore the role of such processes further. But it takes us beyond the topic of the present submission. Regarding homotypic fusion, it is also reasonable to ask why we assume all orphan vesicles can homotypically fuse. This is in fact not a restrictive assumption as long as we are only interested in the homeostatic states, as explained in the revised text. We could, if we wish, assume that only certain pre-defined vesicle subsets can undergo homotypic fusion. Once we run to homeostasis, only such orphan vesicles would be present in the final state. If we now explore over all possible vesicle subsets, we get precisely the same set of homeostatic states. Note that the transient period before we approach homeostasis would indeed be affected by this assumption that all orphan vesicles can fuse. We can use the Boolean framework plus additional ingredients involving homotypic or heterotypic fusion to study in detail how a traffic system recovers homeostasis after a perturbation, and this is an interesting future question to ask.

The text has been modified to discuss these issues:

Fourth paragraph of Results section: “Alternatively assuming only a certain subset of vesicles can undergo homotypic fusion (and exploring over all possible subsets) does not change our results: since no state with accumulating un-fused orphan vesicles can be homeostatic, all orphan vesicles in any homeostatic states we find must fall into this subset. Our approach can be extended to allow heterotypic fusion, or to allow vesicles to simultaneously nucleate new compartments and fuse to existing ones. Additional rules are needed to specify when such processes occur, and we do not consider them here.”

4) The treatment of spatiotemporal aspects of membrane traffic raised two issues:

We apologize; the brief description of this issue in the original text was confusing. We have modified this section in the revision after getting feedback from colleagues about clarity.

We have first started the discussion by motivating the background on compartment spatial localization. We have removed the confusing term “virtual stacking” and have explained the motivation of this analysis. It is a speculative analysis which is why we left it to the Discussion section. Briefly: Spatial locations of compartments are caused by many layers of biophysical mechanisms. We were speculating about the potential function of the precise locations. In particular, we explored whether any of the results from the theory of logistic networks (warehouses locations connected by trucks) might apply to cellular vesicle traffic networks. In the efficient logistics context, the goal is to spread out the warehouses as evenly as possible while minimizing the distances travelled by trucks. If we imagine compartments to be warehouses and vesicles to be trucks, what would the optimal spatial organization of compartments look like? There is a simple algorithm which produces this optimal configuration, as described in “Methods: Spatial Optimization”. It involves minimizing a certain “energy function” which measures how uniformly compartments/warehouses are distributed and how far vesicles/trucks must travel. The intuition behind why this energy function works is that it resembles a system of repelling charges and attracting springs, but that is merely for the sake explanation, the optimization procedure is the main point. In our original analysis the text misleadingly seemed to read that the “springs” and “charges” were the actual physical causes of the locations, this is not the case. Of course it is complex biophysical regulation which actually places compartments at precise locations.

Whether these locations in fact do optimize efficient traffic is still an open question. All we have shown is that Golgi stacks are consistent with this hypothesis, but this observation certainly does not prove this hypothesis.

Figure 4 of the main text in the original has been moved to Figure 4—figure supplement 1 of the revision. We have expanded the text where this issue is discussed:

Third paragraph of Discussion section: “the spatial locations of compartments are determined by complex and largely unknown biophysical mechanisms [Yadav & Linstedt, 2011].”

Third paragraph of Discussion section: “We explored the hypothesis that a cell is like an efficient city-wide logistics system, in which no part of a city is too far from a warehouse, and warehouses with more traffic between them are placed closer to one another […]”

Third paragraph of Discussion section: “Measurements with repositioned organelles might be used to test these ideas further [van Bergeijk et al., 2015].”

Methods section, subsection: “Spatial organization”: “We want to distribute the compartments of a vesicle traffic network in such a way that all parts of a cell are close to at least one compartment, while the distance travelled by vesicles between compartments is minimized […]”

These are important questions, and we will provide a detailed answer here. We also discuss these issues more briefly in the revised text. Most, if not all, previous models of vesicle traffic have attempted to do justice to details such as spatial location, compartment size, reaction kinetics, and so on. In fact we have used such approaches ourselves. Our paper [Ramadas & Thattai, 2013] builds on the classic model of Heinrich and Rapoport, using differential equations and dynamical systems approaches to understand how the number of compartments and their connectivity might be encoded in microscopic molecular parameters.

We tried for a long time unsuccessfully to extend these models to arbitrary network topologies: given the number of parameters, it is technically unfeasible to explore parameter space in an unbiased manner. However, we noticed from our earlier results that the topologies of the networks arising from such complex models were very robustly determined by broad aspects of molecular specificity.

Once the topology was set, the quantitative behavior including rates of cargo flow were determined by more detailed kinetic parameters. This is why we developed the Boolean approach described here. If topology is what one is interested in, the Boolean model provides the same set of topologies are more detailed kinetic models.

Once a topology is obtained form the Boolean approach, the kinetic parameters can be included afterwards. We are currently working on precisely this aspect in an independent project: we are developing a broad mathematical method to put back kinetic parameters onto a given network topology. This turns out to be useful not just because of the Boolean prescription described here, but because cell biological experiments often help us determine network topology (which vesicles flow between which compartments) but not often the kinetics. We will be happy to share with you the results of our project when it is ready. However, it goes beyond the topic of the present submission.

We have modified the introductory text to discuss these issues:

Second paragraph of Results section: “We have shown [Ramadas & Thattai, 2013] that the topological features of a vesicle traffic network – the number of compartments and their connectivity – are robustly determined by molecular specificity alone, while quantitative features such as the rate of flow of cargo depend on additional kinetic parameters. Here we are primarily interested in homeostatic network topologies. We therefore formalize the properties of vesicle traffic systems using a Boolean framework […]”

Second paragraph of Results section: “We also assume the cytoplasm is well mixed, and do not consider spatial location.”

Second paragraph of Discussion section: “This shows that spatial organization is not a pre-requisite for maturation, and supports the idea of a well-mixed cytoplasm.”

In particular, the markers used in your simulation reach a steady-state homeostatic distribution, but is it automatically true that all of the other components, such as lipids, will also undergo balanced flows in a given network?

The lipids themselves can be considered as one of the labels in the system. Therefore, if the network is homeostatic, it is balanced in all its markers. However, there is a subtle point that we now provide new analysis to discuss. For each compartment individually, all flows must balance in a homeostatic network. However, is possible that for larger groups of compartments, molecules might flow in but not out (e.g. if two compartments exchange a molecule with one another, but also that molecule is received from a third compartment).

This means that the network is balanced at fast timescales, but on slower timescales this type of molecule will have to be synthesized elsewhere in the system. We now show how often this type of slow synthesis is required, across all the networks in our system. See Figure 2—figure supplement 2E,F.

New text has been added:

Fifth paragraph of Results section: “We can distinguish true vesicles from non-vesicular transport by explicitly assigning a label to membrane lipids […]”

Results section, subsection “Sampling homeostatic vesicle traffic networks”: “In homeostatic networks, molecular loss must be offset by molecular gain at each compartment, and on fast timescales these processes balance out. However, certain compartment groups could receive particular molecules, yet not give them away. When flows are interpreted in terms of continuous fluxes, such molecular sinks imply the need for compensatory synthesis elsewhere on slower timescales. In general, larger networks tended to require synthesis of more types of molecular components (Figure 2—figure supplement 2E,F).”

Does your model require the unrealistic assumption that every compartment generates the same number and size of vesicles per unit time?

We do not make this unrealistic assumption. Our model specifies the types of cargo carried by the vesicles generated by each compartment. It is agnostic about the relative amounts of this cargo, about the size of the vesicles, and about the rates of vesicle production. In particular (see our remarks above), once a network topology is provided from our Boolean model, we can then go into detail to examine the molecular flows (e.g. see the new Figure 2—figure supplement 2F). Each molecule moves in cycles, and the rate of flux of each cycle can be set as an independent kinetic parameter. We have discussed this in the text, as described above.

New text has been added:

Second paragraph of Results section: “Our approach is agnostic to the relative amounts of molecules on each vesicle, the size of vesicles and compartments, and the flux of vesicles between compartments. We also assume the cytoplasm is well mixed, and do not consider spatial location. Once a homeostatic traffic topology is discovered using this Boolean approach, we can add back more detailed kinetic parameters and examine quantitative molecular flows.”

Is it obvious that movement between compartment is fast relative to formation and fusion of vesicles, so that spatial aspects can be neglected?

This is an important point. It is not at all obvious that the spatial configuration of a cell should be neglected. Indeed, it is extremely likely that local concentration effects ensure that vesicles are more likely to find targets closer to the source compartment. We know the cytoplasm does undergo mixing events, partly driven by a dynamic cytoskeleton. However, to our knowledge there is only partial experimental support for the idea of a truly well-mixed cytoplasm.

Our response to this critique is as follows: we are particularly exploring here how far molecular specificities alone can determine the properties of a vesicle traffic system. If these basic ingredients alone are sufficient to generate complex structures, then it is not necessary to invoke spatial organization as an additional input ingredient.

No model is ever complete, the set of ingredients missing in any given model is infinite.

The key question is, do the set of ingredients that are included provide any insight. We hope that our results here cross this bar: that the surprising emergence of cisternal maturation in the absence of spatial organization at least opens up the possibility that maturation is primarily determined by molecular interactions. The recent observation by Glick and colleagues of retrograde vesicle flow in un-stacked Golgi provides some support for this idea.

Figure 2—figure supplement 2E,F discuss these issues. The text has been expanded in several places to indicate that our Boolean model provides a topological “chassis” on top of which kinetic parameters can be included.

Second paragraph of Results section: “Previous mathematical models of vesicle traffic … add back more detailed kinetic parameters and examine quantitative molecular flows.”

Second paragraph of Results section: “We also assume the cytoplasm is well mixed, and do not consider spatial location.”

Results section, subsection: “Sampling homeostatic vesicle traffic networks”: “In homeostatic networks, molecular loss must be offset by molecular gain at each compartment, and on fast timescales these processes balance out … In general, larger networks tended to require synthesis of more types of molecular components (Figure 2—figure supplement 2E,F).”

Third paragraph of Discussion section: “The connectivity of a vesicle traffic network is primarily determined by molecular specificity, while the spatial locations of compartments are determined by complex and largely unknown biophysical mechanisms [Yadav & Linstedt, 2011].”

Second paragraph of Discussion: “This shows that spatial organization is not a pre-requisite for maturation, and supports the idea of a well-mixed cytoplasm.”

We thank the reviewers for this suggestion, which we have taken to heart. We have circulated the daft among our colleagues in cell biology and have incorporated their suggestions on readability and accessibility. One of the main points we heard was that the model seemed too abstract. To remedy this we have added new text describing how to interpret the molecular labels. We have also added additional clarifying material throughout the text.

New text has been added:

Fifth paragraph of Results section: “This Boolean description appears abstract, but the biology is embodied in the interpretation of the molecular labels. …”

We apologize for the brevity of the discussion in our original submission. This was primarily due to the space constraints of the eLife “Short Reports” format.

We have now added an entire paragraph providing background on vesicle traffic models and motivating the use of the Boolean approach. We also direct the reader to our companion manuscript [Mani & Thattai, 2016] which provides an accessible non-mathematical introduction to our Boolean approach.

New text has been added:

Second paragraph of Results section: “Previous mathematical analyses of vesicle traffic have considered such details as compartment size, location and chemical composition, and used ordinary or partial differential equations to study vesicle and compartment dynamics […]”

We agree this point was confusing in the original submission, and apologize for this. We have significantly expanded our discussion here. To be clear, our analysis proceeded in 3 steps. (1) We explicitly looked for cases of compartmental maturation. (2) We next looked at 3-compartment motifs in an unbiased manner, as discussed above. (3) We finally looked for structures larger than 3-compartment motifs. For step (3), the key to finding larger structures is to shuffle a network while keeping local properties fixed. If this shuffling does not change e.g. the frequency of occurrence of various 3-compartment motifs, then we can be confident that there are no larger repeated structures present. Indeed, this is what we see.

The text has been expanded to discuss this point:

Results section, subsection: “Cell-like networks and vesicle traffic motifs”: “We next checked if our networks contained any large global structures, beyond the scale of local motifs. If such structures are present, they should be disrupted when we shuffle the edges of a network while keeping local incoming and outgoing edges of individual compartments fixed.”

This is an observation we have made from our data, it is not an ingredient we put into the model. The caveat is that we are only modeling a network with a small number of molecular components, and in particular we have focused on the active labels, not passive cargo. In terms of the active labels, imagine there are various Golgi-resident markers constantly treadmilling within the Golgi itself.

What we find is that the very first compartment has fewer active labels than the very last compartment, and this difference causes a gradient within the maturation chain. In a real cell much of the content of the Golgi will be secretory cargo destined for one-way outward flow. These one-way secretions are not considered in our homeostatic framework. Once such passive secretory cargo are introduced, it is less likely that the clear pattern we have observed will remain. In any event, given these various caveats we have opted to remove this particular figure from our revision, and mentioned this result in the text, with the caveat:

Results section, subsection: “Cell-like networks and vesicle traffic motifs”: “The first compartment of a maturation chain tended to be compositionally simpler than its successors (at least in terms of the active labels considered here) due to the treadmilling molecules present on the latter.”

Regarding the maturation chains, one reviewer wrote: "However, these striking observations are not clearly interpretable. The authors should provide much more detail on the characteristics of these chains, on the dynamics of their development, and on the number of the chains that possess these particularly complex features. They should also describe the networks that do not contain maturation chains, which actually represent the majority of the outcomes. They should discuss which parameters lead to realistic maturation chains, and which preclude maturation..… What is interesting to me is not the fact that they observe maturation as this outcome is expected, but the fact that the maturation networks are so complex and so similar to the real ones, and so frequent. Again they should thoroughly describe the maturation chains, the alternative outcomes and the conditions where they obtain. Without this description we cannot judge the value of the simulations."

We agree with the reviewer that there is much more to explore in this diverse dataset. Indeed, we hope the approach we have put forward here is used to uncover further reproducible aspects of these networks. In many ways it is the variability and not the common features that might be important: e.g. during cell differentiation, or during pathogenic re-wiring of a host network. However, all these issues take us beyond the present topic. We will pursue them further.

As described above, in our revision we have devoted a great deal of the text to discussing the properties of all 14,809 homeostatic networks in our dataset, not just the ones with maturation chains. In particular, 6,195 are trivial (all compartments are disconnected from one another). Of the remaining 8,614, about half contain maturation chains. We have now provided a lot of information on the half that do not contain maturation chains, in terms of the top 10 motifs (Figure 3—figure supplement 1) as well as other general features (Figure 2 and Figure 2—figure supplement 2). We have shown which parameter ranges produce maturation chains (Figure 2 and Figure 2—figure supplement 2). We have also closed the Results section with a clear statement of our central finding, about the precise number of chains that display all the diagnostic features of cisternal maturation.

Figure 2 and its supplements discuss these issues in detail. New text has been added:

Results section, subsection: “Cell-like networks and vesicle traffic motifs “: “This diverse sample of networks represents a neutral null hypothesis, which can be contrasted with hypotheses about the selection of various vesicle traffic structures. If some structure of interest frequently occurs in our sample, it suggests such a structure might arise non-adaptively.”

Results section, subsection: “Retrograde vesicles emerge spontaneously, driving cisternal maturation”: “Distilling these observations, here is our central result: across 8,614 non-trivial homeostatic networks, we find 3,111 maturation chains which precisely match all three diagnostic features of the cisternal maturation model (Figure 4).”

This is an interesting point, we thank the reviewer for suggesting it. We have now included a discussion early eukaryote evolution in the introduction:

Fifth paragraph of Results section: “Though GTPases diversified early in eukaryote evolution [Elias et al., 2012], it is plausible that the primordial vesicle traffic system relied on a more basic toolkit of lipidbased compartment identity and SNARE-mediated fusion specificity [Dey et al., 2016].”

[Editors' note: further revisions were requested prior to acceptance, as described below.]

We have significantly revised the manuscript to emphasize spatiotemporal considerations. The stochastic model (Box) unpacks various mechanistic assumptions in detail, e.g. the cooperative recruitment of vesicles, or the effect of compartment size on vesicle fusion. We have also shown quantitative parametric conditions under which we expect maturation to arise. The detailed stochastic dynamics compare very favorably with the live-cell dynamics of compartmental maturation observed by Losev et al. (Nature, 2006). Throughout the text we have updated the presentation to explain the motivation behind our Boolean framework, and highlighted connections with detailed mechanistic or molecular issues.

We appreciate this question, which many other readers will very likely also have. We have therefore addressed it in full. We have presented (Box) a full microscopic model based on fundamental stochastic processes of vesicle budding and fusion, simulated using Gillespie’s exact stochastic simulation algorithm. The mean-field limit of this simulation produces a set of approximate ordinary differential equations. We have presented the parametric conditions under which this set of equations produces a limit-cycle oscillation, of which the Boolean dynamics are a discrete approximation. This discussion provides readers intuition about the meaning of our abstract vesicle traffic graphs, about the mechanistic underpinnings of our approach, about the timescales involved, etc.

We have clarified the discussion of our propensity parameters. These reflect chemical rather than spatial properties. In brief: we imagine that different species might encode different numbers of e.g. adaptors, Arfs, Rabs, and SNARES. Moreoever, these proteins will also have different chemical interaction specificities. A priori we don’t know whether adaptors tend to select only a small proportion or a large proportion of available cargo. Similarly, we don’t know whether SNARE-SNARE pairings are rather promiscuous, or very specific. The propensities g and f are varied so we can sample systems of varying degrees of cargo-adaptor specificity and SNARE-SNARE specificity.

Results section, subsection: “Sampling homeostatic vesicle traffic networks”: “These parameters capture genetically-encoded properties such as the number, and the degree of interaction specificity, of cargo, adaptors, Arf and Rab GTPases, and SNAREs.”

Discussion section, subsection: “Sampling homeostatic vesicle traffic networks”: “All these parameters are ultimately genetically determined: N and A represent the number of protein types involved, while g and f summarize their interaction properties. For example, g depends on cargo-adaptor specificity, and f depends on SNARE-SNARE specificity.”

4) The assumption that orphan vesicles fuse homotypically continues to be troubling. You may not have fully understood the concern raised during the initial submission, so let's try again.

The concern is that if homotypic vesicle fusion is programmed into the model as the default fallback option, then the model may be biased toward compartment formation and subsequent maturation.

We have performed new simulations including the possibility of heterotypic fusion of vesicles governed by the same fusion matrix that governs vesicle-compartment fusion. We find that in the majority of instances this does not significantly deplete the set of orphan vesicles, if at all. Moreover, the fusion matrix itself cannot be the mechanism by which small vesicles fuse to form large compartments de novo, in a homeostatic state. The reason is, the desired compartment would already be present, and therefore the vesicle would already fuse to the compartment and not appear as an orphan. We now discuss at multiple places our treatment of homotypic fusion, to clarify our assumptions. We examined the legitimate concern about biasing the model toward having maturation chains. In fact, the bulk of our homeostatic states have very little homotypic fusion. Over a thousand states have no homotypic fusion and still have maturation cycles. We hope this addresses the concern.

Fifth paragraph of Results section: New section: “Orphan vesicles and homotypic fusion.”

Fifth paragraph of Results section: “We explored allowing orphan vesicles to fuse heterotypically according to the same specificity rules that governed vesicle-compartment fusion.”

Seventh paragraph of Results section: “In practice we find that a small dose of homotypic fusion is often sufficient to achieve homeostasis: over 80% of our homeostatic networks require two or fewer types of homotypically fusing vesicles.”

Results section, subsection: “Cell-like networks and vesicle traffic motifs”: “Out of 3,173 non-trivial networks with no homotypic fusion, over a third contained cycles of maturing compartments (1,053/3,173).”

We apologize, we have clarified the text to avoid any confusion. We now refer to “vesicles”, or to “non-vesicular carriers”. When there is any scope for ambiguity, we refer to “transport vesicles”. We also clarify the many scales of membrane-bound structures in our model.

Fourth paragraph of Results section: “By explicitly assigning a label to membrane lipids, the Boolean framework can accommodate both vesicular and non-vesicular pathways.”

Results section, subsection: “Orphan vesicles and homotypic fusion”: “We assume a hierarchy of membrane-bound structures: compartments are large; transport vesicles are small; vesicles can fuse to compartments but compartments cannot fuse with one-another.”

We have simplified the text as suggested. We have removed the comments about early eukaryotic evolution since they are peripheral to the main discussion.

We hope the extensive new discussion of stochastic and differential equation models, and the connection of such models with our Boolean framework, clarifies this point.

We have omitted the discussion about shuffling edges from the main text. We have replaced it with a brief comment that might be relevant to a subset of readers, and directed them to a new reference [Albert & Barabasi, 2002] for further details.

Results section, subsection “Cell-like networks and vesicle traffic motifs”: “This suggests that vesicle traffic networks might usefully be described by the random graph generation approaches that have provided insights into the structure of metabolic, neural, and ecological networks [Albert & Barabási, 2002] (Methods: Randomly shuffled vesicle traffic networks).”

[Editors' note: further revisions were requested prior to acceptance, as described below.]

1) In cells, many compartments fuse homotypically. For clarity, you should state the assumption that compartments cannot fuse heterotypically with one another.

We have stated our explicit assumption that compartments cannot fuse heterotypically.

We have simplified the first paragraph of the section “Orphan vesicles and homotypic fusion” as suggested.

3) "one another" is two words.

We have fixed all incorrect instances of the phrase “one another”.

https://doi.org/10.7554/eLife.16231.013

Article and author information

Author details

Somya Mani

Simons Centre for the Study of Living Machines, National Centre for Biological Sciences, Tata Institute of Fundamental Research, Bangalore, India

Contribution
SM, Acquisition of data, Analysis and interpretation of data

Competing interests
The authors declare that no competing interests exist.
Mukund Thattai

Simons Centre for the Study of Living Machines, National Centre for Biological Sciences, Tata Institute of Fundamental Research, Bangalore, India

Contribution
MT, Conception and design, Analysis and interpretation of data, Drafting or revising the article

For correspondence
thattai@ncbs.res.in

Competing interests
The authors declare that no competing interests exist.

"This ORCID iD identifies the author of this article:" 0000-0002-2558-6517

Funding

Wellcome Trust-DBT India Alliance (Intermediate Fellowship 500103/Z/09/Z)

Mukund Thattai

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

MT was supported in part by a Wellcome Trust-DBT India Alliance Intermediate Fellowship (500103/Z/09/Z). We thank Joel Dacks, Anjali Jaiman, Ramya Purkanti, and Madan Rao for useful discussions.

Reviewing Editor

Benjamin S Glick, The University of Chicago, United States

Publication history

Received: March 20, 2016
Accepted: August 18, 2016
Accepted Manuscript published: August 19, 2016 (version 1)
Version of Record published: September 6, 2016 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.