Resolving coiled shapes reveals new reorientation behaviors in C. elegans
Figures
Inverting posture analysis to generate worm images.
(A–E) We previously showed that the space of C. elegans body postures is low-dimensional. (A) For a set of images of a freely moving worm, (B) we find the centerline of the body using image thinning (black point indicates the head). (C) At equidistant points along the centerline, we measure the direction of the tangent . After subtracting , this gives a description of the worm’s shape that is intrinsic to the worm itself. (D) Principal Component Analysis reveals that only four eigenvectors of the shape covariance matrix are needed to account for of the variance in . (E) Hence, any body shape can be decomposed as a linear combination of postural ‘eigenworms’. (F) Alternatively, we can think of any body posture as a point in a low-dimensional ‘posture space’, spanned by the eigenworms (gray). Forward crawling is then represented by clockwise progression along a circular trajectory in the plane (blue oval, body wave phase angle ). (G) For any point in this space, we can easily calculate the shape of the backbone. A series of filled circles with radii representing the worm’s thickness, are used to draw an image of the worm’s body (H), inverting the original postural analysis to generate an image. For self-overlapping shapes, image thinning (H, magenta) does not produce an accurate reconstruction of the posture (G, red).

Tracking coiled shapes by searching for image matches in posture space.
Top: tracking algorithm sequence. (A) For each movie frame and reconstituted worm image for posture , we apply two metrics, one based on the shape of the boundary (left), and one based on a coarse-grained pixel density matrix (right). (B) An error function based on these two shape metrics generates a fitness landscape (schematically shown). The position of the global minimum of corresponds to the tracking solution; if a frame is ambiguous, multiple minima may be present. (C) For non-crossed body postures, a simple image thinning algorithm suffices to obtain time series of the modes (blue line, schematically shown). For crossed frames, we use the procedure outlined in A–B. Due to the inherent ambiguity of such images, multiple solutions are generally found for each frame (light gray points). Using the filtering algorithm described in the Materials and methods, we identify the correct solutions (dark gray points). The resulting smooth trajectory (magenta, dotted line) forms the full tracking solution. (D) Sample tracking results (bottom, white background), contrasted with original images (top, gray background), for a turning sequence. Bottom: the inverse algorithm accurately tracks both simple and coiled worm shapes with small error. (E) Histogram of tracking errors for non–self-overlapping worm shapes, quantified as the Euclidean distance between the tangent angle vector from our algorithm, and found by image thinning (magenta). For scale, the error due to dimensionality reduction to five postural eigenmodes is shown in black. We also show the Euclidean distance between in consecutive frames, representing the confidence in due to the finite time resolution of the movie (gray). Even for an extreme value of (gray arrow), backbones from the ‘classic’ algorithm (top) and our algorithm (bottom) are nearly indistinguishable by eye (inset). (F) Tracking error in eigenmode values for the first four modes. For uncrossed worm shapes (yellow/light), our algorithm shows negligible tracking errors. For a smaller set of crossed frames, we compare to a manually found solution (blue/dark). For scale, we show reconstituted images for worms with a single nonzero mode value of ; these ‘error worms’ are essentially flat.
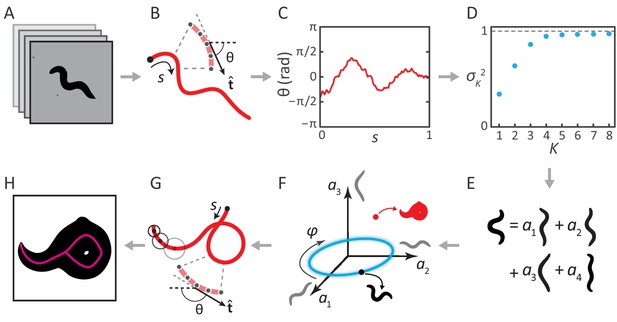
The eigenworms derived from the fully-tracked data show only minor changes compared to those computed without crossings.
We show the original eigenworms (blue) (Stephens et al., 2008); as well as those derived from the current foraging data, but without crossings (red); and those derived from the fully-tracked foraging data (yellow). While the eigenworm shapes are largely similar, and in all cases four modes capture over of the postural variance, the third (turning) eigenmode individually accounts for more variance in the fully-tracked data, as expected given its primary role in deep turns.

Tracking coiled postures and reorientation in the escape response.
(A) Schematic overview (Donnelly et al., 2013) with worm body shapes extracted from tracking data: i forward locomotion and exploratory head motions; ii infrared laser stimulus; iii reversal phase; iv omega turn; v resumption of forward locomotion in the opposite direction. (B) Trajectory through posture space. indicates direction of increasing body wave phase angle, and color encodes time, with blue for t = 0 and red at t = 30 s. The worm’s reorienting coiling behavior is evident as a large excursion along the third mode, starting at the red arrow. (C) The same trajectory as in B, in terms of the body wave phase angle and the postural modes . The heat shock occurs at t = 10 s (pink bar). The omega turn is initiated by a head swing, as seen in , followed by a large pulse in , and is linked to a ‘re-reversal’, a return to forward movement. (D) An important feature of the escape response is the change in the worm’s overall orientation, and we apply our algorithm to track this reorientation for each response segment. While turning accounts for much of the reorientation, the full response distribution is shaped by significant contributions from all three segments. In particular, the small but biased reorientations of the reversal and post-turn segments originate in the fluctuations outside the turn (see the time series in C and also Figure 3—figure supplement 1). This is consistent with the release and presence of the monoamine tyramine during the entire response. (E) The precision of the escape response is evident in the trial-mean reorientation where we find for the full response and if we exclude (four) worms that only make small dorsal reorientations. Notably, the mean reorientation in the reversal and post-turn segments closely cancel, suggesting a correction mechanism at the level of the average response. In the inset to (D, Omega turn), we also show the distribution of amplitudes, which is peaked near coiled shapes in which the worm barely touches.
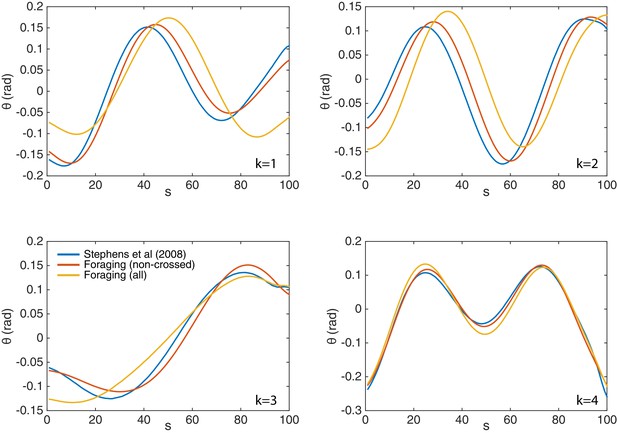
Bias in the turning mode , and resulting reorientation, occurs during all epochs of the escape response.
From previous work on the interpretation of the postural eigenmodes, we know that the third eigenmode (an overall bending of the worm) is linked to reorientation of the worm (Stephens et al., 2008, 2010). We therefore tested if any asymmetry in the fluctuations of during the reversal phase could be linked to the observed reorientations. Such asymmetry is also visible in Figure 3C as a baseline shift of the third mode during the reversal. (Top, left & right) The mean value, versus the resulting orientation change, during the reversal and post-omega behaviors, respectively. The orientation change is strongly correlated with the mean value. (Top, middle) Peak amplitude of the peak corresponding to the omega turn, versus the resulting orientation change. (Bottom, left & right) Histogram of mean values, during the reversal phase and post-omega phase, respectively, showing similarly asymmetric distributions. (Bottom, middle) Histogram of peak amplitudes during the omega turn. We also show a reconstituted worm image for an value of 15, for which the worm is barely self-occluded.

Unraveling coiled shapes during foraging reveals two distinct ventrally-biased classes of large-amplitude turns.
(A) (left) Probability of the amplitude of all local extrema in the time series of the third postural eigenmode . Colors represent the sign of the amplitude, and hence the dorsal (gray) or ventral (blue) direction of the resulting turn. (A) (right) As previously, with all negative amplitudes now plotted as positive. The peaked excess in the distribution for large ventral bends corresponds to ‘classic’ (omega) shapes, and previously undescribed, deeper (delta) turns. Insets in A (left) show reconstructed worm shapes for the indicated amplitudes. (B) Stills from a movie of a worm making a classical omega turn (left, yellow), and a deep delta turn (right, blue). The head is marked with a red dot; dashed lines indicate postures determined from our inverse tracking algorithm. The dynamics of delta turns are largely similar to omega turns, differing primarily in the amplitude of the bending mode , and the overall time to complete the maneuver (see Figure 4—figure supplement 1). (C) Histogram of orientation change () due to ventral omega turns (yellow/light) and ventral delta turns (blue/dark). Ventral reorientations are accomplished through omega turns. To reorient to the dorsal side, however, C. elegans employs delta turns, which ‘over-turn’ through the ventral side. (D) Average turning rate during the tracking experiment. Ventral omega and delta turns are temporally independent, suggesting a separate triggering mechanism, but occur with approximately equal rates that adapt similarly with time spent away from food, a simple strategy to avoid any dorsal-ventral navigational bias.
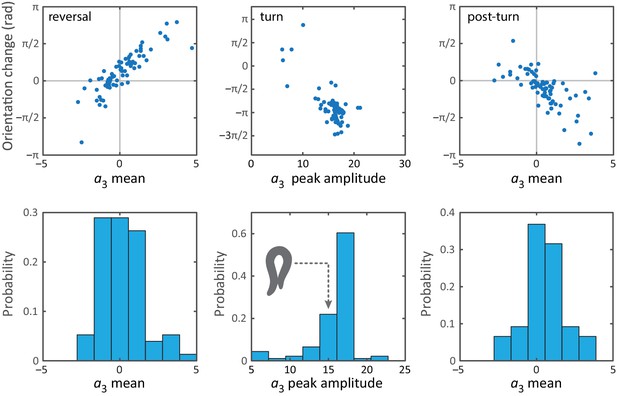
Omega and delta turns follow similar kinematics; while visually quite distinct, the primary difference is the amplitude of the curvature pulse .
(A) Typical time series for the postural eigenmodes during a deep delta turn. is the body wave phase angle, as defined in Figure 1F. Shaded area indicates the delta turn, as defined in the Materials and methods. (B) Average eigenmode time series during a delta turn (blue, N = 348). Gray lines indicate SD. For comparison, the average escape response omega turn is also shown (red dotted line). Time has been normalized with respect to the total length of the turn: (mean ± SD) for delta turns, for escape-response omega turns.
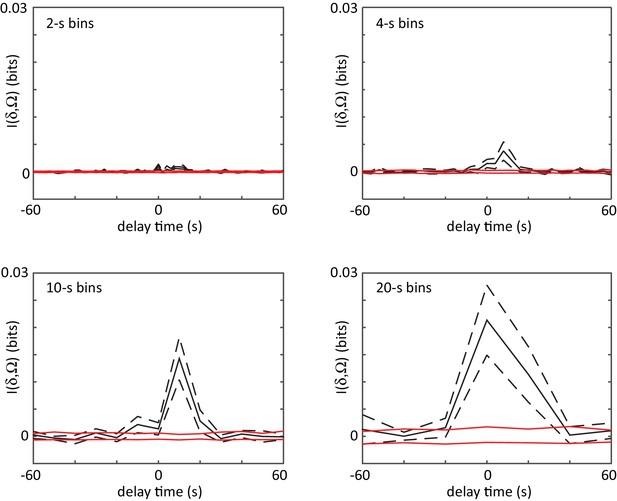
The shifted mutual information between delta turn and omega turn time series.
Events are localized by the large amplitude peaks in the curvature mode , and bins from 2 to 20 s are used to convert these timings into a binary event series. The mutual information is very small in all cases (for scale, the entropy of either event series is ∼1 bit) indicating that the two different turn types occur independently. Dashes are estimated errors from finite sampling. Red lines denote the mutual information between shuffled time series, which would be zero in the infinite data limit.
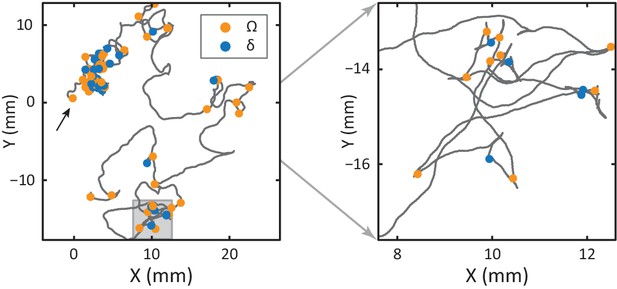
(left) Location of one of the 12 tracked worms over the course of a 35-min tracking experiment (off-food), starting at (0, 0) (black arrow).
Omega turns (orange) and delta turns (blue) are highlighted. (right) An enlargement of the area marked in gray. While both turns occur more frequently at early times, there is no correlated pattern, as consistent with their independence.
Videos
Tracking results for the escape response.
Left images are data, while on the right, there are reconstructed images from our tracking algorithm.
Tracking results for a complex, spontaneous coil.
Left images are data, while on the right, there are reconstructed images from our tracking algorithm.
The dynamics of the escape response in the space of the first three eigenworms.
On the right, we show the full body posture, which turns red at the moment of the thermal stimulus. On the left are the dynamics in mode space. The large-amplitude omega turn is visible as a ‘figure-8’ trajectory. Note that, even during the turn, the body wave is progressing. In general, turning behavior is a superposition of the body wave and curvature dynamics.





