Discovering sparse transcription factor codes for cell states and state transitions during development
Figures
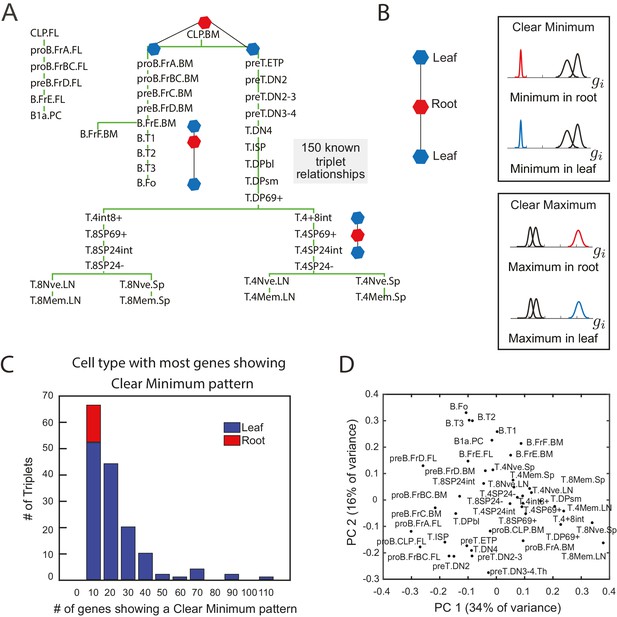
The clear minimum pattern is robustly detected in leaf cell types throughout triplet lineages in B- and T-cell development.
(A) Developmental lineage tree showing relationships among 41 cell types in B- and T-cell development (Heng et al., 2008). Three triplets – the minimal subset of the tree from which relative distances can be studied – are denoted, each including an intermediate root cell type (red) and terminal leaf cell types (blue). 150 triplets among all sets of three cell types within five steps on the lineage tree were extracted for pattern-detection. (B) For each triplet of cell types (left), each gene’s expression level can have the clear minimum pattern in either the root or the leaves (right, top box) where the distribution of gene expression levels in one cell type is well separated from the other two (left, p<0.005 in a two sample t-test); clear maximum pattern (left, bottom) in the root or the leaves: the gene has a clear maximum in one of the cell types (right, p<0.005 in a two sample t-test). (C) A histogram of the number of genes showing the clear minimum pattern among the 150 triplets with known developmental topology. Triplets in which the root has the most genes showing the pattern shown in red; triplets in which one of the leaves has the most genes showing the pattern shown in blue. None of the triplets with more than 10 genes showing the pattern have the most genes with a clear minimum in the root (no red in any histogram bar except for the left most)(D) Principal component analysis of microarray data from the cell types in B- and T- cell development does not reflect known lineage relationships in (A).
-
Figure 1—source data 1
Triplets used for pattern detection.
Sheet 1: The 150 related triplets used for pattern detection are listed, with the root cell type of the triplet in the first column and the two leaves in second and third columns. Cell type names follow (Heng et al., 2008). For each triplet are listed the number of genes with a clear minimum in each cell type and a clear maximum in each cell type (t-test p-value < 0.005). Also listed for each triplet are the length of the triplet, whether the triplet is a lineage progression or a cell fate decision, whether the triplet contains a terminal node, and the entropy in the clear minimum pattern and clear maximum pattern. Sheet 2: The 100 unrelated triplets are listed; cell type names follow (Heng et al., 2008). For each triplet are listed the number of genes with a clear minimum in each cell type and a clear maximum in each cell type (t-test p-value < 0.005) and the entropy in the clear minimum pattern and clear maximum pattern.
- https://doi.org/10.7554/eLife.20488.003
-
Figure 1—source data 2
List of mouse transcription factors.
The list of human transcription factors used to cluster and infer lineages for the hematopoietic and intestinal development trees. The list was adapted from (Thomson et al., 2011).
- https://doi.org/10.7554/eLife.20488.004
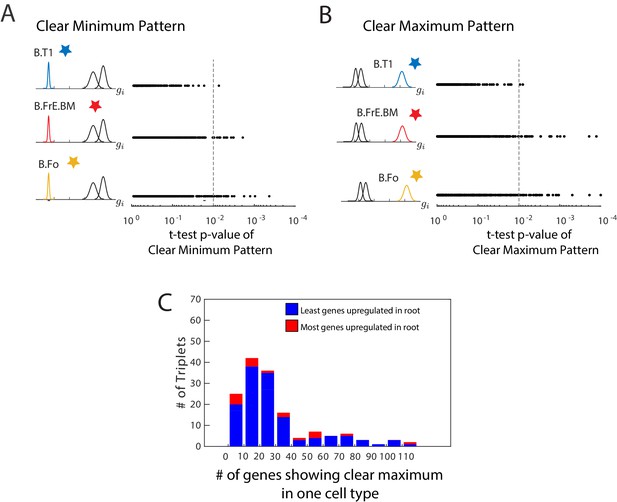
Clear minimum and clear maximum patterns.
(A, B) We used a two-distribution t-test to quantify the likelihood of a gene (each denoted by a single dot) showing either the clear minimum (A) or clear maximum pattern (B).We show the p-value from this t-test and the cell type in which the gene shows differential expression. The p-value cutoff is used to identify genes which show these patterns with high significance (dotted line). In this particular triplet, there are fewer genes with a clear minimum and with a clear maximum in the root of the triplet (B.T1) than in either leaf, as seen by fewer genes in the first row to the right of the cutoff. (C) A histogram of the number of genes showing the clear maximum pattern among the 150 triplets with known developmental topology. Triplets in which the root as the most genes showing the pattern are shown in blue. The clear maximum pattern does not show strong predictive power over the lineage relationships between triplets, and even when a large number of genes exhibit the pattern, the majority often reach their maximum in a leaf.

The clear minimum pattern is observed across different types of triplets.
(A) Histogram of the number of genes showing the clear minimum pattern evaluated over all 25,194 genes among the 150 triplets with known developmental topology. Triplets in which the root has the most genes showing the pattern shown in red; triplets in which one of the leaves has the most genes showing the pattern shown in blue. (B) Histogram of the number of genes showing the clear minimum pattern evaluated over transcription factors, using FDR-adjusted p-values, among the 150 triplets with known developmental topology. Triplets in which the root has the most genes showing the pattern shown in red; triplets in which one of the leaves has the most genes showing the pattern shown in blue. (C) Number of genes showing the clear minimum pattern in the three cell types of each triplet. The number of genes in the root cell type of each triplet is indicated in blue; the number of genes in the two leaves are represented in yellow and red. The triplets are ordered according to the total number of genes showing the pattern in the triplet. (D–F) A histogram of the number of genes showing the clear minimum pattern. As in Figure 1C, triplets in which the root has the most genes showing the pattern shown in red; triplets in which one of the leaves has the most genes showing the pattern shown in blue. Triplets are shaded according to different characteristics: length of triplet (D), presence of terminal node in triplet (E), cell-fate decision or lineage progression (F).

Distinction between related and unrelated triplets.
(A) Plot, for triplets of related and unrelated cell types, of the entropy S of the fraction of genes downregulated in the 3 cell types (x-axis) and the total number of genes showing a minimum in any triplet for 100 unrelated and 150 related triplets (Figure 1—source data 1). Related triplets are shown in blue or red, depending on whether the cell type with the most genes showing the downregulated pattern is the root (red) or a leaf (blue), as in Figure 1C. Unrelated triplets are shown in green. For each triplet, we computed the entropy , where fi is the fraction of the genes which reach a clear minimum in cell type i = A, B, C. Jitter added to triplets with S = 0 for clarity. (B) Histogram of the maximum inferred probability of a non-null topology in the Bayesian algorithm for the set of related triplets (top) and the set of unrelated triplets (bottom). (C) Receiver operating characteristic (ROC) curve for the probability of a non-null topology (B) for binary classification of the related and unrelated triplets. The area under the curve (AUC) is 0.96.
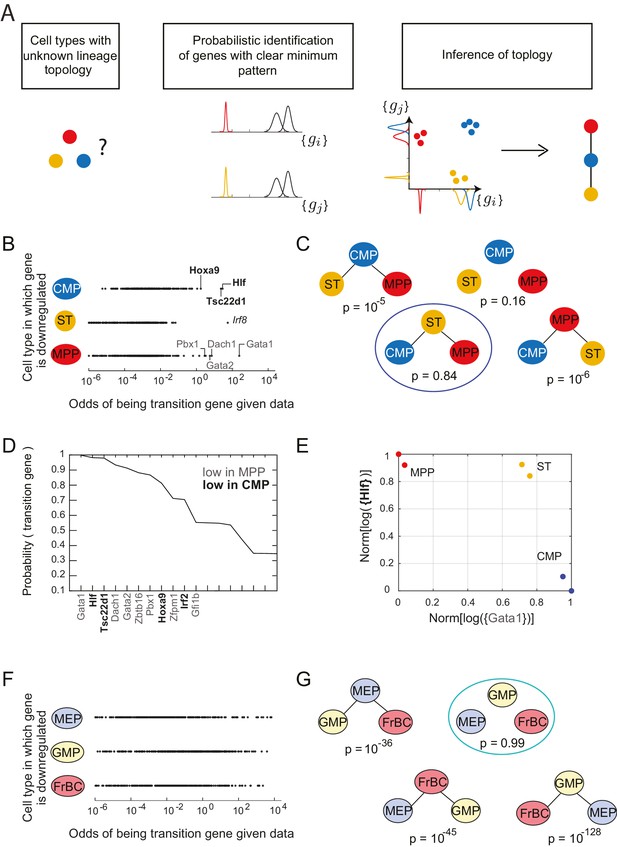
Identification of topology and transition genes (showing clear minimum pattern) for each triplet of cell types.
(A) Schematic for the statistical inference of lineage topology for 3 cell types. Genes with a clear minimum pattern indicate which cell types that are not the root (see Figure 1C) and hence allow inference of the topological relationship. (B) Dot plot (each dot representing a gene) of the cell type that is most likely to have the minimum mean expression of each gene among CMP, ST and MPP as a function of the odds of that gene being a transition gene. Each gene votes against the topology whose root has the minimum mean among the three cell types, and this vote is weighted by the odds that the gene is a transition gene (Equation 1). Two groups of genes, labeled by their names, have high odds of being transition genes and thus cast a strong vote against CMP or MPP being the root.(C) The computed probability of the topology given gene expression data indicates 0.84 probability that ST is the intermediate type.(D) The plot of the probabilities of genes being transition genes for triplet ST/MPP/CMP, given gene expression data and that the topology is MPP – ST – CMP. The names of the 10 genes with the highest probability of being transition genes are shown. Probabilities are calculated assuming the prior odds = 0.05 (see main text). There are two classes of transition genes: one for which gene expression in CMP is greater than expression in MPP (regular font), and another for which gene expression in MPP is greater than expression in CMP (bold font).(E) Plot of the replicates of ST, MPP and CMP in the gene-expression space of the two classes of transition genes (with probability > 0.8). Plotted on each axis is the mean normalized log expression level of the transition genes in the class, each class is denoted in curly brackets by the name of the transition gene with the highest probability.(F) Dot plot for triplet MEP/GMP/FrBC of the cell type that is most likely to have the minimum mean expression as a function of the odds of that gene being a transition gene.(G) The computed probability of the topology given gene expression data is the null hypothesis (p=0.99).
-
Figure 2—source data 1
Early hematopoietic cell types considered.
Listed for each early hematopoietic progenitor whose name is abbreviated in this paper are the Immunological Genome Project descriptor for the cell type, its common name and phenotype, its age and location, and the number of replicates in the data set.
- https://doi.org/10.7554/eLife.20488.009
-
Figure 2—source data 2
Probabilities of topologies for triplets of hematopoietic cell types.
Listed are, for each triplet of cell types, the probabilities of the four topologies for prior odds ; the number of topologies that reach probability for some value of between 10−6 and 102; the non-null topology that has the highest probability over the range of prior odds (if the null topology is the most likely topology for the entire range of prior odds, the topology is marked ‘null’); and the value of highest probability over the range of prior odds; the correct topology and triplet length in the traditional model; and the correct topology and triplet length in the Adolfsson model.
- https://doi.org/10.7554/eLife.20488.010
-
Figure 2—source data 3
Probabilities of transition and marker genes for the hematopoietic lineage tree.
Listed are, for crucial triplets along the lineage tree, the 200 genes with the highest probabilities of belonging to the two transition gene classes and the root marker class, and their associated probabilities.
- https://doi.org/10.7554/eLife.20488.011
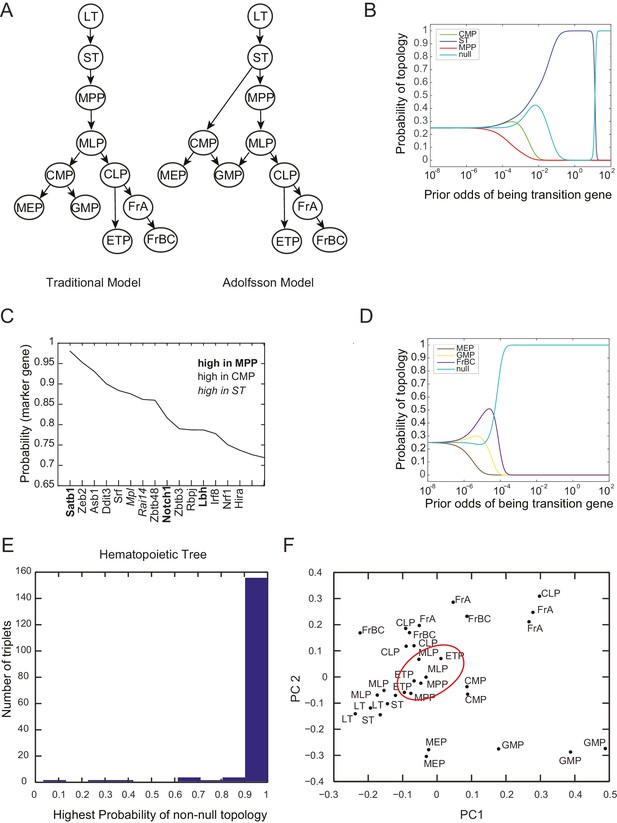
Probability of topology depends on prior odds.
(A) Two models of the hierarchy of early hematopoietic progenitors, both built based on prospective isolation of lineage restricted progenitors, include (left) the traditional model, in which the first split strictly separates myeloid and lymphoid lineages (Akashi et al., 2000; Kondo et al., 1997; Reya et al., 2001) and (right) an alternative hierarchy proposed by Adolfsson and colleagues, in which lymphoid progenitors subsequent to the first split retain some myeloid potential (Adolfsson et al., 2005). (B) The inferred probability of different topological configurations as a function of the prior odds of genes being transition genes. At low values of the prior odds, very few genes are given substantial votes in the inference procedure. The topology MPP-ST-CMP has high probability for a range of prior odds. (C) Genes with high probability of being marker genes for MPP (bold), CMP (plaintext), or ST (italics). (D) The triplet MEP, GMP, FrBC shows no significant probability of a non-null topology for a wide range of prior odds. In this case, our inference method makes no claim as to the topological configuration based on the gene expression evidence provided. (E) Histogram of the maximum inferred probability of a non-null topology for the 165 triplets of hematopoietic progenitors. (F) Projections of the early hematopoietic progenitors along first two principal components. (PC1: 30%; PC2: 17%). Each point represents a different replicate. Note the proximity between ETP and MPP samples (red circle), which does not reflect either of the lineage models shown in (A).
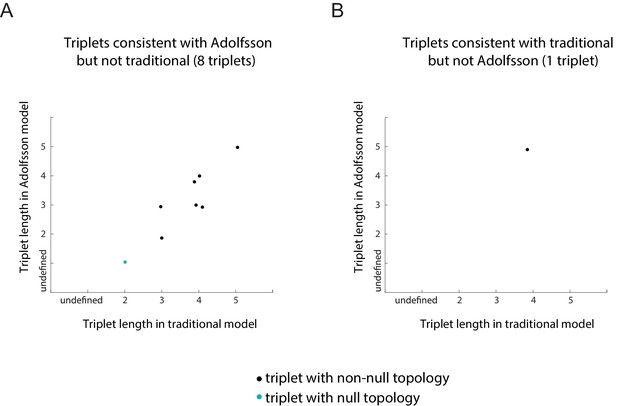
Plots of the length of the triplets distinguishing the traditional model and in the Adolfsson model.
Separate plots are shown for triplets whose inferred topology is consistent with only the Adolfsson model (A) and the traditional model (B) Triplets whose inferred topology is null are shown in turquoise; those whose inferred topology is non-null are shown in black. Jitter was added to the points for clarity.
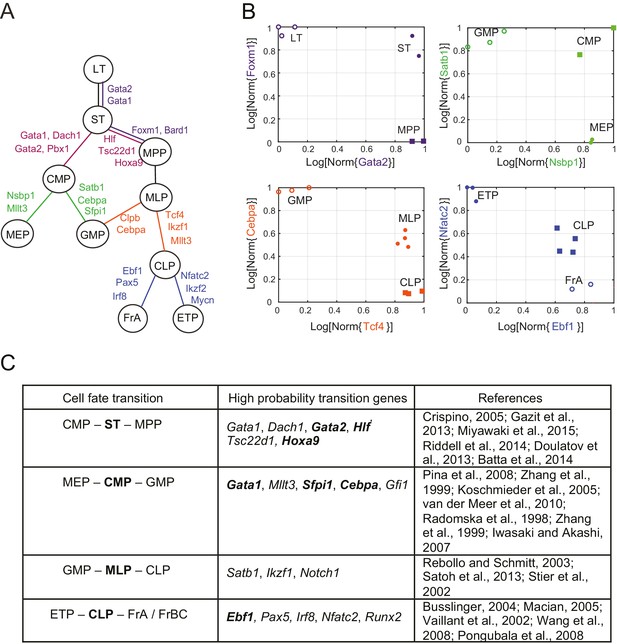
Reconstruction of lineage tree and key transition gene for early hematopoiesis.
(A) Final lineage tree, recapitulating the inferred triplet topologies, with top inferred transition genes indicated along cell fate decisions. (B) Plot of the replicates of different cell types in the gene-expression space of the transition gene classes (probability > 0.8) for 4 cell-fate transitions along the inferred lineage tree in (A). Plotted on each axis is the mean normalized log expression level of the transition genes in the class. The axis labels and data points are color-coded according to the colors in (A). (C) Table with selected transition genes for early hematopoietic cell-fate transitions, along with references to published validations of their functional role. Genes known to be effective for reprogramming are shown in bold.
-
Figure 3—source data 1
Marker genes for early hematopoiesis.
Table with selected marker genes for early hematopoietic cell types, along with references to published validations of their functional role. Genes known to be effective for reprogramming are shown in bold.
- https://doi.org/10.7554/eLife.20488.015
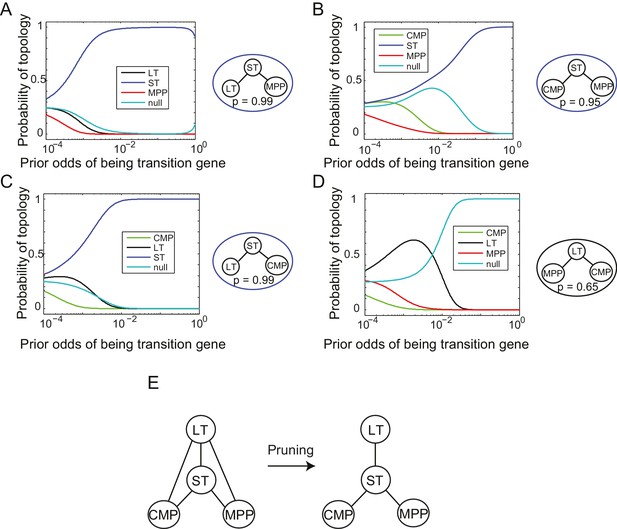
Reconstruction of lineage tree from individual triplets.
(A–D) Probability of all topological configurations for a triplet as a function of prior odds for all triplets between 4 cell types: MPP, ST, LT, and CMP. (A) The LT-ST-MPP triplet, with p=0.99. (B) The CMP-ST-MPP triplet, with p=0.95. (C) The LT-ST-CMP triplet, with p=0.99. (D) The MPP-LT-CMP triplet, with p=0.65. Note that the next highest topology here is the null topology. (E) These four triplets can be combined to infer a simple relationship between all four cell types that is consistent with the topological restrictions inferred from each high probability triplet.

Inferred lineage tree and transition genes for intestinal development.
(A) Inferred lineage tree from intestinal single cell data taken from (Grün et al., 2015).Cluster identifications were taken from RaceID2 (Grün et al., 2016), and a similar tree was inferred from StemID ([Grün et al., 2016], not shown). Using 1369 transcription factors, we inferred these lineage relationships between all cell clusters with more than 10 cells per cluster. The tree differs from that in (Grün et al., 2016) only in the progression from C2 – C8 – C4, while we infer the triplet C8 – C2 – C4 with p>0.99, both of which are consistent with literature (van der Flier and Clevers, 2009), and await experimental validation. (B) High-probability transition genes with known relevance in intestinal homeostasis or differentiation taken from the top 20 transition genes for each lineage progression.
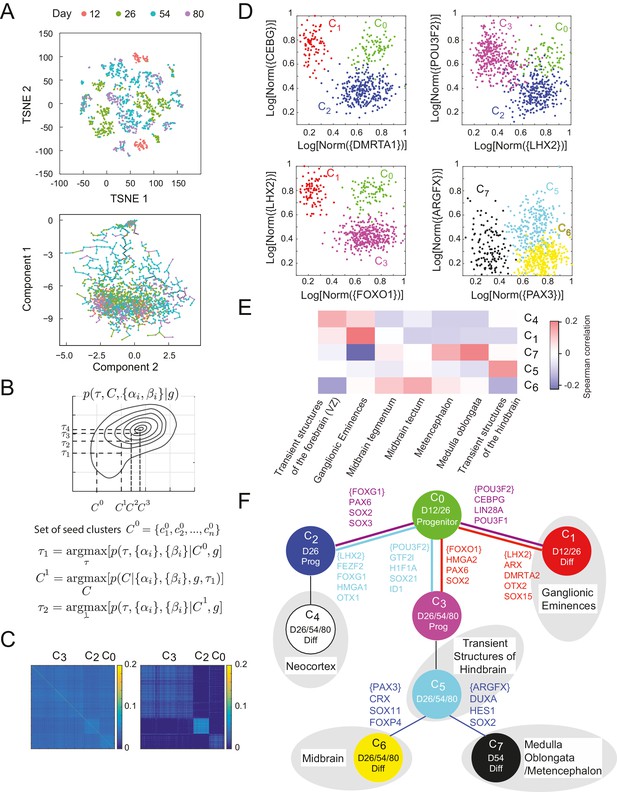
Inference of lineage tree and key transitions genes using single cell expression data from in vitro differentiated developing human brain.
(A) RNA-seq data from single cells collected at days 12, 26, 54, and 80 from a human brain in vitro differentiation protocol (Yao et al., 2017) were analyzed using a variety of existing methods. Partitioning single-cells into cell types through non-linear dimensionality reduction using t-SNE (top) depends on the perplexity parameter (set here to 5, see Figure 4 – Figure Supplement 1A-B) and does not allow for mechanistic understanding. Independent component analysis of all transcription factors with Monocle (bottom) does not show clear structure and could not inform reconstruction of lineage relationships. (B) Maximization algorithm to determine most likely cluster identities , sets of transitions , marker genes () and transition genes (), given single-cell gene expression data . Starting from a seed clustering scheme iterative maximization of the conditional probabilities and converges to most likely set (C) Cell-cell covariance matrix between cells using only the associated high probability marker and transition genes show the final cluster assignments and (right) in contrast to using all transcription factors (left). (D) Selected high probability triplets of clusters plotted in the axes defined by two sets of transition gene classes for each triplet. (top right, ), plotted in transition gene class {CEBPG} also including POU3F1, POU3F2, NR2F1, NR2F2, ARX, LIN28A, TOX3, ZBTB20, PROX1 and SOX15, and class {DMRTA1} also including HES1, HES5, FOXG1, PAX6, HMGA2, SOX2, SOX3, SOX9, SOX6, SP8, OTX2, TGIF, ID4, TCF7L2, and TCFL1. (top left, ), plotted in transition gene class {LHX2} also including FEZF2, FOXG1, HMGA1, SP8, OTX1, SOX11, GLI3, SIX3, ETV5, and class {POU3F2} also including GTF2I, HIF1A, ID1, ID3, PROX1, SALL1, SOX21, TCF12, TRPS1, ZHX2. (bottom left, ), plotted in transition gene class {FOXO1} also including HMGA2, PAX6, and SOX2, and class {LHX2} also including DMRTA2, HMGA1, ARX, LIN28A, OTX2, LITAF, NANOG, POU3F1, SOX15. (bottom right, ), plotted in transition gene class {PAX3} also including CRX, SOX11, EBF2, FOXP4, ASCL1, FOXO3, and SIX3, and class {ARGFX} also including DUXA, HES1, NFIB, PPARA, SOX2, SOX7, and SOX9. (E) Correlations between differentiated cell clusters (Figure 4 – Figure Supplement 4D) and bulk population samples from brain regions (in vivo developmental human data) (Miller et al., 2014). Neuronal cell types can be identified with specific spatial regions of the brain to interpret the topology of the lineage tree. Expression signatures of SOX2+ cell types and were dominated by pluripotency factors, and are not shown. (F) Inferred lineage tree for brain development. Genes associated with neocortical development, and mid-/hind-brain progenitors, and specific neuronal cell types are identified as high probability transition genes and are corroborated by mapping information from in vivo data. Clusters color-coded similarly to (D). D12/26/54/80 labels indicate time of collection of cells within each cell type. Prog refers to SOX2+ cells, Diff refers to SOX2-/DCX+ cells (Figure 4—figure supplement 1C–D).
-
Figure 4—source data 1
Final cluster identities of single cells from in vitro cortical differentiation.
Cells were assigned to a cluster based on an iterative clustering procedure. Their final cluster assignments are shown here. Cell types 8–11 contained bulk brain control cells, and non-neuronal cells which were excluded from the analysis.
- https://doi.org/10.7554/eLife.20488.020
-
Figure 4—source data 2
Probabilities of topologies for triplets of single-cell clusters.
Listed are, for each triplet of clusters, the probability of a given topology and the root of the inferred topology. ‘0’ refers to the null topology. Triplets with p>0.6 were used to construct the lineage tree.
- https://doi.org/10.7554/eLife.20488.021
-
Figure 4—source data 3
Probabilities of Transition and Marker Genes for the Human Brain Developmental Lineage Tree.
Listed are, for crucial triplets along the lineage tree, the genes with the p>0.8 of belonging to the two transition gene classes and the root marker class, and their associated probabilities.
- https://doi.org/10.7554/eLife.20488.022
-
Figure 4—source data 4
Human Brain Development SmartSeq2 Census.
Further detail can be found Materials and methods and in Yao et al. (2017) (Supplemental Information).
- https://doi.org/10.7554/eLife.20488.023
-
Figure 4—source data 5
List of Human Transcription Factors.
List of human transcription factors used to cluster and infer lineages for the cortical differentiation tree. List was adapted from (Ben-Porath et al., 2008).
- https://doi.org/10.7554/eLife.20488.024
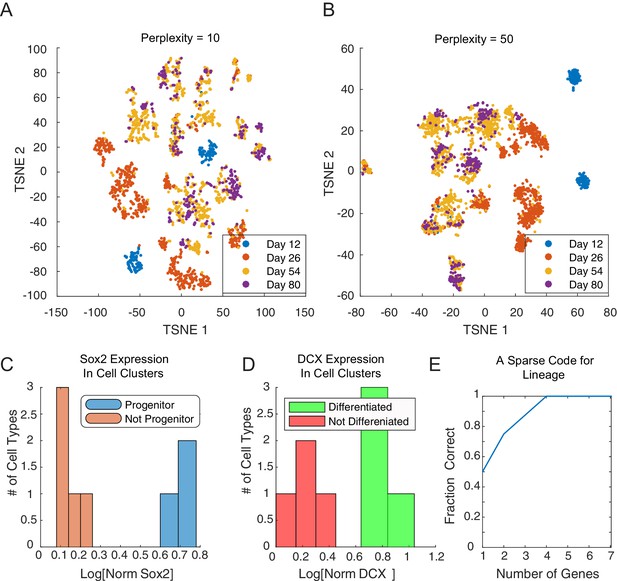
Cluster identity and sparse coding in neuronal differentiation.
(A–B) t-SNE of developing neuronal cells displays seemingly different number of cell types depending on the perplexity parameter.(C) SOX2 expression clearly falls into bimodal distribution. Cell types with high levels of SOX2 (blue, and ) are labeled progenitor cell populations. (D) DCX expression in final clusters is also bimodal, and cell types with high expression (green, and ) are labeled differentiated (post-mitotic) neurons. (E) We assembled 20 triplets that were inferred to be non-null, and had a maximal distance between leaf nodes of less than 5. Amongst these triplets, we attempted to infer the correct topology using a minimal subset of genes. Restricting the inference to the N genes per triplet with the greatest odds ratio of being transition genes, the tree can be reconstructed accurately for any N ≥ 4.
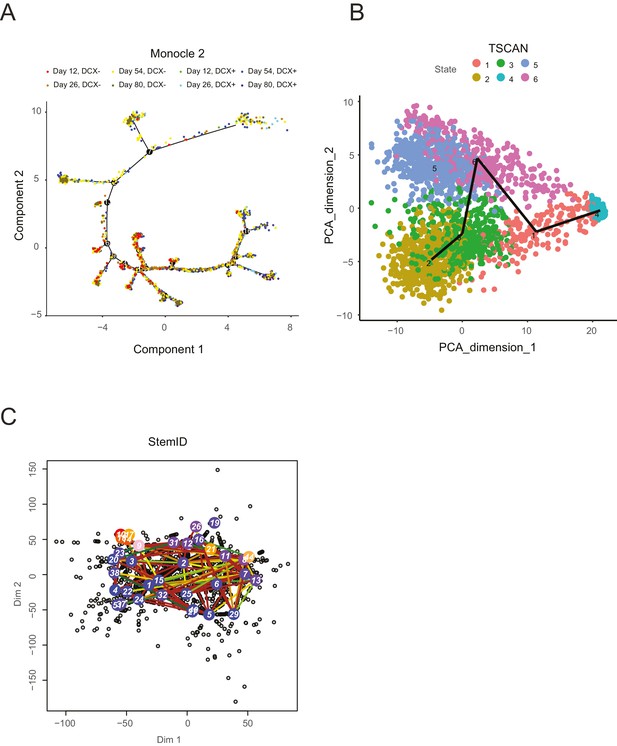
A selection of recent lineage-determination methods for single cell transcriptomic analysis applied to an in vitro neuronal differentiation data set (Yao et al., 2017).
Each of these methods was run with multiple sets of parameters in an attempt to optimize the lineage inference; however, it is possible that an unexplored parameter regime might yield more interpretable results, although it is unclear which parameters these might be. (A) Monocle2 (Trapnell et al., 2014) shows a complex tree with clear progression and multiple branches, but does not separate progenitor cells (DCX- cells) from neurons (DCX+ cells): progenitor cells are known to give rise to neurons, whereas neurons are post-mitotic and do not give rise to progenitors, in contradiction with certain portions of the tree. In addition, portions of the tree are in conflict with the general time point information specifying when cells were collected (Yao et al., 2017). (B) TSCAN (Ji and Ji, 2016) shows separation of DCX- and DCX+ cells along PC dimension 2 (note that cells are not labeled by DCX expression in this plot), but fails to capture structure among the differentiated neurons, particularly a fore-/hind-brain split. (C). StemID (Grün et al., 2016) produces a complex lineage that is not directly interpretable, and no clear separation of progenitors from neurons or forebrain-like from mid/hindbrain-like neurons is apparent.
Videos
Tree-building process for early hematopoietic lineage
Animation of the triplet assembly and pruning process for reconstructing the early hematopoietic lineage. For illustrative purposes, triplets (with p>0.6) are successively selected at random (in practice, the assembly and pruning process was performed on all triplets simultaneously; the resulting tree does not depend on the order in which the triplets are selected). The nodes of the current triplet are highlighted in yellow; if a topology is recognized for the triplet, the root is shown in green and the leaves in yellow, and the triplet edges are shown in magenta. If adding the triplet causes another triplet to be pruned, the soon-to-be-pruned (i.e. offending) edge is highlighted in red. The resulting pruned graph is then shown before adding the next triplet. As more triplets are considered, more edges between nodes are added and then pruned, leading to the final tree.





