Sloppy morphological tuning in identified neurons of the crustacean stomatogastric ganglion
- Brandeis University, United States
Figures
Figure 1 with 4 supplements
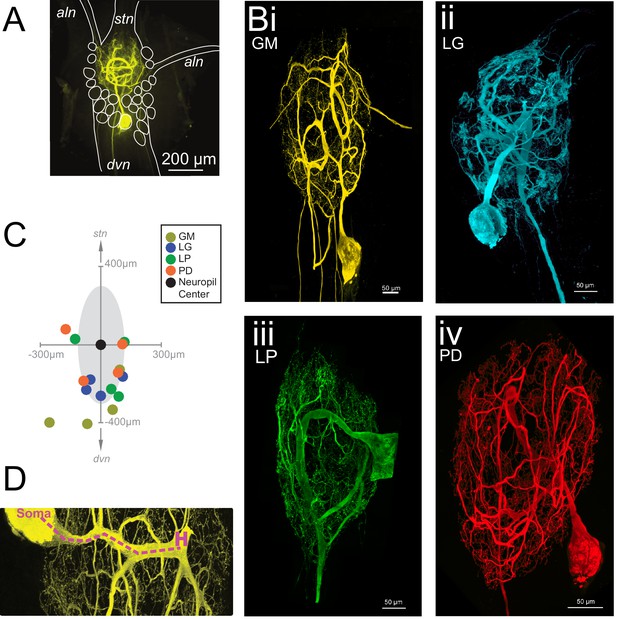
Macroscopic features of four identified neurons of the stomatogastric ganglion.
Each neuron has a primary neurite that ramifies throughout the neuropil and sends one or more axons to peripheral muscles or ganglia via the anterior lateral (aln) or dorsal ventricular (dvn) nerves. (A) Schematic of a gastric mill (GM) neuronal dye-fill as situated in the intact ganglion and the aln, dvn, and stomatogastric nerve (stn). Other cell bodies are outlined in white. (B) Maximum-intensity projections of four Lucifer yellow dye-filled STG neurons. The GM neuron (i) has multiple axons that exit the neuropil bilaterally via the alns, and posteriorly via the dvn. The lateral gastric (LG, ii), lateral pyloric (LP, iii), and pyloric dilator (PD, iv) neurons, respectively, each project only one axon that leaves the neuropil via the dvn. (C) Locations of identified somata across different preparations. Within each preparation, positions were normalized to the ganglion center-of-mass (at origin) and oriented with the stomatogastric nerve (stn) at the top and dorsal ventral nerve (dvn) at the bottom (as described in Materials and methods). (D) Image of neuronal dye-fill (yellow) with path (purple dashed line) from soma to the first multi-furcation, or ‘hand-like’ structure (H).
Figure 1—figure supplement 1
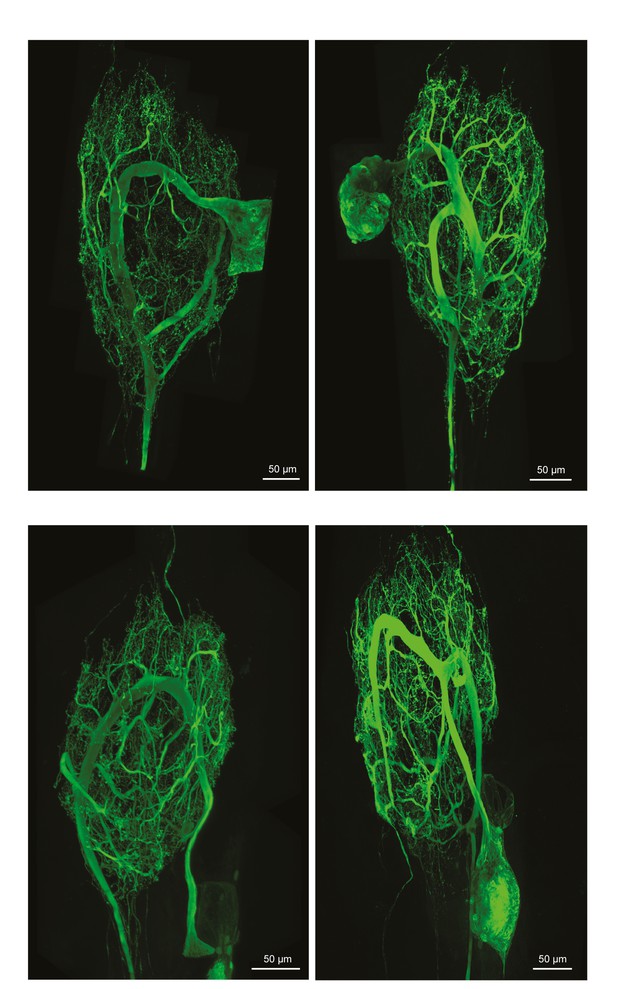
Fluorescent dye-fills of identified lateral pyloric (LP) neurons.
Following physiological identification, Lucifer yellow dye-fills were amplified immunohistochemically and secondarily labeled with an Alexa Fluor 488 fluorophore (Molecular Probes); all images were collected at 63x magnification utilizing a Leica SP5 CLEM confocal microscope (as described in Materials and methods). This figure shows the maximum projections of the complete confocal image stacks of the four LP neurons used in this study. LP neurons have single axons projecting posteriorly to the dorsal ventral nerve (dvn).
Figure 1—figure supplement 2
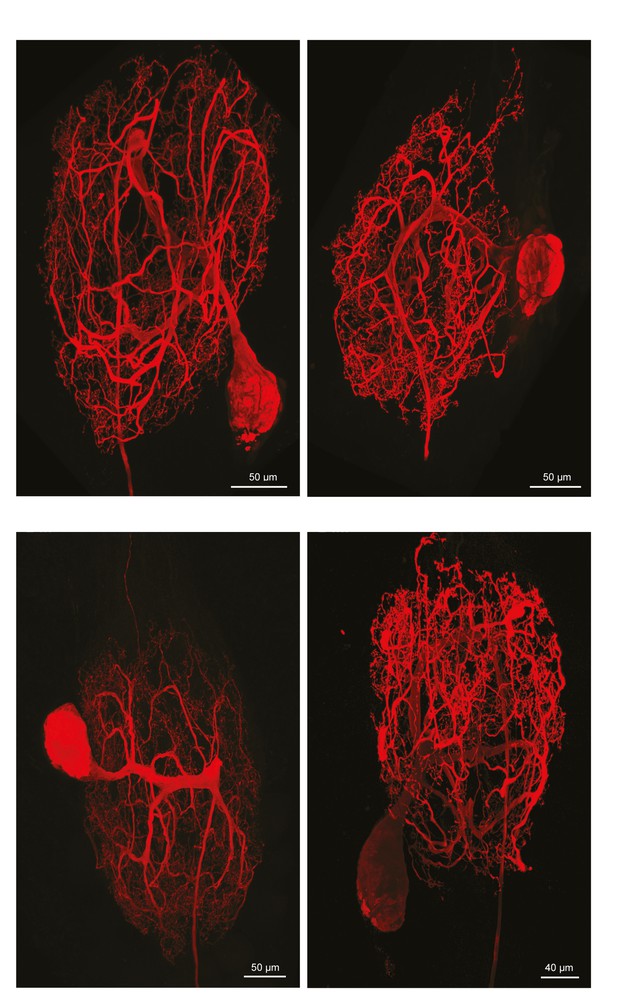
Fluorescent dye-fills of identified pyloric dilator (PD) neurons.
Following physiological identification, Lucifer yellow dye-fills were amplified immunohistochemically and secondarily labeled with an Alexa Fluor 488 fluorophore (Molecular Probes); all images were collected at 63x magnification utilizing a Leica SP5 CLEM confocal microscope (as described in Materials and methods). This figure shows the maximum projections of the complete confocal image stacks of the four PD neurons used in this study. PD neurons have single axons projecting posteriorly to the dorsal ventral nerve (dvn).
Figure 1—figure supplement 3
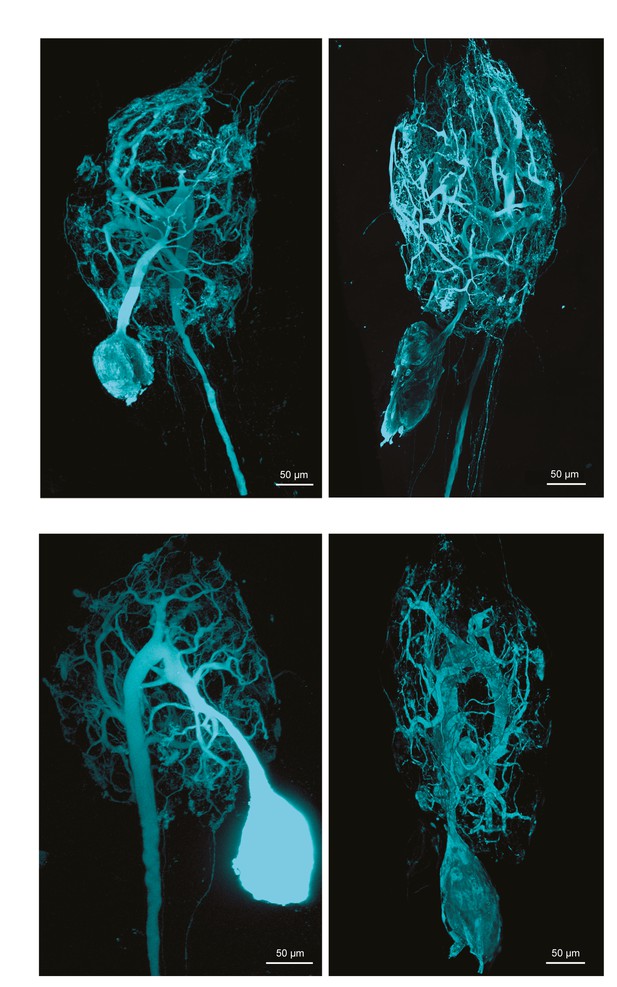
Fluorescent dye-fills of identified lateral gastric (LG) neurons.
Following physiological identification, Lucifer yellow dye-fills were amplified immunohistochemically and secondarily labeled with an Alexa Fluor 488 fluorophore (Molecular Probes); all images were collected at 63x magnification utilizing a Leica SP5 CLEM confocal microscope (as described in Materials and methods). This figure shows the maximum projections of the complete confocal image stacks of the four LG neurons used in this study. LG neurons have single axons projecting posteriorly to the dvn.
Figure 1—figure supplement 4
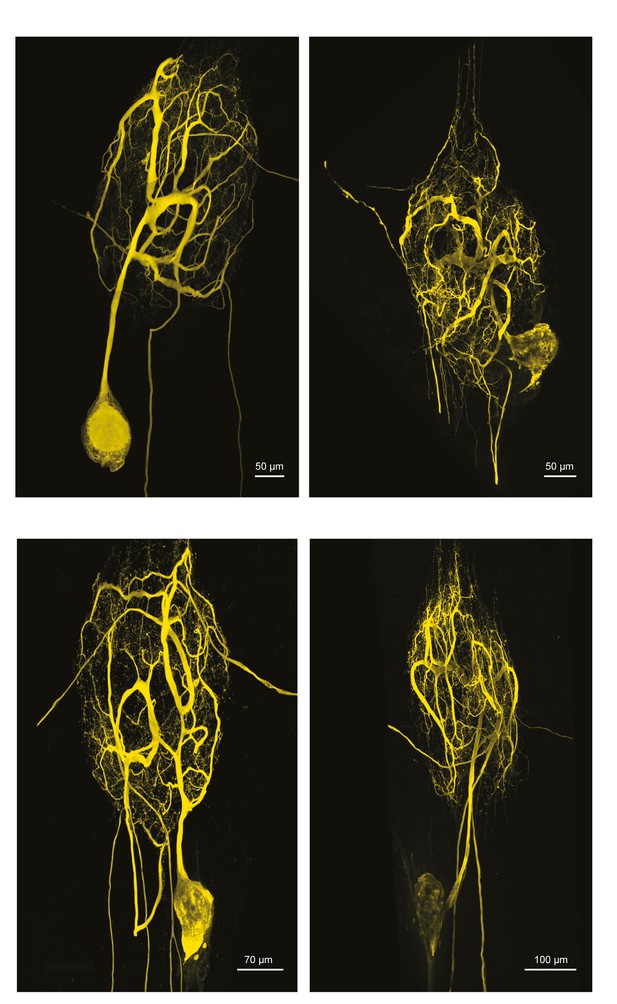
Fluorescent dye-fills of identified gastric mill (GM) neurons.
Following physiological identification, Lucifer yellow dye-fills were amplified immunohistochemically and secondarily labeled with an Alexa Fluor 488 fluorophore (Molecular Probes); all images were collected at 63x magnification utilizing a Leica SP5 CLEM confocal microscope (as described in Materials and methods). This figure shows the maximum projections of the complete confocal image stacks of the four GM neurons used in this study. GM neurons have multiple axons projecting to both the dvn and one or both of the anterior lateral nerves (aln; which exit the ganglion on either side).
Figure 2
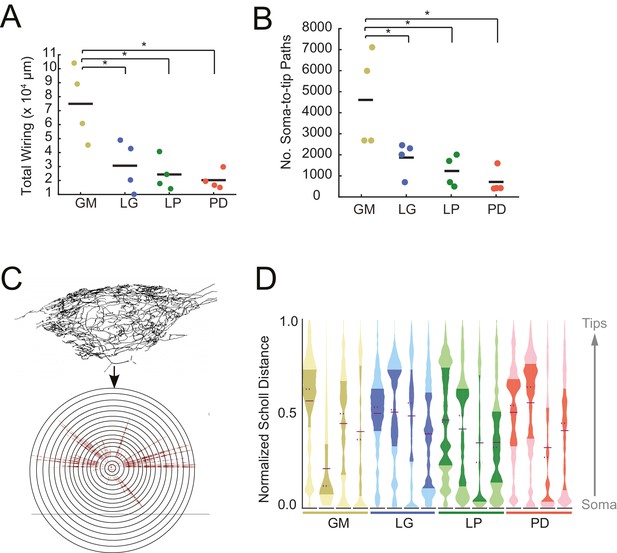
STG neurons have expansive and highly-branched neurite trees.
Total wiring lengths, soma-to-tip neurite path lengths, and Sholl intersections were calculated from three-dimensional skeletal reconstructions generated in KNOSSOS from high-resolution confocal image stacks of Lucifer yellow neuronal dye-fills. (A) Total wiring, excluding axons, was greater than 10,000 µm across all neurons (N = 16; pooled mean ± SD = 37515 ± 27498 µm). GM neurons had greater total wiring than LG, LP, and PD neurons (ANOVA; [F(3,12)=8.34, p=0.0029]; Tukey HSD). (B) Mean soma-to-tip neurite paths varied across neurons but were greater in GM neurons than the other three neuron types (ANOVA; [F(3,12)=7.14, p=0.0052]; Tukey HSD). (C) For each neuron, in order to count the number of Sholl intersections as a function of distance from the soma, we first linearized the neurite paths of the three-dimensional structure (top) relative to the soma. This can be thought of as simply stretching the neurite paths radially from the soma (bottom). The number of neurites per concentric sphere intersection (or Sholl intersections) were quantified as a function of distance from the soma. (D) Sholl intersection violin plots for each neuron. Across neurons, Sholl intersections or neurite densities (counts, normalized to maximum within each neuron, on x-axis) vary with distance from the soma (y-axis, also normalized to the range of neurite path lengths within each neuron; see Materials and methods).
Figure 3
Variable spatial density profiles within and across neuron types.
Spatial density profiles were generated using Gaussian kernel density estimation in the x and y dimensions. This calculation generated a probability distribution function for the points composing each skeletal reconstruction. The black-red-white color map is scaled within each neuron (see Materials and methods) and represents relative neurite density.White values indicate areas of high neurite density and black values indicate areas of low neurite density. White scale bars = 100 µm; black circles indicate somata locations. Each plot is oriented such that the stn is projecting upward and the dvn is projecting downward (as indicated).
Figure 4
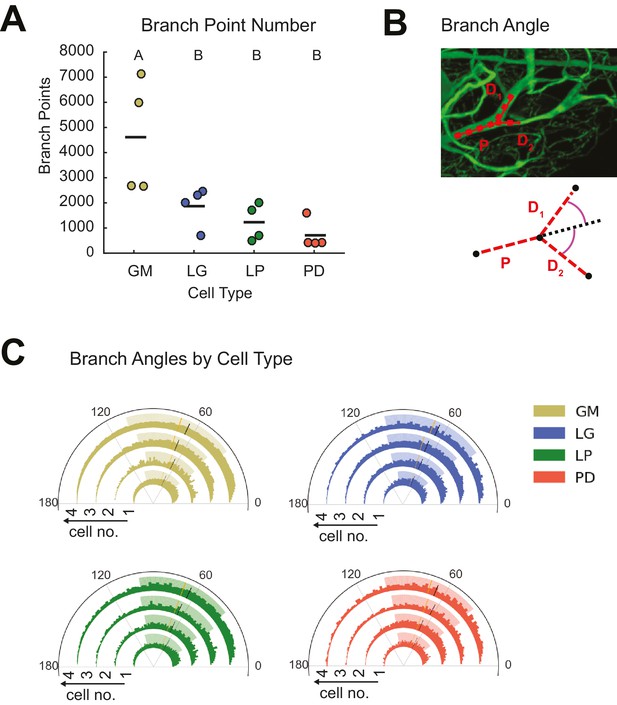
STG neurons present variable branch point numbers and angles.
Branch points numbers and angles were extracted from three-dimensional skeletal reconstructions generated in KNOSSOS from high-resolution confocal image stacks of Lucifer yellow neuronal dye-fills. (A) Branch point numbers were highly variable across neuron types and GM neurons presented higher branch point numbers than other cell types (letters are indicative of ANOVA results; [F(3,12)=7.12, p = 0.0053]; Tukey HSD). (B) Angles were calculated at bifurcating branch points as the angle (purple) between a given daughter branch (D1 or D2) and the hypothetical continuation of the parent (P) branch (dashed line). (C) Branch angle histograms show a wide range of branch point geometries within single neurons. Sets of four concentric histograms show the branch angle distributions of four neurons of a given neuron type (indicated by color in key on right). Solid lines indicate means, dashed lines indicate medians. Shaded ranges of histograms are indicative of the 25–75% confidence interval. There were no measurable statistical differences across individual neurons or neuron types).
Figure 5
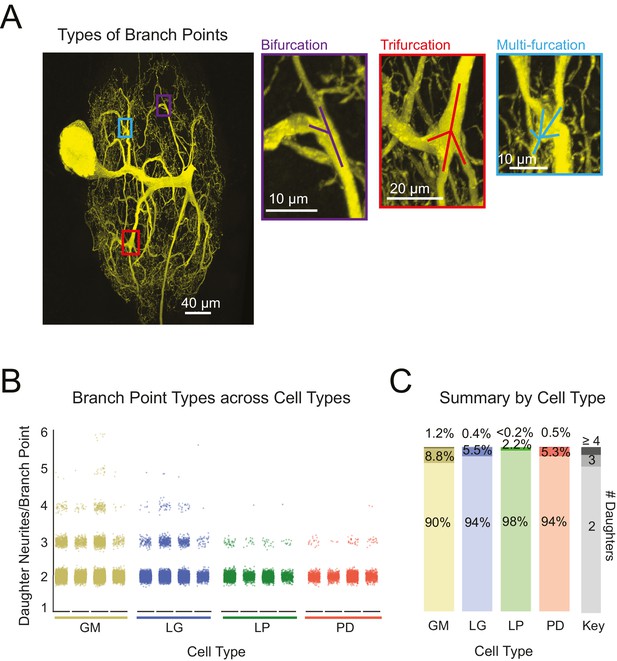
Variable branch point geometries in STG neurons.
Branch point types were detected in three-dimensional skeletal reconstructions generated in KNOSSOS from high-resolution confocal image stacks of Lucifer yellow neuronal dye-fills. (A) Examples of branch point types (right) are indicated as corresponding boxes (color-coded) in a single neuronal dye-fill (left). (B) Scatter plots show the number of daughter branches per branch point (or branch point type, where 2 = bifurcation, 3 = trifurcation, and >4 indicates a multi-furcation) for every branch point in the skeletal structure of an individual neuron (n = 4 for each neuron type, indicated on x-axis). (C) Stacked bars summarize the percentage of branch points that are bifurcations (# daughter branches = 2), trifurcations (# daughter branches = 3), and multi-furcations (# daughter branches ≥ 3), as indicated by gray-shaded key (right). The landscape of branch point types was relatively similar across cell types, wherein multi-furcations accounted for ~10% or less of the branch points within each neuron. Nonetheless, unconventional tri- and multi-furcating branch points were observed in all neurons characterized in this study. Neuron types (n = 4 of each) are color-coded throughout figure: gold = GM neuron, blue = LG neuron, green = LP neuron, red = PD neuron.
Figure 6
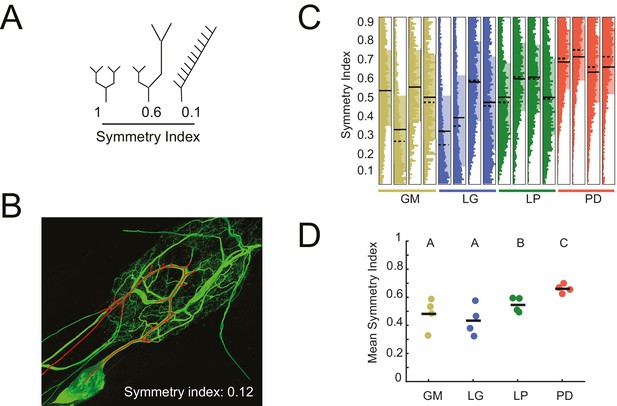
Asymmetric neurite arborizations in STG Neurons.
Symmetry indices (SI) were calculated for every branch point detected in the three-dimensional skeletal reconstructions generated in KNOSSOS from high-resolution confocal image stacks of Lucifer yellow neuronal dye-fills. For a given branch point, the SI was calculated as the ratio of the sums of downstream neurite lengths on either side of the bifurcation (shorter neurite length as the numerator, longer as the denominator). (A) Schematics of branch points with varying SI; SI decreases as neurite lengths on either side of the first branch point become increasingly asymmetrical in length (from left to right). (B) Traced neurite path (red) and its corresponding SI of 0.12, which is akin to the rightmost example in A. (C) Vertical histograms show the distributions of SI values across all branches for each neuron (cell type is indicated by color and labeled on the x-axis). The x-axis scales are normalized to the maximum count within each neuron. All neurons present SI values that span the range of possibilities, between 0 and 1. (D) Mean SI values plotted by cell type. Scatter points indicate mean SI values for individual cells, black line indicates mean SI for each cell type. Letters are indicative of ANOVA results across cell types (F(3,12) = 5.45, p=0.01; Tukey HSD). Neuron types (n = 4 of each) are color-coded in C and D: gold = GM neuron, blue = LG neuron, green = LP neuron, red = PD neuron.
Figure 7
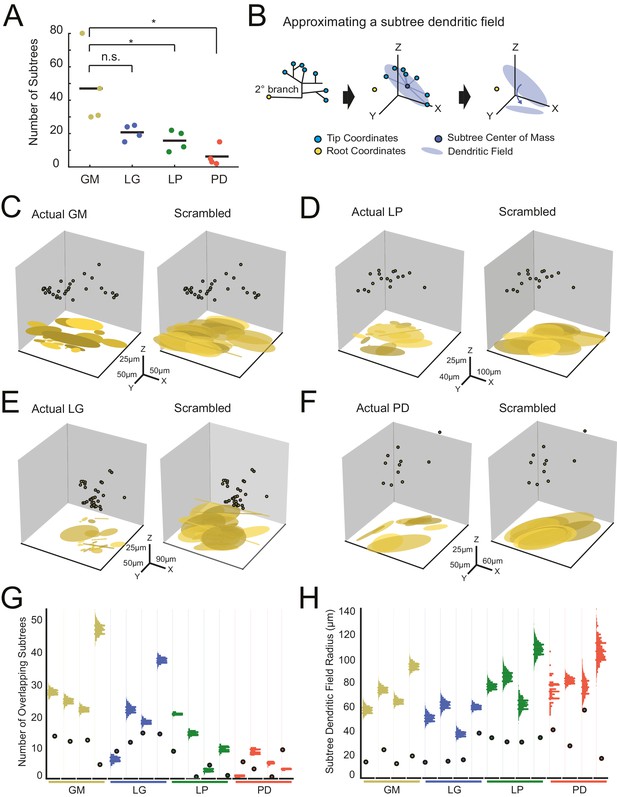
Variable subtrees that tile the neuropil.
Subtrees were defined as neurites sharing a common secondary neurite exiting the main path, or primary neurite, of the neuronal structure. Thus, for each neuron, the number of subtrees was equivalent to the number of secondary neurites in the neurons corresponding to the three-dimensional skeletal reconstruction generated in KNOSSOS. (A) The number of subtrees varied within and across neuron types, such that GM neurons presented more subtrees than LP and PD neurons (letters are indicative of ANOVA results; [F(3,12)=7.6, p=0.0041], Tukey HSD). (B) The neuritic field for a given subtree (example on left) was approximated as an elliptical volume fit (blue shaded area) and centered about the center of mass (dark blue point) of the subtree’s tip coordinates (light blue points; middle). A subtree’s neuritic field was visualized by projecting this elliptical volume into the x-y plane (right), which is representative of a birds-eye view of neuropil space. (C–F) Subtree neuritic field plots for four representative STG neurons (left), juxtaposed to representative scrambled iterations (right). Three-dimensional scatter plots show the subtree root coordinates of individual subtrees (circular data points) and their corresponding neuritic fields projected onto the x-y plane. Left: plots display the subtree neuritic fields given the actual neuronal structure. Right: plots display the subtree neuritic fields for a representative scrambled iteration of tip coordinates for the same neuron on left, wherein tips were re-distributed into the same number of, but different subtrees, while maintaining the same root coordinates (see Materials and methods). For each neuron in C–F scale axes indicate the same x-y-z scale for both the actual and scrambled plots. (G) Scatter plots indicate the number of overlapping subtrees for each neuron (cell type indicated by color and labeled on the x-axis). Overlaid vertical histograms show the number of overlapping subtrees across the scrambled, synthetic population generated from the tip coordinates for each neuron (purple lines indicate the mean radii for each scrambled population). (H) Scatter plots indicate the mean subtree neuritic field radius for each neuron (cell type indicated by color and labeled on the x-axis). Overlaid vertical histograms show the range of subtree neuritic field radii across the scrambled, synthetic population generated from the tip coordinates for each neuron (purple lines indicate the mean radii for each scrambled population). Neuron types (n = 4 of each) are color-coded in A, G, and H: gold = GM neuron, blue = LG neuron, green = LP neuron, red = PD neuron.
Figure 8
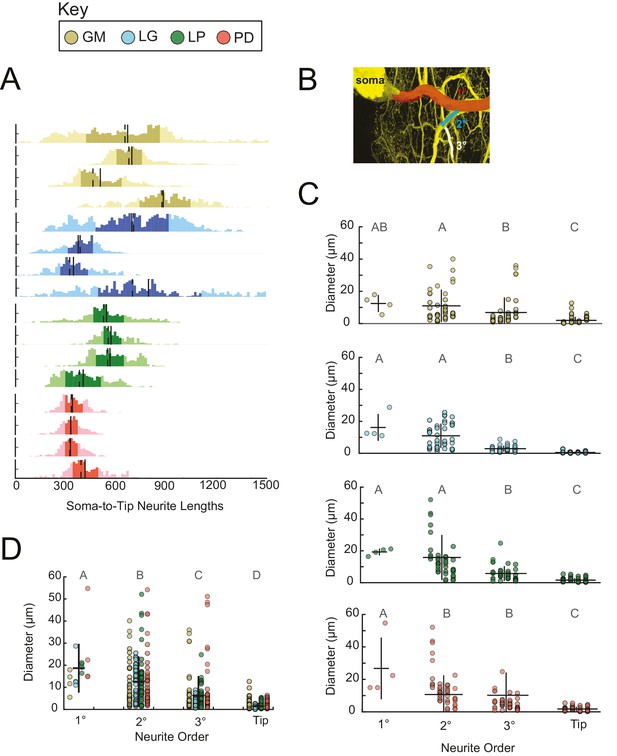
Neurite lengths and diameters.
(A) Histograms for each neuron showing the distribution of neurite lengths across all soma-to-tip paths. Neurite path lengths were measured in three-dimensional skeletal reconstructions generated in KNOSSOS from high-resolution confocal image stacks of Lucifer yellow neuronal dye-fills. There were no cell-type-specific differences in neurite length distributions (ANOVA; [F(3,12)=1.48, p=0.2698]; Tukey HSD). Means are indicated by solid lines; medians are indicated with dashed lines; darker shaded regions indicate 25–75% confidence intervals. Neurite diameters were randomly sampled across primary (1°), secondary (2°), tertiary (3°), and terminating (tip) neurites and manually measured using ImageJ. (B) Illustration of 1° branch (red) and individual 2° (cyan) and 3° (white) branches on one neuron (z-projection of confocal micrograph at 60x magnification, neuron pseudo-colored in yellow). (C) Scatter plots of neurite diameters as a function of neurite order within neuron types show decreasing neurite diameters as a function of neurite order. ANOVA results are: [F(3,149)=14.77, p<<0.001; Tukey HSD)], [F(3,152)=67.16, p<<0.001; Tukey HSD)], [F(3,152)=33.92, p<<0.001; Tukey HSD)], [F(3,146)=16.43, p<<0.001; Tukey HSD)], for GM, LG, LP, and PD, respectively. (D) Scatter plot shows all measured diameters, across all cell types, as a function of neurite order. When all cell types are pooled are together, diameter decreases as a function of neurite order (ANOVA [F(3,611)=89.17, p<<0.001]; Tukey HSD; indicated with letters). ANOVA analyses within each neurite order, across cell types, revealed no significant differences across cell types. For C and D pooled mean ± SD within each neurite order indicated with black lines. In A, C, and D neuron types (n = 4 of each) are color-coded as in key.
Figure 9
Variable Rall powers at neurite branch points.
Rall powers calculated for branch points sampled across different branch orders: initial branch points (or the first branch point relative to the soma), primary-secondary (P–S) branch points, secondary-tertiary (S–T) branch points, and branch points in which at least one daughter branch was a terminating branch (terminal). Parent and daughter neurite diameters were manually measured using ImageJ, directly from the high-resolution confocal image stacks of Lucifer yellow neuronal dye-fills. (A) Examples of initial (red), P-S (blue), and S-T (cyan) branch points are shown on a maximum projection of a neuronal dye-fill. (B–E) Scatter plots show the calculated Rall powers for each neuron (as in Materials and methods and text; N = 16; cell types indicated by color and labeled on x-axis; colored horizontal bars indicate the mean Rall power for each cell) across sampled initial, P-S, S-T, and terminal branch points, respectively (n = 18–20 branch points within each branch point type). The optimal Rall power for current transfer is 3/2 (Rall, 1959). This is indicated on each plot with purple horizontal lines. Mean Rall powers calculated within each cell type are shown in Table 2. There were no statistically significant cell-type-specific differences in this metric.
Figure 10
STG neurons have tortuous neurite paths.
Tortuosities were calculated for every soma-to-tip neurite path detected from the three-dimensional skeletal reconstruction of each neuron (N = 16). (A) An example neurite path (red dashed line) from soma to terminal tip is shown on maximum projection image of an STG neuron section. The tortuosity of such a path is calculated as the ratio of the actual path length (red) over the Euclidean distance from soma to tip (purple). If the actual neurite path follows the most efficient Euclidean path, it will have a tortuosity of 1. If the neurite path deviates from this minimal path, its tortuosity will be >1. (B) Histograms of tortuosities for all neurite paths within each neuron (gold = GM neuron, blue = LG neuron, green = LP neuron, red = PD neuron). Darker shaded regions indicate 25–75% confidence intervals. In all cases, the distributions spanning tortuosities between 1 and 6 are shown (x-axis). In some cases, the distributions extend beyond values of 6 (not shown in this figure).
Figure 11 with 4 supplements
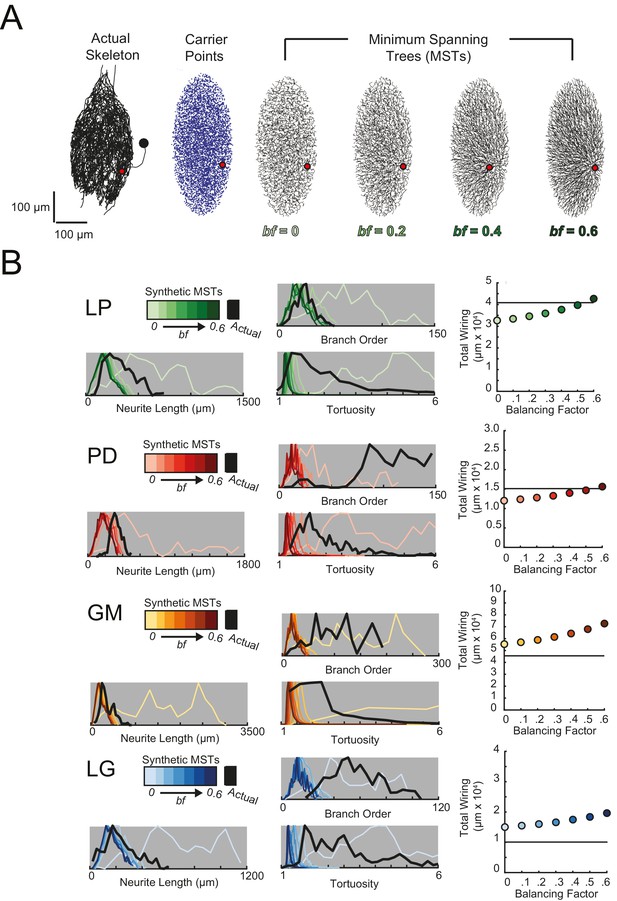
Minimal Spanning Trees (MSTs) adhering to wiring optimization rules do not recapitulate the morphological features of individual STG neurons.
Synthetic MSTs adhering to the wiring cost rule: total cost = wiring cost + bf * path length cost (where bf = balancing factor) were generated using the TREEs toolbox (described in Materials and methods and by Cuntz et al., 2010). (A) An example of four synthetic minimal spanning trees (right) with varying bf values generated from the first branch point (location indicated as red circle on actual skeleton of an LP neuron; left) as the root. The carrier points (blue) were randomly generated from points uniformly distributed across the elliptical volume approximating the actual volume occupied by the neuron. The number of carrier points was tuned such that the MSTs had branch point number within 20% of the actual neuron’s branch point number (Table 3). Scale bars apply to skeleton, carrier point, and MST plots. (B) Morphological features of synthetic trees generated with bf values between 0.1 and 0.6 plotted against measurements from four actual STG neurons (one of each type, indicated on left and by color). Features of actual neurons are shown with black lines, whereas synthetic neurite tree data are plotted in the color scale described in the key for each neuron. Total wiring lengths, branch order distributions, neurite length distributions, and tortuosity distributions were calculated excluding axons for all synthetic and actual neurite trees. Branch order, neurite length, and tortuosity distributions were normalized to the maximum within each data set (for each bf value and actual neurite tree) for direct comparison of distributions despite varying neurite path counts.
Figure 11—figure supplement 1
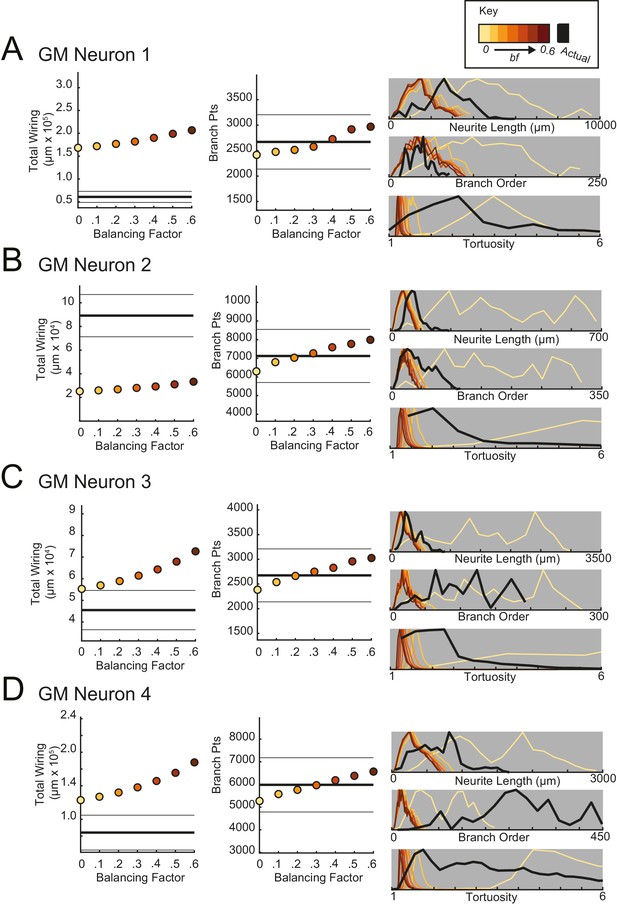
Minimal spanning trees (MSTs) adhering to wiring optimization rules do not recapitulate the morphological features of gastric mill (GM) neurons.
MSTs were generated using the TREEs toolbox (described in Materials and methods and by Cuntz et al., 2010) and adhered to the wiring cost rule: total cost = wiring cost + bf * path length cost (where bf = balancing factor). For each of four GM neurons, MSTs with bf values between 0 and 0.6 were generated from the first branch point as the root. The terminal tip coordinates were randomly generated from points uniformly distributed across the elliptical volume approximating the actual volume occupied by the neuron (as in Figure 11A). The number of terminal tip coordinates was tuned for each neuron, such that the MSTs had branch point numbers within 20% of the actual neuron’s branch point number. A–D present plots comparing morphological features (total wiring, branch point (pts), neurite lengths, branch orders, and tortuosities) of the MSTs to those measured in each of four actual STG neurons. In scatter plots (left), thick lines are indicative of the total wiring or branch point number of the actual neuron, whereas colored points correspond with these metrics for the MSTs of the bf value (indicated in key). Thin black lines indicate 20% above or below the actual neuron’s total wiring or branch point number. For histograms (right), measurements from actual neurons are shown with black lines, whereas synthetic MST data are plotted in the color scale described in the key. Branch order, neurite length, and tortuosity distributions were normalized to the maximum within each data set (for each bf value and actual neurite tree) for direct comparison of distributions despite varying neurite path counts. It is evident that not one bf value capitulates all features of the actual GM neurons.
Figure 11—figure supplement 2
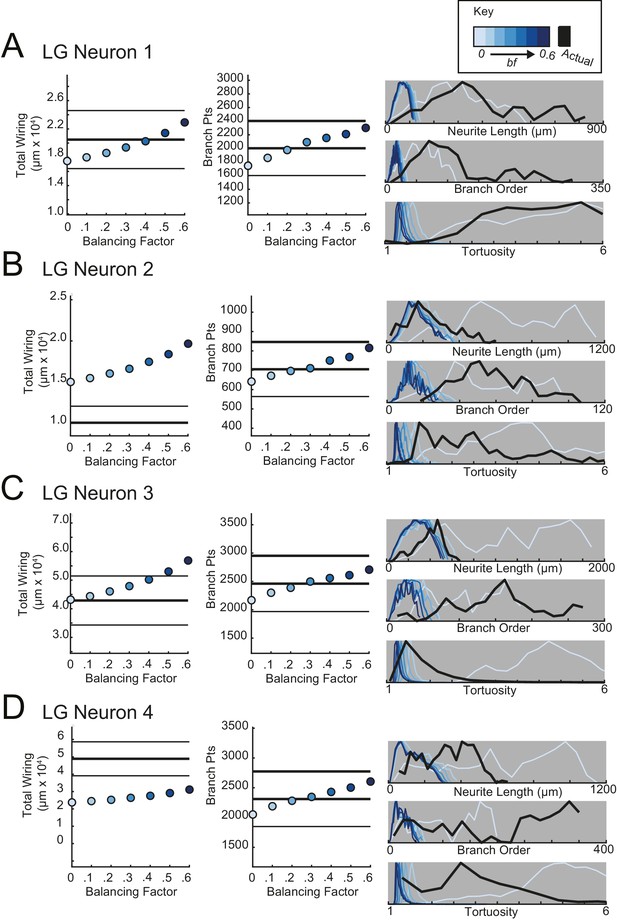
Minimal spanning trees (MSTs) adhering to wiring optimization rules do not recapitulate the morphological features of lateral gastric (LG) neurons.
MSTs were generated using the TREEs toolbox (described in Materials and methods and by Cuntz et al., 2010) and adhered to the wiring cost rule: total cost = wiring cost + bf * path length cost (where bf = balancing factor). For each of four LG neurons, MSTs with bf values between 0 and 0.6 were generated from the first branch point as the root. The terminal tip coordinates were randomly generated from points uniformly distributed across the elliptical volume approximating the actual volume occupied by the neuron (as in Figure 11A). The number of terminal tip coordinates was tuned for each neuron, such that the MSTs had branch point numbers within 20% of the actual neuron’s branch point number. A–D present plots comparing morphological features (total wiring, branch point (pts), neurite lengths, branch orders, and tortuosities) of the MSTs to those measured in each of four actual STG neurons. In scatter plots (left), thick lines are indicative of the total wiring or branch point number of the actual neuron, whereas colored points correspond with these metrics for the MSTs of the bf value (indicated in key). Thin black lines indicate 20% above or below the actual neuron’s total wiring or branch point number. For histograms (right), measurements from actual neurons are shown with black lines, whereas synthetic MST data are plotted in the color scale described in the key. Branch order, neurite length, and tortuosity distributions were normalized to the maximum within each data set (for each bf value and actual neurite tree) for direct comparison of distributions despite varying neurite path counts. It is evident that not one bf value capitulates all features of the actual LG neurons.
Figure 11—figure supplement 3
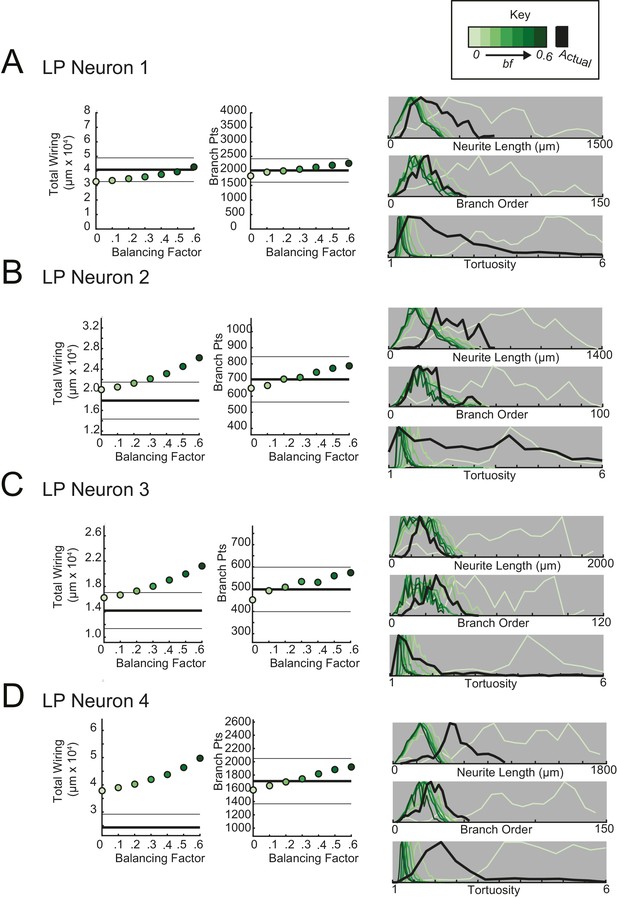
Minimal spanning trees (MSTs) adhering to wiring optimization rules do not recapitulate the morphological features of lateral pyloric (LP) neurons.
MSTs were generated using the TREEs toolbox (described in Materials and methods and by Cuntz et al., 2010) and adhered to the wiring cost rule: total cost = wiring cost + bf * path length cost (where bf = balancing factor). For each of four LP neurons, MSTs with bf values between 0 and 0.6 were generated from the first branch point as the root. The terminal tip coordinates were randomly generated from points uniformly distributed across the elliptical volume approximating the actual volume occupied by the neuron (as in Figure 11A). The number of terminal tip coordinates was tuned for each neuron, such that the MSTs had branch point numbers within 20% of the actual neuron’s branch point number. A–D present plots comparing morphological features (total wiring, branch point (pts), neurite lengths, branch orders, and tortuosities) of the MSTs to those measured in each of four actual STG neurons. In scatter plots (left), thick lines are indicative of the total wiring or branch point number of the actual neuron, whereas colored points correspond with these metrics for the MSTs of the bf value (indicated in key). Thin black lines indicate 20% above or below the actual neuron’s total wiring or branch point number. For histograms (right), measurements from actual neurons are shown with black lines, whereas synthetic MST data are plotted in the color scale described in the key. Branch order, neurite length, and tortuosity distributions were normalized to the maximum within each data set (for each bf value and actual neurite tree) for direct comparison of distributions despite varying neurite path counts. It is evident that not one bf value capitulates all features of the actual LP neurons.
Figure 11—figure supplement 4
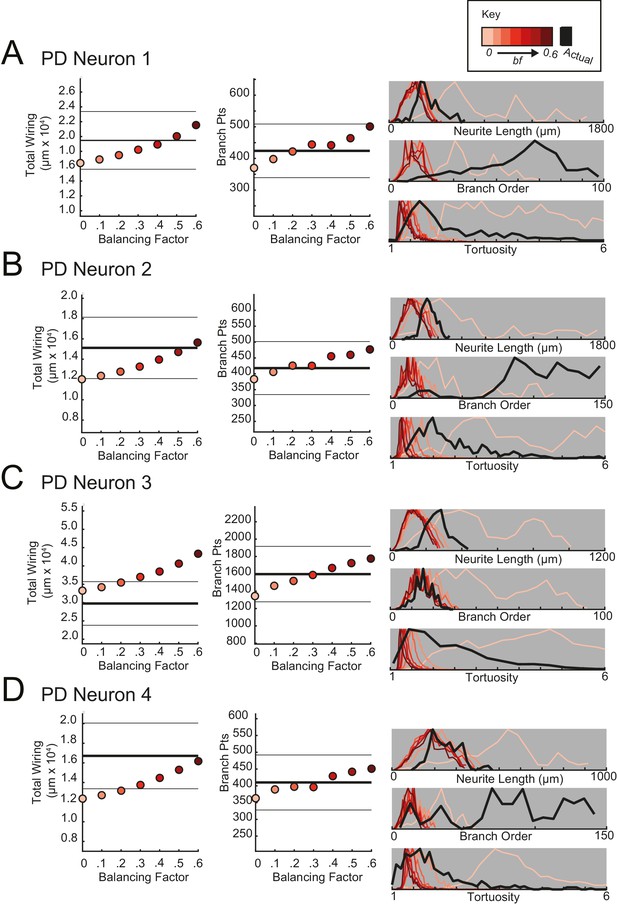
Minimal spanning trees (MSTs) adhering to wiring optimization rules do not recapitulate the morphological features of pyloric dilator (PD) neurons.
MSTs were generated using the TREEs toolbox (described in Materials and methods and by Cuntz et al., 2010) and adhered to the wiring cost rule: total cost = wiring cost + bf * path length cost (where bf = balancing factor). For each of four PD neurons, MSTs with bf values between 0 and 0.6 were generated from the first branch point as the root. The terminal tip coordinates were randomly generated from points uniformly distributed across the elliptical volume approximating the actual volume occupied by the neuron (as in Figure 11A). The number of terminal tip coordinates was tuned for each neuron, such that the MSTs had branch point numbers within 20% of the actual neuron’s branch point number. A–D present plots comparing morphological features (total wiring, branch point (pts), neurite lengths, branch orders, and tortuosities) of the MSTs to those measured in each of four actual STG neurons. In scatter plots (left), thick lines are indicative of the total wiring or branch point number of the actual neuron, whereas colored points correspond with these metrics for the MSTs of the bf value (indicated in key). Thin black lines indicate 20% above or below the actual neuron’s total wiring or branch point number. For histograms (right), measurements from actual neurons are shown with black lines, whereas synthetic MST data are plotted in the color scale described in the key. Branch order, neurite length, and tortuosity distributions were normalized to the maximum within each data set (for each bf value and actual neurite tree) for direct comparison of distributions despite varying neurite path counts. It is evident that not one bf value capitulates all features of the actual PD neurons.
Figure 12
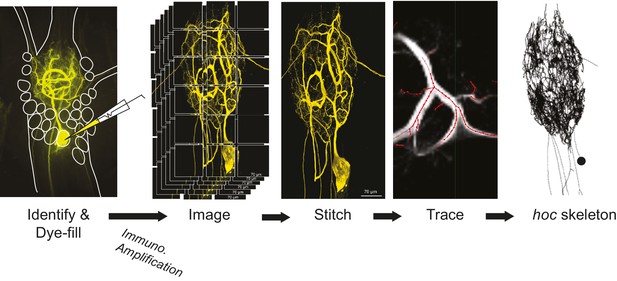
Procedural workflow from dye-fill to morphological analysis.
Neurons were identified physiologically and then filled with Lucifer yellow. Following fixation and immunohistochemical amplification with a rabbit anti-Lucifer yellow primary antibody and an Alexa Fluor 488-tagged secondary antibody, each dye-fill was imaged at 63x magnification as a series of z-stacks that tiled the neuronal structure across the x-y plane (z-stacks contained slices at increments of ~0.5 µm). These z-stacks were stitched together with custom software written in MATLAB. The image stack of each full three-dimensional neuronal structure was then manually traced (image shown is a screenshot from the KNOSSOS platform). The three-dimensional skeletal structures were then converted to hoc files that could be analyzed with a custom quantitative morphology toolbox composed in Python. All conversion and analytical scripts are freely available on the Marder Lab Github repository.
Tables
Table 1
Anatomical properties of GM, LG, LP, and PD neurons. Soma-to tip neurite lengths, tortuosities, and diameters are reported as a mean ± standard deviation, with the exception of the initial primary neurite (1°) diameters (for which there are single values for each neuron). Soma-to-tip neurite, branch point, and subtree values are counts for each neuron. These data are plotted in Figures 2, 4, 7, 8 and 10.
Cell type | Soma-to-Tip neurites | Branch points | Subtrees | Total wiring (µm) | Tortuosity | Soma-to-Tip neurite length (µm) | Neurite diameters (µm) | |||
|---|---|---|---|---|---|---|---|---|---|---|
1° | 2° | 3° | Tip | |||||||
GM | 2675 | 2671 | 30 | 60,796 | 2.6 ± 2.4 | 420.7 ± 113.4 | 14.7 | 13.3 ± 10.4 | 2.4 ± 1.3 | 0.6 ± 0.3 |
GM | 7109 | 7125 | 31 | 89,148 | 2.0 ± 1.3 | 125.9 ± 26.0 | 18 | 6.3 ± 6.7 | 2.8 ± 1.9 | 3.1 ± 3.4 |
GM | 2676 | 2675 | 47 | 45,502 | 1.6 ± 0.7 | 501.7 ± 157.9 | 5.5 | 8.6 ± 5.1 | 4.6 ± 3.9 | 1.1 ± 0.3 |
GM | 5985 | 5984 | 80 | 104,115 | 3.9 ± 2.1 | 664.2 ± 323.9 | 11.7 | 15.8 ± 14.1 | 17.6 ± 13.6 | 3.4 ± 1.2 |
LG | 2003 | 2002 | 25 | 20,489 | 6.8 ± 6.4 | 399.7 ± 201.7 | 12.6 | 9.6 ± 6.4 | 2.1 ± 1.2 | 0.6 ± 0.7 |
LG | 706 | 705 | 15 | 10,061 | 3.2 ± 1.9 | 344.5 ± 127.9 | 12.4 | 7.3 ± 5.6 | 3.0 ± 2.4 | 0.4 ± 0.2 |
LG | 2461 | 2460 | 19 | 42,889 | 1.8 ± 1.0 | 372.9 ± 115.2 | 11 | 15.0 ± 8.6 | 3.1 ± 1.6 | 0.5 ± 0.2 |
LG | 2310 | 2311 | 24 | 48,894 | 3.1 ± 1.5 | 371.4 ± 139.3 | 28.7 | 11.8 ± 8.2 | 3.3 ± 1.9 | 0.6 ± 0.4 |
LP | 2016 | 2015 | 22 | 40,833 | 2.7 ± 1.8 | 402.4 ± 145.4 | 16.4 | 34.0 ± 17.0 | 7.1 ± 4.8 | 1.7 ± 1.1 |
LP | 705 | 704 | 12 | 17,914 | 2.7 ± 1.6 | 561.1 ± 119.2 | 19 | 11.5 ± 3.4 | 7.0 ± 6.5 | 2.2 ± 1.1 |
LP | 500 | 499 | 9 | 14,202 | 1.4 ± 0.5 | 567.5 ± 99.5 | 20.6 | 9.8 ± 5.6 | 5.0 ± 2.9 | 1.1 ± 0.9 |
LP | 1709 | 1708 | 20 | 24,335 | 3.1 ± 2.6 | 540.8 ± 163.5 | 21.1 | 8.0 ± 6.4 | 3.9 ± 3.4 | 1.3 ± 1.3 |
PD | 425 | 424 | 2 | 19,483 | 3.4 ± 3.1 | 414.9 ± 119.2 | 15 | 9.4 ± 4.6 | 9.3 ± 6.1 | 2.1 ± 1.9 |
PD | 419 | 418 | 3 | 15,113 | 2.5 ± 1.2 | 328.1 ± 67.2 | 14.9 | 4.5 ± 3.3 | 9.3 ± 17.0 | 2.0 ± 1.4 |
PD | 1598 | 1597 | 15 | 29,758 | 2.8 ± 1.7 | 329.8 ± 64.4 | 54.8 | 15.8 ± 15.7 | 8.5 ± 16.3 | 1.2 ± 0.7 |
PD | 411 | 410 | 5 | 16,710 | 2.0 ± 1.1 | 339.7 ± 71.0 | 22.4 | 20.6 ± 15.5 | 13.1 ± 15.7 | 1.7 ± 1.0 |
Table 2
Rall powers by cell type. Rall powers were derived from neurite diameters at different branch point categories. Initial-Secondary refers to the Rall power at the first branch point relative to the soma. Terminating tips refers to branch points wherein at least one daughter branch terminates. Pooled means ± standard deviations are shown for each branch point category, for each cell type. For each cell type, pooled means ± standard deviations were calculated from six branch points in each category, for each of four neurons of that cell type. The raw data and mean Rall powers for each neuron are plotted in Figure 9.
Branch point category | Rall power by cell type | |||
|---|---|---|---|---|
Parent-Daughter | GM | LG | LP | PD |
INITIAL-SECONDARY | 0.001 ± 0.001 | 0.001 ± 0.001 | 0.001 ± 0.001 | 0.381 ± 0.658 |
PRIMARY-SECONDARY | 2.132 ± 2.070 | 1.667 ± 0.857 | 4.296 ± 5.331 | 2.215 ± 1.838 |
SECONDARY-TERTIARY | 1.305 ± 0.682 | 6.366 ± 10.098 | 1.332 ± 0.575 | 1.342 ± 0.453 |
TERMINATING TIPS | 1.846 ± 1.449 | 6.847 ± 10.737 | 7.397 ± 10.820 | 1.049 ±. 546 |
Table 3
Minimal spanning trees (MSTs) simulation parameters. 16 STG neuronal structures were simulated using MST analyses from the TREES toolbox (Cuntz et al., 2010). Carrier point numbers (column 4) were tuned to generate MSTs with branch point numbers within 20% of the branch point counts in the actual neurons (column 2, gray shaded). MSTs were generated for balancing factors between 0 and 0.6, at increments of 0.1. Columns 5–18 show branch point numbers and cable lengths for each of these MSTs. The MSTs often had cable lengths within 20% of that measured in the actual neurons (column 3), but in some cases, the MSTs were not a close approximation of the actual cable length.
Cell | Actual neuron | Minimum spanning trees | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Branch Points | Cable length | Carrier Points | Branch point numbers | Cable length (x 104 µm) | |||||||||||||
0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | ||||
GM1 | 2671 | 6.1 | 8500 | 2416 | 2477 | 2512 | 2576 | 2727 | 2916 | 2971 | 16.8 | 17.2 | 17.7 | 18.2 | 19.0 | 19.9 | 20.7 |
GM2 | 7125 | 8.9 | 23000 | 6296 | 6789 | 7030 | 7271 | 7592 | 7773 | 7994 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 3.1 | 3.3 |
GM3 | 2675 | 4.6 | 8800 | 2384 | 2537 | 2665 | 2749 | 2827 | 2959 | 3026 | 5.5 | 5.7 | 5.9 | 6.1 | 6.4 | 6.8 | 7.3 |
GM4 | 5984 | 10.4 | 19000 | 5274 | 5574 | 5762 | 5969 | 6187 | 6379 | 6571 | 14.3 | 14.7 | 15.2 | 15.8 | 16.6 | 17.5 | 18.8 |
LG1 | 2002 | 2.0 | 6500 | 1746 | 1860 | 1976 | 2092 | 2154 | 2209 | 2302 | 1.7 | 1.8 | 1.9 | 1.9 | 2.0 | 2.1 | 2.3 |
LG2 | 705 | 1.0 | 2300 | 641 | 672 | 696 | 710 | 750 | 768 | 815 | 1.5 | 1.5 | 1.6 | 1.7 | 1.7 | 1.8 | 2.0 |
LG3 | 2460 | 4.3 | 8000 | 2168 | 2302 | 2389 | 2498 | 2559 | 2612 | 2707 | 4.3 | 4.4 | 4.6 | 4.8 | 5.0 | 5.3 | 5.7 |
LG4 | 2311 | 4.9 | 7500 | 2050 | 2189 | 2282 | 2346 | 2430 | 2502 | 2603 | 2.4 | 2.4 | 2.5 | 2.6 | 2.8 | 2.9 | 3.1 |
LP1 | 2015 | 4.1 | 6550 | 1825 | 1957 | 1998 | 2059 | 2126 | 2195 | 2263 | 3.3 | 3.3 | 3.5 | 3.6 | 3.8 | 4.0 | 4.3 |
LP2 | 704 | 1.8 | 2330 | 649 | 666 | 706 | 716 | 748 | 773 | 788 | 2.0 | 2.1 | 2.1 | 2.2 | 2.3 | 2.5 | 2.6 |
LP3 | 499 | 1.4 | 1705 | 452 | 493 | 509 | 534 | 531 | 560 | 574 | 1.6 | 1.7 | 1.7 | 1.8 | 1.9 | 2.0 | 2.1 |
LP4 | 1708 | 2.4 | 5650 | 1574 | 1639 | 1697 | 1743 | 1819 | 1883 | 1921 | 3.8 | 3.9 | 4.0 | 4.2 | 4.4 | 4.6 | 5.0 |
PD1 | 424 | 1.9 | 1400 | 370 | 398 | 422 | 444 | 442 | 464 | 501 | 1.6 | 1.7 | 1.8 | 1.8 | 1.9 | 2.0 | 2.2 |
PD2 | 418 | 1.5 | 1400 | 383 | 406 | 426 | 425 | 455 | 460 | 477 | 1.2 | 1.2 | 1.3 | 1.3 | 1.4 | 1.5 | 1.6 |
PD3 | 1597 | 3.0 | 5000 | 1344 | 1462 | 1519 | 1587 | 1667 | 1724 | 1776 | 3.3 | 3.4 | 3.5 | 3.7 | 3.8 | 4.1 | 4.3 |
PD4 | 410 | 1.7 | 1300 | 363 | 389 | 397 | 396 | 429 | 442 | 451 | 1.2 | 1.3 | 1.3 | 1.4 | 1.4 | 1.5 | 1.6 |
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Sloppy morphological tuning in identified neurons of the crustacean stomatogastric ganglion
eLife 6:e22352.
https://doi.org/10.7554/eLife.22352
