Complementary codes for odor identity and intensity in olfactory cortex
- Duke University Medical School, United States
Figures
Figure 1 with 3 supplements
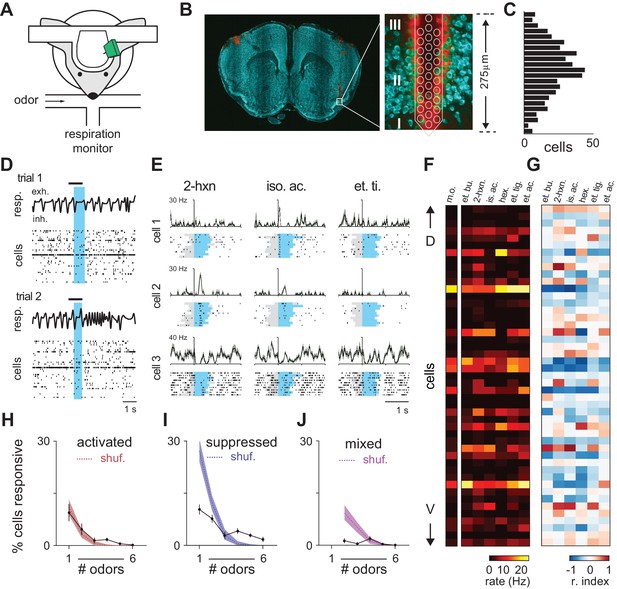
Odor responses in piriform cortex.
(A) Schematic of experimental setup. (B) Left, Coronal brain section showing region of anterior piriform cortex where recordings were obtained. Multielectrode probes were painted with DiI to mark recording locations (red, DiI; green, NeuroTrace). DiI in the left hemisphere is from a separate recording. Right, higher magnification image of boxed area on left, superimposed with a schematic at scale of a 32-channel probe. Numerals indicate piriform layers. Note the electrode tip spans layer II. (C) Dorso-ventral (DV) distribution of 459 isolated cells (n = 9 experiments) determined by measuring the center of mass of each unit’s waveform amplitudes recorded on different channels across the probe. (D) Population activity and timing of odor delivery. One-second odor pulses (black bar, isoamyl acetate) were triggered on exhalation. Blue shaded region indicates first full respiration cycle after odor onset. Population raster plots below display spiking activity of 33 simultaneously recorded cells sorted by estimated DV position within layer II. (E) Inhalation-aligned raster plots showing responses of three simultaneously recorded cells to three different odor stimuli (0.3% v./v.). Gray shading indicates odor delivery. Blue shading indicates respiration cycle. Cells displayed varying degrees of odor specificity, activation or suppression, and temporal precision. (F–G) Population responses in a representative experiment with 48 simultaneously recorded neurons sorted by relative DV location responding to six different monomolecular odorants (0.3%). (F). Firing rates during the first respiration cycle after odor onset. A mineral oil control is shown on left. (G). Same data expressed using a response index where cells with response index values of −1 (blue) and 1 (red) are unambiguously suppressed or activated, respectively. Odors: et. bu., ethyl butyrate; 2-hxn., 2-hexanone; is. ac., isoamyl acetate; hex., hexanal; et. ti., ethyl tiglate; et. ac., ethyl acetate. (H–J) Percent cells responding to different numbers of odorants with significantly increased spiking (H), decreased spiking (I), or mixed polarity responses (J). Filled circles are mean ± s.e.m. (n = 9). The dashed line denotes the expected distribution when cell identities are shuffled; shaded area, 5th–95th percentiles.
Figure 1—figure supplement 1
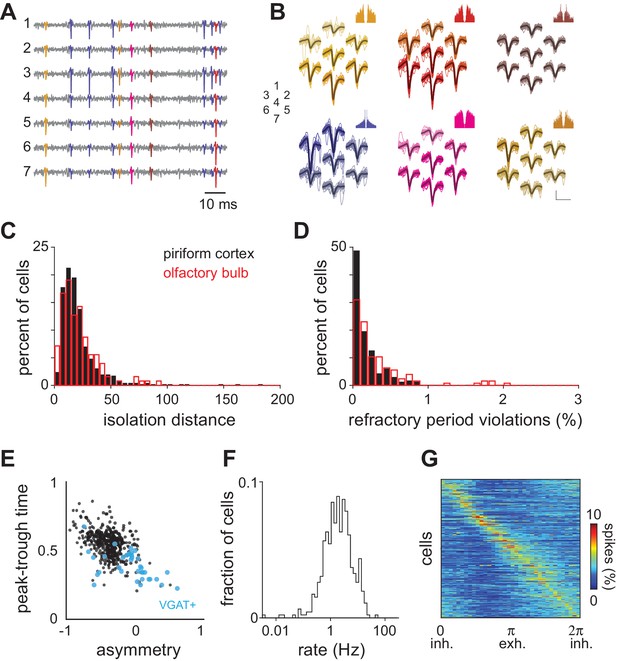
Spike sorting and spontaneous activity.
(A–B) Raw voltage data recorded on seven neighboring channels and waveforms for six different units isolated from these traces. Each unit is differently colored and the spikes in the voltage traces associated with those units are colored accordingly. Autocorrelograms for each unit are shown above. Numbers indicate the spatial arrangement of the seven channels. Scale bar = 50 μV, 1 ms. (C) Isolation distance indicating cluster separation for all recorded piriform (black, mean ± st. dev: 23.74 ± 28.38) and olfactory bulb cells (red, mean ± st. dev: 21.58 ± 16.57). (D) Percent of ISIs shorter than 2 ms for all clustered units. (E) Spike waveform properties for experimental dataset (black circles, n = 459 neurons). Waveform properties for optogenetically identified inhibitory neurons are overlaid in blue (VGAT+, n = 35). Peak-trough time is the time from the negative peak of the extracellular spike to the next positive peak. Waveform asymmetry is the relative difference in the size of the positive peaks surrounding the negative peak of the action potential, measured as in Barthó et al. (2004). (F) Average spontaneous firing rates for all 459 neurons follow a log-normal distribution (mean ± st. dev: 3.09 ± 3.93 Hz). (G) Phase histograms (10° bins) for each isolated unit constructed from spontaneous spiking in awake piriform cortex and sorted according to peak phase. Spontaneous spikes for each cell (n = 459) were assigned a phase in the respiration cycle by linear interpolation between 0 (the start of inhalation) and π (the start of exhalation).
Figure 1—figure supplement 2
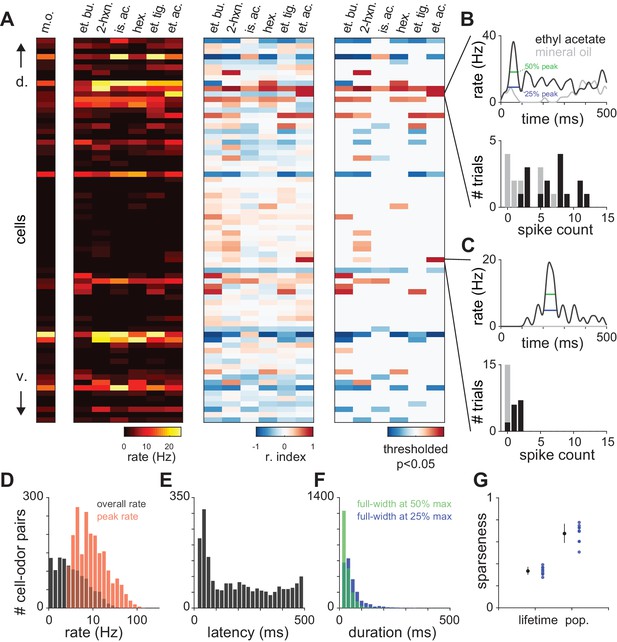
Characterization of piriform odor responses.
(A) Summary representations of responses in a representative experiment with 72 simultaneously recorded neurons. Responses are shown for a blank stimulus (m.o.) or following delivery of 6 different monomolecular odorants (0.3% v./v.). Cells are sorted according to their dorso-ventral positions within layer II, with dorsal on top. Data are represented as firing rate (left), response index (middle), where cells with a response index of −1 (blue) are unambiguously suppressed and values of 1 are unambiguously activated (red), or further thresholded to show only responses that are significantly different from blank trials according to a Wilcoxon rank-sum test (p<0.05, right). Odors: m.o., mineral oil; et. bu., ethyl butyrate; 2-hx, 2-hexanone; is. ac., isoamyl acetate; hex., hexanal; et. ti., ethyl tiglate; et. ac., ethyl acetate. (B–C) Example PSTHs (top) and spike count histograms (bottom) for two cells that are significantly activated by ethyl acetate. Odor responses (black) are compared to mineral oil responses (gray) to determine significant activation. Response latency and duration were measured for the maximum peak in the PSTH (width at 25% and 50% of peak, blue and green, top). Response index and significance were derived from the distributions of spike counts in the first breath after odor delivery across 10–15 trials (bottom). (D–F) Distribution of (D) peak and overall odor-evoked firing rates (peak: red, mean ± st. dev: 13.69 ± 14.7 Hz; overall: black, 2.90 ± 4.22 Hz), (E) latencies to peak for activated responses (208 ± 155 ms), and (F) response duration measured at 25% or 50% of peak (25%: blue, 68.0 ± 44.9 ms; 50%: green, 43.0 ± 22.3 ms) for all responses that contained peaks (2079/2754 cell-odor pairs). (G) Lifetime and population sparseness of odor-evoked piriform firing rates averaged for individual experiments (blue circles) or averaged across experiments (black circles with error bars; mean ± s.e.m., n = 9 experiments).
Figure 1—figure supplement 3
Properties of Activated and Suppressed cells.
(A) PSTHs for six example cells demonstrating exclusively odor-evoked activation (cells 2, 3, and 5, red traces) or odor-evoked suppression (cells 1, 4, and 6, blue traces). Response to mineral oil for each cell is overlaid in gray. (B) Example thresholded response map for a representative experiment with 73 cells showing consistent response polarity across odors (left). Example cells are indicated on the left. Many more mixed polarity responses are expected if responses are randomly assigned to cells within an odor (right). (C) ‘Activated’ (n = 87/459) and ‘Suppressed’ (n = 132/459) cells were identified as having exclusively significant activation or suppression to at least one of six odors. Spontaneous firing was measured during intertrial intervals. Activated cells had lower spontaneous firing rates than Suppressed cells (Activated: mean ± st. dev; 3.07 ± 3.90 Hz, n = 87; Suppressed: 5.16 ± 5.35 Hz; n = 132 p<0.001, unpaired t-test). (D) Waveform properties overlapped completely for Activated and Suppressed cells and both classes were similar to the waveform properties of presumed principal neurons. (E) Relative dorsal-ventral position of Activated and Suppressed cells in piriform layer II. Neither cell type was preferentially positioned in superficial or deep sublaminae.
Figure 2 with 1 supplement
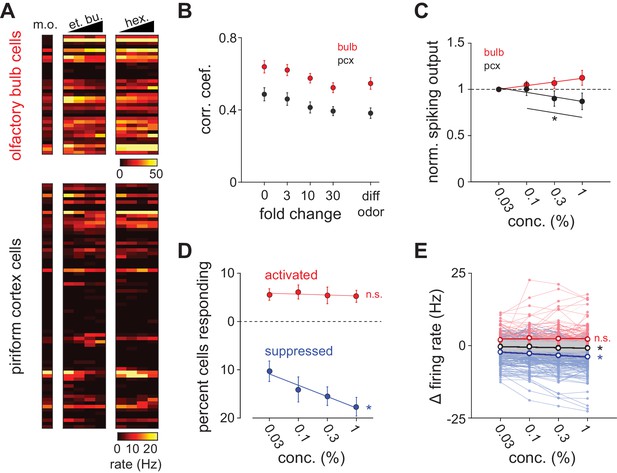
Concentration-dependent suppression in piriform cortex.
(A) Simultaneous population recordings were obtained from olfactory bulb and ipsilateral piriform cortex in 6/9 experiments. Responses are represented as average firing rates over the first respiration cycle after odor delivery for one example experiment. (B) Average trial-by-trial correlation coefficients of population firing rate vectors in olfactory bulb (red circles; n = 6) and piriform cortex (black circles; n = 9), as a function of fold change in concentration for the identical odorant (0–30) or with a distinct odorant at any concentration (diff odor). (C) Total spiking output as a function of concentration in bulb (red circles; repeated measures ANOVA for concentrations 0.1–1%, F(2, 22)=1.66, p=0.21) and piriform cortex (black circles; n = 12, repeated measures ANOVA for concentrations 0.1–1%, F(2, 22)=11.08, p<0.001). Lines are fit to means as a function of concentration. Normalized spiking output did not differ significantly from 1 for any concentration in either region (one sample t-test, p>0.05). (D) Percent piriform cortex neurons significantly responding with increases in firing rate (red circles) or decreases in firing rate (blue circles; p<0.05, Wilcoxon rank-sum test vs. blank stimulus, n = 9). Lines are fit to means as a function of concentration. The percent of suppressed cells increased with concentration but the percent of activated cells did not change (repeated measures ANOVA, activated: F(3, 24)=0.25, p=0.86; suppressed: F(3, 24)=10.83, p<0.001). (E) Average piriform firing rates are not systematically concentration-dependent. Change in firing rate compared to blank responses for all cells for both concentration series (n = 918). Black unfilled circles are mean firing rate changes as a function of concentration for all recorded cells (s.e.m. smaller than marker size). Thin red and blue lines indicate concentration curves for cells that were significantly activated or suppressed for at least one concentration. Unfilled red and blue circles are mean changes in firing rate for these activated and suppressed cells, respectively. Thin gray lines are concentration curves for cells that were unresponsive at any concentration. Average firing rates changed for all responses and for suppressed responses as a function of concentration, but not for activated responses (repeated measures ANOVA, all: F(3, 2751)=23.00, p<0.001; activated: F(3, 354)=1.24, p=0.30; suppressed: F(3, 705)=40.08, p<0.001).
Figure 2—figure supplement 1
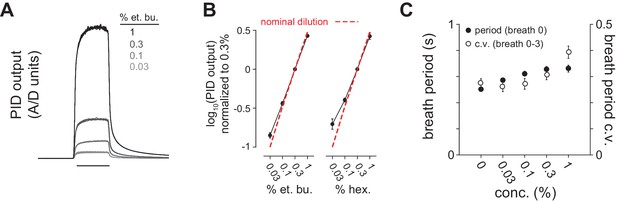
Reliable delivery of odor concentration series and concentration-dependent effects on breathing.
(A) Odor delivery was rapid and reliable across a 30-fold range of concentration. Traces are photoionization detector (PID) output overlaid for 12 trials each of 0.03, 0.1, 0.3 and 1% dilutions of ethyl butyrate in mineral oil. (B) Odor concentration series diluted in mineral oil reliably produced corresponding PID output separated by 0.5 log10 steps. PID output was monitored at final valve exhaust in 8/9 experiments (n = 8). The dashed line shows nominal dilution. (C) Breath period measured immediately after odor delivery (filled circles) and coefficient of variation over four breaths after odor delivery (unfilled circles) as a function of stimulus concentration (n = 12, i.e. 6 experiments x 2 different odorants). Breath period increases systematically with concentration but absolute difference in period is <100 ms. Respiration amplitude and frequency did not change following odor delivery at any concentration in anesthetized mice (not shown). Here, however, we observed small but systematic concentration-dependent changes in sniffing behavior, indicating that these different concentrations are perceived as odors of different intensities (Sirotin et al., 2015).
Figure 3
Distribution of spike times changes with concentration.
(A) Population PSTHs averaged across, and normalized by, all 48 cells in an example experiment are shown as a function of concentration of ethyl butyrate (left) or hexanal (right). Dashed line indicates inhalation onset. (B) As above but with PSTHs averaged across all 459 recorded cells as a function of concentration. (C) The peak/average ratio, which indicates synchrony, increases significantly with concentration for both odors (repeated measures ANOVA, et. bu.: F(3, 24)=7.44, p<0.01, n = 9; hex.: F(3, 24)=6.29, p<0.01, n = 9).
Figure 4 with 1 supplement
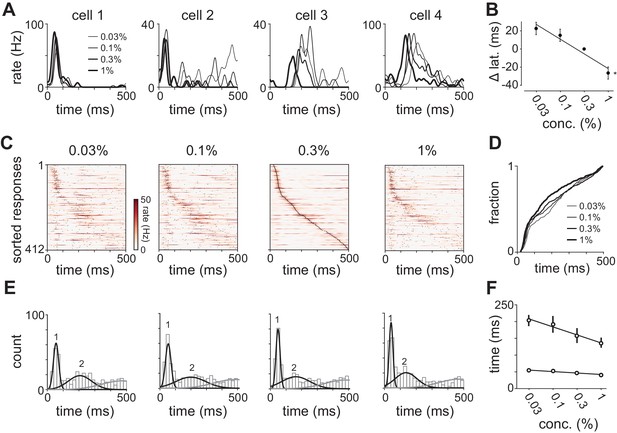
Odor concentration alters response timing.
(A) Odor-evoked changes in firing rate for four cells in response to different odorant concentrations. Response latencies systematically decreased at higher concentrations in some activated cells but not in others. (B) Response latencies averaged across all piriform cortex cells decreased with concentration (repeated measures ANOVA for relative latencies at 0.03%, 0.1%, and 1%, F(2, 1834)=25.85, p<0.001; n = 918). Relative latencies at each concentration were significantly different from 0 (one sample t-test for 0.03%, 0.1%, and 1%, p<0.05, n = 918). Line is fit to relative latency means as a function of concentration. (C) PSTHs for responses in which a peak could be identified within the 500 ms response window. Cells are sorted by their latencies to peak at 0.3% v./v. with the same sorting order maintained for responses at different concentrations. Black dots indicate times of peak response. (D) Cumulative distributions of latencies to response peak at different concentrations. (E) Histograms of latency to peak distribution overlaid with fits for a mixture of three Gaussians. Note that while peak latencies decreased systematically at higher concentrations the timing of the earliest responses was largely concentration-invariant. (F) Timing of the first and second peaks of Gaussian fits (see Figure 4—figure supplement 1) for the distribution of latencies to peak activation (black circles, error bars are 2.5–97.5th percentile of bootstrap model fits).
Figure 4—figure supplement 1
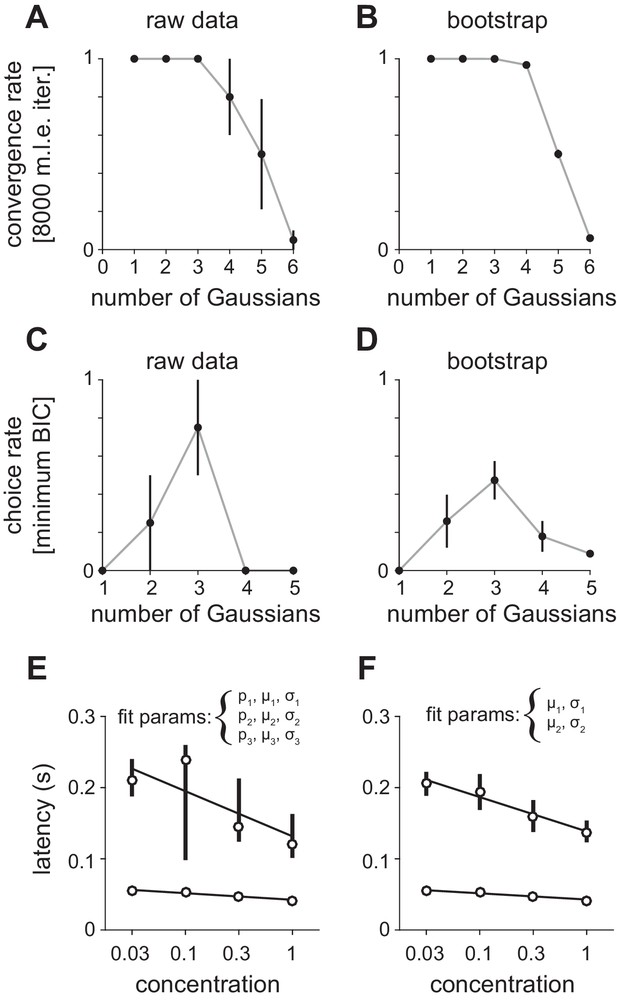
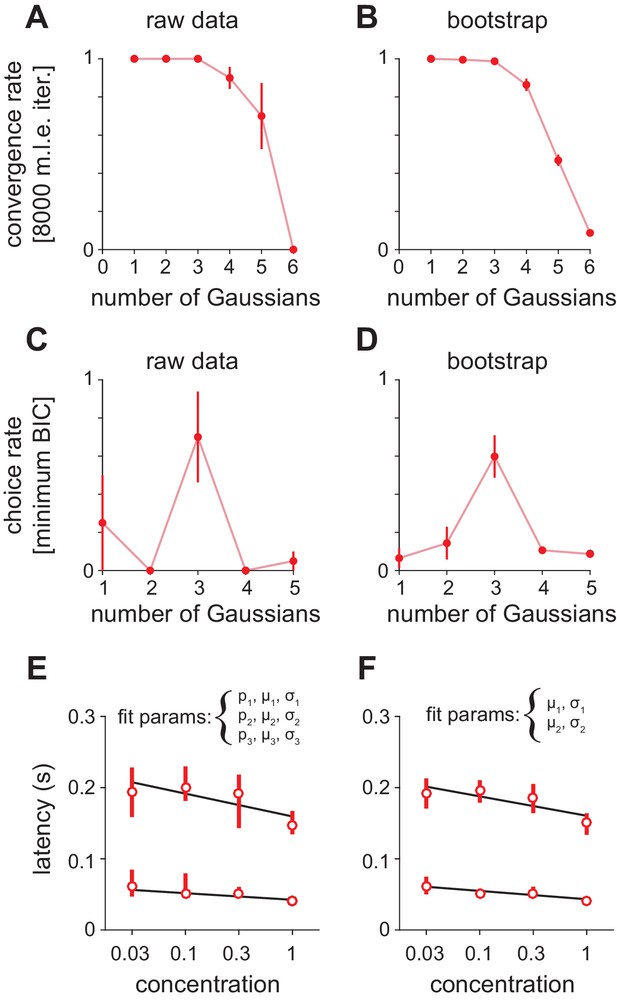
Fitting Gaussian mixture models to peak latency distributions.
(A–D) Distributions were fit with a mixture of truncated Gaussians (truncated between 0 and 500 ms) using maximum likelihood estimation (MLE), including increasing numbers of mixture components in the model. (A) For repeated initialization and fitting to either (A) measured or (B) bootstrapped latency distributions, the MLE algorithm readily converged within 8000 iterations for up to five mixture components. Convergence rates were averaged across concentrations. Attempted fits that failed to converge were not included in any further analysis. Bootstrap latency distributions were obtained by sampling with replacement (1000 bootstrap samples) from the measured latency distributions. The Bayesian Information Criterion (BIC) was used to select the number of mixture components that provided the best fit for each (C) measured or (D) bootstrapped latency distribution, penalizing for extra free parameters. Three components most often provided the best fit for both distributions. (E) MLE estimates for the first two mixture components when proportion (p), mean (μ), and standard deviation (σ) were free for all three distributions. Circles indicate mean latencies estimated from raw data, bars show 2.5–97.5th percentiles of fits to bootstrap samples. Assignment of some later responses into either the second or third mixture component across bootstrap iterations introduced variability. (F) To specifically estimate concentration-dependent changes in the timing of the first two mixture components (corresponding to obvious peaks in the latency distribution) we held constant the mixing proportions for all components, as well as all parameters for the third component, allowing only the mean and standard deviation for the first two components to vary. This substantially reduced the variability of parameter estimates.
Figure 5 with 5 supplements
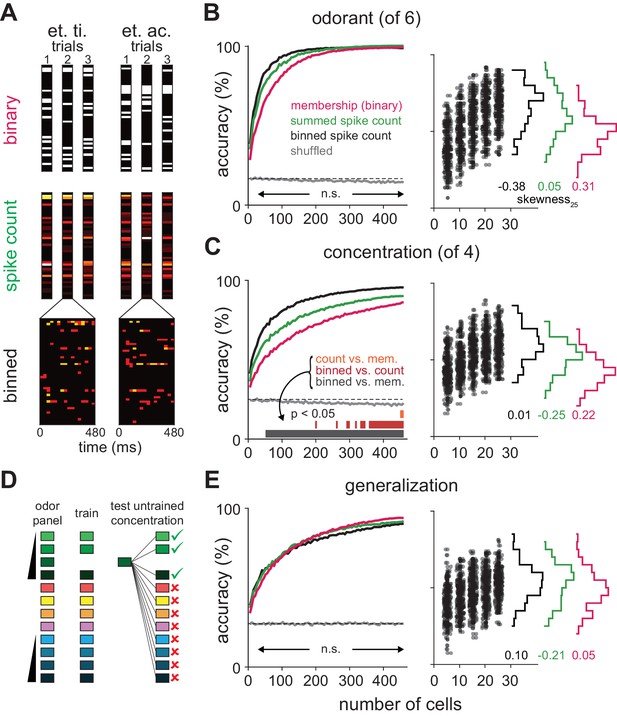
Coding strategies for representations of odor identity and intensity.
(A) Feature vectors for classifier analysis were constructed as either spike counts summed over a 480 ms response window (middle), as binary activation vectors (top), or as spike counts for 16 concatenated 30 ms bins over the same time period (bottom). Binary activation vectors were constructed according to a 1 st. dev. threshold above mean spike counts on blank trials. (B) (Left) Classification accuracy for identifying one of six different odorants as a function of number of cells using binarized spike counts (magenta), summed spike counts (green) or binned spike counts (black). Data are mean accuracy for 200 permutations of pseudopopulation construction. Differences in classification accuracy using different coding schemes failed to reach statistical significance (p>0.05, see Figure 5—figure supplement 2). Classifier performance using shuffled trial label-spike counts (grey) was at chance levels (dashed line). (Right) Points illustrate accuracy for individual pseudopopulations at low sample sizes using binned spike count representations. Distribution of accuracies using different 25-cell populations is shown at the right for each coding scheme. (C) Same as B for classification for one of four concentrations of the same odorant. Spike time information markedly enhances intensity decoding accuracy. Accuracy for each permutation was the average of accuracy for the two different concentration series. Shading indicates points at which decoding accuracy was significantly different (p<0.05) for different coding schemes. (D–E) Odor identity classification accuracy for a classifier trained with all stimuli except for one concentration of the target odorant (n = 11 different stimuli) and then tested using the withheld responses. Accuracy was assessed for correctly identifying the odorant regardless of concentration. Differences in classification accuracy using different coding schemes failed to reach statistical significance (p>0.05).
Figure 5—figure supplement 1
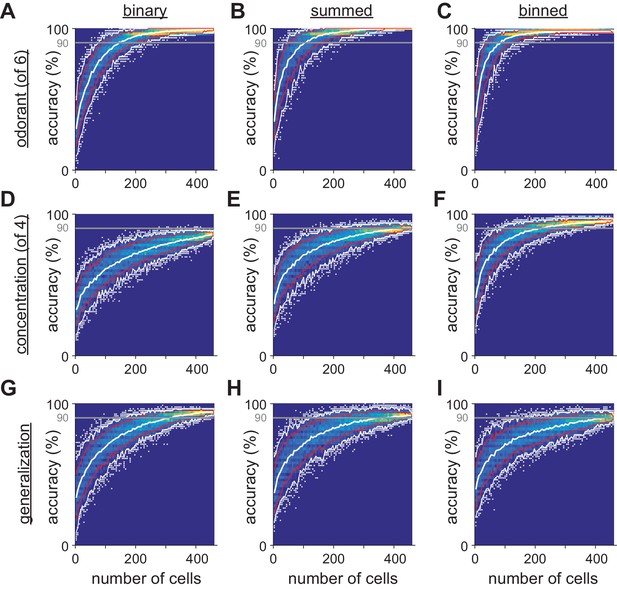
Limited heterogeneity of stimulus information among piriform cortex neurons.
(A–I) The distribution of classifier outcomes for 200 permutations of pseudopopulations of n cells are shown as a heat map for each odor feature and each type of response vector. Curves indicate the 10–90th (red curves) and 2.5–97.5th percentiles (white curves), and white dots show the 5% of most extreme classifier outcomes, indicating the coding efficiency of the most and least informative groups of cells.
Figure 5—figure supplement 2
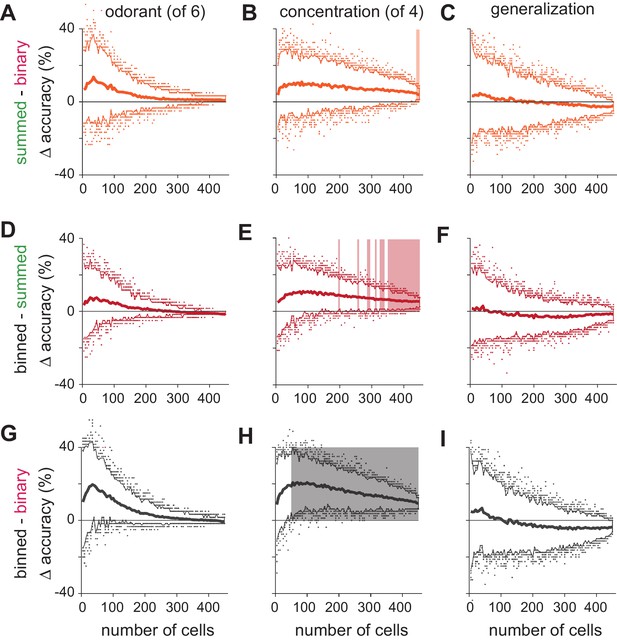
Significance testing of classifier performance.
(A–C) Differences in classification accuracy using spike count vs. binary representations for (A) different odorants, (B) concentrations, and (C) identity generalization tasks. For each permutation, a random pseudopopulation of n cells was selected and differences in classification accuracy using the three types of representations was determined. Data are plotted as mean differences (thick lines) and 2.5–97.5th percentiles (thin lines) for 200 permutations of pseudopopulations of n cells; colored dots show the 5% of most extreme classifier outcomes. Shading indicates significant differences (p<0.05). Note that variance decreases with increasing numbers of cells in large part because more cells are used repeatedly in different permutations. (D–I) As above but for comparisons of (D–F) binned vs. summed representations and (G–I) binned vs. binary representations. Classification accuracies across coding strategies were never significantly different for either odorant classification or generalization. Concentration classification was almost never significantly different using summed vs. binary codes (B) but was significantly better using binned vs. summed codes with ~250 or more cells (E), and significantly better using binned vs. binary codes with as few as 50 cells (H).
Figure 5—figure supplement 3
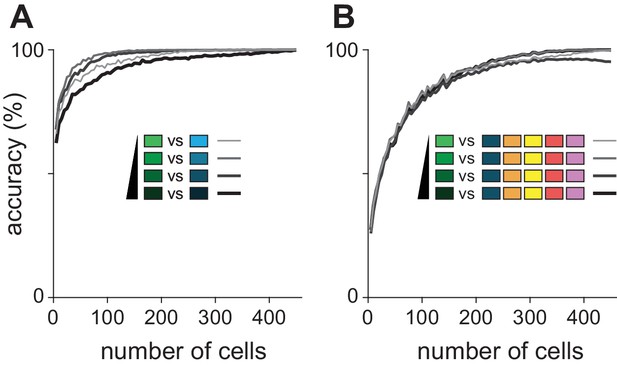
Odorant classification at different concentrations.
(A) Binary distinction between ethyl butyrate and hexanal was assessed over the range of stimulus concentrations. There was little difference in overall performance, though the lowest and highest concentrations were less somewhat less accurately identified. (B) The classifier was tested on ability to identify a target odorant presented at one of four concentrations among five other odorants presented at 0.3% v./v. Again, accuracy varied little with concentration.
Figure 5—figure supplement 4
Classification with real versus pseudopopulations.
Odor identity classification accuracy using spike count vectors as a function of population size either for simultaneously recorded populations (green, mean ± s.e.m.) or pseudo-populations constructed by combining equal numbers of cells from each recording (black, mean ± s.e.m. n = 50 population selection iterations). Classifier performance with pseudo-populations on trials shuffled for odor identity is shown in gray (mean ± s.e.m. n = 50 population selection iterations). Dashed line indicates theoretical chance. The number of individual experiments included in the average decreases as number of cells increases, reflecting the variable number of cells recorded in each experiment.
Figure 5—figure supplement 5
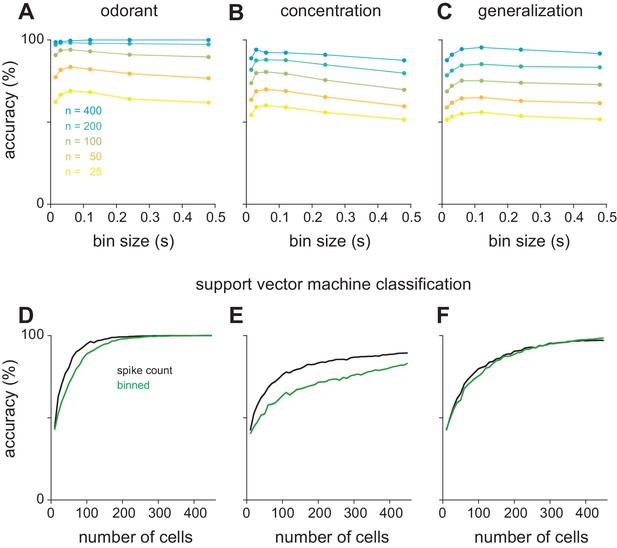
Optimal bin size for classification and alternate classifier method.
(A–C) Performance of the Euclidean distance classifier as a function of bin size for odorant (A), concentration (B), and identity generalization (C) tasks. Concentration decoding generally benefited from small bin sizes (30 ms) while generalization was optimal with larger bins (60 or 120 ms). Colors indicate sample size of pseudopopulation. Each point represents mean of 200 permutations of pseudopopulation selection. Lines and shaded area are mean ± s.e.m. (D–F) Differences between coding efficiency of binned and summed spike count representations are preserved in performance of support vector machine classification on odorant (D), concentration (E), and identity generalization (F) tasks.
Figure 6
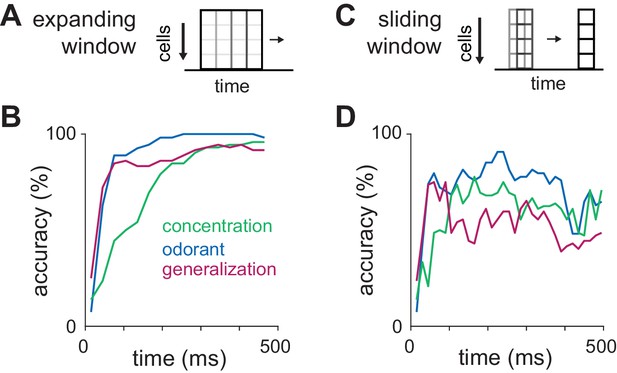
Dissociating identity and intensity coding.
(A–B) Classification accuracy for odorant, intensity, or identity generalization as a function of integration time using an ‘expanding window’ consisting of feature vectors with increasing numbers of 30 ms bins for up to 480 ms. Pseudopopulations were constructed from all recorded cells (n = 459). The accuracy of intensity classification lags behind that for identity classification by ~100 ms and plateaus at a lower value. (C–D) Classification accuracy for odorant, intensity, or identity generalization as a function of time after inhalation using spike counts in a sliding 30 ms window as feature vectors. Note that while odorant classification accuracy remains elevated through the end of the sniff, generalization accuracy falls as concentration accuracy improves.
Figure 7 with 1 supplement
Response latencies for olfactory bulb cells change with concentration.
(A) PSTHs for olfactory bulb responses sorted by their latencies to peak at 0.3% v./v. with the same sorting order maintained for responses at different concentrations. Black dots indicate time of peak responses. (B) Cumulative distributions of latencies to response peak at different concentrations. (C) Histograms of latencies to peak activation for olfactory bulb responses overlaid with fits for a mixture of three Gaussians. Olfactory bulb responses can clearly be divided into two phases but with different dynamics to those in piriform cortex. (D) Timing of the first and second peaks of Gaussian fits for the distribution of latencies to peak activation (red circles, error bars are 2.5–97.5th percentile of bootstrap model fits). Replotted results from Figure 4F show timing of peaks in piriform cortex (black circles).
Figure 7—figure supplement 1
Fitting Gaussian mixture models to olfactory bulb peak latency distributions.
(A–D) Distributions were fit with a mixture of truncated Gaussians (truncated between 0 and 500 ms) using maximum likelihood estimation (MLE), including increasing numbers of mixture components in the model. (A) For repeated initialization and fitting to the measured latency distribution, the MLE algorithm readily converged within 8000 iterations for up to five mixture components. Convergence rates were averaged across concentrations. Attempted fits that failed to converge were not included in any further analysis. (B) Bootstrap latency distributions were obtained by sampling with replacement from the measured latency distributions. (C) For each measured latency distribution, the Bayesian Information Criterion (BIC) was used to select the number of mixture components that provided the best fit, penalizing for extra free parameters. (D) For bootstrap samples, the identical sample was fit with each of the the possible number of mixture components and the model with the lowest BIC was selected. (E) MLE estimates for mean of the first two mixture components. Circles are estimates from the raw data, bars show 2.5–97.5th percentiles of fits to bootstrap samples. When mixing proportion (p), mean (μ), and standard deviation (σ) are free for all three distributions, uncertainty in the attribution of spikes to the second or third (not shown) mixture component introduces substantial variability across bootstrap estimates. (F) As in E but with constant mixing proportions for all components and all parameters for the third component held constant, allowing only the mean and standard deviation for the first two components to vary.
Figure 8
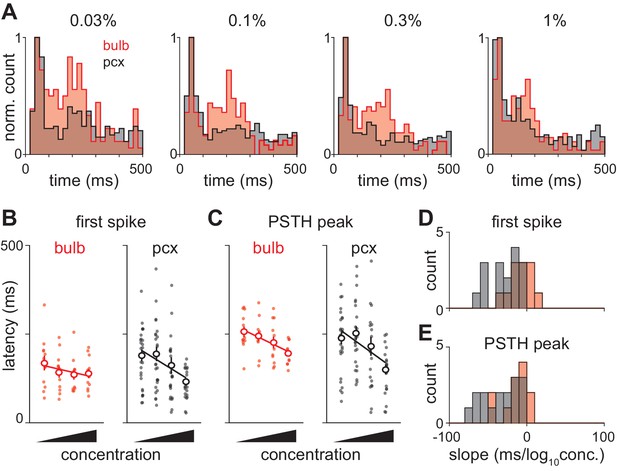
Olfactory bulb input is actively transformed in piriform cortex.
(A) Response peak latency histograms normalized to peak value and overlaid for bulb and piriform. The second phase of responses is more prominent in bulb than in piriform cortex at all but the highest concentration (KS test: 0.03%, 0.0263; 0.1%, 0.0160; 0.3%, 0.0145; 1%, 0.1603). (B–C) Example experiment showing changes in ethyl butyrate response latencies in simultaneously recorded populations of bulb and piriform cells. Response latency for each cell was taken as either the average time to first spike (B) or the average time to PSTH peak (C). Points are average response latencies for each cell at different concentrations. Lines are fit to the average of these points. (D–E) Distribution of fitted slopes for bulb (n = 12, 6 experiments * 2 odors, red) and piriform (n = 16, 8 experiments * 2 odors, red). Fitted slopes were reliably steeper as a function of concentration for piriform populations (unpaired t-test: first-spike, p=0.004; PSTH peak, p=0.016).
Figure 9
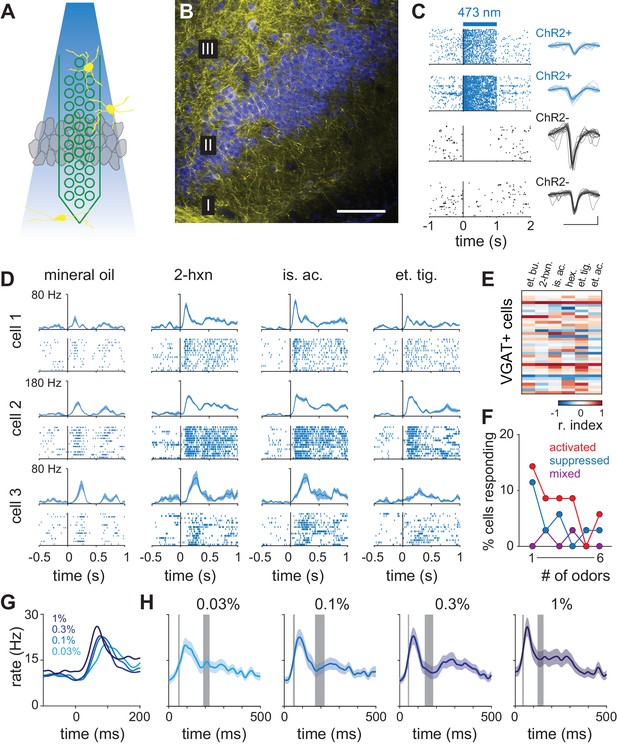
Dynamics of cortical inhibition indicates their role in shaping piriform responses.
(A) Schematic of experiment. Optogenetic identification of ChR2-expressing neurons in piriform cortex of VGAT-ChR2-EYFP transgenic mice. (B) Coronal section of anterior piriform cortex of VGAT-ChR2-EYFP mouse showing dense innervation of layer II/III, consistent with feedback inhibition (yellow, anti-GFP; blue, neurotrace). Scale bar, 100 μm. (C) One second laser pulses (2.5 mW/mm2) evoke sustained responses in presumptive ChR2-expressing neurons (blue raster plots) but sustained suppression in most other cells (black). Scale bar, 50 μV, 1 ms. (D) PSTHs and raster plots for three VGAT+ cells responding to mineral oil control or three different odors. (E) Response matrix for all recorded VGAT+ cells (n = 35) responding to six different odors. (F) Tuning for all recorded VGAT+ cells. Responses tended to be positive and broadly-tuned. (G–H) Average PSTHs for all VGAT+ cell responses (lines and shading are mean ± s.e.m; n = 70, 35 cells x 2 odors) at four concentrations. (G) PSTHs shown on a short time scale. Stronger and earlier peaks occur at higher concentrations. (H) Average VGAT+ PSTHs overlaid with the bootstrap confidence intervals (gray bars) for the first and second peaks of the piriform cortex response latency distributions from Figure 3.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Complementary codes for odor identity and intensity in olfactory cortex
eLife 6:e22630.
https://doi.org/10.7554/eLife.22630
