Sphingomyelin metabolism controls the shape and function of the Golgi cisternae
- ICFO-Institut de Ciencies Fotoniques, The Barcelona Institute of Science and Technology, Spain
- The Barcelona Institute of Science and Technology, Spain
- Universitat Pompeu Fabra, Spain
- National Research Council of Italy, Italy
- Sackler Faculty of Medicine, Tel Aviv University, Israel
- Institució Catalana de Recerca i Estudis Avançats (ICREA), Spain
Figures
Figure 1 with 1 supplement
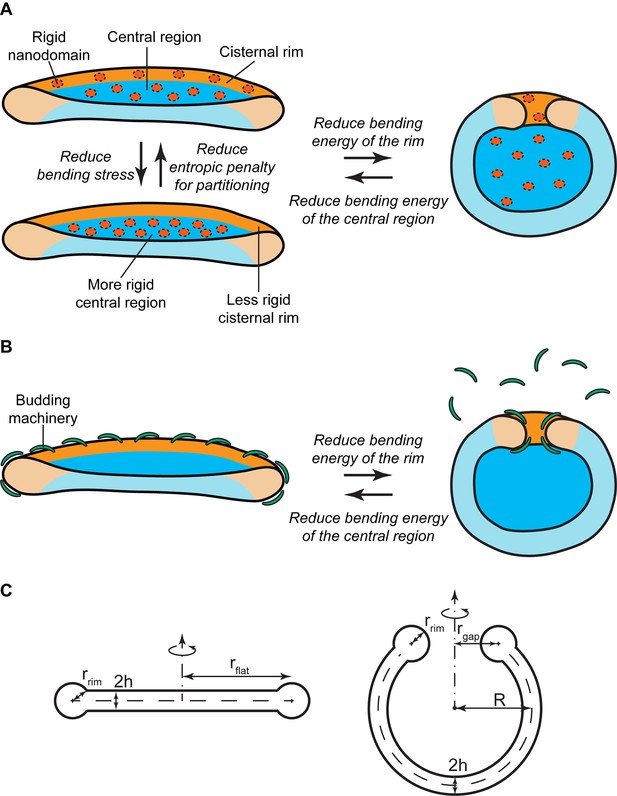
Mechanisms of SM-regulated Golgi cisternae morphology.
(A) Nanodomain partitioning-mediated mechanism. A schematic representation of flat (left) and curled (right) Golgi cisternae is shown, where the highly bent cisternae rims and the flatter central regions are colored in orange and blue, respectively, and rigid nanodomains in red. Non-homogeneous partitioning of rigid nanodomains from the rim to the central region of a flat cisterna (left) reduces the overall bending stress but increases the entropic free energy penalty of partitioning. Flat-to-curled cisterna transition (left to right) reduces the bending energy of the rim in expenses of an increase in the bending energy of the central region. (B) SM-dependent release of budding effectors. Membrane curvature generating proteins, such as components of the budding machinery, present at the cisterna rims are shown in green. Partial release of these proteins from the membranes can lead to destabilization of the flat cisterna rim, and a flat-to-curled cisterna transition can be triggered depending on the balance between the bending energies of the rim and flat regions. (C) Cross section of the geometry of the flat (left) and curled (right) cisterna configurations used in our model. The vertical axes are the axes of symmetry.
Figure 1—figure supplement 1
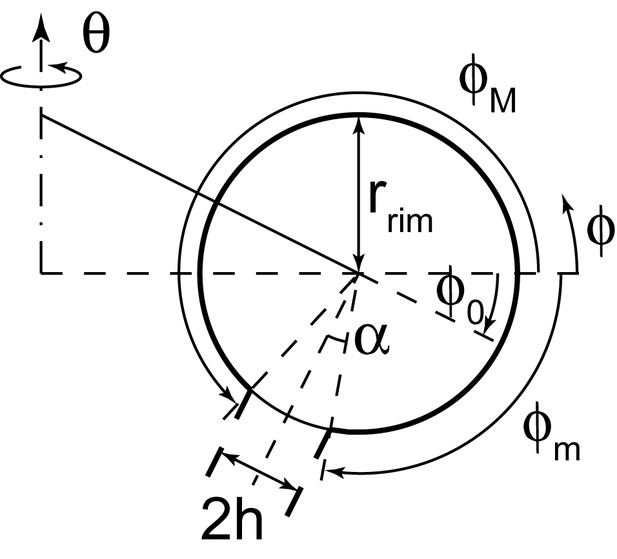
Geometry of the cisterna rim.
A detailed view of the geometrical variables at the rim of a curled cisterna is shown.
Figure 2 with 2 supplements
Shape diagram of a Golgi cisterna as a function of the area fraction of nanodomains and the membrane spontaneous curvature.
(A) The existence of locally stable flat and/or curled cisternae was quantitatively assessed using our model of cisterna morphology, and the results depicted in a shape diagram for different values of the area fraction covered by nanodomains, , and of the membrane spontaneous curvature, , (left panel). Four regions can be distinguished: a region where curled cisternae are the only locally stable shapes (orange), a region with only flat cisternae (blue), and two regions where curled and flat configurations are respectively stable and metastable (orange dashed) or metastable and stable (blue dashed). The designated orange, black and blue lines indicate the boundaries between these regions. In the right subpanel, the energy barriers for the flat-to-curled or curled-to-flat transitions within the bistability regions are shown and color-coded (only energy barriers smaller than are shown for clarity). (B) The total free energy of a cisterna with respect to the flat configuration as a function of the degree of curling, , for two different sets of parameters.
Figure 2—figure supplement 1
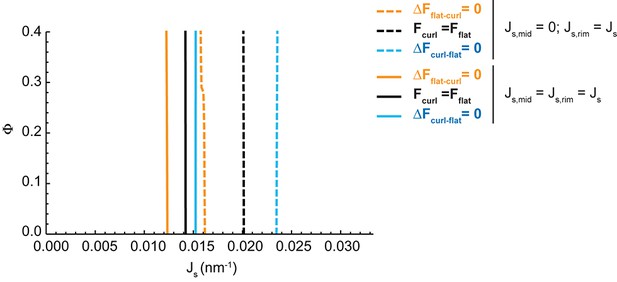
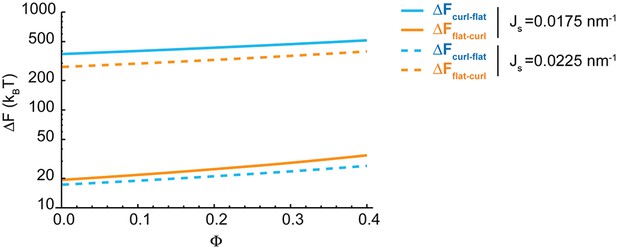
Effect of the distribution of budding effectors along the cisterna on the shape diagram.
Shape diagram boundary curves as designated in the legend plotted as for a range of values of the area fraction covered by nanodomains, , and of the membrane spontaneous curvature, , for a situation where the membrane spontaneous curvature is homogeneously distributed along the entire Golgi cisterna membrane, that is (solid lines). For comparison, the analogous shape diagram boundary curves are shown for the situation corresponding to the shape diagram in Figure 2A, where the membrane spontaneous curvature is zero at the central part of the cisterna and takes the value at the cisterna rims (dashed lines).
Figure 2—figure supplement 2
Effect of the nanodomain area fraction on the shape transitions.
The value of the energy barriers for curled-to-flat (blue lines) and curled-to-flat (orange lines) shape transitions are plotted in logarithmic scale as a function of the total area fraction of rigid nanodomains, , for two different values of the spontaneous curvature, (solid lines), and (dashed lines).
Figure 3
Control of the flat-to-curled cisterna transition by the membrane curvature generators.
(A) The total free energy of a cisterna with respect to the flat configuration as a function of the membrane spontaneous curvature, , for both curled (orange line) and flat (blue line) configurations. The maximum free energy of the energy barrier between flat and curled configurations, , is shown as a solid black line. The different regions are color coded as in Figure 2A. (B) The energy barrier between curled and flat (blue line) and between flat and curled (orange line) configurations is represented in logarithmic scale as a function of the membrane spontaneous curvature, . A horizontal dash line corresponding to a limit of kinetically feasible transitions is shown. (C) The relative enrichment in rigid nanodomains between the rim and central regions of the cisternae is represented as a function of the membrane spontaneous curvature, , for both curled (orange line) and flat (blue line) configurations. (D) The degree of cisterna curling, , is represented as a function of the membrane spontaneous curvature, , for both curled (orange line) and flat (blue line) configurations. Dashed lines represent metastable configurations whereas solid lines represent globally stable configurations. Different arrows representing flat-to-curled or curled-to-flat transitions are detailed in the legend. See text for details on the meaning of circled numbers. (A–D) The area fraction covered by rigid nanodomains has a fixed value of .
Figure 4 with 1 supplement
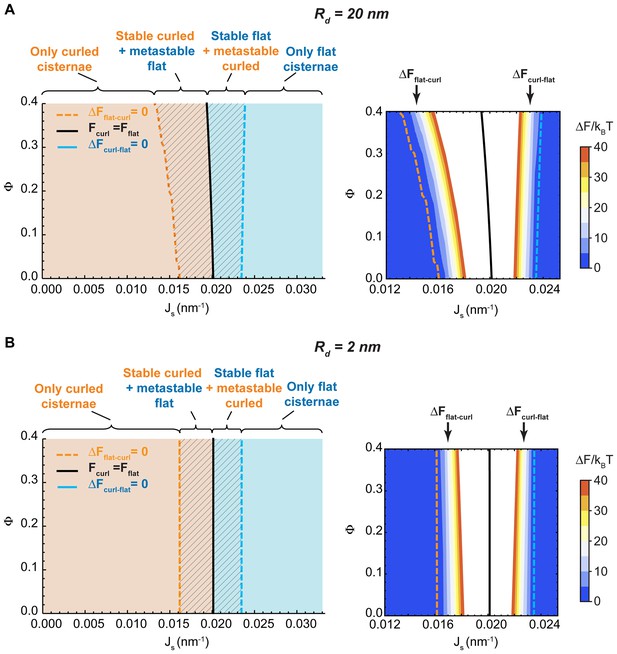
Effect of the nanodomain size on the Golgi cisterna shape diagram.
(A,B) Shape diagrams for different values of the area fraction covered by nanodomains, , and of the membrane spontaneous curvature, , (left panels), for two different values of the nanodomain radius, , (A) and , (B). Four regions can be distinguished: a region where curled cisternae are the only locally stable shapes (orange), a region with only flat cisternae (blue), and two regions where curled and flat configurations are respectively stable and metastable (orange dashed) or metastable and stable (blue dashed). The designated orange, black and blue lines indicate the boundaries between these regions. In the right subpanels, the energy barriers for the flat-to-curled or curled-to-flat transitions within the bistability regions are shown and color-coded (only energy barriers smaller than are shown for clarity).
Figure 4—figure supplement 1
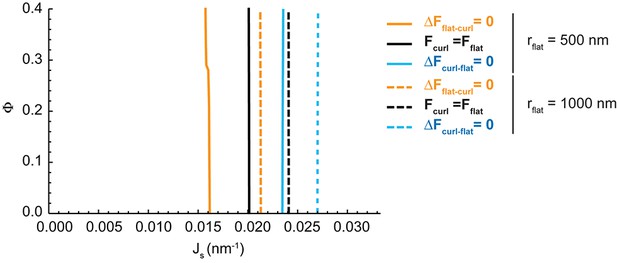
Effect of the cisterna surface area on the Golgi cisterna shape diagram.
Shape diagrams for different values of the area fraction covered by nanodomains, , and of the membrane spontaneous curvature, , for two different values of the flat cisterna radius, (solid lines), and (dashed lines).
Figure 5
Effect of lateral DAG partitioning on the cisterna shape transition.
(A) Schematic representation of the proposed mechanism of non-homogeneous DAG partitioning along the two monolayers of a Golgi cisterna for both flat (left) and curled (right) configurations. Colored triangles represent DAG molecules in the cytosolic (blue) and luminal (red) leaflets of both the top and bottom bilayers of the Golgi membrane. (B) Shape diagram showing the globally stable configuration of the system (curled cisterna in orange, flat cisterna in blue) for different values of the total molar fraction of DAG in the membrane, , and of the membrane spontaneous curvature, . The experimentally observed increase in DAG levels after short-chain ceramide treatment is indicated by the arrow between the two dashed black lines. (C) Optimal molar fraction of DAG in the cytoplasmic (, blue line) and luminal (, red line) monolayers of the cisterna top bilayer plotted as a function of the total molar fraction of DAG, . The dashed line corresponds to a homogeneous DAG distribution.
Figure 6 with 1 supplement
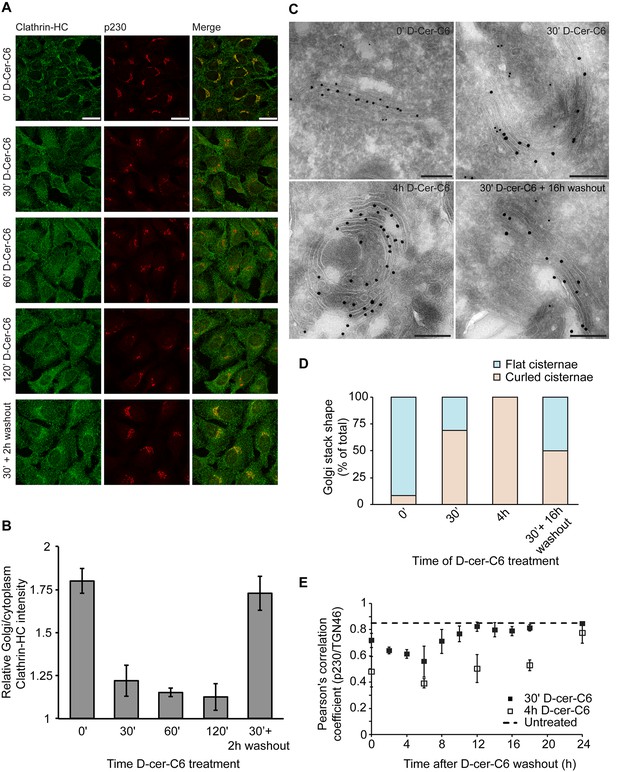
Experimental results.
(A) HeLa cells were treated with 20 µM D-cer-C6 for the indicated times, after which the cells were fixed and the localization of clathrin-HC and the TGN marker protein p230 was monitored by immunofluorescence microscopy. Scale bar is 25 µm. (B) Quantitation of the results in (A) showing the intensity of clathrin-HC in the Golgi area relative to the intensity in the rest of the cytoplasm, for at least 15 cells from three different experiments. Bars represent average values and error bars are the S.E.M. (C) HeLa cells stably expressing the Golgi-resident protein Mannosidase-II-GFP were treated with 20 µM D-cer-C6 for the indicated times, fixed, and the Golgi complex ultrastructure visualized by immunoelectron microscopy. Gold particles of 10 nm and 15 nm label p230 and GFP, respectively. Scale bar is 200 nm. (D) Quantitation of the percentage of flat (blue) and curled (orange) cisternae in the Golgi stacks observed in the experiment presented in (C). (E) HeLa cells were treated with 20 µM D-cer-C6 for either 30' (solid black squares) or 4 hr (empty squares), after which the cells were extensively washed and incubated for different times in complete medium without D-cer-C6. Then, the cells were fixed and the levels of co-localization of two trans-Golgi membrane proteins p230 and TGN46 were quantitated from the immunofluorescence images by means of the Pearson's correlation coefficient, which is plotted here as a function of the washout time. The dashed horizontal line represents the Pearson's correlation coefficient for TGN46 and p230 in untreated HeLa cells.
Figure 6—figure supplement 1
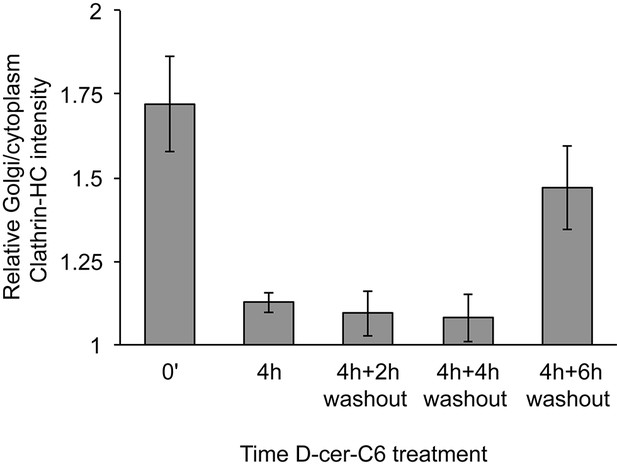
Relative localization of Clathrin-HC at the Golgi area in D-cer-C6 treated cells.
HeLa cells were treated with 20 µM D-cer-C6 for 0 hr or 4 hr, after which the cells were extensively washed and incubate in normal medium for the indicated times. Then the cells were fixed and the localization of Clathrin-HC and the TGN marker protein p230 was monitored by immunofluorescence microscopy and the results quantitated. The bars show the intensity of Clathrin-HC in the Golgi area relative to the intensity in the rest of the cytoplasm, for at least 15 cells from three different experiments. Bars represent average values and error bars are the S.E.M.
Figure 7
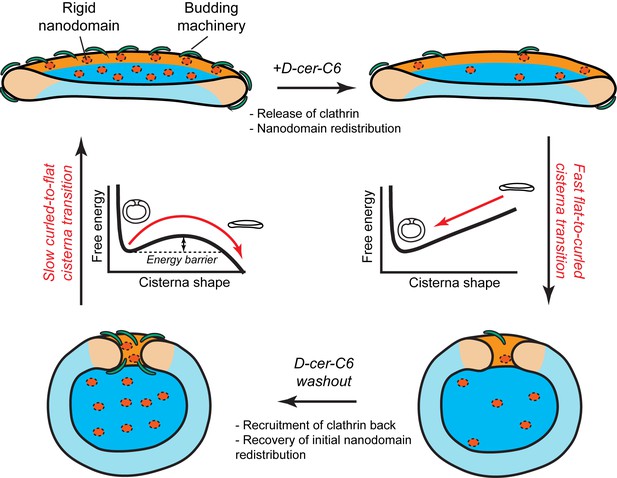
Model of how SM metabolism controls the shape of a Golgi cisterna.
In stationary conditions (top left cisterna), a Golgi cisterna appears as a flat, disc-like structure, with relatively large amounts of budding machinery (green proteins), such as the components of the clathrin-coated vesicles. The Golgi membranes contain about 10% molar fraction of long chain SM, which could be organized in small rigid nanodomains (red patches). Treatment of cells with D-cer-C6 leads to a reduction in the levels of rigid domain-forming SM, a release of clathrin-HC from the Golgi membranes and, according to our physical model, a lateral redistribution of the remaining rigid nanodomains away from the rim (top right cisterna). Under these conditions, the cisterna free energy profile has a single minimum corresponding to a highly curled cisterna configuration and hence, a rapid flat-to-curled cisterna transition is promoted (bottom right cisterna). Washout of D-cer-C6 leads to the recovery of stationary levels of clathrin to the Golgi membranes and, we hypothesize, of the initial levels of rigid SM-rich nanodomains (bottom left cisterna). Under these conditions, the cisterna free energy profile has two local minima corresponding to highly curled and flat cisterna configurations, separated by an energy barrier. The system can thus be kinetically trapped in the curled, metastable configuration and therefore a slow transition back to the flat configuration (top left cisterna) is expected.
Appendix 1—figure 1
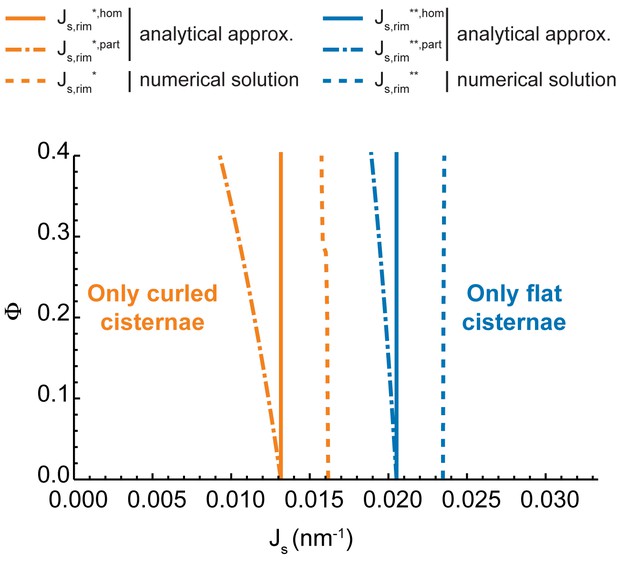
Analytical approximation of the shape diagram.
Comparison between the numerically-computed shape diagram of a Golgi cisterna (simple dashed lines) to the one obtained by using an analytical approximation, for homogeneous nanodomain distribution (solid lines) and complete nanodomain partitioning (dot-dashed lines). We used the same elastic and geometric parameters as in Figure 2A (see Table 1). Orange lines represent the transition lines below which only curled cisternae are locally stable shapes, whereas blue lines represent the loss of local stability of curled cisternae.
Appendix 1—figure 2
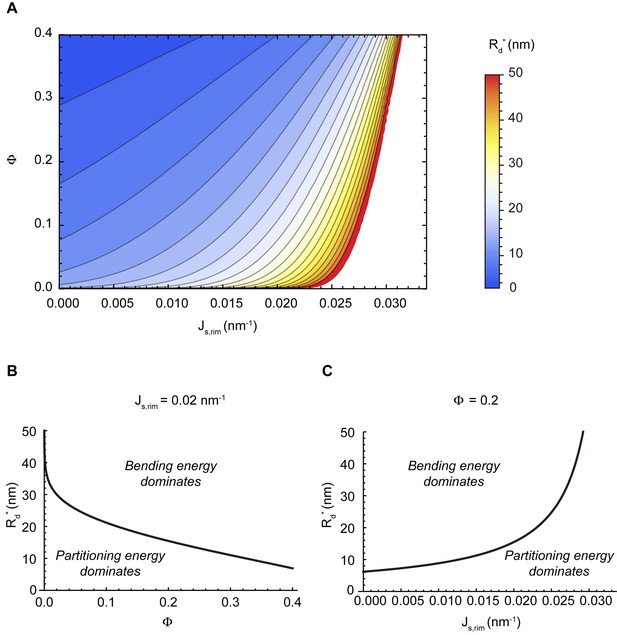
Comparison of the partitioning and bending energy terms of the free energy.
Critical nanodomain size as a function of the nanodomain area fraction and the spontaneous curvature of the rim (A), or plotted separately as a function of the nanodomain area fraction for a fixed value of the rim spontaneous curvature (B), and as a function of the rim spontaneous curvature for a fixed nanodomain area fraction (C). In (B) and (C), the regions where bending energy or partitioning energy dominate are indicated.
Appendix 1—figure 3
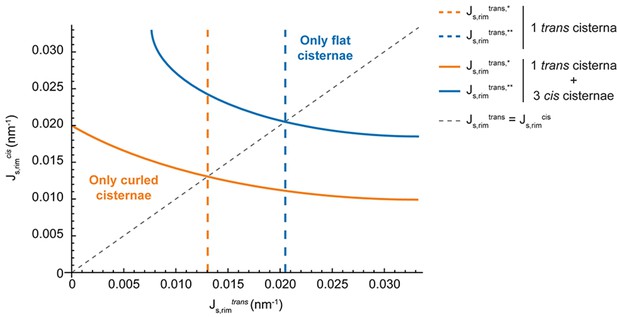
Effect of multiple stacked cisternae on the Golgi shape diagram.
The transition curves where flat (orange) or curled (blue) cisternae cease to be locally stable configurations are shown for a stack composed of 1 trans-like cisterna and 3 cis-like cisternae (solid lines) and compared to the situation of a single trans-like cisterna (dashed lines). In addition, we show the path where the spontaneous curvatures of the trans-like and cis-like cisternae are equal (grey dashed line), showing that under this constraint, the shape diagram does not depend on the number of cisternae of each kind.
Tables
Table 1
Model parameters.
| Parameter | Value(s) |
|---|---|
| 500 nm; 1000 nm | |
| 30 nm | |
| 15 nm | |
| 5 nm; 2 nm; 20 nm | |
| 0–0.4 | |
| 20 kBT | |
| 80 kBT | |
| −0.83 | |
| 0–0.033 nm−1 |
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Sphingomyelin metabolism controls the shape and function of the Golgi cisternae
eLife 6:e24603.
https://doi.org/10.7554/eLife.24603
