Dye-enhanced visualization of rat whiskers for behavioral studies
Figures
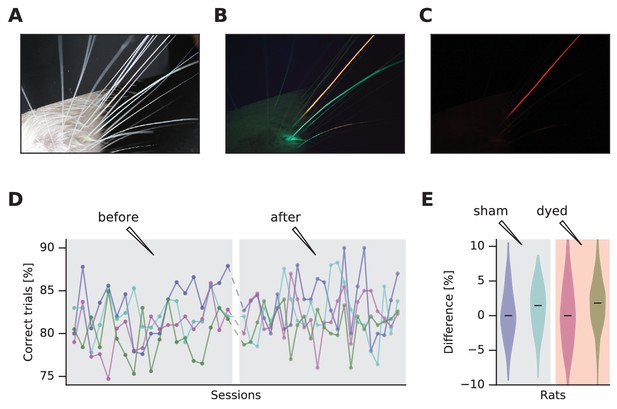
Dye-enhanced whisker visualization and effect on behavior.
(A) Vibrissal pad with two whiskers dyed, under white light. (B) Same as (A) but under blue light and long-pass optical filter. (C) Same as (B) but with red plexiglass. (D) Effect of vibrissal pad coloring (pink, olive) and sham treatment (violet, jade) on daily performance of a vibrissal vibration discrimination task. Chance performance would be 50%. (E) Violin plots of difference in performance before and after treatment. The distributions are generated by permuting every data point before with every data point after.

Whisker modeling and testing.
(A) Log mFRF of the whisker approximated as a tapered beam by FEM model. Three arrowheads indicate the first three modal frequencies. (B) Experimental setup. The blue device at the top is the custom-made orientable lamp mounting. Below is the whisker mounted on a custom-made holder attached to the loudspeaker. To the left is a sample of the shaker input signal, which was estimated by tracking the base of the whisker and has been used as input for the computation of the mFRFs (vertical line corresponds to ± 1 standard deviation, horizontal line corresponds to 200 ms of signal, which has been also zoomed). To the right, image processing is summarized. The image is depicted from the camera’s point of view, with the angle selected so as to maximize the visible motion-induced displacement. From the thresholded raw image, points belonging to the whisker are identified in the region of interest and used to compute n equidistant samples along the whisker deflection using a B-spline model. (C) Log mFRF observed for the whisker modeled in (A). Three arrowheads indicate the first three modal frequencies, perfectly aligned with those of the simulation.
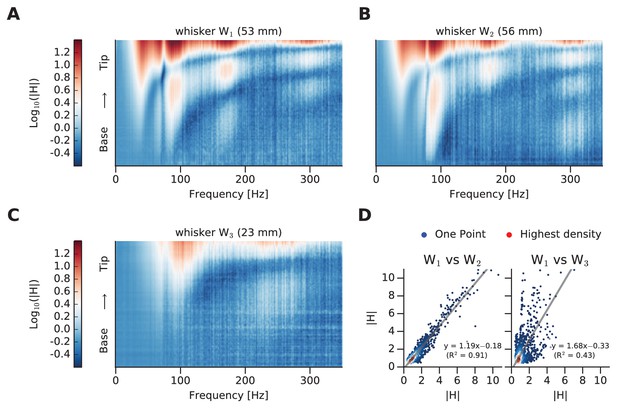
Comparison of whisker dynamic responses.
(A) Log mFRF of whisker W1. (B) Log mFRF of whisker W2. (C) Log mFRF of whisker W3. (D) Each scatter plot compares a pair of transfer functions, where each dot gives mFRF for a given frequency, position of both whiskers. On left panel W1 versus W2; on right panel W1 versus W3. The dot density has been encoded by coloring them from blue (single dot) to red.
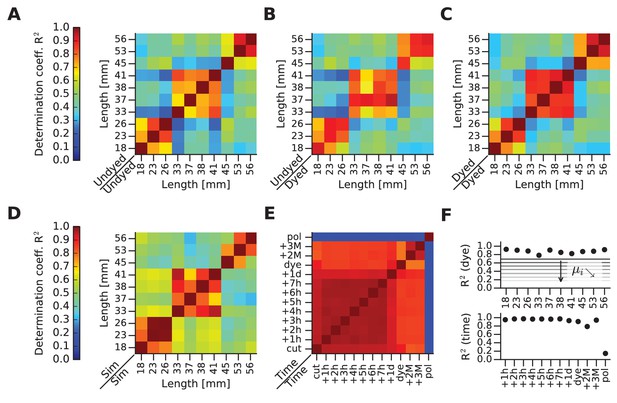
mFRF comparisons across whiskers and time.
(A) This and the next four panels depict matrices of similarity between mFRFs in pairwise (row against column) combinations. This first matrix illustrates similarities before dye application. (B) Matrix comparing the dyed and undyed conditions. (C) Matrix comparing whiskers after dye application. (D) Matrix computed for FEM-simulated (Sim) whiskers. (E) Matrix comparing one whisker over time. Time measures begin with ‘cut’ (immediately after whisker extraction from the snout), ‘dye’ (immediately after dye application) and ‘pol’ (immediately after the application and drying of nail polish). (F) In the upper panel, the diagonal values of the matrix shown in (B) are plotted (each whisker against itself, before and after dyeing). The set of values obtained by taking the i-th sub- and super-diagonal values of the matrix shown in (B) are averaged and represented with horizontal lines labeled i. The further from the main diagonal, the smaller is i, indicating that mFRF similarity decreases with increasing disparity in whisker length. The values of the diagonal are always high, highlighting the absence of dye effect on all samples: despite the application of the dye, each whisker is always more similar to itself rather than to other whiskers. On the lower panel, the supra-diagonal values of the comparison matrix shown in (E), which highlights stability up to the application of polish. In particular, by reference to the horizontal lines shown in the upper panel of (F), the change of the whisker caused by polish can be compared to the difference between the two whiskers of length 18 mm and 56 mm.
Videos
Proof of concept of the method.
https://doi.org/10.7554/eLife.25290.003Demonstration on high-speed video plus whisker tracking.
https://doi.org/10.7554/eLife.25290.004Additional files
-
Supplementary file 1
High-speed video.
A water reward spout armed with a licking sensor triggered the high-speed video recording (this is a frame of Video 2). The field of view is illuminated with four out of seven of the lamp’s LEDs and an orange plexiglass is used as an optical filter, demonstrating a high enough signal-to-noise ratio to allow whisker tracking, which is overlaid.
- https://doi.org/10.7554/eLife.25290.008
-
Supplementary file 2
Dye application method.
After sedation with Domitor: (A) all whiskers are chemically bleached. (B) The bleaching factor is removed with wet cotton and (C) dried with airflow. (D) The single whisker is isolated by paraffin film; (E) color is applied using another paraffin film and after the application time the excess color is washed away as in (B); (F) whisker coloring is tested under the long-pass filter.
- https://doi.org/10.7554/eLife.25290.009
-
Supplementary file 3
Photobleaching.
Normalized fluorescence intensity of the whisker (dark blue); exponential decay fit (light blue); exponential time constant expressed in hours of exposition (dashed line intersection with abscissa).
- https://doi.org/10.7554/eLife.25290.010
-
Supplementary file 4
Geometric and material parameters of the ten whiskers analyzed by the FEM model.
Recall that the modal frequencies do not depend on the Young’s modulus and mass density independently, as they depend on their ratio. This can be inferred from Equation (1) or Equation (5) in Materials and methods. Hence, we have tuned this ratio to fit the experimental results by keeping fixed the mass density and changing the Young’s modulus.
- https://doi.org/10.7554/eLife.25290.011





