Attenuation of dopamine-modulated prefrontal value signals underlies probabilistic reward learning deficits in old age
- Karolinska Institute, Sweden
- Umeå University, Sweden
- University College London, United Kingdom
Figures
Figure 1 with 1 supplement
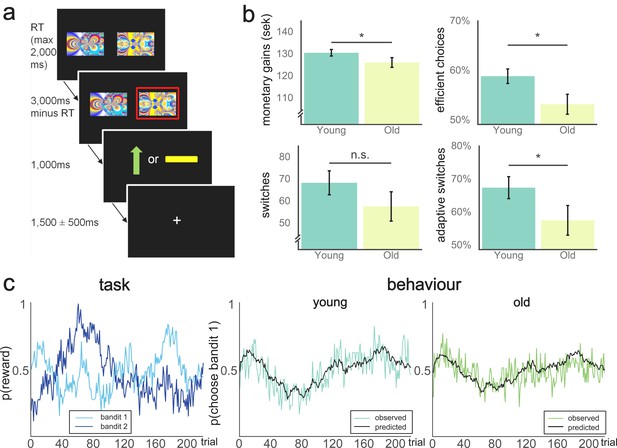
Behavioural paradigm and performance on the two-armed bandit task.
(a) Schematic representation of a trial in the TAB. Participants were presented with two fractal images on each trial and selected one of them through a button press. The maximum response time was 2000 ms, meaning the trial would count as a miss if the response time exceeded this limit and the next trial would start immediately after the next inter-trial interval. If one stimulus was selected, this option was highlighted with a red frame. After 1000 ms, participants were presented with the outcome: either a green arrow pointing upwards, indicating an obtained reward of 1SEK (≈$0.11), or a yellow horizontal bar, indicating no win. The position of the images on the screen varied randomly across the 2 × 110 trials of the experiment. Reward probabilities varied throughout the experiment. (b) Behavioural performance on the TAB, across age group. Younger participants earned more money on the TAB on average (top left, t(49) = 1.69, p(one-tailed)=0.048). Proportion of efficient choices differed significantly between the two groups (top right, Mann-Whitney U = 286.5, p(one-tailed)=0.029). Number of switches did not differ significantly between groups (p=0.19; bottom left), but the proportion of adaptive switches differed between age groups (bottom right, Mann-Whitney = 271.0; p(two-tailed)=0.033). Data are represented as mean ±SEM. (c) Left pane: Varying reward probabilities for obtaining a reward for each bandit on the 220 trials of the experiment. Center/right pane: Model predictions (black lines) and observed behaviour (coloured lines). Model fit did not significantly differ between participants (Mann-Whitney U = 353.0, p=0.406).
-
Figure 1—source data 1
Source data to Figure 1.
- https://doi.org/10.7554/eLife.26424.005
-
Figure 1—source code 1
Code that was used to perform simulation of behavioural data (figure 1c), as well as the creation of Figure 1.
- https://doi.org/10.7554/eLife.26424.006
Figure 1—figure supplement 1
Dopamine D1 binding potential is lower in older adults.
Average BP for young and old participants separately. All BPs significantly differed between groups (p<0.001).
-
Figure 1—figure supplement 1—source data 1
Binding potentials in seven ROIs for young and old participants.
- https://doi.org/10.7554/eLife.26424.004
Figure 2
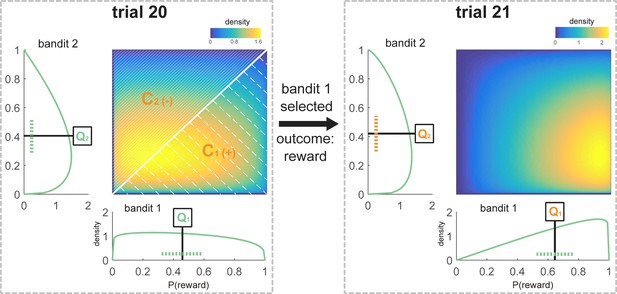
Schematic representation of the Bayesian model values for one participant at the time of choice at trial 21.
All components that are used to model choice at trial 21 are marked in orange. The sequence of choices for this participant was [1 1 1 2 1 1 1 2 2 1 2 2 1 1 1 2 2 2 2 1], and the payout for these choices was [1 1 0 0 1 1 0 1 0 0 0 0 1 1 0 0 1 1 0 1]. According to the participant’s individually fitted model parameters (ω = 0.72; λ = 0.28), and following this sequence of choices and outcomes, the beta distributions defining the subjective value of the bandits were and (see Equations 9–11, Materials and methods) at choice of trial 21. The expected value for each bandit was defined as the mean of the beta distribution (Q1 = 0.65, Q2 = 0.42; see Equation 7, Materials and methods). The variance of the unchosen option was equal to the variance of bandit 2, which was not chosen on trial 20 (Vuc = 0.05, see Equation 8, Materials and methods). Variance is schematically represented as a dotted line (note that this is an approximation because the beta distributions are not symmetrical). The 2-d plot shows the joint distribution P(,) where values of are along the x-axis and along the y-axis. Confidence was calculated based on the values of the distributions at choice on the previous trial. C1 was defined as the probability that a random sample drawn from at the time of choice at trial 20 was greater than a sample drawn from (shaded area below the diagonal, as > there. C1 = 0.56, Materials and methods Equation 15). C2 could be defined as 1-C1 (shaded area above the diagonal, C2 = 0.44, Equation 16, Materials and methods). Crel was equivalent to Cchosen – Cunchosen, in this case C1-C2 (Crel = 0.12, Equation 17). This relative confidence was scaled by and then added to the action that was not chosen on the previous trial (in this case bandit 2).
Figure 3
Value anticipation in vmPFC is related to behavioural performance and D1 BP in NAcc.
(a) Cluster in vmPFC that shows expected value activity at the time of the choice. Peak voxel x,y,z −5,52,–6; p<0.05, FWE corrected. (b) Parameter estimates for younger and older participants extracted from the cluster in Figure 3a. Activity differs significantly between age groups (t(55) = 2.38; p=0.021). Error bars represent standard errors of the means. (c) Time-course visualisation of the expected value signal in vmPFC. Shaded areas indicate standard errors. The expected-value signal is significantly larger and prolonged in the younger compared to the older sample. (d) There is a positive relationship between expected-value signal magnitude and total monetary gains (r(53) = 0.37, p=0.006 when controlling for age and model fit). For display purposes, the correlations are shown with residuals after regressing out age and model fit. (e) DA D1 BP in NAcc is positively related to Q in vmPFC (r(53) = 0.28, p=0.038, when controlling for age). For display purposes the correlations are shown with residuals after regressing out age.
-
Figure 3—source data 1
Source data for figure 3: cluster correponding to Q in vmPFC at the time of choice.
Parameter estimates for all participants of Q in vmPFC at the time of choice. Timecourse data for young and old participants corresponding to Q in vmPFC. BPs in NAcc for all participants.
- https://doi.org/10.7554/eLife.26424.011
Figure 4 with 1 supplement
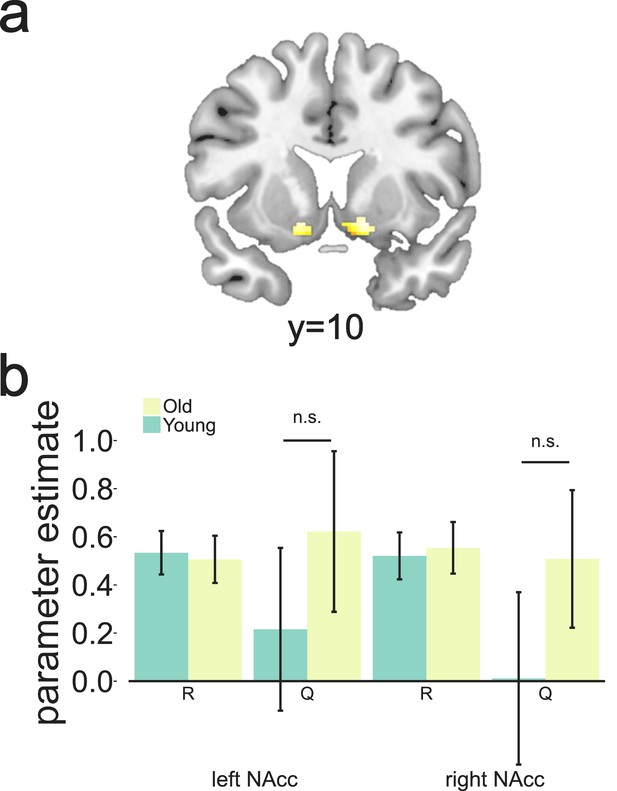
Clusters in bilateral NAcc linked to putative reward prediction error (RPE) at the time of the outcome.
These were selected as candidate regions to test for canonical RPE showing both a positive effect of reward and a negative effect of Q as calculated by the Bayesian observer model. Extracted parameter estimates for R and Q as calculated by the Bayesian observer model from the regions shown in Figure 4a. Although we found a strong effect of reward bilaterally, no expected-value signal was observed for either age group (p>0.10).
-
Figure 4—source data 1
Activation cluster in ventral striatum as defined by the winning Bayesian model, as well as parameter estimates of R and Q in left and right ventral striatum.
- https://doi.org/10.7554/eLife.26424.015
Figure 4—figure supplement 1
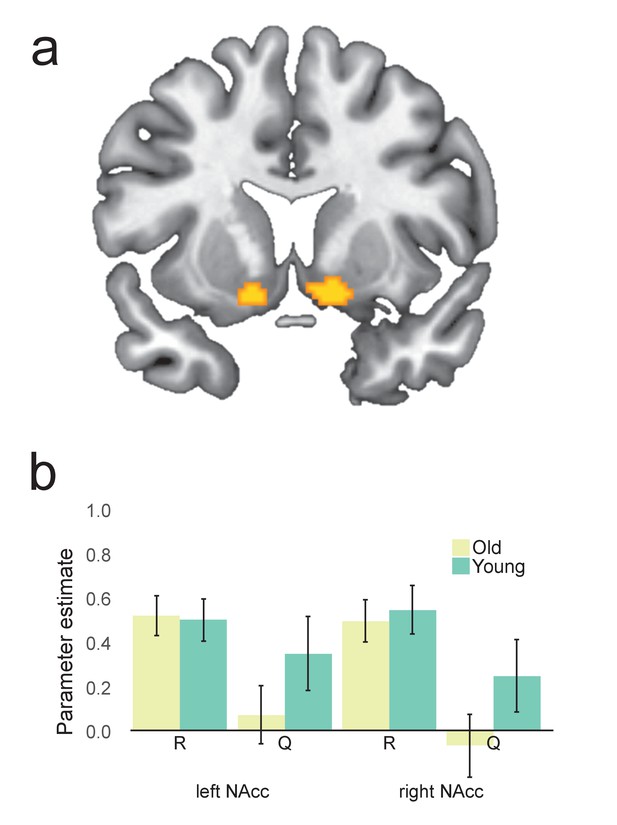
Canonical RPE parameter estimates from the Rescorla-Wagner model.
(a) Clusters in bilateral nucleus accumbens defined with a simple contrast of R-Q in first-level analysis using parameter values put forward by the Rescorla-Wagner model. These were selected as candidate regions conveying canonical reward prediction error (RPE) at the time of outcome. (b) Extracted parameter estimates from the regions shown in Figure 1—figure supplement 1a. Although the nucleus accumbens showed a strong effect of reward bilaterally, no clear expected value signal was observed in the region. Results were not significantly different from beta model parameter estimates.
-
Figure 4—figure supplement 1—source data 1
Activation cluster in ventral striatum as defined by the winning Rescorla-Wagner model, as well as parameter estimates of R and Q in left and right ventral striatum.
- https://doi.org/10.7554/eLife.26424.014
Tables
Table 1
Model comparison statistics for the different models.
The winning model, defined as the model with the lowest integrated BIC (iBIC), was the Bayesian observer model with five parameters. Parameters: β: inverse temperature parameter for softmax, α: learning rate for RW model, b: choice kernel, ϕ: forgetting rate for RW model, ω: learning rate for Bayesian model, λ: forgetting rate for Bayesian model, υ: variance weighting, κ: confidence weighting.
| Family | Parameters | # Param | Likelihood | Pseudo-R² | iBIC |
|---|---|---|---|---|---|
| RW | β, α | 2 | −5636.8 | 0.336 | 11309 |
| β, α, b | 3 | −5317.8 | 0.374 | 10692 | |
| β, α, b, ϕ | 4 | −5140.0 | 0.394 | 10355 | |
| Bayesian observer | β, ω | 2 | −5919.8 | 0.302 | 11877 |
| β, ω, λ | 3 | −5719.2 | 0.326 | 11495 | |
| β, ω, λ, b | 4 | −5154.6 | 0.392 | 10385 | |
| β, ω, λ, υ(chosen) | 4 | −5161.7 | 0.392 | 10399 | |
| β, ω, λ, υ(unchosen) | 4 | −5130.0 | 0.395 | 10335 | |
| β, ω, λ, κ | 4 | −5675.3 | 0.331 | 11426 | |
| β, ω, λ, υ(unchosen), κ | 5 | −5082.5 | 0.401 | 10259 |
Table 2
Summary statistics of the five parameters of the winning model.
https://doi.org/10.7554/eLife.26424.009| Minimum | 25th percentile | Median | 75th percentile | Maximum | |
|---|---|---|---|---|---|
| β | 1.436 | 7.017 | 12.280 | 17.730 | 64.750 |
| ω | 0.042 | 0.238 | 0.408 | 0.558 | 0.851 |
| λ | 0.055 | 0.139 | 0.202 | 0.270 | 0.544 |
| υ | −3.372 | −1.845 | −1.069 | −0.678 | 0.234 |
| κ | −0.202 | 0.152 | 0.260 | 0.359 | 0.896 |
Additional files
-
Source code 1
Computational modelling.
Scripts needed for the entire modelling routine used in the behavioural analysis. See the comments in the file fit_all_models_eLife.m for more details on each of the models and the procedure
- https://doi.org/10.7554/eLife.26424.016
-
Source code 2
fMRI analysis.
All MATLAB scripts required to set up preprocessing of fMRI data, create regressors for fMRI analysis, run the first level analysis and the second level analysis.
- https://doi.org/10.7554/eLife.26424.017
-
Source code 3
PET analysis.
Scripts required to run the segmentation of T1 images, PET analysis and estimation of BPs for the different ROIs.
- https://doi.org/10.7554/eLife.26424.018
-
Source code 4
figures.
R script for ggplot for Figures 1b, 3b, d and e and 4b
- https://doi.org/10.7554/eLife.26424.019
-
Source code 5
MATLAB script that creates joint probability distributions shown in Figure 2.
- https://doi.org/10.7554/eLife.26424.020
-
Source code 6
timecourse extraction.
MATLAB script that extracts the timecourse for expected value from vmPFC for young and old separately.
- https://doi.org/10.7554/eLife.26424.021
-
Supplementary file 1
(A) Correlation coefficients between model parameters and performance.
Coefficients in italics represent significant correlations at p<0.05. Coefficients in bold represent significant correlations at p<0.002 (adjust Bonferroni-corrected threshold). (B) Variance in number of switches as explained by the strongest RW model and winning model. When explaining the number of switches from the individual model parameters, the parameters that weighted V (υ), Crel (κ) and forgetting rate (), in addition to the softmax temperature parameter (β) were found to be significant predictors. Age or other model predictors did not contribute significantly. This regression model explained the number of switches better than the RW model parameters, where only the perseveration parameter b and softmax temperature parameter β were significant predictors of number of switches. (C) Young participants have a higher learning rate in the winning Rescorla-Wagner model according to non-parametric t-tests. None of the other model parameters significantly differed between groups.
- https://doi.org/10.7554/eLife.26424.022
-
Supplementary file 2
(A) No significant correlations between model parameters and dopamine D1 receptor density in any ROI after controlling for age at Bonferroni-corrected threshold of 0.0014.
(B) Partial correlation matrix showing correlation coefficients between the binding potential in the different PET ROIs and their p-values after controlling for age.
- https://doi.org/10.7554/eLife.26424.023
-
Supplementary file 3
Coordinates of clusters responsive to Q at the time of choice.
- https://doi.org/10.7554/eLife.26424.024
-
Transparent reporting form
- https://doi.org/10.7554/eLife.26424.025
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Attenuation of dopamine-modulated prefrontal value signals underlies probabilistic reward learning deficits in old age
eLife 6:e26424.
https://doi.org/10.7554/eLife.26424
