Figures and data in A causal role for right frontopolar cortex in directed, but not random, exploration

Figures
Tables
Additional files

12 figures, 2 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

The horizon task.

Participants make a series of decisions between two one-armed bandits that pay out probabilistic rewards with unknown means. At the start of each game, ‘forced-choice’ trials give participants partial information about the mean of each option. We use the forced-choice trials to set up one of two information conditions: (A) an unequal (or [1 3]) condition in which participants see 1 play from one option and 3 plays from the other and (B) an equal (or [2 2]) condition in which participants see 2 plays from both options. A model-free measure of directed exploration is then defined as the change in information seeking with horizon in the unequal condition (A). Likewise a model-free measure of random exploration is defined as the change choosing the low mean option in the equal condition (B).

https://doi.org/10.7554/eLife.27430.002

Figure 2

Download asset Open asset

The reward-information confound.

The y-axis corresponds to the correlation between the sign of the difference in mean ( $s g n (μ_{l e f t} - μ_{r i g h t})$ ) between options and the sign of difference in the number of times each option has been played ( $s g n (n_{l e f t} - n_{r i g h t})$ ). The forced trials are chosen such that the the correlation is approximately zero on the first free-choice trial. After the first trial, however, a positive correlation quickly emerges as participants choose the more rewarding options more frequently. This strong confound between reward and information makes it difficult to dissociate directed and random exploration on later trials.

https://doi.org/10.7554/eLife.27430.003

Figure 3

Download asset Open asset

Model-free analysis of the first free-choice trial shows that RPFC stimulation affects directed, but not random, exploration.

(A) In the control (vertex) condition, information seeking increases with horizon, consistent with directed exploration. When RFPC is stimulated, directed exploration is reduced, an effect that is entirely driven by changes in horizon 6 (* denotes $p < 0.02$ and ** denotes $p < 0.005$ ; error bars are $\pm$ s.e.m.). (B) Random exploration increases with horizon but is not affected by RFPC stimulation.

https://doi.org/10.7554/eLife.27430.004

Figure 4

Download asset Open asset

Model-based analysis of the first free-choice trial showing the effect of RFPC stimulation on each of the 13 parameters.

Left column: Posterior distributions over each parameter value for RFPC and vertex stimulation condition. Right column: posterior distributions over the change in each parameter between stimulation conditions. Note that, because information bonus, decision noise and spatial bias are all in units of points, we plot them on the same scale to facilitate comparison of effect size.

https://doi.org/10.7554/eLife.27430.006

Figure 5

Download asset Open asset

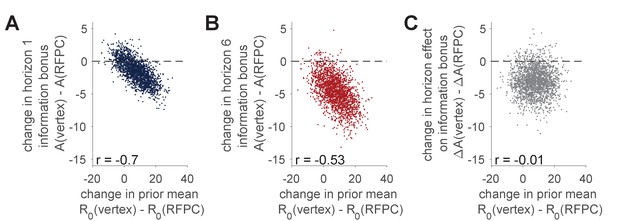
Correlation between TMS-induced changes in information bonus, $A$ , and TMS-induced changes in the prior mean, $R_{0}$ .

(**A, B**) Samples from the posterior distributions over the TMS-related changes in prior mean, $R_{0}$ , and TMS-related change in information bonus in horizon 1 (A) and horizon 6 (B). In both cases we see a negative correlation between the change in $R_{0}$ and the change in $A$ consistent with a tradeoff between these variables in the model. (C) Samples from the posterior over the effect of TMS stimulation on the horizon-related change in information bonus, $Δ A = A (h = 6) - A (h = 1)$ plotted against samples from the TMS-related change in prior mean. Here we see no correlation between variables and the majority of $Δ A (v e r t e x) - Δ A (R F P C)$ samples below zero consistent with an effect of RFPC stimulation on directed exploration.

https://doi.org/10.7554/eLife.27430.007

Figure 6

Download asset Open asset

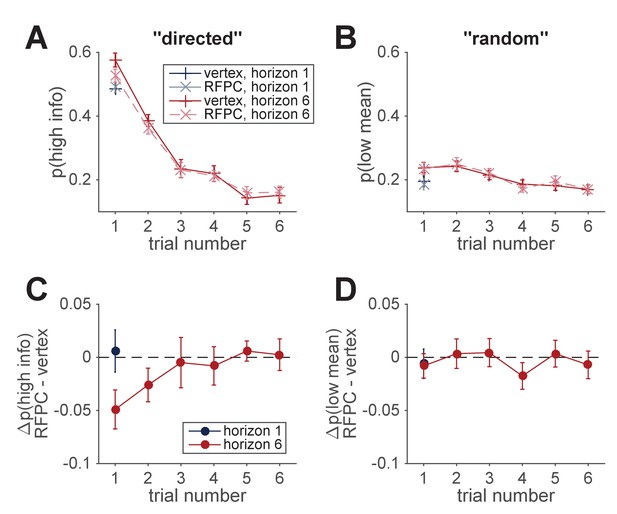
Model-free analysis of all trials.

(**A, B**) Model-free measures of directed (A) and random (B) exploration as a function of trial number suggests a reduction in both directed and random exploration over the course of the game. (**C, D**) TMS-induced change in measures of directed and random exploration as a function of trial number. This suggests that the reduction in directed exploration on the first free-choice trial, persists into the second trial of the game.

https://doi.org/10.7554/eLife.27430.008

Figure 7

Download asset Open asset

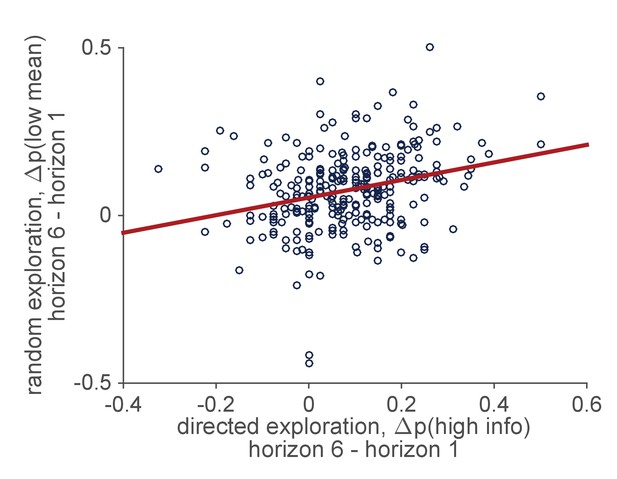
Correlation between individual differences in the levels of directed and random exploration in a sample of 277 people performing the Horizon Task.
https://doi.org/10.7554/eLife.27430.009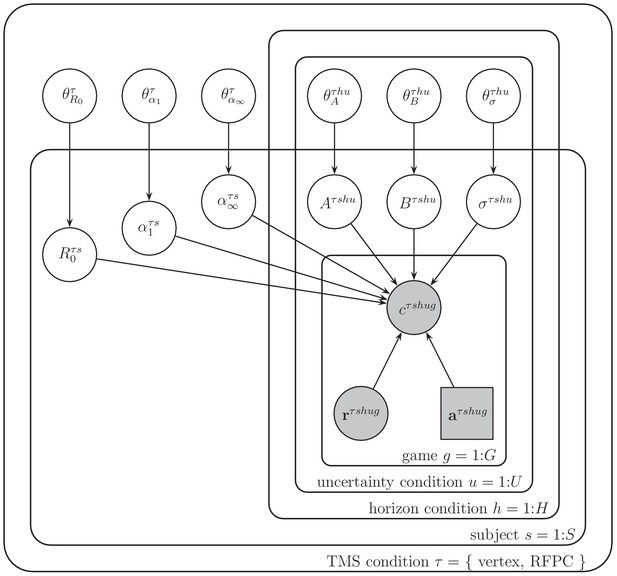

Figure 8

Download asset Open asset

Graphical representation of the model.

Each variable is represented by a node, with edges denoting the dependence between variables. Shaded nodes correspond to observed variables, that is, the free choices $c^{τ s h u g}$ , forced-trial rewards, $𝐫^{τ s h u g}$ and forced-trial choices $𝐚^{τ s h u g}$ . Unshaded nodes correspond to unobserved variables whose values are inferred by the model.

https://doi.org/10.7554/eLife.27430.010

Author response image 1

Download asset Open asset

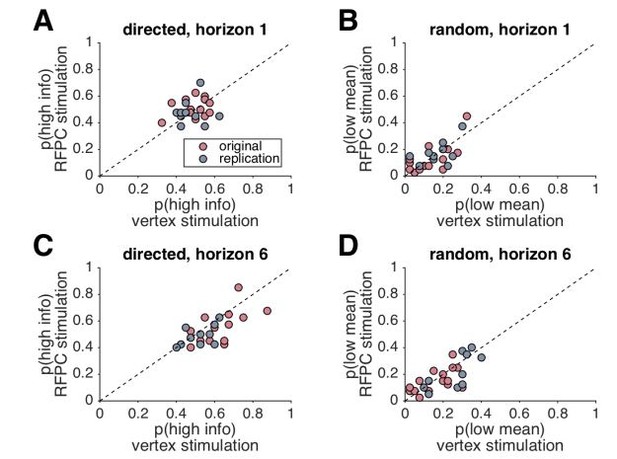
No difference in effects between original and replication experiments.

In each panel we plot the model-free measures of directed and random exploration and how they change between stimulation conditions. For example, in Panel A, we plot p(high info) in horizon 1 for vertex stimulation (x-axis) and RFPC stimulation (y-axis). Each point in this plot is a single subject and the diagonal line represents equality. Participants below the diagonal line have a smaller value of p(high info) in the RFPC stimulation condition. From this we can clearly see that there is no effect of RFPC stimulation on directed exploration in horizon 1 (panel A), or random exploration in either horizon (B, D). However, there is a strong effect of RFPC stimulation on directed exploration in horizon 6 with the majority of points lying below the diagonal (C). Moreover, both the original and replication datasets point to the same conclusions in all four panels.

Author response image 2

Download asset Open asset

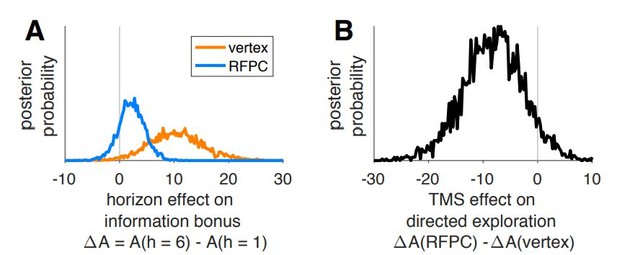
Effect of TMS on information bonus in model with bonus proportional to uncertainty.

Author response image 3

Download asset Open asset

Effect of TMS on decision noise in model in which bonus is a linear function of uncertainty.

Author response image 4

Download asset Open asset

Tables

Table 1

Model parameters.

Subject’s behavior on the first free choice of each session is described by 13 free parameters. Three of these parameters ( $R_{0}$ , $α_{1}$ and $α_{\infty}$ ) describe the learning process and do not vary with horizon or uncertainty condition. Ten of these parameters ( $A$ , $B$ and $σ$ in the different horizon and information conditions) describe the decision process. All parameters are estimated for each subject in each stimulation condition and the key analysis asks whether parameters change between vertex and RFPC stimulation.

https://doi.org/10.7554/eLife.27430.005

Parameter	Horizon dependent?	Uncertainty dependent?	TMS dependent?
prior mean, $R_{0}$	no	no	yes
initial learning rate, $α_{1}$	no	no	yes
asymptotic learning rate, $α_{\infty}$	no	no	yes
information bonus, $A$	yes	n/a	yes
spatial bias, $B$	yes	yes	yes
decision noise, $σ$	yes	yes	yes

Table 2

Model parameters, priors, hyperparameters and hyperpriors.

https://doi.org/10.7554/eLife.27430.011

Parameter	Prior	Hyperparameters	Hyperpriors
prior mean, $R_{0}^{τ s}$	$R_{0}^{τ s} \sim$ Gaussian( $μ_{R_{0}}^{τ}$ , $σ_{R_{0}}^{τ}$ )	$θ_{R_{0}}^{τ} = (μ_{R_{0}}^{τ}, σ_{R_{0}}^{τ})$	$μ_{R_{0}}^{τ} \sim$ Gaussian( 50, 14 ) $σ_{R_{0}}^{τ} \sim$ Gamma( 1, 0.001 )
initial learning rate, $α_{1}^{τ s}$	$α_{1}^{τ s} \sim$ Beta( $a_{α_{1}}^{τ}$ , $b_{α_{1}}^{τ}$ )	$θ_{α_{1}}^{τ} = (a_{α_{1}}^{τ}, b_{α_{1}}^{τ})$	$a_{α_{1}}^{τ} \sim$ Uniform( 0.1, 10 ) $b_{α_{1}}^{τ} \sim$ Uniform( 0.5, 10 )
asymptotic learning rate, $α_{\infty}^{τ s}$	$α_{\infty}^{τ s} \sim$ Beta( $a_{α_{\infty}}^{τ}$ , $b_{α_{\infty}}^{τ}$ )	$θ_{α_{\infty}}^{τ} = (a_{α_{\infty}}^{τ}, b_{α_{\infty}}^{τ})$	$a_{α_{\infty}}^{τ} \sim$ Uniform( 0.1, 10 ) $b_{α_{\infty}}^{τ} \sim$ Uniform( 0.1, 10 )
information bonus, $A^{τ s h u}$	$A^{τ s h u} \sim$ Gaussian( $μ_{A}^{τ h u}$ , $σ_{A}^{τ h u}$ )	$θ_{A}^{τ h u} = (μ_{A}^{τ h u}, σ_{A}^{τ h u})$	$μ_{A}^{τ h u} \sim$ Gaussian( 0, 100 ) $σ_{A}^{τ h u} \sim$ Gamma( 1, 0.001 )
spatial bias, $B^{τ s h u}$	$B^{τ s h u} \sim$ Gaussian( $μ_{B}^{τ h u}$ , $σ_{B}^{τ h u}$ )	$θ_{B}^{τ h u} = (μ_{B}^{τ h u}, σ_{B}^{τ h u})$	$μ_{B}^{τ h u} \sim$ Gaussian( 0, 100 ) $σ_{B}^{τ h u} \sim$ Gamma( 1, 0.001 )
decision noise, $σ^{τ s h u}$	$σ^{τ s h u} \sim$ Gamma( $k_{σ}^{τ h u}$ , $λ_{σ}^{τ h u}$ )	$θ_{σ}^{τ h u} = (k_{σ}^{τ h u}, λ_{σ}^{τ h u})$	$k_{σ}^{τ h u} \sim$ Exp( 0.1 ) $λ_{σ}^{τ h u} \sim$ Exp( 10 )

Additional files

Transparent reporting form: https://doi.org/10.7554/eLife.27430.012
Download elife-27430-transrepform-v2.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Wojciech K Zajkowski
Malgorzata Kossut
Robert C Wilson

(2017)

A causal role for right frontopolar cortex in directed, but not random, exploration

eLife 6:e27430.

https://doi.org/10.7554/eLife.27430

Share this article

Cite this article

The horizon task.

The reward-information confound.

Model-free analysis of the first free-choice trial shows that RPFC stimulation affects directed, but not random, exploration.

Model-based analysis of the first free-choice trial showing the effect of RFPC stimulation on each of the 13 parameters.

Correlation between TMS-induced changes in information bonus, A, and TMS-induced changes in the prior mean, R0.

Model-free analysis of all trials.

Correlation between individual differences in the levels of directed and random exploration in a sample of 277 people performing the Horizon Task.

Graphical representation of the model.

No difference in effects between original and replication experiments.

Effect of TMS on information bonus in model with bonus proportional to uncertainty.

Effect of TMS on decision noise in model in which bonus is a linear function of uncertainty.

Model parameters.

Model parameters, priors, hyperparameters and hyperpriors.

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Correlation between TMS-induced changes in information bonus, $A$ , and TMS-induced changes in the prior mean, $R_{0}$ .