Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins
- Washington University in St. Louis, United States
- Howard Hughes Medical Institute, UT Southwestern Medical Center, United States
Figures
Figure 1
Depiction of gelation without phase separation as opposed to phase separation plus gelation.
(a) Schematic of a synthetic multivalent system. SH3 domains bind to proline-rich modules (PRMs). Multivalent SH3 and PR proteins result from the tethering of multiple SH3 domains (or PRMs) by linkers. (b) Schematic of gelation without phase separation: If the bulk concentration of interaction domains is above the gel point but below the saturation concentration then a system spanning network forms across the entire system volume. In this scenario, a percolation transition is realized without phase separation. (c) Schematic of phase separation plus gelation. Linker-mediated cooperative interactions of multivalent proteins drive phase separation, depicted here as a confinement of molecules into a smaller volume (gray envelope) when compared to the system volume (dashed bounding box). If the bulk concentration of interaction domains is higher than a saturation concentration then a dense phase comprising of multivalent SH3 and PRM proteins will be in equilibrium with a dispersed phase of unbound proteins. A droplet-spanning network will form because the concentration of interaction domains within the dense phase is above the gel point.
Figure 2
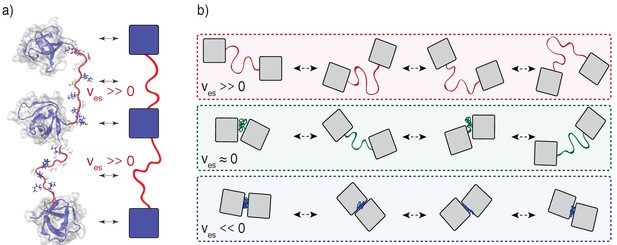
Illustration of the impact of linker effective solvation volumes on the conformational fluctuations and inter-domain distances in linear multivalent proteins.
(a) Schematic of three SH3 domains connected by positive ves linkers. In a cartoon schematic, the SH3 domains are shown as blue squares and the linkers are depicted as red tethers. The bidirectional arrows indicate the mapping between the molecular structures and the cartoon schematic. (b) Comparative schematics of SH3 domains connected by different types of linkers. The top row shows a pair of domains connected by linkers of high positive effective solvation volumes. For linkers with near zero effective solvation volumes, the inter-domain distances are characterized by large fluctuations and this engenders large concentration fluctuations. The bottom row shows the scenario for domains connected by linkers with negative ves values. In this scenario, the inter-domain distances seldom exceed the sum of the individual radii of gyration.
Figure 3
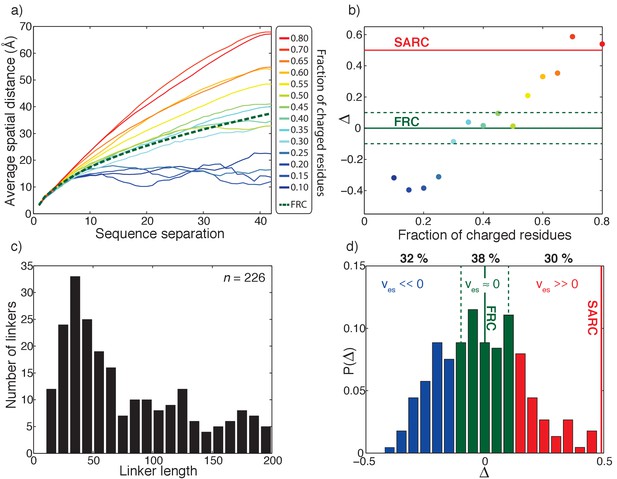
Effective solvation volumes for disordered linkers from the human proteome.
(a) Inter-residue distance profiles for fourteen representative sequences, each 40-residues long. The legend shows the fraction of charged residues within each linker. The green dashed curve shows the inter-residue distance profile for the reference FRC limit. (b) Summary of the variation of ∆ as a function of the fraction of charged residues for the fourteen representative sequences. Here, ∆ , N is the number of linker residues,is the average spatial separation between residue pairs that are k apart in the linear sequence, is the corresponding spatial separation for a FRC chain, and the summation index k runs across all sequence-separations. Linkers for which ∆ < –0.1 will have negative effective solvation volumes (ves < 0); linkers for which –0.1 ≤ ∆≤0.1 will have near zero effective solvation volumes (ves ≈ 0); and linkers for which ∆>0.1, will have positive effective solvation volumes (ves > 0). For the self-avoiding random coil (SARC) linkers, ∆ ≈ 0.5 and this is shown as a horizontal red line. (c) Length distribution of all 226 unique disordered linkers. (d) Distribution of ∆ values extracted from all-atom simulations of all 226 linkers. Based on the results shown in panel (B), we delineate the ∆-distribution into three regimes: ∆ < –0.1 (blue bars), –0.1 ≤ ∆≤0.1 (green bars), and ∆>0.1 (red bars). These regimes correspond, respectively to linkers for which ves is less than zero, near zero, or greater than zero.
Figure 4
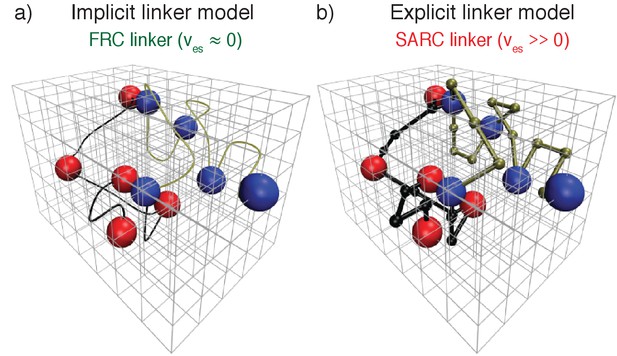
Coarse-grained bead-tether lattice models for modeling the phase behavior of multivalent proteins.
All simulations were performed using 3-dimensional cubic lattice models. In these models, poly-SH3 and poly-PRM proteins were modeled as bead-tether polymers where the red beads mimic an SH3 domain, the blue beads mimic PRMs, and the black or gold tethers mimic linkers that connect domains/modules to one another. Two beads cannot occupy the same lattice site. Panel (a) shows an implicit linker model. To mimic FRC linkers, implicit linkers ensure that two tethered beads cannot move apart beyond a maximum distance, but the linker itself does not occupy any lattice sites. Panel (b) shows the explicit linker model. To mimic SARC linkers, explicit linkers consist of non-interacting beads corresponding to a prescribed number of lattice sites. The explicit linkers tether two folded domains together, but other than occupying sites on the lattice they do not engage in interactions with one another or with the interaction domains. Note that in the explicit linker model each linker bead and interaction domain occupies a single lattice site. This choice was motivated by previous analysis of the comparative effective solvation volumes of FRC and SARC linkers (Mittal et al., 2014). In the figure, the linker beads are represented as being smaller than the interaction beads to emphasize that they are linkers. The real simulation box used is much larger than the lattice dimensions pictured here, which is just for illustration purposes.
Figure 5
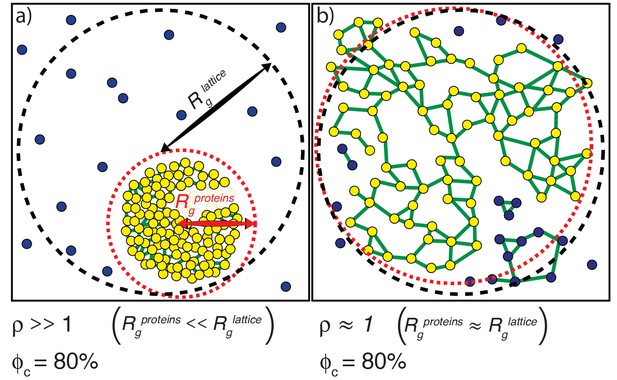
Illustration of how ρand ϕc are calculated.
(a) The scenario where ρ >>1. The radius of gyration over all proteins is the root mean square distance of each of the proteins from the center of mass of the system of proteins and is depicted as the radius of the dashed red envelope. Although the red envelope is centered on the cluster, it extends beyond the cluster boundary due to the presence of proteins outside of the cluster; that is, Rgproteins is always calculated over all proteins in the system. When a majority of the proteins are spatially clustered, the calculated Rgproteins is considerably smaller than the radius of the lattice, and hence the ratio ρ >>1. Rglattice is shown as a black dashed envelope. In panel (a) a majority of the proteins are found within a single droplet-spanning cluster. This cluster encompasses ~ 80% of the modules, hence ϕc ~80%. Modules belonging to the single largest system spanning clusters are shown in yellow, the crosslinks are shown in green, and the ‘system’ here refers to the droplet. (b) The scenario where ρ ≈ 1. In this case, the modules are dispersed across the lattice volume as shown by the fact that the dashed red envelope is essentially coincident with the dashed black envelope. Here, we depict a scenario where 80% of the modules are incorporated into the single largest system-spanning cluster, where the ‘system’ volume corresponds to that of the entire lattice.
Figure 6
Comparative analysis of the connectivity and density transitions for multivalent proteins of fixed linker lengths.
(a) Heat maps showing ϕc as a function of changes to SH3 and PRM concentrations for multivalent proteins with FRC linkers. Progression from cool to hot colors leads to the incorporation of most of the modules into the single largest cluster. The module concentrations at which sharp changes in connectivity are realized will decrease with increasing valence. (b) Heat maps equivalent to those of panel (a) for multivalent proteins with SARC linkers. (c) Analysis of how ϕc changes with module concentration for equal concentrations SH3 modules to PRMs. The solid curves plot ϕc for proteins with SARC linkers and the dashed curves are results for FRC linkers. The legend provides an annotation of the color scheme for the different curves. (d) Heat maps showing ρ as a function of changes to SH3 and PRM concentrations for multivalent proteins with FRC linkers. Comparison to panel (a) shows the congruence between changes to ρ and ϕc, especially for the 5:5, 5:7, 7:5, and 7:7 systems. (e) Heat maps showing ρ as a function of changes to SH3 and PRM concentrations for multivalent proteins with SARC linkers. The value of ρ does not change and remains close to one irrespective of the valence or module concentration. (f) Analysis of how ρ changes with module concentration for equal concentrations SH3 modules to PRMs. The solid curves are for proteins with SARC linkers and this shows that ρ ≈ 1, irrespective of the module concentrations. As discussed in the text and summarized in Figure 7, phase separation is suppressed for systems with SARC linkers and this is reflected in the invariance of ρ. The dashed curves, for the 5:5 and 7:7 systems with FRC linkers show a sharp change above a threshold concentration of the modules. The behavior at high module concentrations is partly an artifact of our approach to increasing concentrations in the simulations, which involves fixing the number of modules and decreasing the volume of the simulation box. Accordingly, the radius of the lattice will decrease, thus decreasing ρ. However, ρ is greater than one above a critical concentration, thus emphasizing the coupling between phase separation and gelation for proteins with FRC linkers.
Figure 7
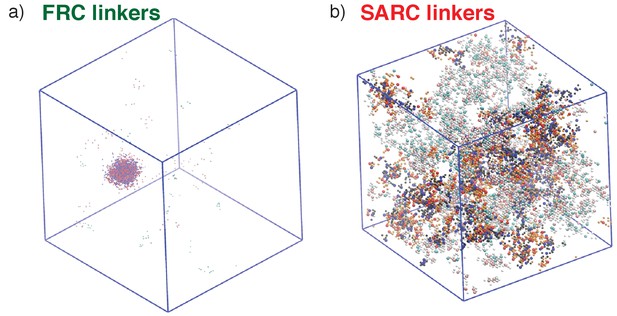
Representative, post-equilibration, snapshots for the 7:7 system above the gel points with FRC, panel (a), and SARC linkers, panel (b) of length n = 5.
In panel (a), the SH3 modules are shown in red and the PRMs in blue. In panel (b), the coloring is similar to panel (a). Additionally, molecules that are part of the single largest, system-spanning cluster are shown in orange. The main message conveyed here is that the SARC linkers suppress phase separation whereas the FRC linkers lead to gelation driven by phase separation.
Figure 8
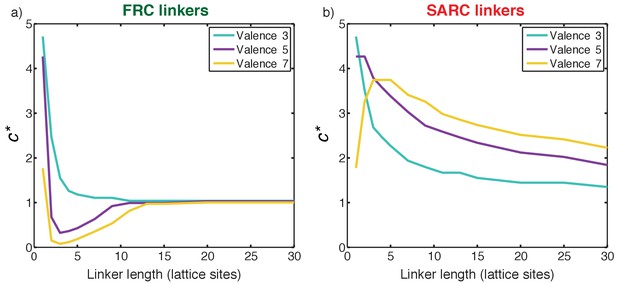
Quantifying cooperativity and the coupling between phase separation and gelation.
(a) Plot of c* as a function of linker length for three symmetric multivalent systems connected by FRC linkers. There is an optimal range for linker lengths where c*<1, implying positive global cooperativity that gives rise to phase separation plus gelation. For long linkers, c* converges to unity, implying an absence of cooperativity and pure sol-gel transitions, in accord with Flory-Stockmayer theories. (b) Plot of c* as a function of linker length for three symmetric multivalent systems connected by SARC linkers. The value of c* is greater than unity for all linker lengths. This points to the suppression of phase separation by linkers with positive effective solvation volumes, and a shifting of the gel point to higher concentrations compared to the Flory-Stockmayer threshold. The linker length in terms of number of amino acids can be written as N ≈ 7 n, where n is the number of lattice sites and N is the number of residues.
Figure 9
Phase diagram for a 5:5 system with a hybrid five-site linker.
Here, for each linker, two of the linker beads were modeled explicitly, while the other three were modeled implicitly. For low binding affinities between SH3 domains and PRMs (<3 kBT), the system undergoes a sol-gel transition as a function of module concentration, and the affinity-specific gel points lie on the green dashed line. The red asterisk denotes the critical point located at an interaction affinity of ~3 kBT and a module concentration of ~10–3polymers/voxel. Above an interaction affinity of ~3 kBT, the system undergoes phase separation plus gelation. Phase separation is characterized by a coexistence curve with two arms, shown in blue and purple. A solution with a bulk concentration that falls within the yellow region will never form a one-phase solution. Instead, it will separate into coexisting dilute and dense phases. The concentrations within these phases are equal to the concentrations taken from coexistence curves that intersect with the corresponding tie line (red dotted line). This is illustrated for interaction strengths of 4.5kBT. Any solution with a bulk concentration along the tie line will phase separate into a dense phase and a dilute phase of a fixed concentration csl and csh, respectively. For this system, the high concentration arm of the coexistence curve always lies beyond the gel-line, and therefore, the dense phase will always form a gel. The gel line within the two-phase region is calculated based on the percolation threshold and is shown as a dotted green line, which is really an extrapolation of the green dashed line. It highlights the fact that csl <cg < csh throughout the two-phase regime. The callouts on the right show schematics of the dilute sol coexisting with a dense gel (top right) and a system spanning gel that forms via gelation without phase separation (bottom right).
Figure 10
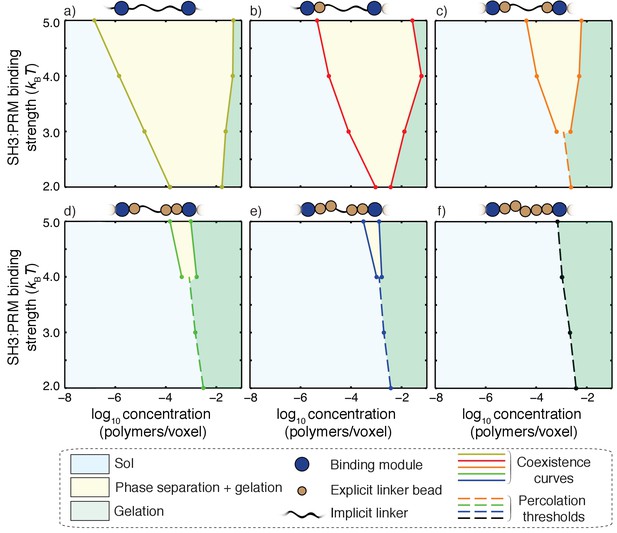
Impact of linker ves values on coupling between phase separation and gelation for 5:5 systems with linkers of length n = 5.
Progressing from panel a) to panel f), the value of ves for each of the linkers increases from 0 to 5 in terms of number of lattice units. The widths of the regimes that correspond to phase separation (yellow regions) shrink as the effective solvation volumes of linkers increase. For the fully implicit, FRC linker (panel a), gelation without phase separation either requires shorter linkers or interaction affinities that are weaker than 2kBT. The sol-gel lines are shown as dashed lines in each panel. Accordingly, for a) and b) the gelation without phase separation are realized for SH3: PRM affinities that are weaker than 2kBT and hence they are not shown in these panels. Each panel is annotated with a schematic to show the design of hybrid linkers and each schematic we shown only a single linker for clarity.
Figure 11
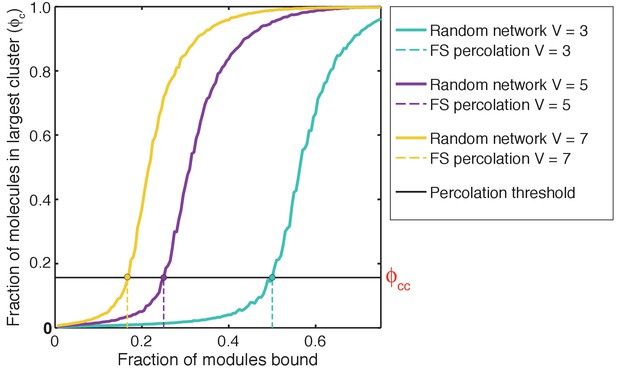
Estimating ϕcc – the critical value of the fraction of molecules in the largest cluster, ϕc that defines the gel point: To estimate ϕcc, we plot ϕc against the fraction of SH3 domains and PRMs that are bound.
ϕc was calculated using a random network model (see Materials and methods) and for a prescribed affinity between interaction domains. ϕc shows a sigmoidal transition that shifts to the right for systems of lower valence (V). For each system, the dashed vertical lines quantify the percolation thresholds, which refer to the fraction of modules for a given valence V that must be bound in order to make a percolated network as prescribed by the theories of Flory and Stockmayer. For a given system of multivalent proteins, the intersection between the solid sigmoidal curve and the dashed vertical line quantifies the value of ϕcc.
Videos
Video 1
Demonstration of gelation driven by phase separation for the 7:7 system of poly-SH3 and poly-PRM.
The color-coding is such that SH3 domains are in red and PRMs are in blue. The simulations start with the molecules dispersed uniformly across the simulation volume. The movie shows droplet formation leading to gelation for bulk concentrations of SH3 domains and PRMs that lie above the saturation concentration csl.
Video 2
Demonstration of gelation without phase separation for the 7:7 system of poly-SH3 and poly-PRM.
The movie shows the formation of a system-spanning network formation leading to gelation for bulk concentrations of SH3 domains and PRMs that lie above the gel point cg.
Tables
Table 1
Summary of the parameters, the physical description of these parameters, and the default values used for the parameters of the lattice model.
https://doi.org/10.7554/eLife.30294.006| Parameter | Physical interpretation | Default value |
|---|---|---|
| Valence | Number of PRMs and SH3 domains per poly-PRM and poly-SH3 | 5 (but titrated for results in Figure 6) |
| Interaction Strength | Intrinsic affinity between PRMs and SH3 domains | –2kBT |
| Linker Length | Length of disordered linker between interaction domains | 5 (but titrated for results in Figure 8) |
| Effective solvation volume (ves) | Degree to which the Linker Prefers Interacting with Solvent | Proportional to the number of explicitly modeled linker beads |
Table 2
Details of the fourteen sequences chosen at random from the human proteome.
All sequences have identical lengths (40 residues) and are enriched in disorder promoting residues. The sequences are listed in descending order of the fraction of charged residues.
| Sequence | FCR* | NCPR† | Fraction of disorder promoting residues | UNIPROT identifier of protein from which the sequence was drawn |
|---|---|---|---|---|
| EDEDSEKEEEEEDKEMEELQEEKECEKPQGDEEEEEEEEE | 0.80 | –0.60 | 0.93 | P37275 |
| DEEGNAYGSEREEEDEEEDEEDGKRELELEEEELGGEEED | 0.70 | –0.55 | 0.88 | P78415 |
| REKDREKYSQREQERDRQQNDQNRPSEKGEKEEKSKAKEE | 0.65 | 0.00 | 0.93 | Q9H0G5 |
| DRVVVTDDSDERRLKGAEDKSEEGEDNRSSESEEESEGEE | 0.60 | –0.30 | 0.88 | Q9BQG0 |
| EAYRLSLEADRAKREAHEREMAEQFRLEQIRKEQEEEREA | 0.55 | –0.10 | 0.88 | Q9UNN5 |
| RRQRRWEDIFNQHEEELRQVDKDKEDESSDNDEVFHSIQA | 0.50 | –0.15 | 0.73 | Q7Z2Y5 |
| NNRKGRGGNRGREFRGEENGIDCNQVDKPSDRGKRARGRG | 0.45 | 0.15 | 0.76 | Q5T6F2 |
| QKQKLRLLSSVKPKTGEKSRDDALEAIKGNLDGFSRDAKM | 0.40 | 0.10 | 0.75 | Q9UMZ2 |
| AEMKVLESPENKSGTFKAQEAEAGVLGNEKGKEAEGSLTE | 0.35 | –0.10 | 0.78 | Q8N3D4 |
| MAAAESDKDSGFSDGSSECLSSAEQMESEDMLSALGWSRE | 0.30 | –0.20 | 0.78 | Q9C0C6 |
| DHFMKSGFASGRNFGNRDAGECNKRDNTSTMGGFGVGKSF | 0.25 | 0.05 | 0.68 | Q9NQI0 |
| TAVSTSGPEDICSSSSSHERGGEATWSGSEFEVSFLDSPG | 0.20 | –0.15 | 0.80 | Q9BQQ3 |
| FSTLGRLRNGIGGAAGIPRANASRTNFSSHTNQSGGSELR | 0.15 | 0.10 | 0.73 | Q9Y252 |
| KSSSQTSGSLVSKSTSLASVSQLASKSSSQTSTSQLPSKS | 0.10 | 0.10 | 0.85 | Q9NXV6 |
-
*FCR: Fraction of charged residues defined as (f++f–) where f+ and f– denote the fraction of positive and negative charges, respectively;
†NCPR: Net charge per residue defined as (f+ – f–)
Additional files
-
Supplementary file 1
Excel spreadsheet summarizing the proteome-wide analysis of naturally occurring intrinsically disordered linkers in linear multivalent proteins.
Data include the Uniprot ID, the name of the protein from which the linker sequence is drawn, the linker length in terms of number of amino acids, the start and end positions in terms of amino acid numbers for each linker, the disorder score on a scale of 0 to 1, the value of ∆ (see Figure 3), the fraction of positively charged residues (f+ or Fpos), the fraction of negatively charged residues (f– or Fneg), location of the diagram-of-states developed by Das and Pappu (Das et al., 2015; Holehouse et al., 2017; Das and Pappu, 2013), amino acid sequence of the linker, Gene Ontology molecular function annotation, Gene Ontology biological process annotation, and Gene Ontology cellular location/component annotation.
- https://doi.org/10.7554/eLife.30294.018
-
Transparent reporting form
- https://doi.org/10.7554/eLife.30294.019
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins
eLife 6:e30294.
https://doi.org/10.7554/eLife.30294
