Gene-free methodology for cell fate dynamics during development
- CNRS / Ecole Normale Supérieure, France
- Rockefeller University, United States
Figures
Figure 1 with 1 supplement
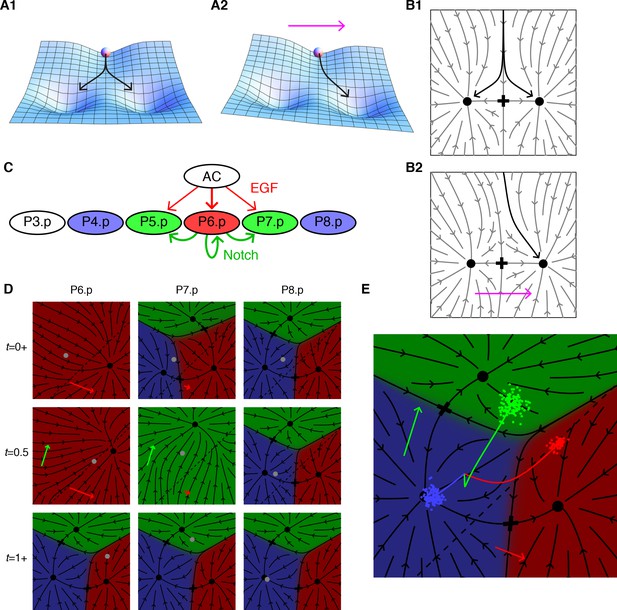
Model dynamics and the vulval patterning network.
(A) Topography with two valleys separated by a ridge. A ball positioned exactly on the ridge will fall with equal probability into either valley. Tilting the topography as suggested by the arrow favors the right valley. (B) The same dynamics as A now represented by arrows showing the direction of movement at each point of the fate plane. The terminal points are shown as dots and the lowest point on the ridge that divides the flows is the saddle point denoted by a cross. (C) The vulva forms from a row of six 6 VPCs, P3.p-P8.p (P3.p differs in competence from other VPCs and is omitted from our model). Fate specification involves EGF signaling (red arrows) from the anchor cell (AC) and lateral Notch signaling among VPCs (green arrows). EGF induces P6.p to the 1° fate (red), while Notch signaling is required for the induction of the 2° fate in P5/7.p (green); this may be facilitated by low levels of EGF from the AC. P4/8.p are uninduced and adopt the default 3° fate (blue). Experiments in which an isolated VPC adopts the 2° fate suggest that the Notch receptor may also respond to autocrine signaling (Sternberg and Horvitz, 1989). (D) Snapshots showing the principal features of our graphical representation of the vulval fate plane following B. The VPC is represented by a grey dot, and all points that limit to a single fate are colored as in C, the arrows show the strength of the EGF (red) and Notch (green) signals, and cells positioned below the dashed line express Notch ligands. At the beginning of competence (t = 0+ signal reception on), all cells in an equivalence group start at the same position, but P6.p receives a strong EGF signal from the AC which makes 1° the only possible fate. Since P6.p is far from the dashed line there is no Notch signaling to P5/7.p. At mid-competence, P6.p reaches the dashed line and produces Notch ligands. This yields autocrine signaling in P6.p (green arrow) and paracrine signaling in P5/7.p that eliminates all fates except 2°. At the end of competence (t = 1+ signal reception off) the fate plane reverts to its configuration in the absence of signaling, which is virtually identical to that for P4/8.p at earlier times since it receives no signals under WT conditions. However, the induced cells find themselves in the red or green regions and progress toward the 1° or 2° fates. Video 1 shows the full dynamics from pre to post competence. (E) A more compact representation of model dynamics, used in subsequent figures, overlays the average trajectories of P6-8.p, colored according to their WT fate, on the fate plane in the absence of signaling following the same notations as D. The clouds of colored dots represent outcomes for individual cells at the end of competence, after allowing for developmental noise. In other genetic backgrounds, this is the source of partial penetrance. Under the WT conditions shown here, each cloud is well inside a single territory, corresponding to an invariant fate pattern.
Figure 1—figure supplement 1
Dynamics and phase diagram of our original model (Corson and Siggia, 2012).
These figures, to be compared with Figure 1C, Figure 1E and Figure 2A, show the dynamics and phase diagram of our model with parameter values from (Corson and Siggia, 2012). We assumed fixed, default directions for EGF and Notch (towards the 1° and 2° fates, making an angle of 120°) and had no information on EGF levels in mutants. The general structure of the phase diagram is the same, and there are just limited quantitative differences. Our estimate of EGF overexpression levels that yield a phenotype was a bit larger than the new data indicates (see the limit of the WT domain for WT Notch). With default directions for EGF and Notch, there is no synergy between low levels of the two signals (in contrast with our current model), thus there are small differences in the slopes of some domain boundaries (e.g. between 33333 and 33133).
Figure 2 with 5 supplements
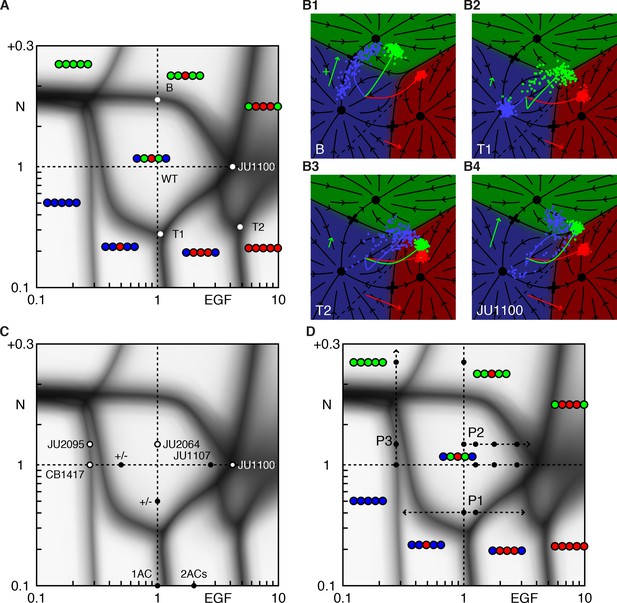
Phase diagram of the model.
(A) Phase diagram of the model showing the vulval pattern as a function of EGF and N(otch) levels normalized to the WT value of one. The horizontal axis represents fold-change in EGF pathway activity, while the vertical is defined to follow (Barkoulas et al., 2013). Notch levels below one are fold changes induced by RNAi, while larger values represent a uniform level of NICD added to the WT level in all cells (in units of the maximum signal produced by a cell). The shaded regions represent zones of partial penetrance marking the transition between two or more discrete fates. Three boundaries meet in triple points, e.g., T1/2. The labeled points are elaborated in B. (B) The fate plane depiction for transition points marked in A. The boundary point B corresponds to mild ectopic Notch activity (symbolized by a green '+'), resulting in partial conversion of P4/8.p to the 2° fate. The triple points T1 and T2 are two dosage combinations such that one pair of cells (P5/7.p and P4/8.p, respectively) can yield all three fates. JU1100 is an EGF over expression line (fit to ~4 × WT; longer red arrow), in which both P4/8.p and P5/7.p are partially transformed. Other symbols follow Figure 1E. (C) The data used to fit the model that admits representation in the phase diagram is shown as solid dots when both the phenotype and signal levels are used, and open circles when only the phenotype was assumed. The +/- denote a half dose of respective signal. (D) The data from (Barkoulas et al., 2013) (dots) overlaid on the phase diagram. The paths P1-3 are discussed in subsequent figures.
Figure 2—figure supplement 1
Phase diagram with a different fate plane topology.
If we assume in A a different fate plane topology, with the 2° fate wedged between 3° and 1° (corresponding to a 'graded' model for induction of vulval fates by EGF; compare with Figure 1E), domains in the phase diagram are also organized in bands, with no triple points (B; compare with Figure 2—figure supplement 2B).
Figure 2—figure supplement 2
Phase diagrams for a deterministic model.
These diagrams show the discrete outcomes (fate patterns) of a deterministic model as a function of EGF and Notch dosage, providing a ‘skeleton’ of the continuous fate variations obtained with stochastic dynamics (Figure 2A). Boundaries are colored according to the cell that changes fate, emphasizing that the phase diagram (and the somewhat complex set of accessible phenotypes) is structured by the boundary lines that originate from a small number of triple points. The presentation is simplified if we first depart from (Barkoulas et al., 2013) and consider multiplicative perturbations along both axes as in A. This also reveals a new triple point (T3) just above WT Notch levels, where P4/8.p adopt all three fates, as observed in the JU1100 EGF overexpression line (see Figures 2 and 3). If we omit the highest levels of Notch (above 4 × WT, where autocrine Notch signaling can override EGF), P6.p (red boundary lines) adopts either the 3° or the 1° fate, depending on EGF dosage; the slight slope of the boundary between 33333 and 33133 reflects synergy with autocrine Notch signaling. The fates of P5/7.p (green lines) are organized around the single triple point T1. For low Notch there is a transition from 3° to 1° fate as EGF increases, while for Notch in excess of the T1 value P5/7.p are fate 2°. P4/8.p (blue lines) display the most complex transitions. Below WT Notch they admit a triple point T2 that is analogous to T1 for P5/7.p, and in a region above this point they are induced to the 2° fate by P5/7.p. But under higher Notch levels P5/7.p adopt the 2° fate and signal less to their neighbors, thus the 2° domain of P4/8.p terminates at a second triple point T3. The Y-like shape of the triple points reflects the geometry of the fate plane (Figure 1E), and the 45° slope of the boundary between 31113 and WT (green line to the right of T1) is a direct consequence of how the signals are combined in the model (linearly). Our assumption of an exponential EGF gradient yields evenly spaced boundaries under low Notch. These generic features, together with a few quantitative phenotypes that position the boundaries, fully specify the structure of the phase diagram. In B, we switch to back to additive Notch as in Figure 2 to examine the fate transitions without the complexity of noise. P6.p admits a triple point T0 under reduced EGF and excess Notch (where ectopic Notch activity becomes sufficient to override EGF from the AC). Synergy between EGF and Notch in the induction of the 2° fate (discussed in the main text) can be seen in the slope of the boundary between 33333 and 33233 (red line to the left of T0). At the lowest EGF levels, the VPCs are all equivalent, going from 3° to 2° at the same level of Notch activity (thus the three boundaries collapse). The 2° domain of P4/8.p fans out above WT Notch instead of closing as in A (here excess Notch activity is independent of P5/7.p).
Figure 2—figure supplement 3
Alternative dynamics with enhanced production of Notch ligands.
A-B WT dynamics and phase diagram of a model that yields 32223 under reduced EGF. Model parameters were set to ‘default’ values (e.g. default EGF/Notch directions; Table 2), except for the lateral signaling threshold (dashed line) that is shifted away from the 1° domain (as seen in A). Then P6.p can strongly signal and induce P5/7.p without adopting the 1° fate (instead P6.p can adopt the 2° fate under reduced EGF due to autocrine Notch signaling). C. Left to right: dynamics under reduced EGF (0.3 × WT), AC ablation at t = 0.5 (also yielding 32223), and EGF overexpression (4 × WT, yielding 22122).
Figure 2—figure supplement 4
Alternative dynamics following Figure 2—figure supplement 3 but without autocrine Notch signaling.
(A-B) WT dynamics and phase diagram of a model that yields a dominant 32323 pattern under reduced EGF. Here again P6.p can induce P5/7.p without adopting the 1° fate, but adopts the 3° fate under reduced EGF. (C) Left to right: dynamics under reduced EGF (0.15 × WT), AC ablation at t = 0.25 (also yielding 32323), and EGF overexpression (4 × WT, yielding 22122).
Figure 2—figure supplement 5
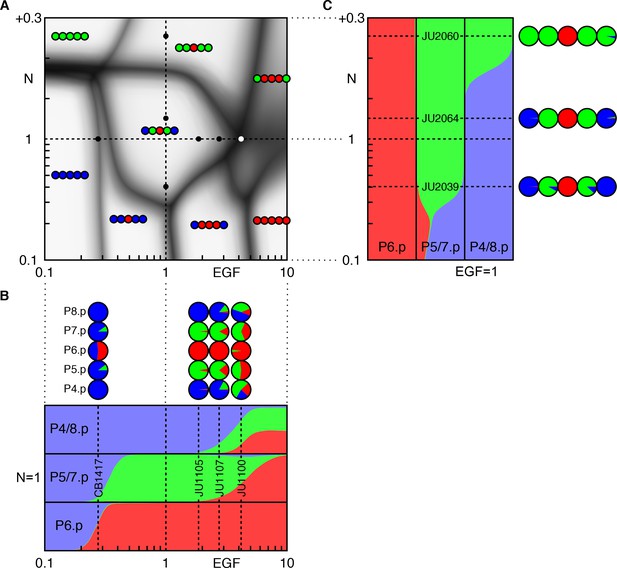
Response to EGF/Notch perturbations.
(A) EGF and Notch perturbation lines from (Barkoulas et al., 2013) (black dots) and the JU1100 line from (Hoyos et al., 2011) (white dot) are overlaid on the phase diagram of the model. EGF levels correspond to the reported values from (Barkoulas et al., 2013), except for the CB1417 line (see text) and JU1100 line (no measurement available), for which they were fit. Notch levels are predictions of the model. (B) Response to EGF perturbations. This corresponds to taking a cut through the phase diagram along the horizontal axis (WT Notch). Vertical dashed lines correspond to experimental lines, with the fate proportions shown as pie charts. Notice that under reduced EGF, loss of the 1° and 2° fates occurs around similar levels. In the experiments, the two phenotypes were never separated (i.e. with loss of 2° fates alone) (Barkoulas et al., 2013). Under increased EGF, P5/7.p are first partially converted to the 1° fate and P4/8.p to the 2° fate. At higher doses P4/8.p can adopt all three fates. (C) Response to Notch perturbations. At the highest Notch doses shown here, P4/8.p are fully converted to the 2° fate but P6.p is unaffected. At yet higher doses the model predicts P6.p is also converted (50% conversion occurs for a Notch level of about WT + 0.6). Notice the non-monotonic variation of 1° fate proportion in P5/7.p under reduced Notch, peaking around 0.2 × WT Notch (a prediction that could be tested with stronger experimental perturbations than reported in (Barkoulas et al., 2013).
Figure 3
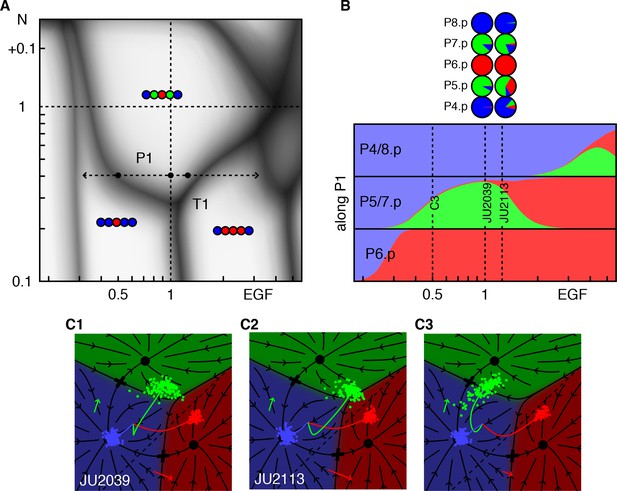
Response to EGF perturbations under reduced Notch.
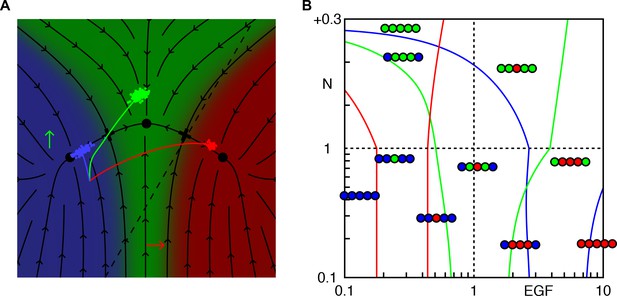
(A) Blowup of the phase diagram of Figure 2 around the triple point T1, where P5/7.p assume three fates. The double-headed arrow (path P1) represents variations in EGF dosage in a background with reduced Notch (lin-12 RNAi (Barkoulas et al., 2013) fit to ~0.4 × WT), which lies just above the lower corner of the wild-type domain. The dots on P1 are examined in panels B,C. (B) Cell fate proportions as a function of EGF dosage from the model and data (pie plots). A 25% increase in EGF already yields a significant fraction of adjacent 1° fates. The pronounced anterior-posterior asymmetry in the data is not seen in the model and may represent enhanced sensitivity to anterior displacements of the AC (Sundaram and Greenwald, 1993). Moving along P1 to 0.5 × WT EGF, we predict loss of 2° fates in P5/7.p. (C) Fate plane for different EGF dosages (WT, 1.25 × WT, and 0.5 × WT). In C1 the fit places the lin-12 RNAi condition just above the triple point T1 of the phase diagram, corresponding to P5/7.p (green dots) just above the center of the fate plane where the three domains meet. In C2, a very minor increase in EGF is sufficient to convert a fraction of the cells to the 1° fate. If instead reduced Notch is combined with a silent reduction in EGF (half dose), a substantial loss of 2° fates is predicted in C3 (Table 4).
Figure 4
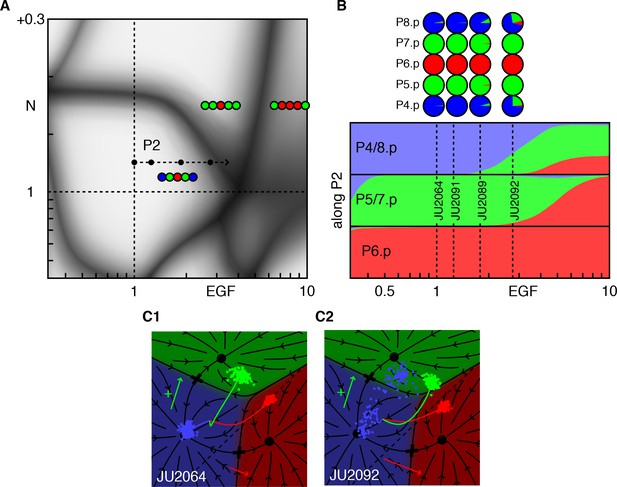
Epistasis between excess EGF and Notch.
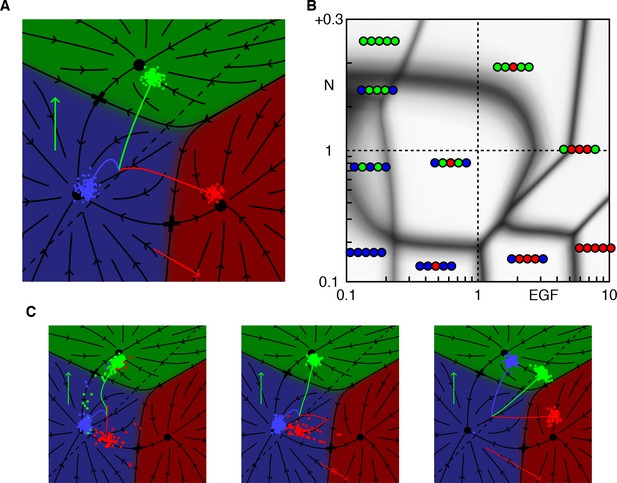
(A) Blowup of the phase diagram of Figure 2 centered on the region with excess EGF and Notch. The arrow (P2 ) represents gradual increases in EGF in a background with mild ectopic Notch activity (fit to ~WT + 0.05). (B) Fate proportions as a function of EGF dosage along path P2, in the model and experiments for the points in A (Table 4). (C) Cell trajectories in the fate plane for the JU2064 line (ectopic Notch and WT EGF) and the JU2092 line, a cross with the strongest EGF overexpression, explaining how excess EGF can produce more 2° fates in P4/8.p (text). See Video 2.
Figure 5
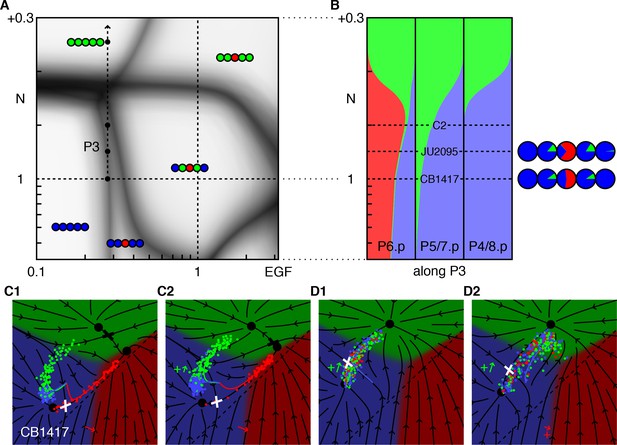
Synergy between low EGF and low ectopic Notch.
(A) Blowup of the phase diagram of Figure 2 showing the region with reduced EGF and excess Notch. The arrow (P3) represents gradual increases in ectopic Notch activity in the background of an EGF hypomorph, lin-3(e1417) or CB1417 in (Barkoulas et al., 2013) (fit to ~0.28 × WT). The boundary between the 33333 and 33133 domains makes a slight angle with the vertical, thus induction of P6.p to the 1° fate is partially rescued by Notch. (B) Fate proportions vs. Notch dosage in the model. The red bump in the left column reflects the partial rescue of P6.p induction by mild ectopic Notch activity. Under higher Notch doses, P6.p is converted to the 2° fate, as observed in a comparable experiment with EGF RNAi (Barkoulas et al., 2013). Correspondence with the data in (Barkoulas et al., 2013) is shown with the pie charts. An extra condition, C2, near maximum induction, was added to illustrate the model in the next panel. (C) Model trajectories for the EGF hypomorph, and the cross with a silent Notch gain-of-function line (N = WT + 0.1, the line C2 in B). In contrast to prior fate plane depictions, we show with arrows the flow experienced by P6.p during the competence window, including autocrine Notch signaling. Thus, the red trajectory follows the arrows. All cells begin at the same location at the beginning of competence (intersection of colored lines). The P6.p cells move toward the saddle or decision point (white cross) that separates the 1° and 2° fates, and then spread out along the line exiting that point. In C2, a small ectopic Notch signal pushes the P6.p points away from the decision point and more flow into the red 1° fate domain. (D) Enhancement of 2° induction by mild EGF activity (Zand et al., 2011). In this Notch sensitized background (N = WT + 0.16, D1), there is no AC or EGF signaling, and cells flow into the saddle point (white cross) separating the 3° and 2° fates and then diverge into two streams, using the same representation as in C. In D2 we add ectopic EGF activity [lin-15(ts)] (EGF = 0.16, +red arrow) which moves cells away from the line that flows into the saddle point. Thus, more cells are deflected toward the 2° fate by the flow around the saddle point. EGF never points toward the 2° fate, yet by acting early in the competence period can effect a large change in outcomes precisely because the background in D1 is poised near the saddle point and the flow around the cross rotates by 90°.
Figure 6 with 2 supplements
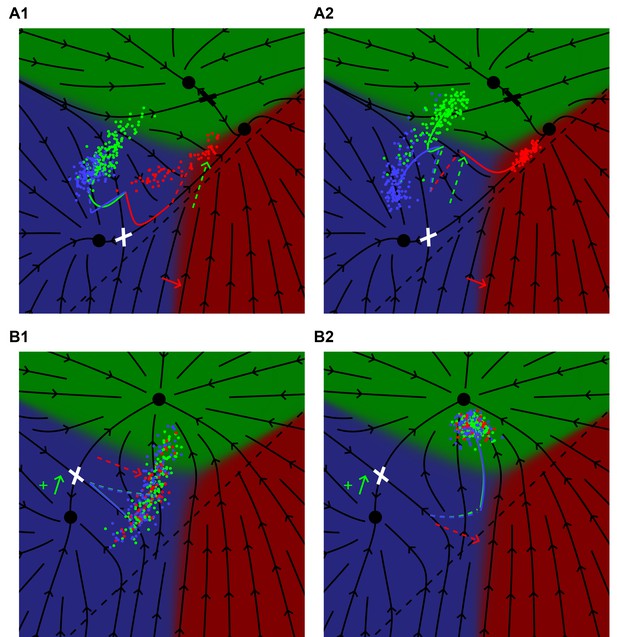
Model predictions for time-dependent perturbations.
(A) A lin-3(e1417) hypomorph subject to a uniform ectopic pulse of Notch (WT + 0.4) late (0.75 < t < 1) (A1) or early (0 < t < 0.25) (A2) in the competence period. The black flow lines represent the behavior of P6.p in the absence of ectopic Notch signaling as defined in Figure 5C1. For a late Notch pulse, the average behavior of P6.p (red curve) follows the flow into the saddle point (white cross) and then out toward fate 1°. At t = 0.75 the red curve has a kink and is dashed to show how the Notch pulse moves the cells toward fates 2° and 3°. An early Notch pulse, A2, pushes the cells across the flow lines (dashed red), but at t = 0.25 there is a kink signifying the end of the Notch pulse, and cells then follow the flow and emerge in the 1° domain, showing nearly complete rescue of fate 1°. See Video 3. (B) A lin-12 mutant with weak ectopic Notch activity (as defined in Figure 5D1) subject to a uniform pulse of EGF (WT + 0.64) either late (0.75 < t < 1) (B1) or early (0 < t < 0.25) (B2) in the competence period. The black lines show the dynamics in the absence of EGF following Figure 5 D1. In B1, the average cell (blue line) moves toward the saddle point as before, but at t = 0.75 has a kink, representing the onset of EGF signaling, and then (dashed) moves across the flow lines toward the 1° domain. The final outcome is a 73% to 25% ratio of 3° to 2° fates. With an early EGF pulse the trajectory (dashed) first moves toward fate 1° across the flow lines and at t = 0.25 has a kink representing the end of EGF signaling, and the trajectory (now solid blue) follows the flow and all cells assume fate 2°. See Video 4.
Figure 6—figure supplement 1
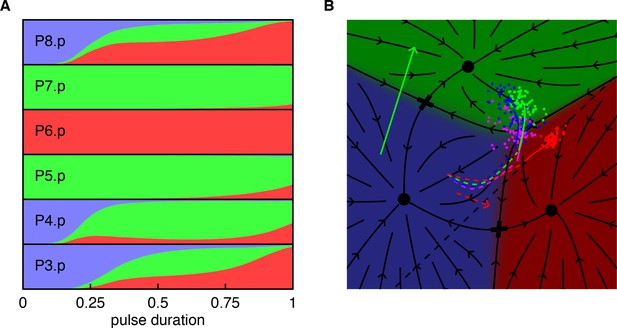
Transient lateral signaling yields adjacent 2° fates.
(A) Predicted fate proportions in response to an early pulse of uniform EGF (WT + 0.5, starting at t = 0), plotted as a function of the duration of the pulse (in an otherwise WT background with an AC). The distal-most VPC, P3.p, which is uninduced in most contexts and elsewhere omitted from the model, is included here as it affects the fate of P4.p (compare with P8.p). Notice that - although excess EGF is applied - ectopic fates are predominantly 2°. (B) Cell trajectories for an EGF pulse ending at t = 0.5 with P3.p shown in magenta (P4-6.p are shown with the usual colors). The dominant pattern for P3-5.p is 222. The initial EGF pulse drives all cells into the 1° domain, and the resulting, transient lateral signal is sufficient to induce adjacent 2° fates. This is similar to the effect of EGF overexpression in a background with mild ectopic Notch (Figure 4), but requires no ectopic Notch activity and yields a stronger effect.
Figure 6—figure supplement 2
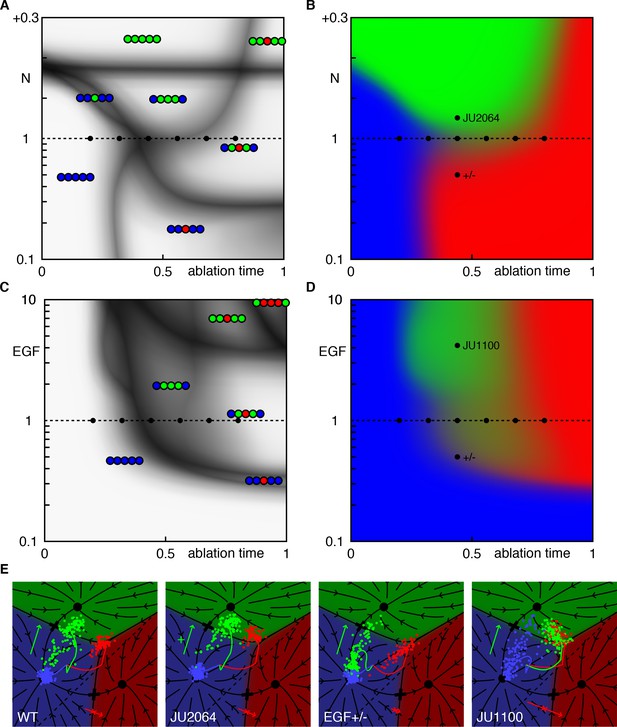
Anchor cell ablations in mutants.
(A) Phase diagram for AC ablation experiments in Notch mutants, showing the outcome as a function of ablation time (in scaled units during the competence period) and Notch dosage. The black dots along the WT Notch axis denote ablation experiments used to fit the model (Table 1). (B) Fate of P6.p. Notice the extended range of ablation times (around t = 0.5) that yield comparable 1°/2° levels. Small changes in Notch dosage are sufficient to shift this balance. The labeled black dots indicate putative ablation experiments (at t = 0.4) in silent backgrounds such that P6.p is predicted to yield mostly 3° fates (half dose of Notch) or mostly 2° fates (JU2064; see trajectories in panel E). In both cases, a higher induction of P6.p (around 90% 1° or 2° fates) is predicted than in WT (below 70% at the same ablation time), reflecting the geometry of the fate plane (E). (C-D) Same as above for ablation time vs. EGF dosage. Moderate reductions (e.g. a half dose) slightly delay induction (only slightly because EGF is saturated in P6.p in WT), but mixed 1°/2° fates remain, in contrast with the effect of Notch mutations. Strong increases in EGF (e.g. 2.75 × WT as in the JU1107 line) are predicted to yield earlier induction and - non-intuitively - a shift towards 2° fates. This is because P5/7.p are pushed toward 1° by EGF and signal to P6.p (see trajectories in E). (E) Model trajectories following AC ablation at an intermediate time (t = 0.4) in different backgrounds for the lines shown in B,D.
Figure 7
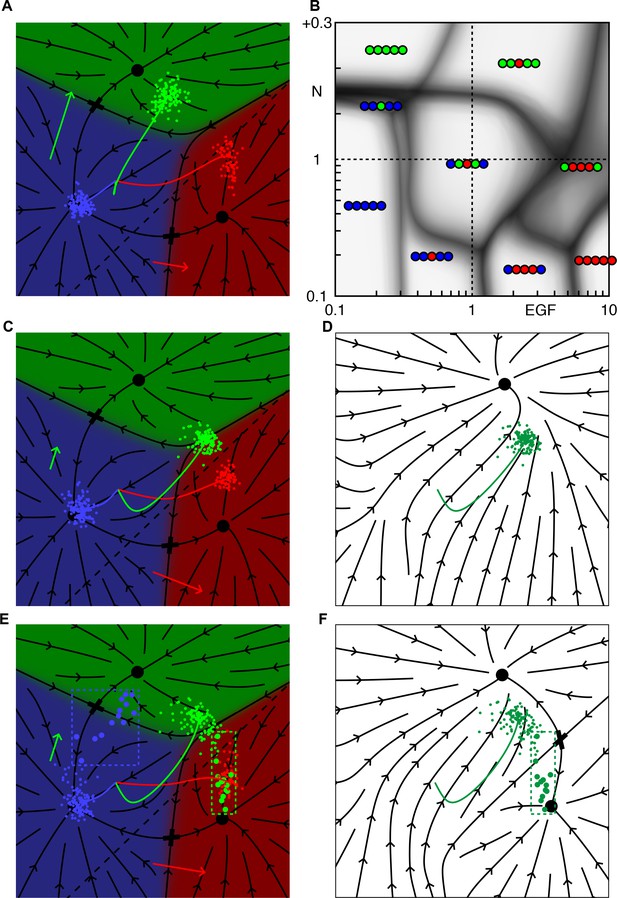
Inhibition of Notch in 1° fated cells clarifies the phase diagram and gives realistic correlated vulval patterns.
(A-B) Notch signaling is down regulated along the same dashed line that defines production of Notch ligand (see Materials and methods). For WT parameters, A, 1° fated cells move further into the red domain (compare with Figure 1E). The modified phase diagram, B, has a well-defined 21112 domain for Notch below WT, and EGF ~5 (compare with Figure 2A). On the boundary with the WT domain, P5-7.p, all change fate simultaneously, demonstrating the correlation. C-F illustrate the relation between multistability and fate correlations along the boundary between WT and 21112 (Notch = 0.4 × WT and EGF = 1.5 × WT). The post competence flow diagram for our primary model is shown in C. The flow seen by P5/7.p near the end of the competence period (including autocrine Notch signaling) has a single attractor (D) and the outcomes are clustered near the 1/2° boundary (green dots in C,D, P4/8.p are not shown). If we allow for down regulation of Notch signaling in 1° fated cells, the saddle point (cross) between 1° and 2° is preserved (F), yielding outcomes for P5/7.p that are spread out (E). Then with some probability P5.p or P7.p signal strongly to their outer neighbors, inducing a 2° fate (the large dots in dashed boxes highlight animals where P5/7.p signal strongly to their neighbors).
Videos
Video 1
Model dynamics of P6-8.p before, during and after the competence period, showing how the secondary Notch signals depend on the state of P6.p (cf. Figure 1).
https://doi.org/10.7554/eLife.30743.005
Video 2
Model dynamics for the JU2092 line with mild ectopic Notch and EGF ~3 xWT in Figure 4C2, showing how EGF can induce some P4/8.p to 2° fate while P5/7.p all remain 2° fate.
At intermediate times, P5/7.p transiently pass through the 1° domain and produce sufficient Notch ligand to divert a fraction of P4/8.p from the 3° fate.
Video 3
Model dynamics for a lin-3 hypomorph, subjected to a pulse of Notch late (left pane) or early (right pane) in the competence period following Figure 6A to show how timing affects outcomes.
The flow lines represent the cell dynamics during the competence period in the EGF hypomorph. The green arrow shows when the Notch pulse is applied.
Video 4
Model dynamics for weak ectopic Notch activity (with no AC and EGF signaling) subjected to an early (left pane) or late (right pane) spatially uniform pulse of EGF from lin-15(ts) showing how timing can affect outcomes, Figure 6B.
The flow lines represent the cell dynamics during competence and in the absence of EGF. The EGF pulse (red arrow) pushes the cells toward the 1° domain.
Tables
Table 1
Experimental data used to fit the model (training set).
Animals heterozygous for null mutations in lin-3 or lin-12 are described in the model by dividing the signal by two (‘half dose’). The EGF level for one overexpression line (JU1107) was set according to the measured lin-3 mRNA level. For other perturbations, the change in signal is included as a fitting parameter, cf. Table S2. * Notch null mutations result in the formation of two anchor cells, thus the effect of suppressing Notch signaling between VPCs it not obvious; however, several lines of evidence suggest that it yields the pattern 33133.
| Experiment | VPC fates (fate or % 1°, 2°, 3°) | References | ||||
|---|---|---|---|---|---|---|
| P4.p | P5.p | P6.p | P7.p | P8.p | ||
| Wild type | 3° | 2° | 1° | 2° | 3° | |
| EGF/Notch mutants | ||||||
| let-23 mosaic (no EGF receptors in P5/7 .p) | wild type | (Koga and Ohshima, 1995; Simske et al., 1995) | ||||
| Half dose of EGF (lin-3/+) | wild type | (Ferguson and Horvitz, 1985) | ||||
| Half dose of Notch (lin-12/+) | wild type | (Greenwald et al., 1983) | ||||
| No Notch signaling * | 3° | 3° | 1° | 3° | 3° | (Sundaram and Greenwald, 1993; Shaye and Greenwald, 2002; Komatsu et al., 2008) |
| Notch null mutant, 2 ACs * (described as 2 × WT EGF) | 3° | 1° | 1° | 1° | 3° | (Greenwald et al., 1983) |
| lin-15 mutant (ectopic EGF; fit to ~0.4 × WT) | alternating 1° and 2° fates (with or without AC) | (Sternberg, 1988) | ||||
| EGF overexpression | ||||||
| JU1107 2.75 × WT EGF (based on measured mRNA level) | 2, 16, 82 | 22, 78, 0 | 100, 0, 0 | 16, 84, 0 | 3, 13, 84 | (Barkoulas et al., 2013) |
| JU1100 (mRNA level not determined; level fit) | 24, 54, 21 | 54, 46, 0 | 96, 4, 0 | 37, 63, 0 | 12, 39, 49 | (Hoyos et al., 2011) |
| AC ablation at successive developmental stages (mapped to evenly spaced time points in the model) | (Milloz et al., 2008) | |||||
| L2 lethargus (t = 0.2) | 3° | 3° | 3° | |||
| early L3 (t = 0.32) | 3, 24, 74 | 18, 19, 64 | 0, 20, 80 | |||
| DU divided (t = 0.44) | 0, 59, 41 | 31, 37, 32 | 0, 53, 47 | |||
| VU divided (t = 0.56) | 0, 95, 5 | 53, 48, 0 | 8, 86, 6 | |||
| 3° divided (t = 0.68) | 3, 98, 0 | 65, 35, 0 | 0, 100, 0 | |||
| two-cell stage (t = 0.8) | 1, 99, 0 | 93, 7, 0 | 1, 99, 0 | |||
| Epistasis between EGF/Notch | (Barkoulas et al., 2013) | |||||
| CB1417 (lin-3(e1417) EGF hypomorph; level fit) | 0, 0, 100 | 0, 10, 90 | 54, 0, 46 | 0, 10, 90 | 0, 0, 100 | |
| JU2064 (mild ectopic Notch activity; level fit) | 0, 1, 99 | 0, 100, 0 | 100, 0, 0 | 0, 100, 0 | 1, 2, 97 | |
| JU2095 (mild ectopic Notch activity in the lin-3(e1417) background) | 0, 0, 100 | 1, 14, 86 | 72, 1, 28 | 0, 16, 84 | 0, 2, 98 | |
Table 2
Model parameters.
The mean value and standard deviation within the parameter ensemble (where applicable) are indicated for each parameter.
| Parameter | Description | Main model | Parameter values from Corson and Siggia (2012) | Model with EGF/Notch coupling (Figure 7) | Alternate models of Figure 2—figure supplements 3 and 4 |
|---|---|---|---|---|---|
| Model parameters | |||||
| Bias towards the default 3° fate | 0.47 ± 0.03 | 0.39 ± 0.03 | 0.51 ± 0.03 | 0.5 | |
| 210 (fixed) | 210 (fixed) | 210 (fixed) | 210 | ||
| Response to EGF* | 3.87 ± 0.52 | 4.60 ± 0.98 | 3.86 ± 0.52 | 6 | |
| −21 ± 8 | −30 (fixed) | −9 ± 6 | −30 | ||
| Response to Notch* | 6.25 ± 1.28 | 5.97 ± 1.07 | 7.72 ± 1.31 | 6 | |
| 73 ± 3 | 90 (fixed) | 73 ± 5 | 90 | ||
| Characteristic time scale of dynamics | 2.02 ± 0.16 | 2.18 ± 0.30 | 2.23 ± 0.25 | 2 | |
| Noise level | 0.12 ± 0.02 | 0.12 ± 0.03 | 0.14 ± 0.02 | 0.14 | |
| Shape of EGF gradient | 0.23 ± 0.02 | 0.16 ± 0.03 | 0.22 ± 0.02 | 0.2 | |
| Relative strength of autocrine signaling | 1.08 ± 0.11 | 1.14 ± 0.17 | 1.24 ± 0.22 | 1/2 (Figure 2—figure supplement 3) or 0 (Figure 2—figure supplement 4) | |
| Threshold for lateral signaling | −1.20 ± 0.09 | −1.23 ± 0.10 | −1.29 ± 0.11 | 0.25 | |
| † | −46 ± 3 | −48 ± 3 | −46 ± 3 | −45 | |
| Signal levels for experiments in the training set | |||||
| Ectopic EGF level in the lin-15 mutant | 0.42 ± 0.11 | 0.55 ± 0.25 | 0.51 ± 0.20 | N/A | |
| EGF level in the JU1100 overexpression line | 4.18 ± 0.49 | 7.39 ± 1.36 | 4.84 ± 0.67 | N/A | |
| EGF level in the lin-3(e1417) hypomorph | 0.28 ± 0.03 | N/A | 0.28 ± 0.03 | N/A | |
| Ectopic Notch activity in the JU2064 line | 0.05 ± 0.03 | N/A | 0.04 ± 0.02 | N/A | |
-
*While the vectors and are parameterized by their Cartesian coordinates, with Gaussian priors, the mean ±SD of their norm and orientation are shown for convenience. Angles (symbolized by ) are relative to the horizontal axis of the fate plane and in degrees.
†As in (Corson and Siggia, 2012), the sharpness of the threshold for lateral signaling was set to a default value, , so that its orientation alone is fit; a similar value for the norm of is recovered when it is not imposed in the fit.
Table 3
Experimental lines from (Barkoulas et al., 2013), and one line from (Hoyos et al., 2011), referred in this study.
Levels used to model the lines were based on measurements of EGF mRNA levels from (Barkoulas et al., 2013) or fit, as indicated. For combined perturbations, we indicate the corresponding single perturbations lines.
| EGF perturbation lines | |
|---|---|
| CB1417 | lin-3(e1417) hypomorph; level included as fitting parameter ~0.28 × WT (measured as ~0.06 × WT in (Barkoulas et al., 2013) and ~0.22 × WT in [Saffer et al., 2011]) |
| JU2036 | measured as ~ 1.25 × WT |
| JU2035 | measured as ~ 1.79 × WT |
| JU1107 | measured as ~ 2.75 × WT |
| JU1100 (Hoyos et al., 2011) | level included as fitting parameter ~4.2 × WT (not measured) |
| Notch perturbation lines | |
| JU2039 | Pn.p cell-specific RNAi; level fit to phenotype strength ~0.4 × WT |
| JU2064 | ectopic Notch activity; level included as fitting parameter ~WT + 0.05 |
| JU2060 | ectopic Notch activity; level fit to yield near-complete P4/8.p conversion ~ WT + 0.26 |
| Combined perturbations | |
| JU2113 | JU2036 × JU2039 |
| JU2091 | JU2036 × JU2064 |
| JU2089 | JU2035 × JU2064 |
| JU2092 | JU1107 × JU2064 |
| JU2095 | CB1417 × JU2064 |
Table 4
Comparison between model predictions and experimental outcomes from (Barkoulas et al., 2013).
The model prediction (mean ±SD within the parameter ensemble) is displayed below the experimental outcome.
| Experiment | VPC fates (% 1°, 2°, 3°) | ||||
|---|---|---|---|---|---|
| P4.p | P5.p | P6.p | P7.p | P8.p | |
| Excess EGF × reduced Notch (Figure 3) The Notch level is our fit for Notch RNAi in the JU2039 line ~ 0.4 × WT. The EGF level is based on the mRNA level measured in the JU2036 EGF perturbation line (Barkoulas et al., 2013). | |||||
| JU2039 (WT EGF) | 1, 0, 99 | 1, 91, 8 | 100, 0, 0 | 1, 87, 11 | 0, 0, 100 |
| 0 ± 0, 0 ± 0, 99 ± 0 | 3 ± 1, 88 ± 1, 8 ± 1 | 99 ± 0, 0 ± 0, 1 ± 0 | 3 ± 1, 89 ± 1, 8 ± 1 | 0 ± 0, 0 ± 0, 99 ± 0 | |
| JU2113 (1.25 × WT EGF) | 7, 10, 83 | 32, 60, 8 | 100, 0, 0 | 4, 79, 17 | 0, 2, 98 |
| 0 ± 0, 0 ± 0, 99 ± 0 | 16 ± 8, 76 ± 9, 9 ± 2 | 99 ± 0, 0 ± 0, 1 ± 0 | 16 ± 9, 75 ± 10, 9 ± 2 | 0 ± 0, 0 ± 0, 99 ± 0 | |
| Excess EGF × ectopic Notch activity (Figure 4) Increasing EGF levels in a background with mild ectopic Notch activity. The level of ectopic Notch activity is our fit for the JU2064 line ~ WT + 0.05. EGF levels are based on measured mRNA levels in the EGF perturbation lines JU2036, JU2035, and JU1107 (Barkoulas et al., 2013). | |||||
| JU2091 (1.25 × WT EGF) | 0, 0, 100 | 0, 100, 0 | 100, 0, 0 | 0, 100, 0 | 0, 1, 99 |
| 0 ± 0, 1 ± 1, 99 ± 1 | 1 ± 0, 99 ± 1, 1 ± 0 | 98 ± 0, 1 ± 0, 1 ± 0 | 1 ± 0, 99 ± 1, 1 ± 0 | 0 ± 0, 1 ± 1, 99 ± 1 | |
| JU2089 (1.79 × WT EGF) | 0, 5, 96 | 2, 98, 0 | 100, 0, 0 | 2, 99, 0 | 1, 7, 92 |
| 0 ± 0, 6 ± 5, 93 ± 5 | 2 ± 1, 97 ± 2, 1 ± 1 | 99 ± 0, 1 ± 0, 1 ± 0 | 2 ± 1, 97 ± 2, 1 ± 1 | 1 ± 0, 6 ± 5, 93 ± 6 | |
| JU2092 (2.75 × WT EGF) | 3, 24, 74 | 0, 100, 0 | 100, 0, 0 | 0, 100, 0 | 8, 24, 68 |
| 1 ± 1, 38 ± 14, 61 ± 14 | 9 ± 4, 88 ± 5, 3 ± 1 | 99 ± 0, 1 ± 0, 1 ± 0 | 8 ± 4, 88 ± 5, 3 ± 1 | 1 ± 1, 38 ± 14, 61 ± 14 | |
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Gene-free methodology for cell fate dynamics during development
eLife 6:e30743.
https://doi.org/10.7554/eLife.30743
