Geometry of antiparallel microtubule bundles regulates relative sliding and stalling by PRC1 and Kif4A

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: October 24, 2018 (This version)
Accepted: September 28, 2018
Received: October 8, 2017

1. Of interest
The neuronal calcium sensor NCS-1 regulates the phosphorylation state and activity of the Ga chaperone and GEF Ric-8A

Daniel Muñoz-Reyes, Levi J McClelland ... Maria Jose Sanchez-Barrena

Research Article Nov 29, 2023
Further reading

Abstract
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Motor and non-motor crosslinking proteins play critical roles in determining the size and stability of microtubule-based architectures. Currently, we have a limited understanding of how geometrical properties of microtubule arrays, in turn, regulate the output of crosslinking proteins. Here we investigate this problem in the context of microtubule sliding by two interacting proteins: the non-motor crosslinker PRC1 and the kinesin Kif4A. The collective activity of PRC1 and Kif4A also results in their accumulation at microtubule plus-ends (‘end-tag’). Sliding stalls when the end-tags on antiparallel microtubules collide, forming a stable overlap. Interestingly, we find that structural properties of the initial array regulate microtubule organization by PRC1-Kif4A. First, sliding velocity scales with initial microtubule-overlap length. Second, the width of the final overlap scales with microtubule lengths. Our analyses reveal how micron-scale geometrical features of antiparallel microtubules can regulate the activity of nanometer-sized proteins to define the structure and mechanics of microtubule-based architectures.

https://doi.org/10.7554/eLife.32595.001

Introduction

The organization of microtubules into specialized architectures is required for a diverse range of cellular processes such as cell division, growth and migration (Dogterom and Surrey, 2013; Subramanian and Kapoor, 2012). Microtubule-crosslinking proteins play important roles in determining the relative orientation, size and dynamics of microtubule-based structures. These proteins include molecular motors that utilize the energy from ATP hydrolysis to mediate the transport of one microtubule over another (referred to as ‘relative sliding’) (Sharp et al., 2000; Tolić-Nørrelykke, 2008; Forth and Kapoor, 2017). Motor proteins frequently act in conjunction with non-motor microtubule crosslinking proteins that oppose relative sliding and regulate both the stability and the size of the arrays (Dogterom and Surrey, 2013; Subramanian and Kapoor, 2012; Bratman and Chang, 2008). The activities of motor and non-motor proteins are in turn modulated by the microtubule cytoskeleton. At the nanometer length-scale, numerous tubulin isotypes and post-translational modifications on tubulin act as a code to tune the activity of microtubule-associated proteins (MAPs) (Gull et al., 1986; Ludueña, 2013; Yu et al., 2015; Gadadhar et al., 2017). In addition, it is becoming apparent that at the micron length-scale, the geometrical properties of microtubule bundles, such as orientation, filament length and overlap length, also modulate the output of motor and non-motor proteins (Fink et al., 2009; Kuan and Betterton, 2016; Shimamoto et al., 2015; Braun et al., 2017). Currently, we have a limited understanding of the mechanisms by which the micron-sized features of a microtubule network are ‘read’ and ‘translated’ by associated proteins.

Arrays of overlapping antiparallel microtubules form the structural backbone of diverse cellular structures. Several insights into the mechanisms underlying the assembly of such arrays have come from examining the non-motor antiparallel microtubule crosslinking proteins of the PRC1/Ase1/MAP65 family. These evolutionarily conserved proteins play an important role in organizing microtubule arrays in interphase yeast and plant cells, and subsets of spindle microtubules in dividing cells in all eukaryotes (Chan et al., 1999; Loïodice et al., 2005; Yamashita et al., 2005; Jiang et al., 1998; Mollinari et al., 2002; Polak et al., 2017). These passive non-motor proteins act in concert with a number of different motor proteins, such as those of the kinesin-4, kinesin-5, kinesin-6 and kinesin-14 families (Jiang et al., 1998; Mollinari et al., 2002; Zhu et al., 2006; Gruneberg et al., 2006; Janson et al., 2007; D'Avino et al., 2007; Fu et al., 2009; Bieling et al., 2010; Braun et al., 2011; Duellberg et al., 2013; Subramanian et al., 2013; Pringle et al., 2013; de Keijzer et al., 2017). A subset of these kinesins, such as Kif4A, Kif23 and Kif20, directly or indirectly bind PRC1/MAP65/Ase1 family proteins (Gruneberg et al., 2006; Fu et al., 2009; Bieling et al., 2010; Subramanian et al., 2013; Kurasawa et al., 2004; Zhu and Jiang, 2005; Vitre et al., 2014). The diversity in the properties of motor proteins that act in conjunction with the different PRC1 homologs affords a powerful model system to elucidate the biophysical principles governing the organization of antiparallel microtubule arrays. However, thus far, the mechanistic studies of PRC1-kinesin systems have mainly focused on elucidating how microtubule sliding by kinesins is regulated by PRC1 homologs (Braun et al., 2011; Subramanian et al., 2010; Lansky et al., 2015). How the geometry of PRC1-crosslinked microtubules, such as lengths of microtubules and the size of the initial overlap, modulates the activities of associated motor proteins is poorly understood.

Here, we address this question by examining the relative sliding of PRC1-crosslinked antiparallel microtubules by the kinesin Kif4A. The collective activity of PRC1 and Kif4A is required for the organization of the spindle midzone, an antiparallel bundle of microtubules that is assembled between the segregating chromosomes at anaphase in dividing cells (Kurasawa et al., 2004; Zhu and Jiang, 2005; Shrestha et al., 2012; Nunes Bastos et al., 2013; Hu et al., 2011). Kif4A, a microtubule plus-end directed motor protein is recruited to the midzone array through direct binding with PRC1, where it acts to suppress microtubule dynamics (Bieling et al., 2010; Subramanian et al., 2013; Nunes Bastos et al., 2013; Hu et al., 2011). Previous in vitro studies with the Xenopus Laevis homologs of these proteins also suggest that they can drive the relative sliding of antiparallel microtubules over short distances (Bieling et al., 2010). However, microtubule sliding by Kif4A and its modulation by the geometrical features of the initial PRC1-crosslinked microtubules remain poorly characterized. In addition to sliding, the processive movement of PRC1-Kif4A complexes and their slow dissociation from the microtubule end result in the accumulation of both proteins in micron-sized zones at the plus-ends of single microtubules (hereafter referred to as ‘end-tags’). It is observed that: (i) the velocity of the motor movement is reduced at end-tags (Subramanian et al., 2013). This hindrance to motor stepping is likely due to molecular crowding at microtubule ends (Subramanian et al., 2013; Leduc et al., 2012). (ii) The size of end-tags increases with microtubule length (Subramanian et al., 2013). How the length-dependent accumulation of PRC1-Kif4A molecules on single microtubules impacts the organization of antiparallel bundles is unknown.

Here, we show using TIRF-microscopy based assays that the collective activity of PRC1 and Kif4A results in relative microtubule sliding and concurrent end-tag formation on antiparallel microtubules. Interestingly, we find that PRC1-Kif4A end-tags act as roadblocks to prevent the complete separation of sliding microtubules. Consequently, sliding and stalling of antiparallel microtubules by PRC1 and Kif4A result in the assembly of a stable overlap that is spatially restricted to the filament plus-ends. Surprisingly, quantitative examination of the data reveals that two aspects of the PRC1-Kif4A-mediated microtubule organization are modulated by the initial geometry of crosslinked microtubules. First, the sliding velocity in this system scales with the initial length of the antiparallel overlap. Second, the size of the final stable antiparallel overlap established by PRC1 and Kif4A scales with the lengths of the crosslinked microtubules. Our observations provide insights into the principles by which the geometrical features of antiparallel arrays can be translated to graded mechanical and structural outputs by microtubule-associated motor and non-motor proteins.

Results

Collision of PRC1-Kif4A end-tags on sliding microtubules results in the formation of antiparallel overlaps of constant length at steady-state

To investigate microtubule sliding in the PRC1-Kif4A system, we reconstituted the activity of the kinesin Kif4A on a pair of antiparallel microtubules crosslinked by the non-motor protein PRC1. For these studies, we adapted a Total Internal Reflection Fluorescence (TIRF) microscopy-based assay that we have previously used to examine relative sliding of PRC1-crosslinked microtubules by the motor-protein Eg5 (Subramanian et al., 2010). First, biotinylated taxol-stabilized microtubules, labeled with rhodamine, were immobilized on a glass coverslip. Next, unlabeled PRC1 (0.2 nM) was added to the flow chamber and allowed to bind the immobilized microtubules. Finally, rhodamine-labeled non-biotinylated microtubules were flowed into the chamber to generate microtubule ‘sandwiches’ crosslinked by PRC1 on the glass coverslip (Figure 1A). After washing out the unbound proteins, the final assay buffer containing Kif4A-GFP, PRC1 and ATP at specified concentrations was flowed into the chamber to initiate end-tag formation and microtubule sliding (Figure 1A). Near-simultaneous multi-wavelength imaging of rhodamine-labeled microtubules and Kif4A-GFP showed that Kif4A preferentially accumulates in the overlap region of PRC1-crosslinked microtubules (Figure 1B–D; $t$ = 0 s; 0.2 nM PRC1 + 6 nM Kif4A-GFP). This is in agreement with prior findings that PRC1 selectively accumulates at regions of antiparallel microtubule overlap regions and recruits Kif4A to these sites (Bieling et al., 2010; Subramanian et al., 2010). In the example shown in Figure 1B-D, the average fluorescence intensity of Kif4A-GFP in the microtubule overlap region is 5-fold higher than the fluorescence intensity in the non-overlapped region at the first time point recorded (Figure 1B–E; $t$ = 0 s). In addition, time-lapse imaging shows an enhanced accumulation of Kif4A-GFP at the plus-ends of both the crosslinked microtubules. We refer to this region of high protein density at microtubule plus-ends as ‘end-tags’ (Figure 1B–E; $t$ = 10–40 s; ~2.5 fold enrichment of Kif4A-GFP at end-tags over the untagged overlap at 10 s). Therefore, under these experimental conditions Kif4A-GFP-containing end-tags are established at the plus-ends of crosslinked microtubules.

Figure 1

Download asset Open asset

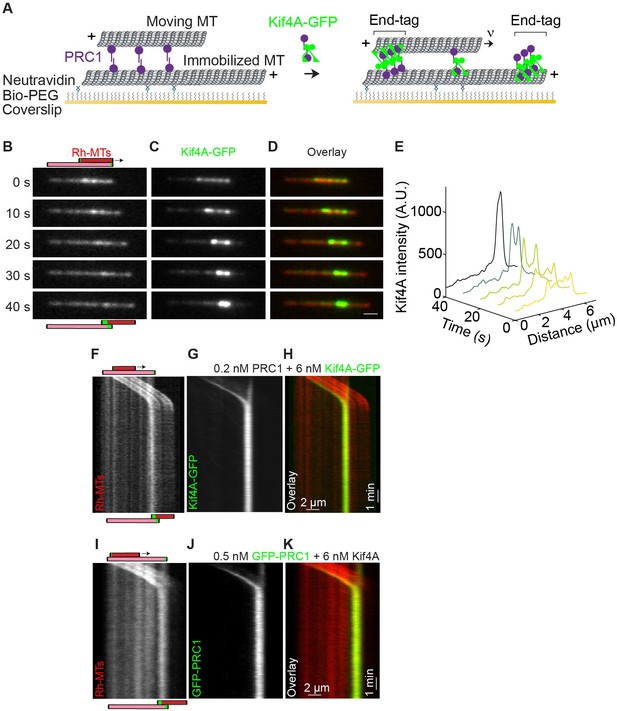
Relative microtubule sliding and the formation of stable antiparallel microtubule overlaps by PRC1 and Kif4A.

(A) Schematic of the in vitro assay. A biotinylated microtubule (‘immobilized MT’, X-rhodamine labeled) immobilized on a PEG coated coverslip and a non-biotinylated microtubule (‘moving MT’, X-rhodamine-labeled) are crosslinked in an antiparallel orientation by PRC1 (purple). Microtubule sliding and end-tag formation are initiated by addition of Kif4A-GFP (green), PRC1 and ATP. (**B–D**) Representative time-lapse fluorescence micrographs of relative microtubule sliding in experiments with 0.2 nM PRC1 and 6 nM Kif4A-GFP. Images show (B) a pair of X-rhodamine-labeled microtubules, (C) Kif4A-GFP, and (D) overlay images (red, microtubules; green, Kif4A-GFP). The schematic in (B) illustrates the position and relative orientation of both the immobilized (pink) and moving (red) microtubules and the end-tags (green) at the beginning and end of the time sequence. Scale bar: x: 2 µm. (E) Line scan analysis of the Kif4A intensity from the micrographs in (C) shows the distribution of Kif4A within the overlap at the indicated time points. (**F–H**) Kymographs show the relative sliding and stalling of antiparallel microtubules (F), associated Kif4A-GFP (G) and the overlay image (red, microtubules; green, Kif4A-GFP) (H). Assay condition: 0.2 nM PRC1 and 6 nM Kif4A-GFP. Scale bar: x: 2 µm and y: 1 min. (**I–K**) Kymographs show the relative sliding and stalling of antiparallel microtubules (I), associated GFP-PRC1 (J) and the overlay image (red, microtubules; green, GFP-PRC1) (K). Assay condition: 0.5 nM GFP-PRC1 and 6 nM Kif4A. Scale bar: x: 2 µm and y: 1 min.

https://doi.org/10.7554/eLife.32595.002

Time-lapse imaging and kymography-based analyses revealed that the end-tagged antiparallel microtubules slide relative to each other (Figure 1B–D and F–H). Strikingly, we find that microtubule sliding stalls when the end-tags arrive at close proximity (Figure 1B–D and F–H). This results in the formation of stable antiparallel overlaps that maintain a constant steady-state width for the entire duration of the experiment (Figure 1B–D and F–H; $t$ = 10 min). We rarely (5%) observe sliding microtubules stall before they arrive at the plus-end of the immobilized microtubule, and these occasional premature stalling events may arise from non-specific sticking to the glass coverslip. Under these experimental conditions, we do not observe any event where the moving microtubule slides past the end-tag of the immobilized microtubule. These observations indicate that the formation of stable antiparallel overlaps is due to the end-tags on the crosslinked microtubule pair arriving at close proximity during relative sliding.

We next examined PRC1 localization on sliding microtubules by conducting experiments similar to that described above, except with GFP-labeled PRC1 and unlabeled Kif4A (Figure 1I–K; 0.5 nM GFP-PRC1 + 6 nM Kif4A). We find that the localization pattern of GFP-PRC1 is similar to Kif4A with the highest fluorescence intensity at the end-tags, intermediate intensity at the untagged microtubule overlap regions and the lowest intensity on single microtubules. Similar to the observations in Figure 1F–H, we find that sliding microtubules stall when their end-tags arrive in close proximity (Figure 1I–K).

Together, these observations suggest that human PRC1-Kif4A complexes can drive the relative sliding of antiparallel microtubules over the distance of several microns. However, sliding comes to a halt at microtubule plus-ends resulting in the formation of stable antiparallel overlaps of constant steady-state length.

Molecular determinants of sliding and cross-bridging in the PRC1-Kif4A system

To investigate the molecular determinants of the observed sliding and cross-bridging in the PRC1-Kif4A system, we examined if Kif4A alone can crosslink microtubules. A common mechanism by which dimeric kinesins crosslink and slide microtubules is by interacting with one microtubule via the motor domains and another microtubule using non-motor C-terminus domains. Whether the C-terminus of human Kif4A, which binds both DNA and PRC1, can also bind microtubules is unknown (Subramanian et al., 2013). To examine this, we purified the C-terminus PRC1 and DNA-binding domain of Kif4A (aa. 733–1232) and performed microtubule co-sedimentation assays (Figure 2A). Dose-dependent microtubule binding of this domain was not observed in the tubulin concentration range tested. Therefore, in the cross-bridging complex, the C-terminus of Kif4A is likely to associate with the N-terminus of PRC1, which forms the link between both microtubules (Figure 2B).

Figure 2

Download asset Open asset

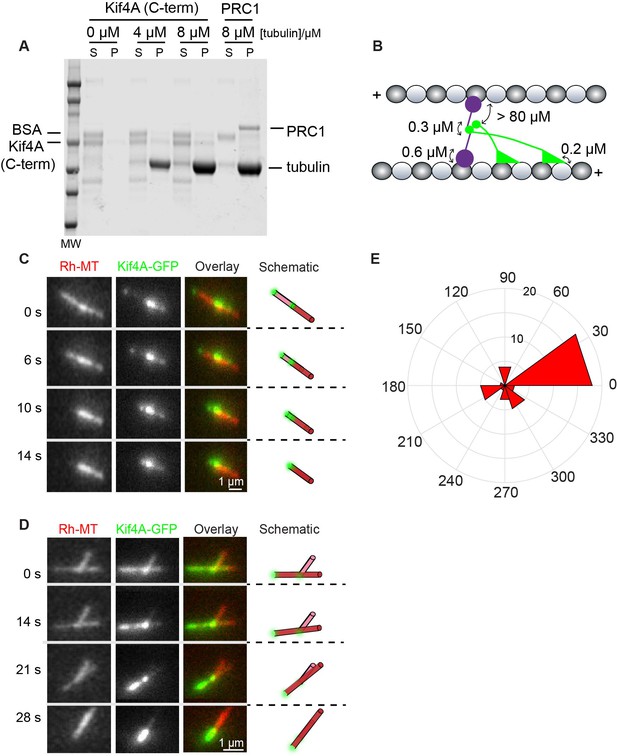
Molecular determinants of cross-bridging and sliding in the PRC1-Kif4A system.

(A) Microtubule co-sedimentation assay. SDS Page analysis of the interaction of Kif4A (C-term) with increasing amounts microtubules (0–8 μM). Full-length PRC1 was included as a control. Quantification of band intensities: Kif4A_pellet = 8% and 6% at 4 μM and 8 μM tubulin. BSA_pellet = 1% and 3% at 4 μM and 8 μM tubulin. (B) Schematic shows the proposed molecular configuration of the cross-bridging PRC1-Kif4A complex in a microtubule overlap. Known dissociation constants are indicated. (**C–D**) Representative time-lapse fluorescence micrographs of relative microtubule sliding in experiments with 6 nM Kif4A-GFP + 2 mM ATP. Images show a pair of X-rhodamine-labeled microtubules, Kif4A-GFP, and overlay images (red, microtubules; green, Kif4A-GFP). The schematic illustrates the position and relative orientation of both the immobilized and moving microtubules (red) and the end-tags (green) at the beginning and end of the time sequence. (E) Rose diagram of the initial angle of attachment of the sliding microtubule. The plot shows the most probable angle of attachment is between 0–30° (N = 39). Assay condition: 6 nM Kif4A-GFP + 2 mM ATP.

https://doi.org/10.7554/eLife.32595.003

Figure 2—source data 1 This spreadsheet contains the initial angle of attachment of the sliding microtubule used to generate the rose diagram shown in Figure 2E.: https://doi.org/10.7554/eLife.32595.004
Download elife-32595-fig2-data1-v1.xlsx

Next, we examined if there was a non-canonical mode of microtubule sliding by Kif4A in the absence of PRC1. For this, we attempted microtubule crosslinking experiments as described in Figure 1 with Kif4A alone (2 mM ATP). Similar to a previous report with Xklp1, full-length human Kif4A does not bundle microtubules in the presence of ATP (not shown) (Bieling et al., 2010). We reasoned that bundle formation might be enhanced if the lifetime of the protein on microtubule was increased. To investigate this, we first bound Kif4A-GFP to immobilized microtubules at low ATP concentrations (6 nM Kif4A-GFP + 10 nM ATP). Under these conditions, due to the slow rate of stepping, the protein is bound along the entire length of the microtubules (Figure 2C and D). Subsequent addition of non-biotinylated microtubules resulted in the formation of pairs of crosslinked microtubules (~20% microtubules are crosslinked per 133 μm² field of view under our experimental conditions). We find that the predominant angle of initial attachment between the two microtubules is 0–30° (Figure 2E). Finally, we flowed in 2 mM ATP and 6 nM Kif4A-GFP, which initiated end-tag formation on all microtubules. We find that contact between the end-tag on the non-biotinylated microtubule with the immobilized microtubule results in tip-mediated movement of one microtubule over the other (Figure 2C–D). Similar to experiments with PRC1 and Kif4A, sliding completely stalls when the Kif4A-GFP end-tags collide. These findings indicate that a Kif4A-dense microtubule tip can slide along another microtubule even though the C-terminus of Kif4A does not bind microtubules with high affinity.

Together these findings suggest that there are two possible modes of cross-bridging and sliding in the PRC1-Kif4A system. First, Kif4A-molecules interacting with microtubule-crosslinking PRC1-molecules can drive sliding. Second, Kif4A molecules at the tips of one microtubule can bind and slide over another microtubule. Currently, we do not know if the second mode of movement occurs in the context of an antiparallel bundle, where the angle between crosslinked microtubules is 180°. Finally, these experiments show that relative microtubule movement can stall at microtubule ends in the absence of PRC1, suggesting that molecular crowding is likely to be the predominant cause of stable overlap formation in the PRC1-Kif4A system.

Characterization of relative microtubule sliding in the PRC1-Kif4A system

To further characterize relative sliding in mixtures of PRC1 and Kif4A, we quantitatively examined the microtubule movement observed in these experiments. Analysis of the instantaneous velocity during microtubule sliding (Figure 3A–C; 0.2 nM PRC1 + 6 nM Kif4A-GFP), reveals three phases: (1) initial sliding at constant velocity, (2) reduction in sliding velocity as the end-tags arrive at close proximity, and (3) microtubule stalling and the formation of stable overlaps that persist for the duration of the experiment.

Figure 3 with 1 supplement see all

Download asset Open asset

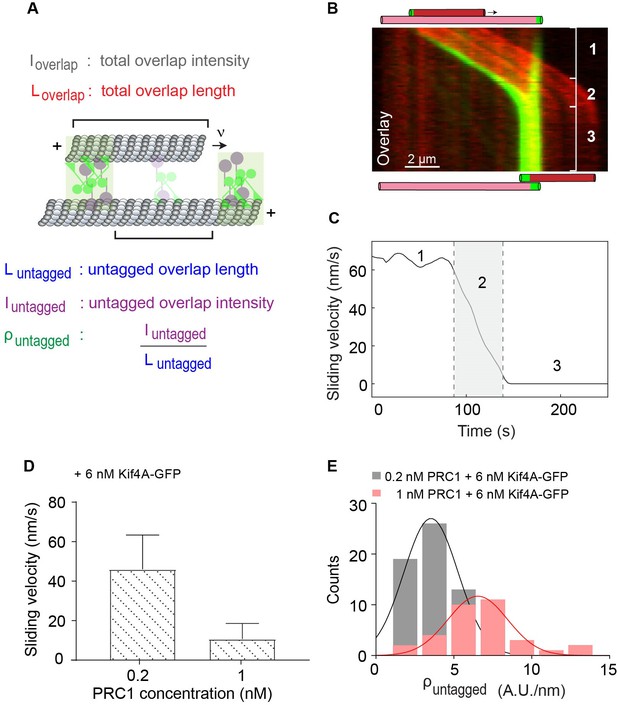
Quantitative analysis of microtubule sliding in the PRC1-Kif4A system.

(A) Schematic of a pair of crosslinked microtubules showing the parameters described in Figures 1 and 4. (B) Kymograph shows the relative sliding and stalling in a pair of antiparallel microtubules (red) and associated Kif4A-GFP (green). Assay condition: 0.2 nM PRC1 and 6 nM Kif4A-GFP. Scale bar: 2 µm. The schematic illustrates the position and relative orientation of both the immobilized (pink) and moving (red) microtubules and the end-tags (green) at the beginning and end of the time sequence. (C) Time record of the instantaneous sliding velocity of the moving microtubule derived from the kymograph in (B). The dashed lines demarcate the three phases observed in the sliding velocity profile: (1) constant phase, (2) slow down and (3) stalling. (D) Bar graph of the average sliding velocity calculated from the constant velocity movement in phase-1. Assay conditions: (i) 0.2 nM and 6 nM Kif4A-GFP (mean: 46 ± 17; N = 98) (ii) 1 nM PRC1 and 6 nM Kif4A-GFP (mean: 11 ± 8; N = 45). Error bars represent the standard deviation of the data. (E) Histograms of the initial GFP-fluorescence density in the untagged region of the overlap, $ρ_{u n t a g g e d}$ . Assay conditions: (i) 0.2 nM PRC1 and 6 nM Kif4A-GFP (black; mean: 3.5 ± 1.7 A.U./nm; N = 64) and (ii) 1 nM PRC1 and 6 nM Kif4A-GFP (red; mean: 6.5 ± 1.9 A.U./nm; N = 33). The mean and error values were obtained by fitting the histograms to a Gaussian distribution.

https://doi.org/10.7554/eLife.32595.005

Figure 3—source data 1 This spreadsheet contains the average sliding velocity used to generate the bar graph shown in Figure 3D and the initial GFP-fluorescence density, $ρ_{u n t a g g e d}$ , used to generate Figure 3E.: https://doi.org/10.7554/eLife.32595.016
Download elife-32595-fig3-data1-v1.xlsx

Figure 4 with 4 supplements see all

Download asset Open asset

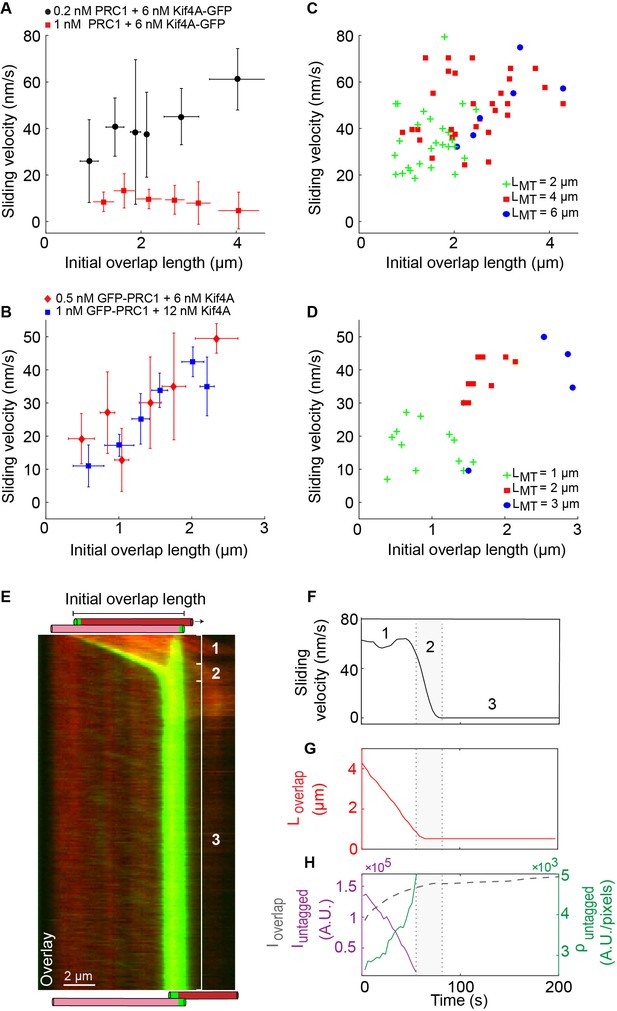
Microtubule sliding velocity in the PRC1-Kif4A system scales with initial overlap width.

(**A–B**) Binned plots of initial sliding velocity versus the initial overlap length. The initial overlap length between the moving MT and immobilized MT is calculated from the rhodamine MT channel. Sliding velocity is calculated from the constant velocity movement in phase-1. (A) Assay conditions: (i) 0.2 nM PRC1 and 6 nM Kif4A-GFP (black; N = 60; Pearson’s correlation coefficient = 0.54) and (i) 1 nM PRC1 and 6 nM Kif4A-GFP (red; N = 42; Pearson’s correlation coefficient = 0.03). (B) Assay conditions: (i) 0.5 nM GFP-PRC1 and 6 nM Kif4A (red; N = 25; Pearson’s correlation coefficient = 0.69) and (ii) 1 nM GFP-PRC1 and 12 nM Kif4A (blue; N = 20; Pearson’s correlation coefficient = 0.74). (**C–D**) Scatter plot of the average sliding velocity versus the initial overlap length color-coded by moving microtubule length, $L_{M T}$ . (C) Assay condition: 0.2 nM PRC1 and 6 nM Kif4A-GFP (green: $L_{M T}$ = 2 ± 0.5 µM, red: $L_{M T}$ = 4 ± 0.5 µM, blue: $L_{M T}$ = 6 ± 0.5 µM; N = 60). (D) Assay condition: 0.5 nM GFP-PRC1 and 6 nM Kif4A (green: $L_{M T}$ = 1 ± 0.5 µM, red: $L_{M T}$ = 2 ± 0.5 µM, blue: $L_{M T}$ = 3 ± 0.5 µM; N = 25). (E) Kymograph shows the relative sliding and stalling in a pair of antiparallel microtubules (red) and associated Kif4A-GFP (green). Assay condition: 0.2 nM PRC1 and 6 nM Kif4A-GFP. Scale bar: 2 µm. The schematic illustrates the position and relative orientation of both the immobilized (pink) and moving (red) microtubules and the end-tags (green) at the beginning and end of the time sequence. (F) Time record of the instantaneous sliding velocity of the moving microtubule derived from the kymograph in (E). The dashed lines demarcate the three phases observed in the sliding velocity profile: (1) constant phase, (2) slow down and (3) stalling. (G) Time record of the overlap length (red; $L_{o v e r l a p}$ ) derived from the kymograph in (E). (H) Time record of the total fluorescence intensity in the antiparallel overlap (dashed gray; $I_{o v e r l a p}$ ), fluorescence intensity in the untagged region of the overlap (solid purple; $I_{u n t a g g e d}$ ), and fluorescence density (intensity per unit overlap length) in the untagged region of the overlap (solid green; $ρ_{u n t a g g e d}$ ) derived from the kymograph in (E).

https://doi.org/10.7554/eLife.32595.006

Figure 4—source data 1 This spreadsheet contains the sliding velocity versus the initial overlap length used to generate the binned plots shown in Figure 4A–B and the scatter plots shown in Figure 4C–D.: https://doi.org/10.7554/eLife.32595.011
Download elife-32595-fig4-data1-v1.xlsx

We first focused on microtubule movement in phase-1 and investigated how the relative solution concentrations of the motor and the non-motor protein impact the initial sliding velocity. This is particularly interesting in the case of PRC1-Kif4A system as the recruitment of Kif4A to microtubules is dependent on PRC1 (Bieling et al., 2010; Subramanian et al., 2013). Therefore, one possible outcome is that motor-protein movement is sterically hindered at higher PRC1 concentrations resulting in lower sliding velocities. Alternatively, it is possible that more Kif4A is recruited to microtubule overlaps at higher PRC1 concentrations and this could counter the potentially inhibitory effects of PRC1. To distinguish between these mechanisms, we compared the maximum microtubule sliding velocity (computed as the average velocity from phase-1) at two different PRC1:Kif4A concentration ratios (Figure 3D). We found that increasing the PRC1 solution concentration 5-fold (0.2 and 1 nM) at constant Kif4A-GFP concentration (6 nM) resulted in a 4-fold reduction in the microtubule sliding velocity (velocity = 46 ± 17 nm/s at 0.2 nM and velocity = 11 ± 8 nm/s at 1 nM). Similarly, in assays with GFP-PRC1 and unlabeled Kif4A, we found that increasing PRC1 concentration 2-fold (0.5 and 1 nM) at constant Kif4A levels (6 nM) resulted in a ~2 fold reduction in the microtubule sliding velocity (Figure 3—figure supplement 1; velocity = 30 ± 13 nm/s at 0.5 nM and velocity = 19 ± 8 nm/s at 1 nM PRC1). Interestingly, in these experiments, we could restore the sliding velocity by compensating the 2-fold increase in the PRC1 concentration with a 2-fold increase in the Kif4A concentration (Figure 3—figure supplement 1).

A possible explanation for the reduced velocity at the higher PRC1:Kif4A concentration is that there are fewer Kif4A molecules in the overlap due to competition from PRC1 for binding sites on the microtubule surface. Therefore, we compared the Kif4A-GFP density in the untagged overlap at two different solution PRC1 concentrations (Figure 3E). The data show that a 5-fold increase in the PRC1 concentrations results in a 2-fold increase in the average Kif4A density in the untagged overlap region, indicating that Kif4A is effectively recruited to antiparallel overlaps at the highest PRC1 concentrations in our assays (Figure 3E). Together, these results are consistent with a mechanism in which the solution concentration ratios of PRC1:Kif4A sets the sliding velocity by determining the relative ratio of sliding-competent PRC1-Kif4A complexes to sliding-inhibiting PRC1 molecules in the antiparallel overlap. The inhibition can arise either due to increased frictional forces or steric inhibition to stepping in crowded overlaps at higher PRC1 concentrations. We elaborate on these possibilities in the discussion section.

Microtubule sliding velocity in the PRC1-Kif4A system scales with initial overlap length

We next examined if the initial width of the PRC1-crosslinked anti-parallel overlap impacts the sliding velocity in phase-1. The initial width is defined as the overlap length at the first time point imaged after flowing in the final assay buffer in our experiment ( $t$ = 0; example: first panel in Figure 1B). Remarkably, analysis of three different datasets suggests that antiparallel microtubules with longer initial overlaps slide at a higher velocity than microtubules with shorter initial overlaps under the same experimental condition (Figure 4A–B). Note: no obvious trend was observed at the higher PRC1 concentration, possibly due to the scatter in the data relative to the low magnitude of sliding velocities (Figure 4A; red squares).

Are molecules in the untagged or end-tagged region responsible for the observed overlap length-dependent sliding? To answer this question, we first analyzed the data from the PRC1-Kif4A experiments to determine if the phase-1 microtubule sliding velocity depended on the amount of protein at the end-tags. However, no significant correlation was observed between the sum of end-tag lengths or sum of end-tag intensities and sliding velocity (Figure 4—figure supplement 1A–B). Consistent with this, the average sliding velocity (75 ± 25 nm/s; N = 25) is independent of end-tag intensity in experiments with Kif4A alone (Figure 2C–D) (Figure 4—figure supplement 1Q). Instead, we find that in experiments with PRC1 and Kif4A, the sliding velocity increases with the initial untagged overlap length under all the conditions where length-dependent sliding is observed (Figure 4—figure supplement 1D–E). Under these conditions, Kif4A-GFP intensity is proportional to both the total and untagged overlap lengths, suggesting that sliding velocity scales with the number of molecules in the overlap (Figure 4—figure supplement 1C–D inset; Note: intensity is a measure of the total number of molecules in the overlap, it is not a direct measure of the number of Kif4A motors involved in binding PRC1 and sliding. We assume that the number of sliding-competent motors is proportional to total intensity). In addition, no correlation is found between sliding velocity and the average motor density in the untagged overlap during phase-1 movement (0.2 nM PRC1 and 6 nM Kif4A-GFP; Pearson’s coefficient: −0.15; N = 20) (Figure 4—figure supplement 1F). These data are consistent with a mechanism in which sliding velocity is set by the total number of sliding-competent PRC1-Kif4A molecules in the untagged region of the antiparallel microtubule overlap.

In order to separate the effect of microtubule length versus antiparallel overlap length on the sliding velocity, we re-plotted the data in Figure 4A–B based on the length of the moving microtubule. A scatter plot of the sliding velocity as a function of initial overlap length color-coded by the moving-microtubule length shows that longer microtubules typically form longer initial overlaps that exhibit faster sliding (Figure 4C–D). However, the observation that long microtubules that form short overlaps exhibit slower sliding than long microtubules that form long overlaps (for example: 6 μm microtubules with ~3 μm overlap in Figure 4C, blue dots), suggests the dominant contribution to the sliding velocity is from the initial overlap length (Figure 4C–D). Our findings indicate that the initial length of the antiparallel overlap can tune the microtubule sliding velocity, such that longer overlaps, which have a greater number of PRC1-Kif4A molecules, slide at a faster rate than shorter microtubule overlaps.

Examining the time-dependent changes during microtubule sliding in the PRC1-Kif4A system

How does the initial antiparallel overlap set the phase-1 sliding velocity? To gain insights into this question, we examined the time-dependent changes in the sliding velocity as a function of overlap length (0.2 nM PRC1 + 6 nM Kif4A-GFP). We focused on a subset of events where the reduction in overlap length ( $L_{o v e r l a p}$ ) begins from the initial time point of recording (34/62 events). We find that in all of these events, movement velocity is constant during phase-1 as the overlap length continually shrinks during sliding (Figure 4E–H and Figure 4—figure supplement 1G–P, 2F-H and N-P). For example, in the kymograph shown in Figure 4E, the reduction in microtubule overlap length begins at 0 s (Figure 4G, solid red line) but a significant reduction in the velocity is not seen until 60 s (Figure 4F, solid black line; see also Figure 4—figure supplement 1N–P, 2F-H and N-P).

The observation that microtubule sliding occurs at a constant velocity even as the overlap shrinks, raises the following question: do the number of Kif4A molecules in the overlap change during relative sliding? Analyses of GFP intensity versus time showed that in phase-1, the total amount of Kif4A-GFP in the microtubule overlap ( $I_{o v e r l a p} = I_{e n d - t a g g e d} + I_{u n t a g g e d}$ ) initially increases and then reaches a constant level that is maintained during all three phases (dashed gray line) (Figure 4H andFigure 4—figure supplement 1N-P and 2). We examined events in which phase-1 sliding continued after the establishment of constant motor number and find that sliding velocity scales with initial overlap length under equilibrium conditions (Figure 4—figure supplement 3). The observation that $I_{o v e r l a p}$ remains constant even as the overlap length reduces suggests that the number of Kif4A molecules per unit length (density) increases in the shrinking overlap during sliding. Is this increase in density in the overlap region entirely due to end-tag formation or is there an increase in the number of Kif4A molecules per unit length of the untagged overlap during microtubule sliding? To answer this question, we quantitatively analyzed the Kif4A-GFP intensity in the untagged region of the overlap during sliding. We find that while the total number of Kif4A-GFP molecules in the untagged overlap region ( $I_{u n t a g g e d}$ ) (Figure 4H; solid purple curve) decreases with shrinking overlap, the Kif4A-GFP density $(ρ_{u n t a g g e d})$ (Figure 4H; solid green curve; fluorescence intensity/pixel) increases.

These data, together with the observation that the number of molecules in the end-tag does not contribute significantly to sliding velocity (Figure 4—figure supplement 1Q and Figure 4—figure supplement 1A–B), indicate that the velocity of microtubule sliding in the PRC1-Kif4A system is determined by the initial width of the PRC1-crosslinked antiparallel overlap, which sets the total number of sliding competent molecules in the untagged overlap. During microtubule sliding at phase-1, the increase in the density of motor molecules could compensate for the reduction in overlap length and the number of sliding-competent motors, ensuring that microtubule-movement proceeds at a constant velocity.

Mechanism for transition from constant velocity sliding to slow-down and stalling in the PRC1-Kif4A system

What is the mechanism underlying the shift from constant to decreasing sliding velocity (phase-1 to phase-2) observed in these experiments? First, we considered the possibility that sliding slows down due to the transition from constant to decreasing overlap length and a concomitant increase in protein density as the moving microtubule slides past the immobilized microtubule. Such a mechanism has been described previously for the slowdown of microtubule sliding in the Ase1-Ncd system (Schizosaccharomyces pombe Ase1 and Drosophila Kinesin-14, Ncd), and by the human kinesin-14 HSET (Braun et al., 2017; Braun et al., 2011). As discussed in the previous section, our results show that the transition from phase-1 to phase-2 does not coincide with a shift from constant to decreasing overlap length during sliding, and there is no inverse correlation between Kif4A-GFP density and the sliding velocity during phase-1 movement under the same experimental condition (See Figure 4E–H, Figure 4—figure supplements 1G–P and and 2). Next, we considered the possibility that the transition from sliding to slowdown coincides with the end-tags on the moving and immobilized microtubules arriving at close proximity. We hypothesized that at the high-density region proximal to the end-tag, sliding first slows down before the microtubule movement is completely halted. We noticed that in 50% of the events (47/98; 0.2 nM PRC1 + 6 nM Kif4A-GFP), the transition from phase 1 to 2 occurs when the end-tags have nearly merged and our image analysis algorithm does not resolve the two end-tags (examples in Figure 4E–H and Figure 4—figure supplement 1G–P). We reasoned that if high protein concentration proximal to end-tags is the reason for slow-down, the protein density at the phase-1 to phase-2 transition should be similar under different experimental conditions. Kif4A-GFP density measurement and fluorescence line-scan analysis at the phase-1 to phase-2 transition time-points in two experimental conditions show that this is indeed the case (Figure 4—figure supplement 4A–B). Furthermore, comparison of the phase-1 to phase-2 transition-point intensity with the average end-tag intensity suggests that on average slowdown occurs when the intensity is >70% of the average end-tag intensity (Figure 4—figure supplement 4B–C). These observations suggest that sliding slows down proximal to end-tags, when the untagged overlap is short and the motors encounter a high-density region, where stepping is inhibited.

The size of stable antiparallel overlaps established by PRC1 and Kif4A are determined by microtubule length and protein concentration

Our findings suggest that in the PRC1-Kif4A system, a stable antiparallel overlap is formed when the end-tags on both microtubules merge during relative sliding. We hypothesized that if stable overlaps form upon the collision of end-tags on the moving and immobilized microtubules, then the final overlap length ( $L_{F O}$ ) should be determined by the sum of the two end-tag lengths ( $L_{E T 1} + L_{E T 2}$ ) (Figure 5A). Consistent with this, the average ratio of the $\frac{L_{F O}}{L_{E T 1 +} L_{E T 2}}$ at 1 nM PRC1 + 6 nM Kif4A-GFP is ~1 (Figure 5B, red). Similar results were observed when the experiments were performed under three different conditions with GFP-PRC1 and untagged Kif4A (Figure 5—figure supplement 1). These findings indicate that the width of the stable microtubule overlap established by PRC1 and Kif4A is approximately equal to the sum of the end-tag lengths on both microtubules. At the lowest concentration of PRC1 tested (0.2 nM PRC1 + 6 nM Kif4A-GFP), the final overlap length was shorter than the $L_{E T 1} + L_{E T 2}$ , as indicated by a ratio of < 1 (Figure 5B, black). A possible reason is that under these conditions, the end-tagged regions of the microtubules have a greater fraction of unoccupied sites that allows for further sliding and reduction in the overlap length after the collision of end-tags.

Figure 5 with 1 supplement see all

Download asset Open asset

The width of the final antiparallel overlap established by PRC1 and Kif4A is determined by end-tag and microtubule lengths.

(A) Schematic shows the formation of a stable antiparallel overlap upon collision of the two end-tags and the stalling of relative microtubule sliding. The initial overlap length is the overlap length of the moving MT on the immobilized MT at $t$ = 0. $L_{E T 1}$ and $L_{E T 2}$ are the lengths of the end-tags consisting Kif4A and PRC1 on the plus-end of each MT. The moving MT with length $M_{L 2}$ moves relative to the immobilized MT with length $M_{L 1}$ , at velocity = $v$ . The collision and the stalling of the end-tags form a stable overlap, which is the final overlap length $L_{F O}$ at $v$ = 0. (B) Histograms of the ratio of sum of the end-tag lengths ( $L_{E T 1} + L_{E T 2}$ ) and final overlap length $L_{F O}$ . Assay conditions: (i) 0.2 nM PRC1 and 6 nM Kif4A-GFP (black; N = 39) and (ii) 1 nM PRC1 and 6 nM Kif4A-GFP (red; N = 33). (**C–E**) Plots of the final overlap length ( $L_{F O}$ ) versus (C) the immobilized microtubule length ( $M_{L 1}$ ), (D) moving microtubule length ( $M_{L 2}$ ), and (E) and the sum of microtubule lengths ( $M_{L 1} + M_{L 2}$ ). Assay conditions: (i) 0.2 nM PRC1 and 6 nM Kif4A-GFP (black; N = 68) and (ii) 1 nM PRC1 and 6 nM Kif4A-GFP (red; N = 30). The Pearson’s correlation coefficient for (E) is (i) 0.65 and (ii) 0.62.

https://doi.org/10.7554/eLife.32595.018

Figure 5—source data 1 This spreadsheet contains the ratio of the sum of the end-tag lengths ( $L_{E T 1} + L_{E T 2}$ ) and final overlap length ( $L_{F O})$ used to generate the histogram in Figure 5B and the final overlap length ( $L_{F O}$ ) versus the immobilized microtubule length ( $M_{L 1}$ ), moving microtubule length ( $M_{L 2}$ ), and the sum of microtubule lengths ( $M_{L 1} + M_{L 2}$ ) used to generate the plots in Figure 5C-E.: https://doi.org/10.7554/eLife.32595.020
Download elife-32595-fig5-data1-v1.xlsx

Prior work shows that the collective activities of PRC1 and Kif4A on single microtubules result in the formation of end-tags whose size scales with microtubule length (Subramanian et al., 2013). This raises the question of whether the width of stable antiparallel overlap established by these proteins depends on the lengths of the two crosslinked microtubules. To examine this, we plotted the final overlap length ( $L_{F O}$ ) as a function of the immobilized microtubule length ( $M_{L 1}$ ), moving microtubule length ( $M_{L 2}$ ) and sum of both microtubule lengths ( $M_{L 1} + M_{L 2}$ ). In all three cases, we find that the final overlap length increases linearly with microtubule length (Figure 5C–E). The slope of the line is higher at greater PRC1 concentration due to longer end-tags formed under these conditions (Figure 5E; 0.2 nM PRC1 + 6 nM Kif4A-GFP, slope = 0.3; 1 nM PRC1 + 6 nM Kif4A-GFP, slope = 0.8). These data suggest that PRC1-Kif4A end-tags act as a barrier to microtubule sliding and establish a stable antiparallel overlap whose size is determined by the microtubule lengths.

Examination of the mechanisms that ensure stability of the overlaps established by PRC1 and Kif4A

Why does the merging of PRC1-Kif4A end-tags during microtubule sliding result in the formation of a stable antiparallel overlap? It has been shown that the entropic forces induced by Ase1p molecules (Schizosaccharomyces pombe PRC1 homolog) can counter the microtubule sliding-associated forces generated by Ncd (Drosophila kinesin-14) molecules to establish a stable antiparallel overlap (Lansky et al., 2015). Similar observations have been reported with the human kinesin-14 HSET (Braun et al., 2017). We therefore examined if entropic forces are generated in the stalled microtubule overlaps established by PRC1 and Kif4A in our experiments. First, we induced the formation of stable overlaps through microtubule sliding and stalling in the presence of GFP-PRC1, Kif4A and ATP. Next, we washed the assay chamber twice with buffer containing no ATP to remove any unbound protein and nucleotide. Under this ‘no-nucleotide’ condition, we expect that the PRC1-Kif4A complexes in the microtubule overlap would essentially function as passive crosslinkers. Dual-wavelength time-lapse images were acquired for 10 min immediately following buffer exchange. Image analysis revealed that while PRC1 was retained in the region of the microtubule overlap under these conditions, the width of the antiparallel overlap did not change during the course of the experiment (Figure 6—figure supplement 1A–B). The lack of overlap expansion in the PRC1-Kif4A system may be due to the tight binding of the kinesin motor domain to microtubules in the absence of a nucleotide. To address this, we performed the experiment as discussed above, except the final buffer was supplemented with 2 mM ADP, a nucleotide that lowers the kinesin-microtubule affinity. As shown in Figure 6—figure supplement 1C–F, no overlap expansion was observed under these conditions. The inclusion of 1 nM PRC1 in addition to 2 mM ADP in the final buffer also did not promote overlap expansion (Figure 6—figure supplement 1G–H). Therefore, neither motor deactivation with ADP nor increasing the number of PRC1 molecules is sufficient to induce entropic expansions of measurable magnitude in this system, suggesting that an alternative mechanism is likely responsible for countering the Kif4A-mediated sliding forces in the antiparallel overlap.

We have previously shown that PRC1-Kif4A end-tags on single microtubules hinder motor-protein stepping (Subramanian et al., 2013). Therefore, we considered if the collision of end-tags on sliding microtubules generated a stable antiparallel overlap simply by providing a steric block to sliding. To test this hypothesis, we generated stable antiparallel overlaps with PRC1, Kif4A-GFP and ATP, and subsequently exchanged the nucleotide to ADP by buffer exchange (Figure 6A–C). As expected, no change in the overlap length was observed upon nucleotide exchange from ATP to ADP. We reasoned that under these experimental conditions, the gradual dissociation of proteins at a slow rate from the overlap should liberate a small fraction of kinesin and PRC1 binding sites on the microtubule (note: intensity analysis suggests a maximum 10% reduction of Kif4A-GFP in 2 min). Therefore, if the moving microtubule had initially stalled due to protofilament crowding, then re-introducing ATP should allow motor-protein stepping and reinitiate microtubule sliding. To test this experimentally, we introduced buffer containing 1 mM ATP (no additional protein) into the chamber 15 min after the ADP exchange step (Figure 6D). We find that relative microtubule sliding is reinitiated under these conditions. Analysis of the GFP fluorescence-intensity profile at different time-points post buffer exchange revealed that new end-tags are established during microtubule sliding, which subsequently collide to establish a new stable antiparallel overlap of shorter width (Figure 6E).

Figure 6 with 1 supplement see all

Download asset Open asset

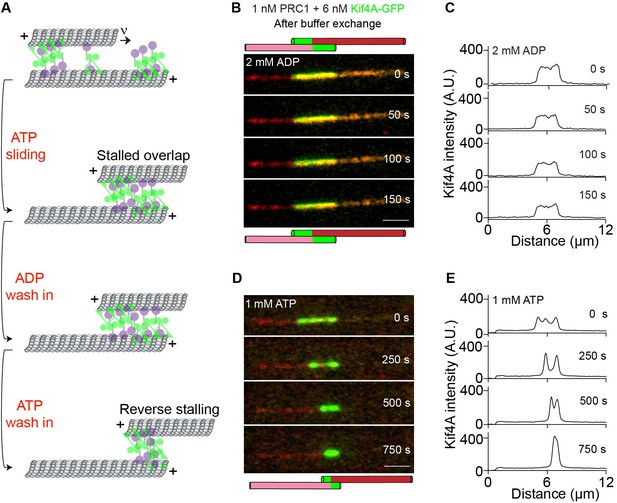
Examination of the mechanisms that ensure stability of the overlaps established by PRC1 and Kif4A.

(A) Schematic of the ADP and ATP wash-in experiments performed with stalled microtubule overlaps Figure 6B-E. (**B–E**) The following figures are representative dual-channel fluorescence micrographs showing microtubules (red) and associated Kif4A-GFP (green) under different experimental conditions. (**B–C**) Time-lapse images (B) and corresponding line-scan profiles (C) of Kif4A-GFP fluorescence of a microtubule pair established as in (Figure 1A ) and subsequent exchange into a buffer containing 2 mM ADP. (**D–E**) Time-lapse images (D) and corresponding line-scan profiles (E) of Kif4A-GFP fluorescence of the microtubule pair in (D) after flowing in 1 mM ATP into the chamber. Scale bar: 2 µm.

https://doi.org/10.7554/eLife.32595.022

Together, these findings are consistent with a mechanism in which PRC1-Kif4A end-tags establish stable overlaps by sterically hindering the relative sliding of antiparallel microtubules. Such a ‘molecular road-block’ based mechanism also provides a simple explanation for the observed correlation between the sum of end-tag lengths and the final overlap length in this system.

PRC1 and Kif4A align the overlap region between multiple antiparallel microtubules

How do microtubule sliding and stalling by PRC1 and Kif4A shape larger microtubule arrays? To gain insights into this question, we carefully examined the few events (N < 10) where we could clearly observe two microtubules slide relative to a single immobilized microtubule. In these events (Figure 7A–C; 0.2 nM PRC1 + 6 nM Kif4A-GFP), we observed that both the sliding microtubules stall proximal to the plus end-tag on the immobilized microtubule. Another example of such an event in experiments with GFP-labeled PRC1 and unlabeled Kif4A is shown in Figure 7D–F (1 nM GFP-PRC1 + 6 nM Kif4A). The data suggest that the formation of end-tags on single microtubules can establish an antiparallel array composed of multiple microtubules with closely aligned plus-ends.

Figure 7 with 1 supplement see all

Download asset Open asset

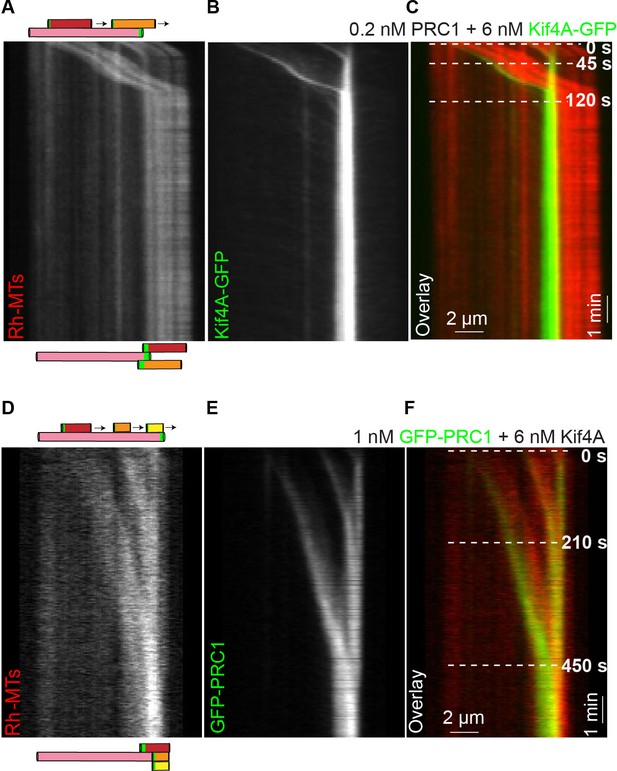
Antiparallel array composed of multiple microtubules are aligned at microtubule plus-ends formed by PRC1 and Kif4A.

(**A–C**) Kymographs show the relative sliding of two microtubules relative to an immobilized microtubule (A), associated Kif4A-GFP (B) and the overlay image (red, microtubules; green, Kif4A-GFP) (C). Both moving microtubules stall at the plus-end of the immobilized microtubule. Assay condition: 0.2 nM PRC1 and 6 nM Kif4A-GFP. Scale bar: x: 2 µm and y: 1 min. (**D–F**) Kymographs show the relative sliding of three microtubules relative to an immobilized microtubule (D), associated GFP-PRC1 (E) and the overlay image (red, microtubules; green, GFP-PRC1) (F). All three moving microtubules stall at the plus-end of the immobilized microtubule. Assay condition: 1 nM GFP-PRC1 and 6 nM Kif4A. Scale bar: x: 2 µm and y: 1 min.

https://doi.org/10.7554/eLife.32595.024

We analyzed five reorganization events where we could reliably measure microtubule and overlap lengths to determine if longer microtubules result in larger final overlaps in these more complex bundles. While we cannot assess the three-dimensional arrangement of the microtubules in the bundles, a simple analysis of microtubule and overlap lengths suggests that in general bundles with longer microtubules are likely to yield longer final overlaps (Figure 7—figure supplement 1).

Together, these observations suggest that microtubule sliding and stalling by PRC1 and Kif4A can align multiple antiparallel filaments such that the region of overlap is restricted to the plus-ends of all the microtubules.

Discussion

Pairs of crosslinked antiparallel microtubules are fundamental structural units in diverse microtubule-based architectures (Dogterom and Surrey, 2013; Subramanian and Kapoor, 2012). Our findings provide insights into how the geometrical features of antiparallel microtubule arrays can be ‘decoded’ by PRC1-Kif4A complexes to govern the dynamics, stability and architecture of microtubule networks.

On the basis of our observations, we propose a mechanism for the organization of stable microtubule length-dependent antiparallel overlaps by the collective activities of PRC1 and Kif4A. PRC1 specifically crosslinks and preferentially localizes to the region of overlap between two antiparallel microtubules (Figure 8A) (Bieling et al., 2010; Subramanian et al., 2010). Kif4A is recruited to the antiparallel overlap through direct interaction with PRC1 (Bieling et al., 2010; Subramanian et al., 2013). The highly processive movement of PRC1-Kif4A complexes on microtubules and the slow dissociation of these proteins from microtubule plus-ends result in the formation of ‘end-tags’, which are highly crowded regions in which motor stepping is inhibited (Figure 8A) (Subramanian et al., 2013; Leduc et al., 2012). In addition, the activity of PRC1-Kif4A complexes within antiparallel overlaps results in robust relative microtubule sliding (Figure 8A). During sliding, as the moving microtubule moves past the length of the immobilized microtubule, the distance between the end-tags at the plus-ends of both microtubules begins to shrink (Figure 8A). Microtubule movement first slows down and then stalls when the two end-tags arrive at close proximity during relative sliding, resulting in the formation of a stable antiparallel overlap (Figure 8A).

Figure 8 with 2 supplements see all

Download asset Open asset

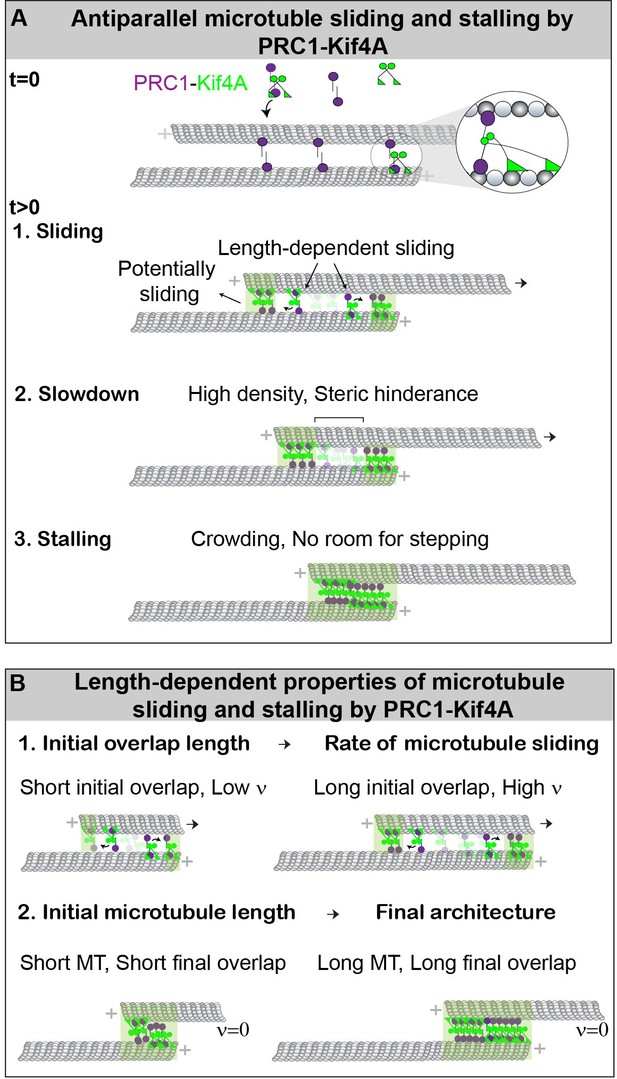
Model for the length-dependent sliding by the collective activity of PRC1 and Kif4A.

(A) Mechanism of microtubule sliding and stalling by PRC1 and Kif4A. At the initial state, $t$ = 0, the ‘immobilized’ and ‘moving’ microtubules are crosslinked by PRC1 to form an antiparallel overlap. The zoomed-in view shows the proposed molecular configuration of the cross-bridging PRC1-Kif4A complex in a microtubule overlap. At $t$ > 0, Kif4A molecules are introduced into the solution, which form a complex with PRC1. This initiates the formation of PRC1-Kif4A end-tags at the plus-ends of both microtubules as well as relative sliding of the moving microtubule. The sliding of microtubules is most likely due to the cross-bridging molecules in the untagged overlap. The slowdown is likely due to the high density of molecules and steric hindrance to motor stepping when the end-tags arrive at close proximity. This eventually halts movement when the end-tags merge, and a stable overlap is established. (B) The schematic shows the length-dependent properties of initial microtubule sliding and subsequent stalling of overlapping antiparallel microtubules established by PRC1 and Kif4A. Our experiments show that: (1) Microtubules that form shorter initial overlaps slide with lower velocity than microtubule pairs that form longer initial overlaps. (2) Since the size of PRC-Kif4A end-tags scale with microtubule length, shorter microtubules form a short overlap and the longer microtubules form a long overlap.

https://doi.org/10.7554/eLife.32595.027

Figure 8—source data 1 This table contains the sliding efficiencies calculated using Equation 3 for $a$ = 1-10%.: https://doi.org/10.7554/eLife.32595.030
Download elife-32595-fig8-data1-v1.docx

Organization of stable antiparallel overlaps by PRC1 and Kif4A

Non-motor crosslinking proteins are primarily thought to contribute to the size and stability of microtubule arrays by opposing the active forces generated by motor proteins (Peterman and Scholey, 2009). Such a mechanism has been proposed for the formation of stable overlaps by the collective activity of the Drosophila Kinesin-14, Ncd and the Schizosaccharomyces pombe Ase1 (Braun et al., 2011). Similarly, the human kinesin-14 HSET, can both generate active and counter-acting entropic forces to generate stable antiparallel overlaps (Braun et al., 2017). In contrast, we propose that the predominant mechanism that leads to the formation of a stable overlap in the PRC1-Kif4A system is steric hindrance to motor stepping at regions of high protein-density for the following reasons. First, sliding microtubules come to a stall when the PRC1-Kif4A end-tags arrive at close proximity. Steric hindrance at an end-tag is expected to be high because the PRC1 and Kif4A binding sites at this region of the microtubule are likely to be nearly saturated (Subramanian et al., 2013; Leduc et al., 2012). Further hindrance to stepping at the crowded end-tags can arise due to the partial overlap of the tubulin-binding interfaces of PRC1 and kinesin (Kellogg et al., 2016). Second, the accumulation of Kif4A alone at microtubule ends can stop sliding, and full-length Kif4A does not have a C-terminus non-motor domain that binds tightly to microtubules and is therefore unlikely to generate significant frictional forces (Figure 2C–D). Third, we do not observe entropic force driven expansion of stable overlaps formed by PRC1 and Kif4A when the motor is deactivated (Figure 6). Fourth, we do not observe an inverse correlation between sliding velocity and changes in protein density during phase-1 sliding as is predicted in models where the buildup of opposing forces in shrinking overlaps stall microtubule sliding (Figure 4—figure supplement 1F). Finally, previous studies have shown that the frictional forces generated by PRC1 are low, and the speed of Kif4A movement on single microtubules is not affected by PRC1 (Duellberg et al., 2013; Forth et al., 2014). Combined with the observation that the number of PRC1 molecules is less than Kif4A motors at the microtubule overlap in our experiments (Figure 8—figure supplement 1), it is unlikely that stable overlaps can be formed solely through the opposition of Kif4A-generated forces by PRC1 at end-tags. For similar reasons as stated above, steric hindrance is likely to play an important role in switching from sliding at constant velocity to slowdown at the phase-1 to phase-2 transition (Figures 3C and 4F), and the reduction in average sliding velocity at high PRC1 concentrations (Figure 3D and Figure 3—figure supplement 1). In the future, it will be interesting to determine the contribution of frictional forces in the slowdown of sliding in the PRC1-Kif4A system. Overall, in contrast to mechanisms where stable microtubule arrays are organized through opposing forces generated by a pair of motor and non-motor protein, the PRC1-Kif4A system reveals an alternative mechanism in which a motor and a non-motor protein act synergistically on antiparallel microtubules to first promote relative sliding and then stall microtubule movement by forming a molecular roadblock.

Some of the distinct features of the roadblock mechanism are as follows. First, in this system, stable arrays can be established under conditions where the non-motor:motor protein ratio may not be not sufficiently high to achieve force-balance. This is particularly advantageous in the case of interacting proteins, such as PRC1 and Kif4A, where increasing the concentration of PRC1 leads to a concomitant increase in both the levels of motor and non-motor proteins further shifting the force-balance point. Second, this system allows for robust relative sliding until the end-tags collide. This in turn leads to the establishment of stable antiparallel overlaps that are spatially restricted to microtubule plus-ends. Third, it provides a simple mechanism by which the formation of length-dependent PRC1-Kif4A end-tags on single microtubules can be readily translated to the organization of microtubule overlaps whose size scales with microtubule length (Figure 8B).

Mechanism of overlap-length dependent sliding by PRC1 and Kif4A

Thus far, the best-studied systems of microtubule sliding are those mediated by crosslinking tetrameric kinesins such as Eg5 or dimeric motors that have non-motor microtubule binding domains such as kinesin-14 (Fink et al., 2009; Kapitein et al., 2005; Korneev et al., 2007; Valentine et al., 2006; Braun et al., 2009). We find that (i) Kif4A alone does not promote antiparallel microtubule crosslinking and (ii) the C-terminus tail of Kif4A does not interact with microtubules with binding affinities comparable to other microtubule binding domains (Figure 2A). In addition, currently there is no evidence for significant oligomerization of full-length Kif4A in the micromolar concentration range (~10 μM). Based on these observations, we consider two alternative modes of microtubule crosslinking and sliding by Kif4A. First, we find that in experiments with Kif4A alone, end-tags on one microtubule can contact and move along another microtubule (Figure 2C and D). We speculate that since end-tags are highly crowded regions, a fraction of Kif4A molecules, especially those at the very tip of the microtubule, may adopt a one-head bound state (as is seen in EM experiments performed at high concentrations of kinesin dimers (Hoenger et al., 2000; Hirose et al., 2000), and collectively mediate microtubule sliding. This is similar to a recent proposal for dynein driven relative-microtubule sliding to form minus-end asters (Tan et al., 2018). Alternatively, it is possible that the high concentration of Kif4A at end-tags may promote intermolecular interactions between motors or binding between the Kif4A C-terminus and microtubule despite these being low-affinity interactions. However, this class of mechanisms, where Kif4A alone is responsible for crosslinking and sliding, is less likely in the untagged overlaps that have lower PRC1 and Kif4A densities. Instead, the C-terminus of Kif4A is likely to interact with the N-terminus of PRC1 (K_d = 0.3 μM) (Subramanian et al., 2013), and the PRC1-tethered Kif4A complexes within the untagged region of the antiparallel overlap drive sliding. However, PRC1 and Kif4A are unlikely to form a stable long-lived complex. Consistent with this, we have not been able to isolate stable PRC1-Kif4A complexes by gel filtration or visualize complexes by single-particle EM (unpublished). However, PRC1-Kif4A complexes have a longer microtubule lifetime than either protein alone, suggesting that PRC1 and Kif4A molecules likely undergo dynamic dissociation and re-association on microtubules (Bieling et al., 2010; Subramanian et al., 2013). As we discuss below, cross-bridging and sliding by the dynamic complex is likely to contribute to the observed length-dependent sliding in this system.

Surprisingly, we find that the sliding velocity in the PRC1-Kif4A system is proportional to the initial antiparallel microtubule overlap length (Figure 8B). While the scaling of movement velocity with motor number has been proposed for microtubule-based transport of cargoes in the cellular cytoplasm (Hill et al., 2004; Kural et al., 2005; Levi et al., 2006), it is not typically observed in microtubule sliding by an ensemble of processive kinesins in in vitro assays. One proposed reason is the low viscous drag experienced by the moving microtubule in aqueous buffers relative to the intracellular environment, and the high magnitude of forces generated by kinesin molecules (Braun et al., 2009; Gagliano et al., 2010). However, this study and in vitro reconstitution experiments with mixtures of Ncd and Ase1 or with the kinesin-14 HSET alone show that scaling of sliding velocity with microtubule overlap length can be observed in the absence of substantial external viscous drag forces (Braun et al., 2017; Braun et al., 2011). However, the mechanisms by which length-dependent sliding is achieved in these systems differ. In both the Ncd-Ase1 and HSET systems, reduction in sliding velocity within shrinking overlap occurs concurrently with an increase in protein density (Braun et al., 2017; Braun et al., 2011). In these systems, increasing Ase1 density opposes Ncd-generated forces, and increasing HSET density generates an entropic force that counteracts its movement. However, in the PRC1-Kif4A system, the initial velocity is constant and does not change with reducing overlap length or changes in motor density during sliding (examples in Figure 4E–H, Figure 4—figure supplements 1G–P and 2). In this constant velocity phase, the rate of microtubule movement is determined by the initial overlap width, which determines the number of associated motor molecules. Therefore, the mechanism of overlap length-dependent sliding by PRC1 and Kif4A is different from systems that involve an increase in forces that oppose motor movement in shrinking overlaps during microtubule sliding.

How might the microtubule sliding velocity scale with initial overlap length? Hints to a possible mechanism come from recent studies that investigate how the physical properties of cargoes impact microtubule sliding by motor proteins (Conway et al., 2012; Grover et al., 2016). For example, when kinesin motors are anchored to a diffusive lipid surface instead of a rigid glass coverslip, the gliding velocity of attached microtubules is dependent on the number of motor molecules (Grover et al., 2016). We consider the nature of the ‘cargo’ borne by the Kif4A molecule. In the untagged overlap of the PRC1-Kif4A system, the cargo is a microtubule polymer that is connected to the Kif4A motor via a PRC1-mediated linkage. The measured dissociation constant between the C-terminus of Kif4A and the N-terminus of PRC1 is 0.3 μM, suggesting that these proteins do not form a stable long-lived complex. Therefore the ‘moving’ microtubule is likely to be loosely coupled to the kinesin walking on an immobilized microtubule, and each 8 nm step of the kinesin does not translate into an 8 nm displacement of the moving microtubule. Other factors, such as force-dependent dissociation of PRC1-microtubule interaction during kinesin stepping, will further reduce the coupling between the two microtubules, and result in the reduction in the ‘sliding efficiency’, and consequently, the sliding velocity in the PRC1-Kif4A system.

We can define the sliding efficiency ( $S$ ), as the fraction of time spent by a PRC1-Kif4A complex bound to both microtubules. In this sliding-competent conformation, PRC1 is bound to Kif4A and the moving microtubule, and Kif4A is bound to the immobilized microtubule. This formulation is analogous to the ‘duty ratio’ of a motor, $f$ , which is the fraction of the catalytic cycle that a motor head spends attached to a microtubule and undergoes a working stroke (Hancock and Howard, 1998; Howard, 1997). However, in the PRC1-Kif4A system, reduction in sliding efficiency due to the uncoupling of motor stepping from microtubule sliding can occur either: (i) during the kinesin ATPase cycle or (ii) between two catalytic cycles. In order to estimate the sliding efficiency for microtubule sliding by PRC1-Kif4A, we followed the method in Ref. (Hamasaki et al., 1995), and first fitted the microtubule sliding velocity as a function of initial microtubule overlap length (0.2 nM PRC1 + 6 nM Kif4A-GFP) to the following equation,

v / v_{0} = L / (L + K_{L})

where $v$ is the microtubule sliding velocity, $v_{o}$ is the maximal velocity, $L$ is the microtubule overlap length and $K_{L}$ is the microtubule overlap length when $v = {0.5 v}_{0}$ . Here, $v$ and $L$ were obtained from experimental data and $v_{o}$ and $K_{L}$ were obtained from the fit (Figure 8—figure supplement 2A).

Next, using $v_{o}$ and $K_{L}$ from above, the sliding efficiency for PRC1-Kif4A, ( $S$ ) was estimated in a manner similar to calculation of motor duty ratios (Uyeda et al., 1990). $S$ represents the probability that a PRC1-Kif4A complex is in a crosslinking conformation compatible with sliding. For simplicity, here we assume that the formation of this crosslinked conformation is sufficient for sliding and do not consider other features of the system such as steric hindrance to motor stepping. Consequently, the probability that the filament is propelled by at least one PRC1-Kif4A complex is ${1 - {(1 - S)}^{N}}$ , where $N$ is the number of available sliding competent complexes (Uyeda et al., 1990). Therefore:

v = v_{0} (1 - {(1 - S)}^{N})

Since $K_{L}$ is defined as the microtubule overlap length where $v = {0.5 v}_{0}$ , Equation 2 leads to

0.5 = {(1 - (1 - S)}^{N (K_{L})})

$N$ can be estimated as

N (K_{L}) = \frac{a K_{L}}{δ}

where $a$ is the experimentally estimated fractional occupancy of sliding-competent motors (molecules per unit length) and $δ =$ 8 nm is the length of a single binding site on microtubules. Based on the experimental fluorescence intensity measurements (see Materials and methods and Figure 8—figure supplement 2B), the occupancy of sliding competent PRC1-Kif4A molecules (a) is estimated to be 1% if PRC1 molecules can crosslink to all 13 microtubule protofilaments of the moving microtubule and 10% assuming that effective crosslinks are only formed with one protofilament. Considering the molecular structure of PRC1, the values are likely to be in the 1-10% range. From the values of $N$ obtained for $a$ = 1-10%, sliding efficiencies, $S$ , calculated using Equation 3 were between 0.3-0.03 (See Figure 8—source data 1). These calculations provide an approximate estimation of the sliding efficiency because (i) we do not reach saturation sliding velocity in our experiments and (ii) the number of sliding-competent molecules is obtained from fluorescence intensity measurements. As a comparison, the estimated values of $S$ are on the same order of magnitude as the duty ratio of motors that exhibits filament length-dependent movement velocities, such as the Paramecium 22S dynein ( $f$ = 0.01) (Hamasaki et al., 1995), β dynein ( $f$ = 0.0050) (Imafuku et al., 1997), myosin ( $f$ = 0.050) (Uyeda et al., 1990), and NcKin3 ( $f$ = 0.03) (Adio et al., 2006). Together, our findings suggest that microtubule sliding by the PRC1-Kif4A complex can be considered as microtubule movement driven by an ensemble of low sliding efficiency motors, which results in the scaling of microtubule sliding velocity with antiparallel overlap length.

Concluding remarks

A defining architectural feature of the spindle midzone is a stable antiparallel microtubule array with overlapping plus-ends (Bratman and Chang, 2008; Glotzer, 2009). While we currently do not know if sliding of end-tagged microtubules by PRC1 and Kif4A contributes to the midzone organization, several properties of this system are relevant to the organization of cell biological structures both during mitosis in eukaryotes and in interphase cells of yeast and plant cells (Dogterom and Surrey, 2013; Subramanian and Kapoor, 2012). The relative sliding of PRC1-crosslinked microtubules by motor proteins such as Cin8 and Kip3p in budding yeast and KLP61F in Drosophila is thought to mediate the spindle elongation during early anaphase and contribute to defining the overlap width (Sharp et al., 1999; Straight et al., 1998; Pellman et al., 1995; Su et al., 2013). Antiparallel sliding of PRC1-crosslinked inter-kinetochore bridges is required for proper chromosome segregation (Polak et al., 2017; Vukušić et al., 2017). At least one of the motors involved in this process is centralspindlin, which also interacts with PRC1. Initial overlap length-dependent sliding could be advantageous in ensuring that microtubules of different lengths arrive at similar rates to the plus-ends of the template microtubule within arrays. The accumulation of proteins at microtubule plus-ends, including multiple mitotic kinesins, is thought to effectively concentrate cytokinesis factors proximal to the site of cell cleavage (Shrestha et al., 2012; Glotzer, 2009; Canman et al., 2003). Microtubule-end localization of PRC1 has been reported during monopolar cytokinesis (Subramanian et al., 2013; Shrestha et al., 2012), and in bipolar cells (Shrestha et al., 2012; Shannon et al., 2005), and both PRC1 and Kif4A have been described to co-localize at the ends of astral arrays of Xenopus egg extracts (Nguyen et al., 2018). These dense regions of proteins at microtubule ends may contribute to the alignment and stability of antiparallel microtubule arrays. Furthermore, the roadblock mechanism may be utilized by other kinesins that accumulate at microtubule plus-ends for the organization of stable arrays of defined size and geometry (Shimamoto et al., 2015; Braun et al., 2017; Bieling et al., 2010; Braun et al., 2011). Our biophysical analyses suggest that the geometrical features of the microtubules in the spindle can in turn tune the activity of associated proteins and regulate the geometry and stability of cellular microtubule arrays such as the spindle midzone.

In summary, our studies show how two microtubule-associated proteins, each with its own distinct filament binding properties, can act collectively to ‘measure’ the geometrical features of microtubules arrays and ‘translate’ them to generate well-defined mechanical and structural outputs. Filament crosslinking, relative-sliding and molecular crowding are likely to represent general features of a number of biological polymers, such as actin filaments and nucleic acids, that are dynamically organized during different cellular processes. The mechanism revealed here can therefore represent general principles that regulate the size and dynamics of cellular architectures built from different polymers.

Materials and methods

Protein purification

Request a detailed protocol

Recombinant proteins used in this study (PRC1, PRC1-GFP, Kif4A and Kif4A-GFP, Kif4A(C-term; aa: 733–1232) were expressed and purified as described previously (Subramanian et al., 2013; Subramanian et al., 2010).

Microtubule polymerization

Request a detailed protocol

GMPCPP polymerized and taxol-stabilized rhodamine-labeled microtubules were prepared with and without biotin tubulin as described previously (Subramanian et al., 2013; Subramanian et al., 2010). Briefly, GMPCPP seeds were prepared from a mixture of unlabeled bovine tubulin, X-rhodamine-tubulin and biotin tubulin, which were diluted in BRB80 buffer (80 mM PIPES pH 6.8, 1.5 mM MgCl₂, 0.5 mM EGTA, pH 6.8) and mixed together by tapping gently. The tube was transferred to a 37°C heating block and covered with foil to reduce light exposure. Non-biotinylated microtubules and biotinylated microtubules were incubated for 20 min and 1 hr 45 min, respectively. Afterwards, 100 µL of warm BRB80 buffer was added to the microtubules and spun at 75000 rpm, 10 min, and 30°C to remove free unpolymerized tubulin. Following the centrifugation step, the supernatant was discarded and the pellet was washed by round of centrifugation with 100 µL BRB80 supplemented with 20 µM taxol. The pellet was resuspended in 16 µL of BRB80 containing 20 µM taxol and stored at room temperature covered in foil.

Microtubule Co-sedimentation assay

Request a detailed protocol

Kif4A (C-term; 0.8 μM) was incubated with microtubules (0–8 μM) for 15 min at room temperature in motility buffer supplemented with 0.1 μg/μL BSA and then subject to sedimentation in TLA 120.1 rotor (Beckman Coulter) at 90000 rpm for 15 min at 27°C. After re-suspending the pellet, the amount of protein in pellet and supernatant was analyzed by SDS PAGE and the Coomassie-stained bands were quantified (LI-COR Odyssey). Full-length PRC1 was included as a control.

In vitro fluorescence microscopy assay

Request a detailed protocol

The microscope slides (Gold Seal Cover Glass, 24 × 60 mm, thickness No.1.5) and coverslips (Gold Seal Cover Glass, 18 × 18 mm, thickness No.1.5) were cleaned and functionalized with biotinylated PEG and non-biotinylated PEG, respectively, to prevent nonspecific surface sticking, according to standard protocols (Subramanian et al., 2013; Subramanian et al., 2010). Flow chambers were built by applying two strips of double-sided tape to a slide and applying to the coverslip. Sample chamber volumes were approximately 6–8 μL.

Experiments were performed as described previously (Subramanian et al., 2013; Subramanian et al., 2010). To make antiparallel microtubule bundles, biotinylated microtubules (referred to as ‘immobilized microtubules’ in text), labeled with rhodamine, were immobilized in a flow chamber by first coating the surface with neutravidin (0.2 mg/ml). Next, 0.2 nM unlabeled PRC1 in BRB80 + 5% sucrose was flushed into the flow chamber. Finally, non-biotinylated microtubules (referred to as moving microtubules) were flushed in the flow cell and incubated for 10–15 min to allow antiparallel overlap formation with the PRC1-decorated immobilized microtubules. To visualize microtubule sliding, PRC1 and Kif4A-GFP and 1 mM ATP were flowed into the chamber in assay buffer (BRB80 buffer supplemented with 1 mM TCEP, 0.2 mg/ml k-casein, 20 µM taxol, 40 mg/ml glucose oxidase, 35 mg/ml glucose catalase, 0.5% b-mercaptoethanol, 5% sucrose and 1 mM ATP) and a time-lapse sequence of images was immediately acquired at a rate of 3 frames/s. Data were collected for 10–15 min. Key experiments and analysis were also performed with GFP-PRC1 and non-fluorescent Kif4A to rule out the effect of GFP on microtubule sliding and stalling by PRC1 and Kif4A. Sliding experiments with Kif4A were performed using the same method.

All experiments were performed on Nikon Ti-E inverted microscope with a Ti-ND6-PFS perfect focus system equipped with a APO TIRF 100x oil/1.49 DIC objective (Nikon). The microscope was outfitted with a Nikon-encoded x-y motorized stage and a piezo z-stage, an sCMOS camera (Andor Zyla 4.2), and two-color TIRF imaging optics (Lasers: 488 nm and 561 nm; Filters: Dual Band 488/561 TIRF exciter). Rhodamine-labeled microtubules and GFP-labeled proteins (either PRC1 or Kif4A) in microtubule sliding assays were imaged by sequentially switching between 488 and 561 channels.

Single molecule analysis

Request a detailed protocol

To visualize single molecules on microtubules, we first immobilized biotinylated microtubule as described above. We then imaged single Kif4A molecules (200 pM Kif4A-GFP and 10 mM AMPMNP) and analyzed the fluorescence intensity distribution.

In order to estimate the total number of molecules in the untagged overlap (both crosslinking and passengers), we measured the fluorescence intensity of microtubule-immobilized single Kif4A-GFP molecules and estimated the number of molecules in the overlap from sliding experiments with 0.2 nM PRC1 + 6 nM Kif4A. Our analyses show that there are on average ~10 molecules/μm the overlap (Figure 8—figure supplement 2).

Image analysis

Request a detailed protocol

ImageJ (NIH) was used to process the image files. Briefly, raw time-lapse images were converted to tiff files. A rolling ball radius background subtraction of 50 pixels was applied to distinguish the features in the images more clearly. From these images, individual microtubules sliding events were picked and converted to kymographs by the MultipleOverlay and MultipleKymograph plug-ins (J. Reitdorf and A. Seitz; https://www.embl.de/eamnet/html/body_kymograph.html). The following criteria were used to exclude events from the analysis: (1) Only kymographs where we could confidently identify exactly two microtubules in the bundle were examined further (except for the data in Figure 7); (2) Sliding microtubules that encounter another bundle were excluded; (3) Pairs of microtubules with proximal plus-ends at initial time points could not be analyzed due to the very short duration of sliding; (4) For the sliding velocity versus initial overlap analysis, we only included kymographs where the initial overlap and the moving end-tag edge could be clearly distinguished (Figure 4); (5) For the microtubule length versus final overlap analysis, we picked kymographs both the immobilized and the moving microtubule edges could be distinguished (Figure 5); and (6) In Figure 4A–D, we excluded data for initial overlaps greater than 5 μm because of the existence of a few data points.

These kymographs were then further analyzed using a custom MATLAB program (Wijeratne, 2018; copy archived at https://github.com/elifesciences-publications/velocity_mt). The program first reads the input image and converts it to an array of intensity values. Next, using the ‘bwboundaries’ function, the high-intensity edges of the GFP channel kymograph were detected. If the features of the kymograph were clear, the edges of the immobilized end-tag and the moving end-tag were detected. Finally, any repeating elements due to a large amount of noise and poor contrast were removed by using the ‘unique’ function. The lines were then converted to x, y coordinates at each time point. For unclear MT or GFP channel kymographs, the kymographs can be further processed by ImageJ using the ‘Find Connected Regions’ plug-in (M. Longair; http://imagej.net/Find_Connected_Regions) to distinguish the features in the kymographs more clearly. This function separates regions in the kymograph based on criteria such as having the same intensity value for the detection of edges. Afterwards, these processed kymographs can be read through the MATLAB program as described above.

To calculate the sliding velocity, the derivative of the position versus time coordinates of the external edge of the moving microtubule end-tag from the GFP channel kymograph was taken. The initial overlap length is calculated from the first time point imaged after flowing in the final reaction mix in our experiment ( $t$ = 0; example first panel in Figure 1B). The initial overlap length, overlap length ( $L_{o v e r l a p}$ ) and untagged overlap length ( $L_{u n t a g g e d}$ ) were measured from the MT channel. The final overlap length ( $L_{F O}$ ) was measured from the MT channel when the end-tags have collided and reached a steady-state. The sum of the end-tag lengths, $L_{E T 1}$ and $L_{E T 2}$ , were determined by measuring the end-tag length before the collision of the end-tags from the GFP channel. The sum of the microtubule lengths, $M_{L 1}$ and $M_{L 2}$ , were measured from the rhodamine-labeled MT channel, and their sum was also plotted.

The overlap intensity ( $I_{o v e r l a p}$ ) and untagged overlap intensity ( $I_{u n t a g g e d}$ ) were measured from the GFP channel. The $ρ_{u n t a g g e d}$ was determined by $I_{u n t a g g e d} / L_{u n t a g g e d}$ . The sum of the end-tag intensities, $I_{E T 1}$ and $I_{E T 2}$ , were determined by measuring the end-tag intensity before the collision of the end-tags from the GFP channel. The sliding velocity and initial overlap length at equilibrium were determined at the time point when $I_{o v e r l a p}$ is constant.

The initial angle of attachment in the Kif4A control experiments is calculated using the ‘Angle’ tool in ImageJ. The average end-tag intensity and the average velocity of the end-tag were calculated using the ‘TrackMate’ plugin (https://imagej.net/TrackMate) in ImageJ.

Data availability

All data generated or analysed during this study are included in the manuscript and supporting files. The underlying source data are also provided.

References

1. Adio S
2. Bloemink M
3. Hartel M
4. Leier S
5. Geeves MA
6. Woehlke G
(2006) Kinetic and mechanistic basis of the nonprocessive Kinesin-3 motor NcKin3
Journal of Biological Chemistry 281:37782–37793.
https://doi.org/10.1074/jbc.M605061200
- PubMed
- Google Scholar
(2010) A minimal midzone protein module controls formation and length of antiparallel microtubule overlaps
Cell 142:420–432.
https://doi.org/10.1016/j.cell.2010.06.033
- PubMed
- Google Scholar
1. Bratman SV
2. Chang F
(2008) Mechanisms for maintaining microtubule bundles
Trends in Cell Biology 18:580–586.
https://doi.org/10.1016/j.tcb.2008.09.004
- PubMed
- Google Scholar
(2009) The kinesin-14 Klp2 organizes microtubules into parallel bundles by an ATP-dependent sorting mechanism
Nature Cell Biology 11:724–730.
https://doi.org/10.1038/ncb1878
- PubMed
- Google Scholar
1. Braun M
2. Lansky Z
3. Fink G
4. Ruhnow F
5. Diez S
6. Janson ME
(2011) Adaptive braking by Ase1 prevents overlapping microtubules from sliding completely apart
Nature Cell Biology 13:1259–1264.
https://doi.org/10.1038/ncb2323
- PubMed
- Google Scholar
1. Braun M
2. Lansky Z
3. Szuba A
4. Schwarz FW
5. Mitra A
6. Gao M
7. Lüdecke A
8. Ten Wolde PR
9. Diez S
(2017) Changes in microtubule overlap length regulate kinesin-14-driven microtubule sliding
Nature Chemical Biology 13:1245–1252.
https://doi.org/10.1038/nchembio.2495
- PubMed
- Google Scholar
1. Canman JC
2. Cameron LA
3. Maddox PS
4. Straight A
5. Tirnauer JS
6. Mitchison TJ
7. Fang G
8. Kapoor TM
9. Salmon ED
(2003) Determining the position of the cell division plane
Nature 424:1074–1078.
https://doi.org/10.1038/nature01860
- PubMed
- Google Scholar
1. Chan J
2. Jensen CG
3. Jensen LC
4. Bush M
5. Lloyd CW
(1999) The 65-kDa carrot microtubule-associated protein forms regularly arranged filamentous cross-bridges between microtubules
PNAS 96:14931–14936.
https://doi.org/10.1073/pnas.96.26.14931
- PubMed
- Google Scholar
1. Conway L
2. Wood D
3. Tüzel E
4. Ross JL
(2012) Motor transport of self-assembled cargos in crowded environments
PNAS 109:20814–20819.
https://doi.org/10.1073/pnas.1209304109
- PubMed
- Google Scholar
1. D'Avino PP
2. Archambault V
3. Przewloka MR
4. Zhang W
5. Lilley KS
6. Laue E
7. Glover DM
(2007) Recruitment of Polo kinase to the spindle midzone during cytokinesis requires the Feo/Klp3A complex
PLoS One 2:e572.
https://doi.org/10.1371/journal.pone.0000572
- PubMed
- Google Scholar
(2017) Shortening of microtubule overlap regions defines membrane delivery sites during plant cytokinesis
Current Biology 27:514–520.
https://doi.org/10.1016/j.cub.2016.12.043
- PubMed
- Google Scholar
1. Dogterom M
2. Surrey T
(2013) Microtubule organization in vitro
Current Opinion in Cell Biology 25:23–29.
https://doi.org/10.1016/j.ceb.2012.12.002
- PubMed
- Google Scholar
(2013) End-binding proteins and Ase1/PRC1 define local functionality of structurally distinct parts of the microtubule cytoskeleton
Trends in Cell Biology 23:54–63.
https://doi.org/10.1016/j.tcb.2012.10.003
- PubMed
- Google Scholar
1. Fink G
2. Hajdo L
3. Skowronek KJ
4. Reuther C
5. Kasprzak AA
6. Diez S
(2009) The mitotic kinesin-14 Ncd drives directional microtubule-microtubule sliding
Nature Cell Biology 11:717–723.
https://doi.org/10.1038/ncb1877
- PubMed
- Google Scholar
1. Forth S
2. Hsia KC
3. Shimamoto Y
4. Kapoor TM
(2014) Asymmetric friction of nonmotor MAPs can lead to their directional motion in active microtubule networks
Cell 157:420–432.
https://doi.org/10.1016/j.cell.2014.02.018
- PubMed
- Google Scholar
1. Forth S
2. Kapoor TM
(2017) The mechanics of microtubule networks in cell division
The Journal of Cell Biology 216:1525–1531.
https://doi.org/10.1083/jcb.201612064
- PubMed
- Google Scholar
1. Fu C
2. Ward JJ
3. Loiodice I
4. Velve-Casquillas G
5. Nedelec FJ
6. Tran PT
(2009) Phospho-regulated interaction between kinesin-6 Klp9p and microtubule bundler Ase1p promotes spindle elongation
Developmental Cell 17:257–267.
https://doi.org/10.1016/j.devcel.2009.06.012
- PubMed
- Google Scholar
(2017) The tubulin code at a glance
Journal of Cell Science 130:1347–1353.
https://doi.org/10.1242/jcs.199471
- PubMed
- Google Scholar
1. Gagliano J
2. Walb M
3. Blaker B
4. Macosko JC
5. Holzwarth G
(2010) Kinesin velocity increases with the number of motors pulling against viscoelastic drag
European Biophysics Journal 39:801–813.
https://doi.org/10.1007/s00249-009-0560-8
- PubMed
- Google Scholar
1. Glotzer M
(2009) The 3Ms of central spindle assembly: microtubules, motors and MAPs
Nature Reviews Molecular Cell Biology 10:9–20.
https://doi.org/10.1038/nrm2609
- PubMed
- Google Scholar
1. Grover R
2. Fischer J
3. Schwarz FW
4. Walter WJ
5. Schwille P
6. Diez S
(2016) Transport efficiency of membrane-anchored kinesin-1 motors depends on motor density and diffusivity
PNAS 113:E7185–E7193.
https://doi.org/10.1073/pnas.1611398113
- PubMed
- Google Scholar
1. Gruneberg U
2. Neef R
3. Li X
4. Chan EH
5. Chalamalasetty RB
6. Nigg EA
7. Barr FA
(2006) KIF14 and citron kinase act together to promote efficient cytokinesis
The Journal of Cell Biology 172:363–372.
https://doi.org/10.1083/jcb.200511061
- PubMed
- Google Scholar
1. Gull K
2. Hussey PJ
3. Sasse R
4. Schneider A
5. Seebeck T
6. Sherwin T
(1986) Tubulin isotypes: generation of diversity in cells and microtubular organelles
Journal of Cell Science 5:243–255.
https://doi.org/10.1242/jcs.1986.Supplement_5.16
- PubMed
- Google Scholar
(1995) Mechanochemical aspects of axonemal dynein activity studied by in vitro microtubule translocation
Biophysical Journal 69:2569–2579.
https://doi.org/10.1016/S0006-3495(95)80128-1
- PubMed
- Google Scholar
1. Hancock WO
2. Howard J
(1998) Processivity of the motor protein kinesin requires two heads
The Journal of Cell Biology 140:1395–1405.
https://doi.org/10.1083/jcb.140.6.1395
- PubMed
- Google Scholar
1. Hill DB
2. Plaza MJ
3. Bonin K
4. Holzwarth G
(2004) Fast vesicle transport in PC12 neurites: velocities and forces
European Biophysics Journal 33:623–632.
https://doi.org/10.1007/s00249-004-0403-6
- PubMed
- Google Scholar
1. Hirose K
2. Henningsen U
3. Schliwa M
4. Toyoshima C
5. Shimizu T
6. Alonso M
7. Cross RA
8. Amos LA
(2000) Structural comparison of dimeric Eg5, Neurospora kinesin (Nkin) and Ncd head-Nkin neck chimera with conventional kinesin
The EMBO Journal 19:5308–5314.
https://doi.org/10.1093/emboj/19.20.5308
- PubMed
- Google Scholar
(2000) A new look at the microtubule binding patterns of dimeric kinesins
Journal of Molecular Biology 297:1087–1103.
https://doi.org/10.1006/jmbi.2000.3627
- PubMed
- Google Scholar
1. Howard J
(1997) Molecular motors: structural adaptations to cellular functions
Nature 389:561–567.
https://doi.org/10.1038/39247
- PubMed
- Google Scholar
(2011) KIF4 regulates midzone length during cytokinesis
Current Biology 21:815–824.
https://doi.org/10.1016/j.cub.2011.04.019
- PubMed
- Google Scholar
(1997) Length dependence of displacement fluctuations and velocity in microtubule sliding movement driven by sea urchin sperm outer arm beta dynein in vitro
Biophysical Chemistry 67:117–125.
https://doi.org/10.1016/S0301-4622(97)00028-8
- PubMed
- Google Scholar
1. Janson ME
2. Loughlin R
3. Loïodice I
4. Fu C
5. Brunner D
6. Nédélec FJ
7. Tran PT
(2007) Crosslinkers and motors organize dynamic microtubules to form stable bipolar arrays in fission yeast
Cell 128:357–368.
https://doi.org/10.1016/j.cell.2006.12.030
- PubMed
- Google Scholar
1. Jiang W
2. Jimenez G
3. Wells NJ
4. Hope TJ
5. Wahl GM
6. Hunter T
7. Fukunaga R
(1998) PRC1: a human mitotic spindle-associated CDK substrate protein required for cytokinesis
Molecular Cell 2:877–885.
https://doi.org/10.1016/S1097-2765(00)80302-0
- PubMed
- Google Scholar
1. Kapitein LC
2. Peterman EJ
3. Kwok BH
4. Kim JH
5. Kapoor TM
6. Schmidt CF
(2005) The bipolar mitotic kinesin Eg5 moves on both microtubules that it crosslinks
Nature 435:114–118.
https://doi.org/10.1038/nature03503
- PubMed
- Google Scholar
1. Kellogg EH
2. Howes S
3. Ti SC
4. Ramírez-Aportela E
5. Kapoor TM
6. Chacón P
7. Nogales E
(2016) Near-atomic cryo-EM structure of PRC1 bound to the microtubule
PNAS 113:9430–9439.
https://doi.org/10.1073/pnas.1609903113
- PubMed
- Google Scholar
(2007) Load-dependent release limits the processive stepping of the tetrameric Eg5 motor
European Biophysics Journal 36:675–681.
https://doi.org/10.1007/s00249-007-0134-6
- PubMed
- Google Scholar
1. Kuan HS
2. Betterton MD
(2016) Motor protein accumulation on antiparallel microtubule overlaps
Biophysical Journal 110:2034–2043.
https://doi.org/10.1016/j.bpj.2016.03.039
- PubMed
- Google Scholar
1. Kural C
2. Kim H
3. Syed S
4. Goshima G
5. Gelfand VI
6. Selvin PR
(2005) Kinesin and dynein move a peroxisome in vivo: a tug-of-war or coordinated movement?
Science 308:1469–1472.
https://doi.org/10.1126/science.1108408
- PubMed
- Google Scholar
(2004) Essential roles of KIF4 and its binding partner PRC1 in organized central spindle midzone formation
The EMBO Journal 23:3237–3248.
https://doi.org/10.1038/sj.emboj.7600347
- PubMed
- Google Scholar
1. Lansky Z
2. Braun M
3. Lüdecke A
4. Schlierf M
5. ten Wolde PR
6. Janson ME
7. Diez S
(2015) Diffusible crosslinkers generate directed forces in microtubule networks
Cell 160:1159–1168.
https://doi.org/10.1016/j.cell.2015.01.051
- PubMed
- Google Scholar
1. Leduc C
2. Padberg-Gehle K
3. Varga V
4. Helbing D
5. Diez S
6. Howard J
(2012) Molecular crowding creates traffic jams of kinesin motors on microtubules
PNAS 109:6100–6105.
https://doi.org/10.1073/pnas.1107281109
- PubMed
- Google Scholar
(2006) Organelle transport along microtubules in Xenopus melanophores: evidence for cooperation between multiple motors
Biophysical Journal 90:318–327.
https://doi.org/10.1529/biophysj.105.067843
- PubMed
- Google Scholar
1. Loïodice I
2. Staub J
3. Setty TG
4. Nguyen NP
5. Paoletti A
6. Tran PT
(2005) Ase1p organizes antiparallel microtubule arrays during interphase and mitosis in fission yeast
Molecular Biology of the Cell 16:1756–1768.
https://doi.org/10.1091/mbc.e04-10-0899
- PubMed
- Google Scholar
1. Ludueña RF
(2013) A hypothesis on the origin and evolution of tubulin
International Review of Cell and Molecular Biology 302:41–185.
https://doi.org/10.1016/B978-0-12-407699-0.00002-9
- PubMed
- Google Scholar
1. Mollinari C
2. Kleman JP
3. Jiang W
4. Schoehn G
5. Hunter T
6. Margolis RL
(2002) PRC1 is a microtubule binding and bundling protein essential to maintain the mitotic spindle midzone
The Journal of Cell Biology 157:1175–1186.
https://doi.org/10.1083/jcb.200111052
- PubMed
- Google Scholar
(2018) Prc1E and Kif4A control microtubule organization within and between large Xenopus egg asters
Molecular Biology of the Cell 29:304–316.
https://doi.org/10.1091/mbc.e17-09-0540
- PubMed
- Google Scholar
1. Nunes Bastos R
2. Gandhi SR
3. Baron RD
4. Gruneberg U
5. Nigg EA
6. Barr FA
(2013) Aurora B suppresses microtubule dynamics and limits central spindle size by locally activating KIF4A
The Journal of Cell Biology 202:605–621.
https://doi.org/10.1083/jcb.201301094
- PubMed
- Google Scholar
1. Pellman D
2. Bagget M
3. Tu YH
4. Fink GR
5. Tu H
(1995) Two microtubule-associated proteins required for anaphase spindle movement in Saccharomyces cerevisiae
The Journal of Cell Biology 130:1373–1385.
https://doi.org/10.1083/jcb.130.6.1373
- PubMed
- Google Scholar
1. Peterman EJ
2. Scholey JM
(2009) Mitotic microtubule crosslinkers: insights from mechanistic studies
Current Biology 19:R1089–R1094.
https://doi.org/10.1016/j.cub.2009.10.047
- PubMed
- Google Scholar
1. Polak B
2. Risteski P
3. Lesjak S
4. Tolić IM
(2017) PRC1-labeled microtubule bundles and kinetochore pairs show one-to-one association in metaphase
EMBO reports 18:217–230.
https://doi.org/10.15252/embr.201642650
- PubMed
- Google Scholar
1. Pringle J
2. Muthukumar A
3. Tan A
4. Crankshaw L
5. Conway L
6. Ross JL
(2013) Microtubule organization by kinesin motors and microtubule crosslinking protein MAP65
Journal of Physics: Condensed Matter 25:374103.
https://doi.org/10.1088/0953-8984/25/37/374103
- PubMed
- Google Scholar
(2005) Taxol-stabilized microtubules can position the cytokinetic furrow in mammalian cells
Molecular Biology of the Cell 16:4423–4436.
https://doi.org/10.1091/mbc.e04-11-0974
- PubMed
- Google Scholar
1. Sharp DJ
2. McDonald KL
3. Brown HM
4. Matthies HJ
5. Walczak C
6. Vale RD
7. Mitchison TJ
8. Scholey JM
(1999) The bipolar kinesin, KLP61F, cross-links microtubules within interpolar microtubule bundles of Drosophila embryonic mitotic spindles
The Journal of Cell Biology 144:125–138.
https://doi.org/10.1083/jcb.144.1.125
- PubMed
- Google Scholar
(2000) Roles of motor proteins in building microtubule-based structures: a basic principle of cellular design
Biochimica et Biophysica Acta (BBA) - Molecular Cell Research 1496:128–141.
https://doi.org/10.1016/S0167-4889(00)00014-8
- PubMed
- Google Scholar
(2015) Measuring pushing and braking forces generated by ensembles of Kinesin-5 crosslinking two microtubules
Developmental Cell 34:669–681.
https://doi.org/10.1016/j.devcel.2015.08.017
- PubMed
- Google Scholar
(2012) PRC1 controls spindle polarization and recruitment of cytokinetic factors during monopolar cytokinesis
Molecular Biology of the Cell 23:1196–1207.
https://doi.org/10.1091/mbc.e11-12-1008
- PubMed
- Google Scholar
(1998) Time-lapse microscopy reveals unique roles for kinesins during anaphase in budding yeast
The Journal of Cell Biology 143:687–694.
https://doi.org/10.1083/jcb.143.3.687
- PubMed
- Google Scholar
1. Su X
2. Arellano-Santoyo H
3. Portran D
4. Gaillard J
5. Vantard M
6. Thery M
7. Pellman D
(2013) Microtubule-sliding activity of a kinesin-8 promotes spindle assembly and spindle-length control
Nature Cell Biology 15:948–957.
https://doi.org/10.1038/ncb2801
- PubMed
- Google Scholar
(2010) Insights into antiparallel microtubule crosslinking by PRC1, a conserved nonmotor microtubule binding protein
Cell 142:433–443.
https://doi.org/10.1016/j.cell.2010.07.012
- PubMed
- Google Scholar
1. Subramanian R
2. Kapoor TM
(2012) Building complexity: insights into self-organized assembly of microtubule-based architectures
Developmental Cell 23:874–885.
https://doi.org/10.1016/j.devcel.2012.10.011
- PubMed
- Google Scholar
1. Subramanian R
2. Ti SC
3. Tan L
4. Darst SA
5. Kapoor TM
(2013) Marking and measuring single microtubules by PRC1 and kinesin-4
Cell 154:377–390.
https://doi.org/10.1016/j.cell.2013.06.021
- PubMed
- Google Scholar
(2018) Cooperative Accumulation of Dynein-Dynactin at Microtubule Minus-Ends Drives Microtubule Network Reorganization
Developmental Cell 44:233–247.
https://doi.org/10.1016/j.devcel.2017.12.023
- PubMed
- Google Scholar
1. Tolić-Nørrelykke IM
(2008) Push-me-pull-you: how microtubules organize the cell interior
European Biophysics Journal 37:1271–1278.
https://doi.org/10.1007/s00249-008-0321-0
- PubMed
- Google Scholar
(1990) Myosin step size. estimation from slow sliding movement of actin over low densities of heavy meromyosin
Journal of Molecular Biology 214:699–710.
https://doi.org/10.1016/0022-2836(90)90287-V
- PubMed
- Google Scholar
(2006) Individual dimers of the mitotic kinesin motor Eg5 step processively and support substantial loads in vitro
Nature Cell Biology 8:470–476.
https://doi.org/10.1038/ncb1394
- PubMed
- Google Scholar
1. Vitre B
2. Gudimchuk N
3. Borda R
4. Kim Y
5. Heuser JE
6. Cleveland DW
7. Grishchuk EL
(2014) Kinetochore-microtubule attachment throughout mitosis potentiated by the elongated stalk of the kinetochore kinesin CENP-E
Molecular Biology of the Cell 25:2272–2281.
https://doi.org/10.1091/mbc.e14-01-0698
- PubMed
- Google Scholar
1. Vukušić K
2. Buđa R
3. Bosilj A
4. Milas A
5. Pavin N
6. Tolić IM
(2017) Microtubule sliding within the bridging fiber pushes kinetochore fibers apart to segregate chromosomes
Developmental Cell 43:11–23.
https://doi.org/10.1016/j.devcel.2017.09.010
- PubMed
- Google Scholar
Software
1. Wijeratne SS
(2018) Velocity_MT, version 6b39bd9
Github.

https://github.com/sitaraw/velocity_mt
1. Yamashita A
2. Sato M
3. Fujita A
4. Yamamoto M
5. Toda T
(2005) The roles of fission yeast ase1 in mitotic cell division, meiotic nuclear oscillation, and cytokinesis checkpoint signaling
Molecular Biology of the Cell 16:1378–1395.
https://doi.org/10.1091/mbc.e04-10-0859
- PubMed
- Google Scholar
(2015) Writing and reading the tubulin code
Journal of Biological Chemistry 290:17163–17172.
https://doi.org/10.1074/jbc.R115.637447
- PubMed
- Google Scholar
1. Zhu C
2. Jiang W
(2005) Cell cycle-dependent translocation of PRC1 on the spindle by Kif4 is essential for midzone formation and cytokinesis
PNAS 102:343–348.
https://doi.org/10.1073/pnas.0408438102
- PubMed
- Google Scholar
(2006) Spatiotemporal control of spindle midzone formation by PRC1 in human cells
PNAS 103:6196–6201.
https://doi.org/10.1073/pnas.0506926103
- PubMed
- Google Scholar

Decision letter

Stefan Diez

Reviewing Editor; Technische Universität Dresden, Germany
Anna Akhmanova

Senior Editor; Utrecht University, Netherlands

In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.

Thank you for submitting your article "Geometry of antiparallel microtubule bundles regulates relative sliding and stalling by PRC1 and Kif4A" for consideration by eLife. Your article has been reviewed by Anna Akhmanova as the Senior Editor, a Reviewing Editor, and three reviewers.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision.

Summary:

The reviewers find that the manuscript addresses an interesting question and presents exciting new results of how motorized sliding of microtubules (by KIF4) is regulated by passive cross-linkers (PRC1) in the case when the motor and the cross-linker directly interact. This topic is important for understanding spindle formation and chromosome segregation.

KIF4 is a multifunctional mitotic kinesin, which localises to the chromosomes during early stages of mitosis and, during anaphase, moves to the spindle midzone through its interaction with PRC1, a microtubule bundling protein, and plays crucial roles in organization of the anti-parallel microtubule bundles. In addition to the motor activity, it has a unique activity to suppress the dynamics of the plus-end of microtubules. Consistent with the latter activity, in vivo depletion phenotypes indicate that KIF4 is important for limiting the anaphase spindle elongation and keeping the central anti-parallel overlap compact. In a previous paper, Subramanian et al., reported on the crystal structures of PRC1 and the formation of high-density regions of KIF4-PRC1 at the microtubule plus-tips, referred to as end-tags. Now it is shown, in a series of nice in vitro experiments (and some modelling), that, as the microtubules slide apart, the tags get closer to each other while the sliding slows down. Sliding stops and stable overlaps are formed when the tags collide. Interestingly, it is observed that structural properties of the initial array regulate PRC1-Kif4A mediated microtubule organization: The sliding velocity scales with the initial microtubule-overlap length and the width of the final overlap scales with the microtubule lengths. Based on these findings, it is suggested that micron-scale geometrical features of antiparallel microtubules can regulate the activity of nanometer-sized proteins to define the structure and mechanics of microtubule-based architectures.

While the reviewers acknowledge that the experiments performed seem very sound (and quite difficult) and that the result in this manuscript provides important new insight, they also raise the concern, whether the progress presented in the current version is large and solid enough to warrant another high impact story (several important ones, including Subramanian et al., 2013, partly by the same authors, have appeared in Cell, Nature Cell Biology). Moreover, the underlying mechanisms (represented by the not yet fully connected experimental and theoretical results) do not seem to be clear at the moment. The following extensive list of major comments would therefore need to be adequately addressed before the paper can be further considered for publication.

Essential revisions:

- It is shown (surprisingly), that the velocity of the KIF4-PRC1 driven sliding scales with the initial overlap length, suggesting that it is dependent on the (untagged?) motor number. This is however not quantified, even though the authors have access to the fluorescence intensities of KIF4-PRC1 (corresponding to motor numbers) in their TIRF data. Please analyze and discuss.

- Similarly, although the motor density is an important parameter (sliding stops at very high density in the "tags"), it is at the moment unclear how does the sliding velocity scale with the density of the motors. Only two stopping events are quantified (Figure 3H and Figure 4—figure supplement 1P) suggesting that it might also be the increase of the density of the untagged motors causing the slowdown. Please analyse from more events and discuss.

- To address the slow-down mechanism, the authors are advised to investigate the sliding of fully overlapping microtubules, in which they can generate different KIF4-PRC1 densities/numbers by different KIF4-PRC1 concentrations in solution. Assembling the microtubule sandwiches for these experiments in ADP and then exchanging ADP to ATP would allow the authors to initially measure the sliding velocities at different KIF4-PRC1 densities homogenously distributed in the overlap (without the presence of the end-tags) and then to observe the change of the velocities during the end-tag formation. Please add such data, analyse and discuss.

- It is somewhat dissatisfying that there is no direct correlation of individual PRC1 and Kif4A complexes. What is the lifetime of the attachment of Kif4A to PRC1? Should one see it as 1:1 complexes that live forever, or is binding more intermittent and should the interaction be seen more as a collective effect (many PRC1s with each Kif4A, at a given moment or after each other)? This could e.g. have important consequences for the mechanism of action. Please discuss.

- KIF4 interacts with PRC1 via its C-terminal tail domain. However, the same domain also has a microtubule-binding activity independent of PRC1 (Bieling, 2010, Figure 7—figure supplement 1). Although it is unclear how strong this interaction is, considering that both the interactions between PRC1 and KIF4 and between PRC1 and unbundled microtubules are weak (K_d ~0.3 μm (Subramanian, 2013) and ~0.6 μm (Bieling, 2010), respectively), it is possible that the KIF4 tail-microtubule interaction might also play an important role in the authors' experimental system. Please perform control experiments and/or discuss.

- The relatively low affinity between KIF4 and PRC1 (~0.3 μM, cf. K_d~8 nM between PRC1 and anti-parallel microtubule bundle) raises the question of what percentages of KIF4 and PRC1 in the tagged and untagged overlaps are in the complex. This might not be important if there is no productive force generation by KIF4 molecules not complexed with PRC1. However, considering the presence of the second microtubule-binding site of the KIF4 tail (see above), it is important to clarify the states of the PRC1-KIF4 complex formation. Reduction of the sliding velocity by increased PRC1 and the reversal by additional KIF4A is consistent with a picture that PRC1 holds the anti-parallel overlap of MTs and KIF4A, which is not in a complex with PRC1, slides them. Please discuss.

- Which fraction of KIF4-PRC1 is driving the sliding and what is causing the slow-down (during the phase-2). Is the decrease of velocity in phase-2 due to the decrease in the number of "untagged" KIF4-PRC1 or an increase in their density? Does friction play any role? Please discuss.

- The description of the result from subsection “Characterization of relative microtubule sliding in the PRC1-Kif4A system” (density and intensity of Kif4A in the different overlap regions) is not very clear. What is meant with "retained"? What is meant by the final sentence of this part? Are these statements based on only two example kymographs (Figure 3E and Supplementary figure 1C-L). For Figure 3H it appears that the overlap keeps on increasing until the end of the experiment (unlike the event in Supplementary figure 1C-L). Please explain more clearly.

- To what extend is the analysis of the end tag lengths (Figure 4AB) affected by the diffraction limited imaging used? How different are the end-tagging lengths on single microtubules and in microtubule overlaps? Please discuss.

- In their theoretical model, the authors implicitly assume that one of the two PRC1 ends that binds the same microtubule with the one that KIF4 interacts with (i.e. the bottom one in Appendix Figure 1A) doesn't interfere with the MT sliding. It is not clear how this is justified. It would be more natural that one end of a PRC1 dimer (upper one in Appendix Figure 1A) works as a supporting point for productive sliding while the other end (bottom one) works as a drag against the stepping of KIF4. Please discuss and resolve the issue.

- On one hand, modeling the PRC1-MT interaction as a slipping tether using the formulation by Grover et al., is an excellent idea. However, the model presented by the authors is not properly describing their experimental conditions. Their model is for a different situation in which KIF4 is tethered on the PRC1 bridging two microtubules (one of them is immobilized) and it drives the sliding of the third, non-immobilized microtubule. Thus, it is not surprising that there is a big inconsistency between the model calculation and the experimental measurements in the order of the sliding velocity. Please resolve.

- On the other hand: Is it really warranted to use a similar model to diffusion (and drag) in a membrane for diffusion of the PRC1 complexes over the MT? PRC1 binds to the MT, most likely with 8 nm periodicity, with relatively large barriers / wells; in the membrane stuff is much more continuous. Would in the current situation such a view not be too simplistic, e.g. not taking into account 'non-linear' / 'out-of-equilibrium' effects due to motor action (i.e. increased loads on the motor which could result in changes in motor action (velocity, release) including a non-linear scaling of friction with motor number (see Lansky et al., 2015).

- According to the authors' formula in the Appendix, 𝑣_𝑀𝑇 is hyperbolic against a dimensionless value x=a∙d∙l/L_MT ("Michaels-Menten" type, passing origin and approaching max value = 𝑣_step). A characteristic parameter is f∙δ, which corresponds to x which gives a half maximal 𝑣_𝑀𝑇 (equivalent to K_M for "Michaels-Menten"). In a regime where x is below this, the 𝑣_𝑀𝑇 ~ x relationship becomes nearly linear. However, calculations with the values in Table A1 result in f∙δ = 1.72 x 10^-5. This is too small, and it is impossible to make x smaller than this by any realistic combinations of a, d, l and L_MT. In other words, 𝑣_𝑀𝑇 is almost equal to 𝑣_step irrespective of l, the lengths of overlap. Please explain how the curves in Appendix Figure 1 were drawn. The actual values of a, d and D used should be presented.

- The modeling should be connected closer to the experiments. For example, a∙d is essentially the line density of PRC1-Kif4A in the overlap and thus should be measurable. Then, the actual D should be able to be determined with actual x and 𝑣_𝑀𝑇 measurements using the authors' formula and can be compared with reported values. Moreover, it would be helpful to indicate what trends (and numbers) belong to the experimentally tested parameter space. The simulations (at least their results) should be discussed more prominently in the main text /Discussion section. Please add this information.

- Biological significance: It is unclear whether the situations studied in this work actually occur in the cell. Although the end-tagging of astral microtubules near spindle poles by PRC1 was demonstrated in Subramanian et al., 2013, it remains unclear whether KIF4A takes part in these tags. Even so, it is unclear whether there is a cellular situation in which microtubules are first tagged (and stabilized) with PRC1 and KIF4A and then bundled. In general, PRC1 localizes on the metaphase spindle although weakly and diffusely while KIF4 is associated with chromosomes before anaphase onset. PRC1 can form midzone bundles without KIF4. Please discuss.

[Editors' note: further revisions were requested prior to acceptance, as described below.]

Thank you for resubmitting your work entitled "Geometry of antiparallel microtubule bundles regulates relative sliding and stalling by PRC1 and Kif4A" for further consideration at eLife. Your revised article has been evaluated by Anna Akhmanova (Senior Editor), a Reviewing Editor, and three reviewers.

The involved editors as well as the reviewers acknowledge that you did a great job of seriously considering the earlier comments, including the performance of additional experiments. The conclusions are now much more solid and the context with previous studies and other systems is discussed much more clearly, highlighting why this study is important and exciting. The manuscript has tremendously gained by the revision and it is felt that the work in general is very well suited for eLife.

However, there are some remaining issues that need to be addressed before your manuscript can possibly be accepted for publication:

1) Please have a look at the following (conclusion of the Figure 4, subsection “Examining the time-dependent changes during microtubule sliding in the PRC1-Kif4A system”): "…velocity of microtubule sliding.… is determined by.…. the total number of sliding competent molecules in the untagged overlap." Velocity increases with increasing (untagged) motor number (Figure 4A-D) and "The microtubule movement can subsequently proceed at a *constant velocity*, even when the overlap shrinks,…" (i.e. when the untagged *motor number decreases* – phase 1 in the Figure 4F and Figure 4—figure supplement 2) "…possibly through increasing the density of motor molecules during relative sliding." This would mean that increasing the motor density should compensate for decreasing the motor number to keep the velocity constant. That is, velocity should increase with increasing motor density.

However: (i) How an increased motor density would result in an increased sliding velocity is intriguing and the authors should probably comment on this. (ii) In contradiction with their statement, the authors show that (at least in some concentration regime) this is not the case (Figure 4—figure supplement 1F).

2) Connected to (1): An essential statement of the paper is that the sliding velocity scales with the initial overlap length. However, Figure 4E-H shows that the sliding velocity stays constant for a shrinking overlap lengths (called phase 1). How is the "initial overlap length" defined here? What means "initial"? Most surprisingly, the overlap intensity increases during this phase. How is that explained? Is there equilibrium in binding achieved before?

3) With regard to the interaction between the C-terminal tail of KIF4A and microtubules it is stated that the interaction between the KIF4A tail and microtubules are not strong. However, the PAGE image in Figure 2 clearly shows there is some interaction between them. The signals of the bands that correspond to KIF4A (but don't appear in 'PRC1' lanes) in the precipitates (KIF4A(C-term) 'P') increase with the increasing amount of microtubules. This indicates a weak but significant interaction between KIF4A C-tail and microtubules. The authors' statements such as "We observed no significant microtubule-association of this domain" (subsection “Molecular determinants of the sliding and cross-bridging in the PRC1-Kif4A system”) or "the C-terminus of Kif4A does not directly bind microtubules" are thus not true.

This interaction is indeed 'very' weak as a MAP. The dissociation constant might be at the orders of 100 µM or 1 mM. However, it should be kept in mind that this domain is not floating alone in solution but is part of a kinesin-like motor protein, which strongly accumulates at the plus-ends of microtubules. The local concentration of the domain can be the order of 1~10 mM, which seems to be comparable with the weak but significant interaction detected in Figure 2A.

Similarly, hydrodynamics data at the protein concentration of 5 µM might not be strong enough to exclude the possibility that Kif4A might form oligomers at the crowded condition. The second (very weak) binding site on the C-terminal tail or oligomerization seems to be more plausible as an explanation of the MT-sliding by Kif4A alone. At least the data are not strong enough to exclude these possibilities. Please discuss all of the above.

4) The response to comment 13 is unsatisfactory. The difference of units doesn't matter if the calculation is performed with physical quantities (numbers + units).

The characteristic parameter (the initial overlap that gives the half maximum velocity, analogous of K_M in the Michaelis-Menten kinetics, here called λ) λ should be at the order of µm or bigger. However, when repeating the calculation with the values provided in the revision, the λ is calculated to be at the order of picometer. Thus, what the authors' theory predicts is that the sliding velocity is independent of the initial overlap length. The theoretical curves in Appendix Figure 1 appear inconsistent with the authors' theory and the parameters provided. Please check.

5) In the calculation, d = 13 and a = 0.4 is assumed – meaning that there should be about 600 molecules active in a 1 micron long MT overlap? Is that a reasonable assumption? Can't an upper bound of the motor number be (roughly) estimated from the fluorescence intensity?

6) With regard to the contribution of the end tags on sliding: Kif4A alone can form an end tag, which drives movement of a non-immobilized microtubule along an immobilized one. It is not clear why the similar end-tag doesn't contribute much to the MT sliding in the Kif4A-PRC1 regime. How fast is the movement driven by Kif4A alone end tags in the experiments represented by Figure 2C and D (can't be currently estimated because scale bars are missing in these panels)?

[Editors' note: further revisions were requested prior to acceptance, as described below.]

Thank you for your second resubmission of your work entitled "Geometry of antiparallel microtubule bundles regulates relative sliding and stalling by PRC1 and Kif4A" for further consideration at eLife. Your revised article has been evaluated by Anna Akhmanova (Senior Editor), a Reviewing Editor, and three reviewers.

The involved editors as well as the reviewers acknowledge that you did a great job in addressing the points raised. Removing the earlier modeling part and replacing it by a kind of "duty ratio" discussion makes sense and is a nice way to extract quantitative information out of the data. While this current description is admittedly not as advanced / informative as a real model (attempted in the last version of the manuscript) it nevertheless provides useful mechanistic insight. Given the enormous amount of very high quality experimental data, the taken approach is regarded fine for this paper. Future work could go into a more advanced model. Hence, the manuscript is now in principle regarded suitable for publication in eLife.

There is one remaining point that the reviewers and editors find of crucial importance before potential acceptance of the paper: The usage of the term/concept "duty ratio" does not seem to be fully appropriate in the presented context. The traditional/authentic "duty ratio" is about the temporal fraction of the crossbridge cycle (= ATPase cycle) of a single motor head in which it is attached to the filament and makes its working stroke. In contrast, the situations the authors imagine are (i) dissociation of the PRC-Kif4A complex from the microtubule, and (ii) slippage of PRC1 on the MT. These will influence the fraction of ATPase cycles that actually result in the sliding of the non-immobilized microtubule, i.e., the fraction of the productive stepping by Kif4A. What the authors call "duty ratio, f", is a mixture of the authentic duty ratio (as to the crossbridge/ATPase cycle) and the effect of the futile cycles. It is not appropriate to skip these details and call the parameter simply "duty ratio". A better term to describe the scenario may be "sliding efficiency". In any case, the authors should explicitly mention that they mean something slightly, but substantially, different than what "duty ratio" has been used for before.

In other words, both the authentic duty ratio and the fraction of productive stepping would influence the sliding velocity in a similar way, following the same form of a mathematical formula (2) in subsection “Mechanism of overlap-length dependent sliding by PRC1 and Kif4A”, as a first approximation. However, their meanings are quite different. A low duty ratio motor can still be highly energy efficient (like dynein). On the other hand, futile sliding simply wastes energy of ATP hydrolysis as a slippery between PRC1 and MTs or a dissociation between PRC1 and KIF4A. Along these lines: Is the low "duty ratio" of the PRC1-Kif4A complex in MT sliding consistent with its highly processive motility along a MT? A quantitative argument is necessary as to the difference in the loads on the PRC1-Kif4A complex between the two conditions; the MT sliding and the single particle motility. Statements like "…microtubule sliding by the PRC1-Kif4A complex can be considered as microtubule movement driven by an ensemble of low duty-ratio motors,.… " need to be revised accordingly.

https://doi.org/10.7554/eLife.32595.041

Author response

Summary:

The reviewers find that the manuscript addresses an interesting question and presents exciting new results of how motorized sliding of microtubules (by KIF4) is regulated by passive cross-linkers (PRC1) in the case when the motor and the cross-linker directly interact. This topic is important for understanding spindle formation and chromosome segregation.

KIF4 is a multifunctional mitotic kinesin, which localises to the chromosomes during early stages of mitosis and, during anaphase, moves to the spindle midzone through its interaction with PRC1, a microtubule bundling protein, and plays crucial roles in organization of the anti-parallel microtubule bundles. In addition to the motor activity, it has a unique activity to suppress the dynamics of the plus-end of microtubules. Consistent with the latter activity, in vivo depletion phenotypes indicate that KIF4 is important for limiting the anaphase spindle elongation and keeping the central anti-parallel overlap compact. In a previous paper, Subramanian et al., reported on the crystal structures of PRC1 and the formation of high-density regions of KIF4-PRC1 at the microtubule plus-tips, referred to as end-tags. Now it is shown, in a series of nice in vitro experiments (and some modelling), that, as the microtubules slide apart, the tags get closer to each other while the sliding slows down. Sliding stops and stable overlaps are formed when the tags collide. Interestingly, it is observed that structural properties of the initial array regulate PRC1-Kif4A mediated microtubule organization: The sliding velocity scales with the initial microtubule-overlap length and the width of the final overlap scales with the microtubule lengths. Based on these findings, it is suggested that micron-scale geometrical features of antiparallel microtubules can regulate the activity of nanometer-sized proteins to define the structure and mechanics of microtubule-based architectures.

While the reviewers acknowledge that the experiments performed seem very sound (and quite difficult) and that the result in this manuscript provides important new insight, they also raise the concern, whether the progress presented in the current version is large and solid enough to warrant another high impact story (several important ones, including Subramanian et al., 2013, partly by the same authors, have appeared in Cell, Nature Cell Biology). Moreover, the underlying mechanisms (represented by the not yet fully connected experimental and theoretical results) do not seem to be clear at the moment. The following extensive list of major comments would therefore need to be adequately addressed before the paper can be further considered for publication.

In recent years, in vitro reconstitution-based studies have revealed the mechanisms by which the collective activities of motor and non-motor proteins regulate the architecture of microtubule arrays. However, there are relatively few studies on how the micron-scale geometrical features of filament arrays, in turn, tune the output of microtubule associated proteins [Braun et al., 2011; Braun at el., 2017; Bieling, Telley and Surrey, 2010; Shimamoto, Forth and Kapoor, 2015]. Our study uncovers new mechanisms by which the geometrical features of antiparallel microtubule bundles, such as filament length and overlap width, can be ‘read’ by associated proteins to regulate the dynamics, stability and architecture of cytoskeletal structures.

While previous studies have characterized the molecular interactions and regulation of microtubule dynamics by PRC1 and Kif4A, microtubule sliding by this protein module is poorly characterized [Bieling, Telley and Surrey, 2010; Nunes et al., 2013; Subramanian et al., 2013]. This study reveals unexpected emergent features of microtubule organization by a protein module composed of a pair of interacting motor and MAP: (i) Microtubule sliding and stalling by PRC1 and Kif4A results in the organization of a stable bundle in which the plus-ends of microtubules are closely aligned. (ii) The size of the final stable antiparallel overlap scales with the lengths of the crosslinked microtubules. Therefore, in addition to preventing microtubules from sliding apart, PRC1-Kif4A end-tags act as ‘molecular rulers’ to define the width of the stable antiparallel overlap. (iii) The microtubule sliding velocity in the PRC1-Kif4A system depends on the initial length of the antiparallel overlap. This is unusual for microtubule movement driven by an ensemble of motor proteins. We have reorganized the discussion to emphasize these findings.

Microtubule sliding and stalling has been described in another motor-MAP system (pombe Ase1 and kinesin-14 Ncd), and more recently with kinesin-14 HSET [Braun et al., 2011; Braun at el., 2017]. While the end result is the formation of a stable antiparallel overlap in all three systems, there are fundamental mechanistic differences between the results here and the published work. (i) In both the published studies, the sliding velocity is not determined by the initial microtubule overlap length as in the PRC1-Kif4A system, but rather changes continuously as the overlap shrinks (i.e. adaptive rather than determined by the initial state). (ii) In both the Ncd-Ase1 and the HSET systems, it is proposed that the reduction in velocity is due to an increase in forces opposing motor stepping as the overlap shrinks. Such a force-balance mechanism cannot account for initial length-dependent sliding in our system, and we discuss an alternative mechanism consistent with our data. (iii) A force balance mechanism also underlies the establishment of a stable overlap in the published studies. We propose an alternative mechanism consistent with our findings. (iv) Scaling of final overlap length with the sum of microtubule lengths is not an inherent feature of the Ase1-Ncd and the HSET systems. Overall, we think our study represents a different class of mechanism for both the formation of a stable array as well as overlap length-dependent sliding.

We have now performed additional experiments, analyses and extended the discussion to clarify the mechanisms underlying microtubule sliding and stalling in this system. Briefly, our main conclusions are: (i) Length-dependent sliding arises from dynamically associating PRC1-Kif4A molecules in the untagged region of the overlap. We discuss the ‘slipping tether model’ as a simple mechanism that is consistent with our data. (ii) Slowdown is due to motors entering the high-density regime proximal to end-tag and the movement stalls when the end-tags merge and stepping by the motor protein is suppressed. We discuss steric hindrance as the predominant mechanism underlying both slow down and stall in this system.

Essential revisions:

1) It is shown (surprisingly), that the velocity of the KIF4-PRC1 driven sliding scales with the initial overlap length, suggesting that it is dependent on the (untagged?) motor number. This is however not quantified, even though the authors have access to the fluorescence intensities of KIF4-PRC1 (corresponding to motor numbers) in their TIRF data. Please analyze and discuss.

As per the reviewer’s suggestion, we are able to quantify fluorescence intensity in the untagged and end-tagged regions of the overlap. Assuming that the number of sliding molecules is proportional to the total number of molecules, our analyses suggest that length dependent sliding arises from molecules in the untagged overlap region. The following data have now been added to the manuscript:

Correlation between overlap length and intensity: We find that the fluorescence intensity of Kif4A-GFP is proportional to total overlap length (Figure 4—figure supplement 1C). From this, we infer that the sliding velocity scales with the number of motor molecules in the overlap. We prefer to plot length rather than intensity because it is overall a less noisy measurement and is not impacted by illumination heterogeneity across the field of view or photobleaching. We have now included a plot showing the correlation (N = 20; Pearson’s correlation coefficient = 0.90) between overlap length and fluorescence intensity of a randomly chosen subset of the data to the Supplement (Figure 4—figure supplement 1C).

In addition, we have now included the following data, which reveal that sliding velocity scales with the untagged overlap length/intensity and not the end-tagged length/intensity:

Untagged overlap vs. sliding velocity (Figure 4—figure supplement 1D-E). The data show a correlation between untagged overlap length and sliding velocity under all conditions where we observe a correlation between total overlap length and sliding velocity. Assay conditions: (i) 0.2 nM PRC1 and 6 nM Kif4A-GFP (Figure 4—figure supplement 1D; black; N = 64; Pearson’s correlation coefficient = 0.54), (ii) 0.5 nM GFP-PRC1 and 6 nM Kif4A (Figure 4—figure supplement 1E; red; N = 20; Pearson’s correlation coefficient = 0.83), and (iii) 1 nM GFP-PRC1 with 12 nM Kif4A (Figure 4—figure supplement 1E; blue; N=22; Pearson’s correlation coefficient= 0.79). We also see a correlation between untagged overlap length and Kif4A-GFP intensity (Figure 4—figure supplement 1D inset). This suggests that the number of motor molecules in the untagged overlap is responsible for length-dependent sliding in this system.

End-tagged overlap vs. sliding velocity data: In the case of end-tags, the intensity is a more reliable measurement than length, as some of the end-tags are very short (less than 5 pixels). Analysis of both end-tag length and intensity as a function of sliding velocity indicate that there is no positive correlation between the number of molecules at the end-tag and the sliding velocity (Figure 4—figure supplement 1A-B, Pearson’s correlation coefficient = between -0.18 and -0.40).

Note: we would like to emphasize that while intensity measurements reflect the total number of molecules in the overlap, measuring the precise number of crosslinking motor proteins within a bundle that contribute to microtubule sliding is challenging for the following reasons. First, fluorescence intensity represents both the Kif4A molecules that are walking on individual microtubules and those that participate in crosslinking and sliding microtubules [Shimamoto, Forth and Kapoor, 2015]. We expect that the number of crosslinking PRC1-Kif4A molecules will be fewer than the number of passenger molecules. This is because PRC1 molecules cross-bridge over a narrow intermicrotubule distance range [Subramanian et al., 2010]. Second, PRC1 and Kif4A do not form a high-affinity stable complex, and sliding is likely sustained by molecules that are dynamically dissociating and reassociating within the bundle (further elaborated in response to comment #4).

2) Similarly, although the motor density is an important parameter (sliding stops at very high density in the "tags"), it is at the moment unclear how does the sliding velocity scale with the density of the motors. Only two stopping events are quantified (Figure 3H and Figure 4—figure supplement 1P) suggesting that it might also be the increase of the density of the untagged motors causing the slowdown. Please analyse from more events and discuss.

We have now included an additional panel of 4 sliding and stalling events along with quantification in the supplement (see Figure 4—figure supplement 2).

How does sliding velocity in phase-1 scale with motor density (as recently reported for HSET)? We find no correlation between sliding velocity and the average untagged overlap motor density in phase-1 for a dataset in which we see a positive correlation between sliding velocity and untagged overlap length/intensity [0.2 nM PRC1 and 6 nM Kif4A-GFP] (Pearson’s coefficient: -0.15; N = 20). This suggests that in this regime, the velocity depends on the number but not the density of motor molecules (Figure 4—figure supplement 1F).

Is the transition from phase-1 to phase-2 due to increase in density of untagged motors?

We analyzed kymographs from experiments conducted with 0.2 nM PRC1 and 6 nM Kif4AGFP and examined the individual Kif4A-GFP density versus time profiles (representative data in Figure 4H and Figure 4—figure supplement 1P and Figure 4—figure supplement 2D, 2H, 2L, 2P). We find that the Kif4A-GFP density in the untagged overlap increases during both phase-1 and phase-2 of movement. So, the transition from phase-1 (constant velocity sliding) to phase-2 (slowdown) does not correspond to a switch from constant to increasing density.

Next, we considered the alternative possibility that the transition from sliding to stalling coincides with the end-tags on the moving and immobilized microtubules arriving at close proximity. At this high-density region, microtubule sliding would first slow down before complete stall is reached. We noticed that in ~50% of the events (47/98; 0.2 nM PRC1 + 6 nM Kif4A-GFP), the transition from phase 1 to 2 occurs when the end-tags have nearly merged and our image analysis algorithm does not resolve the two end-tags (examples: see kymographs in Figure 4E, Figure 4—figure supplements 2I, 2M). We reasoned that if high protein concentration proximal to end-tags is the reason for slow-down, the protein density at the phase-1 to phase-2 transition should be similar under different experimental conditions. Kif4A-GFP density measurement and fluorescence line-scan analysis at the phase-1 to phase-2 transition timepoints in two experimental conditions show that this is indeed the case (Figure 4—figure supplement 4A-B). Furthermore, comparison of the phase-1 to phase-2 transition-point intensity with the average end-tag intensity at the same time point suggests that on average slowdown occurs when the intensity is >70% of the end-tag intensity (Figure 4—figure supplement 4B-C). These observations suggest that sliding slows down proximal to the end-tags, when the untagged overlap is short and the motors encounter a high protein-density.

Together, these analyses suggest that at the (i) phase-1: sliding depends on initial overlap length but not overlap density under the same protein concentrations (ii) phase-1 to -2 transition: sliding slows down due to high protein density. We discuss steric inhibition to stepping as the mechanism underlying slowdown and stall in this system (discussed in response to comment #10 and in the main text under the section ‘Mechanism for transition from constant velocity sliding to slow-down and stalling in the PRC1-Kif4A system’ and Discussion section).

3) To address the slow-down mechanism, the authors are advised to investigate the sliding of fully overlapping microtubules, in which they can generate different KIF4-PRC1 densities/numbers by different KIF4-PRC1 concentrations in solution. Assembling the microtubule sandwiches for these experiments in ADP and then exchanging ADP to ATP would allow the authors to initially measure the sliding velocities at different KIF4-PRC1 densities homogenously distributed in the overlap (without the presence of the end-tags) and then to observe the change of the velocities during the end-tag formation. Please add such data, analyse and discuss.

We have now performed the experiment suggested above and reanalyzed our previous data to address how the sliding velocities change with end-tag formation. Based on the analyses, we conclude that the initial overlap-length dependent sliding is independent of end-tag length. We discuss the findings below:

As suggested by the reviewers, microtubule bundles were assembled with protein and ADP (0.2 nM GFP-PRC1 + 6 nM Kif4A and 2 mM ADP; experimental details in the legend). Under these conditions, no end-tags are observed. Upon exchanging the buffer with ATP (no additional protein in solution), we observe concurrent sliding and end-tag formation even at the earliest time point we could image (Author response image 1). We have also performed this experiment with Kif4A and GFP-PRC1 and obtain the same results. This is expected because the rate of PRC1-Kif4A movement on single microtubules (500 nm/s), which leads to end-tag formation, is faster than the microtubule sliding velocity [Bieling, Telley, and Su, 2010; Subramanian, 2013]. Hence, we cannot measure sliding velocities at homogeneous Kif4A-PRC1 densities by this method. As such, experimentally decoupling end-tag formation and sliding is not feasible. [Note: since solution PRC1/Kif4A is washed out during the ATP exchange, the number of molecules in the overlap is reduced and the sliding velocity is much slower. It is therefore difficult to assess the over-lap-length dependence of sliding under these conditions.] As this experiment is nearly identical to the experiments in Figure 6 of the main text and does not provide additional mechanistic information, we have not included it in the revised manuscript. Instead, we have addressed the question of how velocities change during the end-tag formation through additional analyses of our data as described below.

Author response image 1

Download asset Open asset

Method:Biotinylated rhodamine-labeled microtubules were immobilized in a flow chamber.

0.2 nM un-labeled PRC1 in assay buffer was flushed into the flow chamber. Next, non-biotinylated microtubules were flushed in the flow cell and incubated for 10-15 mins to allow antiparallel overlap formation. Afterwards, 6 nM Kif4A-GFP and 2 mM ADP were flowed into the chamber. To visualize microtubule sliding, 2 mM ATP were flowed into the chamber in assay buffer and a time-lapse sequence of images was immediately acquired at a rate of 5 frames/s for 10-15 min.

https://doi.org/10.7554/eLife.32595.034

(A) Kymograph shows the relative sliding and stalling of antiparallel microtubules (red, microtubules; green, Kif4A-GFP). Assay condition: 0.2 nM PRC1 + 6 nM Kif4A-GFP + 2 mM ADP. Scale bar: x: 1 µm and y: 1 min. (B) Time record of the instantaneous sliding velocity of the moving microtubule derived from the kymograph in (A). The dashed lines demarcate the three phases observed in the sliding velocity profile: (i) constant phase, (ii) slow down and (iii) stalling. (C) Time record of the total overlap length (red; 𝐿_{𝑜𝑣𝑒𝑟𝑙𝑎𝑝}) derived from the kymograph in (A). (D) Total fluorescence intensity (dashed gray; 𝐼_{𝑜𝑣𝑒𝑟𝑙𝑎𝑝}), total fluorescence intensity in the untagged region of the overlap (solid purple; 𝐼_{𝑢𝑛𝑡𝑎𝑔𝑔𝑒𝑑}), and fluorescence density in the untagged region of the overlap (solid green; ρ_{𝑢𝑛𝑡𝑎𝑔𝑔𝑒𝑑}) derived from the kymograph in (A). (E-H) Another representative kymograph from this experiment. Panels E-H are equivalent to panels A-D. (I) Histogram of the average sliding velocity calculated from the constant velocity movement in phase-1. Assay condition: 0.2 nM PRC1 + 6 nM Kif4A-GFP + 2 mM ADP (mean:8 ± 5 nm/s; N=16).</Author response image 1 title/legend>

In order to address the question of whether either the sliding velocity in phase-1 or the transition from phase-1 to phase-2 is correlated with end-tag formation or length, we reexamined our data.

We examined if there was a correlation between end-tag length and average sliding velocity in phase-1. For this analysis, we calculated the end-tag length for phase-1 movement in two different ways (end-tag length at t = 0 and the time point before end-tags collide). No significant positive correlation was observed between end-tag length/intensity and sliding velocity (Figure 4—figure supplement 1A-B; correlation coefficients between -0.18 and -0.40). These results suggest that phase-1 sliding velocity is independent of the end-tag length, instead scales with the untagged overlap length (Figure 4—figure supplement 1D-E).

We analyzed individual events in which we could clearly observe an increase in end-tag length during sliding (the end-tag establishment phase; example: Figure 4—figure supplement 1G-I). We see no significant correlation between instantaneous velocity and increase in end-tag intensity during sliding in 10 events analyzed during phase-1 movement or at the transition from phase-1 to phase-2 (Author response image 2A-B, black arrows indicate phase-1 to -2 transition).

Together these analyses suggest that both phase-1 sliding velocity and the transition from phase-1 to phase-2 are independent of end-tag length (also discussed in response to comment #7).

Author response image 2

Download asset Open asset

Instantaneous sliding velocity versus moving end-tag intensity, 𝐼_𝐸𝑇2.

(A) Instantaneous sliding velocity versus moving end-tag intensity, 𝐼_𝐸𝑇2, plots from 16 kymographs (colored circles). (B) Zoomed-in view of three events in (A). The arrows indicate the phase 1-2 transition point.

https://doi.org/10.7554/eLife.32595.036

4) It is somewhat dissatisfying that there is no direct correlation of individual PRC1 and Kif4A complexes. What is the lifetime of the attachment of Kif4A to PRC1? Should one see it as 1:1 complexes that live forever, or is binding more intermittent and should the interaction be seen more as a collective effect (many PRC1s with each Kif4A, at a given moment or after each other)? This could e.g. have important consequences for the mechanism of action. Please discuss.

This is an excellent question and we think that it does impact the mechanism. The binding affinity between PRC1 and Kif4A is 0.3 μM. Consistent with this, we cannot isolate stable PRC1-Kif4A complexes using size-exclusion chromatography at sub-μM concentrations or observe single particles of the complex on an EM grid. Based on our previous structural data and preliminary chromatography results, the interaction appears to be stoichiometric (unpublished observations). Therefore, under our experimental conditions, PRC1 and Kif4A are not likely to act as stable complexes. However, prior work shows that the lifetime of Kif4A is increased on microtubules in the presence of PRC1 [Bieling, Telley and Surrey, 2010; Subramanian et al., 2013]. This suggests that while the inherent affinity between PRC1 and Kif4A is not high and the estimated dissociation rate is on the order of a few seconds, the localization of these proteins to microtubules results in high rates of re-association. Together, these observations suggest that the interaction between these proteins is best described as a series of dissociation and re-association events of Kif4A with the same or neighboring PRC1 molecule (note: similar to the proposal in Ref. Bieling, Telley and Surrey, 2010).

This result has an important consequence and we briefly mentioned it in the Discussion section of the original submission. We now state it more clearly in the revised submission. Briefly, if PRC1 and Kif4A form a stable high-affinity complex then it would essentially function as single crosslinking molecule where motor stepping is tightly coupled to sliding. Instead, in this system, because of dissociation, every step by the motor may not lead to a corresponding movement of the transport microtubule. The increased decoupling will result in increased dependence of microtubule sliding velocity on motor number. Essentially, even though Kif4A is a high duty ratio motor with respect to its stepping behavior on single microtubules, the PRC1-Kif4A complex may act as a low duty ratio complex with respect to microtubule sliding due to the decoupling of motor stepping from microtubule sliding.

5) KIF4 interacts with PRC1 via its C-terminal tail domain. However, the same domain also has a microtubule-binding activity independent of PRC1 (Bieling, 2010, Figure S4). Although it is unclear how strong this interaction is, considering that both the interactions between PRC1 and KIF4 and between PRC1 and unbundled microtubules are weak (Kd ~0.3 μm (Subramanian, 2013) and ~0.6 μm (Bieling, 2010), respectively), it is possible that the KIF4 tail-microtubule interaction might also play an important role in the authors' experimental system. Please perform control experiments and/or discuss.

In the previous reported work [Bieling, Telley and Surrey, 2010], it is stated that full-length Xenopus Laevis Kif4 did not mediate microtubule bundling in ATP (bundling was only observed with AMPPNP). Similarly, we are also unable to establish aligned bundles with Kif4A in the presence of 1 mM ATP. We see end-tags forming on microtubules but these do not form antiparallel bundles. It is difficult to interpret the microtubule-binding activity of the C-terminus of Kif4A from indirect bundling experiments at high motor concentrations (especially under tight binding conditions such as in the presence of AMPPNP). Therefore, we directly examined microtubule binding by the C-terminus of Kif4A using co-sedimentation assays (Figure 2A).

We expressed and purified a construct (aa 733-1232) that comprises of the globular C-terminus domain of Kif4A (‘tail’; aa 1000-1232) and the coiled coil stalk (aa 732-999; note: we were unable to purify a longer construct due to problems with protein aggregation). This construct contains both the PRC1 and the DNA binding domains of Kif4A, and the globular tail domain is an attractive candidate as a microtubule-binding domain based on the presence of similar domains in other kinesins. However, our results show negligible sedimentation of this construct (< 5%) even in the presence of 8 μM tubulin (Figure 2A). Therefore, it is unlikely that Kif4A molecules crosslink microtubules using the C-terminus domain.

To examine alternative mechanisms of crosslinking by Kif4A, we bound Kif4A-GFP to immobilized microtubules at low ATP concentrations (10 nM). Under these conditions, we do not see end-tag formation and the protein is bound all along the microtubules. However, we observe a few pairs of microtubules interacting at random orientations. We then flow in 1 mM ATP and Kif4A-GFP, which result in end-tag formation on both microtubules. If the end-tag on the nonbiotinylated microtubule can contact the immobilized microtubule, it results in tip-mediated gliding of one microtubule over the other. Interestingly, the angle of attachment is usually low (0-30 degrees), and the movement halts when the end-tags collide (Figure 2C-E). We see no dependence of sliding velocity on Kif4A end-tag intensity (Figure 4—figure supplement 1Q). This result is consistent with our analyses for end-tag intensity versus sliding velocity in the PRC1Kif4A experiments in Figure 4—figure supplement 1A.

These findings indicate that the Kif4A-dense microtubule tip can slide along another microtubule even though the C-terminus of Kif4A does not bind microtubules. How might this be possible? Previous EM studies have shown that under crowded conditions, kinesins adopt a one-head bound conformation [Hirose et al., 2000; Hoenger et al., 2000]. Therefore, it is possible that the end-tags have an array of detached motor domains particularly at the very tip, and the collective activity of single heads could drive microtubule movement. Alternatively, it is possible that at the crowded tip, Kif4A molecules could oligomerize to form tetramers – however, even when concentrated to >5 μM, Kif4A does not elute as oligomers in size exclusion chromatography. We therefore favor the first model at this time. Interestingly, a similar mechanism of aster formation by dynein-dynactin has been suggested recently [Tan et al., 2018].

Currently, it remains unclear if in aligned antiparallel bundles (180 degrees), Kif4A molecules at the end-tags can similarly contribute to sliding. Regardless, based on analyses of sliding velocity as a function of end-tag intensity in both the Kif4A and the PRC1+Kif4A experiments (Figure 4—figure supplement 1A and 1Q), it is clear that movement driven by end-tagged motors does not significantly contribute to the initial overlap length dependent anti-parallel sliding that we see in our PRC1-Kif4A experiments.

We have added these new results to the main text and discussion (Figure 2) (Also see comment #6).

6) The relatively low affinity between KIF4 and PRC1 (~0.3 μM, cf. Kd~8 nM between PRC1 and anti-parallel microtubule bundle) raises the question of what percentages of KIF4 and PRC1 in the tagged and untagged overlaps are in the complex. This might not be important if there is no productive force generation by KIF4 molecules not complexed with PRC1. However, considering the presence of the second microtubule-binding site of the KIF4 tail (see above), it is important to clarify the states of the PRC1-KIF4 complex formation. Reduction of the sliding velocity by increased PRC1 and the reversal by additional KIF4A is consistent with a picture that PRC1 holds the anti-parallel overlap of MTs and KIF4A, which is not in a complex with PRC1, slides them. Please discuss.

We thank the reviewers for raising this interesting point. There are three possible sets of molecules bound to microtubules under these experimental conditions – PRC1 dimer, Kif4A dimer and PRC1-Kif4A complex. Here, we discuss the distribution of these molecules at the untagged and end-tagged regions of the antiparallel overlap.

At the untagged overlap: As discussed above, we find that the C-terminus tail of Kif4A does not directly bind microtubules (Figure 2). We have no evidence that Kif4A oligomerizes to drive sliding (both from gel-filtration as well as the inability to form microtubule bundles with Kif4A alone in ATP). So, the molecules within the untagged region of the antiparallel overlap that are responsible for sliding are likely to be PRC1-Kif4A complexes. However, as noted by the reviewer, the K_d for the PRC1-Kif4A affinity is 0.3 μM. Consistent with this, we have not been able to isolate stable PRC1-Kif4A complexes by gel filtration or visualize complexes by single-particle EM. However, PRC1-Kif4A complexes have a longer microtubule lifetime than either protein alone. Together, these data suggest that the complexes are undergoing dynamic dissociation and re-association on the microtubule lattice. When we increase Kif4A concentration, more PRC1 molecules will be in a sliding-competent complex and contribute to sliding. The cross-bridging and sliding by the dynamic complex is likely to play a key role in the observed length-dependent end-tagging observed in our experiments by further decoupling motor stepping from microtubule sliding (these points have been added to the Discussion section and Appendix sections of the main text).

At the end-tagged regions of the overlap: Analysis of fluorescence intensities suggests that at the time point when the transition to final overlap occurs, there is a 5-fold excess of Kif4A over PRC1 at end-tags. So, the end-tags are likely to be a mixture of PRC1-Kif4A complexes and Kif4A alone.

Our experiments suggest that end-tags composed of Kif4A alone can drive relative microtubule movement [Figures 2C-D]. Since end-tags are highly crowded regions of slowly dissociating protein, it may lead to a fraction of kinesins to adopt a one-head bound state (as is seen in EM experiments performed at high concentrations of kinesin dimers [Luduena, 2013; Yu, Garnham and Roll-Mecak, 2015]). In addition, the molecules at the very tip of the microtubule may also be predominantly in a one-head bound conformation. We propose that one-head bound kinesins can collectively drive end-on attachment and sliding of one microtubule over another. This is similar to a recent proposal for dynein driven relative-microtubule sliding to form minus-end asters [Gadadhar et al., 2017]. Interestingly, the association angle between two microtubules is observed to be low in these experiments. Whether motors at end-tags contribute to sliding in a PRC1 crosslinked antiparallel bundle (180 degrees) is unclear (and difficult to untangle given that the sliding and end-tag formation are linked phenomena).

Can such a mechanism also drive length-dependent sliding in the non-end-tagged overlap? We think this is unlikely for three reasons. First, in our control Kif4A experiments, sliding velocity is independent of the amount of protein at microtubule ends. Second, in the Kif4A experiments, we are unable to form aligned antiparallel bundles at both low and high ATP conditions. This result indicates that Kif4A does not cross-bridge microtubule in the canonical manner. Third, PRC1 crosslinks span an inter-microtubule distance that is in the 35 nm range. The likelihood of two kinesin motor domains connected by a 12 aa long neck-linker spanning that distance is unlikely.

For these reasons, we propose that in the untagged overlap, a cross-bridging PRC1-Kif4A complex drives sliding, whereas in the end-tagged region, sliding may be mediated by the collective action of single motor heads at the microtubule end/tip. However, the scaling of sliding velocity with overlap length only arises from molecules in the untagged overlap. We have now revised our mechanism figure (Figure 8) to reflect the new data.

7) Which fraction of KIF4-PRC1 is driving the sliding and what is causing the slow-down (during the phase-2). Is the decrease of velocity in phase-2 due to the decrease in the number of "untagged" KIF4-PRC1 or an increase in their density? Does friction play any role? Please discuss.

There are two fractions of molecules that can drive sliding: (i) crosslinking PRC1-Ki4A complexes and (ii) Kif4A molecules at the end-tag. However, our data suggest that the microtubule overlap length-dependent sliding only arises from sliding by molecules in the untagged overlap (Figure 4—figure supplement 1D-E).

As previously discussed (response to comment #2), our data suggest that the slowdown is likely due to an increase in density close to end-tags. The transition from sliding to stalling coincides with the end-tags on the moving and immobilized microtubules arriving at close proximity. At this high-density region, microtubule sliding would first slow down before complete stall is reached (Figures 4E-F). We noticed that in ~50% of the events (47/98; 0.2 nM PRC1 + 6 nM Kif4A-GFP), the transition from phase 1 to 2 occurs when the end-tags have nearly merged and our image analysis algorithm does not resolve the two end-tags (example: see kymograph in Figure 4E). We reasoned that if high protein concentration proximal to end-tags is the reason for slow-down, the protein density at the phase-1 to phase-2 transition should be similar under different experimental conditions. Kif4A-GFP density measurement and fluorescence line-scan analysis at the phase-1 to phase-2 transition time-points in two experimental conditions show that this is indeed the case (Figure 4—figure supplement 4A). Furthermore, comparison of the phase-1 to phase-2 transition-point intensity with the average end-tag intensity suggests that on average slowdown occurs when the intensity is >70% of the average end-tag (Figure 4—figure supplement 4B-C). These observations suggest that sliding slows down proximal to end-tags, when the untagged overlap is short and the motors encounter a high-density region, where stepping is inhibited.

While we cannot completely rule out the contribution of friction to the reduction in sliding velocity, the following lines of evidence suggests that it is unlikely to significantly impact the movement velocity in this system. First, previous measurements of frictional forces generated by PRC1 show that the magnitude of these forces is low [Forth et al., 2014]. Second, PRC1 increases processivity without decreasing Kif4A movement velocity suggesting that the drag forces generated by PRC1 are low [Bieling, Telley and Surrey, 2010]. Third, under these conditions, the total number of PRC1 molecules is less than the number of Kif4A molecules in the overlap (Figure 8—figure supplement 1), further arguing against frictional forces being the predominant reason for slow-down.

We have now included these points in the main text.

8) The description of the result from subsection “Characterization of relative microtubule sliding in the PRC1-Kif4A system” (density and intensity of Kif4A in the different overlap regions) is not very clear. What is meant with "retained"? What is meant by the final sentence of this part? Are these statements based on only two example kymographs (Figure 3E and Supplementary figure 1C-L). For Figure 3H it appears that the overlap keeps on increasing until the end of the experiment (unlike the event in sup 1C-L). Please explain more clearly.

Our word choice of ‘retained’was inspired by work from Stefan Diez’s group. However, we realize that this may be a confusing term in our paper and have removed it from the text.

We have analyzed more kymographs and included a panel of examples and quantification (Figure 4—figure supplement 2). These kymographs are representative of the data and the increase in density with overlap shrinkage is observed in all events we have analyzed. The initial increase in overlap intensity represents the equilibrium establishment phase. In Figure 4E in the current manuscript (Figure 3H in the previous submitted manuscript), the time is longer for 𝐼_{𝑜𝑣𝑒𝑟𝑙𝑎𝑝} to reach equilibrium for that particular kymograph. We have now also analyzed equilibrium data when 𝐼_{𝑜𝑣𝑒𝑟𝑙𝑎𝑝} is constant and these data also show scaling of sliding velocity with initial overlap length (Figure 4—figure supplement 3).

9) To what extend is the analysis of the end tag lengths (Figure 4AB) affected by the diffraction limited imaging used? How different are the end-tagging lengths on single microtubules and in microtubule overlaps? Please discuss.

We cannot make reliable length measurements when the end-tags are short (< 5 pixels) but we can measure intensity more accurately at these length scales. It is known that end-tag length and intensity are tightly correlated parameters [Subramanian et al., 2013]. Therefore, we have included both length and intensity data for all analyses requiring quantification of end-tags (Figure 4—figure supplement 1A-B). The method for measuring the end-tag lengths and intensity are in Materials and methods section.

10) In their theoretical model, the authors implicitly assume that one of the two PRC1 ends that binds the same microtubule with the one that KIF4 interacts with (i.e. the bottom one in Appendix Figure 1A) doesn't interfere with the MT sliding. It is not clear how this is justified. It would be more natural that one end of a PRC1 dimer (upper one in Appendix Figure 1A) works as a supporting point for productive sliding while the other end (bottom one) works as a drag against the stepping of KIF4. Please discuss and resolve the issue.

While PRC1 increases processivity of Kif4A, it does not alter motor velocity on single microtubules [Bieling, Telley and Surrey, 2010]. We have also previously observed that Kif4A movement proceeds at high velocities in the presence of PRC1 except at end-tags where motor stepping is inhibited (supplement in [Subramanian et al., 2013]). Further, it has been shown that the frictional force associated with PRC1microtubule interaction is ~2 orders of magnitude less than the typical forces generated by kinesin [Forth et al., 2014]. These observations are the basis for our assumption that the spectrin domain of PRC1 that shares the microtubule with the Kif4A motor domains does not generate significant drag force.

Cryo-EM structural analysis has shown that PRC1 and kinesin have partially overlapping tubulin-binding interface [Kellog et al., 2016]. This result suggests that at high-density PRC1 may sterically impede kinesin movement, as is observed at end-tags on single microtubules [Subramanian at el., 2013]. This is also consistent with our analysis of protein density and intensity at the phase-1 to -2 transition point (Figure 4—figure supplement 4 and response to comment #7). Therefore, while we cannot completely rule out the effects of frictional forces, we propose that steric hindrance to stepping is likely to be the predominant mechanism of slow-down and stall in the PRC1-Kif4A system.

We have modified the text in the Appendix clarifying these points and also revised the schematic that makes our theoretical model assumptions clear.

11) On one hand, modeling the PRC1-MT interaction as a slipping tether using the formulation by Grover et al., is an excellent idea. However, the model presented by the authors is not properly describing their experimental conditions. Their model is for a different situation in which KIF4 is tethered on the PRC1 bridging two microtubules (one of them is immobilized) and it drives the sliding of the third, non-immobilized microtubule. Thus, it is not surprising that there is a big inconsistency between the model calculation and the experimental measurements in the order of the sliding velocity. Please resolve.

We apologize for the lack of clarity. In our experiments (except Figure 7) we only examine pairs of microtubules and our model is describing the same molecular configuration (revised Figure 1 of the Appendix) where Kif4A is linked to the PRC1 molecule bridging two microtubules (one of them is immobilized and the other is the moving microtubule; we show just one protofilament of each microtubule to simplify the schematic). Our goal was to determine if modeling the PRC1-MT interaction as a slipping tether using the formulation by Grover et al., could give rise to overlap length-dependent sliding. We find that even this simple model can recapitulate length dependent sliding with velocities that are roughly in the same range as in our experiments. While other factors, such as steric hindrance, occupancy, and PRC1-Kif4A dissociation and reassociation kinetics will impact the magnitude of the sliding velocity and the extent to which velocity scales with overlap length, the minimal mechanism is sufficient to recapitulate the overall trend observed in our experiments. We therefore propose that this is a possible mechanism for initial overlap-length dependent sliding that is consistent with our experimental observations.

12) On the other hand: Is it really warranted to use a similar model to diffusion (and drag) in a membrane for diffusion of the PRC1 complexes over the MT? PRC1 binds to the MT, most likely with 8 nm periodicity, with relatively large barriers / wells; in the membrane stuff is much more continuous. Would in the current situation such a view not be too simplistic, e.g. not taking into account 'non-linear' / 'out-of-equilibrium' effects due to motor action (i.e. increased loads on the motor which could result in changes in motor action (velocity, release) including a non-linear scaling of friction with motor number (see Lansky et al., 2015).

We agree that the model we consider here is a simple and minimal one. However, the main purpose of the computational work was to determine if modeling the PRC1-MT interaction as a slipping tether could give rise to initial microtubule overlap length-dependent sliding (phase-1) as observed in our experiments. This is especially interesting as current models for reduction of sliding velocity in shrinking overlaps (e.g. Ase1-Ncd and HSET systems) do not apply to the PRC1-Kif4A module [also discussed in response to summary and comments #2].

Currently, we do not have experimental data to model other details of the mechanism. For example, the microtubule binding interactions of PRC1 are mediated by its spectrin domain and an unstructured C-terminus domain (~150 aa) with three stretches of positively charged residues. It is proposed that the unstructured domain in PRC1 interacts with the negatively charged and unstructured ‘tail’ of tubulin. However, the distances over which they interact, periodicity and barriers, occupancy and how these are altered when PRC1 is in a complex with Kif4A are all unknown. Similarly, there are no force measurements that have been performed on this system yet (note: non-linear scaling of frictional forces if present in this system can reduce the magnitude of the sliding velocity but it cannot give rise to the scaling of sliding velocity with overlap as observed in our experiments, which is the focus of this modeling effort). We think that in the future more extensive modeling together with biophysical measurements will reveal other aspects of this system, but they are beyond the scope of this manuscript.

In addition, while certain details of the molecular interactions in this system are unknown, there are some aspects that are known and feed into the model. These include low frictional drag forces generated by PRC1, lack of entropic forces of significant magnitude in this system, diffusive nature of PRC1 interaction, and the moderate PRC1-Kif4A binding affinity. While we only model diffusive tether as the decoupling mechanism (since we have the most experimental data to support this model), there are likely to be others such as dissociation of the PRC1-Kif4A complex that reduce the coupling between motor stepping and microtubule sliding. However, even this minimal model captures the trend and magnitude of scaling observed in our experiments.

13) According to the authors' formula in the Appendix, 𝑣_MT is hyperbolic against a dimensionless value x=a∙d∙l/L_MT ("Michaels-Menten" type, passing origin and approaching max value = 𝑣_step). A characteristic parameter is f∙δ, which corresponds to x which gives a half maximal 𝑣_MT (equivalent to K_M for "Michaels-Menten"). In a regime where x is below this, the 𝑣_MT~ x relationship becomes nearly linear. However, calculations with the values in Table A1 result in f∙δ = 1.72 x 10^-5. This is too small, and it is impossible to make x smaller than this by any realistic combinations of a, d, l and L_MT. In other words, 𝑣_MT is almost equal to 𝑣_step irrespective of l, the lengths of overlap. Please explain how the curves in Appendix Figure 1 were drawn. The actual values of a, d and D used should be presented.

In our theoretical model calculations to produce Appendix Figure 1 𝑘_𝐵𝑇 was converted to units of N∙m units from units of J which is 𝑘_𝐵𝑇~ 4 pN∙nm. The 𝑘_𝐵 value in the Table A1 is in units of J/K. We apologize for the confusion this caused. We have replaced this 𝑘_𝐵 value with consistent units in Table A1. In Appendix Figure 1, the actual values of 𝐿_𝑀𝑇, 𝑎, 𝑑, and 𝐷 are the following:

Figure 1B: for 𝐿_𝑀𝑇 = 2, 4, and 6 μm: 𝑎 = 40%; 𝑑 = 13; and 𝐷 = 2000 nm²/s

Figure 1C; 𝐷 = 200 and 2000 nm²/s: 𝐿_𝑀𝑇 = 6 μm; 𝑎 = 40%; and 𝑑 = 13

Figure 1D; 𝑎 = 10 and 40%: 𝐿_𝑀𝑇 = 6 μm; 𝑑 = 13 and 𝐷 = 2000 nm²/s

These values have also been updated in the legend of Appendix Figure 1 for each subplot.

14) The modeling should be connected closer to the experiments. For example, a∙d is essentially the line density of PRC1-KIF4A in the overlap and thus should be measurable. Then, the actual D should be able to be determined with actual x and 𝑣_𝑀𝑇 measurements using the authors' formula and can be compared with reported values. Moreover, it would be helpful to indicate what trends (and numbers) belong to the experimentally tested parameter space. The simulations (at least their results) should be discussed more prominently in the main text /Discussion section. Please add this information.

We thank the reviewers for raising this point. We have extracted 𝑎 ∙ 𝑑 from the untagged overlap density (intensity/length) from our experimental data. Using the 𝑣_𝑀𝑇 and x values, and the formula from Appendix, Eq. 5, the 𝐷 value is determined to be ~2000 nm²/s (N = 10; 0.2 nM GFPPRC1 + 6 nM Kif4A). In comparison to reported values, our 𝐷 value is consistent with Bieling et al., (𝐷 = 2900 nm²/s) for PRC1 within microtubule overlaps.

Our modeling qualitatively recapitulates the extent of scaling of sliding velocity with initial overlap length (Appendix Figure 1; note: magnitudes are in the experimental range assuming values for occupancy, which we cannot determine from our intensity data as discussed in response #1). The model predicts that the scaling of sliding velocity with initial overlap length depends strongly on motor occupancy and PRC1-diffusivity, and weakly on MT length. Consistent with these trends, our experimental data (Appendix Figure 1; gray circles; 0.2 nM PRC1 + 6 nM Kif4A-GFP), show a weak dependence of the length of the moving microtubule and a stronger dependence of sliding velocity on initial overlap length at higher Kif4A-PRC1 ratios where we would expect a greater percent of complexes in the overlap contributing to sliding (Figure 4A-B).

We have added a discussion of the modeling results to the main text. Since the Appendix will immediately follow the main text in the final publication, we prefer to leave the details of the modeling out of the Discussion section.

15) Biological significance: It is unclear whether the situations studied in this work actually occur in the cell. Although the end-tagging of astral microtubules near spindle poles by PRC1 was demonstrated in Subramanian et al., 2013, it remains unclear whether KIF4A takes part in these tags. Even so, it is unclear whether there is a cellular situation in which microtubules are first tagged (and stabilized) with PRC1 and KIF4A and then bundled. In general, PRC1 localizes on the metaphase spindle although weakly and diffusely while KIF4 is associated with chromosomes before anaphase onset. PRC1 can form midzone bundles without KIF4. Please discuss.

In recent years, the multiple biochemical activities that a single kinesin can perform has been revealed through in vitro characterization of the motor. For example, Kip3p, best known as a regulator of microtubule dynamics was shown to crosslink and slide microtubules to organize microtubule arrays [Su et al., 2013]. Similarly, Eg5, which is best known for crosslinking and sliding, has recently been shown to also regulate microtubule dynamics [Chen and Hancock, 2015]. The role of the PRC1-Kif4A module in regulating microtubule dynamics was first revealed through beautiful reconstitution studies from the Surrey lab [Bieling, Telley and Surrey, 2010]. However, while microtubule sliding was also briefly mentioned in their paper, this activity remains completely uncharacterized. The goal of this study is to address this poorly understood aspect of PRC1-Kif4A function. To test whether sliding contributes to midzone length control, we would need a Kif4A mutant that retains PRC1 binding and sliding and only perturbs microtubule dynamics. Unfortunately, there is currently little understanding of how Kif4A regulates microtubule dynamics at a structural level. The structural investigation and cell biological assays are beyond the scope of this work.

While we do not know if microtubule sliding by Kif4A contributes to the midzone organization, several properties of this system are relevant to cell biological scenarios both during mitosis in eukaryotes and in interphase cells of yeast and plant cells. For example, kinesin accumulation at microtubule ends is observed for several motors [Subramanian et al., 2013; Su et al., 2013; Varga et al., 2006; Leduc et al., 2012; Vitre et al., 2014]. While we only looked at PRC1 localization in monopolar and bipolar spindles, a recent work from Tim Mitchison’s group shows that both PRC1 and Kif4A molecules are at the plus ends of asters in Xenopus egg extracts [Nguyen, Field and Mitchison, 2018]. The ends of microtubules are difficult to image in the midzone of a human cell. However, work from Ted Salmon’s group suggests that when the midzone assembly is perturbed, end-tags are observed even in the central microtubule bundle [Shannon et al., 2005]. This suggests that transport and end-accumulation may be features of the midzone and perhaps contribute to the stability and close alignment of microtubule plus-ends in this antiparallel microtubule array.

Whether sliding of PRC1-crosslinked microtubules contributes to the midzone organization in mammalian cells remains unknown at this time. Recent work from Iva Tolic’s group shows that sliding of PRC1-crosslinked interkinetochore bridges contributes to chromosome segregation in anaphase [Vukusic et al., 2017]. At least one of the motors involved in central spindlin, which also interacts with PRC1. Further, yeast, mammalian and plant cells all have PRC1-crosslinked microtubule arrays that have associated motors with proposed sliding activities [Subramanian and Kapoor, 2012]. Initial overlap length-dependent sliding could be advantageous in ensuring that microtubules of different lengths arrive at similar rates to the plus-ends of the template microtubule within arrays. Therefore, the features uncovered here are likely to inform our models of how the collective activities of these proteins regulate the organization of various cellular microtubule arrays.

Finally, the reconstitution described here, examining microtubule sliding by a pair of interacting motor and non-motor crosslinking protein, reveals unique emergent properties that have not been reported previously. We expect that these findings will inform future models of microtubule self-organization.

We have now added some of the key points from this response to the Discussion section of the main text.

[Editors' note: further revisions were requested prior to acceptance, as described below.]

The involved editors as well as the reviewers acknowledge that you did a great job of seriously considering the earlier comments, including the performance of additional experiments. The conclusions are now much more solid and the context with previous studies and other systems is discussed much more clearly, highlighting why this study is important and exciting. The manuscript has tremendously gained by the revision and it is felt that the work in general is very well suited for eLife.

However, there are some remaining issues that need to be addressed before your manuscript can possibly be accepted for publication:

1) Please have a look at the following (conclusion of the Figure 4, subsection “Examining the time-dependent changes during microtubule sliding in the PRC1-Kif4A system”): "…velocity of microtubule sliding.… is determined by.…. the total number of sliding competent molecules in the untagged overlap." Velocity increases with increasing (untagged) motor number (Figure 4A-D) and "The microtubule movement can subsequently proceed at a *constant velocity*, even when the overlap shrinks,…" (i.e. when the untagged *motor number decreases* – phase 1 in the Figure 4F and Figure 4—figure supplement 2) "…possibly through increasing the density of motor molecules during relative sliding." This would mean that increasing the motor density should compensate for decreasing the motor number to keep the velocity constant. That is, velocity should increase with increasing motor density.

However: (i) How an increased motor density would result in an increased sliding velocity is intriguing and the authors should probably comment on this. (ii) In contradiction with their statement, the authors show that (at least in some concentration regime) this is not the case (Figure 4—figure supplement 1F).

We realize that this statement in the text: "…possibly through increasing the density of motor molecules during relative sliding", may be confusing and we have re-written this subsection “Examining the time-dependent changes during microtubule sliding in the PRC1-Kif4A system”.

Our data show that under a given experimental condition, sliding velocity scales with initial overlap length and intensity. Thus, sliding velocity scales with motor number in the initial overlap. This suggests that for overlaps of the same initial length, increasing the motor density will increase the total number of sliding-competent motors, which in turn should result in higher sliding velocity. In Figure 4—figure supplement 1F, we are plotting the average density during phase-1 movement from events that have different initial overlap lengths. We do not have sufficient events that have the same initial overlap length but different densities under the same experimental condition to perform a correlation analysis.

As an alternative, we re-examined events from the data shown in Figure 3—figure supplement 1, where we plot the average sliding velocity in experiments with 1 nM GFP-PRC1 + 6 nM Kif4A and 1 nM GFP-PRC1 + 12 nM Kif4A. We expect that the density of Kif4A will be greater at the higher motor concentration. We replotted the sliding velocity (phase-1) at comparable initial overlap lengths under these two conditions and find that the sliding velocity is higher at 12 nM Kif4A concentration (Author response image 3A). Intensity analysis of GFP-PRC1 shows that the increase in sliding velocity at 12 nM Kif4A is not due to a decrease in the density of PRC1 molecules at the antiparallel overlap under these conditions (Author response image 3B).

These data suggest that at comparable initial overlap length and comparable PRC1 levels, increasing the Kif4A concentration, which would increase the total number of motor molecules in the initial overlap (and consequently the density in overlaps of similar lengths), results in an increase in sliding velocity.

Author response image 3

Download asset Open asset

Sliding velocity as a function of initial overlap length and untagged overlap density.

A) Sliding velocity as a function of initial overlap length for two bin sizes. Assay condition: 1 nM GFP-PRC1 + 6 nM Kif4A (gray; 500-1500 nm: N = 13, 1500-2500 nm: N = 18) and 1 nM GFP-PRC1 + 12 nM Kif4A (blue; 500-1500 nm: N = 13, 1500-2500 nm: N = 9) B) Histogram of the untagged overlap density of GFP-PRC1. Assay condition: 1 nM GFP-PRC1 + 6 nM Kif4A (gray; N = 38) and 1 nM GFP-PRC1 + 12 nM Kif4A (blue; N = 18).

https://doi.org/10.7554/eLife.32595.037

2) Connected to (1): An essential statement of the paper is that the sliding velocity scales with the initial overlap length. However, Figure 4E-H shows that the sliding velocity stays constant for a shrinking overlap lengths (called phase 1). How is the "initial overlap length" defined here? What means "initial"? Most surprisingly, the overlap intensity increases during this phase. How is that explained? Is there equilibrium in binding achieved before?

In the PRC1-Kif4A experiments connected to Figure 1 of the manuscript, we first set up pairs of PRC1-crosslinked antiparallel microtubules as described in the methods. We then initiate sliding by flowing in a mixture of PRC1, Kif4A and ATP. The initial overlap length is defined as the microtubule overlap length at the first time-point we acquire (𝑡 = 0; example first panel in Figure 1B). We have now emphasized the definition of “initial overlap length” in the text and Materials and methods section, subsection “Image Analysis”).

The initial increase in intensity (note: the intensity reflects both the crosslinking motors that contribute to sliding and passenger molecules that do not contribute to sliding) is due to the establishment of chemical equilibrium and this is observed in all the events we have looked at. As described in our previous response to reviewers (#8) and the submitted revision, we re-analyzed a subset of events in which we could measure sliding velocity in phase-1 after equilibrium is established (i.e. total overlap intensity levels are constant; I_overlap). The results are identical to our findings from analyzing the complete time course of phase-1 (Figure 4—figure supplement 3).

3) With regard to the interaction between the C-terminal tail of KIF4A and microtubules it is stated that the interaction between the KIF4A tail and microtubules are not strong. However, the PAGE image in Figure 2 clearly shows there is some interaction between them. The signals of the bands that correspond to KIF4A (but don't appear in 'PRC1' lanes) in the precipitates (KIF4A(C-term) 'P') increase with the increasing amount of microtubules. This indicates a weak but significant interaction between KIF4A C-tail and microtubules. The authors' statements such as "We observed no significant microtubule-association of this domain" (subsection “Molecular determinants of the sliding and cross-bridging in the PRC1-Kif4A system”) or "the C-terminus of Kif4A does not directly bind microtubules" are thus not true.

This interaction is indeed 'very' weak as a MAP. The dissociation constant might be at the orders of 100 µM or 1 mM. However, it should be kept in mind that this domain is not floating alone in solution but is part of a kinesin-like motor protein, which strongly accumulates at the plus-ends of microtubules. The local concentration of the domain can be the order of 1~10 mM, which seems to be comparable with the weak but significant interaction detected in Figure 2A.

Similarly, hydrodynamics data at the protein concentration of 5 µM might not be strong enough to exclude the possibility that Kif4A might form oligomers at the crowded condition. The second (very weak) binding site on the C-terminal tail or oligomerization seems to be more plausible as an explanation of the MT-sliding by Kif4A alone. At least the data are not strong enough to exclude these possibilities. Please discuss all of the above.

We have quantified the SDS-PAGE gels from the co-sedimentation experiments. The data does not show tubulin concentration dependent binding (Author response image 4; black and orange data points), and therefore we cannot conclude that the C-terminus of Kif4A is a bona-fide microtubule-binding domain from our data. In our experience, most proteins, including BSA, pellet at high concentrations of microtubules to some extent depending on the pH and ionic strength of the assay (Author response image 4; purple and red data points). These quantifications are now included in the figure legend of Figure 2 of the main text. However, we agree with the reviewer that we cannot rule out that this domain is an extremely weak MAP with K_d on the order of 100 µM-1 mM. Whether such low affinity interactions can sustain sliding (due to the high off-rates of the motor from the protofilament) when the motor is concentrated at the microtubule end is currently unknown. Furthermore, the C-terminus of Kif4A also binds PRC1 (K_d = 0.3 μM). Therefore, it is possible that the interaction between the Kif4A-C term and microtubules, if it does occur, is further reduced in the presence of PRC1. We agree with the reviewers that we cannot completely exclude the possibility that some small fraction of motors may form sliding-competent oligomers at the ends of microtubules due to high local concentrations. However, this is not easily to test experimentally.

Overall, the molecular mechanism of Kif4A-end-tag mediated sliding, whether it is through weak Kif4A-Kif4A oligomerization or low-affinity Kif4A-microtubule interaction or through single unattached motor domains at the highly dense end-tags, appears to be different from other crosslinking kinesins. We have revised the text to mention these additional possibilities (subsection “Mechanism of overlap-length dependent sliding by PRC1 and Kif4A”). However, since end-tags alone are not sufficient to generate overlap length-dependent sliding in the PRC1-Kif4A experiments (also see response #6), the specific mechanism by which Kif4A end-tags drive sliding in the absence of PRC1 does not impact the main conclusions from this study and will be examined in the future.

Author response image 4

Download asset Open asset

Quantitative analysis of SDS-PAGE gels from two co-sedimentation assays.

The percentage of Kif4A (black and orange) and BSA (red and purple) in the pellet is plotted against tubulin concentration. The curves labeled bound-1 are connected to the gel in Figure 2 of the main text. Inset: Zoomed-in view of the plot.

https://doi.org/10.7554/eLife.32595.038

4) The response to comment 13 is unsatisfactory. The difference of units doesn't matter if the calculation is performed with physical quantities (numbers + units).

The characteristic parameter (the initial overlap that gives the half maximum velocity, analogous of K_M in the Michaelis-Menten kinetics, here called λ) λ should be at the order of µm or bigger. However, when repeating the calculation with the values provided in the revision, the λ is calculated to be at the order of picometer. Thus, what the authors' theory predicts is that the sliding velocity is independent of the initial overlap length. The theoretical curves in Appendix Figure 1 appear inconsistent with the authors' theory and the parameters provided. Please check.

5) In the calculation, d = 13 and a = 0.4 is assumed – meaning that there should be about 600 molecules active in a 1 micron long MT overlap? Is that a reasonable assumption? Can't an upper bound of the motor number be (roughly) estimated from the fluorescence intensity?

We are extremely thankful to the reviewers for discovering this error during the peer review process. We discovered that there was a mistake (in converting units) when extracting the diffusion constant as described in the Appendix of the manuscript. A summary of new analyses and outcomes is as follows.

(1) The recalculated diffusion constant is 9x10⁷ – 3x10⁸ nm²/s (for 1-8% protein occupancy estimated from experimental data; see below). These values are ~10⁵ fold greater than the reported diffusion constant of PRC1 within antiparallel overlaps (2900 nm²/s; Bieling et al., 2010). As pointed out in comment # 4, the published values do not quantitatively explain the overlap-length dependent rate of sliding observed in our experiments. Therefore, we need to consider mechanisms other than diffusive anchorage of PRC1 that can decouple motor stepping from microtubule sliding. At the molecular level, we can imagine at least two other possibilities: (i) dissociation of the PRC1-Kif4A complex within overlaps and (ii) increased dissociation rate of PRC1 from the moving microtubule due to motor stepping. However, we feel that determining the precise molecular mechanism by which motor stepping is decoupled from microtubule sliding is beyond the scope of this paper.

Based on the above findings, we took a step back and decided to estimate the duty ratio of the PRC1-Kif4A molecules instead of assuming specific mechanisms. These calculations, which are summarized in Author response image 5A, provide an approximate estimate of the duty ratio (approximate because (a) we do not reach saturation sliding velocity in our experiments and (b) we are estimating number of sliding-competent molecules from fluorescence data (now calculated experimentally – see next point)). We find that the estimated values of duty ratio are less than 1, and in the same range as those published for myosin [Uyeda, Kron and Spudich, 1990], β dynein [Imafuku, Toyoshima and Tawada, 1997], 22S dynein [Hamasaki et al., 1995], and NcKin3 [Adio et al., 2006], which exhibit filament length/motor-number-dependent movement velocities. This suggests to us that while the precise molecular mechanism underlying the scaling of sliding velocities with initial microtubule overlap-length is currently unknown, it is reasonable to think about microtubule sliding by the PRC1-Kif4A complex as microtubule movement driven by an ensemble of low duty-ratio motors. We have altered the Discussion section to focus on duty ratio and the potential molecular mechanisms that could result in a reduction of the duty ratio and give rise to length-dependent sliding in the PRC1-Kif4A system.

Author response image 5

Download asset Open asset

A) Calculation of the duty ratio of the PRC1-Kif4A molecules. B) Estimation of the number of molecules/µm from experimental fluorescence intensity measurements. C) The fitting of Eq. 1. (red line) to the microtubule sliding velocity as a function of initial microtubule overlap length data (Assay condition: 0.2 nMPRC1 + 6 nM Kif4A-GFP (gray circles; N = 84).

https://doi.org/10.7554/eLife.32595.039

We thank the reviewer for raising the point of occupancy number in a microtubule overlap. We have now measured intensities of single Kif4A-dimers and used it to estimate the maximum protein occupancy in microtubule overlaps (see Author response image 5B). The average occupancy (𝑎) is estimated to be 1% if PRC1 molecules can crosslink to all 13 microtubule protofilaments of the moving microtubule and 10% assuming that effective crosslinks are only formed with one protofilament. Considering the molecular structure of PRC1, the values are likely to be in the 1-10% range. These values were used to calculate the duty ratio (Author response image 5A).

6) With regard to the contribution of the end tags on sliding: Kif4A alone can form an end tag, which drives movement of a non-immobilized microtubule along an immobilized one. It is not clear why the similar end-tag doesn't contribute much to the MT sliding in the Kif4A-PRC1 regime. How fast is the movement driven by Kif4A alone end tags in the experiments represented by Figure 2C and D (can't be currently estimated because scale bars are missing in these panels)?

As noted by the reviewers, we find that Kif4A end-tags alone can drive the movement of one microtubule over another (Figure 2). The velocity data for the Kif4A-alone driven sliding was presented in Figure 4—figure supplement 1Q inset (v = 75 ± 25 nm/s). Scale bars have now been added to Figure 2C-D. Indeed, it is possible that end-tags contribute to antiparallel microtubule sliding in the PRC1/Kif4A system, and we indicated this as ‘potentially sliding’ in the schematic in Figure 8. However, the extent to which PRC1-Kif4A end-tags contribute to sliding is unclear at this time due to the following reasons:

Sliding velocity in the PRC1-Kif4A experiments scale with untagged overlap length and not the end-tag length (Figure 4—figure supplements 1A, B, D, E). We do not observe a correlation between end-tag intensity and sliding velocity in Kif4A-alone experiments (Figure 4—figure supplement 1Q). Together, these data suggest that molecules in the untagged overlap and not those at the end-tag drive length-dependent antiparallel sliding in the PRC1-Kif4A experiments.

We can compare the sliding velocities in the standard PRC1-Kif4A sliding experiments (Figure. 1 of main text) with the velocities in the ‘wash-out’ experiments (Figure Author response image 1; Author response image 6). Briefly, in the wash-out experiments that were performed during the previous round of revision, we first establish microtubule bundles with proteins and ADP (0.2 nM GFP-PRC1 + 6 nM Kif4A and 2 mM ADP). Next, the solution protein was washed-out and exchanged with buffer containing ATP (no additional protein included). Under these conditions, when the protein concentration in the solution is low, it is observed that end-tags are re-established through depletion of PRC1 and Kif4A from the untagged overlap, and sliding is simultaneously reinitiated. Therefore, the washout experiments present a scenario in which end-tags are robustly established but the amount of protein in the untagged overlap is low.

If end-tags are sufficient to drive antiparallel sliding and molecules in the untagged overlap do not contribute to velocity, then the sliding velocities in the wash-out experiment would be in the same range as those seen in Kif4A sliding experiments. Instead, we find that the average velocity in the wash-out experiments is lower (v = 15 ± 5 nm/s) suggesting that motors in the untagged overlap play a significant role in microtubule sliding in the PRC1-Kif4A system (Author response image 6). The predominant initial interaction angle between microtubules in the Kif4A-alone experiments is between 0-30° (Figure 2). It is possible that there are geometrical constraints that inhibit end-tag mediated sliding when microtubules are anti-parallel.

In summary, it is possible that Kif4A end-tags can slide antiparallel microtubules but this mechanism alone is neither sufficient to generate movements at the observed velocities nor give rise to overlap-length dependent sliding.

Author response image 6

Download asset Open asset

Average sliding velocity for PRC1-Kif4A no wash-out experiment (0.2 nM PRC1 + 6 nM Kif4A-GFP, N = 84; 60 ± 17nm/s) and wash-out experiment (0.2 nM PRC1 + 6 nM Kif4A-GFP + 2 mM ADP, N = 22; 15 ± 5 nm/s).
https://doi.org/10.7554/eLife.32595.040

[Editors' note: further revisions were requested prior to acceptance, as described below.]

Thank you for your second resubmission of your work entitled "Geometry of antiparallel microtubule bundles regulates relative sliding and stalling by PRC1 and Kif4A" for further consideration at eLife. Your revised article has been evaluated by Anna Akhmanova (Senior Editor), a Reviewing Editor, and three reviewers.

The involved editors as well as the reviewers acknowledge that you did a great job in addressing the points raised. Removing the earlier modeling part and replacing it by a kind of "duty ratio" discussion makes sense and is a nice way to extract quantitative information out of the data. While this current description is admittedly not as advanced / informative as a real model (attempted in the last version of the manuscript) it nevertheless provides useful mechanistic insight. Given the enormous amount of very high quality experimental data, the taken approach is regarded fine for this paper. Future work could go into a more advanced model. Hence, the manuscript is now in principle regarded suitable for publication in eLife.

There is one remaining point that the reviewers and editors find of crucial importance before potential acceptance of the paper: The usage of the term/concept "duty ratio" does not seem to be fully appropriate in the presented context. The traditional/authentic "duty ratio" is about the temporal fraction of the crossbridge cycle (= ATPase cycle) of a single motor head in which it is attached to the filament and makes its working stroke. In contrast, the situations the authors imagine are (i) dissociation of the PRC-Kif4A complex from the microtubule, and (ii) slippage of PRC1 on the MT. These will influence the fraction of ATPase cycles that actually result in the sliding of the non-immobilized microtubule, i.e., the fraction of the productive stepping by Kif4A. What the authors call "duty ratio, f", is a mixture of the authentic duty ratio (as to the crossbridge/ATPase cycle) and the effect of the futile cycles. It is not appropriate to skip these details and call the parameter simply "duty ratio". A better term to describe the scenario may be "sliding efficiency". In any case, the authors should explicitly mention that they mean something slightly, but substantially, different than what "duty ratio" has been used for before.

In other words, both the authentic duty ratio and the fraction of productive stepping would influence the sliding velocity in a similar way, following the same form of a mathematical formula (2) in subsection “Mechanism of overlap-length dependent sliding by PRC1 and Kif4A”, as a first approximation. However, their meanings are quite different. A low duty ratio motor can still be highly energy efficient (like dynein). On the other hand, futile sliding simply wastes energy of ATP hydrolysis as a slippery between PRC1 and MTs or a dissociation between PRC1 and KIF4A. Along these lines: Is the low "duty ratio" of the PRC1-Kif4A complex in MT sliding consistent with its highly processive motility along a MT? A quantitative argument is necessary as to the difference in the loads on the PRC1-Kif4A complex between the two conditions; the MT sliding and the single particle motility. Statements like "…microtubule sliding by the PRC1-Kif4A complex can be considered as microtubule movement driven by an ensemble of low duty-ratio motors,.… " need to be revised accordingly.

We fully agree that the usage of the term ‘duty ratio’ in the text is not completely accurate. We thank the reviewers for suggesting ‘sliding efficiency’ and have re-named and clarified this parameter in the Discussion section of the text (subsection “Mechanism of overlap-length dependent sliding by PRC1 and Kif4A”). We have also distinguished the difference between the authentic duty ratio and sliding efficiency in the text.

The highly processive movement of Kif4A on single immobilized microtubules in the presence of PRC1 arises from an increase in the lifetime of Kif4A motors under these conditions. At a molecular level, this can be achieved through transient interactions of PRC1 and Kif4A on the immobilized microtubule. In contrast, for relative sliding, crosslinks between two microtubules need to be formed by PRC1-Kif4A complexes such that motor stepping can be translated to microtubule displacement (example: Kif4A dissociation from one PRC1 molecule and reassociation with a neighboring PRC1 will increase its lifetime but not lead to microtubule displacement). Such a difference in the molecular mechanisms between stepping and sliding by the PRC1-Kif4A complex can explain how a motor that is highly processive on a single microtubule is characterized by low sliding efficiency.

Additional references:

Chen, Y. and W.O. Hancock. Kinesin-5 is a microtubule polymerase. Nat Commun, 2015. 6: p. 8160.

Varga, V., J. Helenius, K. Tanaka, A.A. Hyman, T.U. Tanaka, and J. Howard. Yeast kinesin-8 depolymerizes microtubules in a length-dependent manner. Nat Cell Biol, 2006. 8(9): p. 957-62.

https://doi.org/10.7554/eLife.32595.042

Article and author information

Author details

Sithara Wijeratne
1. Department of Molecular Biology, Massachusetts General Hospital, Boston, United States
2. Department of Genetics, Harvard Medical School, Boston, United States
Contribution
Data curation, Software, Formal analysis, Investigation, Methodology, Writing—original draft, Writing—review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-3935-926X
Radhika Subramanian
1. Department of Molecular Biology, Massachusetts General Hospital, Boston, United States
2. Department of Genetics, Harvard Medical School, Boston, United States
Contribution
Conceptualization, Data curation, Funding acquisition, Writing—original draft, Writing—review and editing

For correspondence
radhika@molbio.mgh.harvard.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-3011-9403

Funding

Pew Charitable Trusts

Radhika Subramanian

Richard and Susan Smith Family Foundation

Radhika Subramanian

National Institutes of Health (1DP2GM126894)

Radhika Subramanian

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

The authors would like to thank Tarun Kapoor (Rockefeller Univ., USA) for generous support during initial stages of this project and feedback on the manuscript. The authors would also like to thank Yuta Shimamoto (NIG, Japan), Scott Forth (RPI, USA), Meredith Betterton (Univ. of Colorado Boulder, USA) and Doug Martin (Lawrence College, USA) for helpful comments.

Senior Editor

Anna Akhmanova, Utrecht University, Netherlands

Reviewing Editor

Stefan Diez, Technische Universität Dresden, Germany

Version history

Received: October 8, 2017
Accepted: September 28, 2018
Version of Record published: October 24, 2018 (version 1)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.

Metrics

2,107

Page views
292

Downloads
33

Citations

Article citation count generated by polling the highest count across the following sources: Scopus, Crossref, PubMed Central.

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Sithara Wijeratne
Radhika Subramanian

(2018)

Geometry of antiparallel microtubule bundles regulates relative sliding and stalling by PRC1 and Kif4A

eLife 7:e32595.

https://doi.org/10.7554/eLife.32595

Share this article

Cite this article

Relative microtubule sliding and the formation of stable antiparallel microtubule overlaps by PRC1 and Kif4A.

Molecular determinants of cross-bridging and sliding in the PRC1-Kif4A system.

Figure 2—source data 1

Quantitative analysis of microtubule sliding in the PRC1-Kif4A system.

Figure 3—source data 1

Microtubule sliding velocity in the PRC1-Kif4A system scales with initial overlap width.

Figure 4—source data 1

The width of the final antiparallel overlap established by PRC1 and Kif4A is determined by end-tag and microtubule lengths.

Figure 5—source data 1

Examination of the mechanisms that ensure stability of the overlaps established by PRC1 and Kif4A.

Antiparallel array composed of multiple microtubules are aligned at microtubule plus-ends formed by PRC1 and Kif4A.

Model for the length-dependent sliding by the collective activity of PRC1 and Kif4A.

Figure 8—source data 1

Method:Biotinylated rhodamine-labeled microtubules were immobilized in a flow chamber.

Instantaneous sliding velocity versus moving end-tag intensity, 𝐼𝐸𝑇2.

Sliding velocity as a function of initial overlap length and untagged overlap density.

Quantitative analysis of SDS-PAGE gels from two co-sedimentation assays.

Average sliding velocity for PRC1-Kif4A no wash-out experiment (0.2 nM PRC1 + 6 nM Kif4A-GFP, N = 84; 60 ± 17nm/s) and wash-out experiment (0.2 nM PRC1 + 6 nM Kif4A-GFP + 2 mM ADP, N = 22; 15 ± 5 nm/s).

Author details

Sithara Wijeratne

Contribution

Competing interests

Radhika Subramanian

Contribution

For correspondence

Competing interests

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Categories and tags

Further reading

Instantaneous sliding velocity versus moving end-tag intensity, 𝐼_𝐸𝑇2.