Phylogenetic divergence of cell biological features
- Arizona State University, Arizona
Figures
Figure 1
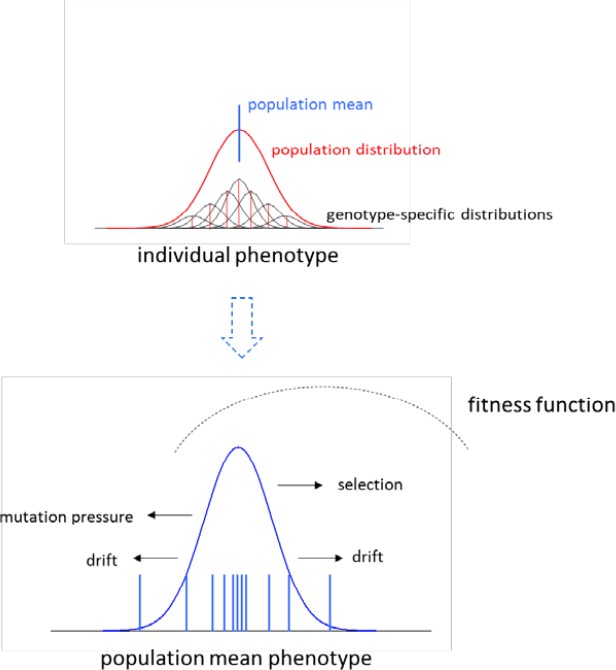
An idealized overview of the model for the evolution of the distribution of mean phenotypes, given here for a trait under stabilizing selection.
The upper panel denotes a hypothetical phenotype distribution at a single point in time. The population consists of multiple genotypes, each having an expected genotypic value (red) but a range of phenotypes (black distributions) resulting from variance in residual deviations (environmental effects and nonadditive genetic factors). The phenotype distribution for the entire population (red) is the sum of these genotype-specific curves, and has a mean denoted by the blue line. The exact location of this overall distribution can wander over time, owing to the joint forces of selection, mutation, and random genetic drift. The lower panel gives the overall distribution of population means over a long evolutionary time span, with 11 locations at specific points of time being denoted by the short vertical lines. Persistent mutational bias towards smaller phenotypes prevents the overall distribution of means from coinciding with the fitness-function optimum, and random genetic drift causes a dispersion of means around the overall average value.
Figure 2
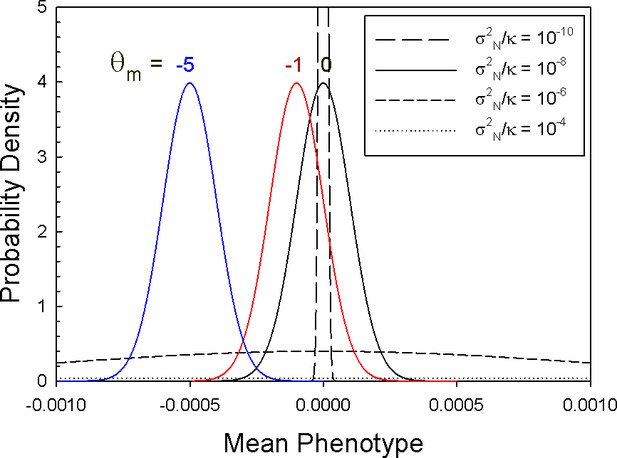
Stationary distributions of mean phenotypes, with optimum phenotype and
Results are given for three different values of for the condition in which (colored curves), and four different values of for the case in which the mutational mean coincides with the optimum (black curves). The parametric values used in these plots assume a scale on which the phenotypic standard deviation is 1.0, so a mean phenotype of is equivalent to a shift of 0.1% phenotypic standard deviations from the optimum.
Figure 3
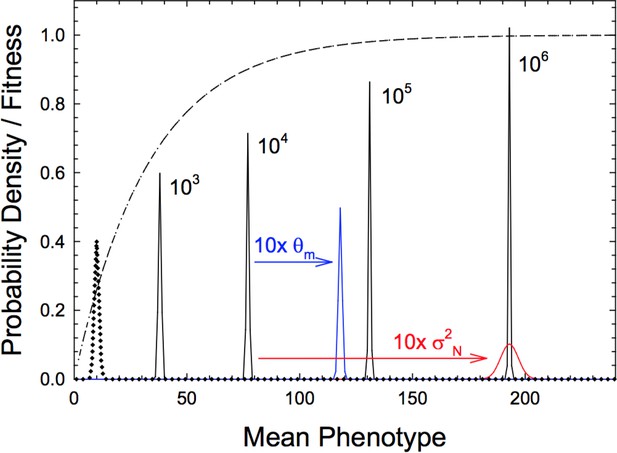
Stationary distributions of mean phenotypes with a hyperbolic fitness function, Equation (14) with and and denoted by the dashed line.
Black distributions denote results for various effective population sizes ( to ), with phenotypic variance , mutational variance and the mean phenotype under neutrality (distribution given by the dotted line) Blue and red distributions denote the effects of altering and
Figure 4
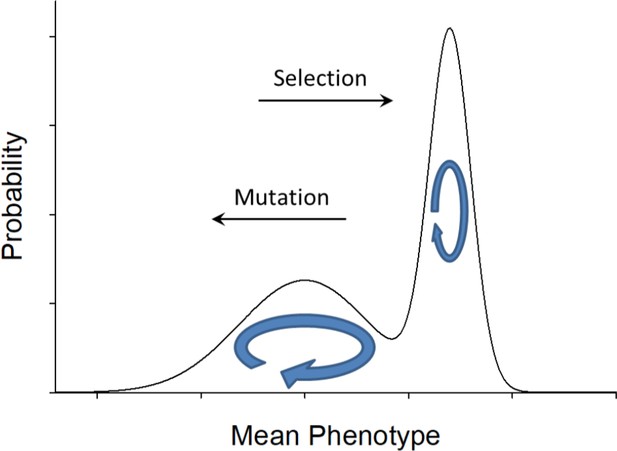
An example of a bimodal stationary distribution of mean phenotypes, with mutation pressure to the left and selection pressure to the right, with the forms of these two functions being such that their product is a minimum at the valley in the landscape.
Most of the time, a population will reside in one domain or the other, wandering over a range of phenotype space to the left or the right of the valley, but occasionally a transition will be made across the valley impelled by a stochastic series of drift and mutational events. Populations crossing the valley to the right are pulled by selection pressure, whereas those crossing to the left are pulled by the multiplicity of mutational opportunities.
Tables
Table 1
Formulae for mean population fitness, , and the rate of change of the mean phenotype resulting from selection, , obtained from Equations (4) and (6), respectively.
https://doi.org/10.7554/eLife.34820.004| Model | ||
|---|---|---|
| Gaussian | ||
| Hyperbolic | ||
| Sigmoid |
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.34820.008
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Phylogenetic divergence of cell biological features
eLife 7:e34820.
https://doi.org/10.7554/eLife.34820
