Theta-modulation drives the emergence of connectivity patterns underlying replay in a network model of place cells
- Centre de Recerca Matemàtica, Spain
- New York University Shanghai, China
- NYU-ECNU Institute of Brain and Cognitive Science at NYU Shanghai, China
- Universitat Pompeu Fabra, Spain
- Max Planck Florida Institute for Neuroscience, United States
- Barcelona Graduate School of Mathematics, Spain
Figures
Figure 1
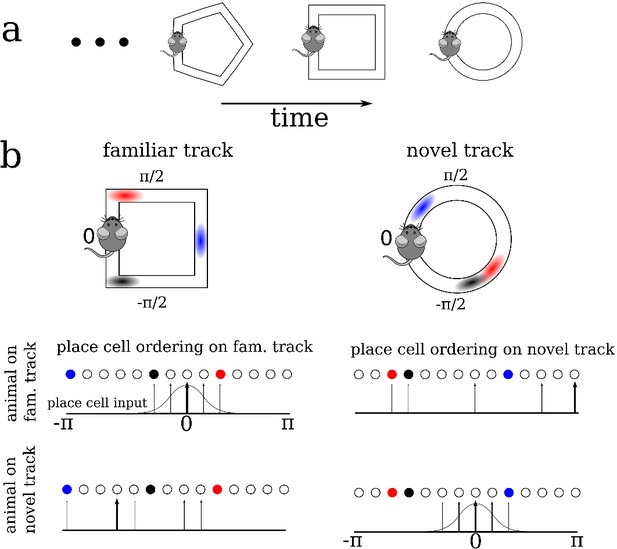
A schematic description of the model.
(a) We model the sequential exploration of a number of distinct linear tracks. (b) The network consists of N place cells. The ordering of the place fields is randomly remapped on each track. Therefore, if the cells are properly ordered in any given environment the place field input is represented by a spatially localized bump of activity (upper left and lower right). Sequential activity on a familiar track would look random given an ordering on a novel track, and vice versa (upper right and lower left respectively).
Figure 2 with 8 supplements
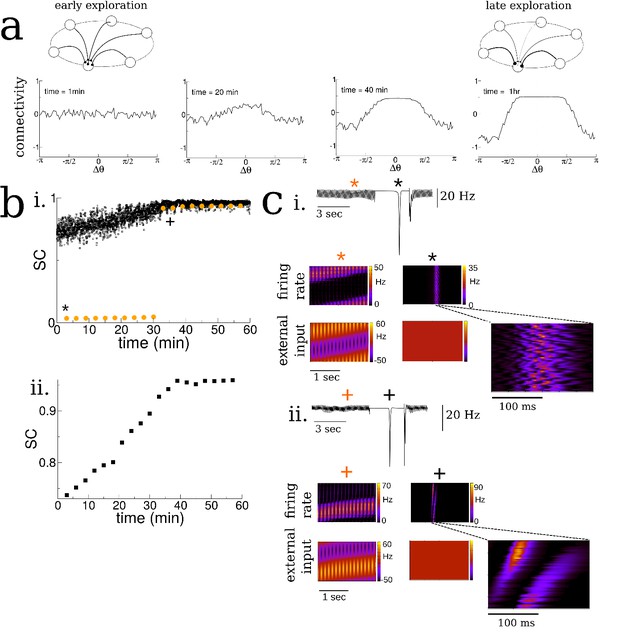
Spatial exploration gives rise to plasticity-dependent emergence of spatio-temporal structure in spontaneous activity.
(a) Snapshots of the connectivity during the exploration of a novel environment. During early exploration, the connectivity is not correlated with the place-field ordering, while during late exploration cells with neighboring place-fields are more strongly connected. (b) i. The mean cross-correlation of the activity of place cells with adjacent place fields on a novel track during exploration (sequential correlation SC). Black: SC during active exploration (theta-activity), Orange: SC during spontaneous bursts. Note the sharp transition in the SC of burst activity. ii. The SC of the total activity binned into 3 min intervals shows a steady increase preceding the transition. (c) Burst activity exhibits replay after a critical period. i. Early exploration. Top: average input to place cells before (blue star), during (black star) and after period of ‘quiet wakefulness’. Bottom: space-time plots of the place cell input and firing rate. Note the disordered spatio-temporal structure of the burst activity. ii. Later exploration. After a critical transition time bursts exhibit sequential replay of activity from the novel track. Note the sequential structure of the burst activity.
Figure 2—figure supplement 1
The evolution of the recurrent connectivity during exploration of 10 distinct tracks.
(a) The mean synaptic weight of recurrent excitatory connections as a function of time for 10 consecutive simulations of 1 hr each. The initial condition was all the weights identical and set to a value of 40. (b) the distribution of synaptic weights at the end of the 10 hr of simulation. About 10% of synaptic weights are maximally depressed to zero, 40% are maximally potentiated (threshold set to 80) and 50% take on intermediate values. As new environments are explored the distribution remains largely fixed but individual synapses change in time.
Figure 2—figure supplement 2
The emergence of replay for unidirectional motion.
(a) The evolution of the mean synaptic weight over the course of exploration of 10 distinct tracks and the resulting distribution of synaptic weights (right). (b) Snapshots of the profile of the recurrent connectivity and firing rate during exploration of a novel track, up to 15 hr. The place cell activity is calculated with respect to the maximum of the subthreshold input. Note that at later times the maximum of the place cell activity is shifted to the right (clockwise, in the direction of motion) compared to the input. In experiment this would be seen as a backward shift in the place field of cells. Note also the negative skewness in the activity. (c) Transition in the SC of burst activity (black circles) reflecting the change in the spatio-temporal structure of the bursts. The SC of the sensory-driven theta-activity shows an increase leading up to the transition. Inset: The same over 16 hr of simulation time. (d) ‘LFP’ and space-time plots of the network firing rate and external input before and after the transition. (e) The amplitudes of the even and odd Fourier modes of the recurrent connectivity after 1 hr of exploration. (f) A transition in the SC occurs only for a range of frequencies. (g) An anti-symmetric plasticity rule (left) or a rule with dominant depression at short latencies (right) does not lead to an emergence of spontaneous bursts. All parameters are the same as in Figures 2 and 3 with the exception of the following. The modulation frequency during training on the 10 tracks for one hour each is f = 5 Hz, = 22 Hz, and the velocity of the animal is constant with a value = 1 rad/sec. Finally, during the training period of 1 hr on each of ten distinct tracks, theta activity was always present, that is there were no bursts. Allowing for bursts during training did not alter the results qualitatively.
Figure 2—figure supplement 3
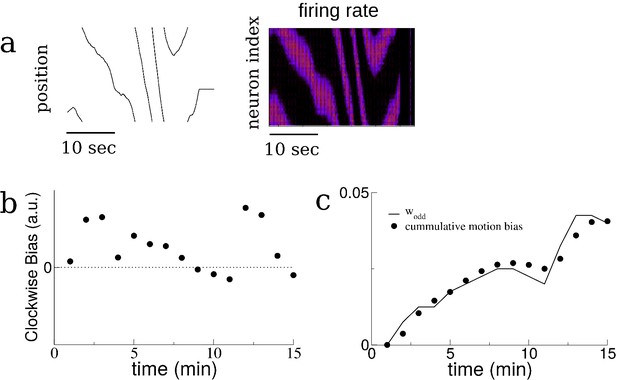
The growth of the odd mode of the recurrent connectivity is determined by the bias in the motion of the virtual animal.
(a) A sample trajectory of the virtual animal. The velocity is modeled as an Ornstein-Uhlenbeck process. Left: Position of virtual animal, i.e. the position of the maximum in the place-field input. Right: Place-cell activity. (b) The bias in the motion of the virtual animal during the first 15 min of a simulation, averaged in one-minute bins. Specifically the bias is the difference in the time spent moving clockwise versus moving counter-clockwise. The velocity of the virtual rat is an Ornstein-Uhlenbeck process with a non-zero mean as described in Materials and methods; the non-zero mean results in an overall clockwise bias. (c) The growth of the odd Fourier mode (sine mode) over time (solid line) compared to the cumulative motion bias. The cumulative motion bias is the time integral of the motion bias, scaled to match amplitudes with the normalized odd mode of the connectivity.
Figure 2—figure supplement 4
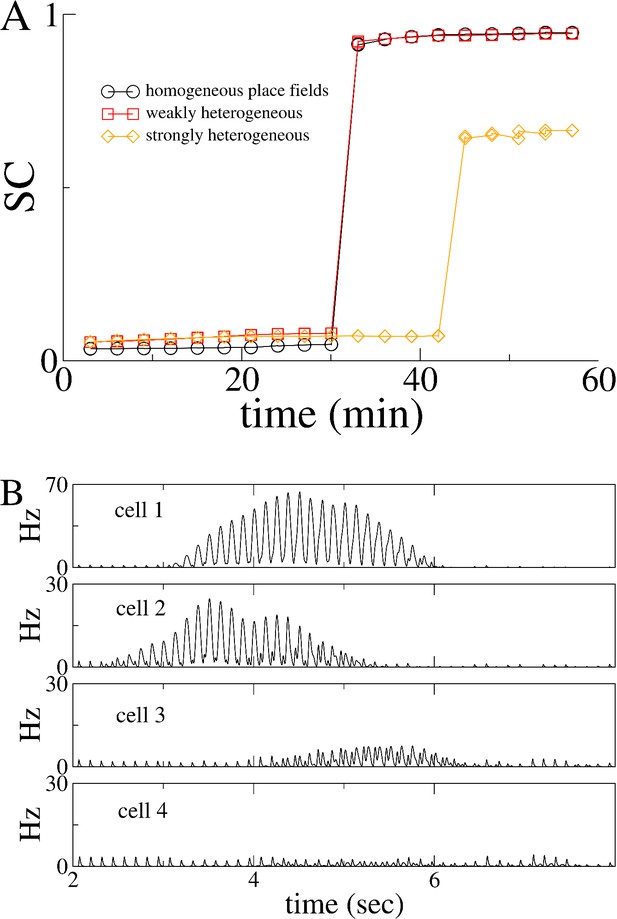
Heterogeneity in place-cell activity does not qualitatively alter the transition to replay.
(A) The SC for three identical simulations with the only difference being the degree of heterogeneity in the place-field input to place-cells. The curve with the black circles is identical to the simulation in Figure 2 of the main text, for which = 25 Hz. The red squares are a simulation for which is uniformly distributed between 20 and 30 Hz (and hence the mean is the same as before). The orange diamonds show an extreme case where is uniformly distributed between 0 and 50 Hz. B. Examples of place-cell activity for the strongly heterogeneous case. Note that in this case some cells are only very weakly selective to place, for example cell 3, while others have no place field whatsoever, for example cell 4.
Figure 2—figure supplement 5
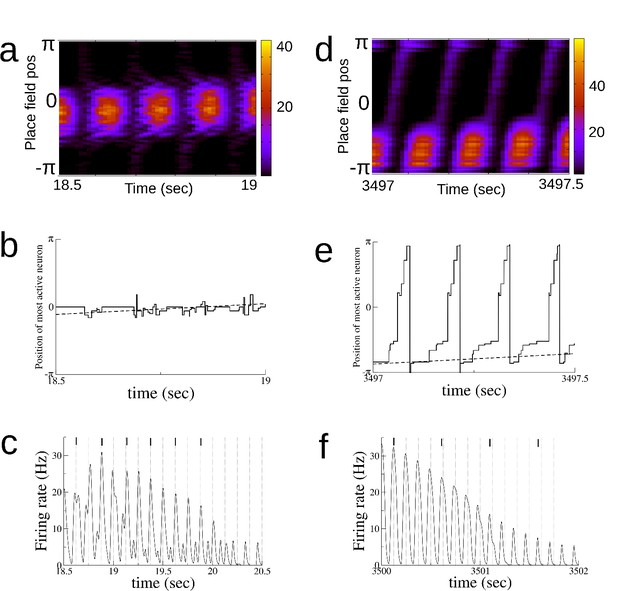
Theta sequences and phase precession emerge over time.
(a) A space-time plot of the firing rate (Hz) during early exploration. (b) The position of the most active place cell over time (solid line). The position of the animal is given by the dashed line. (c) The firing rate of a single place cell. Peaks in the theta rhythm are given by dotted vertical lines, and most likely spike times by solid lines. (d)-(f) The same as (a)-(c) for late exploration. Parameters are the same as those used for Figure 2—figure supplement 2, with the exception of = 8 Hz.
Figure 2—figure supplement 6
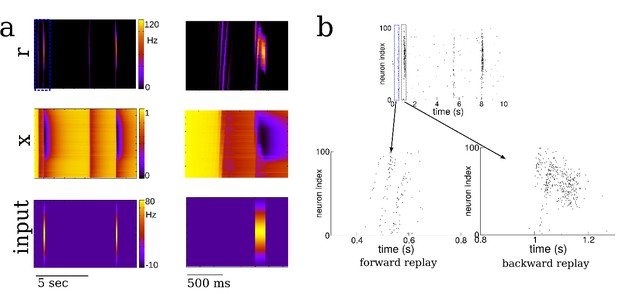
Forward replay occurs spontaneously, but backward replay requires location-specific input.
(a) The firing rate r (top), short-term synaptic depression variable x (middle) and external input to place cells (bottom) during a period of ßleep’ or ‘quiet wakefulness’, that is in the absence of theta-modulated place field input. Spontaneously occurring bursts always travel forward when the input is globally homogeneous, reflecting the asymmetry in the underlying recurrent connectivity. However, a strong location-specific input (just after 1 s and 8 s) can transiently depress the synapses in downstream neurons, facilitating the propagation of activity backwards. Right: blow-up of activity showing forward and backward replay. (b) Raster plot generated from the same simulation as in (a). The external input is Hz except for the two spatially-modulated inputs which are presented for 50 ms each and have the form Hz.
Figure 2—figure supplement 7
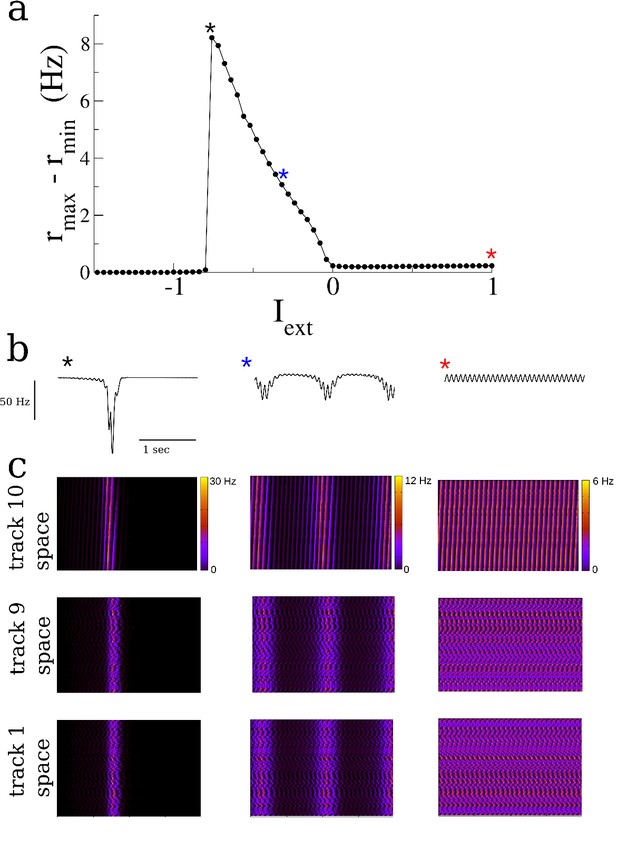
The degree of ‘burstiness’ of spontaneous activity can be modulated by a global external input.
(a) The temporal maximum of the mean firing rate (averaged over the network) as a function of the external input. The input is a constant, that is there is no place-specific input. Simulations are run for 100 s and the first 10 s are discarded to avoid transients. (b) 'LFP's of the spontaneous activity, actually the total input to the network for I = −0.8 (left), −0.35 and 1 respectively. (c) Space-time plots of the spontaneous activity shown with neurons ordered according to their place fields in the last, next-to-last and first environments explored. Parameter values are identical to those in Figure 2.
Figure 2—figure supplement 8
Changes in the recurrent connectivity stabilize in an extended, 10 hr simulation.
(a) The amplitude of the even mode of the recurrent connectivity over time. (b) Top: The SC of the SWR activity. Bottom: The mean firing rate in the network over time. The initial condition for the recurrent connectivity is the same as for the simulation shown in Figure 2, in other words that resulting from the exploration of 10 distinct tracks.
Figure 3
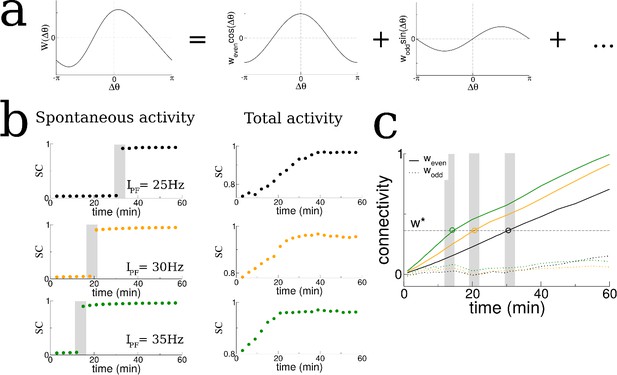
The transition in the structure of burst activity occurs when the even component of the recurrent connectivity reaches a critical value.
This mode grows only for STDP rules with dominant potentiation, and grows fastest when periodic modulation is in the theta range. (a) The profile of the recurrent connectivity at any point in time can be decomposed into a series of even (cosine) and odd (sine) modes. Only the first two modes are shown. (b) As the amplitude of the place-field input is increased from 25 Hz (black), 30 Hz (orange) and 35 Hz (green) the transition shifts to earlier times. The SC of the SWR activity shows a sharp transition (shaded grey bars), while the total activity displays a smooth increase leading up to the transition. (c) In all cases the value of the even mode reaches approximately the same critical value at the time of the transition (shaded grey bars). The growth of the odd mode (dotted lines) is much more irregular, and its value does not correlate with the transition time.
Figure 4
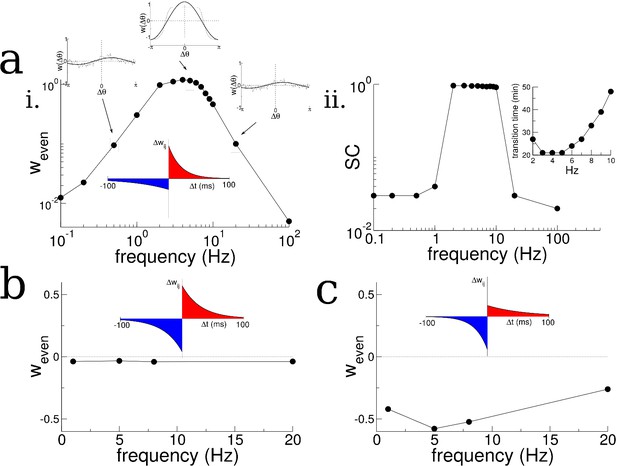
Theta-modulation accelerates emergence of connectivity mode which drives replay.
(a) A temporal asymmetric plasticity rule with dominant potentiation at short latencies. i. The amplitude of the even mode of the connectivity after 1 hr of exploration, as a function of the modulation frequency. The even mode grows maximally over a range of approximately 1–10 Hz and it is strongly attenuated at lower and higher frequencies. Note the logarithmic scale. On the other hand, the growth of the odd mode is largely independent of the modulation frequency, see text for details. ii. The degree of SC of spontaneous bursting after 1 hr of exploration. Replay occurs only when the frequency lies between 2–10 Hz. Inset: The time at which a transition in the SC takes place as a function of frequency, for times up to 1 hr. (b) A purely anti-symmetric plasticity rule leads to recurrent connectivity which has only odd Fourier modes. There is no increase or transition in the SC of bursts in these simulations even after 1 hr. (c) An asymmetric plasticity rule with depression dominating at short latencies leads to connectivity with a negative amplitude of the even mode, that is recurrent excitation is weaker between pairs of place cells with overlapping place fields than those with widely separated place fields. In this case bursts are actually completely suppressed (not shown).
Figure 5
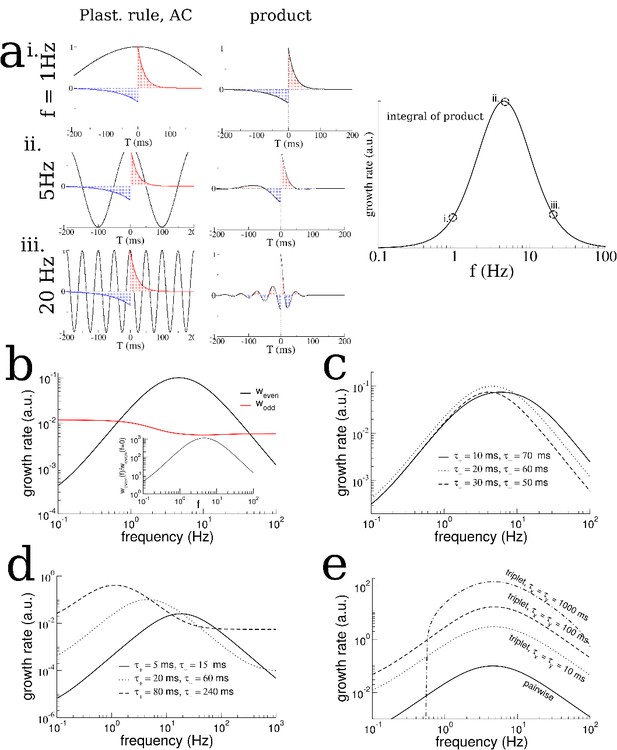
Analysis of a linear firing rate model with plasticity reveals the mechanism by which the plasticity rule and periodic modulation shape connectivity.
(a) The growth rate of the symmetric mode is proportional to the integral of the product of the autocorrelation (AC) of place cell activity with the plasticity window (PW). Left: The AC of place cell activity overlaid on the PW with dominant potentiation at short latencies. Middle: Product of the PW and the AC. Right: The growth rate of the symmetric (cosine) mode of the connectivity as a function of frequency. i. When the activity is modulated at 1 Hz (top), the product returns nearly the original plasticity window, which being balanced yields near-zero growth rate. ii. For 5 Hz the potentiating lobe is maintained and some of the depression lobe changes sign and becomes potentiating leading to higher growth rate. iii. For 20 Hz the plasticity window undergoes sign reversals at a rate faster than the width of the lobes, meaning the integral is again near zero. (b) The growth rate of the even (cosine) and odd (sine) spatial Fourier coefficients as a function of the modulation frequency (black curve is the same as in (a) except on a log-log scale). Inset: The growth rate of the even mode normalized by its value for no periodic modulation. Rule parameters are = 0.1, = 20 ms, = 0.1/3, = 60 ms (c) Increased growth rate in the theta range does not require fine tuning. (d) The frequency at which growth is maximal depends on the overall width of the plasticity window. Broader windows favor slower frequencies. (e) A triplet rule increases the growth rate at all frequencies compared to the pairwise rule, but does not significantly shift the optimal frequency range. The parameters for pairwise interactions are as before. The time constants for triplet interactions are indicated on the figure, while the remaining parameters are chosen to make the rule balanced.
Figure 6
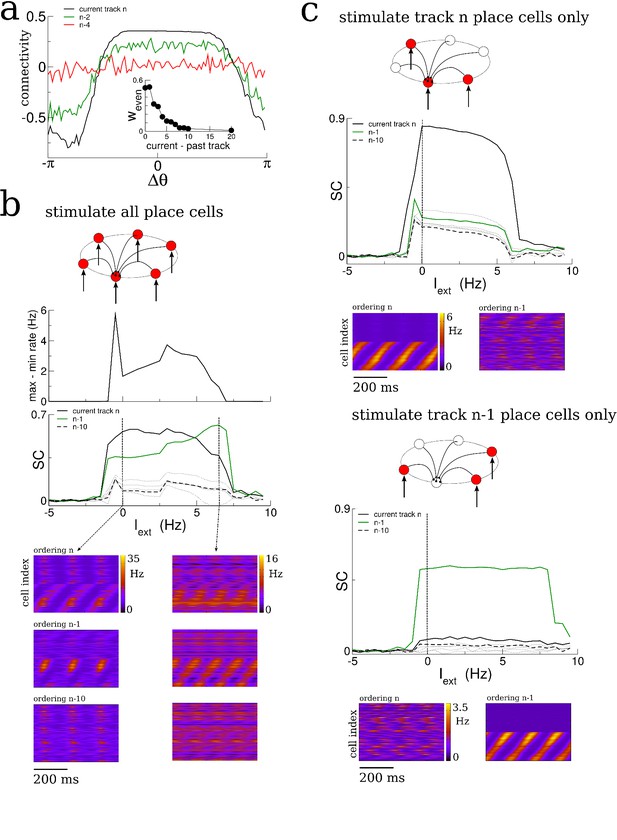
Sparse coding allows for the replay of multiple previously experienced environments.
(a) The connectivity profile after exploration of 30 environments in a network in which one half of the neurons are place cells on any given track. The same connectivity can be visualized using the ordering of the place cells on the most recently explored track (track n, black curve) or using the ordering of past explored tracks (green and red curves). The spatial structure which emerges during exploration on any given track eventually gets overwritten as new tracks are explored. Nonetheless the connectivity stores structure from several past explored tracks simultaneously. Inset: The amplitude of the even Fourier mode as a function of the recency of the corresponding track. (b) A global stimulus applied to all the neurons in the network generates replay which is highly correlated with the past two tracks. (c) Selective stimulation of only those neurons which were place cells in the most recently explored track (top) or next-to-last track (bottom) generates replay which is highly correlated only with the corresponding environment. N = 200 neurons in all simulations.
Figure 7 with 4 supplements
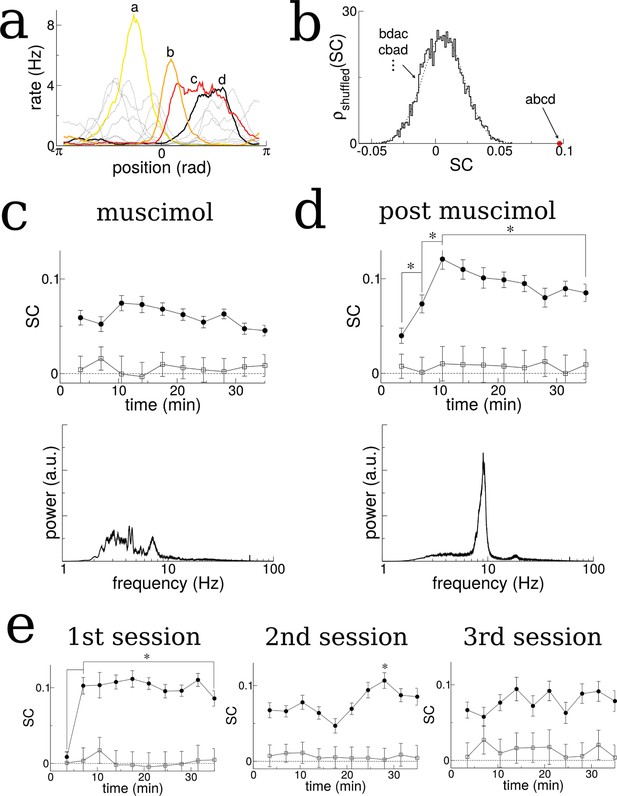
The SC of place cells in rat hippocampus during the exploration of a novel track shows an initial increase and plateau, but only when theta is present.
(a) Sample firing rate profiles from place cells recorded from CA1 of rat hippocampus during exploration of a novel periodic track with an illustration of how cells can be ordered according to their phases. (b) The SC calculated over the entirety of the experiment (35 min) given the correct ordering (red dot) and for 5000 reshuffled orderings. (c) The time course of SC given the proper ordering (solid symbols) does not show any dynamics when the medial septum is reversibly inactivated with muscimol. Note, however, the clear separation with the shuffled data (open symbols), indicating that place fields are intact even though theta is disrupted. (d) After a rest period the animal is placed back onto the same track; the SC now exhibits a significant increase given the proper ordering (solid symbols) over the first 10 min of exploration and then plateaus. Note that the bottom plots in (c) and (d) show the power spectrum of hippocampal LFP (CA1), indicating a large reduction of theta power in the muscimol condition. (e) When the animal is allowed to explore a novel track and then placed back on the track for a second and third session, there is a significant increase in the SC only during the first session. Error bars are S.E.M.
Figure 7—figure supplement 1
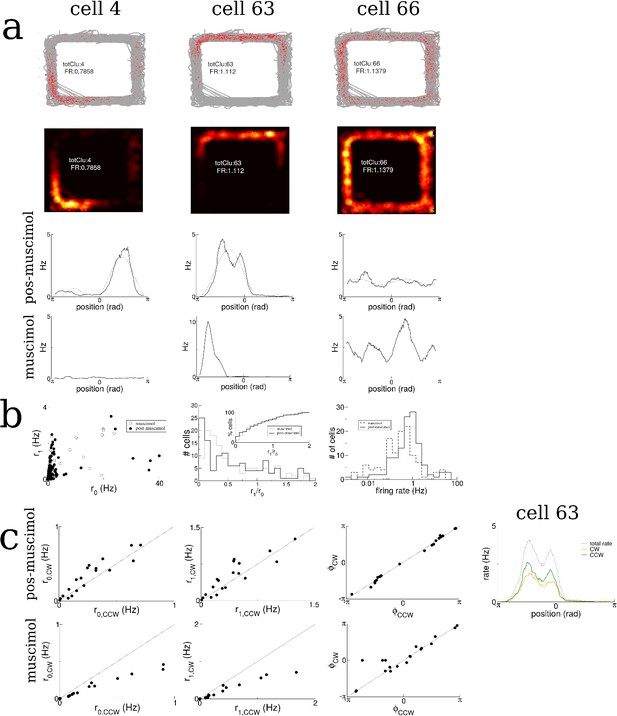
Place cell statistics for rat A991.
(a) Three sample cells. Spike maps (top), rate maps (middle) and linearized rate along the track with muscimol and post-muscimol (bottom). Each linearized rate profile is fit by a curve and the coefficients extracted. (b) Left: The values of the coefficients of the first cosine mode vs. the spatially homogeneous mode for all cells. Middle: The histogram of the tuning index ratio for all cells. Right: Histogram of firing rates. (c) There is only weak rate-remapping for clockwise versus counter-clockwise motion. (Left to right) The first two Fourier coefficients and phase of the fit to the linearized rate profiles in the clockwise versus the counter-clockwise direction, and a sample cell.
Figure 7—figure supplement 2
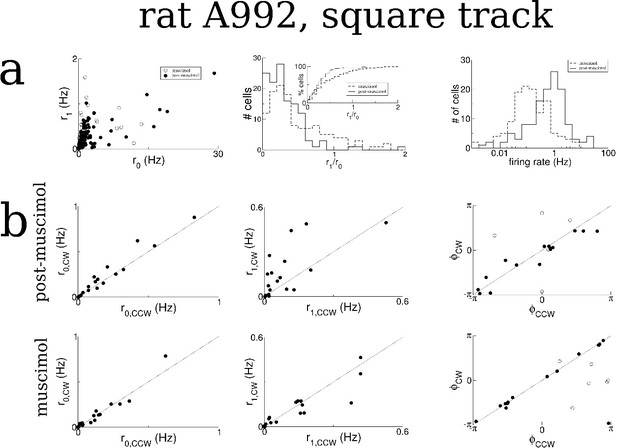
Same as Figure 7—figure supplement 1 for rat A992.
https://doi.org/10.7554/eLife.37388.018
Figure 7—figure supplement 3
Figure 7—figure supplement 3 SC and statistics for cells recorded during three sessions exploring a novel hexagonal track, from two rats.
(a) Time-resolved SC for each session. Asterix and shaded regions as above, in Figure 7—figure supplement 4. (b) First Fourier coefficient plotted versus the zeroth order coefficient of average place field activity for all cells. (c) Histogram of the TI for all cells (dashed line) and for those cells with mean firing rate 0.4 Hz (solid lines). (d) Histogram of firing rates. e. Norrmalized TI histograms.
Figure 7—figure supplement 4
The time-resolved SC for both rats both with medial septum inactivation (muscimol) and after recovery (post muscimol) and for different selection criteria of the tuning index (TI) of place fields.
Asterix indicates a significant difference with the first data point (t-test p0.006 corrected for multiple comparisons) except for the second asterix in the plot of SC for which indicates a significant difference between the second and third data points. Shaded regions indicate a significant difference between SC and that of 5000 shuffles with randomized ordering (t-test p0.005, corrected for multiple comparisons). Bottom: Power spectra of LFP recorded during each session.
Author response image 1
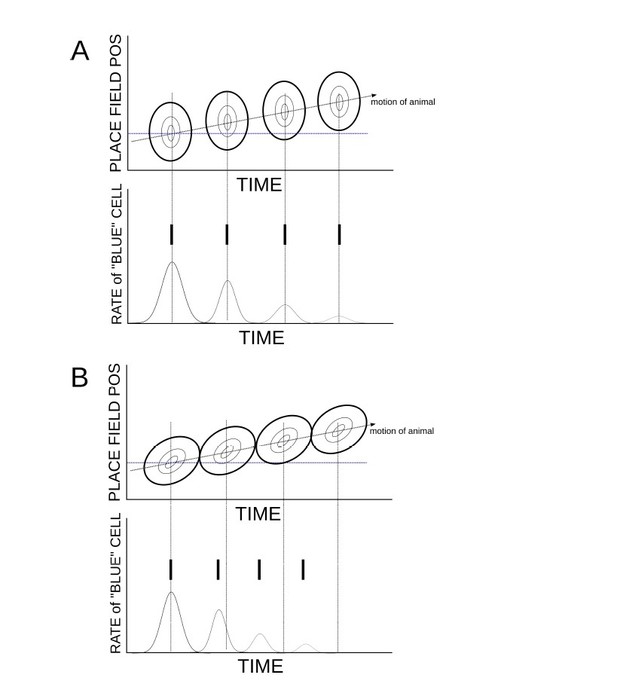
Temporally asymmetric place-cell activity leads to phase precession.
(A) When place-cell activity is symmetric, and hence there are no theta sequences, there is also no phase precession. (B) The presence of theta sequences generates phase precession.
Author response image 2
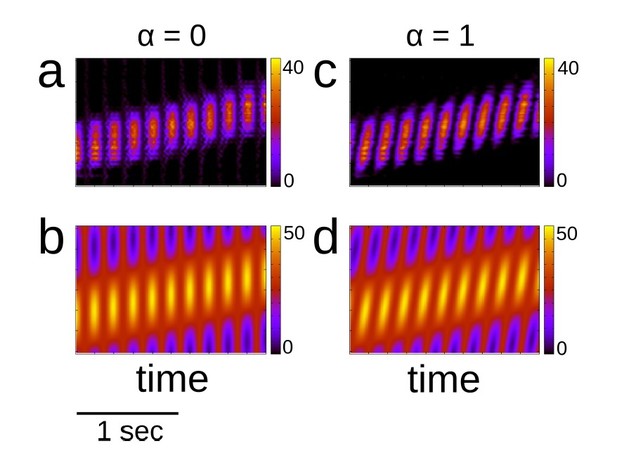
Place cell activity and place cell input with and without theta sequences.
(a) Place cell activity with no theta sequences (α = 0). (b) Input with no theta sequences. (c)-(d) Same as (a) and (b), but with theta sequences (α = 1). Color indicates activity or input in Hz.
Author response image 3
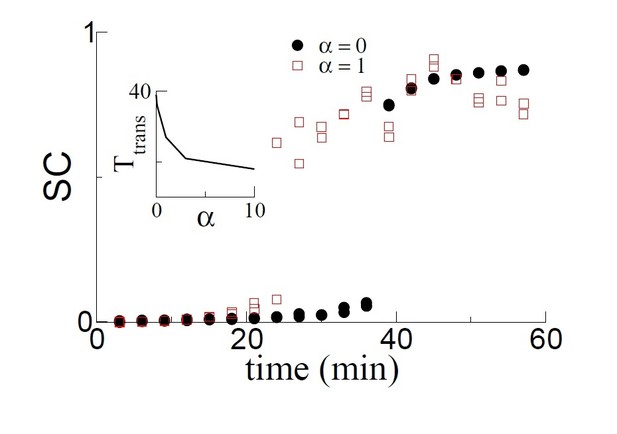
The SC as a function of time for two simulations: α = 0, i.e. no theta sequences and α = 1, i.e. with theta sequences.
Learning is faster and hence the transition occurs earlier with theta sequences. The transition time decreases monotonically as a function of α, which sets the velocity of the theta sequences.
Author response image 4
Growth rate of the mean connectivity as a function of the average neuronal firing rate.
https://doi.org/10.7554/eLife.37388.026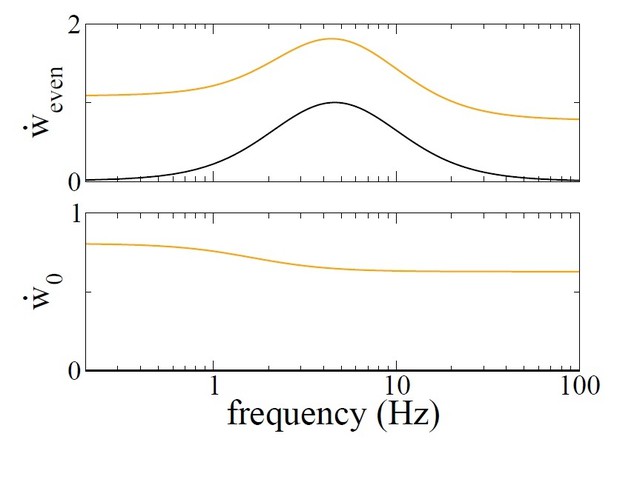
Author response image 5
Growth rate of the even mode (top) and mean connectivity (bottom) as a function of modulation frequency f with a balanced rule (black) and an unbalanced rule (orange).
r0 = 10Hz.
Author response image 6
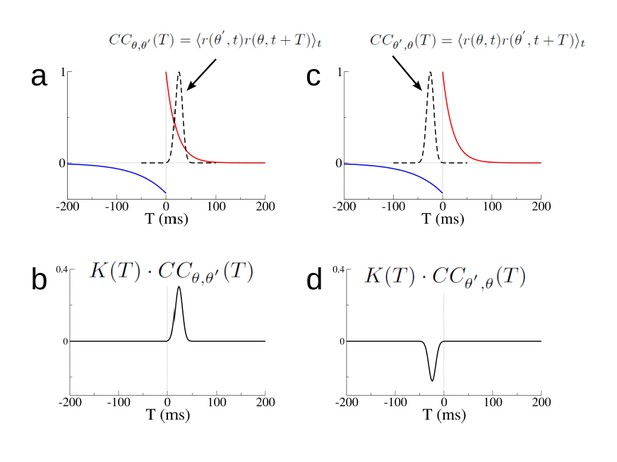
Changes in individual synapses depend on the cross-correlation of the firing rate of pre- and post-synaptic cells.
(a) The STDP window K(T) (red and blue curves) and the cross-correlation CCθ,θ′(T) (dashed black line) for two hypothetical place cells. (b) The product K(T) · CCθ,θ′(T). (c)-(d) Same as (a)-(b) but for Cθ′,θ(T). The rate of change of the synaptic weight is found by integrating the curves in (b) and (d) respectively.
Author response image 7
The spontaneous dynamics in a model with asymmetric versus symmetric recurrent connectivity.
(a) The amplitude of spontaneous activity as a function of the external drive (uniform, non-specific drive to all place cells) in an asymmetric network. This is a reproduction of Figure 2—figure supplement 8; the parameters are all the same. (b) A space-time plot of the activity. Replay is always in one direction. (c) Blow-up of the replay activity. (d)-(f) The same for a network with symmetric recurrent activity. In this case we take the synaptic connection from a cell j to a cell i to be ˜wij = (wij + wji)/2, where wij and wji are the weights after the exploration of 10 tracks for one hour each. These are exactly the (asymmetric) weights used in (a)-(c). The external input is Iext = −0.8.
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.37388.021
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Theta-modulation drives the emergence of connectivity patterns underlying replay in a network model of place cells
eLife 7:e37388.
https://doi.org/10.7554/eLife.37388
