Figures and data in Competition for synaptic building blocks shapes synaptic plasticity

Figures
Tables
Additional files

8 figures, 4 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

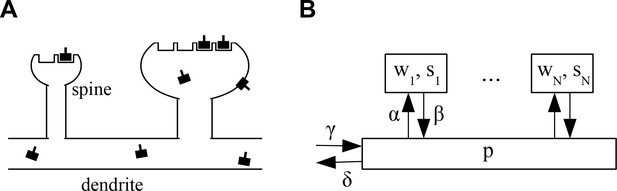
Architecture of the model.

(A) Sketch of the architecture of the model. Neurotransmitter receptors, e.g. AMPA receptors, are trafficked through the dendrite and bind to ‘slots’ inside of dendritic spines. The efficacy of a synapse is assumed to be proportional to the number of receptors attached to its slots. (B) Abstract description of the stochastic process indicating the rates at which receptors move in and out of slots in the synapses and the receptor pool in the dendrite. See text for details.

https://doi.org/10.7554/eLife.37836.002

Figure 2

Download asset Open asset

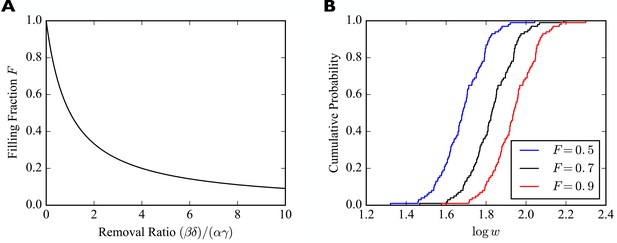
Synaptic filling fraction.

(A) Filling fraction $F$ as a function of the removal ratio $(β δ) / (α γ)$ . (B) Example empirical cumulative distribution functions (CDFs) of the numbers of receptors bound in individual synapses for fixed numbers of slots drawn from a lognormal distribution and three different filling fractions $F$ . The simulated piece of dendrite has 100 synapses and 100 receptor slots per synapse on average.

https://doi.org/10.7554/eLife.37836.004

Figure 3

Download asset Open asset

Filling fraction $F^{*}$ in the short-term approximation of constant receptor number as a function of the ratio of transition rates $ρ = β / α$ for different combinations of $R$ and $S$ .

(A) $F^{*}$ for a fixed number of $S = 10 000$ slots and three different receptor numbers as a function of $ρ$ . (B) For fixed number of $R = 10 000$ receptors and three different numbers of slots. Note that $F^{*}$ reacts particularly sensitively to changes in $ρ$ when $ρ$ is small and when $R = S$ (black curves). In this regime, small changes to, say, the rate of detaching from slots $β$ have a great influence on the filling fraction. In all cases, the shown solution $F^{*}$ is only transient. Eventually the filling fraction will assume its steady state value $F$ given by Equation 7.

https://doi.org/10.7554/eLife.37836.006

Figure 4

Download asset Open asset

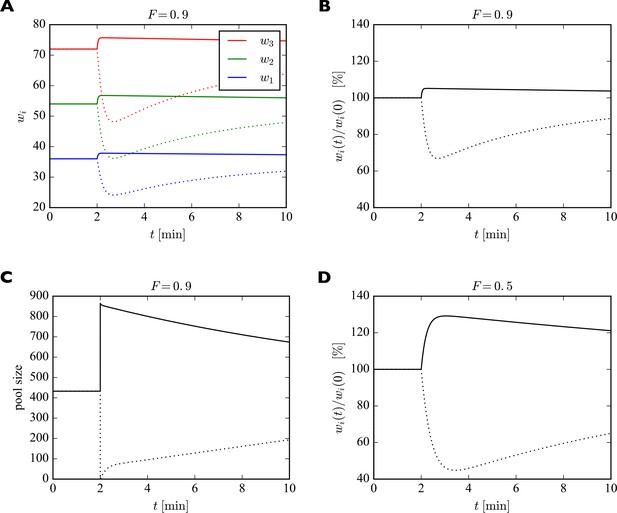
Effect of sudden change of the pool size $p$ on synaptic efficacies.

(A) After 2 min, the pool size is either doubled (solid curves) or set to zero (dotted curves). In response, the synaptic efficacies are scaled multiplicatively as receptors are redistributed through the system. Doubling the receptor pool has a relatively weak effect in this example, as the system starts with a high filling fraction of 0.9, meaning that 90% of the slots are already filled at the beginning and there are few empty slots to which the additional receptors can bind. (B) Same as A. but showing relative change in synaptic efficacies, which is identical for all synapses. (C) Change in pool size. After the sudden increase or decrease in pool size at 2 min, there is first a rapid relaxation of the pool size followed by a much slower return towards the original value. (D) Same as B. but for a filling fraction of $1 / 2$ . The smaller filling fraction leads to bigger relative changes of the synaptic efficacies. Parameters used were: $β = 1 / 43 s^{- 1}$ , $δ = 1 / 14 {min}^{- 1}$ . The desired relative pool size was set to $ϕ = 2.67$ . The production rate $γ$ and attachment rate $α$ were calculated according to Equation 12 and Equation 13, respectively.

https://doi.org/10.7554/eLife.37836.007

Figure 5

Download asset Open asset

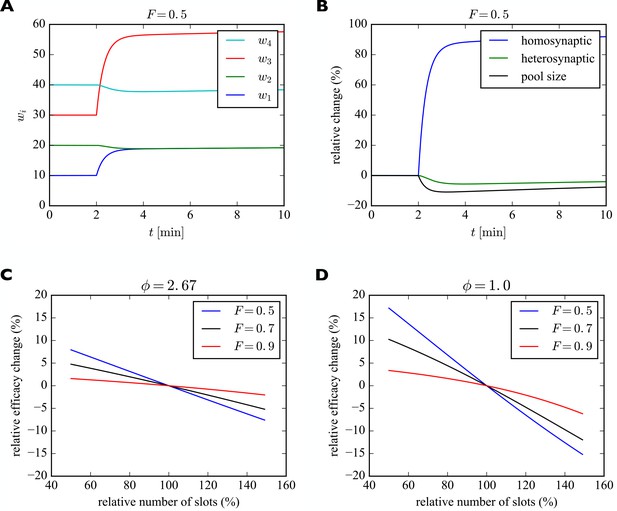
Induction of transient heterosynaptic plasticity.

(A) Illustration of transient heterosynaptic plasticity. After 2 min, the number of slots in synapses 1 and 3 is increased instantaneously. The system quickly reaches a new (transient) equilibrium, where the non-stimulated synapses 2 and 4 are slightly weakened. At the same time, the number of receptors in the pool is reduced. Parameters were: $β = 1 / 43 s^{- 1}$ , $δ = 1 / 14 {min}^{- 1}$ . The filling fraction was set to $F = 0.5$ and the relative pool size was set to $ϕ = 2.67$ . The production rate $γ$ and attachment rate $α$ were calculated according to Equation 12 and Equation 13, respectively. (B) Time course of relative changes in synaptic efficacies due to homosynaptic and heterosynaptic plasticity for the experiment from A. (C) Approximate maximum relative change of synaptic efficacy due to heterosynaptic plasticity as a function of the number of receptor slots after homosynaptic plasticity induction for different filling fractions. (D) Same as C but for a smaller relative pool size of $ϕ = 1.0$ . See text for details.

https://doi.org/10.7554/eLife.37836.008

Figure 6

Download asset Open asset

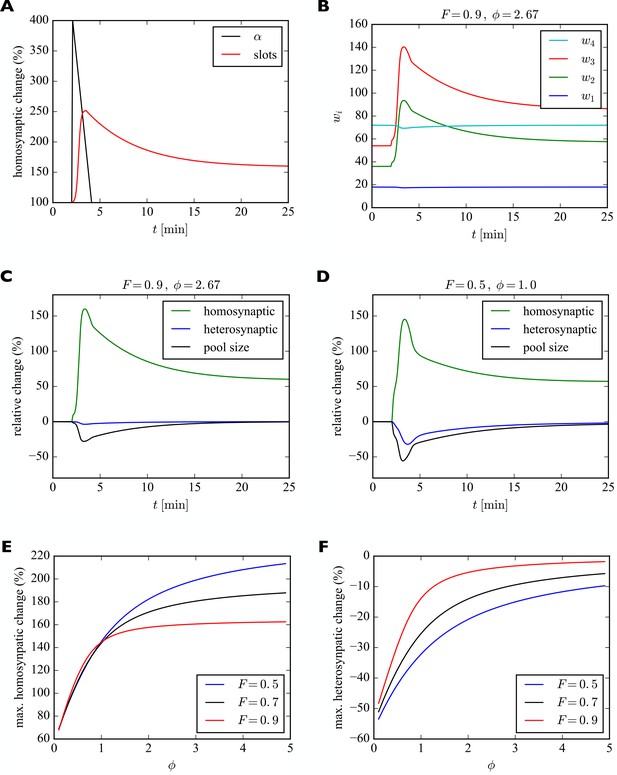
Model of homosynaptic LTP accompanied by heterosynaptic LTD.

After 2 min, LTP is induced in synapses 2 and 3. This entails a transient synapse-specific change in the insertion rate $α$ of these synapses and a gradual change in their slot numbers. (A) Time course of relative change of receptor insertion rate $α$ and slot numbers of stimulated synapses undergoing homosynaptic LTP. (B) Time course of synaptic efficacies for a filling fraction of $F = 0.9$ and a relative pool size of $ϕ = 2.67$ . Only a very small amount of heterosynaptic LTD can be observed in unstimulated synapses 1 and 4. (C) Relative change of synaptic efficacies and pool size due to homosynaptic LTP and heterosynaptic LTD in B as a function of time. (D) Same as C but for a smaller filling fraction of $F = 0.5$ and a smaller relative pool size of $ϕ = 1.0$ . Note the smaller transient increase in efficacy of potentiated synapses (compare peaks of green curves in C and D) and the increased amount of heterosynaptic LTD (compare troughs of blue curves). (**E, F**) Maximum amount of homosynaptic LTP (E) and heterosynaptic LTD (F) as a function of relative pool size $ϕ$ for three different filling fractions.

https://doi.org/10.7554/eLife.37836.009

Figure 7

Download asset Open asset

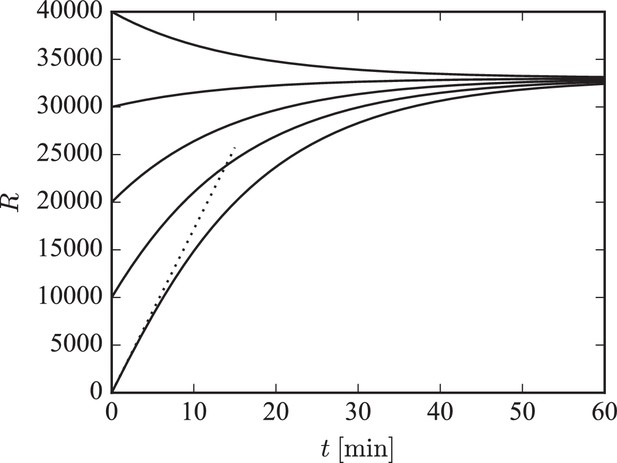
Illustration of long-term behavior under the separation of time scales assumption.

Parameters were: $β = 1 / 43 s^{- 1}$ , $δ = 1 / 14 {m i n}^{- 1}$ . The desired relative pool size was set to $ϕ = 2.67$ and the desired filling fraction to $F = 0.9$ . The production rate $γ$ and attachment rate $α$ were calculated according to Equation 12 and Equation 13, respectively. The steady-state total number of receptors in this example is given by $R^{\infty} = (1 + ϕ) F S = 33 030$ .

https://doi.org/10.7554/eLife.37836.010

Figure 8

Download asset Open asset

Quantification of spontaneous synaptic efficacy fluctuations due to the fast exchange of receptors between synapses and the receptor pool.

(A) Example simulation of a piece of dendrite with 7 synapses during 10 min of simulated time. The number of receptor slots in each synapse is given in the legend. The relative pool size was set to $ϕ = 2.67$ and the filling fraction was set to $F = 0.5$ by choosing the binding rate to receptor slots $α$ via Equation 13. (B) Same as A. but for a higher filling fraction of $F = 0.9$ . (C) Size of synaptic efficacy fluctuations as measured by the coefficient of variation (CV) as a function of the steady state number of receptors in each synapse, which is given by the product of the filling fraction $F$ and the number of slots $s_{i}$ in synapse $i$ . The relative pool size was set to $ϕ = 2.67$ . Data points represent averages over 10 simulations of 30 min simulated time each. Lines represent linear fits through the data points in double log space. (D) CV as a function of steady state number of receptors for different relative pool sizes $ϕ$ achieved by holding the binding rate to receptor slots $α$ fixed and varying the externalization rate $γ$ .

https://doi.org/10.7554/eLife.37836.011

Tables

Table 1

Standard parameters of the model.

https://doi.org/10.7554/eLife.37836.003

	Value	Description	Reference
$β$	${(43 s)}^{- 1}$	unbinding rate from slots	Henley and Wilkinson (2013); Henley and Wilkinson (2016)
$δ$	${(14 min)}^{- 1}$	internalization rate	Ehlers et al. (2007)
$ϕ$	2.67	relative pool size	M. Renner, personal communication
$F$	unknown	filling fraction	set by hand to {0.5, 0.7, 0.9}
$γ$	unknown	externalization rate	set via Equation 12 to achieve desired $ϕ$
$α$	unknown	binding rate to slots	set via Equation 13 to achieve desired $F$

Table 2

Summary of model predictions.

Further predictions are mentioned in the Discussion.

https://doi.org/10.7554/eLife.37836.005

Prediction	Explanation
Filling fraction	Synapses in a local group have identical filling fractions in the basal state.
Pool Size	Manipulation of local pool size scales synapses multiplicatively.
Sensitivity	Filling fraction is most sensitive when pool size matches slot numbers.
Heterosynaptic I	High pool size and filling fraction reduce heterosynaptic plasticity.
Heterosynaptic II	Heterosynaptic plasticity is only transient.
Homosynaptic	Pool size and filling fraction modulate homosynaptic plasticity.
Fluctuations	Spontaneous efficacy fluctuations are bigger for small synapses.

Table 3

Fitting results from the stochastic version of the model, cf. Figure 8C.

The externalization rate $γ$ and the attachment rate of receptors to slots $α$ are set to obtain different filling fractions while maintaining a relative pool size of $ϕ = 2.67$ . Parameters $β$ and $δ$ are as in Tab. 1. $a$ and $b$ give the parameters of the power law fits.

https://doi.org/10.7554/eLife.37836.012

$F$	$α [{min}^{- 1}]$	$γ [{min}^{- 1}]$	Scale factor $a$	Exponent $b$
0.5	0.0056	12.1	71.4	−0.52
0.7	0.0093	9.4	55.6	−0.51
0.9	0.0278	6.7	31.8	−0.50

Table 4

Fitting results from the stochastic version of the model, cf. Figure 8D.

The attachment rate of receptors to slots is chosen as $α = 0.0093 min^{- 1}$ to obtain a filling fraction of $0.7$ for a relative pool size of $ϕ = 2.67$ . Parameters $β$ and $δ$ are as in Tab. 1. $γ$ is varied to obtain different relative pool sizes $ϕ$ and filling fractions $F$ .