A prediction model of working memory across health and psychiatric disease using whole-brain functional connectivity
- Advanced Telecommunications Research Institute International, Japan
- Kyoto University, Japan
- Showa University, Japan
- The University of Tokyo, Japan
- National Institute of Radiological Sciences, Japan
- Hiroshima University, Japan
- Kyoto Prefectural University of Medicine, Japan
- University of Cambridge, United Kingdom
- National Institute of Information and Communications Technology, Japan
Figures
Figure 1
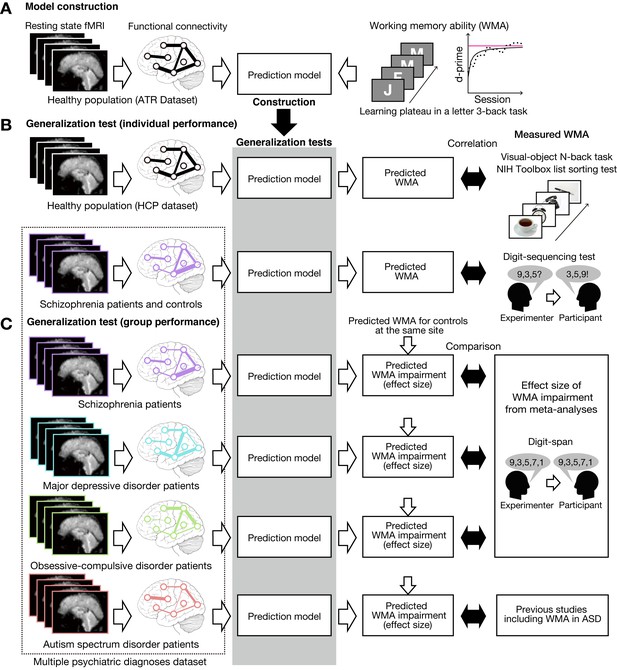
Schematic diagram of model construction and generalization tests using independent datasets.
(A) Model was developed using a whole-brain resting state FC and a learning plateau of a letter 3-back task within healthy individuals from ATR dataset. (B) We applied the model to resting state FC patterns and predicted individual participant’s working memory ability. We first examined the external validity using an independent USA healthy dataset (HCP dataset: the upper flow chart in (B)). The predicted working memory ability was compared to actual working memory performance (visual-object N-back task and the NIH toolbox list sorting test). Then we examined the generalizability to a clinical population using a schizophrenia dataset (the lower flow chart in (B)). The predicted working memory ability was compared to actual working memory score measured by Digit sequencing test. (C) Using the multiple psychiatric diagnoses dataset, degree of working memory impairment for each diagnosis was predicted as differences from corresponding controls. The predicted impairments were validated by previous meta-analysis studies on digit-span across multiple diagnoses. Note that the HCP dataset’s task stimuli images are just illustration purpose and different from the original stimuli.
Figure 2 with 1 supplement
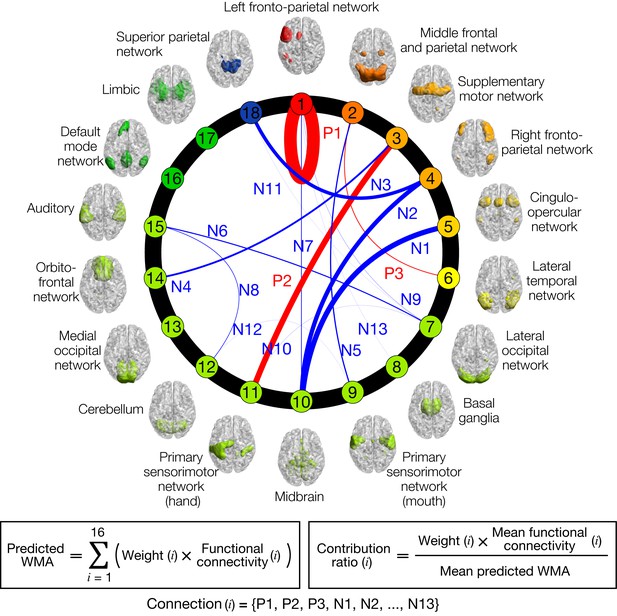
Normative model of working memory ability (WMA).
Circle plot of networks and their connections in the model. Individual letter 3-back learning plateaus are predicted by a linear weighted summation of 16 FC values at 16 connections selected by a sparse linear regression algorithm. Connection thicknesses indicate contribution ratios (weight x FC at each connection). Connections are labeled ‘Positive/Negative (P/N)’ based on correlation coefficient signs with letter 3-back learning performances, whereas numbers indicate descending orders of contribution ratio. Each network’s color indicates relevance with working memory function based on BrainMap ICA (Laird et al., 2011); warmer colors indicate closer relevance to working memory function. See Table 1 for the networks connected by the selected 16 connections, and precise values of contribution ratio of each connection. Each network’s label and regions included in it are summarized in Supplementary file 2.
Figure 2—figure supplement 1
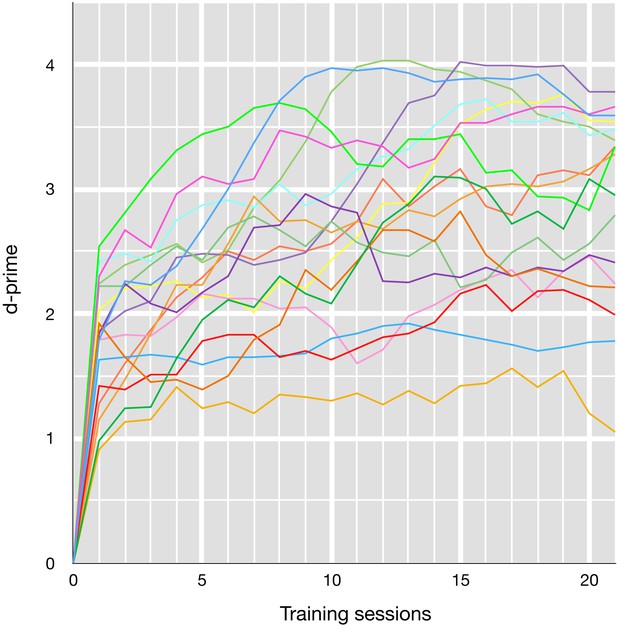
Letter 3-back learning curves for each participant.
Data points were five-session moving averaged (e.g. training session one plots average d-prime from sessions 1 to 5).
Figure 3 with 3 supplements
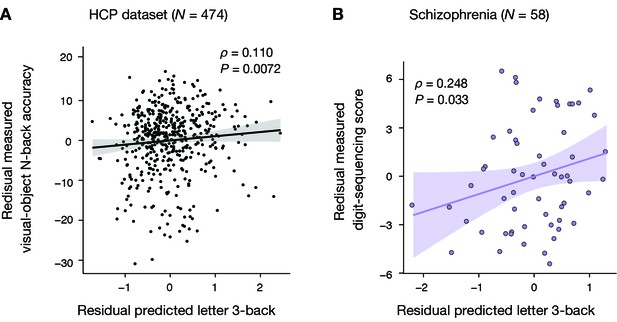
Generalizability to HCP dataset and schizophrenia dataset.
(A) Significant Spearman’s rank partial correlation between predicted letter 3-back learning performance and measured visual-object N-back accuracy while factoring out general fluid intelligence and head motion (ρ = 0.110, p = 0.0072). (B) Significant Pearson partial correlation between predicted letter 3-back performances and measured digit-sequencing scores while factoring out the composite BACS score and age (ρ = 0.248, p = 0.033).
Figure 3—figure supplement 1
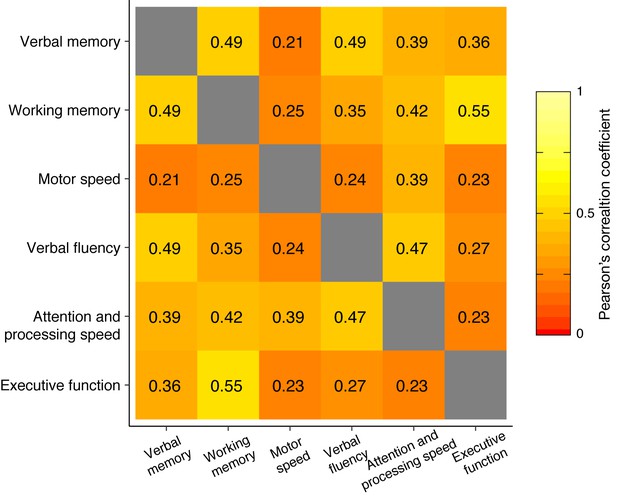
Spearman’s rank correlation matrix for HCP dataset.
https://doi.org/10.7554/eLife.38844.006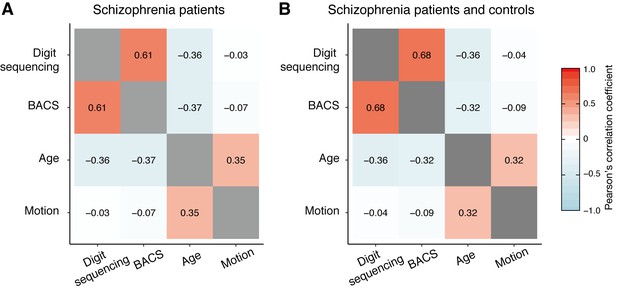
Figure 3—figure supplement 2
Pearson’s correlation matrices for schizophrenia samples.
(A) Correlation among schizophrenia patients (N = 58). (B) Correlation among schizophrenia patients and controls (N = 118).
Figure 3—figure supplement 3
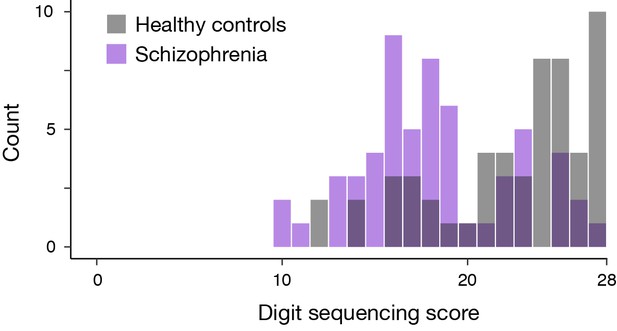
Distribution of BACS digit-sequencing score.
The count of healthy controls increased toward the maximum score (28), and the largest count was found for the maximum score. This suggests a ceiling effect in the healthy controls.
Figure 4 with 1 supplement
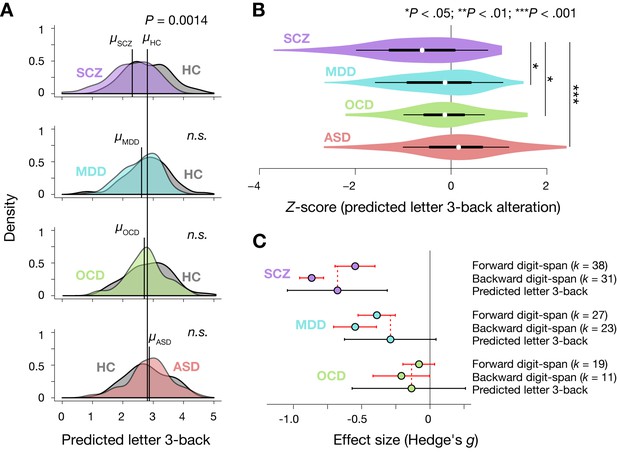
Prediction of diagnosis-specific alterations of working memory ability.
(A) Predicted letter 3-back working memory ability for patients (N = 58, 77, 45, and 69 for SCZ, MDD, OCD, and ASD, respectively) and their age- and gender-matched healthy/typically developed controls (HC, N = 60, 62, 47, and 71) shown as kernel density. For illustration purposes, distribution of each control group was standardized to that of the ATR dataset, and the same linear transformation was applied to patients’ distributions. μ indicates mean value for each group. (B) Violin plots of Z-scores for predicted working memory ability alterations. White circles indicate medians. Box limits indicate 25th and 75th percentiles. Whiskers extend 1.5 times interquartile range from 25th and 75th percentiles. (C) Comparison of estimated effect sizes for working memory deficits. k indicates number of studies included in the meta-analyses (Forbes et al., 2009; Snyder, 2014; Snyder et al., 2015). Error bars indicate 95% confidence intervals.
Figure 4—figure supplement 1
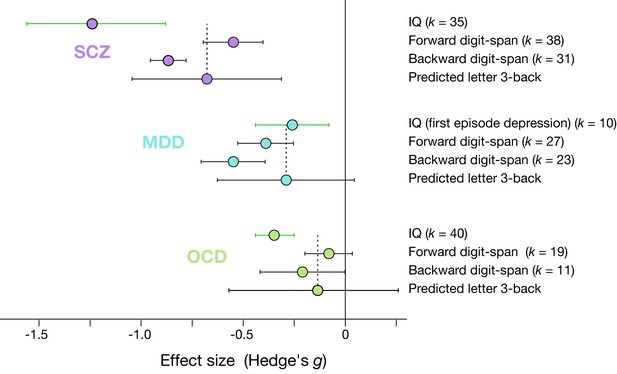
Effect sizes of IQ, digit-span, and predicted working memory ability.
k indicates number of studies included in the meta-analyses (Abramovitch et al., 2018; Ahern and Semkovska, 2017; Heinrichs and Zakzanis, 1998). Error bars indicate 95% confidence intervals.
Figure 5 with 3 supplements
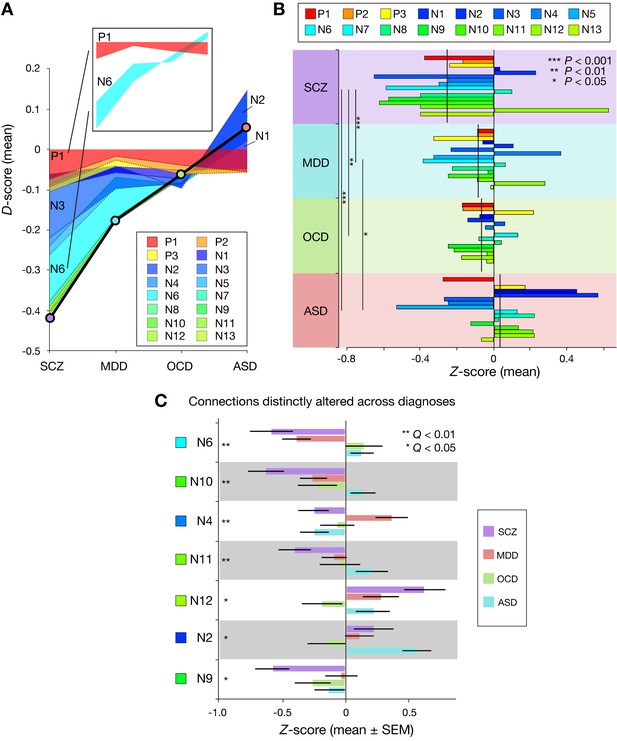
Accumulation of function connectivity differences exhibits diagnosis-specific working memory ability.
(A) Accumulation of averaged D-scores for all 16 connections. Bold black line indicates summation of contributions by all connections, corresponding to predicted working memory ability alteration. This figure shows how diagnosis-specific working memory impairment results from complex disturbances of multiple connections. Upper panel depicts two representative alteration patterns across diagnoses. While connection P1 commonly decreased working memory ability across diagnoses, connection N6 distinctly affected working memory ability (decrease in SCZ and MDD and increase in OCD and ASD). (B) Z-scores (normalized D-scores) for each diagnosis. Left asterisks and lines indicate significant differences in mean Z-scores between two diagnoses (p < 0.05, Bonferroni corrected). Vertical lines across horizontal bars indicate Z-scores averaged across connections. (C) Z-scores for connection that showed a significant effect of diagnosis. Connections were sorted by small p values of diagnosis effect (Kruskal-Wallis test, Q < 0.05, FDR corrected).
Figure 5—figure supplement 1
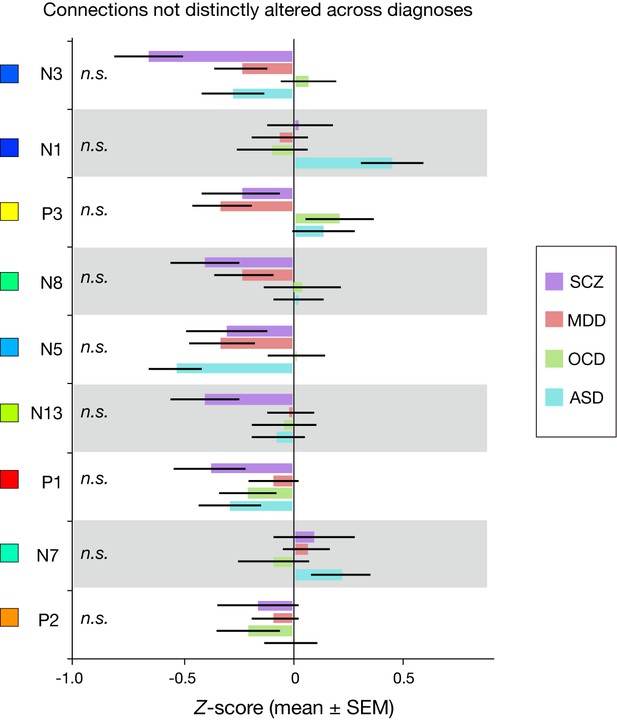
Connections of non-significant effect of diagnosis.
https://doi.org/10.7554/eLife.38844.014
Figure 5—figure supplement 2
Distribution of magnitude of diagnosis effect on connectivity change between the connections in the model and other connections.
The horizontal axis shows chi-square values of a Kruskal-Wallis test for each connection. There was no significant difference between the two groups (two-sample Kolmogorov-Smirnov test, p = 0.30).
Figure 5—figure supplement 3
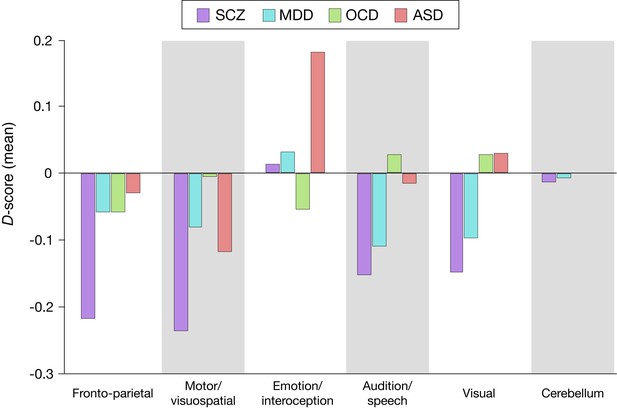
D-scores related to network clusters.
https://doi.org/10.7554/eLife.38844.016
Author response image 1
Pearson’s correlation matrix of BACS sub-scores.
Tables
Table 1
Selected connections and their contribution to working memory ability.
https://doi.org/10.7554/eLife.38844.012| Label | Connection (rank) | Contribution ratio [%] | ||
|---|---|---|---|---|
| Positive features | ||||
| P1 | Left fronto-parietal network (1) | (within-network) | 33.9% | |
| P2 | Supplemental motor network (3) | Primary sensorimotor network (hand) (11) | 15.4% | |
| P3 | Middle frontal and parietal network (2) | Lateral temporal network (6) | 1.9% | |
| Negative features | ||||
| N1 | Cingulo-opercular network (5) | Midbrain (10) | 13.9% | |
| N2 | Right fronto-parietal network (4) | Midbrain (10) | 11.4% | |
| N3 | Right fronto-parietal network (4) | Superior parietal network (18) | 9.2% | |
| N4 | Supplemental motor network (3) | Orbitofrontal network (14) | 5.0% | |
| N5 | Middle frontal and parietal network (2) | Primary sensorimotor network (mouth) (9) | 3.0% | |
| N6 | Lateral occipital network (7) | Auditory (15) | 2.6% | |
| N7 | Left fronto-parietal network (1) | Midbrain (10) | 1.8% | |
| N8 | Cerebellum (12) | Auditory (15) | 1.3% | |
| N9 | Left fronto-parietal network (1) | Lateral occipital network (7) | 0.3% | |
| N10 | Lateral occipital network (7) | Primary sensorimotor network (hand) (11) | 0.3% | |
| N11 | Lateral occipital network (7) | Superior parietal network (18) | 0.1% | |
| N12 | Primary sensorimotor network (mouth) (9) | Cerebellum (12) | −0.0% | |
| N13 | Left fronto-parietal network (1) | Basal ganglia (8) | −0.2% | |
-
Rank indicates relevance with working memory function according to the BrainMap ICA.
Table 2
Demographic data of the multiple psychiatric diagnoses dataset.
https://doi.org/10.7554/eLife.38844.011| Diagnosis | Site | Measure | Patients | Controls | Test | P-value |
|---|---|---|---|---|---|---|
| SCZ | KYU | N | 58 | 60 | - | - |
| Age | 37.9 | 35.2 | t116 = 1.7 | 0.1 | ||
| (9.3) | (8.4) | |||||
| Male % | 52% | 67% | Fisher’s exact test | 0.13 | ||
| MDD | HRU | N | 77 | 63 | - | - |
| Age | 41.6 | 39.3 | t138 = 1.3 | 0.21 | ||
| (11.2) | (12.0) | |||||
| Male % | 56% | 46% | Fisher’s exact test | 0.31 | ||
| OCD | KPM | N | 46 | 47 | - | - |
| Age | 32.2 | 30.3 | t91 = 1.1 | 0.28 | ||
| (9.9) | (8.7) | |||||
| Male % | 37% | 45% | Fisher’s exact test | 0.53 | ||
| ASD | UTK (site1) | N | 33 | 33 | - | - |
| Age | 32.8 | 34.7 | t64 = −1.0 | 0.3 | ||
| (8.4) | (7.0) | |||||
| Male % | 64% | 55% | Fisher’s exact test | 0.62 | ||
| SHU (site2) | N | 36 | 38 | - | - | |
| Age | 29.9 | 32.5 | t72 = −1.5 | 0.14 | ||
| (7.2) | (7.4) | |||||
| Male % | 100% | 100% | Fisher’s exact test | 1 | ||
| Pooled | N | 69 | 71 | - | - | |
| Age | 31.3 | 33.5 | t138 = −1.8 | 0.08 | ||
| (7.9) | (7.2) | |||||
| Male % | 83% | 79% | Fisher’s exact test | 0.67 |
-
Site: KYU, Kyoto University; HRU, Hiroshima University; KPM, Kyoto Prefectural University of Medicine; UTK, University of Tokyo; SHU, Showa University. Measure: ‘N’ indicates the number of subjects; ‘Age’ is shown as mean (SD); ‘Male %” is the fraction of male. The tests and p-values compare the patient and control groups within-site.
Additional files
-
Supplementary file 1
Resting state fMRI scan parameters and their values.
- https://doi.org/10.7554/eLife.38844.017
-
Supplementary file 2
Whole-brain intrinsic functional network labels and their component regions.
- https://doi.org/10.7554/eLife.38844.018
-
Transparent reporting form
- https://doi.org/10.7554/eLife.38844.019
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
A prediction model of working memory across health and psychiatric disease using whole-brain functional connectivity
eLife 7:e38844.
https://doi.org/10.7554/eLife.38844
