Extrinsic and intrinsic dynamics in movement intermittency
- Newcastle University, United Kingdom
Figures
Figure 1 with 3 supplements
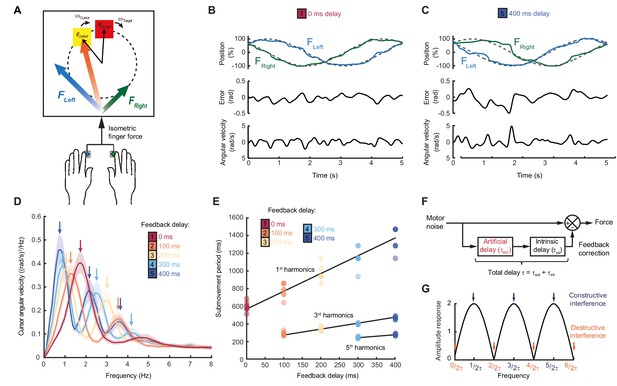
Movement intermittency during visuomotor tracking depends on feedback delays.
(A) Schematic of human tracking task. Bimanual isometric finger forces controlled 2D cursor position to track slow, circular target motion. Kinematic analyses used the angular velocity of the cursor …
-
Figure 1—source data 1
Subject information, time periods of submovement peaks and associated regression analysis.
- https://doi.org/10.7554/eLife.40145.006
Figure 1—figure supplement 1
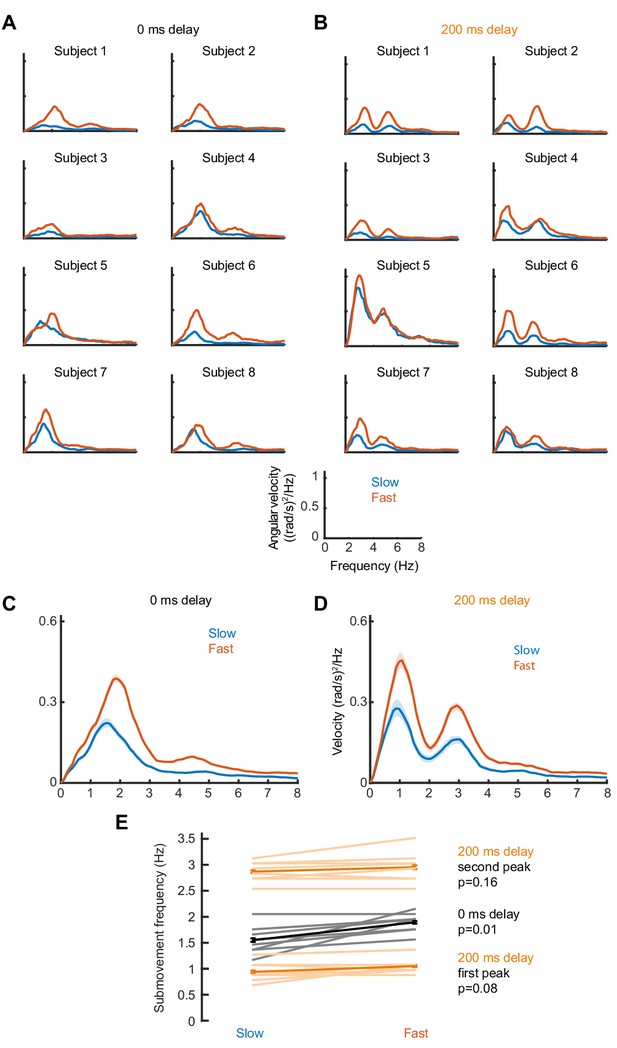
Effect of target speed on movement intermittency.
(A) Power spectra of cursor angular velocity for individual subjects with slow (0.1 cycles/s) or fast (0.2 cycles/s) target rotation, and no feedback delay. (B) Power spectra of cursor angular …
Figure 1—figure supplement 2
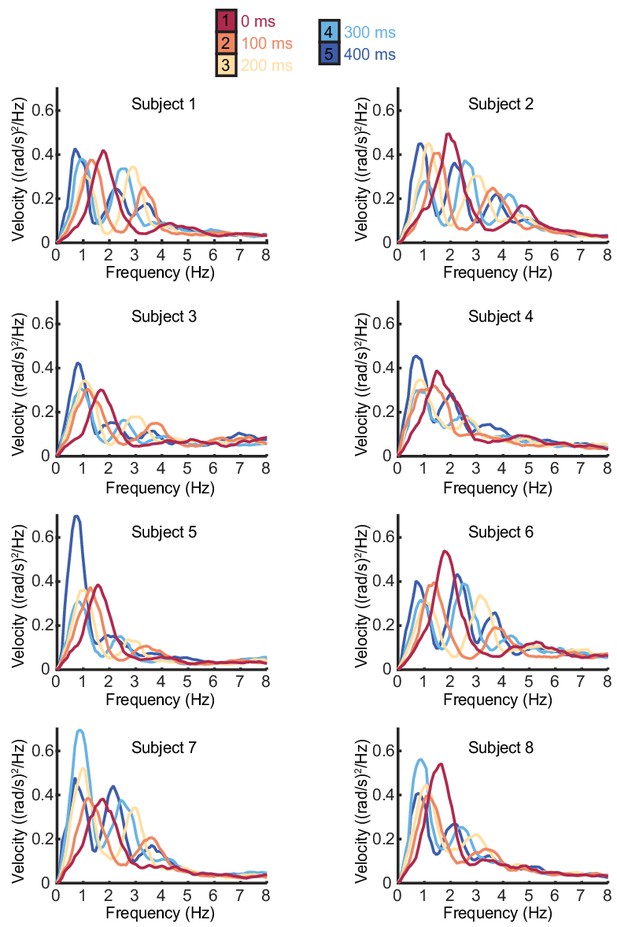
Individual subject power spectra of cursor velocity with different feedback delays.
Power spectra of cursor angular velocity for individual subjects with 0–400 ms feedback delay. The average over subjects is shown in Figure 1D.
Figure 1—figure supplement 3
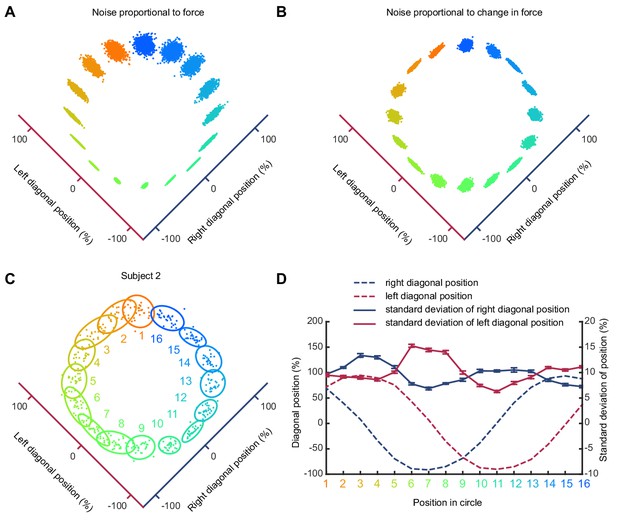
Trajectory variability depends on change in isometric force.
(A) Simulated pattern of trial-to-trial variability if motor noise is proportional to absolute force. (B) Simulated pattern of trial-to-trial variability if motor noise is proportional to derivative …
Figure 2 with 3 supplements
Frequency responses and phase delays to artificial motor errors.
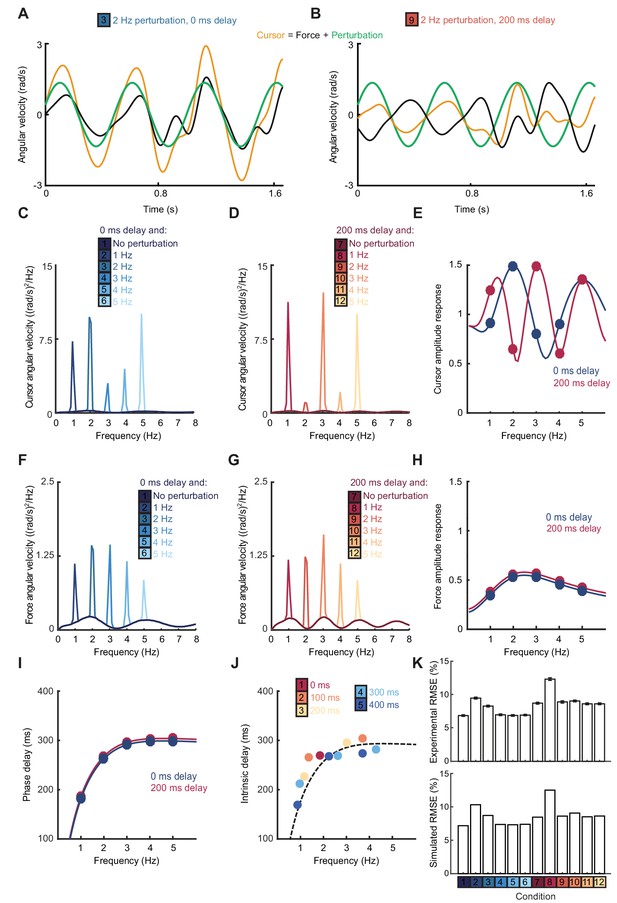
(A) Example force (black) and cursor (yellow) angular velocity traces in the presence of a 2 Hz perturbation (green) when no feedback delay was added. The force response and perturbation sum to …
-
Figure 2—source data 1
Subject information, perturbation responses and feedforward amplitude responses.
Data for individual subjects in Experiment 2 (summarized in Figure 2C–I) and Experiment 3 (summarized in Figure 2K).
- https://doi.org/10.7554/eLife.40145.012
Figure 2—figure supplement 1
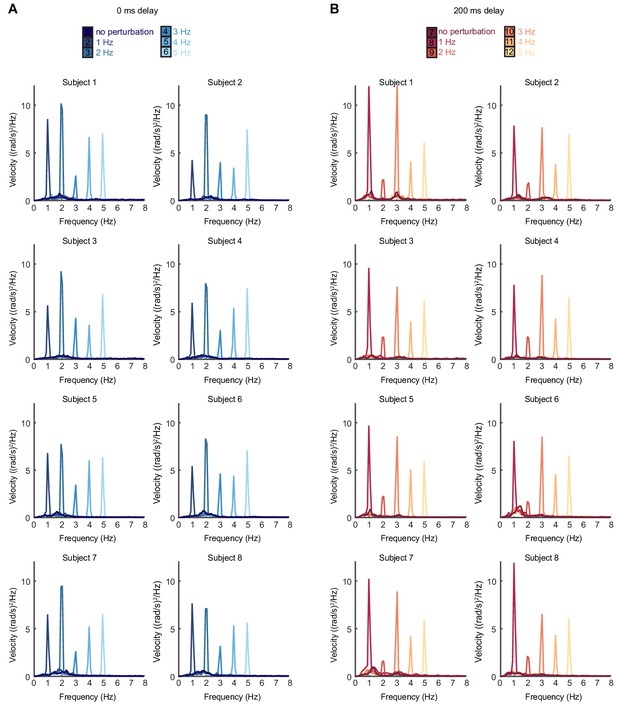
Individual subject power spectra of cursor velocity with perturbations.
(A) Power spectra of cursor angular velocity for individual subjects with 1–5 Hz perturbations and no feedback delay. The average over subjects is shown in Figure 2C. (B) Power spectra of cursor …
Figure 2—figure supplement 2
Individual subject power spectra of force velocity with perturbations.
(A) Power spectra of force angular velocity for individual subjects with 1–5 Hz perturbations and no feedback delay. The average over subjects is shown in Figure 2F. (B) Power spectra of force …
Figure 2—figure supplement 3
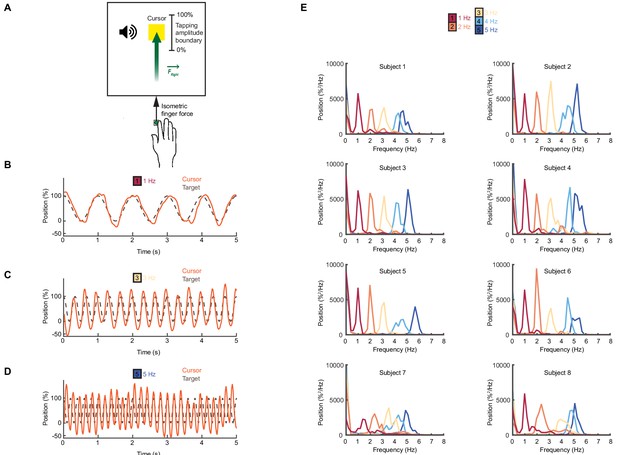
Feedforward task.
(A) Schematic of the feedforward isometric task. Subjects generated sinusoidal forces within a set range, at a frequency indicated by an auditory cue. (B–D) Performance of an example subject for …
Figure 3
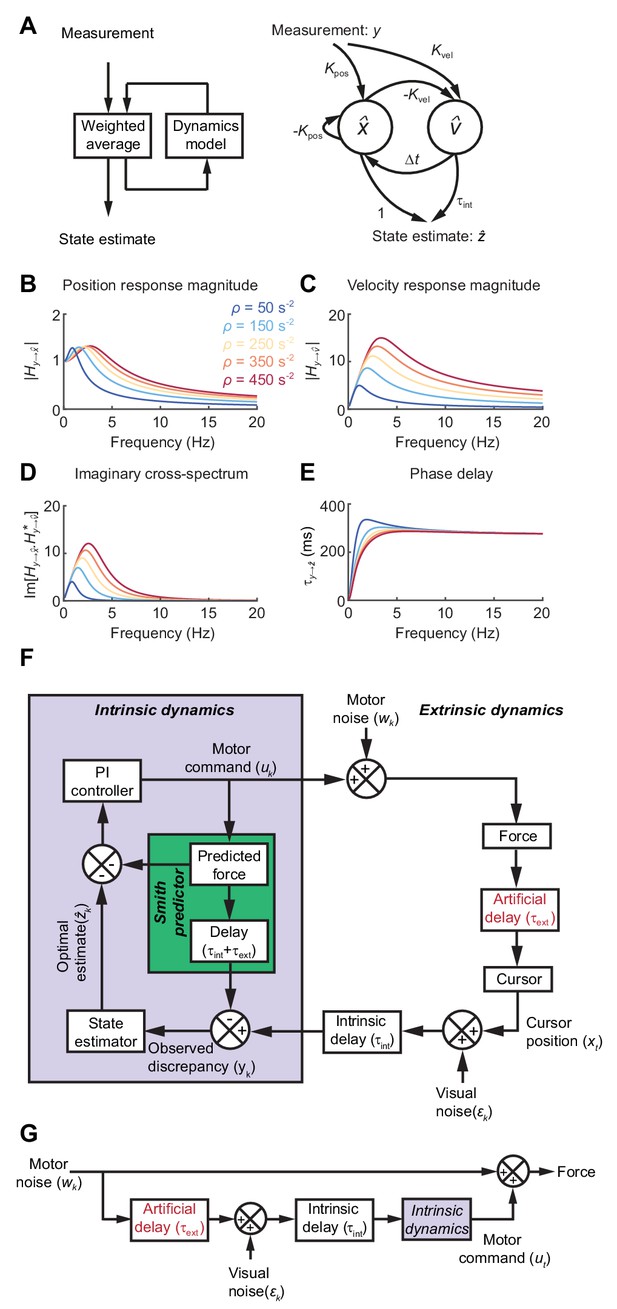
State estimation with a Kalman filter.
(A) Left: Schematic of a Kalman filter. Noisy measurements are combined with an internal model of the external dynamics to update an optimal estimate of current state. Right: A dynamical system for …
Figure 4
Smith Predictor model with optimal state estimation reproduces human behavioral data.
(A) Simulated tracking performance of the model with a 2 Hz sinusoidal perturbation and no feedback delay. (B) Simulated tracking performance of the model with a 2 Hz sinusoidal perturbation and 200 …
Figure 5
Emergence of predictive control strategies within individual trials.
(A) Schematic of a simple feedback controller with intrinsic gain, and time delay, . (B) A Smith Predictor with intrinsic gain, , time delay and calibrated internal feedback loop. (C,D) …
Figure 6
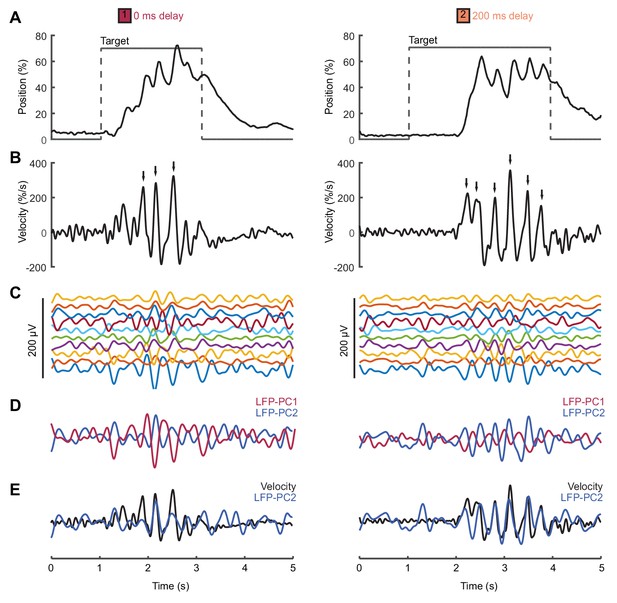
Movement intermittency in a non-human primate tracking task.
(A) Radial cursor position during a typical trial of the center-out isometric wrist torque task under two different feedback delay conditions. Data from Monkey U. (B) Radial cursor velocity. …
Figure 7
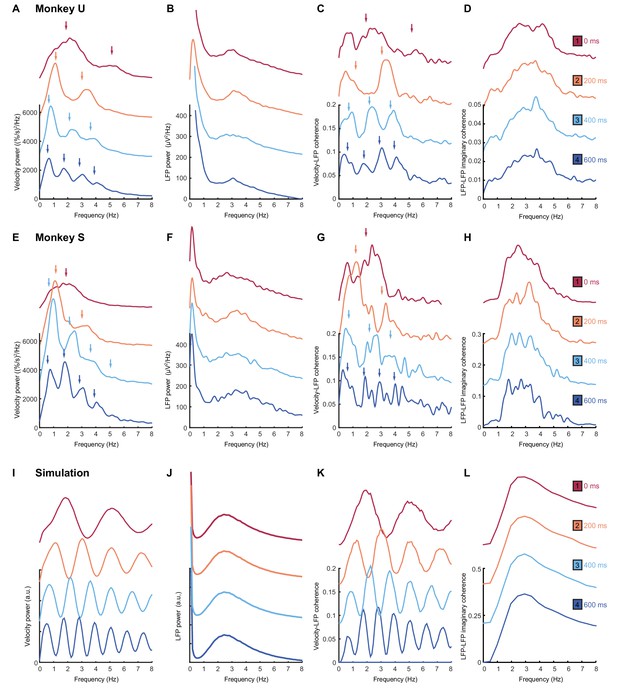
Frequency-domain analysis reveals delay-dependent and delay-independent spectral features.
(A) Power spectrum of radial cursor speed with 0–600 ms feedback delay. Traces have been off-set for clarity. Arrows indicate expected frequencies of peaks from OFC model. Data from Monkey U. (B) …
Figure 8 with 1 supplement
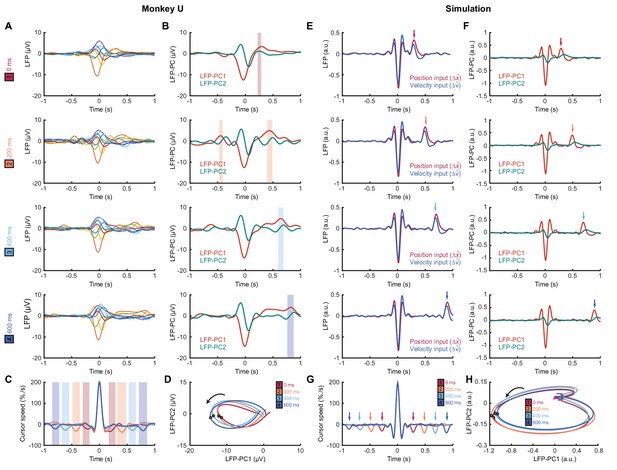
Submovement-triggered averages of M1 LFPs.
(A) Average low-pass filtered LFPs from M1, aligned to the peak speed of submovements with 0–600 ms feedback delay. Note the second feature, which follows submovements by an extrinsic, …
Figure 8—figure supplement 1
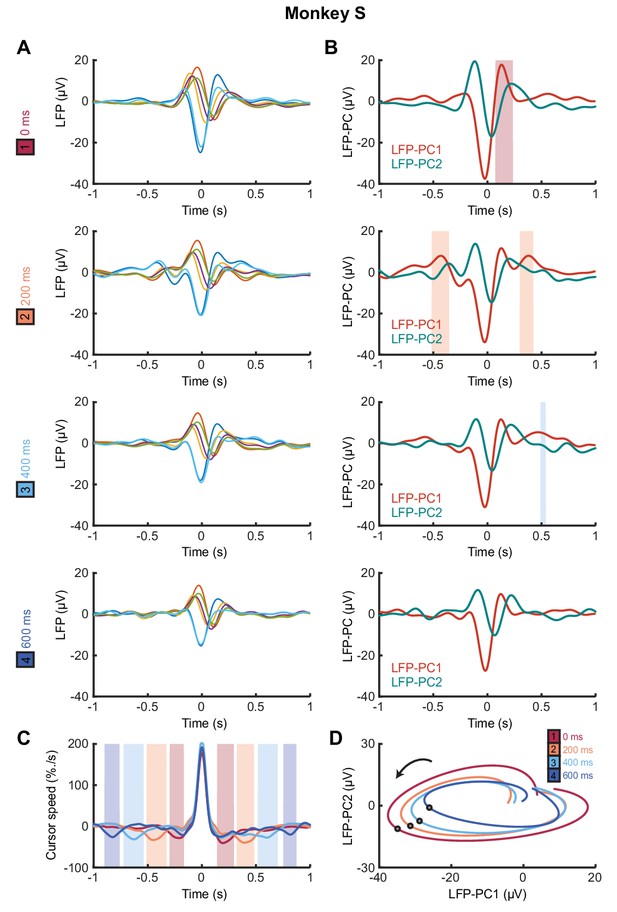
Submovement-triggered averages of M1 LFPs for Monkey S.
(A) Average low-pass filtered LFPs from M1, aligned to the peak speed of submovements with 0–600 ms feedback delay. Data from Monkey S. (B) Average of first two LFP-PCs aligned to submovements. …
Figure 9
Schematic of delay-dependent and delay-independent relationships in the OFC model.
The boxes show how the various frequency-domain and submovement-triggered average (SmTA) relationships are explained by the OFC model. Top row, from left to right: Broad spectrum motor noise drives …
Figure 10
Simulated LFP dynamics during movement and sedation.
(A) K-complex events in LFP from M1 recorded under ketamine sedation. (B) Average low-pass filtered multichannel LFPs aligned to K-complex events. LFPs are color-coded according to phase relative to …
Tables
Table 1
The dependency of submovement period on feedback delay.
Shown in the table are the gradients and intercepts of regression lines fitted to each harmonic group in Figure 1E. The time period of each spectral peak was regressed against feedback delay. Shown …
| Harmonic (N) | Predicted slope = 2/N | Measured slope | Measured intercept (ms) | R2 | P | τint = Intercept*N/2 |
|---|---|---|---|---|---|---|
| 1 | 2 | 1.89 [1.69,2.09] | 589 ms [539,638] | 0.90 | <0.00001 | 294 ms [270,319] |
| 3 | 0.67 | 0.59 [0.53,0.65] | 226 ms [211,242] | 0.94 | <0.00001 | 340 ms [316,362] |
| 5 | 0.4 | 0.33 [0.22,0.45] | 146 ms [106,185] | 0.75 | <0.00001 | 364 ms [266,463] |
Additional files
-
Source code 1
MATLAB implementation of feedback controller model.
Code used to generate Figure 4.
- https://doi.org/10.7554/eLife.40145.022
-
Transparent reporting form
- https://doi.org/10.7554/eLife.40145.023
