Figures and data in Biophysical mechanisms in the mammalian respiratory oscillator re-examined with a new data-driven computational model

Figures
Tables
Additional files

11 figures, 1 table and 2 additional files

Figures

Figure 1

Download asset Open asset

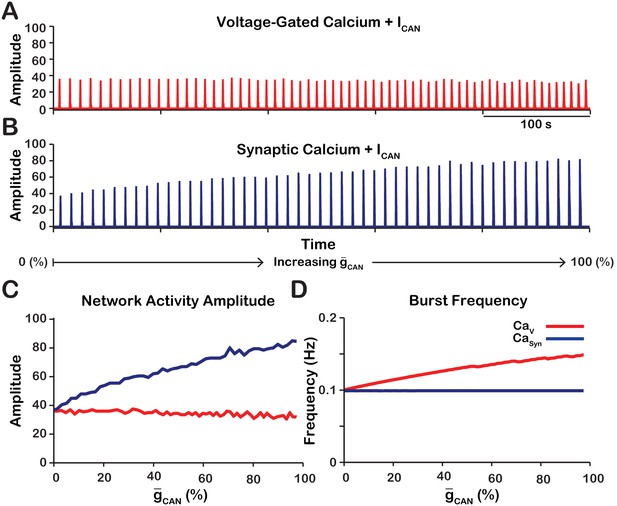
Manipulations of ${\bar{g}}_{C A N}$ in the ${C a}_{V}$ and ${C a}_{S y n}$ networks produce opposite effects on network activity amplitude (spikes/s) and frequency.

(A and B) Histograms of neuronal population activity amplitude in the ${C a}_{V}$ , and ${C a}_{S y n}$ networks with linearly increasing ${\bar{g}}_{C A N}$ . (C) Plot of ${\bar{g}}_{C A N}$ (% of the baseline mean value for the simulated population) vs. network activity amplitude for the ${C a}_{V}$ and ${C a}_{S y n}$ networks in A and B. (D) Plot of ${\bar{g}}_{C A N}$ (%) vs. network frequency for the ${C a}_{V}$ and ${C a}_{S y n}$ networks in A and B. ${C a}_{V}$ network parameters: ${\bar{g}}_{C a} = 1.0 (n S)$ , $P_{C a} = 0.0$ , $P_{S y n} = 0.05$ and $W_{m a x} = 0.2 (n S)$ . ${C a}_{S y n}$ network parameters: ${\bar{g}}_{C a} = 0 (n S)$ , $P_{C a} = 0.01$ , $P_{S y n} = 0.05$ and $W_{m a x} = 0.2 (n S)$ .

https://doi.org/10.7554/eLife.41555.002

Figure 2

Download asset Open asset

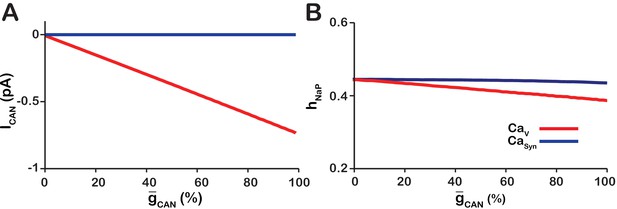
Calcium source and ${\bar{g}}_{C A N}$ -dependent effects on cellular properties regulating network frequency for the simulations presented in Figure 1.

(A) Average magnitude of $I_{C A N}$ in pacemaker neurons during the interburst interval for the ${C a}_{V}$ (red) and ${C a}_{S y n}$ (blue) networks. (B) Average inactivation ( $h_{N a P})$ of the burst generating current $I_{N a P}$ in pacemaker neurons immediately preceding each network burst as a function of ${\bar{g}}_{C A N}$ (%) for the voltage-gated and synaptic calcium networks. ${C a}_{V}$ network parameters: ${\bar{g}}_{C a} = 1.0 (n S)$ , $P_{C a} = 0.0$ , $P_{S y n} = 0.05$ and $W_{m a x} = 0.2 (n S)$ . ${C a}_{S y n}$ network parameters: ${\bar{g}}_{C a} = 0 (n S)$ , $P_{C a} = 0.01$ , $P_{S y n} = 0.05$ and $W_{m a x} = 0.2 (n S)$ .

https://doi.org/10.7554/eLife.41555.003

Figure 3

Download asset Open asset

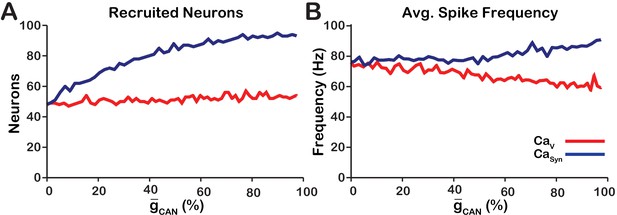
Calcium source and ${\bar{g}}_{C A N}$ -dependent effects on cellular properties regulating network activity amplitude for the simulations presented in Figure 1.

(A) Number of recruited neurons in the modeled population of 100 neurons as a function of ${\bar{g}}_{C A N}$ (%) for voltage-gated and synaptic calcium sources. The number of recruited neurons is defined as the peak number of spiking neurons per bin during a network burst. (B) Average spiking frequency of recruited neurons as a function of ${\bar{g}}_{C A N}$ for the voltage-gated and synaptic calcium mechanism. Average spiking frequency is defined the number of spikes per bin divided by the number of recruited neurons. The parameters used in these simulations are: ${C a}_{V}$ : ${\bar{g}}_{C a} = 1.0 (n S)$ , $P_{C a} = 0.0$ , $P_{S y n} = 0.05$ and $W_{m a x} = 0.2 (n S)$ . ${C a}_{S y n}$ : ${\bar{g}}_{C a} = 0 (n S)$ , $P_{C a} = 0.01$ , $P_{S y n} = 0.05$ and $W_{m a x} = 0.2 (n S)$ .

https://doi.org/10.7554/eLife.41555.004

Figure 4

Download asset Open asset

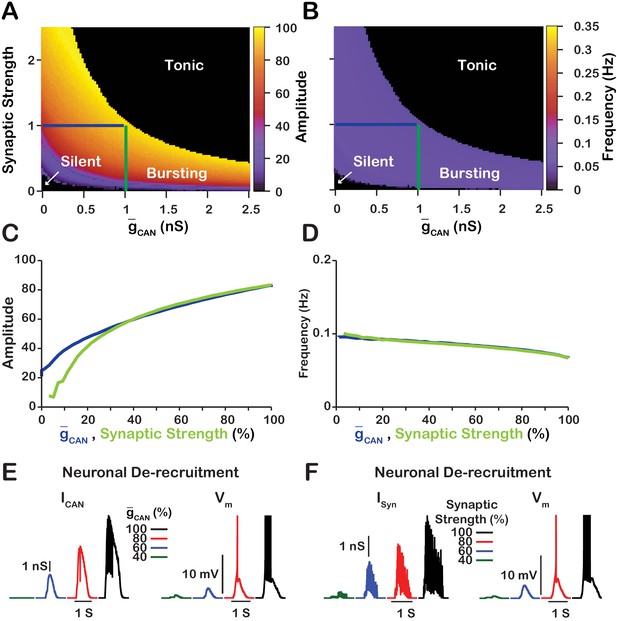
Manipulations of synaptic strength ( $N \cdot P_{S y n} \cdot \frac{1}{2} W_{m a x}$ ) and ${\bar{g}}_{C A N}$ have equivalent effects on network activity amplitude, frequency and recruitment of inspiratory neurons not involved in rhythm generation.

(A and B) Relationship between ${\bar{g}}_{C A N}$ (mean values for the simulated populations), synaptic strength and the amplitude and frequency in the ${C a}_{S y n}$ network. Notice the symmetry about the X=Y line in panels A and B, which, indicates that changes in ${\bar{g}}_{C A N}$ and or synaptic strength are qualitatively equivalent. Synaptic strength was changed by varying $W_{m a x}$ . (C) Relationship between network activity amplitude and the reduction of ${\bar{g}}_{C A N}$ (blue) or synaptic strength (green). (D) Relationship between network frequency and the reduction of ${\bar{g}}_{C A N}$ (blue) or synaptic strength (green). (E and F) Decreasing ${\bar{g}}_{C A N}$ or synaptic strength de-recruits neurons by reducing the inspiratory drive potential, indicated by the amplitude of subthreshold depolarization, right traces. The solid blue and green lines in panels A and B represent the location in the 2D parameter space of the corresponding blue and green curves in C and D. The action potentials in the right traces of E and F are truncated to show the change in neuronal inspiratory drive potential. The parameters used for these simulations are ${C a}_{S y n}$ : ${\bar{g}}_{C a} = [0,0]$ , $P_{C a} = 0.01$ , $P_{S y n} = 1.0$ and $W_{m a x} = v a r$ .

https://doi.org/10.7554/eLife.41555.005

Figure 5

Download asset Open asset

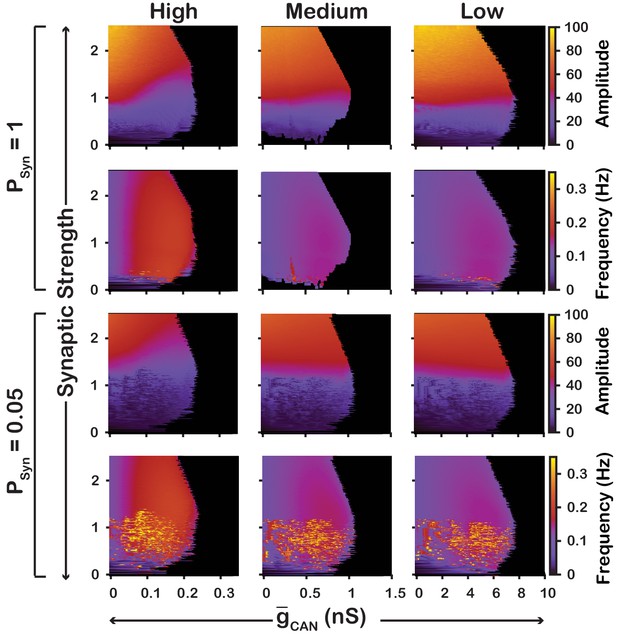
Robustness of amplitude and frequency effects to changes in ${\bar{g}}_{C A N}$ and synaptic strength in the ${C a}_{V}$ network for ‘high’ (left), ‘medium’ (middle) and ‘low’ (right) conductance of the voltage-gated calcium channel $I_{C a}$ as well as ‘high’ (top) and ‘low’ (bottom) network connection probabilities.

Amplitude and frequency are indicated by color (scale bar at right). Black regions indicate tonic network activity. Values of ${\bar{g}}_{C A N}$ indicated are the mean values for the simulated neuronal populations.

https://doi.org/10.7554/eLife.41555.006

Figure 6

Download asset Open asset

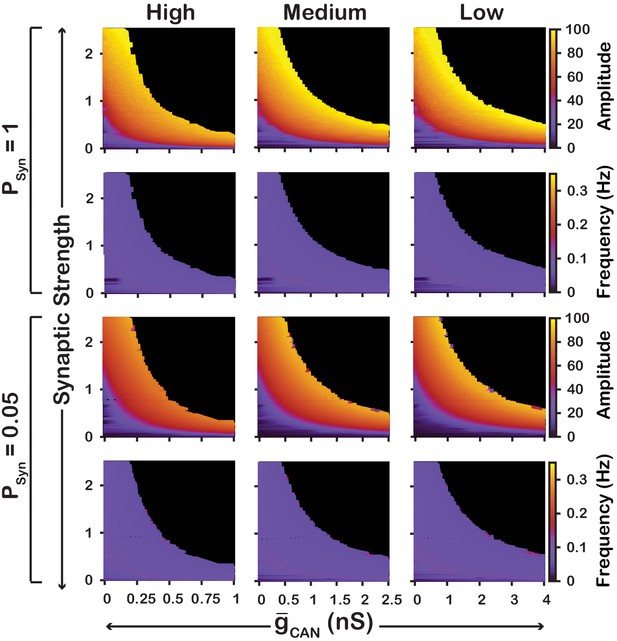
Robustness of amplitude and frequency effects to changes in ${\bar{g}}_{C A N}$ and synaptic strength in the ${C a}_{S y n}$ network for ‘high’ (left), ‘medium’ (middle) and ‘low’ (right) calcium conductance in synaptic currents as well as ‘high’ (top) and ‘low’ (bottom) network connection probabilities.

Amplitude and frequency are indicated by color (scale bar at right). Black regions indicate tonic network activity. Values of ${\bar{g}}_{C A N}$ indicated are the mean values for the simulated neuronal populations.

https://doi.org/10.7554/eLife.41555.007

Figure 7

Download asset Open asset

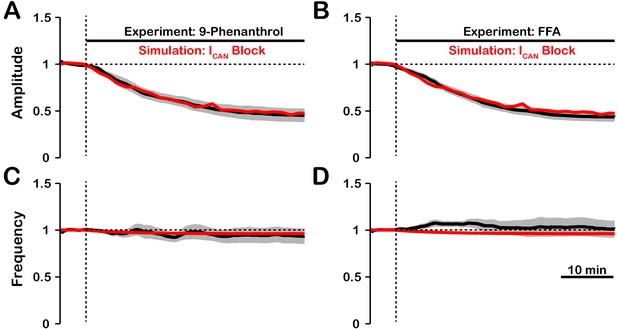
Experimental and simulated pharmacological blockade of $I_{C A N}$ by (**A and C**) 9-phenanthrol and (**B and D**) flufenamic acid (FFA).

Both voltage-gated and synaptic sources of intracellular calcium are included. Experimental blockade of $I_{C A N}$ (black) by 9-phenanthrol and FFA significantly reduce the (**A and B**) amplitude of network oscillations while having little effect on (**C and D**) frequency. The black line represents the mean and the gray band is the S.E.M. of experimental integrated XII output recorded from neonatal rat brainstem slices in vitro, reproduced from Koizumi et al., 2018. Simulated blockade of $I_{C A N}$ (red) closely matches the reduction in (**A and B**) amplitude of network oscillations and slight decrease in (**C and D**) frequency seen with 9-phenanthrol and FFA. Simulated and experimental blockade begins at the vertical dashed line. Blockade was simulated by exponential decay of ${\bar{g}}_{C A N}$ with the following parameters: 9-phenanthrol: $?_{B l o c k} = 0.85$ , $t_{B l o c k} = 357 s$ ; FFA: $?_{B l o c k} = 0.92$ , $t_{B l o c k} = 415 s$ . The network parameters are: ${\bar{g}}_{C a} = 0.00175 (n S)$ , $P_{C a} = 0.0275$ , $P_{S y n} = 0.05$ and $W_{m a x} = 0.096 (n S)$ .

https://doi.org/10.7554/eLife.41555.008

Figure 8

Download asset Open asset

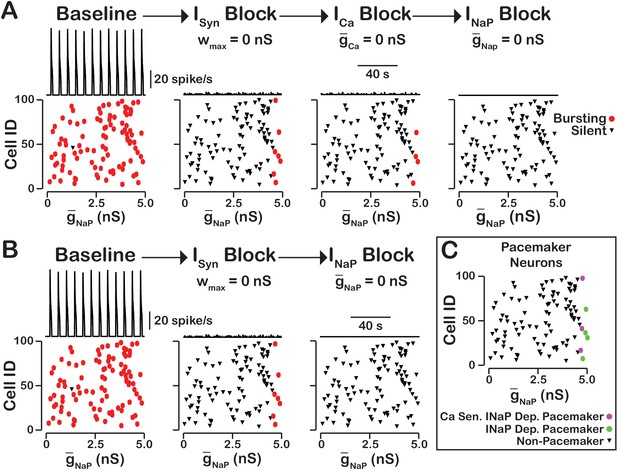
$I_{N a P}$ -dependent and ${C a}^{2 +}$ -sensitive intrinsic bursting.

(A) From left to right, intrinsic bursters (pacemakers) are first identified by blocking synaptic connections. Cells whose activity is elminated under these conditions are non-pacemaker neurons. Then, calcium sensitive neurons are silenced and identified by $I_{C a}$ blockade. The remaining neurons are identifed as sensitive to $I_{N a P}$ block. Top traces show the network output and Cell ID vs. ${\bar{g}}_{N a P}$ scatter plots that identify silent and bursting neurons under each condition. (B) $I_{N a P}$ blockade after synaptic blockade eleminates bursting in all neurons. Therefore, all intrinsic bursters are $I_{N a P}$ dependent. (C) Identification of calcium-sensitive and $I_{N a P}$ -dependent as well as calcium-insensitive and $I_{N a P}$ -dependent intrinsic bursters. Notice that only the neurons with the highest value of ${\bar{g}}_{N a P}$ are intrinsic bursters and that a subset of these neurons are sensitive to calcium blockade but all are dependent on $I_{N a P}$ . The network parameters are: ${\bar{g}}_{C a} = 0.00175 (n S)$ , $P_{C a} = 0.0275$ , $P_{S y n} = 0.05$ and $W_{m a x} = 0.096 (n S)$ . The values of ${\bar{g}}_{N a P}$ given in the scatter plots indicate the magnitude of ${\bar{g}}_{N a P}$ for each neuron in the network and show the range of the ${\bar{g}}_{N a P}$ distribution.

https://doi.org/10.7554/eLife.41555.009

Figure 9

Download asset Open asset

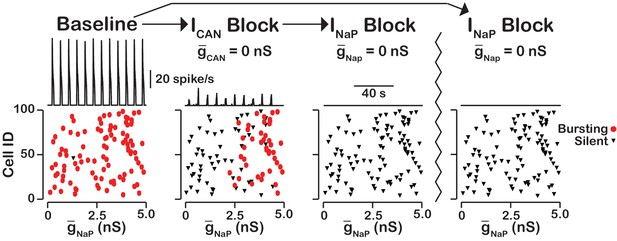
$I_{C A N}$ blockade reveals an $I_{N a P}$ -dependent rhythmogenic kernel.

The top traces show the network output at baseline, after $I_{C A N}$ blockade and $I_{N a P}$ blockade. The bottom Cell ID vs. ${\bar{g}}_{N a P}$ scatter plots identify silent and bursting neurons in each conditon. Notice that only neurons with relitively high ${\bar{g}}_{N a P}$ remain active after $I_{C A N}$ block. The network parameters used are: ${\bar{g}}_{C a} = 0.00175 (n S)$ , $P_{C a} = 0.0275$ , $P_{S y n} = 0.05$ and $W_{m a x} = 0.096 (n S)$ . The values of ${\bar{g}}_{N a P}$ given in the scatter plots indicate the magnitude of ${\bar{g}}_{N a P}$ for each neuron in the network and show the range of the ${\bar{g}}_{N a P}$ distribution.

https://doi.org/10.7554/eLife.41555.010

Figure 10

Download asset Open asset

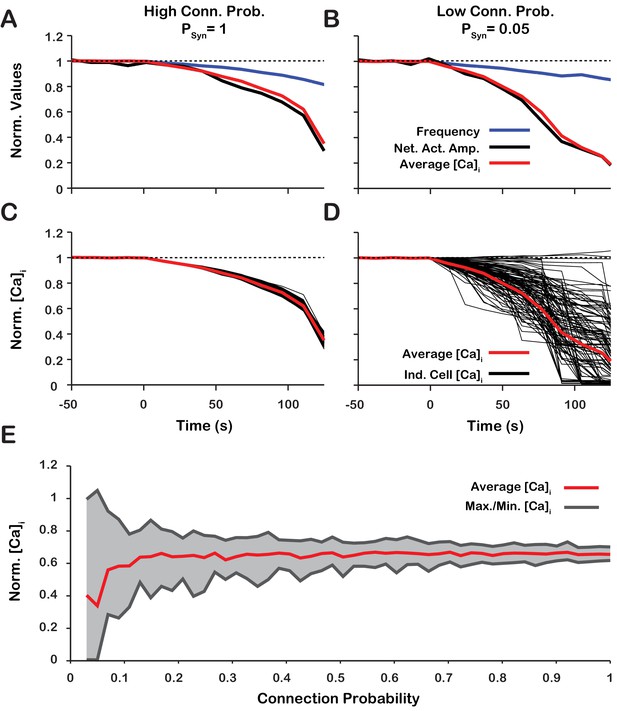
Changes of network activity amplitude, average network intracellular calcium concentration ${[C a]}_{i}$ amplitude, and single model neuron ${[C a]}_{i}$ amplitude during simulated $I_{C A N}$ blockade.

(**A and B**) Effect of $I_{C A N}$ block on network activity amplitude, network calcium amplitude and frequency for network connection probabilities (A) P = 1 and (B) P = 0.05. (**C and D**) Effect of $I_{C A N}$ block on changes in the magnitude of peak cellular calcium transients for network connection probabilities (C) $P_{S y n} = 1$ and (D) $P_{S y n} = 0.05$ . (E) Maximum, minimum and average change in the peak intracellular calcium transient of individual neurons as a function of synaptic connection probability. All curves in A through E are normalized to their baseline values. Synaptic weight was adjusted to keep the average synaptic strength ( $N \cdot P_{S y n} \cdot \frac{1}{2} W_{m a x} = c o n s t$ ) constant. Notice that lowering the synaptic connection probability increases the variability in the peak intracellular calcium concentration during $I_{C A N}$ blockade. Interestingly, for connection probabilities below approximately 5%, blocking ${\bar{g}}_{C A N}$ can increase the peak calcium transient in a small subset of neurons. The network parameters used are: ${\bar{g}}_{C a} = 0.00175 (n S)$ and $P_{C a} = 0.0275$ and $W_{m a x} = v a r$ .

https://doi.org/10.7554/eLife.41555.011

Figure 11

Download asset Open asset

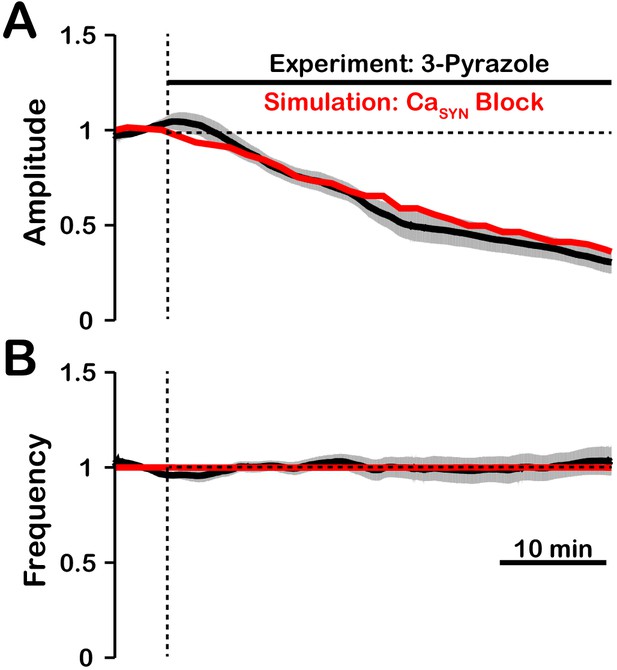
Comparison of experimental (black) and simulated (red) TRPC3 blockade (by ${C a}_{S y n}$ block) on network activity amplitude (A) and frequency (B).

Simulated and experimental blockade begins at the vertical dashed line. The black line represents the mean and the gray band represents the S.E.M. of experimental integrated XII output recorded from neonatal rat brainstem slices in vitro, reproduced from Koizumi et al., 2018. Blockade was simulated by exponential decay of $P_{C a}$ with the following parameters: 3-pyrazole: $?_{B l o c k} = 1.0$ , $τ_{B l o c k} = 522.5 s$ . The network parameters are: ${\bar{g}}_{C a} = 0.00175 (n S)$ , $P_{C a} = 0.0275$ , $P_{S y n} = 0.05$ and $W_{m a x} = 0.096 (n S)$ .

https://doi.org/10.7554/eLife.41555.012

Tables

Table 1

Model parameter values.

The channel kinetics, intracellular Ca²⁺ dynamics and the corresponding parameter values, were derived from previous models (see Jasinski et al., 2013) and the references therein).

https://doi.org/10.7554/eLife.41555.013

Channel	Parameters
$I_{N a}$	${\bar{g}}_{N a} = 150.0 n S$ , $E_{N a} = 55.0 m V$ , $V_{m_{1 / 2}} = - 43.8 m V$ , $k_{m} = 6.0 m V$ , $V_{τ m_{1 / 2}} = - 43.8 m V$ , $k_{τ_{m}} = 14.0 m V$ , $τ_{m_{m a x}} = 0.25 m s$ , $V_{h_{1 / 2}} = - 67.5 m V$ , $k_{h} = - 10.8 m V$ , $V_{τ h_{1 / 2}} = - 67.5 m V$ , $k_{τ_{h}} = 12.8 m V$ , $τ_{h_{m a x}} = 8.46 m s$
$I_{K}$	${\bar{g}}_{K} = 160.0 n S$ , $E_{K} = - 94.0 m V$ , $A_{α} = 0.01$ , $B_{α} = 44.0 m V$ , $κ_{α} = 5.0 m V$ $A_{β} = 0.17$ , $B_{β} = 49.0 m V$ , $κ_{β} = 40.0 m V$
$I_{L e a k}$	${\bar{g}}_{L e a k} = 2.5 n S$ , $E_{L e a k} = - 68.0 m V$
$I_{N a P}$	${\bar{g}}_{N a P} \in [0.0, 5.0] n S$ , $V_{m_{1 / 2}} = - 47.1 m V$ , $k_{m} = 3.1 m V$ , $V_{τ m_{1 / 2}} = - 47.1 m V$ , $k_{τ_{m}} = 6.2 m V$ , $τ_{m_{m a x}} = 1.0 m s$ , $V_{h_{1 / 2}} = - 60.0 m V$ , $k_{h} = - 9.0 m V$ , $V_{τ h_{1 / 2}} = - 60.0 m V$ , $k_{τ_{h}} = 9.0 m V$ , $τ_{h_{m a x}} = 5000 m s$
$I_{C A N}$	${\bar{g}}_{C A N} \in [0.5, 1.5] n S$ , $E_{C A N} = 0.0 m V,$ ${C a}_{1 / 2} = 0.00074 m M$ , $n = 0.97$
$I_{C a}$	${\bar{g}}_{C a} = 0.01 n S$ , $E_{C a} = R ∙ T / F ∙ l n ({[C a]}_{o u t} / {[C a]}_{i n})$ , $R = 8.314 J / (m o l ∙ K)$ , $T = 308.0 K$ , $F = 96.485 k C / m o l$ , ${[C a]}_{o u t} = 4.0 m M$ $V_{m_{1 / 2}} = - 27.5 m V$ , $k_{m} = 5.7 m V$ , $τ_{m} = 0.5 m s$ , $V_{h_{1 / 2}} = - 52.4 m V$ , $k_{h} = - 5.2 m V$ , $τ_{h} = 18.0 m s$
${C a}_{i n}$	$α_{C a} = 2.5 ∙ 10^{- 5} m M / f C$ , $P_{C a} = 0.01$ , $C a_{m i n} = 1.0 ∙ 10^{- 10} m M$ , $τ_{C a} = 50.0 m s$
$I_{S y n}$	$g_{T o n i c} = 0.31 n S$ , $E_{S y n} = - 10.0 m V$ , $τ_{S y n} = 5.0 m s$

Additional files

Source code 1 Phillips et al. model source code.: https://doi.org/10.7554/eLife.41555.014
Download elife-41555-code1-v1.cc
Transparent reporting form: https://doi.org/10.7554/eLife.41555.015
Download elife-41555-transrepform-v1.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Ryan S Phillips
Tibin T John
Hidehiko Koizumi
Yaroslav I Molkov
Jeffrey C Smith

(2019)

Biophysical mechanisms in the mammalian respiratory oscillator re-examined with a new data-driven computational model

eLife 8:e41555.

https://doi.org/10.7554/eLife.41555

Figures

Manipulations of ${\bar{g}}_{C A N}$ in the ${C a}_{V}$ and ${C a}_{S y n}$ networks produce opposite effects on network activity amplitude (spikes/s) and frequency.

Calcium source and ${\bar{g}}_{C A N}$ -dependent effects on cellular properties regulating network frequency for the simulations presented in Figure 1.

Calcium source and ${\bar{g}}_{C A N}$ -dependent effects on cellular properties regulating network activity amplitude for the simulations presented in Figure 1.

Manipulations of synaptic strength ( $N \cdot P_{S y n} \cdot \frac{1}{2} W_{m a x}$ ) and ${\bar{g}}_{C A N}$ have equivalent effects on network activity amplitude, frequency and recruitment of inspiratory neurons not involved in rhythm generation.

Experimental and simulated pharmacological blockade of $I_{C A N}$ by (A and C) 9-phenanthrol and (B and D) flufenamic acid (FFA).

$I_{N a P}$ -dependent and ${C a}^{2 +}$ -sensitive intrinsic bursting.

$I_{C A N}$ blockade reveals an $I_{N a P}$ -dependent rhythmogenic kernel.

Changes of network activity amplitude, average network intracellular calcium concentration ${[C a]}_{i}$ amplitude, and single model neuron ${[C a]}_{i}$ amplitude during simulated $I_{C A N}$ blockade.

Comparison of experimental (black) and simulated (red) TRPC3 blockade (by ${C a}_{S y n}$ block) on network activity amplitude (A) and frequency (B).

Tables

Model parameter values.

Additional files

Source code 1

Transparent reporting form

Download links

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Be the first to read new articles from eLife

Share this article

Cite this article

Manipulations of g-CAN in the CaV and CaSyn networks produce opposite effects on network activity amplitude (spikes/s) and frequency.

Calcium source and g-CAN-dependent effects on cellular properties regulating network frequency for the simulations presented in Figure 1.

Calcium source and g-CAN-dependent effects on cellular properties regulating network activity amplitude for the simulations presented in Figure 1.

Manipulations of synaptic strength (N·PSyn·12Wmax) and g-CAN have equivalent effects on network activity amplitude, frequency and recruitment of inspiratory neurons not involved in rhythm generation.

Experimental and simulated pharmacological blockade of ICAN by (A and C) 9-phenanthrol and (B and D) flufenamic acid (FFA).

INaP-dependent and Ca2+-sensitive intrinsic bursting.

ICAN blockade reveals an INaP-dependent rhythmogenic kernel.

Changes of network activity amplitude, average network intracellular calcium concentration Cai amplitude, and single model neuron Cai amplitude during simulated ICAN blockade.

Comparison of experimental (black) and simulated (red) TRPC3 blockade (by CaSyn block) on network activity amplitude (A) and frequency (B).

Model parameter values.

Source code 1

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Manipulations of ${\bar{g}}_{C A N}$ in the ${C a}_{V}$ and ${C a}_{S y n}$ networks produce opposite effects on network activity amplitude (spikes/s) and frequency.

Calcium source and ${\bar{g}}_{C A N}$ -dependent effects on cellular properties regulating network frequency for the simulations presented in Figure 1.

Calcium source and ${\bar{g}}_{C A N}$ -dependent effects on cellular properties regulating network activity amplitude for the simulations presented in Figure 1.

Manipulations of synaptic strength ( $N \cdot P_{S y n} \cdot \frac{1}{2} W_{m a x}$ ) and ${\bar{g}}_{C A N}$ have equivalent effects on network activity amplitude, frequency and recruitment of inspiratory neurons not involved in rhythm generation.

Experimental and simulated pharmacological blockade of $I_{C A N}$ by (A and C) 9-phenanthrol and (B and D) flufenamic acid (FFA).

$I_{N a P}$ -dependent and ${C a}^{2 +}$ -sensitive intrinsic bursting.

$I_{C A N}$ blockade reveals an $I_{N a P}$ -dependent rhythmogenic kernel.

Changes of network activity amplitude, average network intracellular calcium concentration ${[C a]}_{i}$ amplitude, and single model neuron ${[C a]}_{i}$ amplitude during simulated $I_{C A N}$ blockade.

Comparison of experimental (black) and simulated (red) TRPC3 blockade (by ${C a}_{S y n}$ block) on network activity amplitude (A) and frequency (B).