Length regulation of multiple flagella that self-assemble from a shared pool of components
- Brandeis University, United States
- Harvard University, United States
Figures
Figure 1
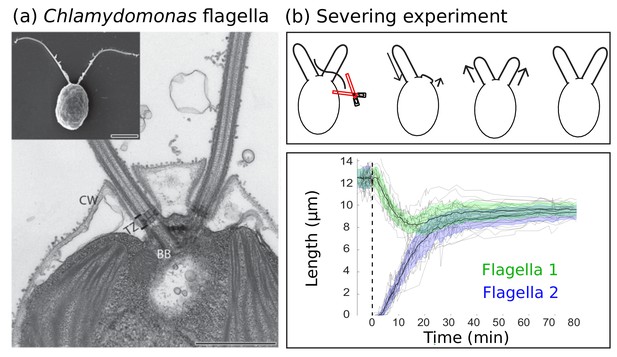
Experimental background.
(a) Electron microscopy images of the biflagellate green algae Chlamydomonas and its flagella captured by Elisa Vannuccini and Pietro Lupetti (University of Siena, Italy) and reproduced from Morga …
Figure 2
IFT in Chlamydomonas with diffusive return of kinesin-2 to the base.
(a) Kinesin-2, dynein, and tubulin combine to form a complex with other IFT components in the basal pool and are injected into the flagellum. The kinesin-2 motors move toward the tip of the …
Figure 3 with 6 supplements
Length dynamics of two flagella assembling from shared pools of building blocks.
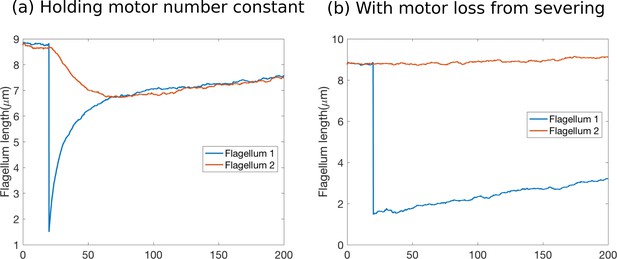
(a) Flagellar assembly in Chlamydomonas reinhardtii and modes of coupling between basal proteins pools. (b) Simulations of the severing experiment using different modes of coupling between basal …
Figure 3—video 1
The constant disassembly model with tubulin separate and motors shared does not yield length equalization.
Figure 3—video 2
The constant disassembly model with tubulin shared and motors separate does not yield length equalization.
Figure 3—video 3
The constant disassembly model with both tubulin and motors shared does not yield length control.
Figure 3—video 4
Replenishing protein pools in the constant disassembly model with tubulin separate and motors shared does not yield length control.
Figure 3—video 5
Replenishing protein pools in the constant disassembly model with tubulin shared and motors separate does not yield length control.
Figure 3—video 6
Replenishing protein pools in the constant disassembly model with both tubulin and motors shared does not yield length control.
Figure 4 with 2 supplements
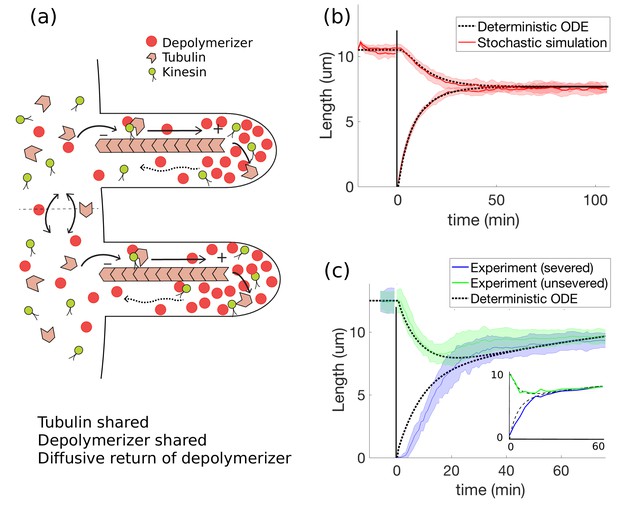
Concentration-dependent disassembly model: simultaneous length control is achieved using shared tubulin and shared depolymerizers.
(a) The depolymerizer moves ballistically to the flagellar tip and diffuses back, (b) The model Equations 20 and 21 captures rapid length equalization, (c) Protein replenishment with timescale …
Figure 4—video 1
The active disassembly model with both tubulin and motors shared but without protein replenishment exhibits rapid length equalization.
Figure 4—video 2
Replenishing protein pools in the active disassembly model with both tubulin and motors shared exhibits rapid length equalization and slow recovery.
Figure 5
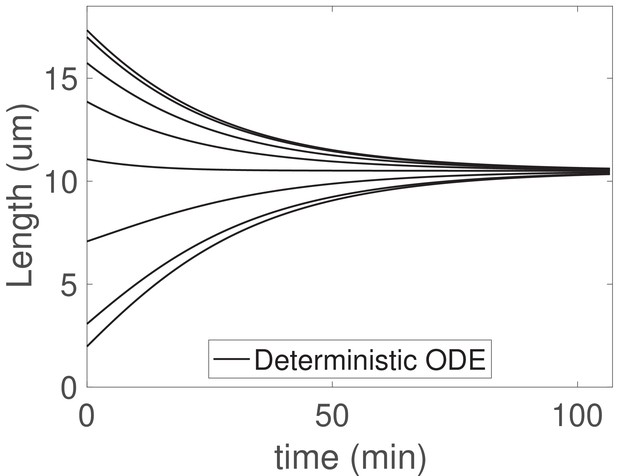
The concentration-dependent disassembly model generalizes to arbitrary flagellar number .
We solve (Equations 25) with flagella and the larger shared pool , , and ; otherwise all parameters are as in Table 1.
Appendix 3—figure 1
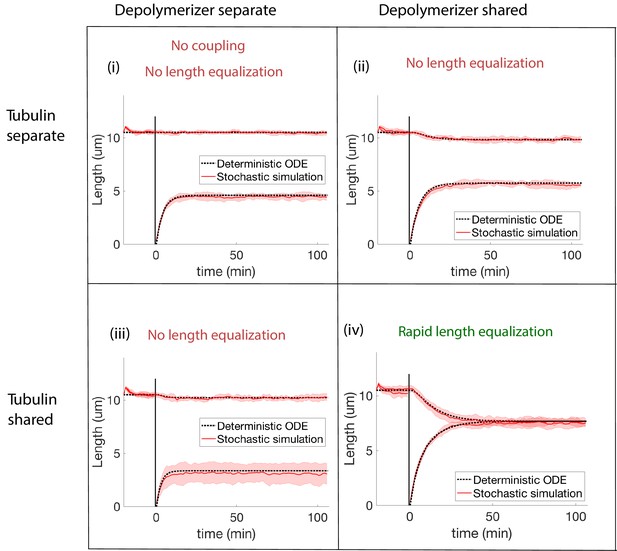
Concentration-dependent disassembly model: simulations of severing experiment with different modes of coupling between basal pools (and no replenishment of protein levels).
We conclude that biomolecule pools are fully shared after ruling out all models that disagree with the rapid length equalization that occurs in severing experiments. (i) In the case of separate …
Appendix 3—figure 2
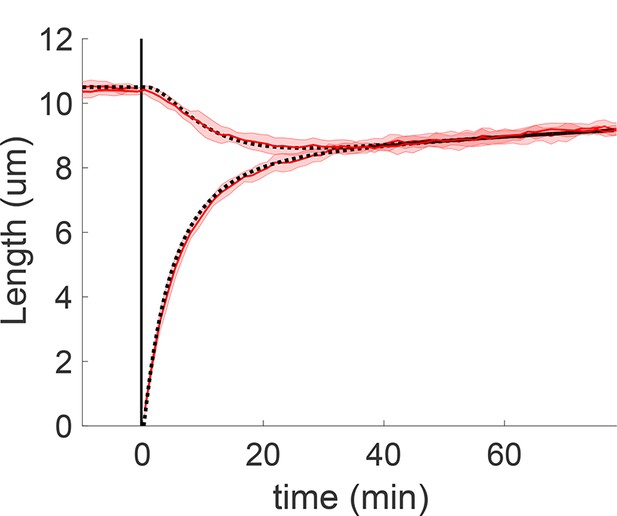
Concentration-dependent disassembly model Equation 68 and 69 with tubulin in excess yields rapid length equalization consistent with severing experiments, here with replenishment timescale .
Appendix 3—figure 3
Simultaneous length control is achieved by different versions of the concentration-dependent disassembly model.
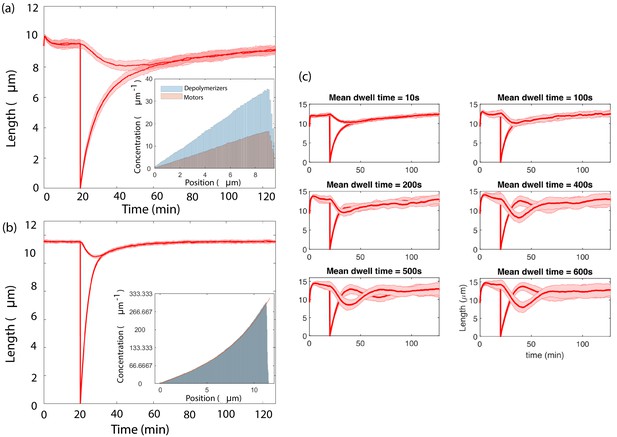
(a) Results from agent-based simulations with different populations of depolymerizer and rate-limiting IFT protein, using capacity , (inset) Concentrations along the flagellum of diffusing IFT …
Author response image 1
Tables
Table 1
Parameter values and definitions.
| Symbol | Definition | Value | Units | References |
|---|---|---|---|---|
| Parameters | ||||
| Steady-state length | 10–12 | µm | Marshall and Rosenbaum, 2001; Rosenbaum et al., 1969 | |
| Tubulin pool per flagellum | 38–47 | µm | Marshall et al., 2005 | |
| Disassembly speed | 0.5 | µm/min | Marshall and Rosenbaum, 2001; Ludington et al., 2012 | |
| IFT speed | 2.5–3 | µm/s | Kozminski et al., 1993; Buisson et al., 2013 | |
| Diffusion coefficient | 1.7 | µm2/s | Chien et al., 2017 | |
| Assembly rate per tubulin | 2.3 × 10-2 –3.6 × 10-2 | min−1 | Fit | |
| Injection rate constant | 0.8–4 | min−1 | Fit | |
| Prefactor in Equation 5 | 2.5 × 10-4 | Estimate (Appendix 2) | ||
| Variables | ||||
| Number of flagella | ||||
| Free tubulin | µm | |||
| Total motors | ||||
| Free motors | ||||
| Ballistic motors | ||||
| Diffusing motors | ||||
| Flux | min−1 | |||
| Motor concentration | µm−1 | |||
| Average concentration | µm−1 |
