Representational untangling by the firing rate nonlinearity in V1 simple cells
- MTA Wigner Research Center for Physics, Hungary
- Central European University, Hungary
- Rutgers University, United States
- University of California, Los Angeles, United States
- David Geffen School of Medicine, University of California, Los Angeles, United States
- West Los Angeles VA Medical Center, United States
- University of Cambridge, United Kingdom
Figures
Figure 1
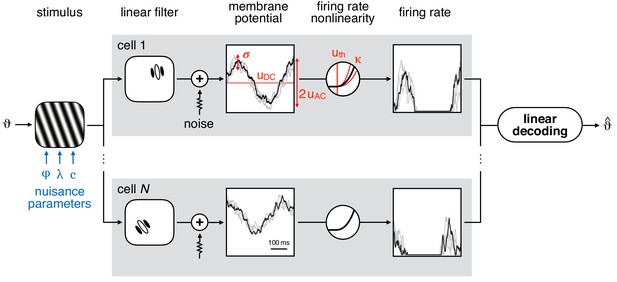
Model schematic.
Left: sine wave grating stimulus used as input to the model population. The stimulus is parametrised by orientation () and nuisance parameters phase (φ), spatial period (λ), and contrast (). Middle: simple cell membrane potential (MP) responses (grey boxes) are obtained using localised, oriented Gabor filters and temporally correlated additive noise (Gaussian, with standard deviation σ). The mean response varies sinusoidally (with amplitude ) around the baseline () as the phase of the grating stimulus is changing. The stochastic component of the MP response of each neuron is variable in time (black line) and across trials (gray lines). Firing rate is obtained by transforming the MP through a threshold-power-law firing rate nonlinearity (FRNL), characterised by threshold uth and exponent κ. Right: linear decoding of orientation from the population response of simple cells yields the estimated orientation ().
Figure 2
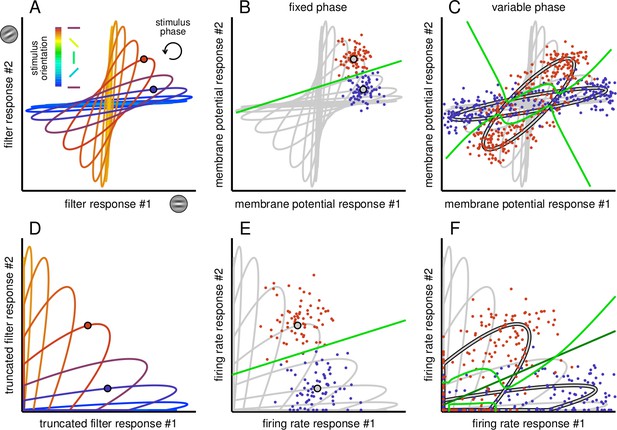
Effect of phase variability on the linear separability of the responses of a pair of simple cells.
(A) Filter responses of a pair of model simple cells to gratings with various orientations (different colours) and phases (position along ellipses). Circles mark a pair of example stimulus phases at two different orientations. (B) Stochastic membrane potential responses of the pair of cells (dots) at the reference pair of stimulus orientations and phases (gray circles with black contour). Gray lines show average responses at other phases and orientations for reference. The optimal decision boundary (green line) constructed for membrane potential responses is a straight line and it is thus achievable by a linear decoder. (C) Membrane potential responses (coloured dots) to stimuli with the same pair of orientations as in B but for variable stimulus phase (gray ellipses with black contour). Phase variability abolishes the linear separability of responses given to different orientations: the decision boundary of the optimal decoder (green line) is highly nonlinear. (D) Filter responses as in A but truncated due to the threshold linear transformation of the FRNL. (E–F) Same as B-C, but for firing rate responses. Note that the decision boundary of the optimal decoder of firing rate responses (F, green line) can be well approximated by a linear decoder (F, dark green line).
Figure 3 with 3 supplements
Effect of phase variability on decoding performance.
Orientation decoding from firing rates (FR) was performed for grating stimuli with fixed (black and grey) or unknown phase (dark and light blue) using an optimal (lighter colours) or linear decoder (darker colours). (A) Decoding performance as a function of the FRNL threshold (solid lines). Black dotted line shows chance performance. Green shaded area shows the distribution of membrane potentials for reference. Red line shows sparseness of responses as a function of the FRNL threshold. Inset shows the performance of the linear decoder against the performance predicted by the normalised optimal decoder (the combined effect of total information and sparseness) at different values of the FRNL threshold under variable phase (blue dots). Note that decoding from firing rates with FRNL threshold values below the membrane potential distribution is equivalent to decoding from membrane potentials. (B) Performance of the linear decoder using firing rates (FR) obtained with the optimal FRNL thresholds (diamonds on A) and membrane potentials (MP). Horizontal lines show the performance of the optimal decoder at the corresponding FRNL threshold values. (C) Performance of linear decoder with fixed (black bars) and unknown phase (blue bars) for a neuron population with pixel-like receptive fields. As no optimal threshold existed with this population, the firing rate decoder was evaluated at the optimal FRNL threshold of the Gabor population. (D) Same as panel C but for a population with center-surround receptive fields.
Figure 3—figure supplement 1
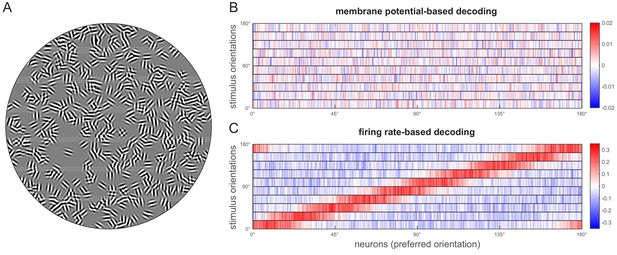
Properties of the model neuron population.
(A) Gabor filters characterising the model neurons. A fixed set of Gabor filters was used throughout the simulations (but see Figure 4—figure supplement 1) that characterise the receptive field properties of the model neuron population. Receptive field locations were randomly sampled on a 90 degree circle (approximating the visual field), with random orientations and phase but fixed spatial frequency and receptive field size (see Materials and methods and Table 1). (B) Representation of the linear decoder parameters trained for membrane potential decoding (top panel) and firing rate decoding (lower panel). Colour code shows the strength of the connection between model neurons and the orientations the decoder distinguishes. There is no clear pattern in the connection strengths of the membrane potential decoder. In the case of the firing rate decoder, however, stronger weights are characteristic of neurons with preferred orientations matching the orientations represented by the decoder. Note the different colour scales in B and C.
Figure 3—figure supplement 2
Alternative measures for the characterisation of decoding performance.
(A) Linear decoding performance as a function of the FRNL threshold for fraction correct (blue), probabilistic faction correct (black), and cosine error (yellow). For fraction correct, in any given trial the class with the maximal class probability is chosen and the fraction of correct choices across trial is plotted. For the probabilistic fraction correct, class probabilities are normalised and the mean normalised class probability of the correct choice is calculated. The cosine error measure (yellow) is based on a weighted sum of the orientations characterising the classes and the cosine of the angular deviation of the resulting orientation from the true orientation is measured. While the performance of the performance measures is not equal, the optimal threshold (diamonds and ticks on the horizontal axis) is only marginally affected by the choice of measure. (B) Optimal decoding performance as measured by fraction correct (blue) and probabilistic fraction correct (black), similar to panel A. Mutual information between the population responses and the stimulus orientation (yellow) is a shifted and exponentiated version of the probabilistic fraction correct (see text). At low threshold levels, the mutual information equals the logarithm of the number of decoded orientations.
Figure 3—figure supplement 3
Linear decoding performance with variable phase for narrow and wide field of view.
Receptive fields are distributed either on a 90-degree circle (blue) or a 3-degree circle (red). Shaded area shows the full range of variance (between maximal and minimal decoding performance in 25 simulations). Representational untangling is not affected by assessing local orientation instead of global orientation. The blue line is identical to the one shown on Figure 3A of the main text.
Figure 4 with 2 supplements
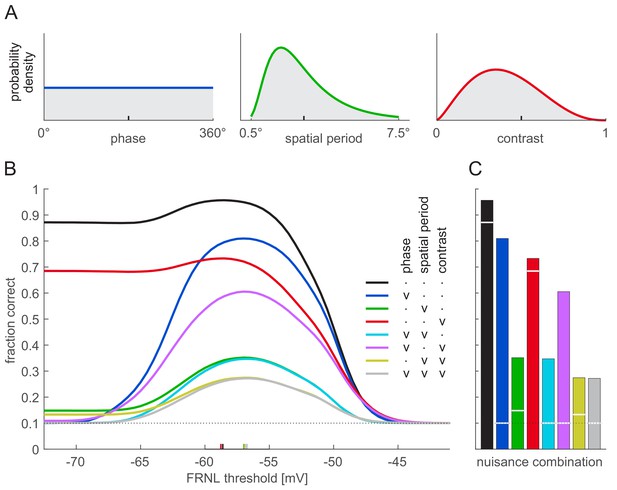
Effect of nuisance parameter variability on decoding performance.
Nuisance parameters were varied individually (blue: phase; green: spatial period; red: contrast) or in combination (mixture colours). (A) Parameter distributions used for varying nuisance parameters: uniform for stimulus phase (left), lognormal for spatial period (middle), and beta distribution for contrast (right). Ticks on x-axes show parameter values used when the corresponding parameter was fixed. (B) Linear decoding performance as a function of the FRNL threshold for different combinations of variable nuisance parameters (colours, see legend for details: ‘v’ denotes variable, ‘.’ denotes fixed parameter). Coloured ticks on x-axis show optimal thresholds for the corresponding combinations of variable nuisance parameters (i.e. the locations of peaks on the corresponding performance curves). Note that even when all nuisance parameters are variable, a linear decoder performs above chance around the optimal threshold. (C) Linear decoding performance for firing rates obtained with optimal FRNL threshold values under different nuisance parameter uncertainties (bars, colours as in B) and for membrane potentials (white lines). Note that the only nuisance parameter that shows membrane potential decoding performance considerably above chance is contrast (red). Simulations without nuisance parameter variability (black) and with only phase variability (blue) are replotted from Figure 3A.
Figure 4—figure supplement 1
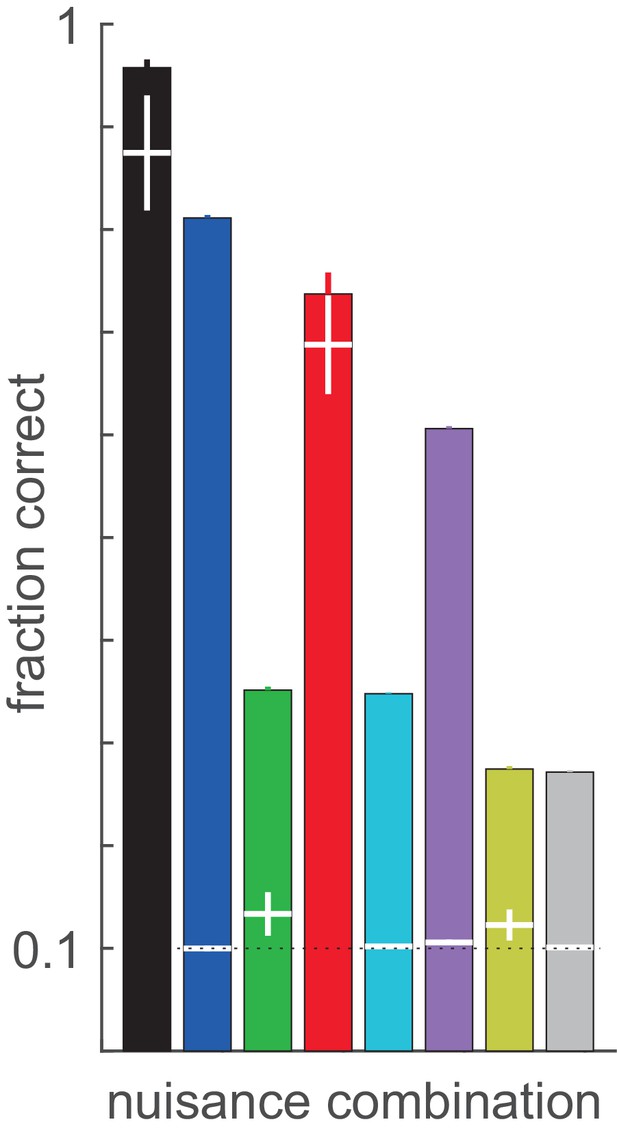
Variance in decoding performance as a result of variations in receptive field parameters of model neurons.
Randomness was introduced by resampling the positions and phases of the Gabor filters that characterise the receptive fields of the model neurons. Means (bars) and 2 s.D. (error bars) are calculated from 25 random settings of the population. Sensitivity of the optimal performance of firing rate (filled bars) and membrane potential decoders (white horizontal lines on the bars) to variations in encoding population parameters for different nuisance parameter combinations. All of the membrane potential decoders where nuisance parameters are present (white lines on coloured bars) are significantly lower than that of the no-nuisace membrane potential decoder (white line on black bar), unpaired t-test: p=1.5e-33, t[22.1]=−132.5; p=4.0e-39, t[27.7]=−119.3; p=5.0e-27, t[43.3]=−24.5; p=1.9e-33, t[22]=−132.3; p=1.8e-33, t[22.1]=−131.5; p=2.2e-36, t[25]=−124.7; p=1.8e-33, t[22]=−132.4 for the seven bars, respectively. Firing rate decoders (coloured bars) were consistently outperforming membrane potential decoders for all conditions except for the case where contrast was the only nuisance parameter, consistent with the fact that contrast introduces variations that do not directly affect linear decoding boundaries (unpaired t-test: p=1.9e-33, t[22]=132.6; p=0.58, t[24]=−0.6; p=3.3e-14, t[24]=15.8; p=1.1e-33, t[23]=120.0; p=1.6e-12, t[24]=13.2; p=3.9e-17, t[24]=21.3; p=1.0e-13, t[24]=15.1; p=5.8e-06, t[23]=5.8543 for the eight conditions, respectively). Colours match those at Figure 4. Notice that the variance of optimal performance of the FR decoder is almost negligible, except for the no nuisance (black) and contrast nuisance (red) cases, where variance of membrane potential decoder performances are also high.
Figure 4—figure supplement 2
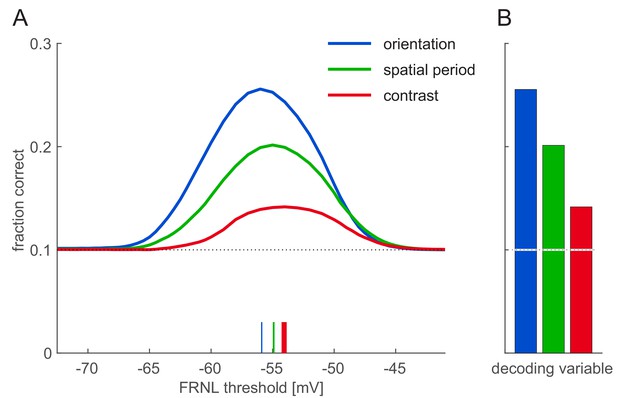
Orientation, spatial period, and contrast decoding from firing rate responses.
(A) Decoding performance for orientation, spatial period, and contrast from firing rate responses as a function of FRNL threshold. Of the four investigated variables (phase, orientation, spatial period, contrast) one was selected as a target for the linear decoder while the other three were treated as nuisance parameters for the decoder. The number of decoding classes were ten in every case. FRNL threshold-dependence showed a peak similar to orientation decoding, with slight variation in the optimal FRNL threshold (coloured ticks). (B) Linear decoding performance for firing rates at the optimal FRNL threshold (colours as in A).
Figure 5
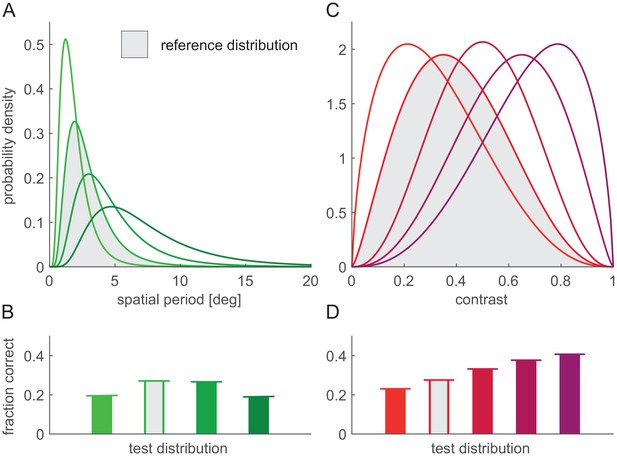
Robustness of the optimal FRNL threshold to changes in nuisance parameter statistics.
(A) Distributions of spatial period. Grey-shaded distribution is the reference distribution used in other figures where spatial period was a nuisance parameter. (B) Performance of the linear decoder under different period distributions (colours as in A) with the ‘default’ FRNL threshold which was optimised to the reference spatial period distribution (bars). As an upper bound, performance with the FRNL threshold re-optimised for each spatial period distribution is also shown (horizontal lines). Note that bars reach horizontal lines in all cases, indicating that performance with the default FRNL threshold is indistinguishable from that achieved with the re-optimised FRNL threshold. (C–D) Same as (A–B) but for changes in the distribution of stimulus contrast.
Figure 6 with 2 supplements
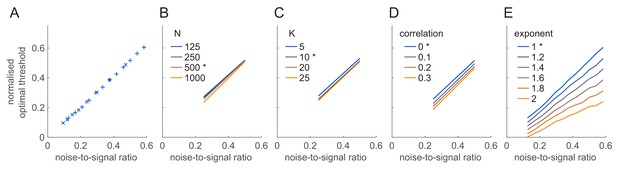
Dependence of the optimal threshold on model parameters.
(A) Dependence of the normalised optimal threshold (y-axis) on the noise-to-signal ratio (x-axis). The normalised optimal threshold is the deviation of the optimal threshold from the baseline membrane potential, normalised by the magnitude of membrane potential noise: (see text for details). Noise-to-signal ratio is the ratio between the magnitude of noise and the strength of the signal: . Note the same linear dependence irrespective of whether signal strength (×) or noise magnitude is varied (+). (B–E) Same as (A) for different population sizes (B), decoder resolutions (C), correlation strengths (D) and exponents of the FRNL nonlinearity (E). Asterisks mark the default values of the parameters used in other figures. Scaling of the optimal threshold with noise-to-signal ratio is largely independent from changes in these network and cellular parameters except for the exponent of the FRNL nonlinearity which substantially changes the noise-dependence of the optimal threshold.
Figure 6—figure supplement 1
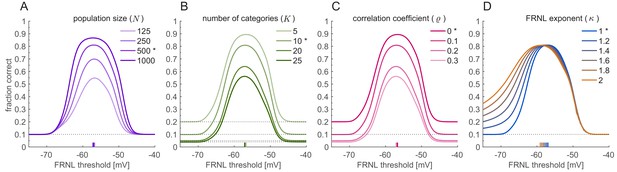
Parameter-dependence of optimal FRNL threshold.
Linear decoding performance was assessed for the linear firing rate decoder under phase uncertainty as a function of FRNL threshold. Stars indicate the default values of the parameters used in other figures. Ticks on the horizontal axis show the optimal FRNL threshold. (A) Population size. (B) Resolution of the decoder. (C) Level of correlation in the noise corrupting membrane potential responses (correlations are homogeneous across all the pairs in the population). (D) Exponent of the FRNL. Parameter values match those shown on Figure 6.
Figure 6—figure supplement 2
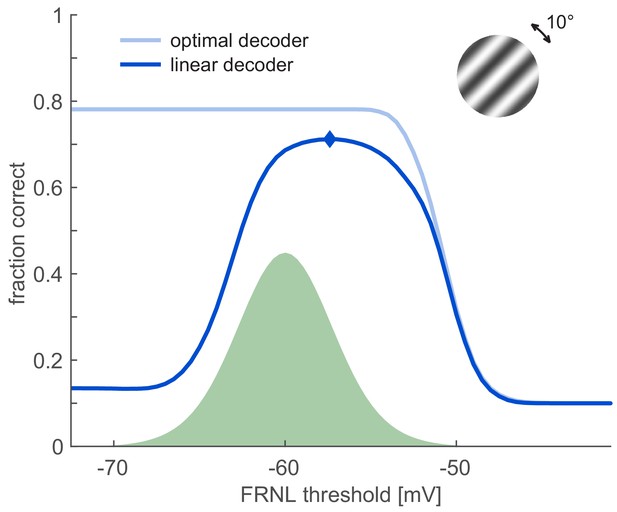
Effect of information-limiting correlations on decoding performance.
Information-limiting correlations were induced in the population by introducing random rotations in the orientation of the stimulus. Standard deviation of the noise was five degrees (inset). Average standard deviation of the membrane potential resulting from such stimulus orientation noise was 1.5 mV. So that marginal noise variance on individual neurons is matched with that of the non-correlated case (green shaded area), private noise was introduced with 2.59 mV standard deviation. Information limiting correlations reduce the performance of the Bayesian decoder (light blue). The linear decoder (dark blue) shows a maximum performance close to the optimal FRNL threshold characterising the non-correlated case.
Figure 7 with 3 supplements
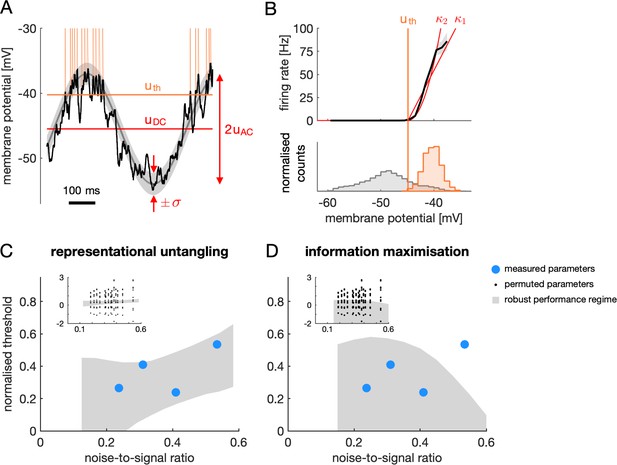
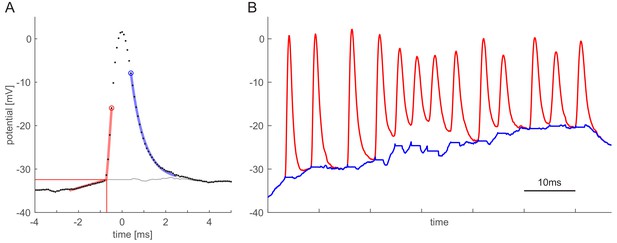
Comparison of optimal firing thresholds derived from the model and firing thresholds of V1 simple cells.
(A) Intracellularly recorded ‘generator’ membrane potential trace of a V1 simple cell (black) with spikes clipped off (see Materials and methods). Orange vertical lines show spike times, orange horizontal line shows estimated firing threshold (). Red marks show response baseline (), signal variance (), and noise magnitude (σ) estimated from the generator potential responses to multiple cycles of the moving grating stimulus. (B) Illustration of estimating the FRNL from electrophysiological data. The firing rate of a cell as a function of the membrane potential (top panel, black line, gray shaded area shows s.e.m.) is obtained as the normalised ratio of the probability distributions of the generator potential at spike times and at all times (bottom panel, orange and gray histograms, respectively). A threshold-power-law function was fitted to the firing rate function and the threshold linear fit was used to estimate the firing threshold (vertical orange line). Threshold-power-law fits with different levels of the FRNL exponent (red traces, , ) were largely consistent with the firing rate estimated from the data. (C) Normalised thresholds of four V1 simple cells as a function of the noise-to-signal ratio of their membrane potential responses (blue circles). Normalised thresholds and noise-to-signal ratios were computed from the original cellular parameters (panels A-B) as in Figure 6. Shaded area shows robust decodability regime of RU (range of normalised thresholds within which > 90% of maximal linear decoding performance is achieved across all values between 1 and 2, cf. Figure 6E, Figure 7—figure supplement 2). Inset: same as main panel but black dots correspond to normalised threshold values and noise-to-signal ratios obtained by shuffling the experimentally measured parameters across recorded neurons ( = −46.8, –42.4, –47.3, –36.9 mV; = 7.15, 9.1, 4.48, 7.83 mV; = 1.7, 2.83, 2.39, 3.21; and = −44.9, –38.6, –44.9, –35.1 mV). (D) Same as panel (C) but recorded data is compared with the prediction of maximal information transmission on the normalised threshold.
Figure 7—figure supplement 1
Spike fitting.
(A) Location of a spike is determined by searching a local maximum (time axis aligned to this point for illustration purposes) in the raw membrane potential data (corresponding to peaks with steepness exceeding a given threshold). Inflection points before (right circle) and after (blue circle) the peak are determined. Initiation time of the spike (vertical thin red line), and the spike threshold (horizontal thin red line) are determined by a piecewise linear fit on the membrane potential in a time window preceding the left inflection point. The tail of the spike is fitted by an exponential (blue curve) on the time window between 2.5 ms succeeding the peak and the right inflection point. The fitted exponential is used for removing the spike tail in a 6 ms window. Between the starting point of the spike and the right inflection point the generator potential is taken to be equal to the spiking threshold. (B) Illustration of a high firing rate segment of the intracellular recording (red line) and the estimated generator potential (blue line). The spike fitting method is capable of estimating generator potentials for spikes separated by not less than 5 ms. The high firing rate shown here is not typical and was chosen to demonstrate the performance under circumstances that are challenging for spike fitting.
Figure 7—figure supplement 2
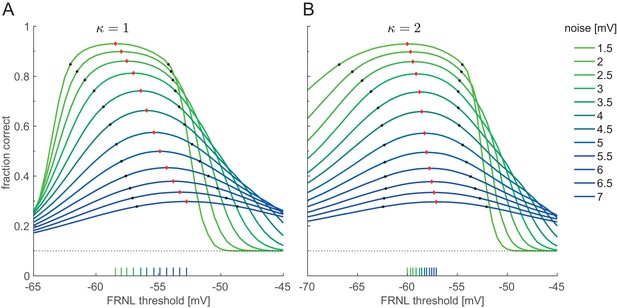
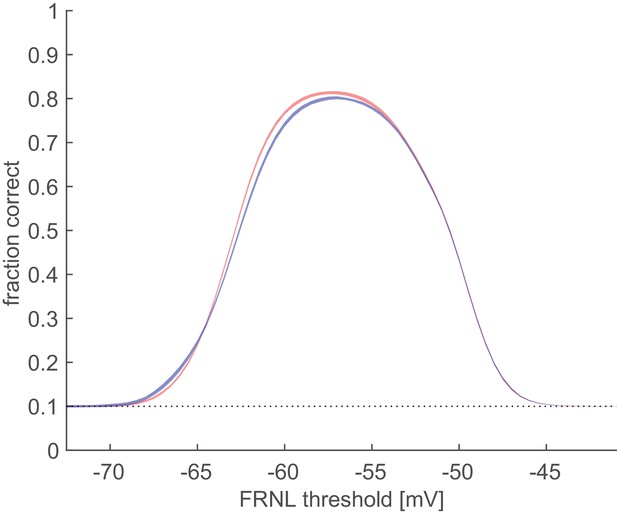
Dependence of the optimal threshold on the level of membrane potential noise.
Linear decoding performance is measured at various FRNL threshold levels with a threshold-linear nonlinearity (κ = 1, (A) and with a threshold quadratic nonlinearity (κ = 2, (B). As the amplitude of membrane potential noise increases, the optimal threshold progressively shifts to higher values (red diamonds and corresponding ticks on the x axis). Black dots indicate the minimum and maximum of the FRNL threshold range in which decoding performance exceeds the 9% of the performance measured at the optimal threshold.
Figure 7—figure supplement 3
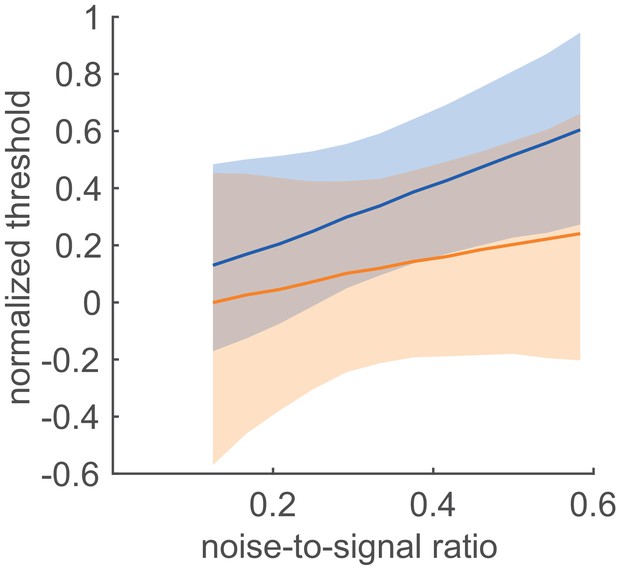
Robust decodability of population responses.
Relationship between the normalised optimal threshold on the signal-to-noise ratio at two FRNL exponents (see Figure 6E) considered to be the extremes of feasible values of FRNLs characterising neuronal responses: at threshold linear nonlinearity, corresponding to κ = 1 (thick blue line), and threshold quadratic nonlinearity, corresponding to κ = 2 (thick orange line). Shaded areas represent the range of normalised thresholds where the performance of the linear decoder exceeds the 90% of the performance measured at the optimal normalised threshold (see Figure 7—figure supplement 2). Robust decodability is defined by the regime where linear decoding performance is close to the performance measured at the optimal threshold irrespective of the exact value of the FRNL exponent (overlap between shaded areas).
Figure 8
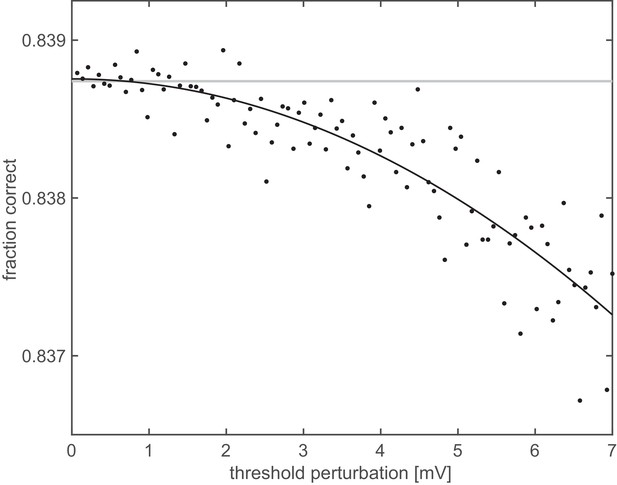
Representational untangling in a heterogeneous population.
Orientation decoding performance from a population (N = 500) of neurons with heterogeneous properties as a function of the magnitude of deviation (Euclidean distance) from the optimal firing thresholds determined based on the assumption of a homogeneous population. Both the exponent of the FRNL and the level of membrane potential noise were chosen from a set of five possible values (1, 1.2, 1.4, 1.6, 1.8, and 2, 2.5, 3, 3.5, 4 mV, respectively), yielding 25 different parameter combinations. Thus, twenty neurons with different receptive fields were assigned to each parameter combination. For each of the 25 parameter combinations, the optimal firing threshold was established by simulating a homogeneous population with those parameters. In the heterogeneous population, the threshold for each cell was set to the value optimised for the corresponding homogeneous population. Decoding performance was measured after perturbing these thresholds (black dots). Grey line shows decoding performance with the unperturbed thresholds, black line is a quadratic fit to the perturbed performance levels.
Tables
Table 1
Parameters of the decoding model under phase uncertainty and their default values are shown or their generator methods are indicated (first column).
Description of the parameters and methods are expounded (second column). The performance curve of the above described standard model is shown by the thick blue curve on Figure 3A and Figure 4B and used as a reference simulation on Figures 5 and 6 where parameters of the model are varied.
| Parameters of the encoder Gabor population | |
|---|---|
| Number of Gabor cells in the encoder population (with the exception of Figure 6B) | |
| | coordinates of the center of Gabor filter n measured from the line of sight; randomly chosen from a uniform distribution over a disk with radius R (with the exception of Figure 3—figure supplement 3) |
| period of the plane wave component of Gabor filters; identical for all cells (with the exception of Figure 4—figure supplement 2) | |
| preferred orientation of cell n; evenly distributed on the entire range | |
| phase offset of the sinusoidal wave component of the Gabor filter relative to the center; evenly distributed on the entire range, but the order is randomly permuted to avoid correlation with the preferred orientation (with the exception of no-nuisance simulations where ) | |
| standard deviation of the circular Gaussian envelope of Gabor filters; identical for all cells | |
| Parameters of the rescaling of filter responses to membrane potential values | |
| mean value of phase modulated filter responses | |
| peak amplitude of maximally modulated filter responses; numeric value is chosen as a typical value (Carandini, 2004) (but varied on Figure 6A) | |
| Variability and covariability of membrane potential responses | |
| std of Gaussian membrane potential noise is measured relative to the signal amplitude; identical for all cells (but varied on Figures 6, 7C and 8) | |
| off-diagonal elements of the covariance matrix; no correlation structure is assumed (with the exception of Figure 6) | |
| Firing rate nonlinearity | |
| power-law exponent of the FRNL (but varied on Figures 6E, 7C and 8) |
| threshold of the FRNL; this is always a running variable in the simulations | |
| prefactor of the FRNL of Gabor cells | |
| Parameters of the categorisation task | |
| number of discrete orientation categories (varied only on Figure 6C) |
| Parameters of the stimulus set used for training the decoder | |
| number of bins for stimulus orientation, , within an orientation category (represents orientation uncertainty) | |
| number of bins for stimulus phase, (represents phase uncertainty) | |
| number of stimulus repetitions at a given () with independent noise |
| total number of stimuli used for training the decoder | |
| Spatial period of sine wave stimuli; matched to the spatial period of the Gabor filters (but see Figures 4 and 5 and respective captions) | |
| contrast of the sine wave stimuli; chosen to be the mean value of the natural distribution used later in Figure 4 or Figure 6 (but see Figure 5) |
| orientation of the grating stimulus (), 0 being the horizontal direction |
| phase of grating stimulus m relative to line of sight; generated such that () pairs come from the rectangular grid covering uniformly the – parameter space |
| Parameters of the stimulus set used for testing the decoder | |
| number of stimulus repetitions with given (); other parameters of the testing stimulus bank is the same as the training parameters above |
Additional files
-
Transparent reporting form
- https://doi.org/10.7554/eLife.43625.021
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Representational untangling by the firing rate nonlinearity in V1 simple cells
eLife 8:e43625.
https://doi.org/10.7554/eLife.43625
