Figures and data in Calcium-driven regulation of voltage-sensing domains in BK channels

Figures
Tables
Additional files

7 figures, 1 table and 1 additional file

Figures

Figure 1

Download asset Open asset

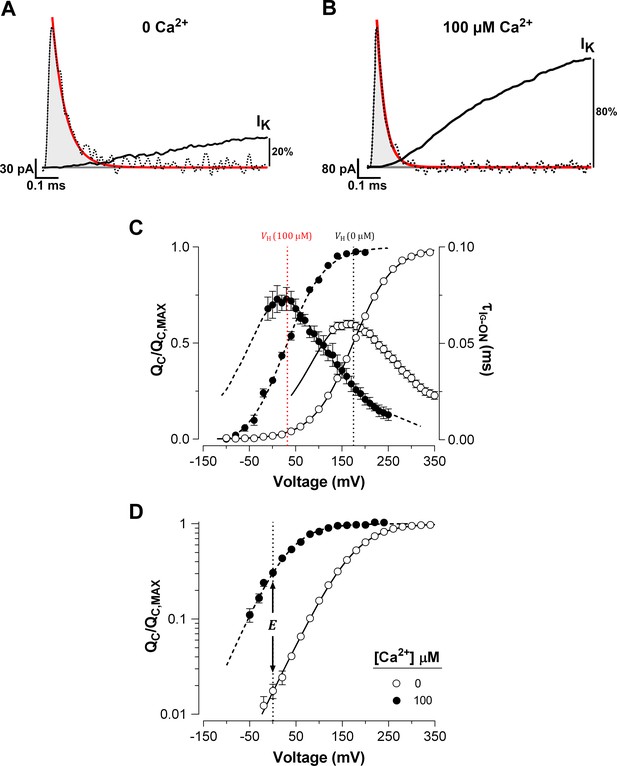
Ca²⁺ binding strongly affects the activation of VSD in BK channels.

(**A–B**) Fast component of the ON-gating current (*I_G*-ON) at 0 and 100 μM internal Ca²⁺ concentration, respectively. The representative *I_G*-ON records were evoked by applying a 160 mV voltage step of 1 ms duration. The first 100 µs of the *I_G*-ON were fitted to a single exponential function (red line; $τ_{I_{G} - O N (0 C a^{2 +})}$ = 58 µs and $τ_{I_{G} - O N (100 μ M)}$ = 30 µs). The area under the curve described by the monoexponential fit (gray areas) was integrated to obtain the charge displaced between closed states ( $Q_{C}$ ). For comparison, the initial time course of the macroscopic K⁺ current (*I_K*) activation (solid black line) obtained at 0 and 100 μM Ca²⁺ were superimposed on the *I_G*-ON under the same internal Ca²⁺ conditions. The *I_K* were evoked by a 15 ms pulse to 160 mV. The *I_K* is described by an exponential function with initial delay: $Δ t_{I_{K} (0 C a^{2 +})}$ = 0.16 ms and $τ_{I_{K} (0 {C a}^{2 +})}$ = 3.37 ms at 0 Ca²⁺; and $Δ t_{I_{K} (100 μ M)}$ = 0.08 ms and $τ_{I_{K} (100 μ M)}$ = 0.66 ms at 100 μM Ca²⁺. After 1 ms, the *I_K* increased to about 20% and 80% of its steady-state amplitude in 0 Ca²⁺ and 100 μM Ca²⁺, respectively. (C) Voltage-dependence of the $Q_{C}$ and of the gating current time constants ( $τ_{I_{G} - O N}$ ) at 0 Ca²⁺ (open circles) and 100 μM Ca²⁺ (filled circles). Gating charge-voltage relationships ( $Q_{C} (V) / Q_{C, M A X}$ ) were obtained by integrating the fast component for each ON *I_G* trace (from −90 mV to 350 mV). Boltzmann fitting to the experimental data (mean ± SEM) is indicated by solid line at ‘zero’ Ca²⁺ ( $V_{H}$ = 174.5 ± 2.4 mV, $z_{Q}$ = 0.60 ± 0.01, $n$ = 25) and by a dashed line at 100 µM Ca²⁺ ( $V_{H}$ = 31.9 ± 4.5 mV, $z_{Q}$ = 0.66 ± 0.01, $n$ = 7). Right ordinate shows the time constants data (mean ± SEM) of the exponential decays of *I_G*-ON ( $τ_{I_{G} - O N}$ ) plotted against the voltage. The best fit to a two-state model of the VSD activation where the $z_{J}$ was constrained to the values found for the $Q_{C} (V)$ relation ( $z_{Q}$ ) is indicated by solid lines at ‘zero’ Ca²⁺ ( $α_{0}$ = 3.73 ms⁻¹, $β_{0}$ = 76.10 ms⁻¹ and $δ$ = 0.29) and dashed line at 100 µM Ca²⁺ ( $α_{0}$ = 7.28 ms⁻¹, $β_{0}$ = 6.98 ms⁻¹ and $δ$ = 0.36). The corresponding $V_{H}$ at each internal Ca²⁺ concentration is indicated by a vertical line. (D) Semi-logarithmic plot of the $Q_{C} (V) / Q_{C, M A X}$ curves at 0 Ca²⁺ and saturating Ca²⁺ concentration (100 µM). The allosteric parameter $E$ determines the vertical displacement of the 0 mV intercept (dashed vertical line) of the $Q_{C} (V) / Q_{C, M A X}$ curve at 100 µM Ca²⁺ relative to the 0 Ca²⁺ condition.

https://doi.org/10.7554/eLife.44934.002

Figure 2 with 2 supplements

Download asset Open asset

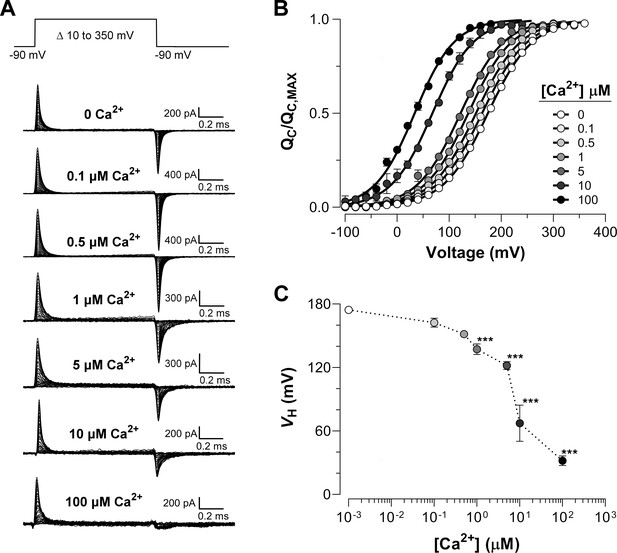
Ca²⁺-dependent effects on VSD activation in BK channels.

(A) Representative gating current (*I_G*) recordings at different internal Ca²⁺ concentrations (from 0 to 100 μM). *I_G* was evoked by the indicated voltage protocol of 1 ms duration. Representative gating current records are from different patches with the exception of 0 and 100 μM Ca²⁺. (B) Gating charge-voltage relationships ( $Q_{C} (V)$ ) were obtained by integrating the fast component for each ON *I_G* trace. Normalized gating charge data $(Q_{C} (V) / Q_{C, M A X})$ (mean ± SEM) were fitted using a single Boltzmann function (solid lines). The fit parameters are as follows: ‘zero’ Ca²⁺ ( $V_{H}$ = 174.5 ± 2.4 mV, $z_{Q}$ = 0.60 ± 0.01, $n$ = 25); 0.1 µM Ca²⁺ ( $V_{H}$ = 162.4 ± 4.2 mV, $z_{Q}$ = 0.59 ± 0.01, $n$ = 5); 0.5 µM Ca²⁺ ( $V_{H}$ = 151.6 ± 1.3 mV, $z_{Q}$ = 0.60 ± 0.01, $n$ = 5); 1 µM Ca²⁺ ( $V_{H}$ = 137.1 ± 5.1 mV, $z_{Q}$ = 0.61 ± 0.01, $n$ = 5); 5 µM Ca²⁺ ( $V_{H}$ = 121.9 ± 3.8 mV, $z_{Q}$ = 0.63 ± 0.01, $n$ = 5); 10 µM Ca²⁺ ( $V_{H}$ = 67.3 ± 17.1 mV, $z_{Q}$ = 0.64 ± 0.08, $n$ = 4); 100 µM Ca²⁺ ( $V_{H}$ = 31.9 ± 4.5 mV, $z_{Q}$ = 0.66 ± 0.01, $n$ = 7). (C) $V_{H}$ obtained from the $Q_{C} (V)$ curves as a function of Ca²⁺ concentration (mean ± SEM). Ca²⁺ binding produces a leftward shift in $V_{H} (Δ V_{H})$ : 0.1 µM Ca²⁺ ( $Δ V_{H}$ = −12.1 ± 3.5 mV); 0.5 µM Ca²⁺ ( $Δ V_{H}$ = −22.9 ± 1.8 mV); 1 µM Ca²⁺ ( $Δ V_{H}$ = −37.1 ± 3.5 mV); 5 µM Ca²⁺ ( $Δ V_{H}$ = −50.3 ± 4.7 mV); 10 µM Ca²⁺ ( $Δ V_{H}$ = −107.1 ± 17.1 mV); 100 µM Ca²⁺ ( $Δ V_{H}$ = −142.6 ± 4.5 mV). One-way ANOVA followed by Dunnett’s post-hoc test analysis was used to assess statistical significance of the Ca²⁺-induced shifts in $V_{H}$ (***p<0.001).

https://doi.org/10.7554/eLife.44934.003

Figure 2—figure supplement 1

Download asset Open asset

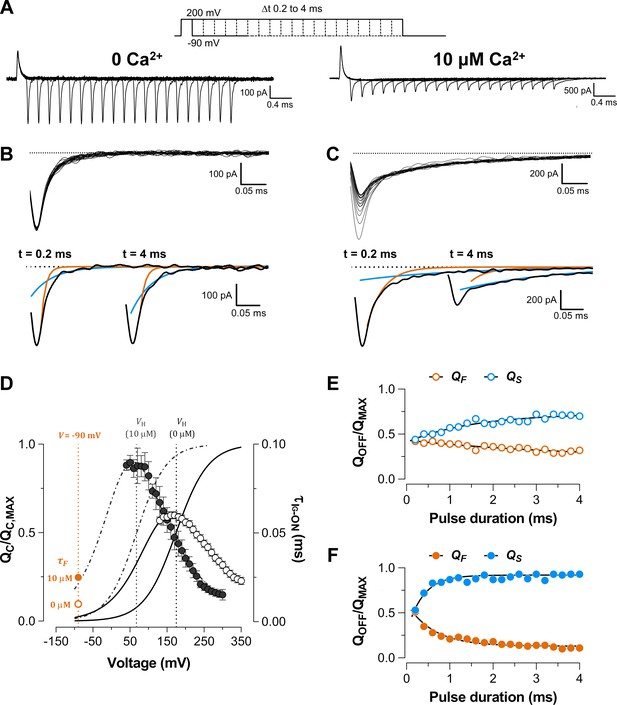
Ca²⁺ increases the slow component of the OFF gating currents.

(A) Recording of gating current (*I_G*) evoked by 200 mV pulses of different durations (from 0.2 to 4 ms) at 0 and 10 μM [Ca²⁺] conditions, respectively. (**B–C**) The top panels show the superimposed traces of the *I_G*-OFF recorded at −90 mV evidencing a decrease in amplitude and a slower decay of the OFF current as the duration of the pulse increases at 10 μM Ca²⁺. The dashed line represents the baseline for each experiment. *I_G*-OFF were fitted with an exponential function of two-components (fast and slow components). *I_G*-OFF traces at 0.2 ms and 4 ms pulse duration are displayed for each Ca²⁺ condition. Orange and blue lines correspond to fast and slow components of the two-exponential fits, respectively: (B) ‘zero’ Ca²⁺ ( $τ_{F}$ = 10 μs and $τ_{S}$ = 44 μs) and (C) 10 μM Ca²⁺ ( $τ_{F}$ = 25 μs and $τ_{S}$ = 212 μs). (D) Plots of the gating currents time constants measured at 0 Ca²⁺ (open symbols, solid line) and 10 μM Ca²⁺ (filled symbols, dot-dashed line). Data are well described using the equations of the two-sate model (see Materials and methods) with the following parameters: $α_{0}$ = 3.73 ms⁻¹, $β_{0}$ = 76.10 ms⁻¹ and $δ$ = 0.29 at 0 Ca²⁺and $α_{0}$ = 3.98 ms⁻¹, $β_{0}$ = 10.61 ms⁻¹ and $δ$ = 0.37 at 10 μM Ca²⁺. The fast OFF time constants at −90 mV for 0 Ca²⁺ (10 μs, orange open circles) and 10 μM Ca²⁺ (25 μs, orange filled circles) from panels B and C are shown. Time constants extrapolated to −90 mV from the two-state model are close to the experimental measurements: 3 μs and 21 μs for 0 Ca²⁺ and 10 μM Ca²⁺, respectively. Boltzmann fit of the $Q_{C} (V)$ curves for 0 Ca²⁺ (solid line) and 10 μM Ca²⁺ are also drawn (dot-dashed line). (**E–F**) The relative amplitude of the OFF-charge components, the fast ( $Q_{F}$ , orange symbols) and slow ( $Q_{S}$ , blue symbols) charge components were plotted against the pulse duration and fitted with an exponential function representing the time course of the opening of the channel: (E) ‘zero’ Ca²⁺ (open circles, $τ_{0 {C a}^{2 +}}$ = 1.8 ms) and (F) 10 μM Ca²⁺ (filled circles, $τ_{10 μ M}$ = 536 μs).

https://doi.org/10.7554/eLife.44934.004

Figure 2—figure supplement 2

Download asset Open asset

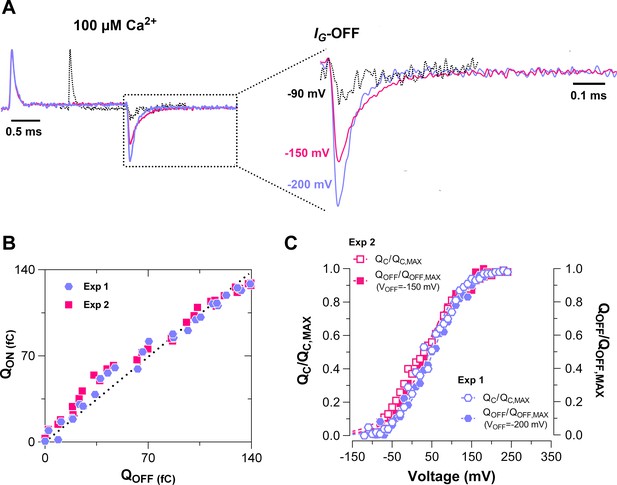
Voltage-dependent movement of the ON and OFF gating charge has a similar behavior at saturating Ca²⁺ conditions.

(A) Normalized gating current (*I_G*) trace at 160 mV voltage step for three different experiments recordings in 100 μM of internal Ca²⁺ conditions. The *I_G*-160 mV trace represented by the black dashed line corresponds to the representative *I_G* at 100 μM Ca²⁺ in Figure 2A. In this record, the *I_G*-ON was evoked by 1 ms voltage steps of 10 mV, going from −90 to 350 and the OFF-gating currents (*I_G*-OFF) recorded at −90 mV of 1 ms duration. For the *I_G* represented by the purple and pink lines, the *I_G*-ON was evoked by 2 ms voltage steps of 10 mV, going from −90 to 350 and the *I_G*-OFF recorded at −200 mV (Experiment 1) and −150 mV (Experiment 2) of 2 ms duration, respectively. For comparison, only the *I_G* trace at 160 mV voltage step of each experiment was shown . (B) $Q_{O N}$ plotted against $Q_{O F F}$ are linearly related in Experiment 1 (Exp 1: purple symbols) and Experiment 2 (Exp 2: pink symbols). $Q_{O N}$ was obtained by integrating the fast component for each ON *I_G* trace ( $Q_{O N}$ = $Q_{C}$ ), and the $Q_{O F F}$ was determined by integrating *I_G*-OFF for each pulse. (C) Normalized ON gating charge data (open symbols: $Q_{C} (V) / Q_{C, M A X}$ ) and OFF gating charge data (filled symbols: $Q_{O F F} (V) / Q_{O F F, M A X}$ ) were fitted using a single Boltzmann function for each experiment: $Q_{C} (V) / Q_{C, M A X}$ ( $V_{H}$ = 44.5 mV, $z_{Q}$ = 0.59) and $Q_{O F F} (V) / Q_{O F F, M A X}$ ( $V_{H}$ = 52.8 mV, $z_{Q}$ = 0.62) for the Exp 1 (V_OFF = −200 mV); and $Q_{C} (V) / Q_{C, M A X}$ ( $V_{H}$ = 29.5 mV, $z_{Q}$ = 0.53) and $Q_{O F F} (V) / Q_{O F F, M A X}$ ( $V_{H}$ = 35.3 mV, $z_{Q}$ = 0.62) for the Exp 2 (V_OFF = −150 mV).

https://doi.org/10.7554/eLife.44934.005

Figure 3 with 2 supplements

Download asset Open asset

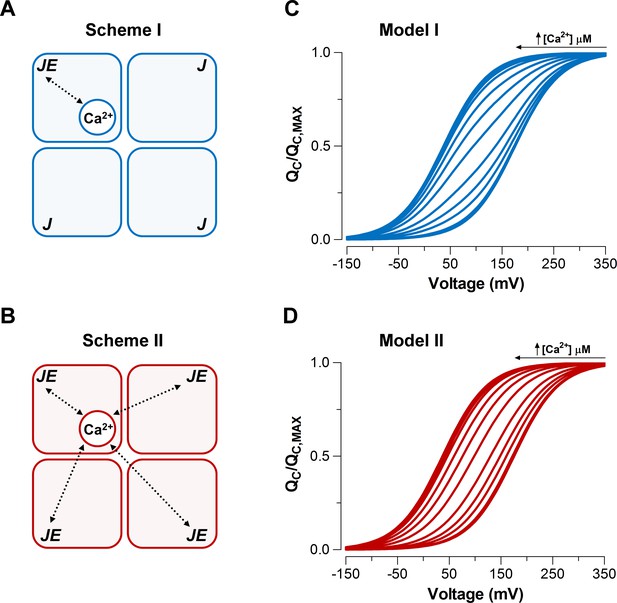
Model-dependent behavior of the $Q_{C} (V)$ curves based on the CTD-VSD interaction mechanisms according to the fractional occupancy of Ca²⁺-binding sites.

(**A–B**) Cartoons representing two interaction schemes between voltage sensors and Ca²⁺-binding sites (modified from Horrigan and Aldrich, 2002). Scheme I (A) assumes that Ca²⁺-binding only affects the voltage sensor of one α-subunit ( $E_{M 1}$ ), whereas Scheme II (B) predicts that binding of Ca²⁺ to one α-subunit will affect VSD in all subunits equally, increasing the voltage sensor equilibrium constants ( $J$ ) $E_{M 2}$ -fold in all four subunits ( $E_{M 2}^{4}$ , when the four Ca²⁺ sites are occupied). In both schemes, a single Ca²⁺-binding site is considered in each α-subunit. (**C–D**) Predictions of $Q_{C} (V)$ relationships at different internal calcium concentration (from 0 to 10 mM) by two distinctive interaction mechanisms between Ca²⁺-binding sites and voltage sensors (Scheme I and Scheme II), respectively. $Q_{C} (V)$ curves were generated using Equation 4 (blue: Model I) or Equation 6 (red: Model II), and the following set of parameters: $z_{J}$ = 0.58, $J_{0}$ = 0.018, $K_{D}$ = 11 µM and $E_{M 1}$ = $E_{M 2}^{4}$ = 25.

https://doi.org/10.7554/eLife.44934.006

Figure 3—figure supplement 1

Download asset Open asset

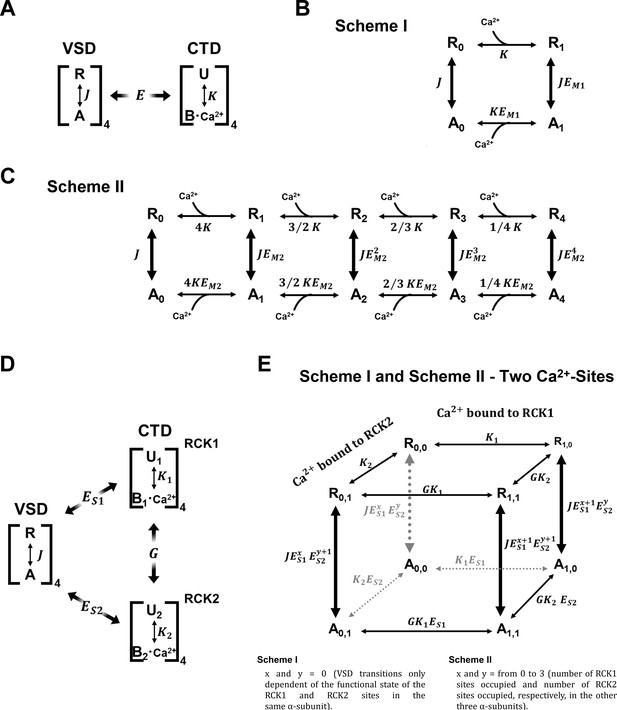
Kinetic models of the VSD activation according to the CTD-VSD interaction schemes.

(A) Sub-scheme describing calcium and voltage allosteric interaction for closed channels. The VSD transit between two resting (R) and active (A) configuration governed by the equilibrium constant $J$ , where each Ca²⁺ site undergoes unbound (U) - Ca²⁺ bound (B) transitions governed by the equilibrium constant $K$ . The allosteric factor $E$ accounts for the coupling between the calcium and voltage sensors (CTD-VSD). (**B–C**) VSD kinetic models in the presence of Ca²⁺ according to CTD-VSD interaction schemes I and II (Figure 3A–B), respectively, where the vertical transitions (R-A) represent the VSD movement and the horizontal transitions (R-R and A-A) are Ca²⁺-binding reactions when the VSD is in the resting or active conformation. For Scheme I (B), each VSD can undergo R₀-A₀ or R₁-A₁ transitions depending on the unbound or bound state of the Ca²⁺ site in the α-subunit, respectively. Thus, the R₁-A₁ equilibrium is defined by $J$ increased $E_{M 1}$ -fold ( $J E_{M 1}$ ). For Scheme II (C), the R₀-A₀ to R₄-A₄ transitions represent the VSD equilibrium with 0, 1, 2, 3, and four occupied Ca²⁺ sites in the channel. Thus, for each Ca²⁺ bound the equilibrium constant $J$ increase $E_{M 2}$ -fold reaching to $J E_{M 2}^{4}$ when the four Ca²⁺ sites are occupied. The thickness of the arrows indicates the probability of transitions. (D) General sub-scheme of the CTD-VSD interaction including two Ca²⁺ sites for each CTD (RCK1 and RCK2 sites). For each RCK1 and RCK2 site the unbound-Ca²⁺ bound transitions are governed by the equilibrium constants $K_{1}$ and $K_{2}$ . The factor $G$ describes the cooperativity between the sites within the same α-subunit; and the $E_{S 1}$ and $E_{S 2}$ factors define the allosteric coupling between the RCK1 and RCK2 sites and the VSD, respectively. (E) Schematic representation of VSD kinetic model according to the extended version of the Scheme I (B) and Scheme II (C) accounting for both RCK1 and RCK2 Ca²⁺-sites on each α-subunit. The VSD transitions in Scheme I only depend on the unbound or bound state of the RCK sites within the same α-subunit: unliganded (R_0,0-A_0,0), RCK1 site occupied (R_1,0-A_1,0), RCK2 site occupied (R_0,1-A_0,1) and both sites occupied (R_1,1-A_1,1). For sake simplicity, Scheme II, only depicts VSD transitions described for the Scheme I. In this case, x and y represent the number of RCK1 sites occupied and number of RCK2 sites occupied, respectively, in the other three α-subunits (x = from 0 to 3 and y = from 0 to 3).

https://doi.org/10.7554/eLife.44934.007

Figure 3—figure supplement 2

Download asset Open asset

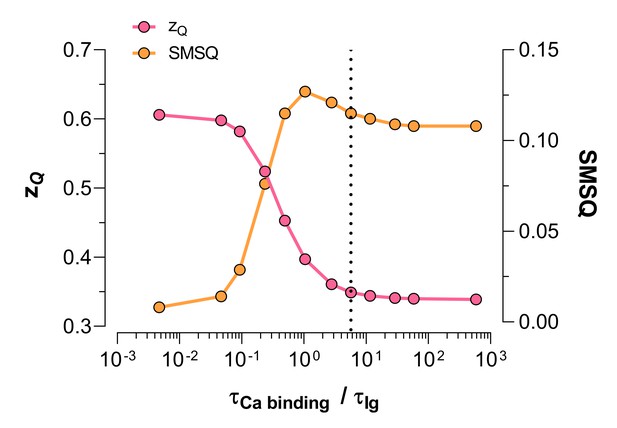
The resting-active transition of the voltage sensor is fast enough to assume no Ca²⁺ re-equilibration during gating currents measurements.

Simulation of, as a function of the time constant ratios of Ca²⁺ binding and gating currents are shown. Gating currents were simulated for a BK Scheme I (Figure 3A). The Ca²⁺ binding rate constant was $k_{b}$ = 1.81×10⁸ M^-1s^-1 (Hou et al., 2016) and the unbinding rate constant $k_{u}$ = 1150. s^-1 was calculated using a $K_{D}$ = 6.4×10^-6 M (Table 1). Voltage-dependent rates for the voltage sensor activation were taken from Figure 1. Gating current were simulated using different calcium-binding time constants: $τ_{C a b i n d i n g} = 1 / x (k_{b} [C a^{2 +}] + k_{u})$ scaled with different x-factors ranging from 0.01 to 1000. We fitted the simulated gating current at 10 μM Ca²⁺ to a single exponential using the first 100 μs of the gating current decay. The maximum gating current time constant was used to calculate the time constant ratios shown in the horizontal axis of the figure. The vertical dashed line marks the time constant ratio calculated for x = 1. The $Q_{C} (V)$ data obtained by integration of the area under the exponential function were fitted using a Boltzmann function. The sum of the residuals squared, SMSQ, was used as an indication of the goodness of the fit. The figure shows that the fit was good (low SMSQ) and the experimental $z_{Q}$ value (0.61) was recovered for calcium-binding/gating current time constant ratio 0.04 or less; that is fast calcium re-equilibration, which is obtained for a calcium-binding rated constant one hundred times faster than the reported by Hou et al. (2016). We conclude that the good fit to a single Boltzmann sigmoidal function to our experimental $Q_{C} (V)$ curves is not due to fast calcium re-equilibration but due to the failure of Model I to describe our data. This conclusion is the same for analysis based on the first 30 μs of the simulated gating currents.

https://doi.org/10.7554/eLife.44934.008

Figure 4 with 1 supplement

Download asset Open asset

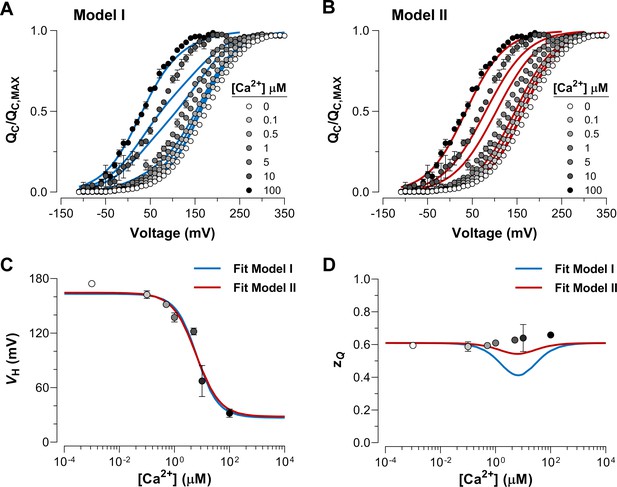
Dose-dependent effect of Ca²⁺ on voltage sensor activation is predicted by a Ca²⁺-VSD interaction mechanism in which Ca²⁺-binding affects equally the VSD in all four α-subunits.

(**A–B**) The experimental $Q_{C} (V)$ data were fitted using the two possible allosteric interaction mechanisms between voltage and calcium sensors described by Scheme I and Scheme II. The blue and red lines represent the global fits by Model I and Model II, respectively. The allosteric factor $E$ ( $E_{M 1}$ and $E_{M 2}$ ) was constrained to the value obtained from the individual fitting of the $Q_{C} (V) / Q_{C, M A X}$ curves at 0 and 100 µM Ca²⁺ (experimental $E$ ( $E_{e x p}$ ) equal to 26.4, see Table 1). The $z_{J}$ , $J_{0}$ and $K_{D}$ parameters were allowed to vary freely. Note that the allosteric factor $E$ for Model I ( $E_{M 1}$ ) and Model II ( $E_{M 2}$ ) have different interpretations, since $E_{M 1} = E_{e x p}$ whereas $E_{M 2} = \sqrt[4]{E_{e x p}}$ given that the four voltage sensor will be altered in 2.3-fold ( $E_{M 2}$ = 2.27) with each additional Ca²⁺ bound. (**C–D**) The Ca²⁺-dependence of $z_{Q}$ - $Q_{C} (V)$ (C) and $V_{H}$ - $Q_{C} (V)$ (D) curves are superimposed with the $z_{Q}$ and $V_{H}$ values predicted by Model I (blue line) and Model II (red line).

https://doi.org/10.7554/eLife.44934.009

Figure 4—figure supplement 1

Download asset Open asset

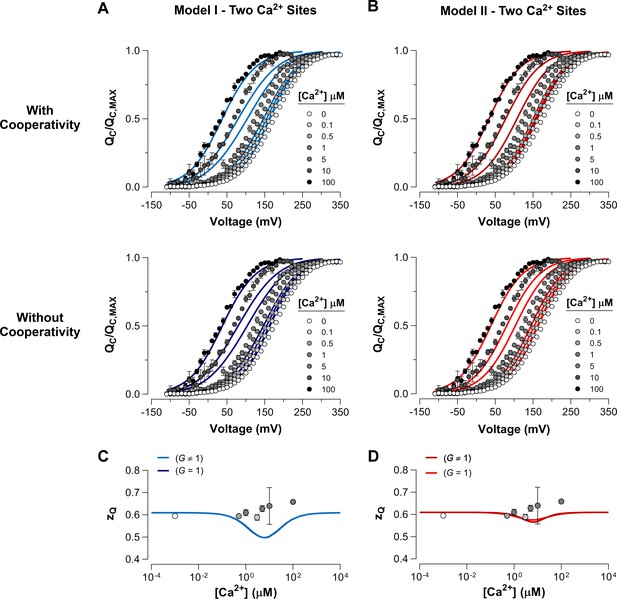
Fitting of experimental $Q_{C} (V)$ data by the Ca²⁺-VSD interaction mechanisms including two Ca²⁺-binding sites per α-subunit.

(**A–B**) The blue and red lines represent the global fits to the experimental $Q_{C} (V)$ curves by Model I (A) and Model II (B), respectively, with two Ca²⁺ sites in each α-subunit. For each model a cooperativity factor between the Ca²⁺ sites within the same subunit ( $G$ ≠ 1) (*Uppe*r) or no cooperative interactions between the Ca²⁺ sites ( $G$ = 1) (*Bottom*) was introduced. The estimated parameters for each model are shown in Table 1. The Ca²⁺-dependence of $z_{Q}$ - $Q_{C} (V)$ data are superimposed with the $z_{Q}$ values predicted by Model I (C) and Model II (D). The statistical analysis using one-way ANOVA followed by Dunnett’s post-hoc test showed no significant effect of Ca²⁺ on $z_{Q}$ (p>0.05).

https://doi.org/10.7554/eLife.44934.010

Figure 5

Download asset Open asset

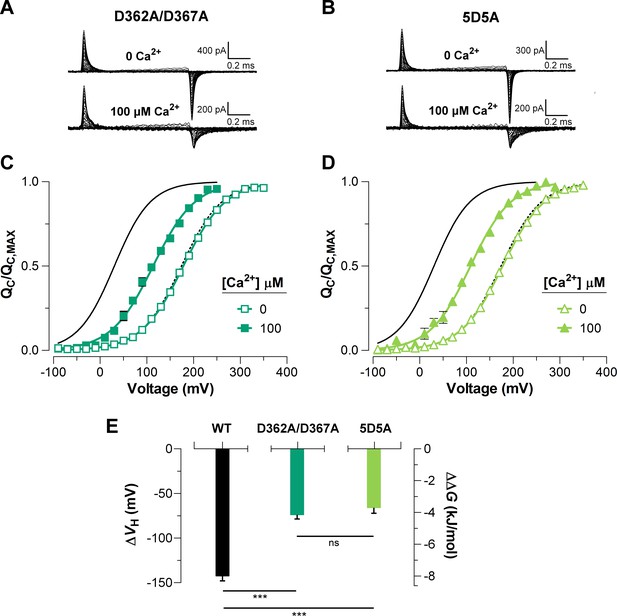
The high-affinity Ca²⁺-binding sites contribute equally to the allosteric coupling between calcium and voltage sensors in BK channels.

(**A–B**) Representative gating current (*I_G*) recordings at 0 and 100 μM of [Ca²⁺]_i for the RCK1 site mutant (D362A/D367A) and the RCK2 site mutant (5D5A), respectively. (**C–D**) Gating charge-voltage curves ( $Q_{C} (V)$ ) were obtained at 0 Ca²⁺ (open symbols) and 100 μM Ca²⁺ (filled symbols) for D362A/D367A and 5D5A mutants, respectively. Boltzmann fitting to the experimental data (mean ± SEM) is indicated by solid lines ( $V_{H}$ _{(D362A/D367A)}= 178.0 ± 2.7 mV, $z_{Q}$ = 0.58 ± 0.01, $n$ = 12 and $V_{H}$ _(5D5A)= 176.4 ± 4.6 mV, $z_{Q}$ = 0.58 ± 0.01, $n$ = 17 at ‘zero’ Ca²⁺; $V_{H}$ _{(D362A/D367A)}= 104.2 ± 7.3 mV, $z_{Q}$ = 0.56 ± 0.02, $n$ = 7 and $V_{H}$ _(5D5A)= 110.8 ± 6.7 mV, $z_{Q}$ = 0.58 ± 0.02, $n$ = 6 at 100 µM Ca²⁺). For comparison, all $Q_{C} (V)$ plots include the Boltzmann fit of the $Q_{C} (V)$ curves for WT at 0 Ca²⁺ (dashed black line) and 100 μM Ca²⁺ (solid black line). (E) Quantification of the $V_{H}$ shift $(Δ V_{H})$ in the $Q_{C} (V)$ curves and the free energy change $(Δ Δ G_{V}^{C a})$ induced by 100 μM Ca²⁺. The non-parametric t-test was used to evaluate statistical significances between WT BK channel and the RCK sites mutants (***p<0.001).

https://doi.org/10.7554/eLife.44934.011

Figure 6

Download asset Open asset

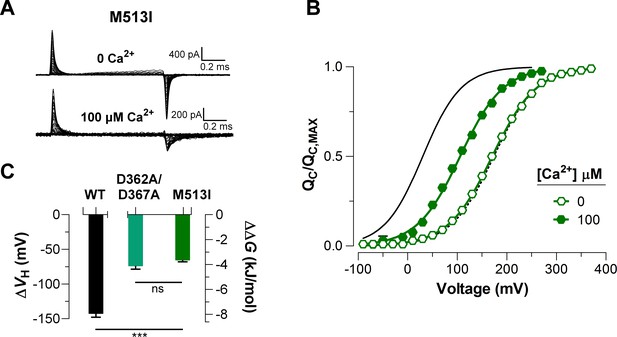
Mutations abolishing Ca²⁺-sensing by the RCK1 binding-site reduce the Ca²⁺-induced effect on voltage sensors activation similarly.

(A) Representative gating current (I_G) recordings at 0 and 100 μM [Ca²⁺]_i for the RCK1 site mutant M513I. (B) Gating charge-voltage curves $Q_{C} (V)$ were obtained at 0 Ca²⁺ and 100 μM Ca²⁺ (open and filled symbols) for the M513I mutant. Boltzmann fit to the experimental data (mean ± SEM) is indicated by solid lines ( $V_{H}$ _(M513I)= 170.4 ± 4.4 mV, $z_{Q}$ = 0.58 ± 0.01, $n$ = 17 at ‘zero’ Ca²⁺ and $V_{H}$ _(M513I)= 105.0 ± 6.3 mV, $z_{Q}$ = 0.62 ± 0.03, $n$ = 4 at 100 µM Ca²⁺). For comparison, the $Q_{C} (V)$ plot includes the Boltzmann fit of the $Q_{C} (V)$ curves for WT at 0 Ca²⁺ and 100 μM Ca²⁺ (dashed and solid black line). (C) Quantification of the $V_{H}$ shift $(Δ V_{H})$ in the $Q_{C} (V)$ curves and the free energy change induced by 100 μM Ca²⁺ $(Δ Δ G_{V}^{C a})$ . A non-parametric t-test was used to compare WT and RCK1-site mutants BK channels (***p<0.001).

https://doi.org/10.7554/eLife.44934.012

Author response image 1

Download asset Open asset

Boltzmann sigmoidal curve fits of the Q(V) curves simulated for a BK model where the occupancy of the calcium binding site of one subunit alters the voltage sensor of only the same subunit.

Using the on binding rate constant of Hou et al., 2016 kb = 1.81⋅108 M^-1s^-1 and the unbinding rate constant ku = 650 s^-1, calculated from the calcium dissociation constant of 3.6⋅10-6. We fitted the simulated the gating current at 15 μM Ca²⁺ to a single exponential using the first 30 μs of the gating current decay. Q(V) data obtained by integration of the area under the exponential function were fitted using a Boltzmann function. The sum of squared residual indicates that the fit is good for the calcium-binding time constant one hundred times shorter than gating current time constant. Also, we recover the zd value (0.58) we used for the simulation, only when the Ca²⁺ binding is 20 to 200 times faster than the voltage sensor kinetics. The high sum of squared residuals and the low zδ value obtained for calcium binding time constant three or more times slower than the gating currents time constant (pointed with arrows) indicates that the Q(V) curve is not a simple Boltzmann sigmoidal function.

Tables

Table 1

Parameters for the best fits of the $Q_{C} (V)$ data using different Ca²⁺-VSD interaction models.

https://doi.org/10.7554/eLife.44934.013

One Ca²⁺-site per α-subunit			Two Ca²⁺-sites per α-subunit
	Model I	Model II		Model I		Model II
Parameters	Model I	Model II	Parameters	With cooperativity	Without cooperativity	With cooperativity	Without cooperativity
*z_J*	0.61	0.61	z_J	0.61	0.61	0.61	0.61
J₀	0.020	0.018	J₀	0.019	0.019	0.021	0.019
E	26.4^*	2.27^*	E_S₁	4.57^*		1.46^*
E	26.4^*	2.27^*	E_S₂	5.35^*		1.52^*
K_D (µM)	6.4	6.1	K_D₁ (µM)	3.2	4.9	837.7	5.9
K_D (µM)	6.4	6.1	K_D₂ (µM)	631.7	6.9	6.6	5.9
			G	56.1	1^*	120.4	1^*
AIC	−948.4	−1150.9		−1088.9	−1090.3	−1162.0	−1147.5
L_i	4^*10⁻⁴⁷	0.004		1^*10⁻¹⁶	3^*10⁻¹⁶	1	7^*10⁻⁴
w_i	4^*10⁻⁴⁷	0.004		1^*10⁻¹⁶	3^*10⁻¹⁶	0.995	0.001

^*Fixed parameters in the model fitting. AIC values correspond to Akaike Information Criterion to select the best fit model. ℒ_i and w_i are the relative likelihood and the weight of each model within the set of candidate models.

Additional files

Transparent reporting form: https://doi.org/10.7554/eLife.44934.014
Download elife-44934-transrepform-v2.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Yenisleidy Lorenzo-Ceballos
Willy Carrasquel-Ursulaez
Karen Castillo
Osvaldo Alvarez
Ramon Latorre

(2019)

Calcium-driven regulation of voltage-sensing domains in BK channels

eLife 8:e44934.

https://doi.org/10.7554/eLife.44934

Share this article

Cite this article

Ca2+ binding strongly affects the activation of VSD in BK channels.

Ca2+-dependent effects on VSD activation in BK channels.

Ca2+ increases the slow component of the OFF gating currents.

Voltage-dependent movement of the ON and OFF gating charge has a similar behavior at saturating Ca2+ conditions.

Model-dependent behavior of the QC(V) curves based on the CTD-VSD interaction mechanisms according to the fractional occupancy of Ca2+-binding sites.

Kinetic models of the VSD activation according to the CTD-VSD interaction schemes.

The resting-active transition of the voltage sensor is fast enough to assume no Ca2+ re-equilibration during gating currents measurements.

Dose-dependent effect of Ca2+ on voltage sensor activation is predicted by a Ca2+-VSD interaction mechanism in which Ca2+-binding affects equally the VSD in all four α-subunits.

Fitting of experimental QC(V) data by the Ca2+-VSD interaction mechanisms including two Ca2+-binding sites per α-subunit.

The high-affinity Ca2+-binding sites contribute equally to the allosteric coupling between calcium and voltage sensors in BK channels.

Mutations abolishing Ca2+-sensing by the RCK1 binding-site reduce the Ca2+-induced effect on voltage sensors activation similarly.

Boltzmann sigmoidal curve fits of the Q(V) curves simulated for a BK model where the occupancy of the calcium binding site of one subunit alters the voltage sensor of only the same subunit.

Parameters for the best fits of the QC(V) data using different Ca2+-VSD interaction models.

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Ca²⁺ binding strongly affects the activation of VSD in BK channels.

Ca²⁺-dependent effects on VSD activation in BK channels.

Ca²⁺ increases the slow component of the OFF gating currents.

Voltage-dependent movement of the ON and OFF gating charge has a similar behavior at saturating Ca²⁺ conditions.

Model-dependent behavior of the $Q_{C} (V)$ curves based on the CTD-VSD interaction mechanisms according to the fractional occupancy of Ca²⁺-binding sites.

The resting-active transition of the voltage sensor is fast enough to assume no Ca²⁺ re-equilibration during gating currents measurements.

Dose-dependent effect of Ca²⁺ on voltage sensor activation is predicted by a Ca²⁺-VSD interaction mechanism in which Ca²⁺-binding affects equally the VSD in all four α-subunits.

Fitting of experimental $Q_{C} (V)$ data by the Ca²⁺-VSD interaction mechanisms including two Ca²⁺-binding sites per α-subunit.

The high-affinity Ca²⁺-binding sites contribute equally to the allosteric coupling between calcium and voltage sensors in BK channels.

Mutations abolishing Ca²⁺-sensing by the RCK1 binding-site reduce the Ca²⁺-induced effect on voltage sensors activation similarly.

Parameters for the best fits of the $Q_{C} (V)$ data using different Ca²⁺-VSD interaction models.