Figures and data in Surface-to-volume scaling and aspect ratio preservation in rod-shaped bacteria | eLife

Figures
Additional files

4 figures and 3 additional files

Figures

Figure 1 with 1 supplement

Download asset Open asset

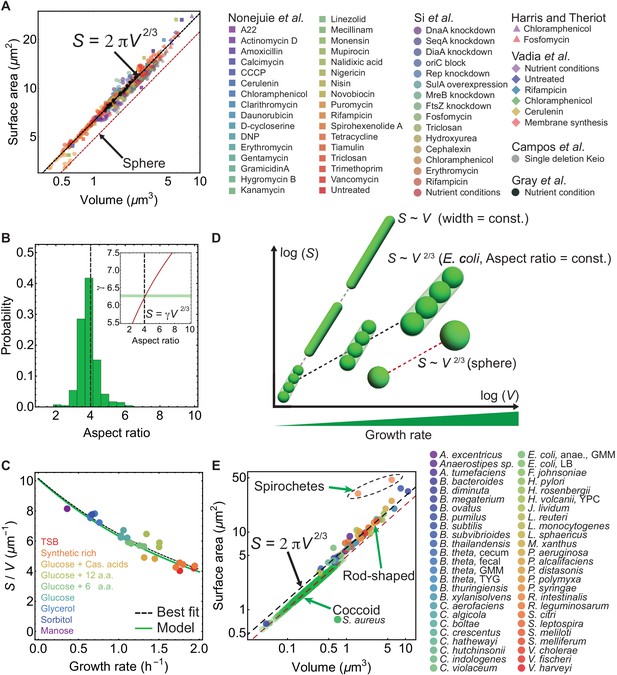
Surface-to-volume scaling in E. coli and other rod-shaped bacteria.

(A) E. coli cells subjected to different antibiotics, nutrient conditions, protein overexpression/depletion, and single gene deletions (Nonejuie et al., 2013; Si et al., 2017; Harris and Theriot, 2016; Vadia et al., 2017; Campos et al., 2018; Gray et al., 2019), follow the scaling relation between population-averaged surface area ( $S$ ) and volume ( $V$ ): $S = γ V^{2 / 3}$ (legend on the right, 5011 data points; Supplementary file 1). Best fit shown in dashed black line for steady-state data from Si et al. (2017) gives γ = 6.24 ± 0.04, and a power law exponent 0.671 ± 0.006. For single deletion Keio set (Campos et al., 2018), the best fit curve is $S = 5.79 V^{2 / 3}$ . (B) Aspect-ratio distribution for cells growing in steady-state, corresponding to the data in (A) (Si et al., 2017). (Inset) Relationship between $γ$ and aspect ratio $η$ for a sphero-cylinder (red line). Best fit from (A) shown with horizontal green band gives aspect ratio 4.14 ± 0.17. (C) $S / V$ vs growth rate. Model line uses $S = 2 π V^{2 / 3}$ and the nutrient growth law (Equation 1). Data from Si et al. (2017). (D) $S$ - $V$ relation for various bacterial cell shapes. Black dashed line: Small, medium, and large rod-shaped cells with a conserved aspect ratio of 4 follow the relation: $S = 2 π V^{2 / 3}$ . Gray dashed line: Filamentous cells with constant cell width follow the scaling law: $S \sim V$ . Red dashed line: Spheres follow $S = 6^{2 / 3} π^{1 / 3} V^{2 / 3}$ . (E) $S$ vs $V$ for 49 different bacterial species (Sato, 2000; Trachtenberg, 2004; Pelling et al., 2005; Wright et al., 2015; Deforet et al., 2015; Desmarais et al., 2015; Harris and Theriot, 2016; Ojkic et al., 2016; Quach et al., 2016; Carabetta et al., 2016; Chattopadhyay et al., 2017; Lopez-Garrido et al., 2018; Gray et al., 2019), and one rod-shaped Archaea (H. volcanii) (Supplementary file 2). Rod-shaped cells lie on $S = 2 π V^{2 / 3}$ line, above the line are Spirochete and below the line are coccoid. For coccoid S. aureus exposed to different antibiotics best fit is $S = 4.92 V^{2 / 3}$ , with preserved aspect ratio η = 1.38 ± 0.18. Red dashed line is for spheres.

https://doi.org/10.7554/eLife.47033.002

Figure 1—figure supplement 1

Download asset Open asset

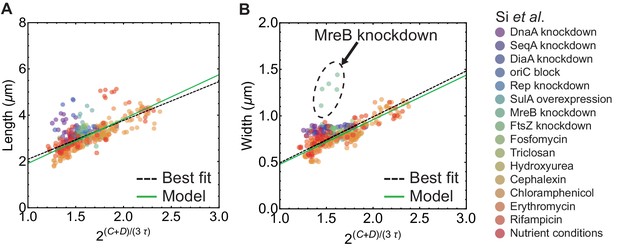
Control of cell width and length in E. coli.

Cell length (A) and width (B) vs $2^{(C + D) / τ}$ . Data used from Si et al. (2017). Here $C$ is time from initiation to termination of DNA replication, $D$ is time from termination of DNA replication to cell division, and $τ$ is doubling time. Green solid lines are calculated assuming $S = 2 π V^{2 / 3}$ . Dashed black lines are best fit curves.

https://doi.org/10.7554/eLife.47033.003

Figure 2 with 1 supplement

Download asset Open asset

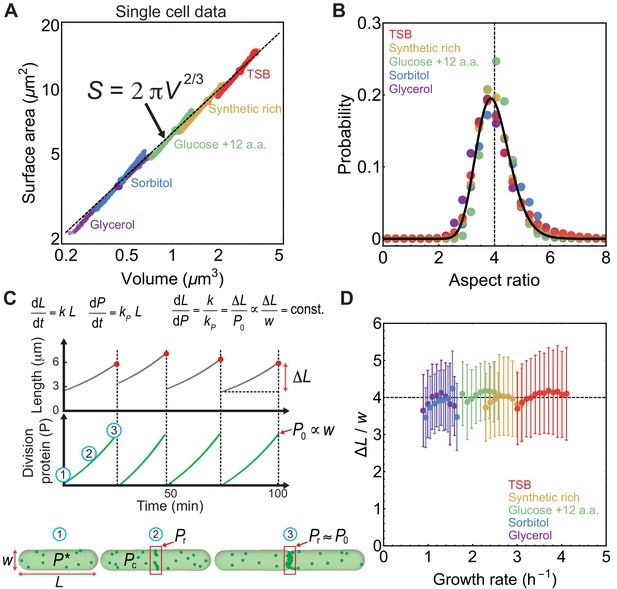
Aspect ratio control in E. coli at the single cell level.

(A) $S$ vs $V$ for newborn E. coli cells grown in mother machine (Taheri-Araghi et al., 2015). Single cell data (small circles) binned in volume follow population averages (large circles). For sample size refer to Supplementary file 1. (B) Probability distribution of newborn cell aspect ratio is independent of growth rate, fitted by a log-normal distribution (solid line) (C) Model schematic. Cell length $L$ increases exponentially during the division cycle at a rate $k$ . Division proteins ( $P$ ) are produced at a rate $k_{P}$ , and assembles a ring in the mid-cell region. At birth, cells contain $P^{*}$ molecules in the cytoplasm. Amount of FtsZ recruited in the ring is $P_{r}$ . Cells divide when $P_{r} = P_{0} \propto w$ , where $w$ is cell width. $P$ vs time and $L$ vs time are reproduced from model simulations. (D) Ratio of the added length ( $Δ L$ ) and cell width ( $w$ ) during one cell cycle is constant and independent of growth rate. Error bars: ±1 standard deviation.

https://doi.org/10.7554/eLife.47033.004

Figure 2—figure supplement 1

Download asset Open asset

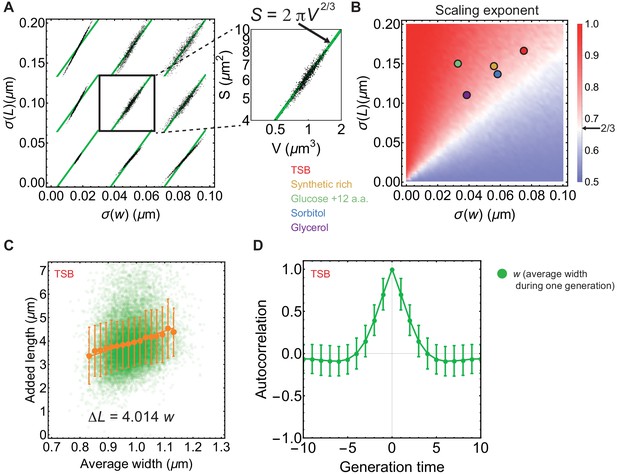
Deviation from average surface-to-volume scaling law, and correlation between added length and width from single-cell E. coli data.

(A) Surface area vs volume for sphero-cylindrical bacterium, computed using normal distribution for cell widths ( $μ_{w}$ , $σ (w)$ ) and log-normal distribution ( $μ_{L}$ , $σ (L)$ ) of cell lengths. Green line is $S = 2 π V^{2 / 3}$ . (B) Surface-to-volume scaling exponent computed for different values of $σ (w)$ and $σ (L)$ while keeping $L / w = 4$ . For each pair of values ( $σ (w)$ , $σ (L)$ ) we pick 10⁴ random numbers from corresponding distributions and computed surface-to-volume scaling exponent. Total of 2500 pairs ( $σ (w)$ , $σ (L)$ ) were used. We obtained $σ (w)$ and $σ (L)$ of newborn cells grown in mother machine by fitting experimental distributions. These values are shown by coloured points that correspond to different growth media (Taheri-Araghi et al., 2015). Large fluctuation in new born lengths for a given cell width results in scaling exponents slightly above 2/3, as expected. (C–D) Single cell data are obtained from Suckjoon Jun lab (UCSD) (Taheri-Araghi et al., 2015). (C) Single cell added length ( $Δ L$ ) vs average width ( $w$ ) during one cell cycle for cell grown in TSB. Green circles represent single cell data, orange circles are average of binned data in width, error bars are ±1 standard deviation, and orange line is best fit to binned data ( $Δ L = 4.014 w$ ). (D) Intergeneration autocorrelation function of average cell width during one cell cycle for cell grown in TSB. Once perturbed, cell width takes ≈4 generations to equilibrate to its steady state population average. Error bars: ±1 standard deviation.

https://doi.org/10.7554/eLife.47033.005

Figure 3 with 1 supplement

Download asset Open asset

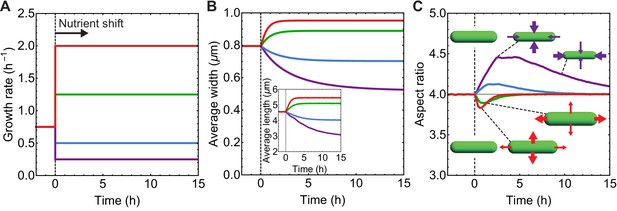
Simulations of aspect ratio preservation during nutrient upshift or downshift.

(A–C) At t = 0 h cells are exposed to nutrient upshift or downshift. Population average of n = 10⁵ simulated cells. (A) Growth rate ( $k$ ) vs time used as input for our simulations. (B) Population-averaged cell length and width vs time. (C) Population-averaged aspect ratio of newborn cells vs time. Changes in cell width and length result in a transient increase in aspect ratio during nutrient downshift, or a transient decrease during nutrient upshift.

https://doi.org/10.7554/eLife.47033.006

Figure 3—figure supplement 1

Download asset Open asset

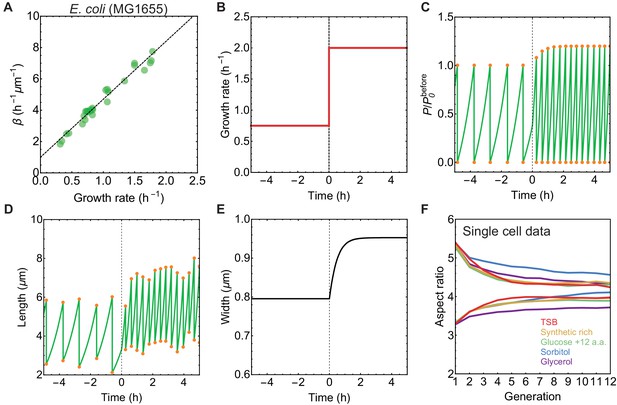
Simulations of nutrient upshift and aspect ratio equilibration at the single cell level.

(A) From experimental measurement of growth rate $k$ and cell width $w$ we calculated surface area production rate $β = 4 k / w$ . Data from Si et al. (2017). Dashed black line is best fit that we used in nutrient shift simulations. (B–E) Single cell traces for simulation of cell shape dynamics during nutrient upshift. (B) Division protein vs time normalised by $P_{0}$ before the nutrient shift. (C) Growth rate vs time. (D) Length vs time. Length fluctuations at division is a consequence of noise in division ratio (see Materials and methods). (E) Cell width vs time. (F) Aspect ratio of newborn cells vs generation number for single cell data from mother machine (Taheri-Araghi et al., 2015). Newborn cells with aspect ratio between 5–6 or 3–3.5 were tracked over generations. Population average for given generation number over 737–2843 cells for different growth condition is shown.

https://doi.org/10.7554/eLife.47033.007

Figure 4 with 1 supplement

Download asset Open asset

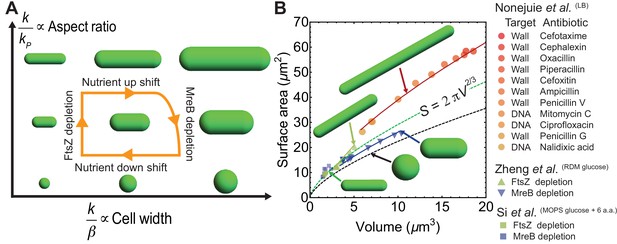
Model predictions for aspect ratio and shape control under perturbations.

(A) Model parameters that control changes in cell aspect ratio ( $k / k_{P}$ ) or width ( $k / β$ ). For quantification see Figure 4—figure supplement 1A. (B) Surface area vs volume for cells under antibiotic treatment (Nonejuie et al., 2013), FtsZ knockdown and MreB depletion (Si et al., 2017; Zheng et al., 2016). Solid lines are best fit obtained using our model and data from Zheng et al. (2016) (see Materials and methods). Cells with depleted FtsZ have elongated phenotypes, while depleted MreB have smaller aspect ratio and larger width. Cell wall or DNA targeting antibiotics induce filamentation. Dashed green line: $S = 2 π V^{2 / 3}$ , dashed black line: spheres.

https://doi.org/10.7554/eLife.47033.008

Figure 4—figure supplement 1

Download asset Open asset

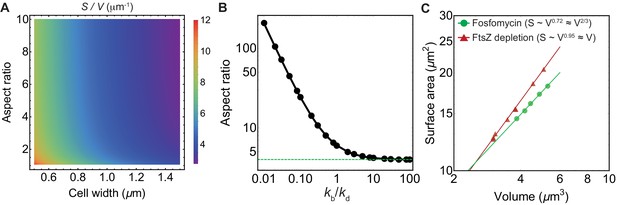
Impact of surface-to-volume ratio and FtsZ depletion on cell aspect ratio.

(A) Quantification of surface-to-volume ratio for the schematic shown in Figure 4A. (B) Model prediction for cellular aspect ratio (average over newborn cells) as a function of $k_{b} / k_{d}$ . Here $k_{b}$ is the rate of binding of cytoplasmic FtsZ to the Z-ring, and $k_{d}$ is the rate of disassembly of Z-ring bound FtsZ. Dashed green horizontal line corresponds to aspect ratio of 4, obtained in the limit $k_{b} ≫ k_{d}$ . (C) Comparison of surface-to-volume scaling for E. coli treated with fosfomycin (Harris and Theriot, 2016) and under FtsZ knockdown (Zheng et al., 2016).

https://doi.org/10.7554/eLife.47033.009

Additional files

Supplementary file 1 Sample size for collected bacterial shape data.: https://doi.org/10.7554/eLife.47033.010
Download elife-47033-supp1-v2.docx
Supplementary file 2 Sample size for rod-shaped bacterial and archeal cell shapes.: https://doi.org/10.7554/eLife.47033.011
Download elife-47033-supp2-v2.docx
Transparent reporting form: https://doi.org/10.7554/eLife.47033.012
Download elife-47033-transrepform-v2.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Nikola Ojkic
Diana Serbanescu
Shiladitya Banerjee

(2019)

Surface-to-volume scaling and aspect ratio preservation in rod-shaped bacteria

eLife 8:e47033.

https://doi.org/10.7554/eLife.47033

Sign up for email alerts

Privacy notice