Single-cell modeling of routine clinical blood tests reveals transient dynamics of human response to blood loss
- Massachusetts General Hospital, United States
- Harvard Medical School, United States
- Sports Medicine Research and Testing Laboratory, United States
Figures
Figure 1
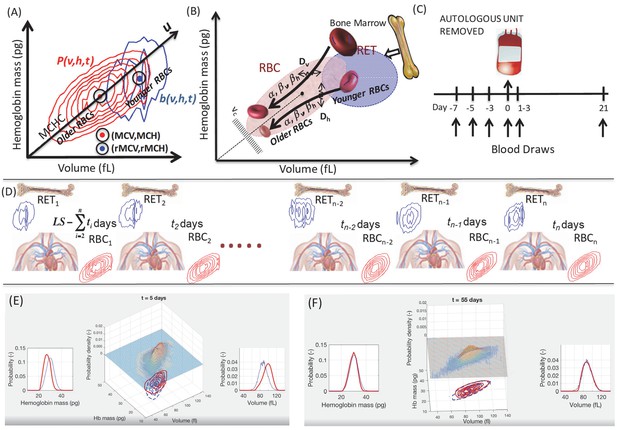
Unsteady-state modeling of single-RBC volume and hemoglobin dynamics.
(A) Routine complete blood counts (CBC) measure the single-cell volume and hemoglobin for young RBCs (b(v,h,t), blue contours showing ‘reticulocytes’ that are <~3 days old) as well as for all circulating RBCs (P(v,h,t), red contours showing RBCs of all ages from 0 up to 90–120 days, with RBC lifespan well-controlled in each person but varying from one person to the next). The black line through the origin shows the mean hemoglobin concentration (mean corpuscular hemoglobin concentration, MCHC) for the sampled population and this major axis of the distribution (u) provides a very rough estimate of RBC age, with higher u corresponding to younger age. (B) Schematic of the model of single-RBC volume-hemoglobin dynamics. Individual RBCs are produced as reticulocytes (RET) in the top right and lose about 30% of their volume and about 20% of their hemoglobin during their 90–120 day lifespan, with volume and hemoglobin reductions occurring during an early fast phase parameterized by βv and βh and a later slow phase parameterized by α, with fluctuations in rates of single-RBC volume and hemoglobin change quantified by Dv and Dh. As the single-RBC volume and hemoglobin continue to fall, the probability of clearance increases dramatically as the RBC’s trajectory approaches the boundary region shown as vc. (C) Four measurements were made to establish each subject’s baseline before controlled blood loss. Additional measurements were made 1–3 days and 21 days later. (D) The modeling integrated serial CBCs into the parameter estimation process in a piecewise manner. The first CBC (left) is assumed to be at steady state, and the model is used to estimate dynamic parameters which produce RBC1 given RET1. These model parameters and RET1 are then used to estimate the initial condition leading to timepoint t2, and the model estimates the dynamics between timepoints t1 and t2. These steps for timepoint t2 are then repeated to estimate the transient dynamics between each successive timepoint. LS refers to the lifespan of RBCs. Panels (E–F) are frames from Video 1 that shows a simulation of the evolution of P(v,h,t) from t = 0 to t = 105 days for a typical study subject. Equal-probability contours for P(v,h) are shown at the bottom, with the empirical measurement as blue lines, and the simulation in solid red. The surface plot also shows the simulated P(v,h,t). The plot of the empirical measurement in dashed blue is serially updated during the movie to the measurement subsequent to the value of t. Marginal P(v,t) and P(h,t) are shown on the left and right.
Figure 2 with 1 supplement
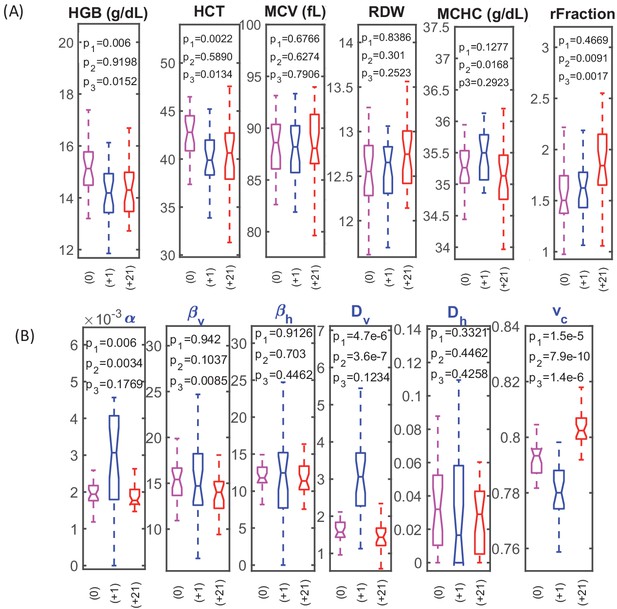
RBC dynamics are more sensitive to blood loss than RBC population statistics.
(A) Complete blood count (CBC) statistics for 28 healthy subjects before (0), 1–3 days after blood loss (+1), and 21 days after blood loss (+21). Intensive quantities (HGB, concentration of hemoglobin per unit volume of blood; HCT, volume fraction of RBCs in the blood) change significantly immediately following blood loss due to fluid shift, but single-RBC population statistics do not change significantly. MCV, mean RBC volume; RDW, coefficient of variation in RBC volume; MCHC, mean RBC hemoglobin concentration; rFraction, percentage of identified reticulocytes. See Figure 2—figure supplement 1 for rMCV, mean reticulocyte volume; rRDW, coefficient of variation in reticulocyte volume; MCH, mean RBC hemoglobin mass; CHDW, coefficient of variation in single-RBC hemoglobin concentration. By 21 days after blood loss, the CHDW and rFraction have increased significantly relative to baseline. MCHC at 21 days has decreased relative to 1–3 days. See main text and supplementary information for more detail. (B) Single-RBC volume and hemoglobin dynamics show significant change soon after blood loss. α and Dv increase significantly, and vc drops. (p1 compares +0 with +1, p2 compares +1 and +21, p3 compares 0 and +21.) Boxplots show the median (middle horizontal line), the 25th and 75th percentiles, and whiskers extend to data points not more than 1.5-times the interquartile range from the median. Notches show a 95% confidence interval for the median, and any additional outliers are shown as discrete points.
-
Figure 2—source data 1
Source data for boxplots in Figure 2.
- https://cdn.elifesciences.org/articles/48590/elife-48590-fig2-data1-v1.xlsx
Figure 2—figure supplement 1
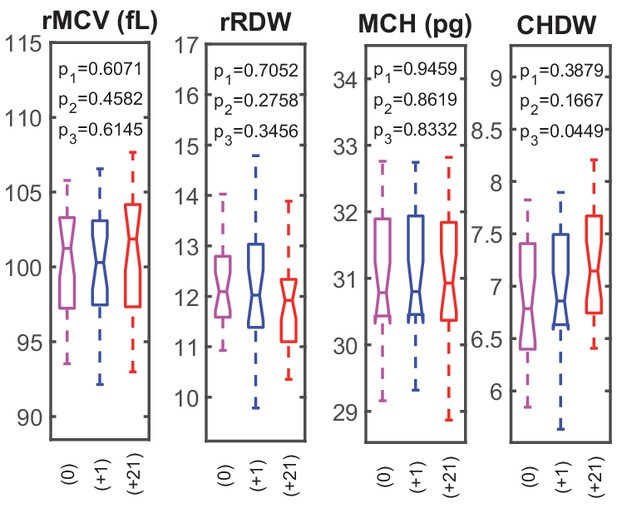
RBC dynamics are more sensitive to blood loss than RBC population statistics.
Supplementary complete blood count (CBC) statistics for 28 healthy subjects before (0), 1–3 days after blood loss (+1), and 21 days after blood loss (+21). rMCV, mean reticulocyte volume; rRDW, coefficient of variation in reticulocyte volume; MCH, mean RBC hemoglobin mass; CHDW, coefficient of variation in single-RBC hemoglobin concentration. By 21 days after blood loss, the CHDW has increased significantly relative to baseline.
-
Figure 2—figure supplement 1—source data 1
Source data for boxplots in Figure 2—figure supplement 1.
- https://cdn.elifesciences.org/articles/48590/elife-48590-fig2-figsupp1-data1-v1.xlsx
Figure 3
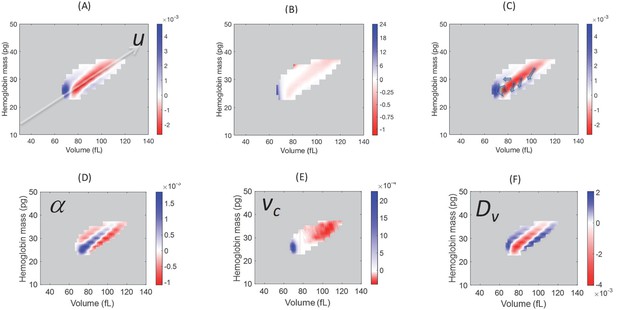
Model simulations show that blood loss causes a shift of probability density from the central axis of the (v,h) distribution, mostly to the low volume-low hemoglobin tail.
Comparison of the absolute (A) and relative (B) changes in the simulated single-RBC volume-hemoglobin probability density when setting Dv’=4Dv, α’=2α, and vc’=0.9vc, to match the median changes shown in Figure 2B. (C) Arrows depict the typical movement in probability density 1–3 days after blood loss. (D–F) show the effects of isolated changes to individual parameters, with changes to α and vc corresponding to retention of older RBCs (delayed clearance), and changes to Dv adding density in the high-volume, low-hemoglobin region where new RBCs appear, corresponding, in part, to increased production.
Figure 4
Single-cell model provides a mechanistic link between dynamics of the (v,h) distribution and the balance between increased RBC production and delayed RBC clearance in response to blood loss.
(A) Schematic of the single-cell volume-hemoglobin distribution for RBCs. The major axis of the distribution (u) corresponds to the mean single-RBC hemoglobin concentration (MCHC). An RBC’s position when projected onto u corresponds roughly to its age, with younger RBCs generally appearing in the upper right, and aging along the u axis toward the origin in the bottom left. We can compare changes in the fraction of older RBCs by integrating density along u as shown in the inset in the top left. We can compare changes in the fraction of newly produced RBCs by conditioning on higher u and integrating density along the [Hb] axis as show in the inset in the top right of panel (A). (B) The top panel shows a typical (v,h) distribution that has been transformed onto the u-[Hb] plane in the bottom panel. (C) The typical blood loss response after 1–3 days includes an increase in the fraction of newly produced cells which will have [Hb] more than one standard deviation below the median and u more than one standard deviation above the median (p<1e-3), corresponding to the top right inset in panel (A) and consistent with increased production. (D) 1–3 days following blood loss, the typical response also involves an increase in the fraction of older RBCs, located more than one standard deviation (15%) below the median u (p<1e-3), corresponding to the top left inset in panel (A) and consistent with a delayed clearance. (E) The mean RBC age (MRBC), as estimated by the glycated hemoglobin fraction, has decreased on average by about 4% after 21 days, but there is significant variation, with some subjects seeing an increase in MRBC. (F) The model characterizes the relative balance between increased production and delayed clearance in each subject’s blood response by the dimensionless parameter ratio . The time-weighted average of this ratio after blood loss for each subject is significantly correlated with the estimated change in MRBC (ρ = −0.59), suggesting that the model of (v,h) dynamics has accurately captured the balance of the typical subject’s blood loss response. The red line is a least-squares linear fit. (G) The dimensionless parameter ratio distinguishes subjects whose MRBC becomes shorter (production-dominated) during response to blood loss from those whose MRBC becomes longer (clearance-dominated). (See Figure 2 caption for boxplot description.)
-
Figure 4—source data 1
Source data for boxplots in Figure 4.
- https://cdn.elifesciences.org/articles/48590/elife-48590-fig4-data1-v1.xlsx
Figure 5
Following blood loss, the MCHC rise and fall and the sustained CHDW rise are consistent with a combination of delayed RBC clearance and increased RBC production.
(Top) The intra-subject MCHC tends to increase immediately after blood loss (left, p<0.05) and then decreases below baseline by 21 days later (right, p<0.01). (Bottom) The intra-subject CHDW increases immediately after blood loss (p<0.002) and then increases again by 21 days later (p<0.002).
-
Figure 5—source data 1
Source data for boxplots in Figure 5.
- https://cdn.elifesciences.org/articles/48590/elife-48590-fig5-data1-v1.xlsx
Videos
Video 1
The video shows a simulation of the evolution of P(v,h,t) from t = 0 to t = 105 days for a typical study subject.
Equal-probability contours for P(v,h) are shown at the bottom, with the empirical measurement as blue dashed lines, and the simulation in solid red. The surface plot also shows the simulated P(v,h,t). The plot of the empirical measurement in dashed blue is serially updated during the movie to the measurement subsequent to the value of t. Marginal distributions, P(v,t), and P(h,t), are shown at the sides along with empirical measurements in blue.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Single-cell modeling of routine clinical blood tests reveals transient dynamics of human response to blood loss
eLife 8:e48590.
https://doi.org/10.7554/eLife.48590
