Measuring the distribution of fitness effects in somatic evolution by combining clonal dynamics with dN/dS ratios
- Centre for Genomics and Computational Biology, Barts Cancer Institute, Barts and the London School of Medicine and Dentistry, Queen Mary University of London, United Kingdom
- Computational Oncology, Department of Epidemiology and Biostatistics, Memorial Sloan Kettering Cancer Center, United States
- Evolutionary Genomics and Modelling Lab, Centre for Evolution and Cancer, The Institute of Cancer Research, United Kingdom
- Department of Cell and Developmental Biology, University College London, United Kingdom
Figures
Figure 1 with 1 supplement
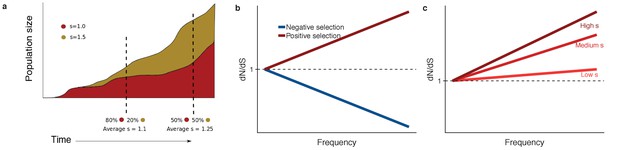
dN/dS in somatic evolution depends on the frequency of clones.
(a) Variants under positive selection are enriched at high frequency, this means dN/dS estimates are dependent on the frequency of mutation, (b). The strength of selection influences the degree to which positively selected variants are enriched at high frequencies (c).
Figure 1—figure supplement 1
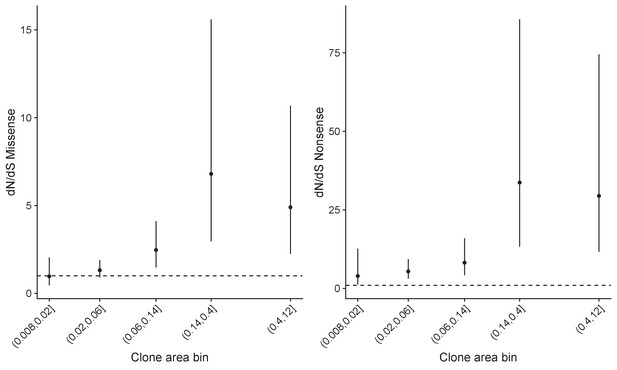
Global dN/dS values in different frequency bins for patient PD31182 showing that the values depend on the frequency of mutations.
Figure 2 with 4 supplements
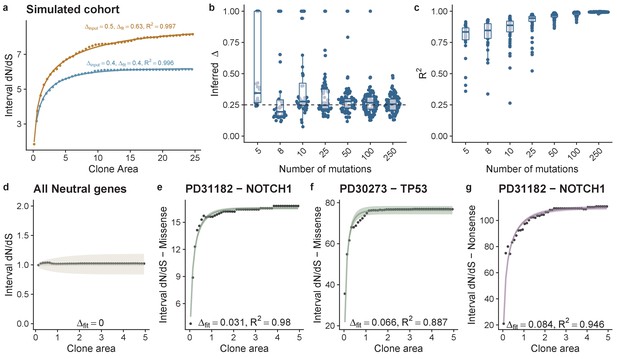
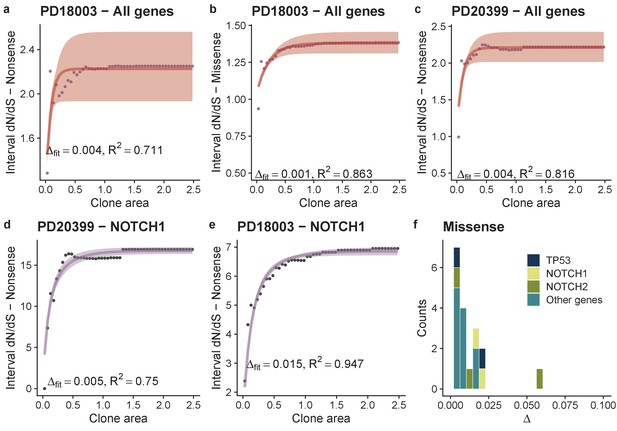
Theoretical model of interval dN-dS fitted to simulated data and data from deep sequencing of the oesophagus.
(a) Interval dN/dS as a function of clone area for 2 simulated cohorts where driver mutations induce different biases, theoretical model captures the dynamics well and enables us to recover the bias ∆, accurately. As the number of mutations increases ability to recover the correct ∆ and the model fit (measured using R2) improves (b) and (c). (d) Data and model fit for all neutral genes, shows i-dN/dS = 1 across the frequency range and inferred bias of 0. Data and model fit for (e) NOTCH1 missense mutations in patient PD31182, (f) missense TP53 mutations in PD30273 and NOTCH1 nonsense mutations in PD31182 (g). Data are black points and model fits are solid lines with shaded areas denoting 95% CI.
Figure 2—figure supplement 1
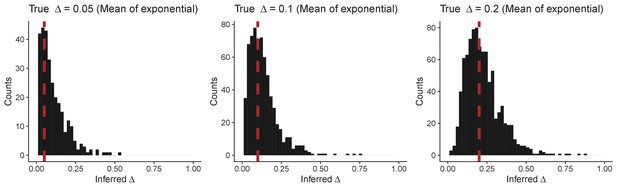
Histogram of inferred Δ values from simulations using an exponentially distributed fitness effect.
For each panel the mean of the exponential distribution used for Δ is stated above and illustrated by the red dashed lines.
Figure 2—figure supplement 2
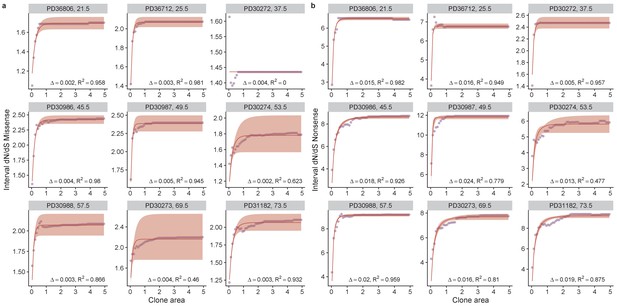
Model fits for all patients in the oesophagus data set.
Purple points are data and red lines model fits, shaded areas denote 95% confidence intervals. Fits were performed separately for missense, (a) and nonsense mutations, (b). Each plot is annotated with the inferred bias ∆ and the R2 value.
Figure 2—figure supplement 3
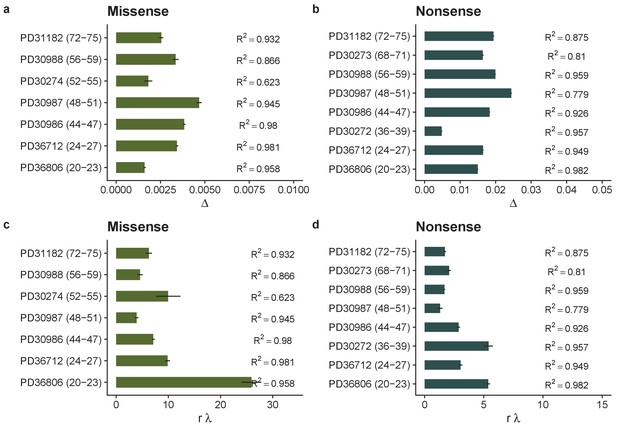
Inferred biases for for each patient in the oesophagus dataset based on missense, (a) and nonsense mutations, (b).
Inferred loss replacement rates, rλ for each patient based on missense, (c) and nonsense mutations, (d).
Figure 2—figure supplement 4
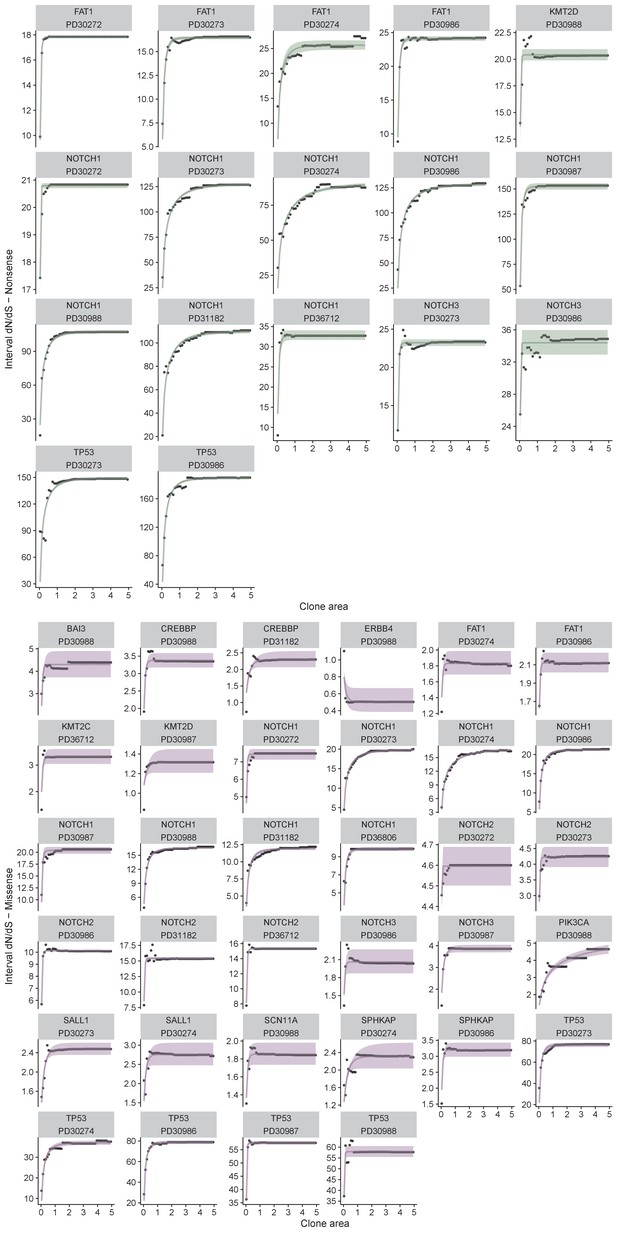
Individual fits for each gene in each patient in the oesophagus dataset.
Points are data and lines are model fits. Analysis performed separately for nonsense, a and missense, b.
Figure 3 with 1 supplement
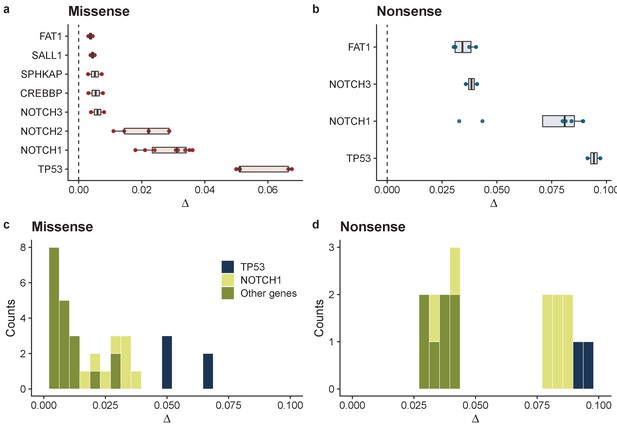
Summary of model fits across all patients for normal oesophagus data.
Inferred biases ∆ for genes where at least 2 patients had good model fits (R2 > 0.6 & >7 mutations) for missense mutations (a), and nonsense mutations (b). Inferred distribution of fitness effects for all genes across all patients for missense mutations (c), and nonsense mutations (d).
Figure 3—figure supplement 1
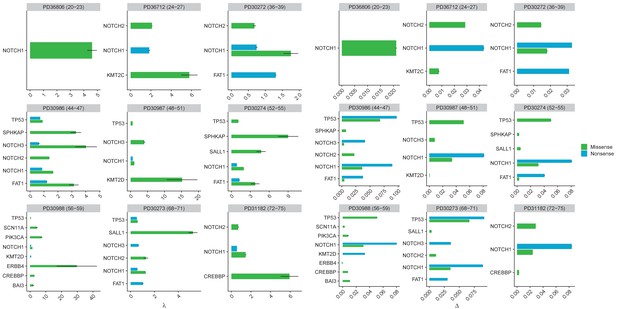
Inferred parameters for each gene in each patient in the oesophagus dataset where there were sufficient mutations to perform the analysis.
Left hand plot shows inferred loss replacement rates λ and right hand plot inferred biases ∆.
Figure 4
Analysis of skin dataset shows similar DFE to oesophagus.
Model fits per patient and per gene per patient when there were sufficient mutations in the skin dataset. Points are data and lines are model fits, (a-e). (f) Shows the distributions of fitness effects for missense mutations across the cohort. There were insufficient nonsense mutations in the majority of genes to draw the equivalent plot for nonsense mutations.
Figure 5 with 5 supplements
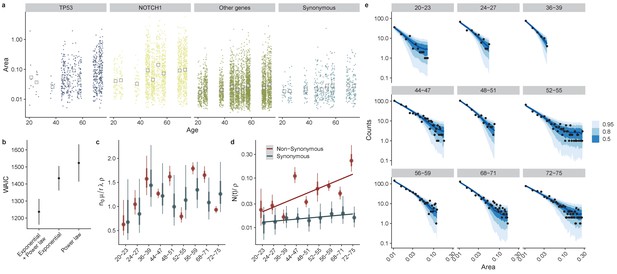
Directly fitting site frequency specta supports interval dN/dS inferences.
(a) Site frequency spectra become wider for older donors, with increases in the median clone area which is more pronounced for mutations in TP53 and NOTCH1. (b) Using WAIC to perform model selection, we found a model with an exponential term and a power law to be the best fitting model (lowest WAIC). (c) Posterior parameter estimates for . (d). The characteristic frequency , Interval represent 66% and 95% credible intervals respectively. (e) Site frequency spectra from data (black dots) and posterior predictive fits for 50, 80% and 95% credible intervals (blue ribbons) for non-synonymous mutations in each don or.
Figure 5—figure supplement 1
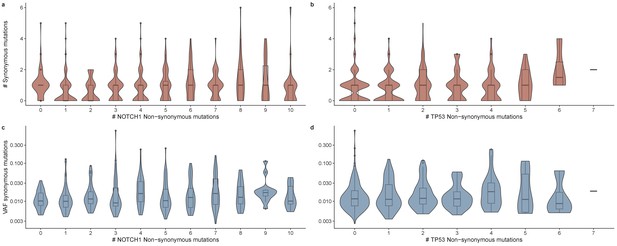
The number of synonymous mutations as a function of the number of NOTCH1 (a) and TP53 (b) mutations per tissue piece.
The mean VAF of synonymous mutations as a function of the number of NOTCH1 (c) and TP53 (d) mutations per tissue piece.
Figure 5—figure supplement 2
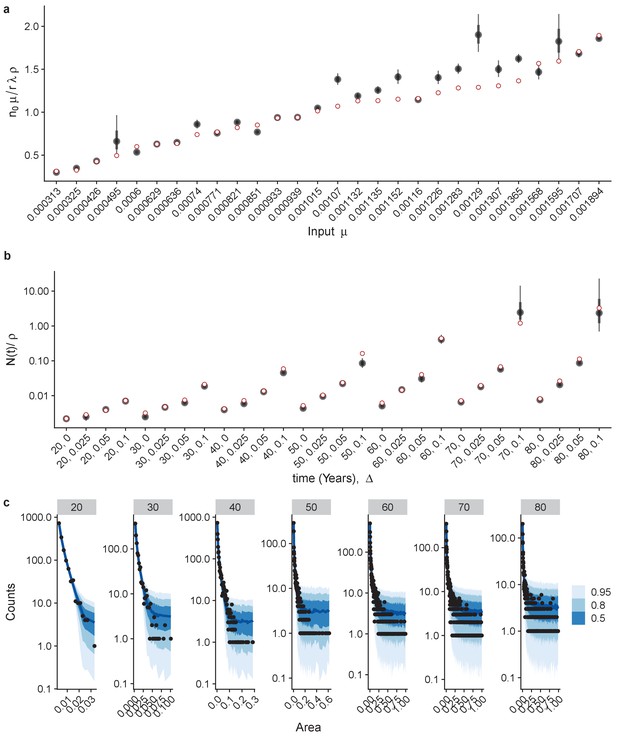
Inferring parameters from the site frequency spectrum of a simulated dataset.
Inferred values for n0μ, (a) and N(t)/ρ, (b). Red points are true values, black points are median posterior values and whiskers are 66% and 95% credible intervals. Example fits across ages for Δ = 0.1. Individual fits across different age cohorts (c), black dots are data points (from simulation) and blue shaded areas are 50%, 80% and 95% credible intervals.
Figure 5—figure supplement 3
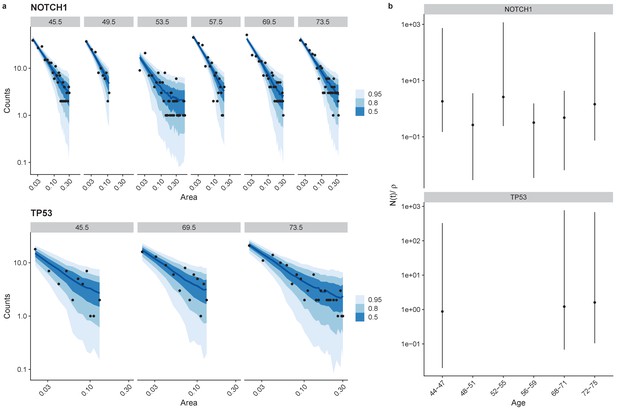
Site frequency spectra fits for NOTCH1 and TP53 non-synonymous mutations, (a).
Posterior values for N(t)/ρ showing large uncertainty in these values (b).
Figure 5—figure supplement 4
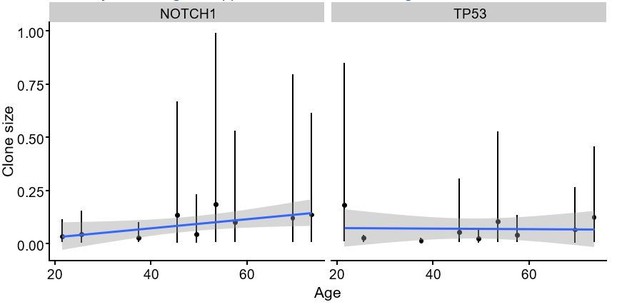
Regression of clone size against age.
(a) Summary of all posterior regression coefficients for all genes showing TP53 and NOTCH1 cause the largest increase in frequency as a function of age. (b) Regression coefficients with inferred selection coefficients from interval-dN/dS are positively correlated.
Figure 5—figure supplement 5
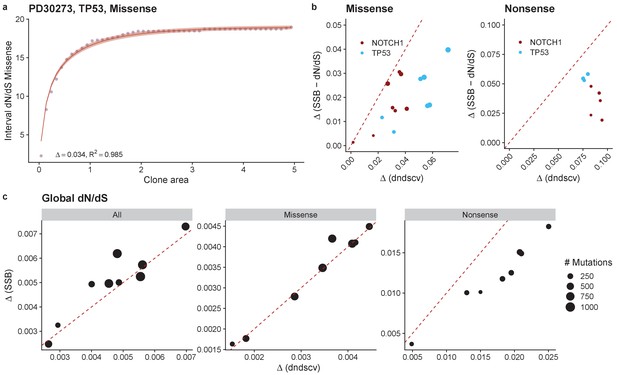
Comparison of results using dndscv and SSB-dN/dS.
Fit for TP53 missense mutations in donor PD30273 using SSB-dN/dS results (a). Comparison of inferred Δ values for NOTCH1 and TP53 mutations (b). Comparison of global dN/dS values for all mutations, missense and nonsense mutations (c).
Author response image 1
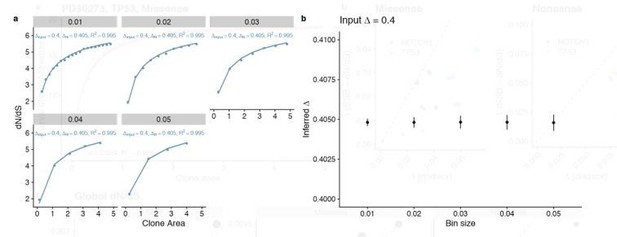
Comparison of different bin sizes.
(a) Fits to simulation with different bin sizes (b) Summary of inferred ∆ for the different bin sizes shows highly consistent results with a small increase in variance at larger bin sizes.
Author response image 2
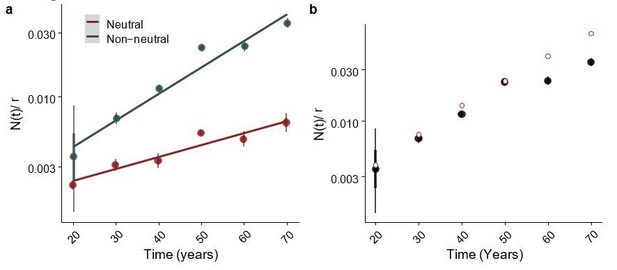
Fitted parameter values of a simulated dataset as a function of time.
(a) Inferred N(t) as a function for age in a simulated cohort, equivalent to Figure 5D. (b) Posterior estimates for inferred values in black, with ground truth shown with red circular points, for this “ground truth” we calculated N(t) using Δ=0.05, the mean of the exponential distribution used in the simulations..
Author response image 3
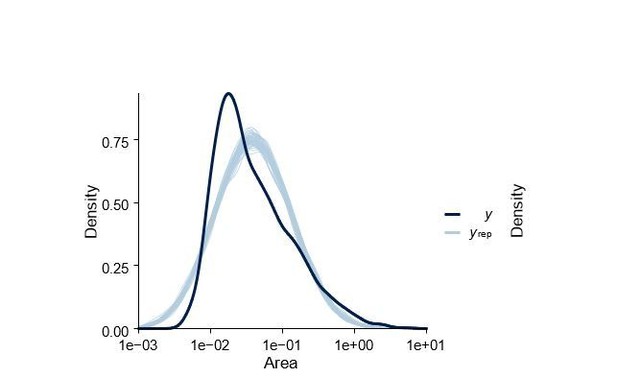
Posterior predictive check of statistical model shown in Figure 5—figure supplementary 1.
Dark blue density labelled y is the real data and lighter blue lines labelled yrep are datasets simulated from the posterior.
Author response image 4
Mean clone size as a function of age for NOTCH1 and TP53.
Points represent the mean values and lines show 95% intervals.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Measuring the distribution of fitness effects in somatic evolution by combining clonal dynamics with dN/dS ratios
eLife 9:e48714.
https://doi.org/10.7554/eLife.48714
