Single molecule mechanics resolves the earliest events in force generation by cardiac myosin
- University of Pennsylvania, United States
- Rutgers University, United States
- LENS - European Laboratory for Non-linear Spectroscopy, Italy
- University of Florence, Italy
Figures
Figure 1
Myosin biochemical model and example UFFC traces.
(a) Mechano-chemical model of acto-myosin interaction (Goldman and Ostap, 2012). Steps are numbered to remain consistent with the myosin literature. The working stroke is shown in two phases, the latter one coupled to ADP release from AM⋅ADP. Inset: The primary working stroke is depicted either before or after phosphate release from AM⋅ADP⋅Pi. (b) Applied forces acting on the bead-actin-bead dumbbell in the ultra-fast force clamp at ± 3.75 pN. Dashed line indicates zero force. (c) Position of the optical trap, which approximates the actin filament position. Dashed boxes in (b and c) indicate regions containing myosin binding events expanded in panels (d and e). (d and e) The dumbbell force and position signals expanded during a myosin binding event under hindering (positive) 3.75 pN load. (f) Further expanded section of panel f showing myosin binding (red triangle) and dissociation (blue triangle) distinguished by the sudden changes in slope of the position trace. (g) Further expanded view of (f) showing a displacement (green triangle) of ~10 nm occurring ~1 ms of actin binding.
-
Figure 1—source data 1
Matlab figure files with data from Figure 1.
- https://doi.org/10.7554/eLife.49266.003
Figure 2 with 3 supplements
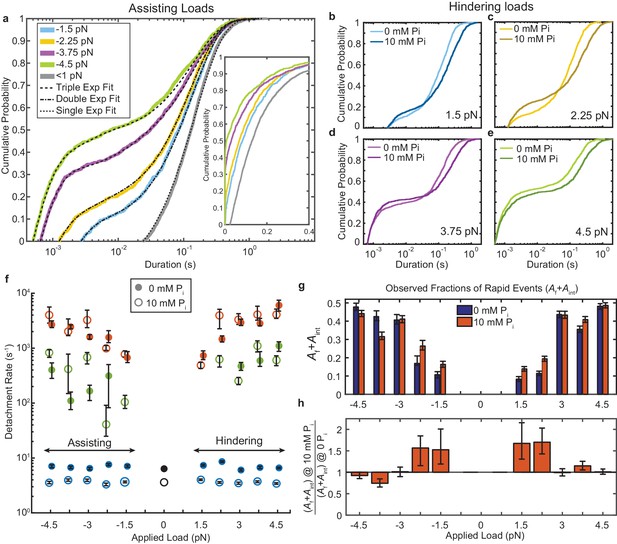
Kinetics of actomyosin attachment durations under mechanical load.
(a) Cumulative distributions of actomyosin attachment event durations at 1 μM ATP under assisting loads (solid lines) plotted on semi-log axes. Best fits from the loglikelihood ratio test (Woody et al., 2016) are shown as dashed lines. Low-load data (<0.5 pN) from non-feedback experiments are shown in grey with a single exponential fit. The other fitted curves are double or triple exponential cumulative distributions as explained in the text. Inset shows the same data on a linear scale. (b–e) Comparison of cumulative distributions of durations under hindering loads listed in each panel with no added phosphate (lighter lines) and 10 mM added phosphate (dark lines). (f) Fitted rate constants from the multi-exponential functions which describe the data with no added phosphate (solid symbols) and 10 mM Pi (open symbols). Positive forces (hindering loads) are defined as the direction that opposes the progression of the myosin working stroke. Blue symbols give the slowest of the fitted rates (ks), red the fastest rates (kf), and green the intermediate rate (kint) in the cases where three rates were statistically justified. Black symbols are the single rate constant fitted to the non-feedback data from the same molecules. (g) Fraction of observed interactions that were rapid (Af + Aint) from the multicomponent exponential fits for no added Pi (blue) and 10 mM Pi (red). (h) Relative fraction of rapid events for 10 mM added Pi compared to 0 Pi, {(Af+Aint) at 10 mM Pi} / {(Af+Aint) at 0 mM Pi}. Error bars in f) – h) give 68% confidence intervals (90% in h)) from 500 rounds of bootstrapping (Woody et al., 2016). Numbers of events, 784 to 1502, from 5 to 8 molecules at each [Pi] (See Supplementary file 1 Table 1 for details).
-
Figure 2—source data 1
Matlab figure files with data from Figure 2.
- https://doi.org/10.7554/eLife.49266.008
Figure 2—figure supplement 1
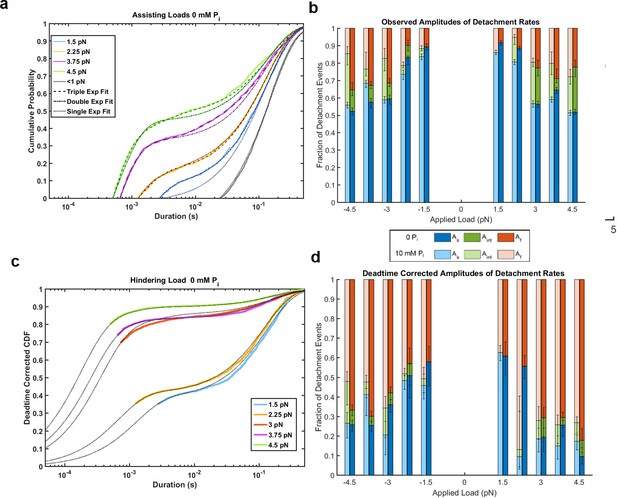
Attachment durations and fitted distributions.
(a) Data from Figure 2a plotted as cumulative density functions (CDFs) with fitted distributions incorporating 1–3 exponential components as indicated in the symbol key, showing that for forces > 2.25 pN the sum of three exponential components was statistically justified. (b) The amplitudes (relative fraction) of each fitted rate constant, kf (Af, red), kint (Aint, green), and ks (As, blue) for data with 0 (dark bars) and 10 mM (light bars) added Pi. (c) Plot of the cumulative distribution functions at 0 mM Pi and hindering loads correcting for events that are missed by the experimental deadtime assuming exponential distributions (see Materials and methods). Most of the events lost in the deadtime are part of the fastest phase. Black dotted lines show fits to the data and extrapolate back to the zero CDF and duration (not shown). (d) Similar plot to panel b, but showing the amplitudes of each component after correcting for the experimental deadtime. The amplitude of the fast component (red) is considerably larger at each force than in panel b due to the loss of these events in the deadtime. Error bars are 68% confidence intervals from 500 rounds of bootstrapping for all panels.
Figure 2—figure supplement 2
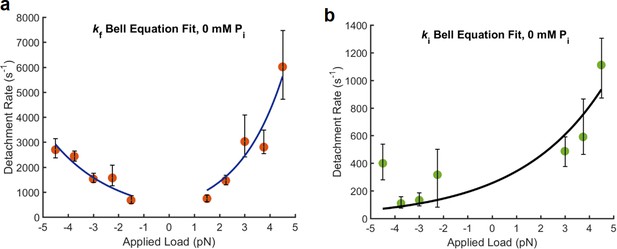
Force dependence of fast and intermediate detachments at 0 Pi and 1 μM MgATP.
(a) Data for kf from Figure 2a. To describe the force dependence of these rates, the Bell equation was used: where k is the force dependent rate, k0 is the unloaded rate, (F) is the applied force, (d) is the distance parameter indicating the force dependence of the transition, k is Boltzmann’s constant, and T is the absolute temperature. Because the data show increasing rates as the magnitude of the force increases under either positive or negative loads, the Bell equation was fitted to the kf values separately for assisting (negative) and hindering (positive) loads. For assisting loads k0 = 579 (369–789, 68% CI) s−1 and d = −1.47 (−1.84 – −1.06), 68% CI) nm, and for hindering loads k0 = 354 (127–581, 68% CI) s−1, d = 2.54 (1.90–3.18, 68% CI) nm. (b) Because kint shows a general trend of increasing rate as the load becomes more positive (more hindering load), the fit for kint was performed on positive and negative data but excluded the point at −4.5 pN. k0 = 256 (131–381, 68% CI) s−1, d = 1.18 (0.67–1.68, 68% CI) nm.
Figure 2—figure supplement 3
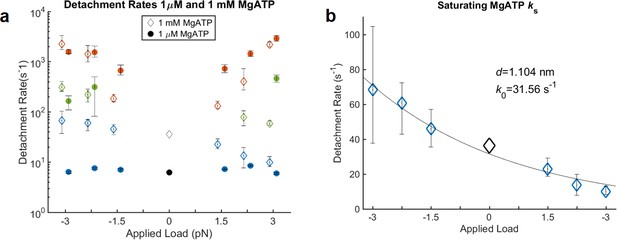
Kinetics of actomyosin detachment in the presence of 1 mM MgATP.
(a) Fitted detachment rate constants, kf (red), kint (green), and ks (blue) in the presence of 1 μM MgATP (closed circles, same data as in text Figure 2f) and 1 mM MgATP (open diamonds). The zero-load rates (black) are from non-feedback experiments. kf and kint do not vary systematically between low and high ATP concentration, while ks is faster and more force dependent at 1 mM than at 1 μM MgATP. (b) ks at 1 mM MgATP with a fitted Bell equation, yielding a distance parameter of 1.1 nm. The estimated unloaded rate (k0 = 31.5 s−1) is slightly less than some previous measurements (50–70 s−1), which may be at least partially due to mixing of the slow and intermediate phases in the fitted parameters. Such mixing may also be responsible for the differences in kint for 1 μM vs. 1 mM MgATP under resisting loads.
Figure 3 with 1 supplement
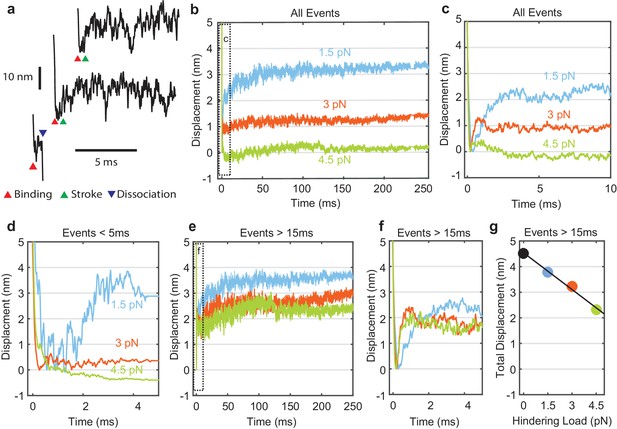
Myosin working stroke dynamics under hindering load.
(a) Example traces of the position of the actin filament (reported by the leading trap position) during individual actomyosin interactions under 3.75 pN of hindering load. Red triangles indicate approximately when myosin binds to actin, stopping the motion of the filament. Green triangles indicate positive displacements expected from the myosin working stroke. The blue triangle shows dissociation for an event shorter than 5 ms. (b) Ensemble averages of all events from data at 0 added Pi at 1.5, 3, and 4.5 pN hindering load. Dashed box shows a region that is shown expanded in panel (c). (d) Ensemble averages of events shorter than 5 ms. The average working stroke step is greatly reduced for forces above 1.5 pN apparently due to force-dependent detachment before the working stroke. (e) Ensemble averages of events lasting longer than 15 ms. (f) Expanded view of boxed area of (e) showing a similar initial displacement across forces. (g) Total measured step for events longer than 15 ms plotted against applied load with a linear fit, leading to an estimate of the stiffness of the myosin and its lever arm of at least 2.3 pN/nm.
-
Figure 3—source data 1
Matlab figure files with data from Figure 3.
- https://doi.org/10.7554/eLife.49266.011
Figure 3—figure supplement 1
Quantification of ensemble average displacements from force-binned groups plotted against the minimum event duration (MED) included in each group for (a) 0 Pi and (b) 10 mM added Pi.
For example, the averages MED = 10 ms represent the average displacement of all events > 10 ms. The plotted displacement is normalized to the largest displacement observed at each force. As more events are excluded (increasing x-axis), the total observed displacement rises, until it nearly plateaus at MED ≥ 15 ms for 0 Pi. This result justifies analyzing events longer than 15 ms separately from short events (e.g. Figure 3) for this data. For 10 mM Pi, the total displacement continued to increase until events shorter than 25 ms were excluded, and thus 25 ms was used as a threshold for the 10 mM Pi data, and the 0 Pi data that were directly compared to it (Figures 4 and 5).
Figure 4 with 1 supplement
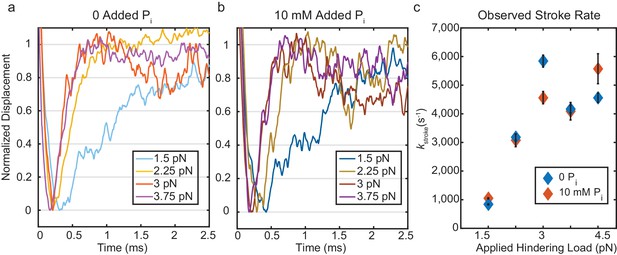
Kinetics of the initial working stroke displacement.
(a) and (b) Ensembles averages from events longer than 25 ms plotted after normalizing the amplitudes of the initial displacements. (a) without added Pi and (b) with 10 mM Pi for 1.5 pN to 3.75 pN hindering loads. (c) Observed stroke rates from single exponential fits for no added Pi (blue), and 10 mM added Pi (red). Error bars show 95% confidence intervals from the fits.
-
Figure 4—source data 1
Matlab figure files with data from Figure 4.
- https://doi.org/10.7554/eLife.49266.014
Figure 4—figure supplement 1
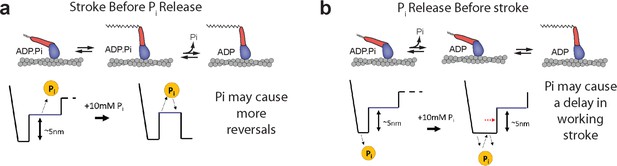
Models for the effect of free Pi on single-molecule displacements in the presence of hindering mechanical load.
(a) If the working stroke occurs before Pi release, Pi is expected to cause more reversals and reversals which occur later in the events and would not delay the initial stroke. (b) If Pi is released before the working stroke, solution Pi is expected to delay the working stroke due to Pi binding to AM·ADP and then having to dissociate again before the stroke.
Figure 5 with 3 supplements
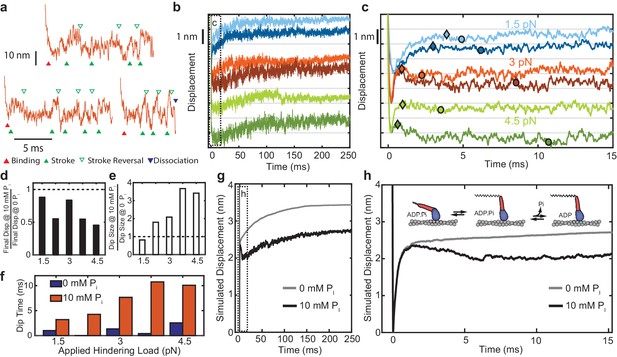
Effect of added Pi on reversals of the working stroke.
(a) Example traces of displacements in individual interactions under 3 pN of load at 10 mM Pi with apparent strokes (filled green triangles) and reversals (open triangles) identified. (b) Ensemble averages of events longer than 25 ms at 1.5 pN (blue), 3 pN (red), and 4.5 pN (green) with 0 (lighter colored traces) and 10 mM Pi (dark traces). Traces at the various forces are offset by 2 nm for visualization. (c) Expanded view of the boxed region in b) showing the initial stroke and later ‘dip’ attributed to stroke reversals. Triangles indicate the detected maximum initial displacement, and circles indicate the location and timing of the maximum ‘dip' in the signal using a moving average, as described in Materials and methods. (d) Total displacement for events longer than 25 ms at 10 mM Pi relative to that with no added Pi, ({displacement at 10 mM Pi} / {displacement at 0 Pi}). (e) Relative amplitude of the dip for 10 mM vs. 0 added Pi. (f) Comparison of the time between the maximum initial displacement and minimum of the dip for no added Pi (blue) and 10 mM added Pi (red). (g) Simulated ensembles averages from the model described in the text and Materials and methods with Pi release occurring after the working stroke. (h) Expanded view of the boxed region in g) showing the dip in the displacement predicted by this model, similar to the experimental data. Inset shows a simplified view of the working-stroke-first model used in the simulations.
-
Figure 5—source data 1
Matlab figure files with data from Figure 5.
- https://doi.org/10.7554/eLife.49266.019
Figure 5—figure supplement 1
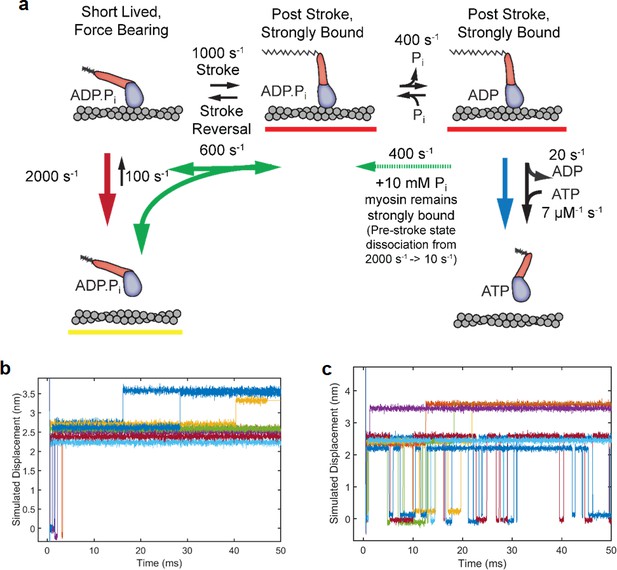
Simulations of ensembles averages with and without added Pi.
The scheme in (a) is the same as text Figure 6, but with rate constants used in the ensemble average simulations shown in Figure 5g-h in the main text. The rate constants reflect the rates at 3pN of hindering load. The fast detachment rate of 2000 s−1, with a 1000 s−1 stroke rate leads to an observed stroke and detachment rate of 3000 s−1, similar to the observed rates at 3pN of load (Figure 2f, Figure 4c) and sets the fraction of short lived events near 60% (Figure 2—figure supplement 1). The stroke reversal rate of 600 s−1 corresponds approximately to the interpolated kint from the Bell equation fit in Figure 2—figure supplement 2b. The phosphate release and rebinding rates at 10 mM Pi were both set to 400 s−1 to recapitulate the ensemble average data, and are consistent with previous estimates of 600 s−1 and 400 s−1 respectively from muscle fiber experiments (Araujo and Walker, 1996). The rate of M·ADP·Pi binding to actin was set to 100 s−1 to produce an estimated ensemble rate of Pi release to be 18 s−1, in agreement biochemical findings (Rohde et al., 2017; Liu et al., 2015) (b) and (c) Examples of 8 individual traces simulated using the above pathway with added Gaussian noise. Averages of 450 such traces are shown in the main text Figure 5-g and h. (b) Traces simulated with no Pi rebinding and (c) simulated with Pi rebinding at 400 s−1, showing more reversals of the working stroke, especially those occurring later during the attachment.
Figure 5—figure supplement 2
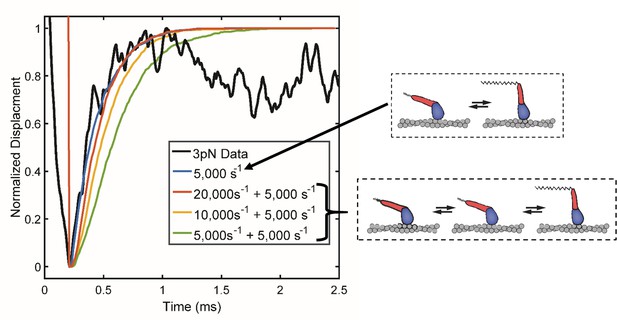
Simulations of the initial ensemble displacement for immediate (blue) vs. multistep processes (red, yellow, green) occurring between actin binding and the working stroke compared to the observed data at 3 pN load (black).
Only the single process at 5000 s−1 (blue) or a multistep reaction scheme with one rate being ≥10,000 s−1 (red and yellow) exhibit rapid displacement stroke like that observed (black). This comparison indicates that if extra processes occur between binding and completion of the working, they must be extremely fast. The high speed of the stroke thus rules against extra reaction steps.
Figure 5—figure supplement 3
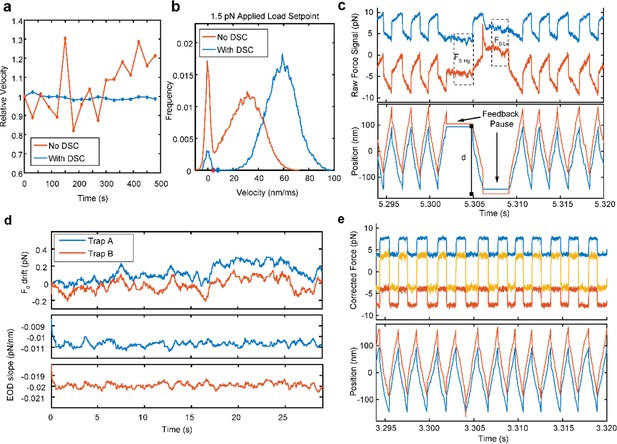
UFFC Real Time Drift and EOD Slope Correction (DSC) system.
(a) Relative velocities of one trap under 1.5 pN applied load from sequential traces over 12 min without the real time corrections (orange) shows a 20% change in the velocity, while the DSC system reduces the variability to <3% change in velocity over the same period. (b) Distributions of velocities from single traces when 1.5 pN of load is applied (traces are from different days). The distribution without DSC is broader and has a lower unbound velocity (orange) than the DSC enabled trace (blue). The difference in height of the peak at zero velocity (the velocity when myosin is bound) is not due to the DSC system, but rather represents the stochastic variation between the number and length of binding events in a particular trace. (c) Approximately 25 ms of raw force and position signals are shown when the DSC is engaged with the force set point at 4.5 pN. Upper and lower pauses are indicated. The bar indicated ‘d’ is the distance between trigger points for reversing the direction of the applied force. (d) Calculated drift and EOD slope values for both traps over the full 30 s trace of c., calculated as described in the Supplementary Materials and methods (e) The estimated real force and position traces from the data in (c) with the pauses removed for further analysis.
Figure 6
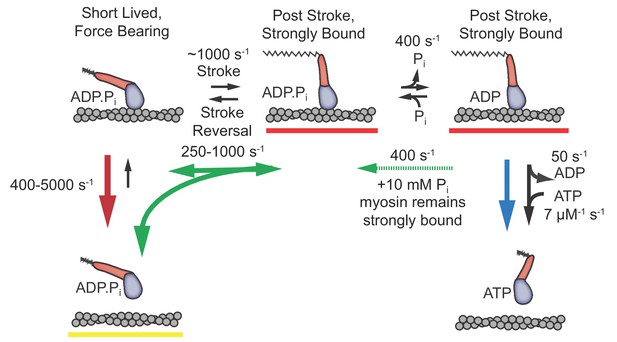
Proposed model with short-lived, weakly-bound attachments directly preceding the working stroke, which is followed by phosphate release and potential phosphate rebinding.
Rates constants are estimates at zero load (lowest values) to 4.5 pN of hindering load (highest values). Colored arrows indicate processes associated with detachment rate kf (red), kint (green), and ks (blue). Dashed green arrow is only relevant when 10 mM Pi is added. Red underlined states indicate myosin is strongly bound, while yellow underlines indicate a weakly bound or unbound state.
Additional files
-
Supplementary file 1
File containing three supplementary tables which provides n-values for experiments, measured stroke rates, and ionic strength conditions.
- https://doi.org/10.7554/eLife.49266.021
-
Transparent reporting form
- https://doi.org/10.7554/eLife.49266.022
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Single molecule mechanics resolves the earliest events in force generation by cardiac myosin
eLife 8:e49266.
https://doi.org/10.7554/eLife.49266
