Single molecule mechanics resolves the earliest events in force generation by cardiac myosin
- University of Pennsylvania, United States
- Rutgers University, United States
- LENS - European Laboratory for Non-linear Spectroscopy, Italy
- University of Florence, Italy
Figures
Figure 1
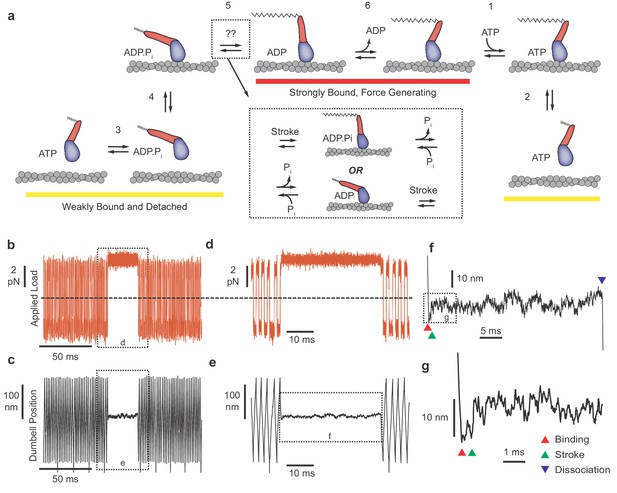
Myosin biochemical model and example UFFC traces.
(a) Mechano-chemical model of acto-myosin interaction (Goldman and Ostap, 2012). Steps are numbered to remain consistent with the myosin literature. The working stroke is shown in two phases, the …
-
Figure 1—source data 1
Matlab figure files with data from Figure 1.
- https://doi.org/10.7554/eLife.49266.003
Figure 2 with 3 supplements
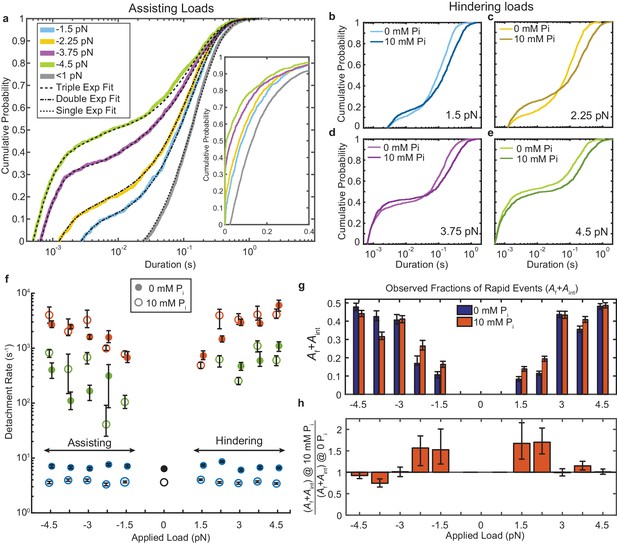
Kinetics of actomyosin attachment durations under mechanical load.
(a) Cumulative distributions of actomyosin attachment event durations at 1 μM ATP under assisting loads (solid lines) plotted on semi-log axes. Best fits from the loglikelihood ratio test (Woody et …
-
Figure 2—source data 1
Matlab figure files with data from Figure 2.
- https://doi.org/10.7554/eLife.49266.008
Figure 2—figure supplement 1
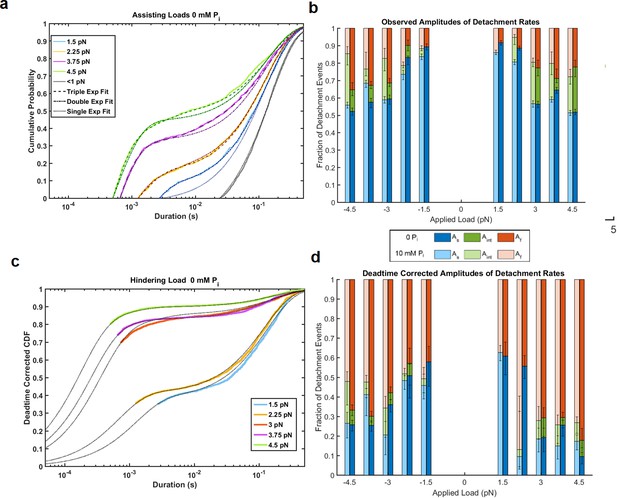
Attachment durations and fitted distributions.
(a) Data from Figure 2a plotted as cumulative density functions (CDFs) with fitted distributions incorporating 1–3 exponential components as indicated in the symbol key, showing that for forces > 2.2…
Figure 2—figure supplement 2
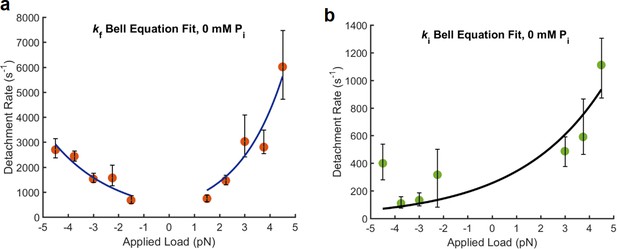
Force dependence of fast and intermediate detachments at 0 Pi and 1 μM MgATP.
(a) Data for kf from Figure 2a. To describe the force dependence of these rates, the Bell equation was used: where k is the force dependent rate, k0 is the unloaded rate, (F) is the applied …
Figure 2—figure supplement 3
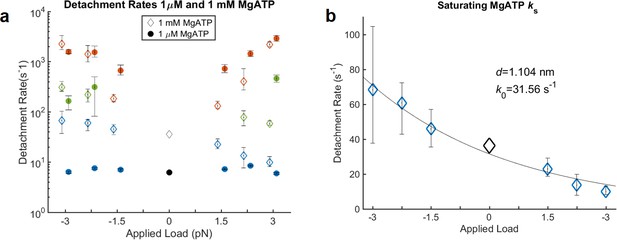
Kinetics of actomyosin detachment in the presence of 1 mM MgATP.
(a) Fitted detachment rate constants, kf (red), kint (green), and ks (blue) in the presence of 1 μM MgATP (closed circles, same data as in text Figure 2f) and 1 mM MgATP (open diamonds). The …
Figure 3 with 1 supplement
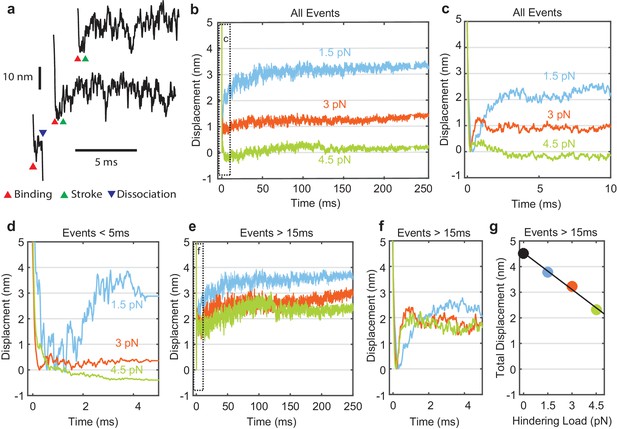
Myosin working stroke dynamics under hindering load.
(a) Example traces of the position of the actin filament (reported by the leading trap position) during individual actomyosin interactions under 3.75 pN of hindering load. Red triangles indicate …
-
Figure 3—source data 1
Matlab figure files with data from Figure 3.
- https://doi.org/10.7554/eLife.49266.011
Figure 3—figure supplement 1
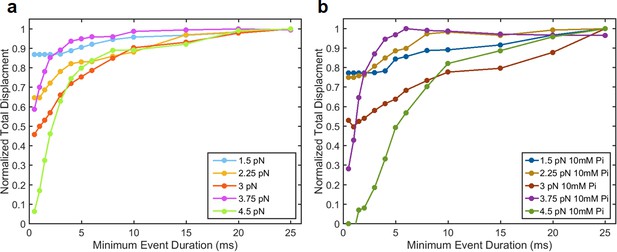
Quantification of ensemble average displacements from force-binned groups plotted against the minimum event duration (MED) included in each group for (a) 0 Pi and (b) 10 mM added Pi.
For example, the averages MED = 10 ms represent the average displacement of all events > 10 ms. The plotted displacement is normalized to the largest displacement observed at each force. As more …
Figure 4 with 1 supplement
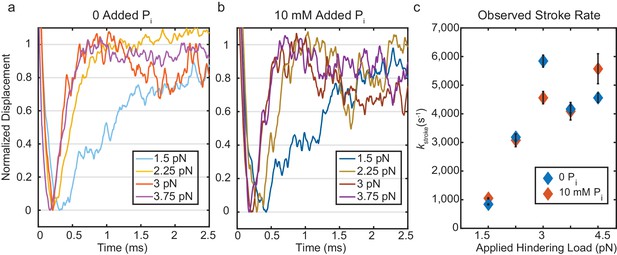
Kinetics of the initial working stroke displacement.
(a) and (b) Ensembles averages from events longer than 25 ms plotted after normalizing the amplitudes of the initial displacements. (a) without added Pi and (b) with 10 mM Pi for 1.5 pN to 3.75 pN …
-
Figure 4—source data 1
Matlab figure files with data from Figure 4.
- https://doi.org/10.7554/eLife.49266.014
Figure 4—figure supplement 1
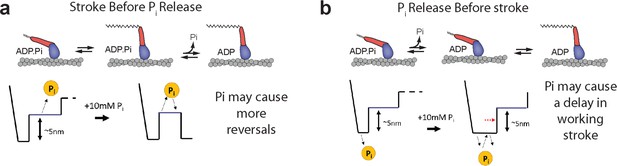
Models for the effect of free Pi on single-molecule displacements in the presence of hindering mechanical load.
(a) If the working stroke occurs before Pi release, Pi is expected to cause more reversals and reversals which occur later in the events and would not delay the initial stroke. (b) If Pi is released …
Figure 5 with 3 supplements
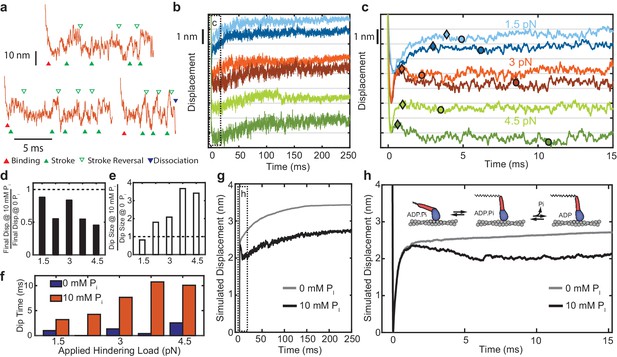
Effect of added Pi on reversals of the working stroke.
(a) Example traces of displacements in individual interactions under 3 pN of load at 10 mM Pi with apparent strokes (filled green triangles) and reversals (open triangles) identified. (b) Ensemble …
-
Figure 5—source data 1
Matlab figure files with data from Figure 5.
- https://doi.org/10.7554/eLife.49266.019
Figure 5—figure supplement 1
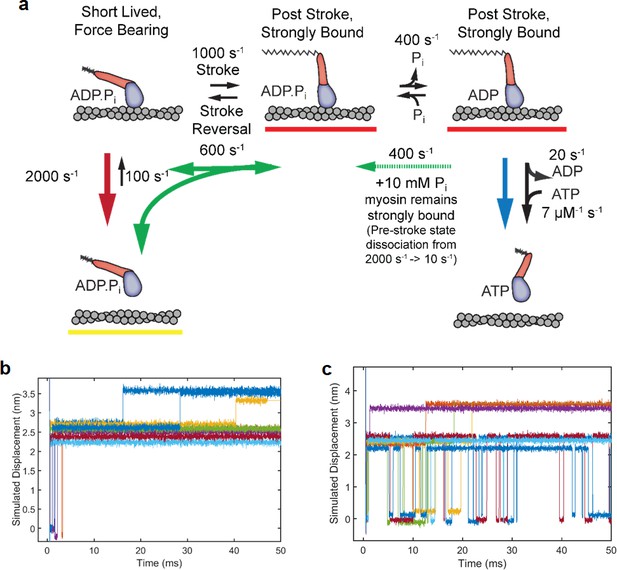
Simulations of ensembles averages with and without added Pi.
The scheme in (a) is the same as text Figure 6, but with rate constants used in the ensemble average simulations shown in Figure 5g-h in the main text. The rate constants reflect the rates at 3pN of …
Figure 5—figure supplement 2
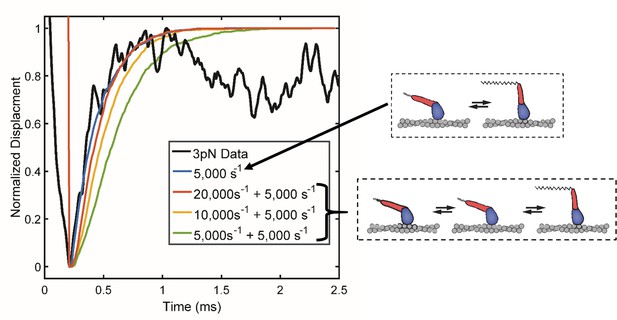
Simulations of the initial ensemble displacement for immediate (blue) vs. multistep processes (red, yellow, green) occurring between actin binding and the working stroke compared to the observed data at 3 pN load (black).
Only the single process at 5000 s−1 (blue) or a multistep reaction scheme with one rate being ≥10,000 s−1 (red and yellow) exhibit rapid displacement stroke like that observed (black). This …
Figure 5—figure supplement 3
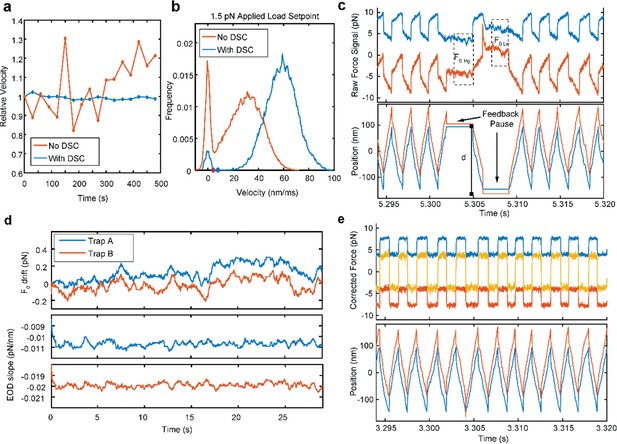
UFFC Real Time Drift and EOD Slope Correction (DSC) system.
(a) Relative velocities of one trap under 1.5 pN applied load from sequential traces over 12 min without the real time corrections (orange) shows a 20% change in the velocity, while the DSC system …
Figure 6
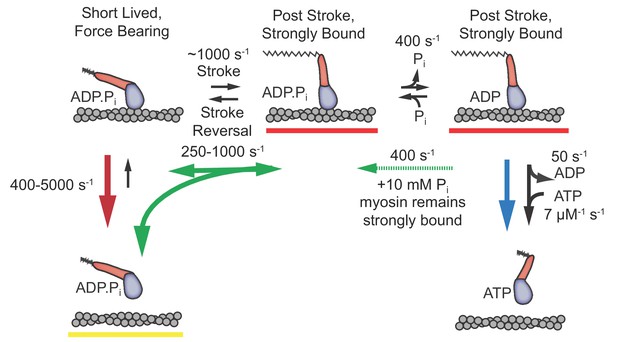
Proposed model with short-lived, weakly-bound attachments directly preceding the working stroke, which is followed by phosphate release and potential phosphate rebinding.
Rates constants are estimates at zero load (lowest values) to 4.5 pN of hindering load (highest values). Colored arrows indicate processes associated with detachment rate kf (red), kint (green), and …
Additional files
-
Supplementary file 1
File containing three supplementary tables which provides n-values for experiments, measured stroke rates, and ionic strength conditions.
- https://doi.org/10.7554/eLife.49266.021
-
Transparent reporting form
- https://doi.org/10.7554/eLife.49266.022
