Reinforcement biases subsequent perceptual decisions when confidence is low, a widespread behavioral phenomenon
- Department of Physiology, Anatomy and Genetics, University of Oxford, United Kingdom
- UCL Institute of Ophthalmology, University College London, United Kingdom
- Department of Molecular and Cellular Biology and Center for Brain Science, Harvard University, United States
- RIKEN-MIT Laboratory at the Picower Institute for Learning and Memory at Department of Biology and Department of Brain and Cognitive Science, Massachusetts Institute of Technology, United States
- McGovern Institute for Brain Research at Department of Brain and Cognitive Sciences, Massachusetts Institute of Technology, United States
- Cold Spring Harbor Laboratory, United States
- Graduate School of Brain Science, Doshisha University, Kyotanabe, Japan
- Watson School of Biological Sciences, United States
- Departments of Neuroscience and Psychiatry, Washington University School of Medicine, United States
- Department of Neurophysiology, University Medical Center, Hamburg-Eppendorf, Germany
- Howard Hughes Medical Institute at Massachusetts Institute of Technology, United States
Figures
Figure 1 with 1 supplement
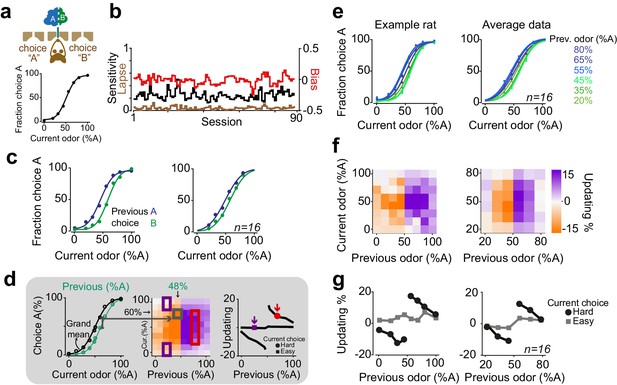
Rats update their trial-by-trial perceptual choice strategy in a stimulus-dependent manner.
(a) Top: Schematic of a 2AFC olfactory decision-making task for rats. Bottom) Average performance of an example rat. (b) Following learning, the psychometric curves showed minimal fluctuations across test sessions. Bias, sensitivity and lapse were measured for each test session. (c) After successful completion of a trial, rats tended to shift their choice toward the previously rewarded side. Left and right panels illustrate example animal and population average. (d) Schematic of analysis procedure for computing conditional psychometric curves and updating plots. Left: Black curve shows the overall psychometric curve and the green curve shows the curve only after trials with 48% odor A (i.e. conditional on the stimulus (48% A) in the previous trial). Middle: Each point in the heatmap indicates the vertical difference between data points of the conditional psychometric curve and the overall psychometric curve. Red and purple boxes indicate data points which are averaged to compute data points shown in the rightmost plot. Right: Updating averaged across current easy trials (in this case the easiest two stimulus levels) and current difficult trials. (e) Performance of the example rat (left) and population (right) computed separately based on the quality of olfactory stimulus (shown as colors mixtures from blue to green) in the previously rewarded trial. After successful completion of a trial, rats tended to shift their choices towards the previously rewarded side but only when the previous trial was difficult. (f) Choice updating, that is the size of shift of psychometric curve relative to the average psychometric curve, as a function of sensory evidence in the previously rewarded trial, and current trial. Positive numbers refer to a bias towards choice A and negative numbers refer to a bias toward the alternative choice. The left and right plots refer to the example rat and population, respectively. (g) Choice updating as a function of previous stimulus separated for current easy (square) and difficult (circle) trials. These plots are representing averages across graphs presented in f.
Figure 1—figure supplement 1
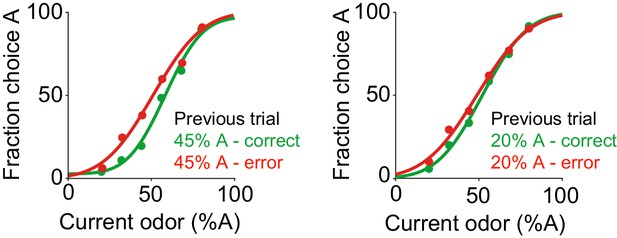
Left: Performance of population of rats (n=16) computed from trials in which the previous stimulus was difficult (45% odor A, 55% odor B), separated based on whether the previous choice was rewarded (correct) or unrewarded (error).
Right: Performance of population of rats (n=16) computed from trials in which the previous stimulus was easy (20% odor A, 80% odor B), separated based on whether the previous choice was rewarded (correct) or unrewarded (error).
Figure 2 with 1 supplement
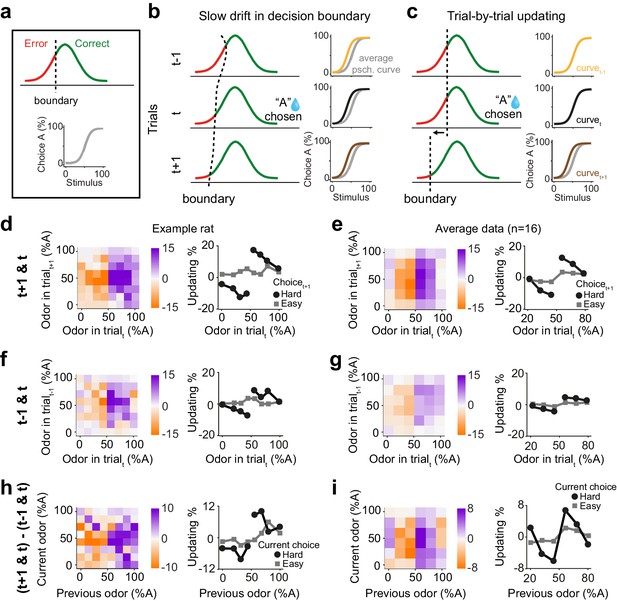
Choice updating is not due to slow and nonspecific drift in response bias.
(a) Signal detection theory-inspired schematic of task performance. The psychometric curve illustrates the average choice behavior. (b) Slow non-specific drift in choice bias, visualized here as drift in the decision boundary, could lead to shift in psychometric curves which persisted for several trials and was not specific to stimulus and outcome of the previous trial. This global bias effect is cancelled when subtracting the psychometric curve of trialt-1 (orange) from trialt+1 (brown). (c) Trial-by-trial updating of decision boundary shifts psychometric curves depending on the outcome and perceptual difficulty of the preceding trial. Subtracting psychometric curves does not cancel this effect. (d) Choice bias of the example rat following a rewarded trial. (e) Similar to d but for population. (f) Choice bias of the example rat in one trial prior to current trial, reflecting global nonspecific bias visualized in b. (g) Similar to f but for population. (h) Subtracting choice bias in trialt-1 from trialt+1 reveals the trial-by-trial choice updating in the example rat. (i) Similar to h but for the population. See Figure 2—figure supplement 1 for details of the normalization procedure.
Figure 2—figure supplement 1
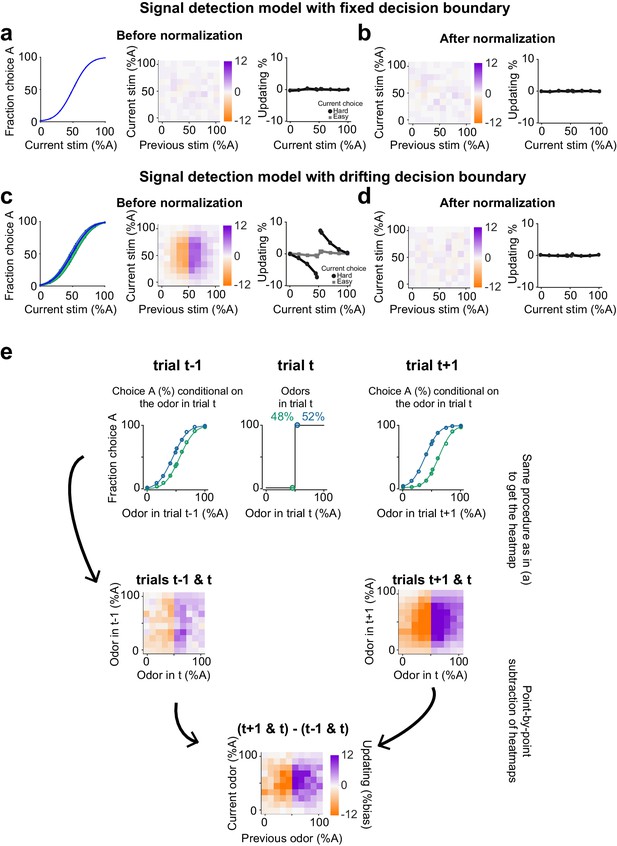
Isolation and correction of slowly drifting non-specific choice bias.
(a,b) A simple signal detection theory-based simulation with a fixed decision boundary. In this model, stimuli are drawn from a normal distribution and are compared to a fixed decision boundary (50%) for choice computation. This model generates psychometric curves that are not depending on the previous trial (left panel in a) and hence no updating is observed (middle and right panel in a). Our normalization (explained in e) does not influence updating in this model, as shown in b. (c,d) A signal detection theory-based simulation using a slowly drifting decision boundary. Psychometric curves appear to depend on the previous trial (left panel in c), resulting in apparent updating effect (middle and right panels in c). However, this effect is removed after applying our normalization as shown in d. (e) The normalization procedure for isolating trial-by-trial updating. Upper row middle panel shows the performance for two levels of stimuli (48 and 52%) which were both rewarded, hence the delta function. Upper row left panel shows the psychometric curves separately for trials followed by 48% or 52% stimuli. Any separation between these curves indicates a side bias which extend beyond a single trial. Upper right panel shows psychometric curves separately computed based on whether the stimulus in trial t was 48 or 52%. The full conditional psychometric curves in trial t-1 and t and in trial t and t+1 were used to compute heatmaps (middle row). The heatmap of t-1 was subtracted from the heatmap of t+1 to compute normalized trial-by-trial updating (lowest row).
Figure 3 with 1 supplement
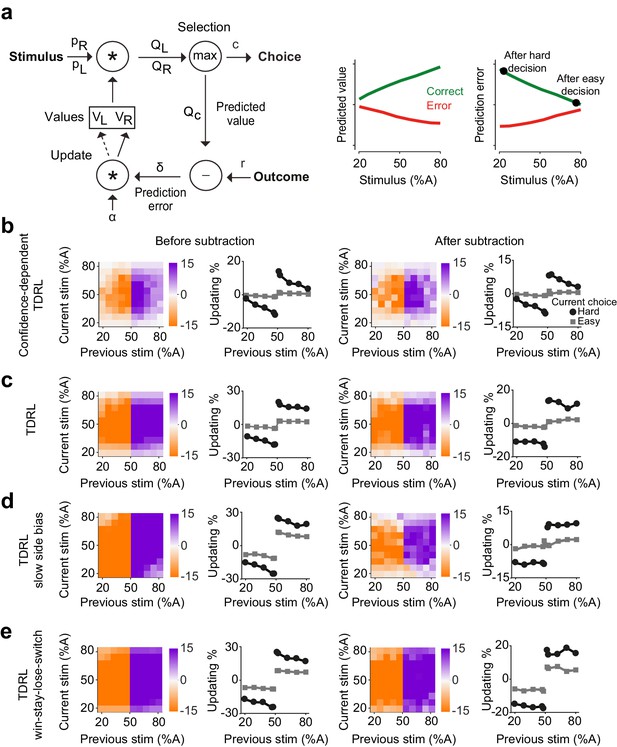
Belief-based reinforcement learning model accounts for choice updating.
(a) Left: schematics of the temporal difference reinforcement learning (TDRL) model that includes belief state reflecting perceptual decision confidence. Right: predicted values and reward prediction errors of the model. After receiving a reward, reward prediction errors depend on the difficulty of the choice and are largest after a hard decision. Reward prediction errors of this model are sufficient to replicate our observed choice updating effect. (b) Choice updating of the model shown in a. This effect can be observed even after correcting for non-specific drifts in the choice bias (right panel). The model in all panels had =0.2 and =0.5. (c) A TDRL model which follows a Markov decision process (MDP) and that does not include decision confidence into prediction error computation produces choice updating that is largely independent of the difficulty of the previous decision. (d) A MDP TDRL model that includes slow non-specific drift in choice bias fails to produce true choice updating. The normalization removes the effect of drift in the choice bias, but leaves the difficulty-independent effect of past reward (e) A MDP TDRL model that includes win-stay-lose-switch strategy fails to produce true choice updating. For this simulation, win-stay-lose-switch strategy is applied to 10% of randomly-selected trials. See Figure 3—figure supplement 1 and the Materials and methods for further details of the models.
Figure 3—figure supplement 1
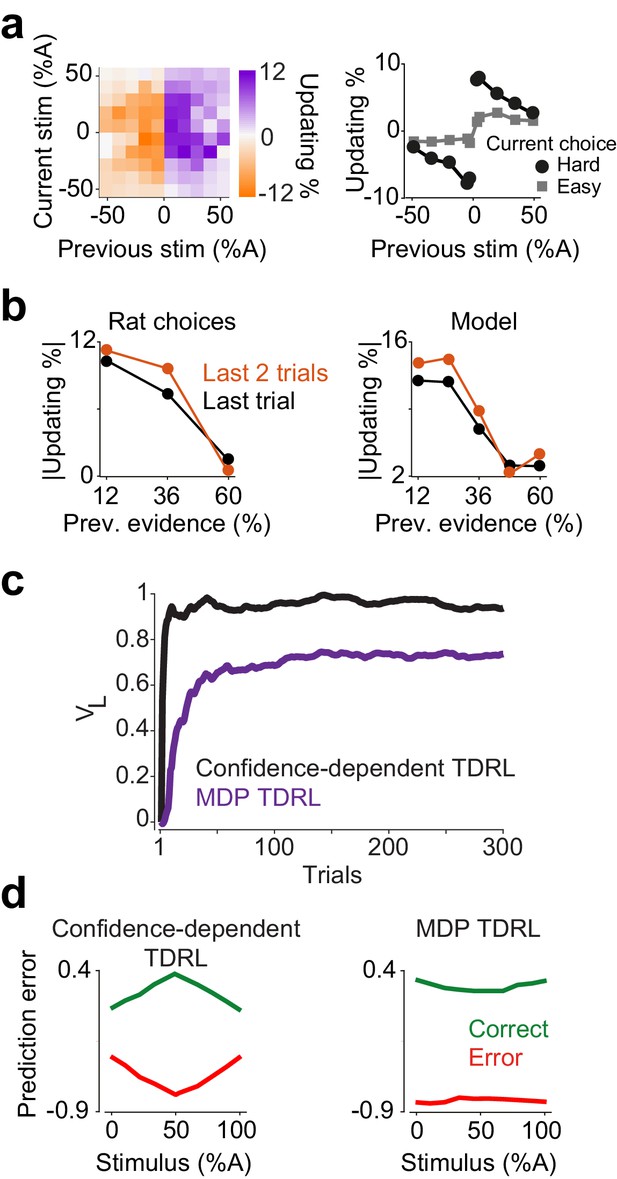
Further characteristics of the confidence-dependent TDRL model and the MDP TDRL model.
(a) Confidence-dependent TDRL model which uses a softmax for computing choice produces confidence-dependent updating similar to the model run that uses argmax for choice computation. (b) Confidence-dependent choice updating is stronger after two rewarded difficult trials (left), consistent with the model predictions (right). Left panel shows the absolute size of choice updating computed after one rewarded difficult choice (black) and after two rewarded difficult choices to the same choice side (light red) (n=16 rats). Right panel shows the size of updating after one reward and two rewarded difficult choices. (c) The stored values of actions converge to different quantities in the confidence-dependent model and the MDP TDRL model. The stored value of left actions averaged over 1000 model runs are shown (the results would be same for the right actions). In both models, the size of delivered reward in correct trials was 1. (d) The difference in the prediction errors of the confidence-dependent model and the MDP TDRL model. The prediction errors in the confidence-dependent model results in choice updating in the next trial.
Figure 4
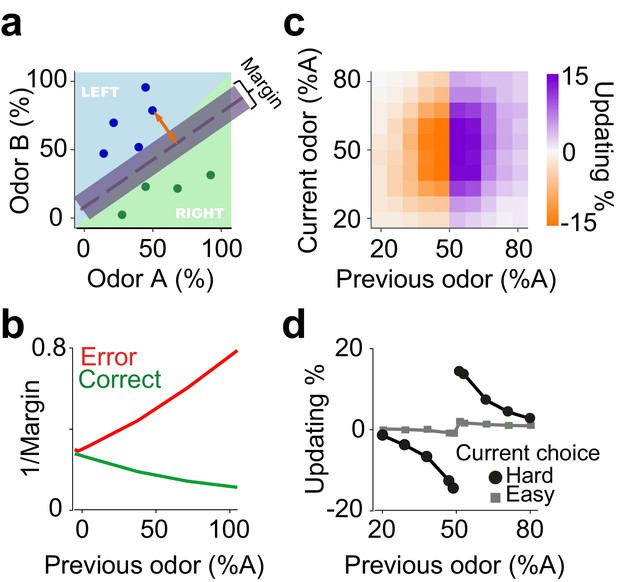
An on-line statistical classifier accounts for choice updating.
(a) Schematic of a classifier using Support Vector Machine for learning to categorize odor samples. The dashed line shows one possible hyperplane for classification and shaded area around the dashed line indicates the margin. Orange arrow indicates the distance between one data point and the classification hyperplane, that is the margin for that data point, given the hyperplane. Each circle is one odor sample in one trial. (b) Average estimates of the margins of the classifier. (c) The size of shift in the classification as a function of previous and current stimulus. (d) Choice updating as a function previous odor separated for current easy and hard choices.
Figure 5
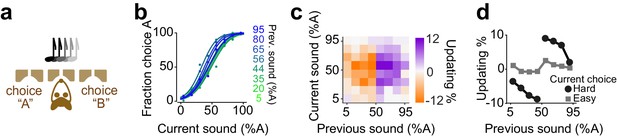
Rats update their trial-by-trial auditory choices in a confidence-dependent fashion.
(a) Schematic of a 2AFC auditory decision-making task for rat. (b) Performance of an example rat computed separately based on the quality of auditory stimulus (shown as colors from blue to green) in the previously rewarded trial. (c) Choice updating as a function of sensory evidence in the previous and current trial in the population of rats (n = 5). (d) Choice updating as a function of previous stimulus separated for current easy (square) and difficult (circle) trials, averaged across rats.
Figure 6
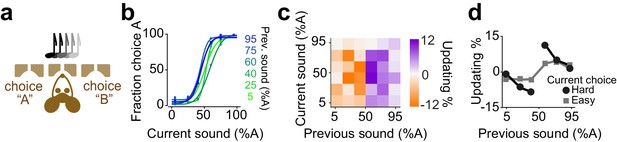
Mice update their trial-by-trial auditory choices in a confidence-dependent fashion.
(a) Schematic of a 2AFC auditory decision making task for mice. (b) Performance of an example mouse computed separately based on the quality of auditory stimulus (shown as colors from blue to green) in the previously rewarded trial. (c) Choice updating as a function of sensory evidence in the previous and current trial in the population of mice (n = 6). (d) Choice updating as a function of previous stimulus separated for current easy (square) and difficult (circle) trials, averaged across mice.
Figure 7
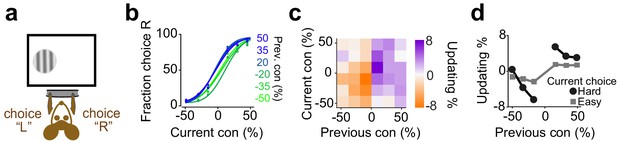
Mice update their trial-by-trial visual choices in a confidence-dependent fashion.
(a) Schematic of a 2AFC visual decision making task for mice. (b) Performance of an example mouse computed separately based on the quality of visual stimulus (shown as colors from blue to green) in the previously rewarded trial. (c) Choice updating as a function of sensory evidence, that is the contrast of stimulus, in the previous and current trial in the population of mice (n = 12). (d) Choice updating as a function of previous stimulus separated for current easy (square) and difficult (circle) trials, averaged across mice.
Figure 8
Humans update their trial-by-trial visual choices in a confidence-dependent fashion.
(a) Schematic of a 2IFC visual decision making task in human subjects. (b) Performance of an example subject computed separately based on the quality of visual stimulus (shown as colors from blue to green) in the previously rewarded trial. (c) Choice updating as a function of sensory evidence, that is the difference in coherence of moving dots between two intervals, in the previous and current trial, averaged across subjects (n = 23). (d) Choice updating as a function of previous stimulus strength, separated for current easy (square) and difficult (circle) trials, averaged across subjects.
Figure 9 with 1 supplement
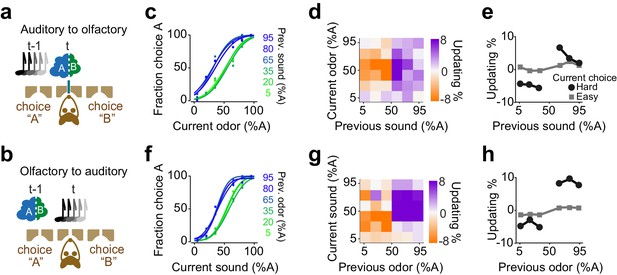
Confidence-dependent choice updating transfers across sensory modalities.
(a-b) Schematic of a 2AFC task in which rats performed either an olfactory (a) or auditory (b) decisions in randomly interleaved trials. (c) Performance of an example rat computed for olfactory trials separately based on the quality of auditory stimulus (shown as colors from blue to green) in the previously rewarded trial. (d) Choice updating as a function of sensory evidence (auditory stimulus) in the previous trial and odor mixture in the current trial, averaged across subjects (n = 6). (e) Choice updating as a function of previous auditory stimulus separated for current odor-guided easy (square) and difficult (circle) trials, averaged across subjects. (f-h) Similar to c-e but for trials in which the current stimulus has been auditory and the previous trial has been based on olfactory stimulus.
Figure 9—figure supplement 1
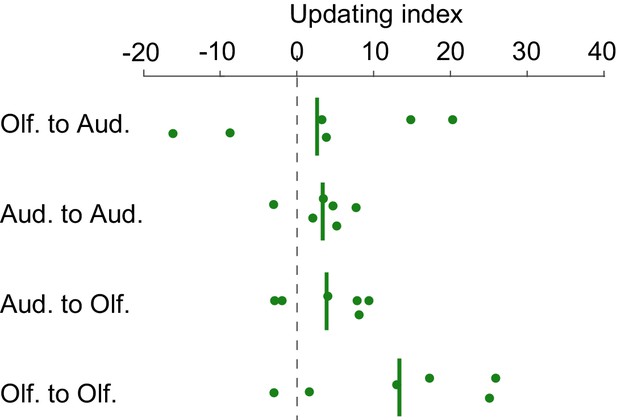
Choice-updating in rats performing a task in which the modality of sensory stimulus in different trials is either auditory or olfactory.
See Figure 10 for the definition of Updating Index.
Figure 10
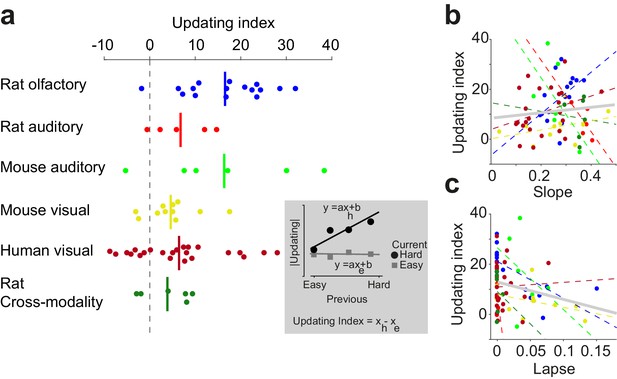
Confidence-guided choice updating is strongest in individuals with well-defined psychometric behavior.
(a) The strength of choice updating among individuals. The vertical lines show the mean. Inset: schematics illustrates the calculation of updating index. The index is defined as the difference in the slope of lines fitted to the data. (b) Scatter plot of choice updating as a function of the slope of psychometric curve. Each circle is one individual. Dashed lines illustrate a linear fit on each data set, and the gray solid line shows a linear fit on all subjects. (c) Scatter plot of choice updating as a function of the lapse rate of the fitted psychometric curve.
Figure 11
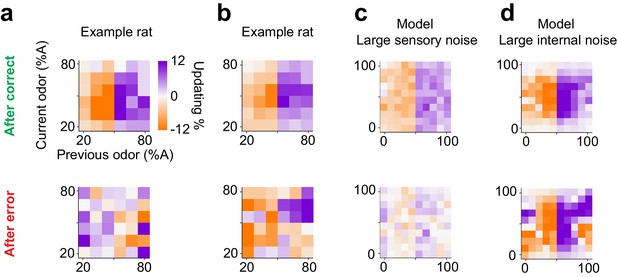
Diverse learning effects after error trials.
(a) Choice updating after correct trials (top) and after error trials (bottom) in one example rat. (b) Similar to a for another example rat. (c) Choice updating of the TDRL model ran with large sensory noise ( 0.5). This model exhibit choice updating qualitatively similar to the rat shown in a. (d) Choice updating in the TDRL model with large internal noise (). This model run exhibits choice updating similar to the rat shown in b.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Reinforcement biases subsequent perceptual decisions when confidence is low, a widespread behavioral phenomenon
eLife 9:e49834.
https://doi.org/10.7554/eLife.49834
