Patterned perturbation of inhibition can reveal the dynamical structure of neural processing
- Bioengineering Department, Imperial College London, United Kingdom
Figures
Figure 1 with 1 supplement
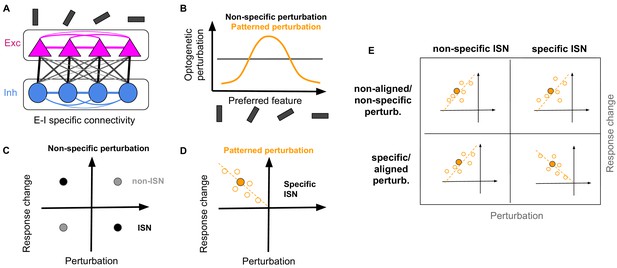
Random and patterned perturbation of inhibition to asses inhibitory stabilized networks.
(A) Schematic of network with specific EI connectivity. (B) Optogenetic perturbation of inhibition can either be non-specific (independent of preferred features of the perturbed inhibitory neurons) or patterned (specifically addressing inhibitory neurons with similar feature selectivity). (C) Non-specific perturbation only reveals the average paradoxical effect in an ISN (black circle), by revealing that the average activity of perturbed inhibitory neurons is changing in the opposite direction of perturbations. In non-ISNs (gray circle), perturbations and response changes have the same sign. (D) Patterned perturbation of specific ISNs reveals specific paradoxical effects, where inhibitory neurons with more (negative) perturbations show more (positive) response changes. The negative correlation of perturbations and response changes is indicated by the dashed line with a negative slope. The mean activity of inhibitory neurons (filled orange circle) still shows the non-specific paradoxical effect, similar to (C). The specific paradoxical effect is, however, reflected in the slope of the pattern, and cannot be distinguished by the mean activity. (E) Expected patterns for the response changes of inhibitory neurons versus their perturbations under four scenarios: non-specific or specific perturbation of non-specific of specific ISNs. Similar to (D), open circles denote the response change of individual inhibitory neurons upon perturbation, the filled circle is the average across those neurons, and the dashed line indicates the slope of correlation. While all combinations show non-specific paradoxical effect (reflected in the similar behaviour of the mean response), only specific perturbation of specific ISNs reveal the specific paradoxical effect (reflected in the negative slope of the line).
Figure 1—figure supplement 1
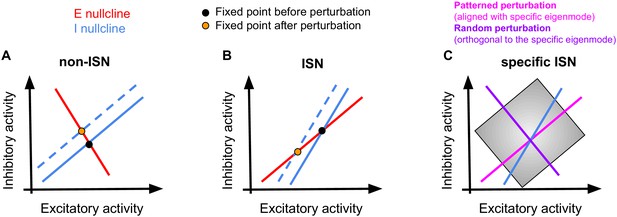
Paradoxical effects of perturbing inhibition in ISNs and specific ISNs.
(A) Effect of perturbing the inhibitory population in networks with weak coupling of excitatory and inhibitory populations (non-ISNs). Here, increasing the activity of inhibitory neurons (demonstrated by the shift in the I nullcline from the solid blue line to the dashed one) leads to a new fixed point with higher inhibitory and lower excitatory activity, in the expected direction. (B) In networks with strong coupling of excitation and inhibition, increasing the input to inhibition leads to a new fixed point with lower activity of both excitation and inhibition. Perturbation of inhibition, therefore, changes the activity of the inhibitory population in a paradoxical direction. (C) In specific ISNs, patterned stimulation of the network can change the fixed point (in the specific direction; ‘specific fixed point’) either in ISN or non-ISN fashion, depending on the alignment of the perturbation pattern with the specific eigenmode of the network. Perturbation patterns aligned with the specific eigenmode (magenta) change the specific fixed point in the ISN direction (similar to (B)), hence leading to the specific paradoxical effect. Perturbation patterns orthogonal to the specific eigenmode (purple) change the specific fixed point in the non-ISN direction (similar to (A)), hence failing to reveal the specific paradoxical effect.
Figure 2 with 7 supplements
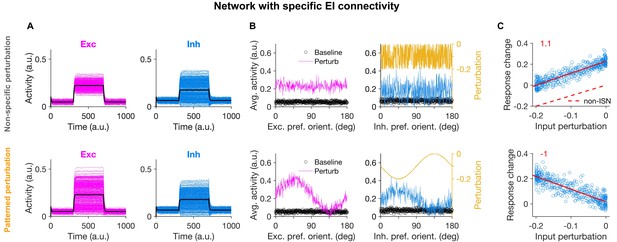
Patterned perturbation of inhibition is necessary to reveal specific inhibitory stabilization.
(A) Activity of individual excitatory (magenta) and inhibitory (blue) neurons, and their average activity (black), in the baseline state and during perturbation (from T = 300 to 700) applied by reducing the input to inhibitory neurons (see Materials and methods). Perturbations are induced either non-specifically (upper) or in a patterned manner (lower), where the decrease in the input is proportional to the preferred orientation of respective inhibitory neurons (Figure 1B). Both modes of optogenetic perturbations lead to the non-specific paradoxical effect, as reducing the input to inhibitory neurons paradoxically increases their average activity. (B) Average activity of individual excitatory and inhibitory neurons during baseline (black dots) and perturbed states as a function of their preferred orientations. The amount of perturbation of the input to each inhibitory neuron is plotted on the right side (orange) for comparison. The non-specific perturbation is the same pattern as the specific perturbation but randomized over neurons. (C) Response change as a result of perturbation (calculated as the difference in the average activity of neurons in the perturbed states compared to the baseline) for inhibitory neurons as a function of their input perturbation. This is shown for specific EI networks in response to nonspecific perturbation (upper) and patterned perturbations (lower). Solid red lines show the best fitted regression line to the data points, with the slope of the line indicted on top (red). The dashed line in (upper) illustrates how a non-ISN would have behaved under a similar perturbation (Figure 2—figure supplement 2).
Figure 2—figure supplement 1
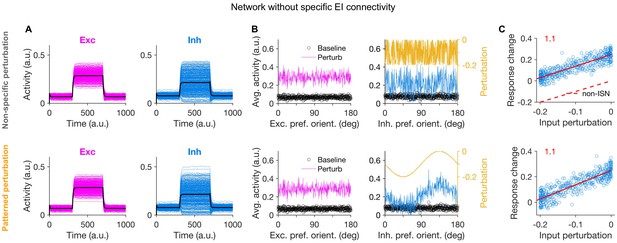
Lack of specific paradoxical effect in networks without specific EI connectivity.
(A-C) Similar plots as in Figure 2A-C, respectively, for neuronal networks without feature-specific EI connectivity. Here, both nonspecific and patterned perturbation fail to yield a specific paradoxical effect (as quantified by lack of negative slopes in C), consistent with lack of specific ISNs in networks without specific connectivity. Note that the nonspecific paradoxical effect is still present, as reflected in the increase in the average activity of inhibitory neurons despite negative perturbations.
Figure 2—figure supplement 2
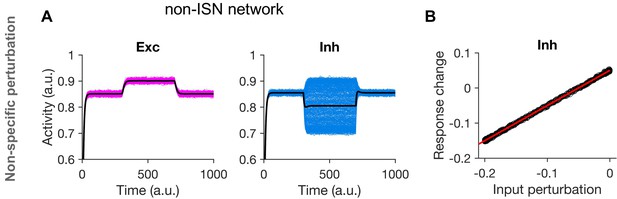
Non-paradoxical effect in non-ISN networks.
(A,B) Similar plots as Figure 2A,C, respectively, for a network operating in a non-ISN regime of activity.
Figure 2—figure supplement 3
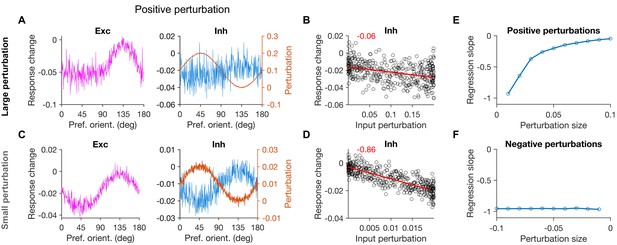
Specific paradoxical effect with positive perturbations.
(A,B) Similar to Figure 2B,C, respectively, for positive patterned perturbations. The pattern of perturbation of inhibitory neurons is the same but reversed in sign. (C,D) Similar as (A,B) for a 10 times smaller perturbation size. The slope of the best fitted regression line is denoted on the top (red) in each case. (E,F) The slope of the best fitted lines to response changes versus input perturbations, for positive (E) and negative (F) perturbations of different size.
Figure 2—figure supplement 4
Patterned perturbation of inhibitory neurons in networks with fewer inhibitory neurons and broader inhibitory connectivity.
(A) Response change versus input perturbations (similar to Figure 2C), in a network with fewer inhibitory neurons. The network is the same as in Figure 2, but it has inhibitory and excitatory neurons, and , . Upper: Patterned perturbation; Lower: Randomized patterns over neurons. (B) Same as (A) for the network with broader inhibitory connectivity. The network is the same as Figure 2, but the specificity of all weights other than EE connections has reduced by 20% (i.e., and ), and , . (C) Same as (A), for a network with fewer inhibitory neurons and broader connectivity of inhibition. Differing parameters from Figure 2 are the following: , , , , , . Red lines denote the best fitted regression lines to the data in each case, with the slope of the regression indicated in red.
Figure 2—figure supplement 5
Patterned perturbation of inhibitory neurons in networks with heterogeneous specificity of excitatory and inhibitory connections.
(A) Left: Distribution of connection specificity (m) of synapses in the network. Instead of a single value (e.g. m = 1 in Figure 2), connection specificity is now drawn from a uniform distribution between 0 (non-specific) to 1 (highly specific). Right: The weight matrix of the EE subnetwork generated with connection specificity as shown on the left. Neurons are sorted according to their initial preferred orientations. (B) Average activity of neurons in the network during baseline and perturbed states (c.f. Figure 2) as a function of their initial preferred orientation. Conventions are the same as Figure 2B. (C) Average response change of neurons versus their input perturbations for patterned perturbations (as in (B)) (upper) and a randomized version of the input perturbations (lower). Conventions similar to Figure 2C. Red lines denote the best fitted regression lines to the data, with the slope of the regression indicated in red.
Figure 2—figure supplement 6
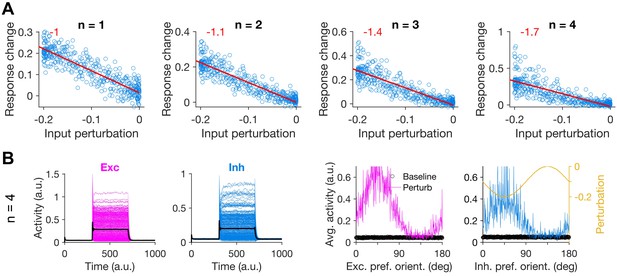
Feature-specific paradoxical effects in networks with nonlinear transfer functions.
(A) Response change as a function of input perturbation of inhibitory neurons in rate-based networks with nonlinear transfer function (see Materials and methods). The power of expansive nonlinearity of the transfer function is specified by n, with n = 1 recapitulating the same dynamics as in Figure 2. Other conventions are the same as Figure 2C. Note different scales of y-axes. (B) Left: Sample activity of excitatory and inhibitory neurons before, during and after patterned perturbation, for n = 4 (similar to Figure 2A). Right: Average activity of individual excitatory and inhibitory neurons during baseline state and during perturbation, as a function of their initial preferred orientation. Conventions the same as Figure 2B.
Figure 2—figure supplement 7
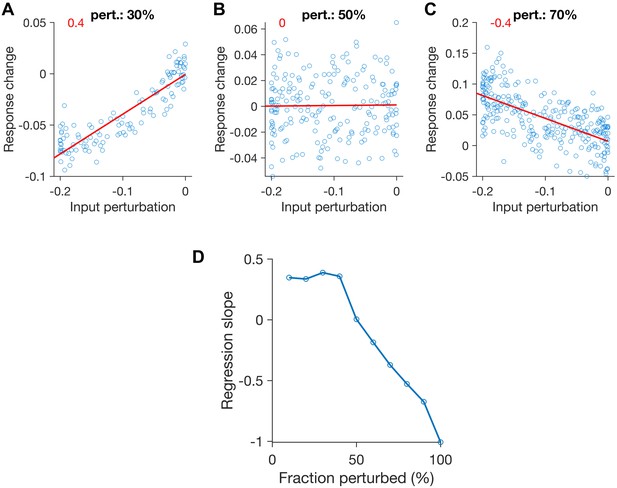
Feature-specific paradoxical effects in networks with partial perturbation of inhibition.
(A–C) Response change as a function of input perturbations for perturbed inhibitory neurons under patterned perturbations (similar to Figure 2C). Different fraction of inhibitory neurons are perturbed in (A): 30%, (B): 50% and (C): 70%. Other parameters and conventions are otherwise the same as Figure 2. (D) The slope of regression line fitted to the data (red lines in (A-C), with the slope denoted with the numbers in red) for different fractions of patterned perturbation. More than 50% of the inhibitory population should be perturbed to observe the specific paradoxical effect (assayed by the negative slope of the regression).
Figure 3 with 1 supplement
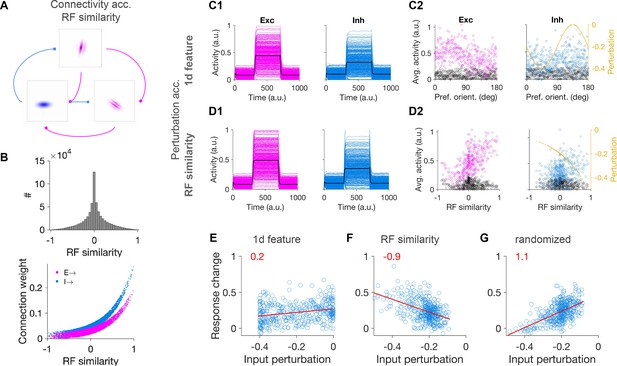
Patterned perturbation of inhibition based on receptive field similarity is necessary to reveal specific inhibitory stabilization.
(A) Sample neuronal RFs for excitatory (magenta) and inhibitory (blue) neurons and schematics of connectivity between neuronal pairs. (B) Upper: Distribution of RF similarity of all neuronal pairs in the network, as quantified by pairwise correlations of RFs. Lower: Weights of connections between neurons as a function of their RF similarity. (C1) Activity of excitatory and inhibitory neurons in response to patterned perturbation along the 1D dimension of orientation (similar to Figure 2A). (C2) The average activity of neurons during baseline and perturbed states, along with the profile of inhibitory perturbation, as a function of the preferred orientation of neurons (similar to Figure 2B). (D1,D2) Similar to (C1,C2) for patterned perturbation along RF similarity (see Materials and methods). The average activity of neurons in (D2) is plotted against the RF similarity of respective neurons to a reference inhibitory cell. (E) Response change of individual inhibitory neurons as a result of perturbation versus their respective input perturbations, along with the best fitted regression line (red), similar to (C). Patterned perturbation along the 1d feature of orientation does not reveal a negative slope, although it yields a nonspecific paradoxical effect (average increase of inhibition as a result of negative perturbations). (F) Patterned perturbation along RF similarity (with regard to a reference cell) shows the specific paradoxical effect (negative slope). (G) Same pattern of perturbation as in (F) but randomized over inhibitory neurons, does not lead to a specific paradoxical effect (lack of negative slope).
Figure 3—figure supplement 1
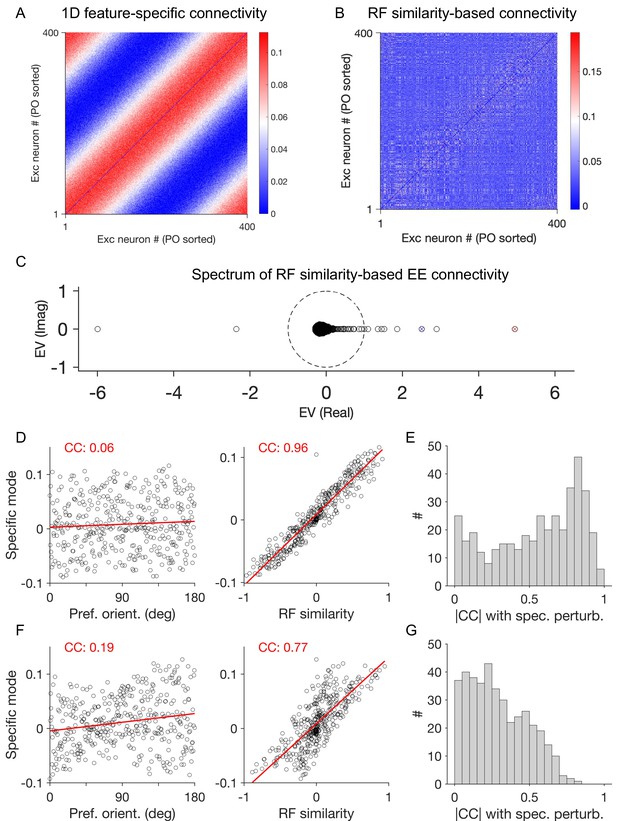
Spectral analysis of specific perturbations.
(A) Connectivity matrix of the excitatory subpopulation (E-to-E) in a network with feature-specific connectivity based on a one-dimensional feature (preferred orientation, PO), as in Figure 2. (B) Connectivity matrix of excitatory neurons based on RF similarity (similar to networks in Figure 3). Neurons are sorted according to their preferred orientations (PO) in both (A) and (B). (C) Spectrum of weight matrix in (B), when specific connectivity is only preserved within excitatory (EE) subnetwork. Connectivity between other connection subtypes (E-to-I, I-to-E, and I-to-I) is replaced with the mean value of the respective subpopulation. The eigenvalue marked in red thus reveals the most unstable eigenmode resulting from specific E-to-E connectivity. (D) Structure of the first specific eigenmode of E-to-E (i.e., the eigenvector corresponding to the eigenvalue marked in red in (C)) versus different features of excitatory neurons: their preferred orientation (Pref. orient.) in left and RF similarity of neurons to a reference neuron in the network on right. Correlation coefficient (CC) between the specific eigenvector and neuronal features are indicated in red in each case. Red lines show the best fitted regression line to the data. (E) Distribution of the absolute value of the correlation coefficient (|CC|) between the specific eigenvector and the vector of RF similarity of neurons to different excitatory neurons in the network. (F,G) Similar to (D,E) for another specific eigenvector (the third unstable eigenvalue marked in blue in (C)).
Figure 4 with 2 supplements
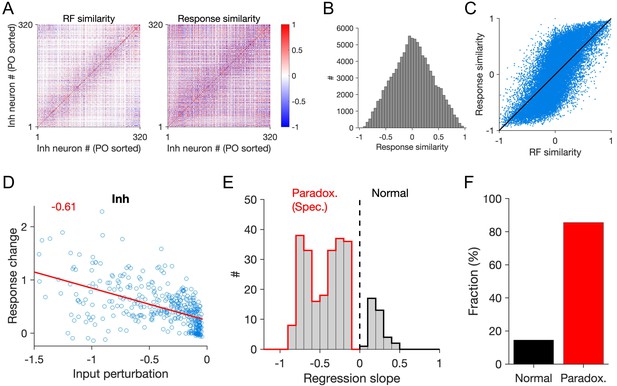
Patterned perturbation of specific ISNs according to response similarity.
(A) Left: RF similarity (quantified as pairwise RF correlation) of responsive inhibitory neurons in the network. Right: Response similarity of same inhibitory neurons, calculated as correlation of activity in response to a sequence of stimuli, composed of RFs with similar statistics as the neuronal RFs (see Materials and methods). Responsive units are identified as neurons with average activity more than the 20th percentile of the population and sorted according to their preferred orientation (PO sorted). (B) Marginal distribution of response similarity of all neuronal pairs in (A). (C) Response correlation of the neuronal pairs versus their RF correlation. (D) Response change of inhibitory neurons versus their input perturbation, when patterned perturbation is applied according to response similarity with regard to an example reference inhibitory cell. Red line shows the best fitted regression line and the slope is denoted in red. (E) The slope of the fitted regression line to the data points (as in (D)) for different inhibitory neurons used as the reference. Only significant regression lines (p-value<0.05) have been included. Negative slopes denote specific paradoxical effects. (F) Fraction of inhibitory neurons that would reveal a specific paradoxical effect (significant negative slope; red) or not (significant positive slope; black), if used as reference for delivering patterned perturbations.
Figure 4—figure supplement 1
Patterned perturbation of specific ISNs according to response similarity when full-field gratings are used as stimuli.
(A) Example stimuli used to probe the response similarity of inhibitory neurons. Full-field gratings with different orientation, but with a fixed spatial frequency (0.04 cpd), are interleaved with gray images, to measure the activity of neuronal networks. (B) Response correlation of neuronal pairs obtained from the responses to stimuli in (A) versus their RF correlations. (C) Left: Distribution of inhibitory neurons that would elicit significant negative regression slopes (specific paradoxical effect) or significant positive slopes, if the patterned perturbation is delivered according to response similarity with regard to them (similar to Figure 4E, but when stimuli as in (A) are used to probe neuronal responses). Right: Fraction of reference inhibitory neurons with specific paradoxical effects or normal. (D-F) Similar to (A-C) when stimuli with different orientations and a wide range of spatial frequencies (examples shown in (D)) are used to probe the neuronal responses and response similarities guiding patterned perturbations. Same as in Figure 4, all results are shown for responsive inhibitory neurons, identified as neurons with average activity of more than the 20th percentile of the population.
Figure 4—figure supplement 2
Feature-specific paradoxical effects obtained by perturbing inhibitory neurons based on their response similarity to natural images.
(A) Example natural images used to probe the response similarity of inhibitory neurons. (B) Distribution of response similarity of responsive inhibitory neurons, when the network is stimulated with natural images (see Materials and methods). (C) Response similarity versus RF similarity. (D) Distribution of patterned perturbations based on reference inhibitory neurons leading to a significant negative slope (specific paradoxical effect; red) or not (significant positive slope; black). (E) Fraction of patterned perturbations (based on response similarity to reference inhibitory cells) leading to paradoxical effect or not. Other conventions are the same as Figure 4.
Figure 5 with 1 supplement
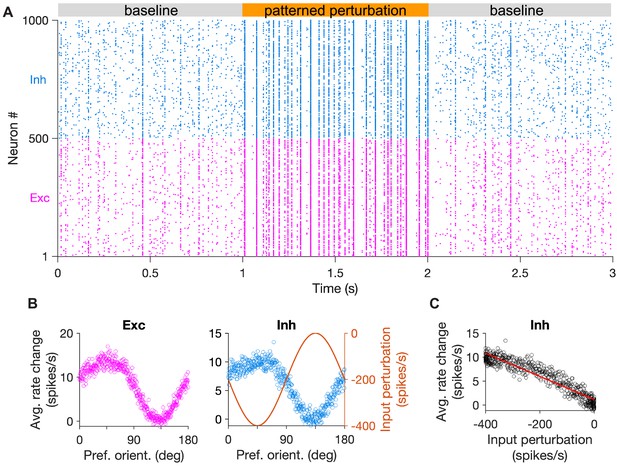
Spiking networks with specific EI connectivity show specific inhibitory stabilization.
(A) Sample raster plot of spiking activity of excitatory (red) and inhibitory (blue) neurons in the baseline states (gray) and during patterned perturbation (orange). The network has all-to-all connectivity and connection weights are modulated as a function of the preferred orientation of neurons (see Materials and methods). (B) Average activity of excitatory and inhibitory neurons during the baseline and perturbed states, across 10 repetitions of the simulation in (A). Input perturbation of inhibitory neurons is shown on the right for comparison. (C) Average response change of inhibitory neurons versus their input perturbation. The red line shows the best fitted regression line to the data points.
Figure 5—figure supplement 1
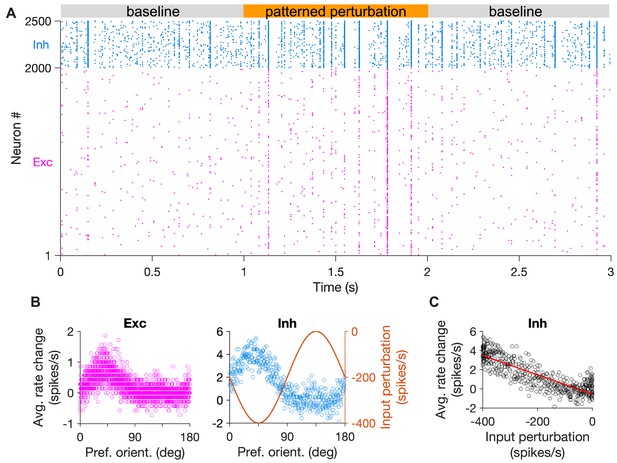
Specific inhibitory stabilization in spiking networks with fewer inhibitory neurons.
(A-C) Same as Figure 5A-C, respectively, for a network with 20% inhibitory and 80% excitatory neurons (). E-to-E connection probability is 25%, while other connections (E-to-I, I-to-E, I-to-I) are all-to-all as before. Other parameters and conventions are the same as Figure 5.
Figure 6 with 1 supplement
Spontaneous transition between selective states during spontaneous activity in specific EI networks.
(A) Sample raster plots of spontaneous spiking activity of excitatory and inhibitory neurons for network with nonspecific EI connectivity. Neurons are sorted according to their preferred orientation (from 0 to 180 degrees). Population preferred orientation (pop. PO, black) and population orientation selectivity index (pop. OSI, red) are shown at the bottom, for the activity of the excitatory population rendered in bins of 10 ms (Materials and methods). Only bins in which at least five excitatory neurons are active are included in the analysis. (B) Same as (A) for the spontaneous activity of networks with specific EI connectivity (Specific connectivity: 100%, corresponding to m = 1; see Materials and methods). Neurons show clustered activity around different preferred orientations, in the absence of a tuned external input with a specific orientation. The transition between highly selective states with different neuronal patterns (clustering of activity around different POs) is highlighted for two example regions (shaded). Note population activity patterns with different pop. POs and high pop. OSI in the vicinity of each other. (C,D) Same as (A,B), respectively, for evoked activity. During evoked activity, stimulus with a specific orientation (90°) is shown, conveying tuned input (Specific input: 100%) to neurons according to their preferred orientations. See Materials and methods for details.
Figure 6—figure supplement 1
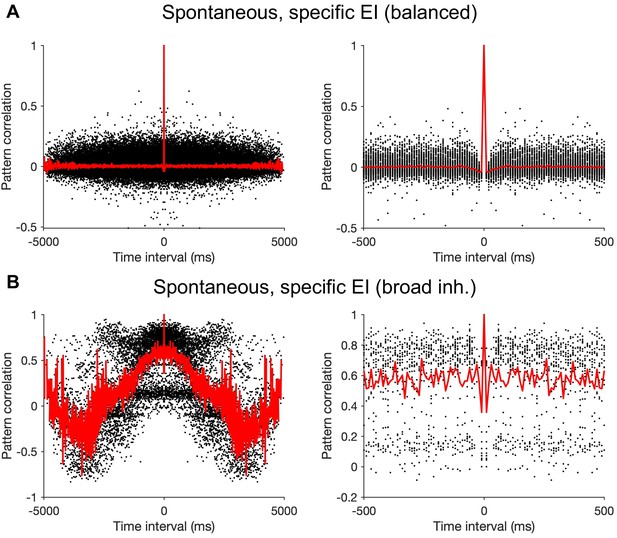
Time scale of transitions between selective states during spontaneous activity.
(A) Pattern correlations of excitatory neurons as a function of the time interval between each pair of patterns. For each pair of highly selective excitatory population patterns (defined as pop. OSI > 0.5), the correlation coefficient between the population activity and the time interval between their occurrence is calculated (black dots). Average pattern correlations are calculated for different pairs of population activity patterns at a given time interval (red). Right: A zoomed in version to show shorter time scales of pattern correlations. Parameters of connectivity are the same as Figure 6B (mEE = mEI = mIE=mII = 1). J = 1 and simulation time is 5s. Other parameters are the same as Figure 6. (B) Same as (A), but for a network connectivity with sharper EE connectivity than the rest: mEE = 1, mEI = mIE = mII=0.5.
Figure 7
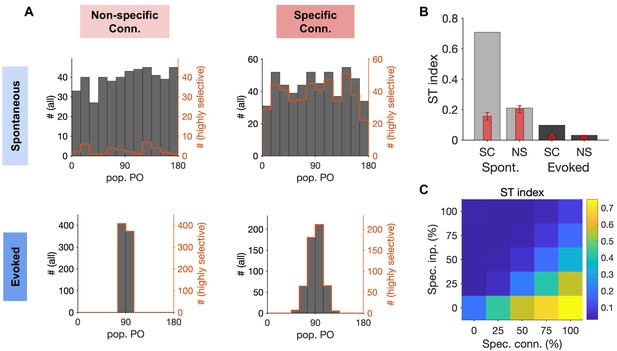
Quantification of spontaneous transition in networks with nonspecific and specific EI connections.
(A) Distribution of population POs derived from the four raster plots shown in Figure 6, for all the data (black) and for highly selective (orange) moments of population activity (pop. OSI > 0.5). (B) The spontaneous transition (ST) index (Materials and methods) for all four combinations of spontaneous (Spont.) and evoked activity of networks with nonspecific (NS) or specific (SC) EI connectivity. Red bars show the mean and std of shuffled data for each case (see Materials and methods for details). (C) ST index for responses of networks with different degrees of specific connectivity (Spec. Conn.) and in response to inputs with different levels of specificity (Spec. Inp.). All results in this figure are obtained from similar networks as in Figures 5 and 6, but with longer simulation times (10s).
Figure 8
Correlation between specific paradoxical effects and spontaneous transitions between selective states.
(A) Sample raster plots of spiking activity from networks with different degree of specific EI connectivity (m = 0, 10, 100%, respectively). Networks and conventions are otherwise similar to Figure 6. (B) Normalized response change of inhibitory neurons as a function of the normalized change in their input due to patterned perturbations. Response changes (Resp. change) and input perturbations (Inp. perturb.) are normalized to the average firing rate and the average input in the baseline state, respectively. The network is simulated for 5s in the baseline state, and another 5s during patterned perturbation. Numbers in red denote the slope of the best fitted regression line to the data (red line). The procedure and conventions are otherwise similar to Figure 5C. (C) The ST index (as in Figure 7) as a function of the slope of perturbations for different networks (back dots). The mean and std of the ST index for shuffled activity (100 repetitions) are shown for comparison (grey). (D) The bootstrapped ST index for networks with negative (specific paradoxical effect) and positive (normal) slopes of perturbations. (E) Bootstrapped ST index and the normalized specific ISN effect (Spec. ISN) in networks as a function of feature-specific connectivity (m). Spec. ISN for each network is calculated by normalizing the slope of the perturbation by slope in the network with the maximum specific connectivity (m = 100%).
Tables
Table 1
Parameters of rate-based networks.
| Description | Type | Symbol | Figure 2 | Figure 2—figure supplement 2 | Figure 2—figure supplement 1 | Figure 3, 4 |
|---|---|---|---|---|---|---|
| Number of neurons | E | 400 | 400 | 400 | 400 | |
| I | 400 | 400 | 400 | 400 | ||
| Time constant | E and I | 10 | 10 | 10 | 10 | |
| Synaptic weight | E→E | 0.05 | 0.001 | 0.05 | 0.05 | |
| E→I | 0.05 | 0.001 | 0.05 | 0.05 | ||
| I→E | −0.075 | −0.0015 | −0.075 | −0.075 | ||
| I→I | −0.075 | −0.0015 | −0.075 | −0.075 | ||
| Synaptic specificity | E→E | 1 | 1 | 0 | 0.5 | |
| E→I | 1 | 1 | 0 | 0.5 | ||
| I→E | 1 | 1 | 0 | 0.5 | ||
| I→I | 1 | 1 | 0 | 0.5 | ||
| Specificity exponent | η | - | - | - | 2 |
Table 2
Parameters of spiking networks.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Patterned perturbation of inhibition can reveal the dynamical structure of neural processing
eLife 9:e52757.
https://doi.org/10.7554/eLife.52757
