Complexity of frequency receptive fields predicts tonotopic variability across species
- Department of Physiology, Anatomy & Genetics, University of Oxford, United Kingdom
Figures
Figure 1 with 2 supplements
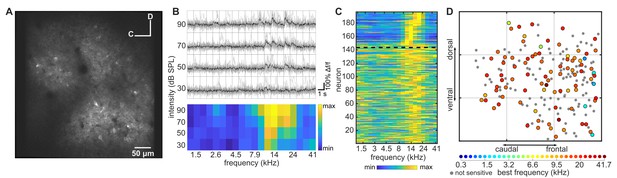
Imaging neuronal responses to pure tones in ferret A1.
(A) An example cortical field in A1 of ferret 1, imaged 120 µm below the pial surface. (B) Responses of one neuron in (A) to pure tones presented at different frequencies and sound levels. Top panel: single trial (gray) and trial-averaged (black) ΔF/F0 traces, measured for 1 s from sound onset. Bottom panel: Frequency Response Area (FRA) of the same neuron. Color scale indicates the trial-averaged response of the neuron to tones presented at each frequency/level combination, calculated from the deconvolved fluorescence trace (see Materials and methods). (C) Frequency-response profile (i.e. level-averaged tuning curves) of all neurons in (A). Neurons above the dashed black line were significantly modulated by frequency (two-way ANOVA, p<0.05) and are sorted by their Best Frequency (BF). Neurons below the line were not sensitive to sound frequency and are sorted by the p-value of the frequency predictor in the two-way ANOVA (bottom neurons have the largest p-value). (D) Map of the neurons in (A) color-coded according to their BF (see color scale below). Gray dots represent neurons that were not sensitive to tone frequency. Each gray grid is 100 µm2.
Figure 1—figure supplement 1
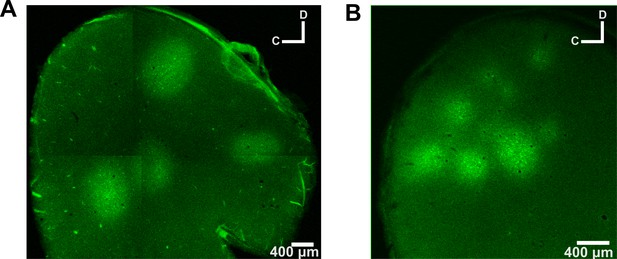
GCaMP6 expression in ferret auditory cortex.
Tangential sections of the auditory cortex are shown to visualize the locations and spread of GCaMP6 injections. Sections were 50 µm thick and were acquired at 200 µm below the cortical surface. (A) The auditory cortex of ferret 3 was injected with a 1:1 solution of AAV1.Syn.GCaMP6f.P2A-nls-dTomato.WPRE.SV40 and AAV1.mDlx.GFP-GCaMP6f-Fishell-2.WPRE.SV40 in four cortical locations. The typical spread of these injections was ~800 µm in diameter per site. (B) Auditory cortex shown as in (A), but for ferret 7. Here, a 1:1 solution of AAV1.Syn.GCaMP6m.WPRE.SV40 and PBS was injected at seven injection sites, and the typical spread was ~400 µm in diameter per site.
Figure 1—figure supplement 2
Imaging in layer 2/3 of ferret A1.
(A) A series of z-projections acquired in vivo using two-photon imaging in ferret 7. The projections have the same fronto-caudal and dorso-ventral axis as the imaged field shown in Figure 1A. Projections were selected to show 10 µm increments in cortical depth. While imaging, the most superficial neuronal bodies were visible ~ 60 μm below the cortical surface. (B) A coronal section of the A1 of ferret 4 showing the extent of GCaMP6 labeling throughout the cortical depth. (C) Distribution of the number of fields imaged at each cortical depth.
Figure 2 with 4 supplements
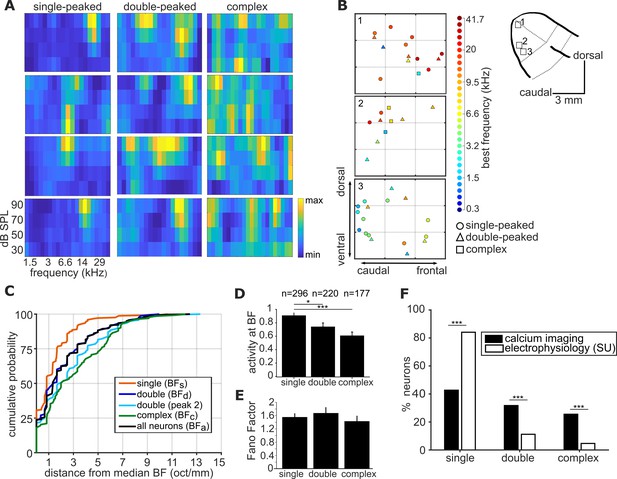
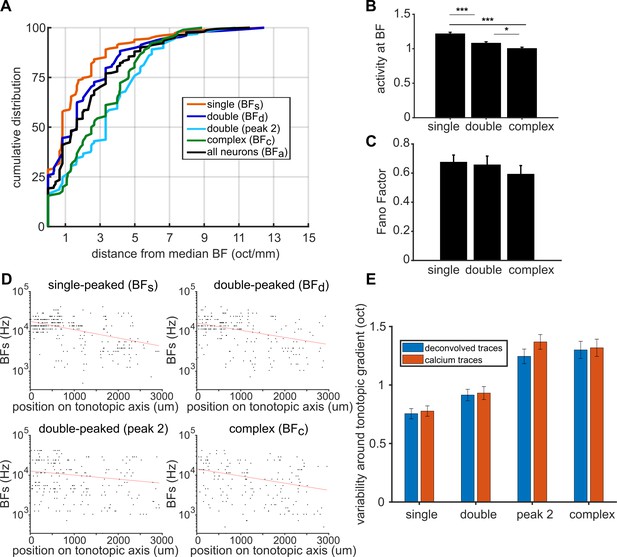
Complexity of frequency receptive fields predicts local variability in ferret A1 tonotopy.
(A) FRA plots of four example neurons from ferret 6 for each of the three FRA classes. (B) Three 300 x 300 µm spatial maps of frequency-sensitive neurons along the tonotopic axis of ferret 6. Their anatomical locations within the ferret’s ectosylvian gyrus are represented in the schematic to the right. The color of each neuron indicates its BF (see color scale, right), and the shape corresponds to the classification of its FRA. (C) Cumulative probability plots of the difference (in octaves) between each neuron’s BF and the median BF of all neurons of the same FRA class in the same imaging field. Distributions for different FRA classes are plotted separately: single-peaked BFs; double-peaked BFd; double-peaked peak 2; complex BFc; and the BFa of all three FRAs together. (D) Magnitude of the trial-averaged response at BF, calculated from deconvolved fluorescence traces in two-photon imaging experiments. Responses were averaged across all neurons in each FRA class, pooled across imaging fields and ferrets (mean ± SEM). (E) Fano Factor values (mean ± SEM) for single-peaked, double-peaked, and complex neurons. (F) Percentage of neurons classified into each FRA class from two-photon calcium imaging (black) and single unit microelectrode recordings (white). The results of t-tests are indicated above the bars in (D) and (E), and Likelihood Ratio Tests in (F) (*p < 0.05 and *** p < 0.001).
Figure 2—figure supplement 1
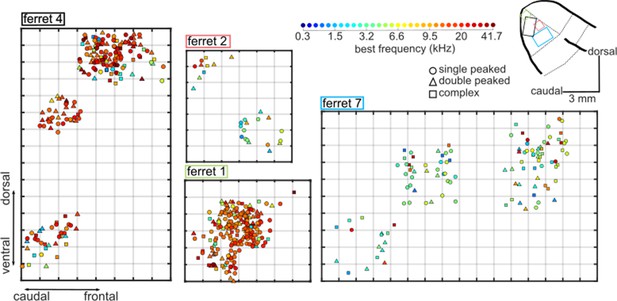
Spatial maps of best frequency in A1 of 4 ferrets.
Each plot is a map of frequency-responsive neurons imaged in individual ferrets (ferrets 1, 2, 4 and 7). Neurons are plotted along the rostro-caudal and dorso-ventral axes. The color of each neuron indicates its BF, while the shape corresponds to the classification of its FRA (see legend, top center), as in Figure 2B. Each gray grid in the maps corresponds to a cortical area of 100 × 100 µm. The locations of the four maps within A1 are represented on a common map of ferret auditory cortex as colored rectangles (top right, color matches ferrets’ numbers).
Figure 2—figure supplement 2
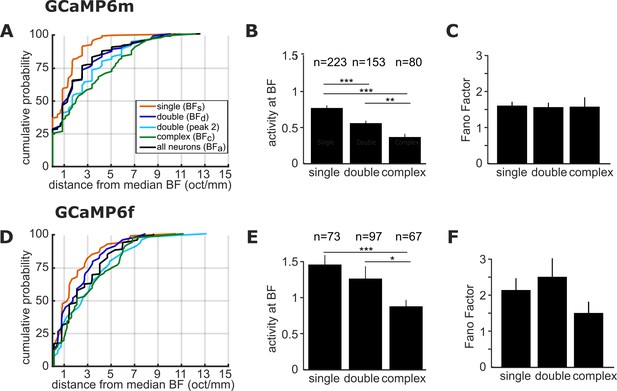
BF variance, response strength and response reliability are comparable in GCaMP6m and GCamP6f ferret datasets.
Top row (A, B, C): results from imaging experiments using GCaMP6m as calcium indicator. Bottom row (D, E, F): same analyses as in A, B, C above, but using data from GCaMP6f experiments. (A, D) Cumulative probability plots of the difference (in octaves) between each neuron’s BF and the median BF of all neurons of the same FRA class in the same imaging field. Distributions for different FRA classes are plotted separately as colored lines, as in Figure 2C (see legend in A). (B, E) Magnitude of the trial-averaged response at BF and best level, calculated from deconvolved fluorescence traces. Responses were averaged across all neurons in each FRA class, and pooled across imaging fields and ferrets (mean ± SEM). (C, F) Fano Factor values (mean ± SEM) for single-peaked, double-peaked, and complex neurons. The results of t-tests are indicated above the bars in (B, E) (*p < 0.05, **p < 0.01 and *** p < 0.001).
Figure 2—figure supplement 3
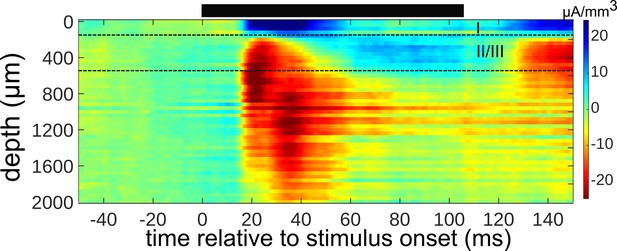
Determining cortical layers from an inverse Current Source Density (iCSD) map of electrophysiological responses.
The iCSD shown was constructed from local field potential recordings of responses to tones presented near BF (±1/3 octave) in one microelectrode penetration. The black bar above the plot indicates stimulus presentation time. The depth (µm) relative to the cortical surface is plotted on the y-axis. The boundary between layers 1 and 2 (upper black dotted line) was inferred based on the reversal in the iCSD profile, and the boundary between layers 3 and 4 (lower black dotted line) was estimated to be 400 µm below the beginning of layer 2.
Figure 2—figure supplement 4
Magnitude of the trial-averaged response at the best frequency and level combination, calculated from spike rates measured with microelectrodes.
Responses were averaged across all neurons in each FRA class, pooled across penetrations and ferrets (mean ± SEM). The number of neurons per group is given above each bar.
Figure 3 with 1 supplement
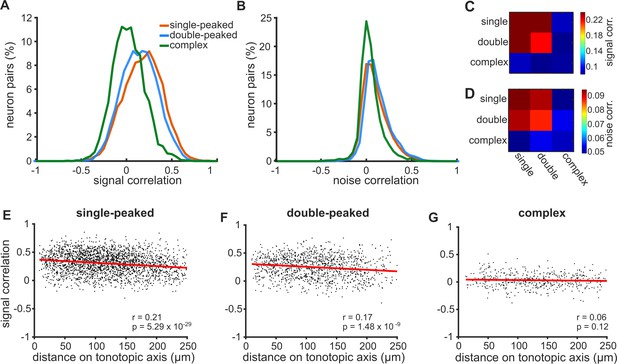
Correlations in neural activity are weaker and less spatially ordered for neurons with more complex FRAs.
(A) Distributions of signal correlations in the pure tone responses of pairs of simultaneously imaged neurons with single-peaked (orange), double-peaked (blue) or complex (green) FRAs. (B) Distributions of noise correlations for the same neural pairs shown in (A). (C) The color scale (right) shows the average signal correlation for pairs of neurons across all 9 combinations of the three FRA classes. (D) Noise correlations across FRA classes, presented as in (C). (E) Pairwise signal correlations for single-peaked neurons plotted as a function of the distance between the two neurons along the tonotopic axis. The best linear fit to the data is shown (red line), with Pearson’s correlation coefficient (r) and p-value (p) in the bottom right of the plot. (F) Same as (E), but for double-peaked neurons. (G) Same as in (E), but for complex neurons.
Figure 3—figure supplement 1
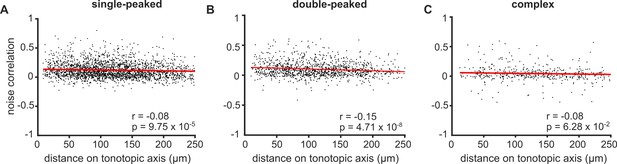
Noise correlations in neurons with single-peaked, double-peaked and complex FRAs.
(A) Noise correlations for pairs of single-peaked neurons imaged simultaneously, as a function of the distance between the two neurons along the tonotopic axis. (B) Same as (A) for double-peaked neurons. (C) Same as (A) for complex neurons. Red lines indicate the best linear fit to the data. Pearson’s correlation coefficient (r) and p-value (p) are shown.
Figure 4 with 4 supplements
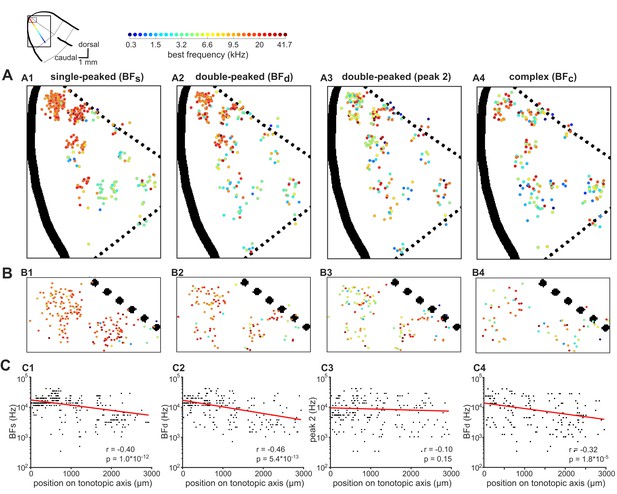
Global tonotopic organization of frequency preferences in ferret A1.
The anatomical locations of neurons imaged across eight ferrets were projected onto a template map of auditory cortex, shown in the top-left corner. Thick black solid lines indicate sulci, and black dotted lines indicate approximate borders between known cortical fields. The two boxes represent the location of A1 (large box; A) and the most dorsal region of A1 (small box; B). The colored line illustrates the tonotopic gradient. (A) The BFs of individual neurons are color-coded (legend above) and mapped onto A1. The spatial distributions of BFs (A1), BFd (A2), peak 2 of double-peaked neurons (A3), and BFc (A4) are plotted separately. (B) Frequency preferences are mapped as in (A) for the dorsal tip of A1, where many neurons are occluded in (A). (C) BFs (C1), BFd (C2), peak 2 (C3), and BFc (C4) of each neuron are plotted against the neuron’s position along the tonotopic axis on the template A1. Red lines show the best single-term exponential fits to the data, and Pearson’s correlations (r) with their p-values (p) are also shown.
Figure 4—figure supplement 1
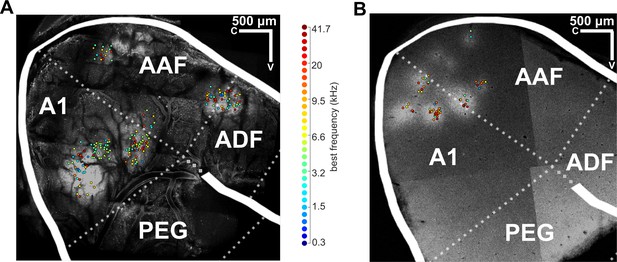
Mapping data from individual ferrets onto a common template of auditory cortex.
(A) An image of the brain surface of ferret 3, acquired in vivo using two-photon calcium imaging. Individual frequency-sensitive neurons imaged across all fields are plotted on this map according to their anatomical position, where their color indicates their BF (color scale, right). The common template of auditory cortex is superimposed, where white solid lines indicate sulci and white dotted lines indicate approximate borders between known cortical fields (names in white text). The brain image and template were aligned according to the positions of sulci, and frequency responses of imaged neurons. Only neurons in A1 were included in our analyses. (B) A post mortem section of the auditory cortex of ferret 7, which was sliced parallel to the two-photon imaging plane (i.e. parallel to the surface of auditory cortex) and imaged with a confocal microscope. The BF of imaged neurons and the cortical template are superimposed, as in (A). A1 = primary auditory cortex; AAF = anterior auditory field; PEG = posterior ectosylvian gyrus (containing the posterior pseudosylvian and posterior suprasylvian fields); ADF = anterior dorsal field.
Figure 4—figure supplement 2
Mapping the peak-to-peak distances in double-peaked neurons.
(A), (B) Double-peaked neurons imaged across all ferrets are mapped onto the template A1, as in Figure 4A and B. Here, the color scale (below B) indicates the difference, in octaves, between BFd (i.e. the frequency eliciting the strongest response) and peak 2 (i.e. the frequency eliciting the second-strongest response) for each neuron. (C) The octave difference between BFd and peak 2 is plotted for each double-peaked neuron, as a function of its position along the tonotopic axis (as in Figure 4C). The red line represents the best single-term exponential fit to the data, and the coefficient (r) and p-value (p) of Pearson’s correlation are shown. (D) Distribution of the difference (in octaves) between BFd and peak 2, across all double-peaked neurons. BFd and peak two were on average 1.74 ± 0.07 (mean ± SEM) octaves apart, and their octave distances did not differ when BFd was lower or higher than peak 2 (t-test: t = −0.17, p=0.87).
Figure 4—figure supplement 3
Comparison between deconvolved and non-deconvolved traces.
(A) Cumulative probability plots of the difference (in octaves) between each neuron’s BF and the median BF of all neurons in the same FRA class and imaging field. Distributions for different FRA classes are plotted separately: single-peaked BFs; double-peaked BFd; double-peaked peak 2; complex BFc; and the BFa of all three FRAs together. (B) Magnitude of the trial-averaged response at BF, calculated from non-deconvolved fluorescence traces. Responses were averaged across all neurons in each FRA class, pooled across imaging fields and ferrets (mean ± SEM). Significant results of t-tests are shown above the bars: * p < 0.05, *** p < 0.001. (C) Fano Factor values calculated at BF (mean ± SEM) for single-peaked, double-peaked, and complex neurons in non-deconvolved fluorescence traces. T-tests show no significant differences between groups (p > 0.05). (D) BFs , BFd, peak 2, and BFc of each neuron are plotted against the neuron’s position along the tonotopic axis on the template A1. Red lines show the best single-term exponential fits to the data. (E) Average octave distance of each BF from the fit (red curves in D and Figure 4C) for deconvolved traces (blue) and non-deconvolved fluorescence traces (red) (mean ± SEM). T-tests show no significant differences between results of the two methods for each FRA type (p > 0.05).
Figure 4—figure supplement 4
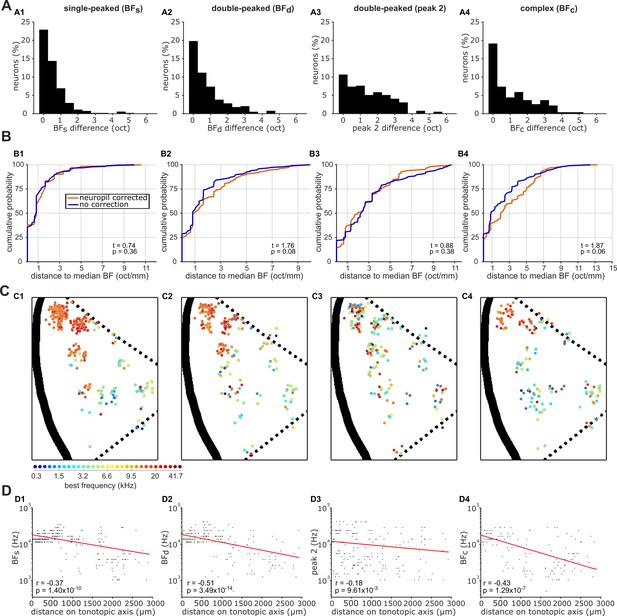
Effects of neuropil contamination on local and global tonotopic organization.
(A) Distributions of the difference (in octaves) between BFs (A1), BFd (A2), peak 2 (A3) and BFc (A4) calculated with and without neuropil signal subtraction. (B) Cumulative probability plots of the difference (in octaves) between each neuron’s BF and the median BF of all frequency sensitive neurons in the same imaging field. Distributions for BFs obtained with (red) and without (blue) neuropil correction are plotted separately. The results of t-tests between the two distributions are given in the bottom right of each plot. (C) Frequency preferences are mapped onto a template A1 as in Figure 4A, but here without neuropil correction. (D) Scatterplots show the frequency preferences of neurons as a function of their position along the tonotopic axis of the maps in C (as in Figure 4C), for neuropil-uncorrected data.
Figure 5 with 4 supplements
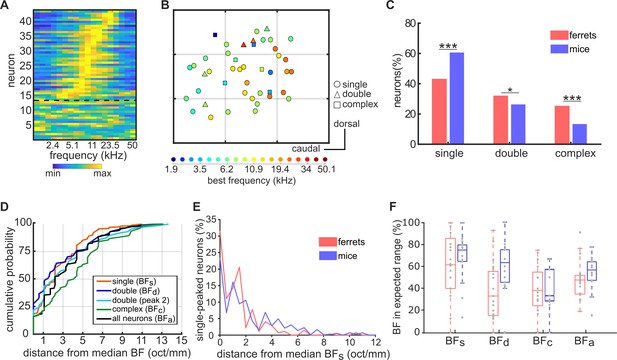
Similar tonotopic organization in the primary auditory cortex of ferrets and mice.
(A) Frequency-response profile (i.e. level-averaged tuning curves) of all neurons imaged in one imaging field in one mouse. Data are presented as in Figure 1C. (B) Map of the anatomical locations of the neurons in (A), plotted as in Figure 2B. Neurons are color-coded according to their BF, and their shape corresponds to their FRA class. Each gray grid corresponds to a cortical area of 100 x 100 µm. (C) Proportion of frequency-sensitive neurons from each FRA class for ferrets (red) and mice (blue). The results of Likelihood Ratio tests are indicated above (*p < 0.05 and *** p < 0.001). (D) Cumulative probability plots of the difference (octaves/mm) between the BF of each neuron and the median BF of all neurons in the same imaging field. As in Figure 2C, distributions were calculated separately for BFs (orange), BFd (dark blue), peak 2 of double-peaked neurons (light blue), BFc (green), and BFa (black). (E), Distributions of the distance in octaves per mm between the BFs of each single-peaked neuron in an imaging field and the median BF of these neurons. Data are shown for ferrets (red) and mice (blue). (F) Box plots showing the percentage of neurons having a BF within the expected frequency range, given the species, size and average BF of each imaging field. Percentages were calculated separately for BFs, BFd, BFc and BFa, and percentages for individual imaging fields are shown as gray dots. Boxplots for ferrets (red) and mice (blue) show the median, upper quartile, and lower quartile of each dataset.
Figure 5—figure supplement 1
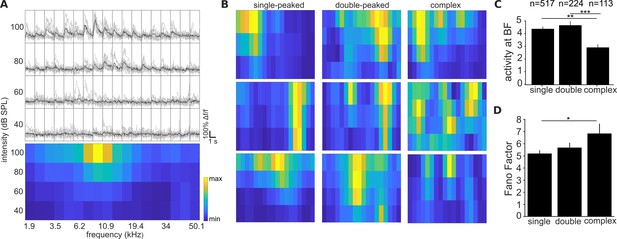
All 3 FRA types are present in the mouse primary auditory cortex.
(A) Responses of one neuron to pure tones presented at different frequencies and sound levels. Top panel: single trial (gray) and trial-averaged (black) ΔF/F0 traces, measured for 1.5 s from sound onset. Bottom panel: Frequency Response Area (FRA) of the same neuron. The color scale indicates the trial-averaged response of the neuron to tones presented at each frequency/level combination, calculated from the deconvolved fluorescence trace. (B) FRA plots of three example neurons for each of the three FRA classes, imaged in one mouse. (C) Magnitude of the trial-averaged response at BF and best level, calculated from deconvolved fluorescence traces, as in Figure 2D. Responses were averaged across all neurons in each FRA class, pooled across imaging fields and mice (mean ± SEM). (E) Fano Factor values (mean ± SEM) at the best frequency and level combination for single-peaked, double-peaked, and complex neurons. The results of t-tests are indicated above the bars in (C) and (D) (* p < 0.05, ** p < 0.01, and *** p < 0.001).
Figure 5—figure supplement 2
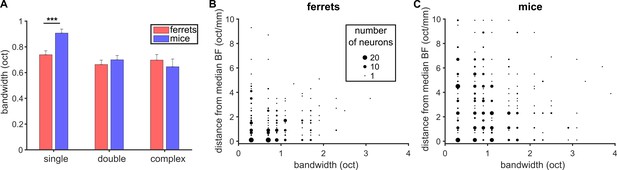
FRA bandwidth does not predict local tuning heterogeneity.
(A) Average (mean ± SEM) frequency tuning bandwidth around BF for single-peaked, double-peaked and complex neurons in ferrets and mice (t-test; *** p < 0.001). (B, C) Scatterplots show the frequency tuning bandwidth as a function of the distance of the BF for each neuron from the median BF value in each imaging field in ferrets (B) and mice (C). Data are shown for single-peaked neurons only. Dot size is proportional to the number of neurons (see legend).
Figure 5—figure supplement 3
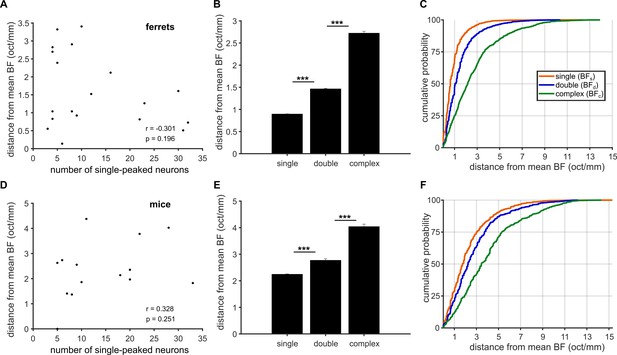
The BF variance within an imaging field does not depend on the number of neurons in the field.
(A) BF variance for single-peaked neurons in ferrets is plotted as a function of the number of these neurons within an imaging field, for all imaging fields containing at least three single-peaked, three double-peaked, and three complex neurons. The statistics of a Pearson’s correlation of these two values are given in the bottom right of the plot. (B) For each ferret imaging field, we estimated the BF variance for each neuron class using only three neurons, and this calculation was repeated for every possible combination of 3 neurons. The bar plot shows the average (mean ± SEM) BF variance across all iterations for each neuron type (t-test; *** p < 0.001). (C) Cumulative probability of the bootstrapped BF variance within ferret imaging fields, for single-peaked (orange), double-peaked (blue) and complex (green) neurons. (D - F) Results plotted as in A, B, C above (respectively), but for mouse data.
Figure 5—figure supplement 4
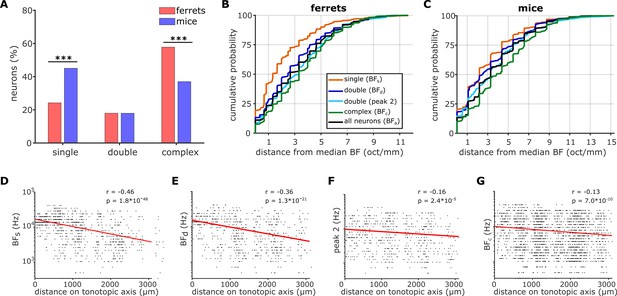
Effects of FRA complexity on BF organization hold across all imaged neurons.
(A) Proportion of neurons in each FRA class are shown for ferrets (red) and mice (blue), classified as in Figure 5C. The results of Likelihood Ratio tests are indicated above (*** p < 0.001). (B) Cumulative probability plots of the difference (octaves/mm) between the BF of each neuron imaged in ferrets and the median BF of all neurons in the same imaging field. Distributions were calculated separately for BFs (orange), BFd (dark blue), peak 2 of double-peaked neurons (light blue), BFc (green), and BFa (black). (C) Results plotted as in B, but for all neurons imaged in mice. (D-G) Global tonotopic gradients in ferrets, presented as in Figure 4C. BFs (D), BFd (E), peak 2 (F), and BFc (G) of individual neurons (black dots) are plotted against the neuron’s position along the tonotopic axis. Red lines show the best single-term exponential fits to the data, and Pearson’s correlations (r) with their p-values (p) are given in the top right corner of each plot.
Author response image 1
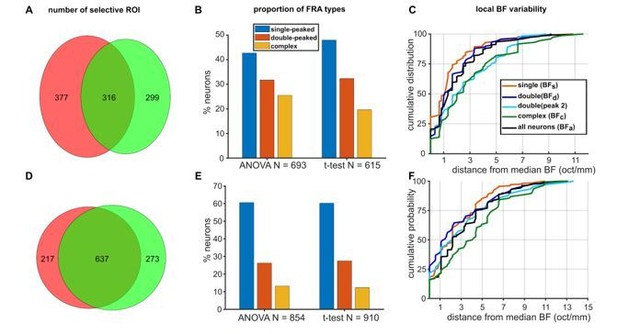
Comparison of 2-way ANOVA and paired t-test as ROI inclusion tests.
(A) Venn diagram showing the overlap in the number of ferret ROIs passing the ANOVA (pink) and the t-test (green). (B) Proportions of single-peaked, double-peaked and complex FRAs within the population of neurons identified using either the ANOVA (left) or t-test (right). (C) Cumulative probability plots of the difference (in octaves) between each neuron’s BF and the median BF of all neurons of the same FRA class in the same imaging field. Distributions for different FRA classes are plotted separately as colored lines, as in Figure 2C. Data are for neurons identified as responsive by the t-test. D, E, F. Mouse data plotted as in A, B, C (respectively) for ferret data above.
Author response image 2
Pairwise signal correlations for all pairs of simultaneously recorded ferret neurons.
The signal correlation (SC) was calculated as in our original manuscript (x-axis) or after doubling the response strength of one neuron in each pair (y-axis). This scaling of the response strength has no effect on the resulting signal correlation. Signal correlations of individual pairs of neurons are plotted as blue dots, and these all fall on the line of equality (red).
Author response image 3
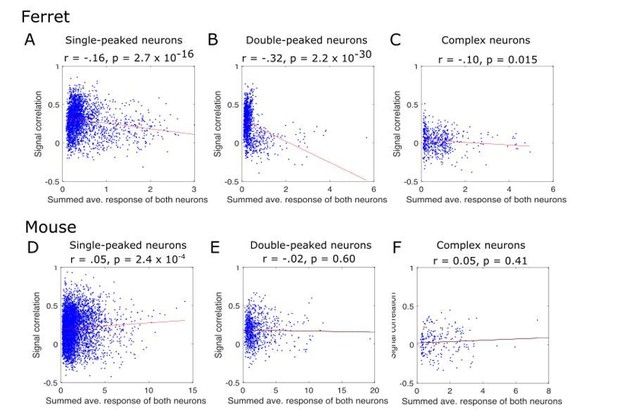
Pairwise signal correlations as a function of the summed response strength of paired neurons.
The signal correlation was calculated as in our original manuscript (y-axis), and is plotted as a function of the response strength of the pair of neurons (x-axis). The response strength was calculated as the two neurons’ summed extracted spikes, each averaged across all stimulus conditions (x-axis). Individual neuron pairs are shown as blue dots and the regression line is overlaid. The results of the regression of signal correlation on response strength is given below each panel title. Results are plotted separately for ferrets (A, B, C) and mice (D, E, F), and for single-peaked (A, D), double-peaked (B, E) and complex (C, F) cells.
Author response image 4
FRA overlap between pairs of simultaneously recorded neurons, plotted as a function of their distance along the tonotopic gradient.
Y-axis shows the number of stimuli eliciting a response >50% maximum for both neurons in a given pair. Each blue dot represents a pair of neurons. The red line is the fitted linear regression, and statistics for the fit are provided below the titles above each plot. Results are plotted separately for ferrets (A, B, C) and mice (D, E, F), and for single-peaked (A, D), double-peaked (B, E) and complex (C, F) cells.
Tables
Table 1
Details of stimuli presented to ferrets.
| Ferret | Stimulus duration (ms) | Repetitions | Interstimulus interval (s) | Frequency range (Hz) |
|---|---|---|---|---|
| 1 | 100 | 10 | 0.75 | 1259–41687 |
| 2 | 500 | 12 | 1.50 | 1047–28840 |
| 3 | 100 | 10 | 1.33 | 1259–41687 |
| 4 | 100 | 10 | 1.33 | 1259–41687 |
| 5 | 500 | 12 | 1.50 | 346–28840 |
| 6 | 500 | 20 | 1.50 | 346–28840 |
| 7 | 500 | 12 | 1.50 | 1047–28840 |
| 8 | 500 | 12 | 1.50 | 1047–28840 |
Additional files
-
Supplementary file 1
Supplementary statistics for t-tests and ANOVAs described in the main figures.
- https://cdn.elifesciences.org/articles/53462/elife-53462-supp1-v2.docx
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/53462/elife-53462-transrepform-v2.docx
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Complexity of frequency receptive fields predicts tonotopic variability across species
eLife 9:e53462.
https://doi.org/10.7554/eLife.53462
