Chromosome organization by one-sided and two-sided loop extrusion
- Institute for Medical Engineering & Science, Massachusetts Institute of Technology, United States
- Department of Physics, Massachusetts Institute of Technology, United States
- Harvard Graduate Program in Biophysics, Harvard University, United States
- Departments of Molecular Biosciences and Physics & Astronomy, Northwestern University, United States
Figures
Figure 1
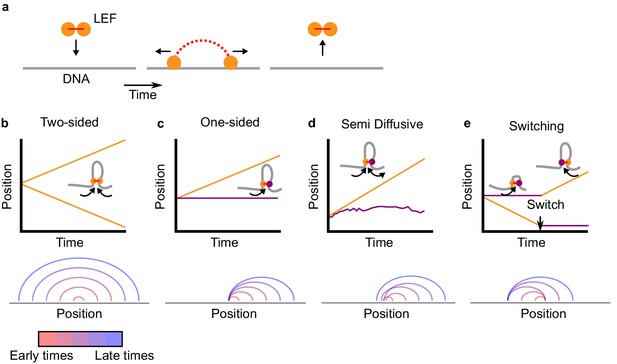
Two-sided loop extrusion and variants of one-sided loop extrusion.
(a) A schematic of the loop extrusion model. The two subunits of the LEF bind to sites on a one-dimensional lattice representing DNA/chromatin. Over time, the subunits may translocate along DNA, and the LEF eventually unbinds from DNA. In 3D polymer simulations, the two subunits remain in spatial proximity (in 3D) while translocating along DNA (in 1D), thereby extruding loops. (b) Top: The positions of the two LEF subunits versus time for a two-sided LEF. Inset: Cartoon of a two-sided LEF on DNA extruding a loop. Bottom: Arch diagram showing the positions of the LEF subunits from early times (red) to late times (blue). (c) Top: Time trace of a one-sided LEF with inset schematic. In the example in the schematic, the active subunit is on the left, but in the model LEFs are loaded with random orientations. Bottom: Arch diagram for a one-sided LEF, where the left subunit is stationary (passive). (d) Top: The positions of the two LEF subunits versus time for the semi-diffusive model. The speed of loop growth increases as the loop grows because the entropic cost of loop growth most strongly affects small loops. Bottom: Arch diagram for the semi-diffusive model, where the left subunit is diffusive. (e) Top: Schematic and a time trace of the switching model. Bottom: Example of an arch diagram for a LEF in the switching model. Note: the arch diagrams do not correspond to the time traces, but rather, they are illustrative examples.
Figure 2 with 7 supplements
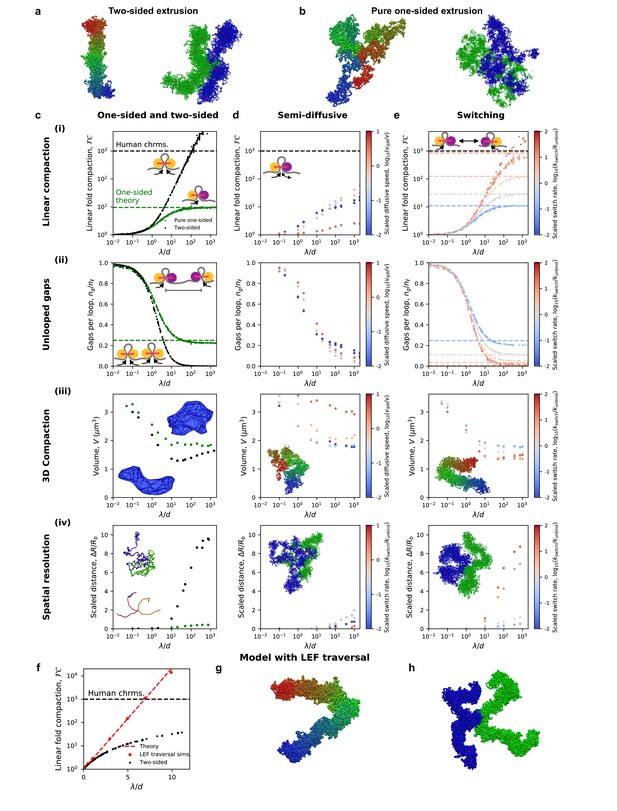
Chromosome compaction and structure in the one-sided loop extrusion model and model variants.
(a) Simulation snapshots of chromosomes compacted (left) and spatially resolved (right) by two-sided extrusion. (b) Simulation snapshots showing deficient compaction (left) and resolution (right) of chromosomes with pure one-sided loop extrusion. (c) One-sided loop extrusion model, as compared to the two-sided model. (i) Linear fold compaction, FC, as a function of the dimensionless ratio, λ/d, of the processivity to the mean distance between LEFs. Pure one-sided extrusion (green) saturates at ≈10-fold compaction for large λ/d, as predicted by mean-field theory (green dashed line). FC by two-sided extrusion (black) surpasses the 1000-fold linear compaction expected for human chromosomes (black dashed line) for λ/d > 50. Insets: cartoons of extrusion of chromatin (gray) by active LEF subunits (yellow). Stationary passive subunit for one-sided LEF is purple. (ii) Number of gaps per parent loop, ng/nℓ, saturates at ≈0.25 (dashed line) as λ/d increases in the pure one-sided model (green), as expected from theory. For two-sided extrusion, ng/nℓ approaches 0 (black). Insets: mechanisms of gap formation and closure. (iii) Chromosome volume, V, decreases as λ/d increases. V achieves smaller values in the two-sided model (black) than in the one-sided model (green). Insets: Images of concave hulls of simulated chromosomes compacted by one- and two-sided extrusion (top and bottom, respectively). (iv) Scaled distance, ΔR/Rb, between sister chromatid backbones in one- or two-sided models. Insets: chromatid backbones in simulations of one- and two-sided extrusion (top and bottom, respectively). (d) Semi-diffusive model. (i) FC <1000 for λ/d < 1000. Color from blue to red indicates increasing scaled diffusive stepping speed, vdiff/v. Inset: a semi-diffusive LEF. (ii) Number of gaps per loop, ng/nℓ, versus λ/d. (iii) Compacted chromosome volume, V, versus λ/d. Inset: chromosome compacted by semi-diffusive LEFs with vdiff/v = 1. (iv) Scaled distance, ΔR/Rb, between chromatid backbones. Inset: image of spatial resolution with vdiff/v = 1. (e) Switching model. (i) FC can surpass 1000-fold linear compaction for rapid scaled switching rates, kswitch/kunbind > 10 (red). Simulations with large λ/d match mean-field theoretical predictions (colored dashed lines). Inset: illustration of the model. (ii) Number of gaps per loop, ng/nℓ, with mean-field theoretical predictions (dashed lines). (iii) Compacted chromosome volume, V. Inset: image of compacted chromosome with kswitch/kunbind = 30. (iv) Scaled distance, ΔR/Rb, between chromatid backbones. Inset: spatial resolution in simulations with kswitch/kunbind = 30. (f) Linear fold-compaction for a chromosome with LEFs that are able to traverse each other. Dashed line shows theoretical fold compaction, as quantified by loop coverage, FC = eλ/d. (g) Simulation snapshot of chromosome compacted by LEFs that may traverse each other. (h) Simulation snapshot of chromatids resolved by LEFs that may traverse each other. Each data point is a mean quantity (see Materials and methods). Standard deviation of the mean for each point is <15% of the mean, or else smaller than the size of a data point.
Figure 2—figure supplement 1
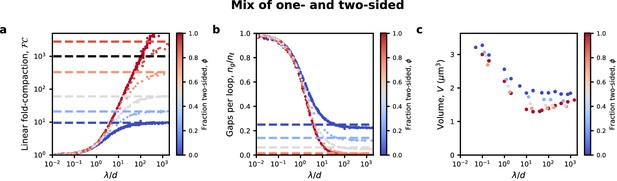
Compaction in model with a mix of one- and two-sided LEFs.
(a) Strong linear compaction can only be achieved with a high fraction of two-sided LEFs. Colored dashed lines show prediction from mean-field theory (Banigan and Mirny, 2019) for compaction in the limit of large λ/d, while black dashed line indicates FC = 1000, expected for human chromosomes. (b) Gaps remain in systems with a one-sided LEFs, as quantified by the number of gaps per loop, ng/nℓ. Dashed lines indicate the expected number of gaps per loop. (c) Volumetric compaction for different fractions of two-sided extrusion.
Figure 2—figure supplement 2
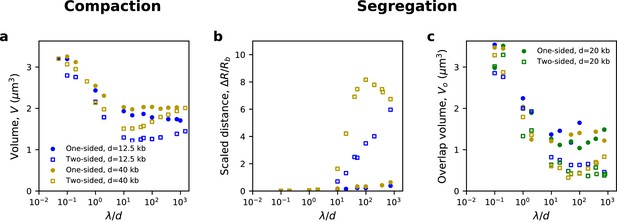
Measures of compaction and segregation with different densities of LEFs.
(a) Volumetric compaction of individual chromosomes and (b) scaled distance between the backbones of sister chromatids are shown for one-sided and two-sided extrusion (filled circles and open squares, respectively) with LEF densities of 1 per 12.5 kb (blue) and 1 per 40 kb (gold). (c) Sister chromatid overlap volume is shown as a supplementary measure of chromatid resolution. Overlap volume decreases as λ/d increases, but the decrease in volume is limited for chromatids compacted by one-sided extrusion (filled circles) as compared to those compacted by two-sided extrusion (open square).
Figure 2—figure supplement 3
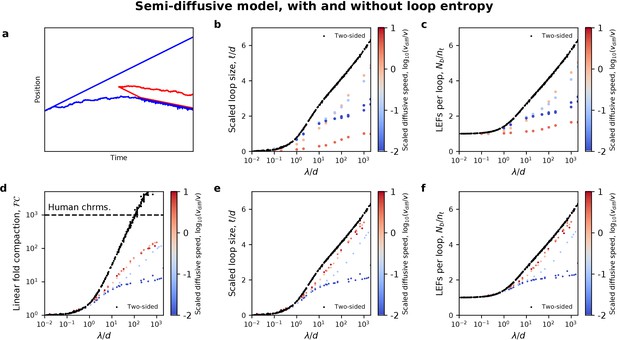
Loop sizes and LEF nesting explain the ineffectiveness of the semi-diffusive model.
(a) Example trajectory of a semi-diffusive LEF (blue) that is ratcheted open by another LEF (red) that binds within the extruded loop. (b) Mean loop sizes, ℓ, are small in the semi-diffusive model because loop growth is opposed by entropy. (c) Consequently, the number of LEFs per loop, which quantifies LEF nesting, remains small. (d) In a semi-diffusive model that ignores the effects of polymer conformational entropy, a higher degree of linear compaction, FC, can be obtained, but FC < 1000 for λ/d < 1000. (e) This can occur due to the growth of larger loops, which (f) facilitates LEF nesting, and thus Brownian ratcheting. Two-sided extrusion data is shown in black in (b-f) for comparison.
Figure 2—figure supplement 4
Models in which the active subunits of nested LEFs can push passive LEF subunits.
(a) Cartoon arch diagrams of ‘weak’ and ‘strong’ pushing models (top two and bottom two panels, respectively). One-sided LEFs are composed of active subunits (yellow) connected to passive subunits (purple); active subunits translocate in the direction indicated by the arrow along the chromatin polymer (gray), shown as a series of discrete sites. In the weak pushing model, an active LEF subunit can only push a single passive LEF subunit. In the strong pushing model, an active LEF subunit can simultaneously push multiple consecutive passive LEF subunits. See Appendix 1 for more details. (b) Fold linear compaction shown for the two-sided model (black), the strong pushing model (gray), and the weak pushing model (brown). Purple and brown dashed lines indicate large λ/d predictions from mean-field theory for one-sided and weak pushing models, respectively. (c) Number of gaps per loop for the two-sided, strong pushing model, and weak pushing models, with the brown dashed line showing the mean-field prediction for the weak pushing model.
Figure 2—figure supplement 5
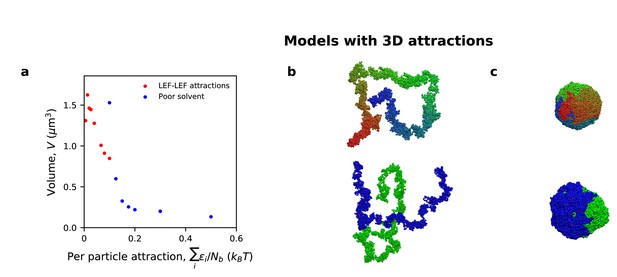
Defective compaction and segregation with 3D attractive interactions.
(a) Volumetric compaction plotted as a function of average attraction energy per monomer, for simulations with LEF-LEF attractive interactions (red) and attractive interactions between all monomers (i.e., poor solvent conditions; blue). (b) Simulation images of chromosome compaction (top) and sister chromatid resolution (bottom) in simulations with LEF-LEF attractions. (c) Simulations images of chromosome compaction (top) and sister chromatid resolution (bottom) in simulations with poor solvent.
Figure 2—figure supplement 6
Fold linear compaction in pure one-sided extrusion models in which LEF residence times are altered by contact with other LEFs.
(a) Fold linear compaction in a model in which blocked one-sided LEFs have a different unbinding rate, kunbind,blocked. A LEF is blocked if it cannot extrude because it has encountered another LEF. Red and pink denote LEFs that unbind more rapidly when blocked; dark blue denotes LEFs that unbind more slowly when blocked. (b) Fold linear compaction in a model in which each (one-sided) LEF has a different unbinding rate, kunbind,adjacent, if it is directly adjacent to another LEF. Dark blue denotes LEFs that unbind more slowly when adjacent to each other. For both panels, light blue is data for pure one-sided extrusion, with kunbind,blocked=kunbind and kunbind,adjacent=kunbind, respectively.
Figure 2—figure supplement 7
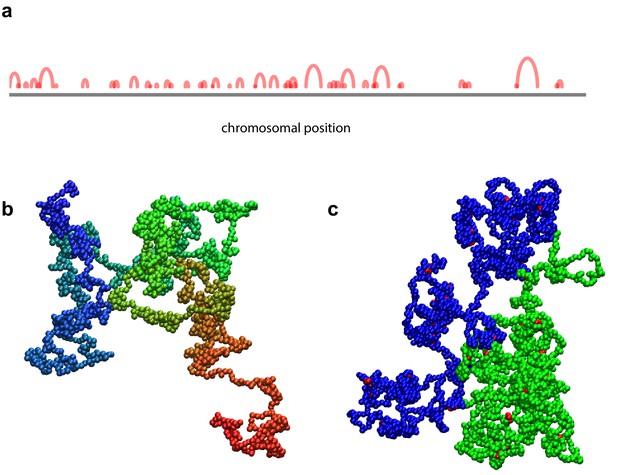
Compaction and resolution of chromosomes with limited loop coverage.
(a) Arch diagram for a 1 Mb yeast chromosome with one-sided loop extruders with 40% loop coverage. (b) 3D polymer simulation image of the same chromosome. (c) Spatial resolution of 1 Mb chromatids with 40% loop coverage.
Figure 3 with 8 supplements
TADs and corner peaks for variations on one-sided loop extrusion.
(a) A TAD in Hi-C of cortical neurons (Bonev et al., 2017), visualized by HiGlass (Kerpedjiev et al., 2018) at a resolution of 8 kb. Two characteristic features of TADs, stripes and dots, are indicated. (b) Contact maps computed from polymer simulations with two-sided (left) and one-sided (right) LEFs. The residence time and density of LEFs have been chosen to approximate the WT conditions (d=λ=200 kb) (Materials and methods and Figure 3—figure supplement 1). (c) Percentage of ungapped TADs for the same LEF separation and processivity as in (b). The percentage of ungapped TADs is computed over 100,000 LEF turnover times, for a system of 20 TADs of size 400 kb, the same size as the largest TAD in the contact maps. The standard error in the mean of the percentage of ungapped TADs is less than 0.05%. (d) Contact maps computed from polymer configurations for the semi-diffusive model, the one-sided model with biased loading, the switching model, and the model with a mix of one- and two-sided LEFs. WT values of d and λ are used for every map. The parameter values, from top to bottom and from left to right, are: vdiff/v = 0.1, 1, and 3.5 (with v = 1 kb/s, D = 0.2, 2, and 7 kb2/s), bias for loading at CTCF = 10, 100, and 1000, kswitch/kunbind = 0.1, 1, and 10 and percentage two-sided = 20, 40, and 60.
Figure 3—figure supplement 1
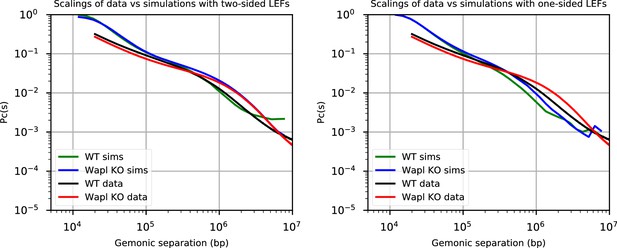
Comparison of the contact probability as a function of genomic separation (scalings) of experiments (Haarhuis et al., 2017) and simulations to validate the chosen parameters for the simulations.
We present simulations for two-sided extrusion (left) and one-sided extrusion (right) for both wild-type (WT) and Wapl depletion conditions. With one monomer = 2 kb, λ = d = 200 kb for WT simulations and λ = 2 Mb and d = 200 kb for Wapl depletion simulations. Since the processivity is given by λ = qv/kunbind, with q = 1 or 2 for one- and two-sided LEFs, respectively (see main text), the unbinding rate, kunbind, for one-sided LEFs is chosen to be half that of two-sided LEFs with the same λ. In Figure 3, we used values of λ and d close to their experimental values in WT (Cattoglio et al., 2019; Fudenberg et al., 2016; Holzmann et al., 2019). In Figure 3—figure supplements 4–7 we also consider sweeps of λ and d, including values that match Wapl depletion conditions.
Figure 3—figure supplement 2
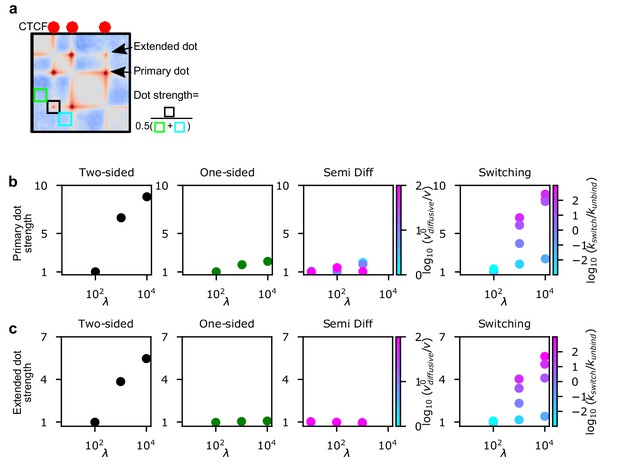
The primary and extended dot strength for two-sided, one-sided, semi-diffusive and switching LEFs.
(a) The definition of dot strength and primary and extended dots. The divergent color scale of the contact map emphasizes that dot strengths are computed on contact maps after computing observed-over-expected (Materials and methods). (b) Strength of primary dots for increasing processivity at a constant LEF separation, d = 200 kb. (c) Strength of extended dots for increasing processivity at a constant LEF separation, d = 200 kb.
Figure 3—figure supplement 3
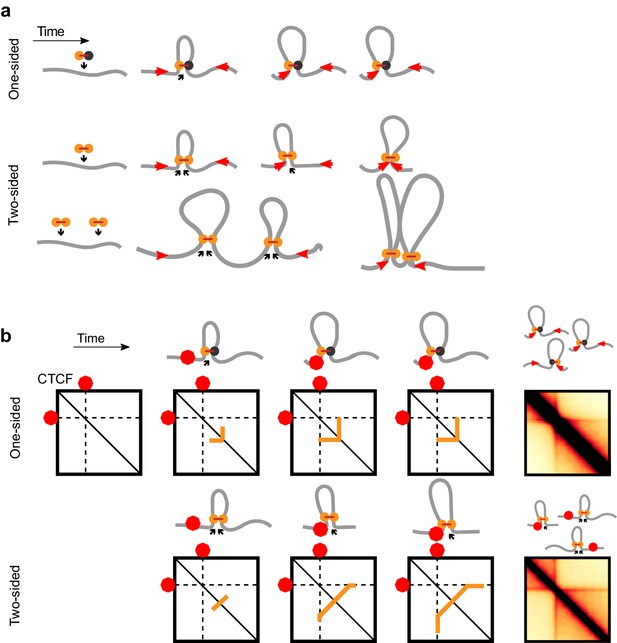
Illustrations of loop extrusion by one-sided and two-sided LEFs.
(a) One-sided LEFs leave a gap between the passive LEF subunit and a barrier, unless they are loaded at a barrier (top row). Two-sided LEFs, on the other hand, can pair barriers while loading between barriers in two possible ways; a single two-sided LEF can pair two barriers (middle row), or barriers can be paired through the collective extrusion of multiple LEFs (bottom row). (b) Illustration of stripe formation by one- and two-sided LEFs.
Figure 3—figure supplement 4
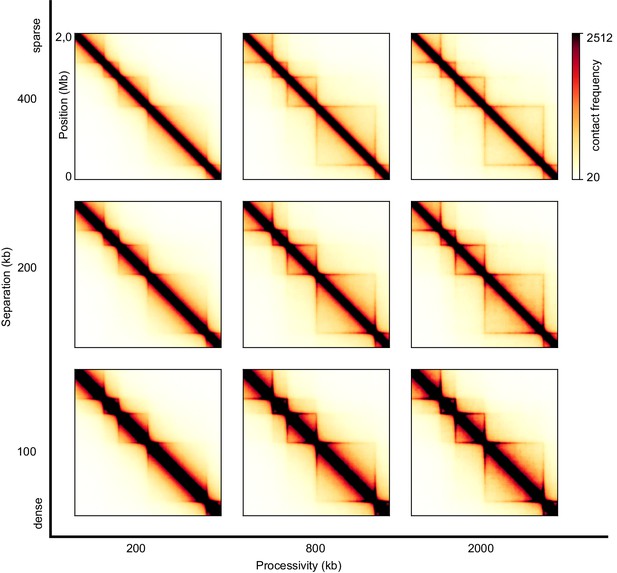
Sweep of the separation between LEFs and the processivity of LEFs for one-sided LEFs.
The TAD sizes from left to right are 200 kb, 400 kb, and 800 kb respectively. A processivity of λ = 200 kb gives scalings that best match wild-type conditions, while a processivity of λ = 2 Mb results in scalings that best match Wapl depletion conditions (Figure 3—figure supplement 1).
Figure 3—figure supplement 5
Sweep of the separation and the processivity of LEFs for two-sided LEFs.
The TAD sizes from left to right are 200 kb, 400 kb, and 800 kb respectively.
Figure 3—figure supplement 6
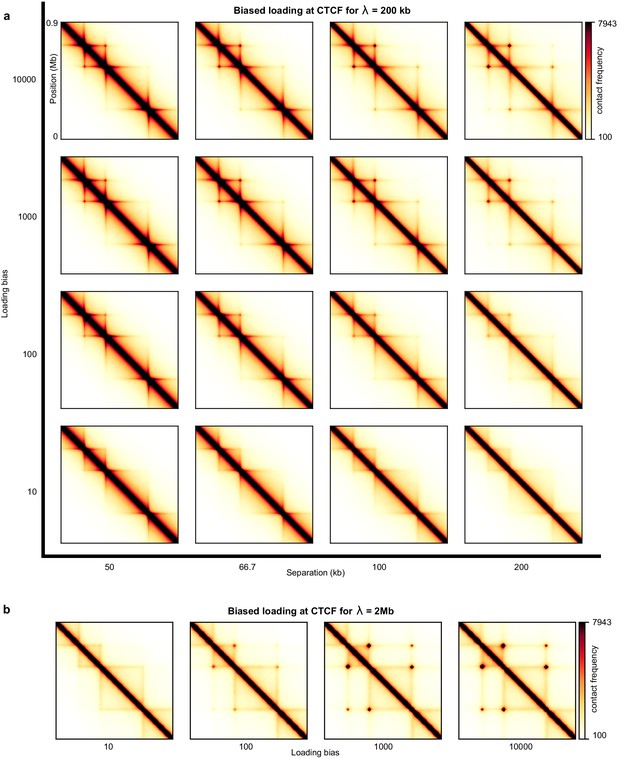
Sweep of the separation and the processivity of LEFs for one-sided LEFs with a loading bias at CTCF sites.
(a) Sweep of the separation between LEFs, d, for one-sided LEFs that load 1000 times more likely at a CTCF site as compared to an arbitrary site within the TAD, where each CTCF site has two loading sites. For the smallest TAD (which consists of 100 monomers, 200 kb), this loading bias implies that at most 95% of all LEFs load at a boundary. For the largest TAD (which has a size of 200 monomers, 400 kb), at most 90% of the LEFs load at a boundary. Note that, once a boundary is occupied, a LEF is forced to load somewhere else, and therefore we only give an upper estimate for the fraction of LEFs loaded at a boundary. The processivity is λ = 200 kb for all panels. (b) Sweep of the loading bias for λ = 2 Mb, d = 200 kb.
Figure 3—figure supplement 7
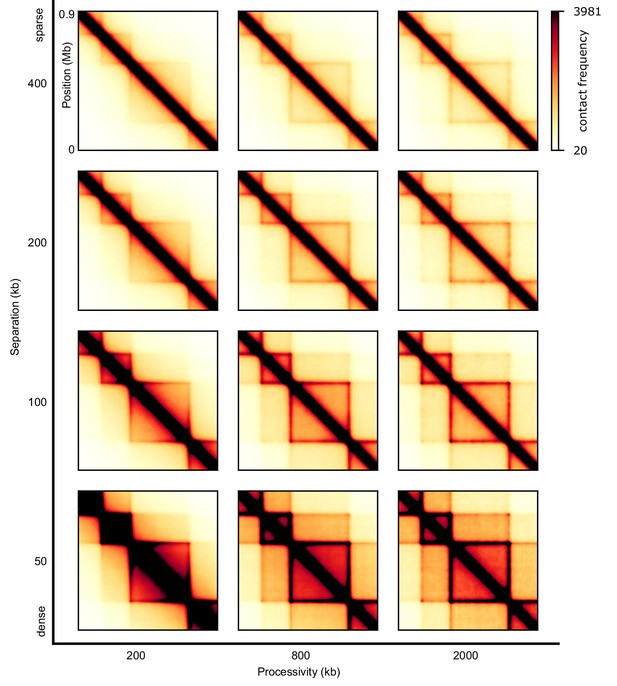
Sweep of the separation and the processivity of LEFs for one-sided LEFs that may traverse each other.
The TADs are 200 kb and 400 kb in size.
Figure 3—figure supplement 8
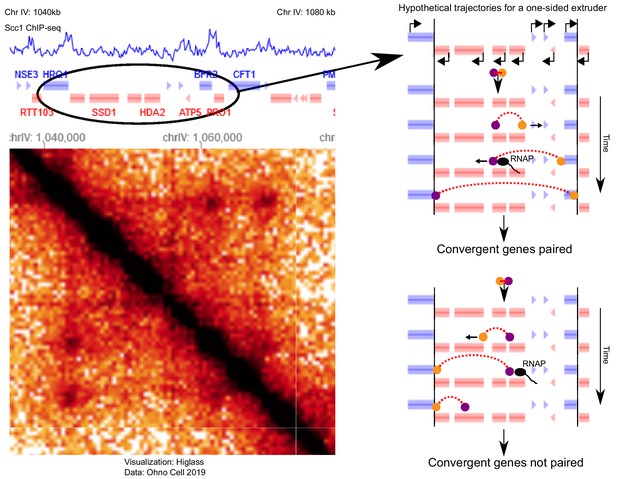
Illustration of how the moving barrier mechanism (Brandão et al., 2019) combined with one-sided LEFs may result in dots in Hi-C of S. cerevisiae.
In the moving barrier model, RNA polymerase (RNAP) can push LEF subunits along chromatin. Left panel: ChIP-seq of the cohesin subunit Scc1 (Hu et al., 2015) and Hi-C (Ohno et al., 2019) in the S phase of S. cerevisiae. The selected region shows two dots between pairs of convergent genes that are enriched by Scc1. Right panels: two hypothetical trajectories for a one-sided LEF combined with the moving barrier mechanism for the region shown on the left. In the top scenario, a one-sided extruder is oriented such that the active subunit (yellow) extrudes to the right pair of convergent genes. The passive subunit (purple) is pushed by RNAP, resulting in 3D pairing of two pairs of convergent genes. Note that we assume that the passive subunit can be pushed across multiple genes; experiments have yet to show that this can actually happen. In the bottom trajectory, the one-sided LEF loads in a different orientation, such that the passive subunit is not pushed in the correct direction, and convergent genes are not paired. Since the orientation of loading of the LEF, as well as the orientation, activity, and density of genes determines whether a one-sided LEF pairs convergent genes, the moving barrier mechanism with one-sided LEFs is less efficient at pairing barriers than two-sided LEFs. However, the moving barrier mechanism may explain dot formation by one-sided LEFs between convergent gene pairs in S. cerevisiae (Dauban et al., 2020; Ohno et al., 2019), and we will discuss this mechanism elsewhere.
Figure 4 with 8 supplements
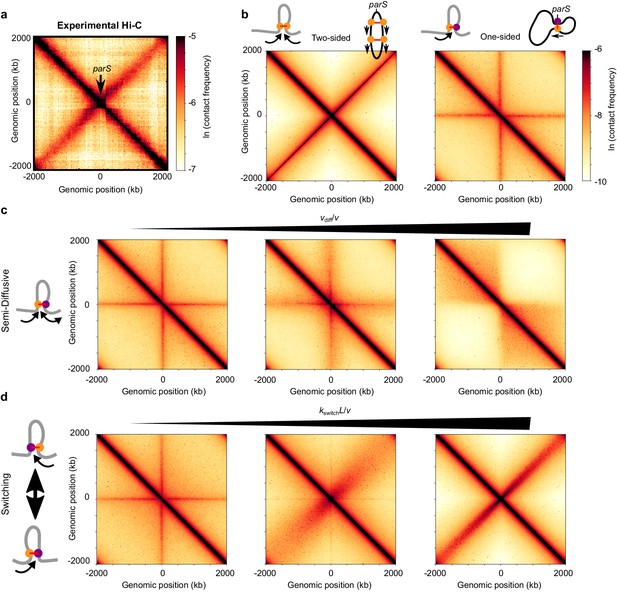
Effect of different extrusion rules on bacterial contact maps.
(a) Experimental Hi-C map for B. subtilis with a single parS site (SMC complex loading site) near the ori in the strain BDR2996 from Wang et al. (2015). Simulations of (b) the pure two-sided model (left map, and schematic of a single two-sided LEF and a chromosome extruded by two-sided LEFs) and the pure one-sided model (right map and schematic). (c) Simulations of the semi-diffusive model (with diffusive stepping rates, from left to right, of vdiff/v = 0.005, 0.1, and 3.5 (D = 0.005, 0.1, and 3.5 kb2/s with v = 1 kb/s)), and (d) the switching model (with switching rates, from left to right, of kswitchL/v = 4, 40, and 400, or kswitch = 0.001, 0.01, and 0.1 s−1, respectively). All simulations displayed were performed with N = 5 LEFs per chromosome.
Figure 4—figure supplement 1
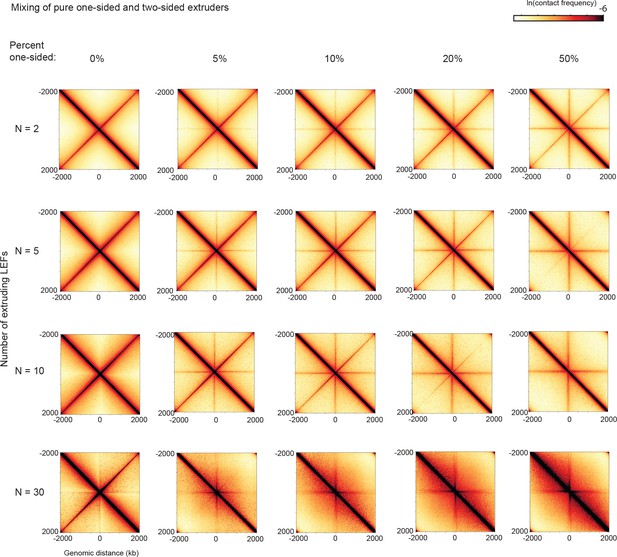
Contact maps from simulations for different mixes of one- and two-sided LEFs and numbers of LEFs for bacterial chromosomes.
The fraction of one-sided LEFs increases from left to right, with 0% indicating the case of pure two-sided extrusion. The number of LEFs increases from top to bottom. Note that in these simulations, each LEF is randomly designated as either one- or two-sided each time it is loaded onto the chromosome.
Figure 4—figure supplement 2
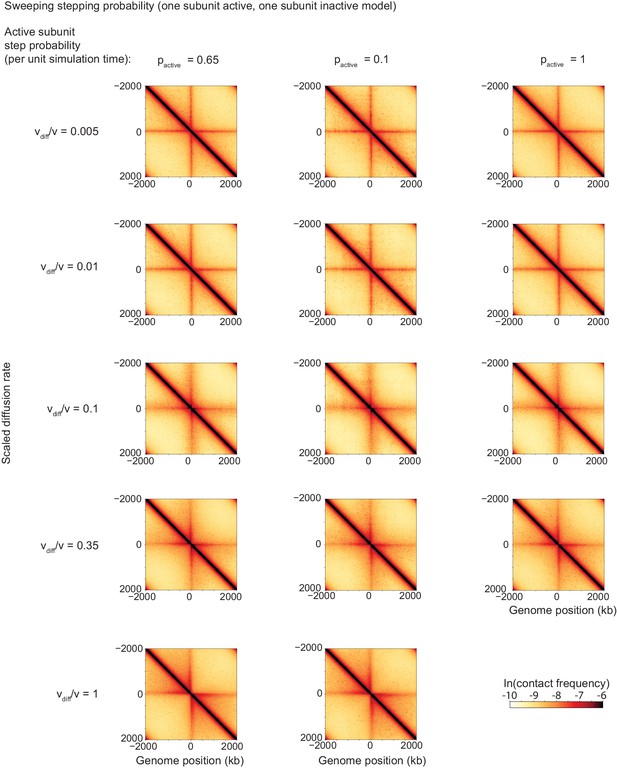
Contact maps from simulations for different values of the LEF stepping probability (per simulation step), with N = 5 LEFs on each chromosome.
These results indicate that the scaled diffusion rate, vdiff/v is the invariant quantity giving the contact maps their shape in the case of the model of a semi-diffusive LEF.
Figure 4—figure supplement 3
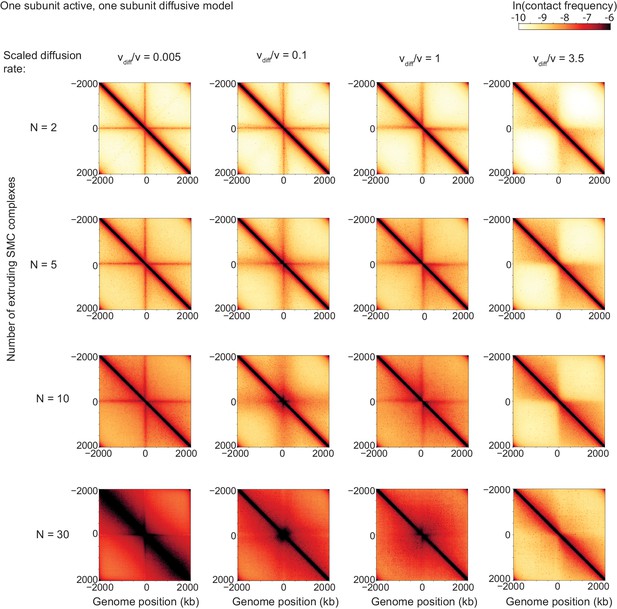
Sweep of the diffusive stepping rate and the number of LEFs for bacterial chromosomes.
Scaled diffusive stepping rate increases from left to right, and number of LEFs (i.e. extruding SMC complexes) increases from top to bottom.
Figure 4—figure supplement 4
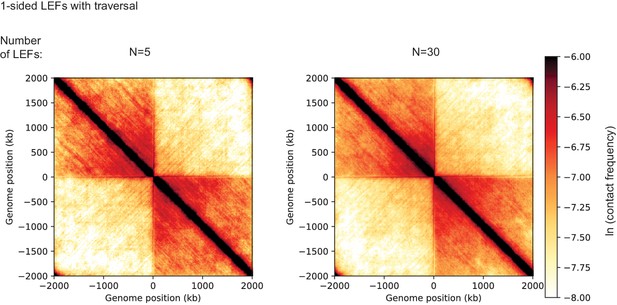
Contact maps from 3D polymer simulations of an extrusion model in which LEFs may traverse each other and may occupy the same lattice sites.
Polymer simulations were performed as described in Appendix 3. Maps result form 10,000 different conformations of the bacterial chromosome polymer, with contacts captured with a radius of 6 monomer units (i.e., approximately 90 nm). These simulations demonstrate that one-sided LEFs with traversal do not reproduce the juxtaposition of bacterial chromosome arms observed in B. subtilis.
Figure 4—figure supplement 5
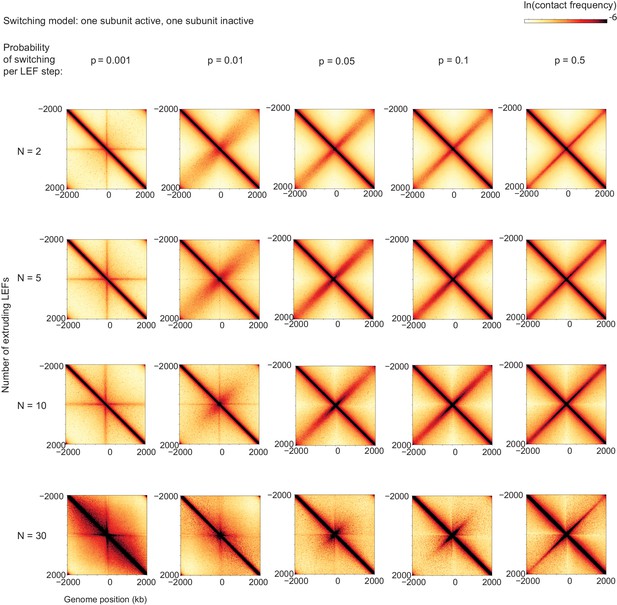
Contact maps from simulations for scaled switching rates and numbers of LEFs for bacterial chromosomes.
Switching probability per active translocation step increases from left to right and number of LEFs increases from top to bottom. Note that switching probabilities are given in simulation step units; from left to right, these correspond to units of of 4, 40, 200, 400, 2000; in units of switching rate, , from left to right these correspond to 0.001 s−1, 0.01 s−1, 0.05 s−1, 0.1 s−1 and 0.5 s−1 for B. subtilis.
Figure 4—figure supplement 6
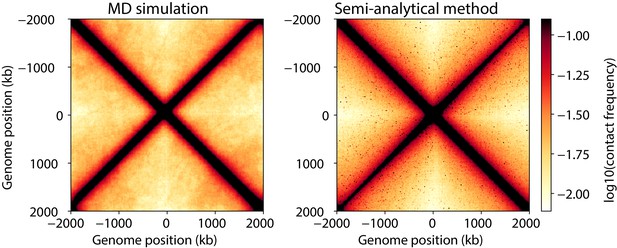
Contact maps generated from molecular dynamics simulations as compared to the semi-analytical method.
Figure 4—figure supplement 7
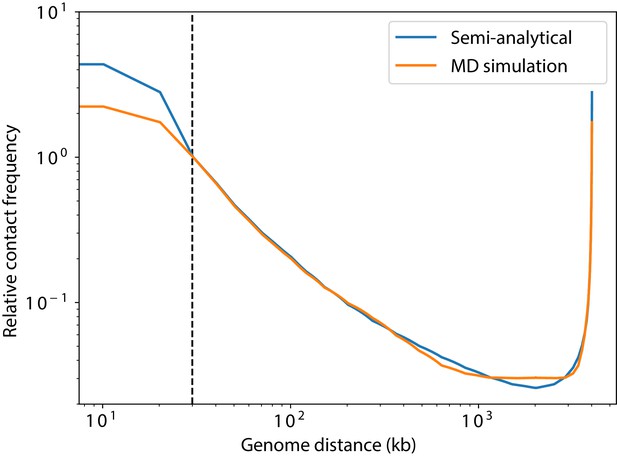
Contact probability as a function of genomic distance generated from molecular dynamics simulations as compared to the semi-analytical method.
Data from molecular dynamics (MD) simulations is shown in orange, while the contact probability calculated from the semi-analytical method is shown in blue.
Figure 4—figure supplement 8
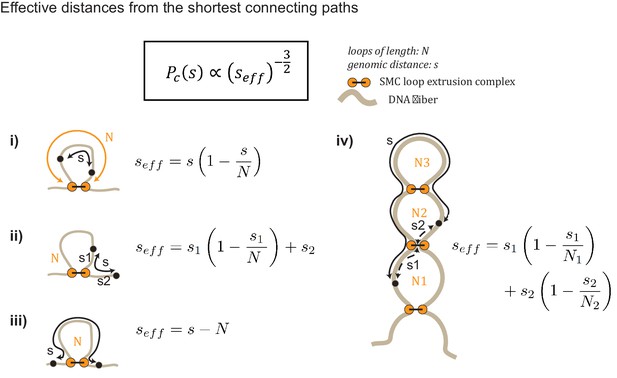
Generating Gaussian chain contact maps analytically from loop configurations.
The contact probability Pc(s) is calculated by converting the true genomic distance, s, to its effective genomic distance seff. For example, in (i), the effective genomic distance is simply harmonic mean distance between the two paths in a loop (i.e., seff=(1/s+1/(N–s))−1 = s(1 - s/N)). Diagrams (i)-(iv) schematically illustrate the types of transformations used to calculate contact probability given a loop diagram.
Tables
Table 1
Summary of model results.
Each entry indicates whether there are parameters for the specified model (column headings) that can explain chromosome organization in the specified scenario (row headings). A dash indicates that the model/scenario combination was not explored. *Indicates theoretical result from Banigan and Mirny, 2019.
| Pure 1-sided | 2- sided | 1-sided + 2-sided mix | Semi- diffusive | 1-sided + loading bias | Switching | 1-sided with traversal | 1-sided + 3D attraction | |
|---|---|---|---|---|---|---|---|---|
| Mitosis | No | Yes | Yes with > 80% 2-sided | No | Yes with > 1000 fold bias* | Yes with kswitch/kunbind > 10 | Yes | No |
| Interphase | No | Yes | Yes with > 50% 2-sided | No | Yes with > 100 fold bias | Yes with kswitch/kunbind > 10 | Yes for d ≤ 50 kb or λ > 2 Mb | No** |
| Bacteria | No | Yes | No | No | No | Yes with kswitchL/v > 200 | No | - |
-
**Indicates inferred from simulation results of Fudenberg et al., 2016.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Chromosome organization by one-sided and two-sided loop extrusion
eLife 9:e53558.
https://doi.org/10.7554/eLife.53558
