1. Computational and Systems Biology

Neural arbitration between social and individual learning systems

  1. Andreea Oliviana Diaconescu  Is a corresponding author
  2. Madeline Stecy
  3. Lars Kasper
  4. Christopher J Burke
  5. Zoltan Nagy
  6. Christoph Mathys
  7. Philippe N Tobler
  1. Translational Neuromodeling Unit, Institute for Biomedical Engineering, University of Zurich & ETH Zurich, Switzerland
  2. Laboratory for Social and Neural Systems Research, Department of Economics, University of Zurich, Switzerland
  3. University of Basel, Department of Psychiatry (UPK), Switzerland
  4. Krembil Centre for Neuroinformatics, Centre for Addiction and Mental Health (CAMH), University of Toronto, Canada
  5. Rutgers Robert Wood Johnson Medical School, United States
  6. Institute for Biomedical Engineering, MRI Technology Group, ETH Zürich & University of Zurich, Switzerland
  7. Interacting Minds Centre, Aarhus University, Denmark
  8. Scuola Internazionale Superiore di Studi Avanzati (SISSA), Italy
https://doi.org/10.7554/eLife.54051
Share this article
Cite this article
  1. Andreea Oliviana Diaconescu
  2. Madeline Stecy
  3. Lars Kasper
  4. Christopher J Burke
  5. Zoltan Nagy
  6. Christoph Mathys
  7. Philippe N Tobler
(2020)
Neural arbitration between social and individual learning systems
eLife 9:e54051.
https://doi.org/10.7554/eLife.54051
  2. Download BibTeX
  3. Download .RIS
11 figures, 7 tables and 2 additional files

Figures

Figure 1 with 2 supplements
Download asset Open asset
Experimental paradigm.

(a) Binary lottery game requiring arbitration between individual experience and social information. Volunteers predicted the outcome of a binary lottery, that is whether a blue or green card would be drawn. They could base predictions on two sources of information: advice from a gender-matched advisor (video, presented for 2 s) who was better informed about the color of the drawn card, and on an estimate about the statistical likelihood of the cards being one or the other color that the participant had to infer from own experience (outcome, 1 s). After predicting the color of the rewarded lottery card (user-controlled, maximum 3 s), participants also wagered one to ten points (user-controlled, maximum 6 s), which they would win or lose depending on whether the prediction was right or wrong. After the outcome, participants viewed their cumulative score on the feedback screen (1 s). (b) Contingencies of individual reward and social advice information: Card color probability corresponds to the likelihood of a given color (e.g. blue) being rewarded. The probabilities were matched on average for the two information sources (55% for the card color information and 56% for the advice information). Additionally, the two sources of information were uncorrelated as illustrated by phases of low (yellow) and high (light grey) volatility, enabling a factorial analysis of information source and volatility.

Figure 1—figure supplement 1
Download asset Open asset
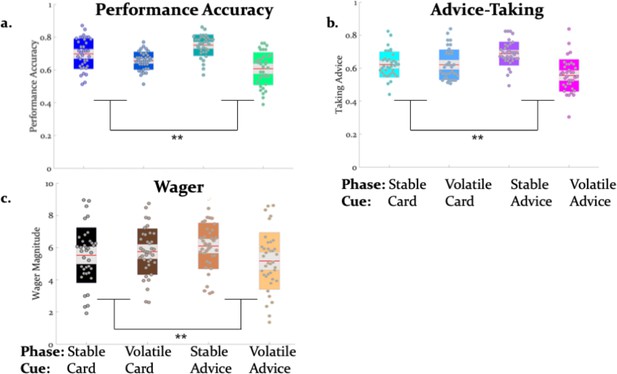
Behavior influenced by volatility.

Average lottery prediction accuracy (a), decisions to take the advice (b), and amount of points wagered per trial (c) were reduced during volatile phases of the paradigm, particularly with regard to social information. The average values across all trials were 68.2 ± 6.2% (mean accuracy ± standard deviation) lottery prediction accuracy, 62.1 ± 6.9% advice-taking, and 5.6 ± 1.5 points wagered (participants on average accumulated 378.6 ± 173.2 points). Jittered raw data (i.e., means over all trials of each behavioral measure per subject) are plotted for each behavioral measure. Red lines indicate the mean, grey areas reflect 1 SD of the mean, and colored areas the 95% confidence intervals of the mean. **p<0.001 is indicated to emphasize the phase ×cue interactions.

Figure 1—figure supplement 2
Download asset Open asset
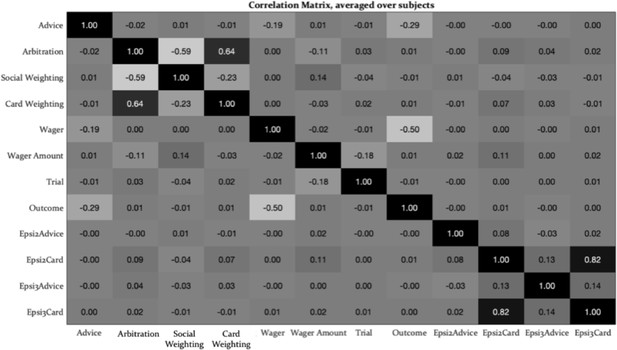
|Average pairwise correlations between regressors.

Using the Fisher-transformation, we computed averages of the pairwise correlations between regressors. Overall, the correlations between time periods and between parametric modulators were small to moderate, with the exception of the correlation between second- and third-level precision-weighted prediction errors about the card color outcome (Epsi2Card with Epsi3Card).

Figure 2 with 1 supplement
Download asset Open asset
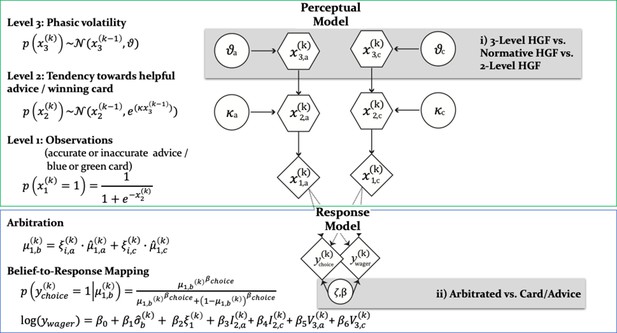
Computational learning and arbitration model.

In this graphical notation, circles represent constants whereas hexagons and diamonds represent quantities that change in time (i.e. that carry a time/trial index). Hexagons in contrast to diamonds additionally depend on the previous state in time in a Markovian fashion. The two-branch HGF describes the generative model for advice and card probability: x1 represents the accuracy of the current advice/card color probability, x2 the tendency of the advisor to offer helpful advice tendency of card color to be rewarded, and x3 the current volatility of the advisor’s intentions/card color probabilities. Learning parameters describe how the states evolve in time. Parameter κ determines how strongly x2 and x3 are coupled, and ϑ represents the meta-volatility of x3. The response model maps the predicted color probabilities to choices. The response model also assumes that trial-wise wagers and predictions arise from a linear combination of arbitration, informational uncertainty (advice and card), and volatility (advice and card). For model selection, we combined three perception with three response models (see Figure 3). All the models considered can be grouped according to common features and divided into model families: (i) the Perceptual model families distinguish between more (non-normative and normative three-level) and less (two-level) complex types of HGFs. More specifically, the distinction between three-level and two-level HGFs refers to estimating or fixing the volatility of the third level; normative in contrast to non-normative HGFs assume optimal Bayesian inference. (ii) Response model families distinguish between arbitrated and single-information source – advice or card only – models, which correspond to estimating parameter ϑ or fixing it to reduce arbitration to either the advice prediction or the card color prediction.

Figure 2—figure supplement 1
Download asset Open asset
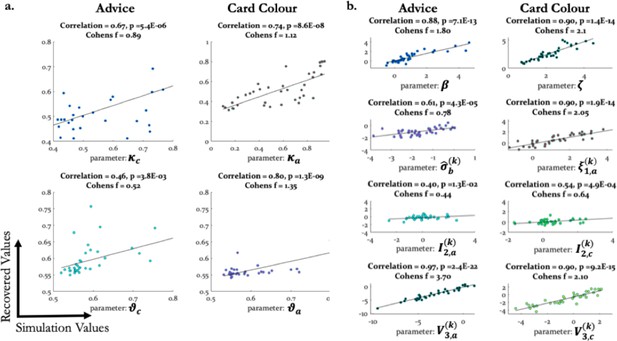
Parameter recovery when using empirical parameter values (Binary HGF).

Parameter recovery for perceptual (a) and response model parameters (b). The correlation coefficients (with corresponding p-values) and Cohen’s f values are included to quantify and compare parameter recovery results across all estimated parameters of the model. We saved the seed of the random number generator to ensure reproducibility of the results.

Figure 3
Download asset Open asset
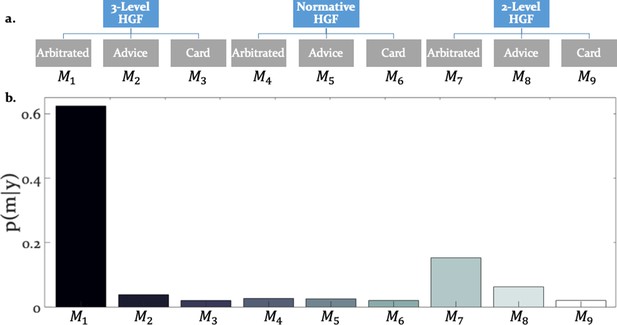
Hierarchical structure of the model space and model selection results.

(a) The learning and arbitration models considered in this study have a 3 × 3 factorial structure and can be displayed as a tree. The nodes at the top level represent the perceptual model families (three-level HGF, normative HGF, two-level non-volatility HGF). The leaves at the bottom represent response models which integrate and arbitrate between social and individual sources of information (‘Arbitrated’) or exclusively consider social (‘Advice’) or individual (‘Card’) information. (b) Random effects Bayesian model selection revealed one winning model, the Arbitrated three-level HGF. Posterior model probabilities or p(m|y) indicated that this model best explained participants’ behavior in the majority of the cases.

Figure 4
Download asset Open asset
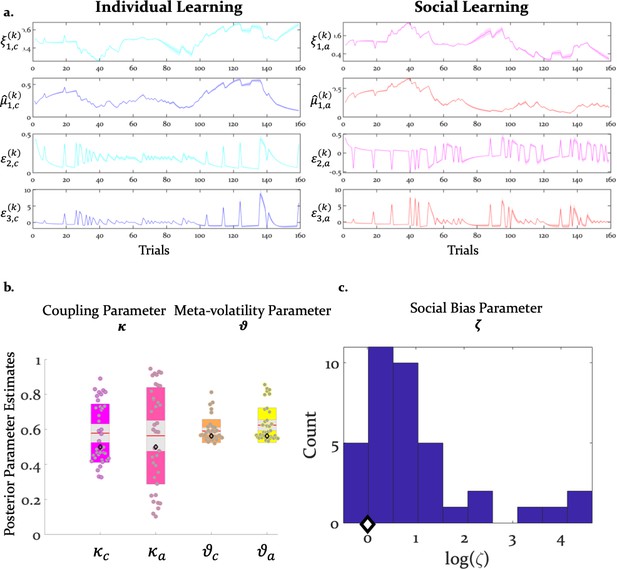
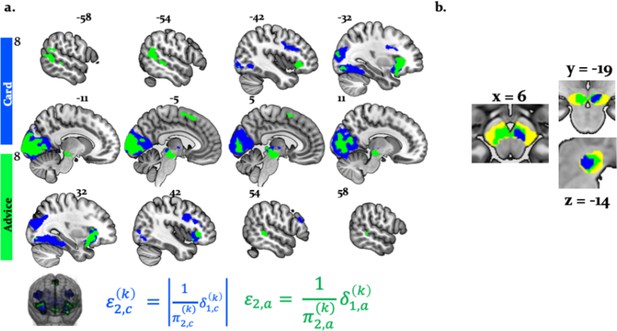
Inference and arbitration of individual and social learning.

(a) Average trajectories for arbitration and hierarchical precision-weighted PEs for individual and social learning (see Materials and methods for the exact equations): ξa = arbitration in favor of the advice (Equation 19); ξc = arbitration in favor of individually estimated card color probability (Equation 20). μ^1,a = estimated advice accuracy (Equation 4); μ^1,c = individually estimated card color probability (Equation 18). ε2,a = precision-weighted prediction error (PE) of advisor fidelity (Equation 8); ε2,c = unsigned (absolute) precision-weighted PE of card outcome (absolute value of Equation 14). ε3,a = precision-weighted advice volatility PE (Equation 13); ε3,c = precision-weighted card color volatility PE (Equation 15). Line plots were generated by averaging the computational trajectories of the winning (Arbitrated 3-HGF: Figure 2) model across all participants for each of the 160 trials. The shaded area around each line depicts +/- standard error of the mean over participants. (b) Group means, standard deviations and prior values for the perceptual model parameters determining dynamics of computational trajectories in (a). Jittered participant-specific estimates are plotted for each perceptual model parameter, red lines indicate the group mean, grey areas reflect 1 SD of the mean, and colored areas the 95% confidence intervals of the mean. (c) Distribution of log(ζ) values. In (b) and (c), black diamonds denote the priors of each parameter (for details, see Table 2).

Figure 5 with 1 supplement
Download asset Open asset
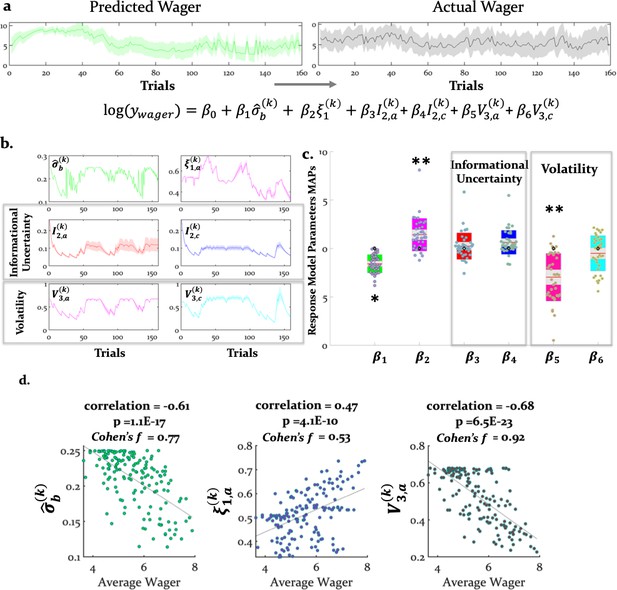
Computational quantities and model parameters explaining wager amount.

(a) With our response model, we predicted that the actual trial-wise wager (right) could be explained (left and bottom) by the six key trajectories (see Equation 21) given in (b). These include (i) (irreducible) belief uncertainty (based on the integrated belief of individual and advice predictions; Equation 24); (ii) arbitration in favour of advice (Equation 19); (iii) informational uncertainty (Equation 25) and volatility of the advice (Equation 26) and (iv) informational uncertainty and volatility of the card (same Equations 25 and 26, but for the card modality). (a) and (b) show group averages (see Materials and methods for the exact equations). For the model-based parameters, the line plots were generated by averaging the computational trajectories of the winning (Arbitrated 3-HGF: Figure 2) model across all participants for each of the 160 trials. The shaded areas depict +/- standard error of this mean over participants. (c) Group means, standard deviations and prior values for the response model parameters determining the impact of those trajectories (i.e. uncertainties and arbitration) on trial-wise wager amount. Jittered raw data are plotted for each parameter. Red lines indicate the mean, grey areas reflect 1 SD from the mean, and the colored areas the 95% confidence intervals of the mean. The black diamonds denote the prior of the parameters, which in this case is zero. *p<0.05, **p <0.001. (d) Scatter plots with average actual wager on the x-axis and average of the computational variables assumed to impact the trial-wise wager: belief uncertainty, arbitration in favor of advice, and volatility of advice on the y-axes, respectively. The correlation coefficients (with corresponding p values), regression slopes, and effect sizes (Cohen’s f) are included to quantify the relationship between the actual wager and the computational quantities that showed a significant relation to wagers.

Figure 5—figure supplement 1
Download asset Open asset
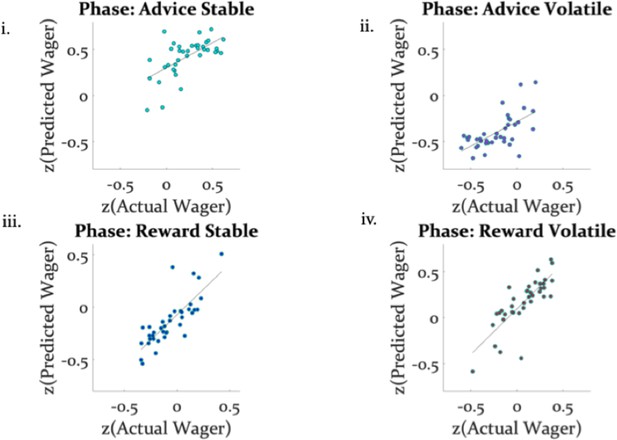
Model validity with regard to wager amount.

The z-transformed wager amount predicted by the model strongly correlated with the z-transformed number of points participants actually wagered across all four conditions of the task ((i) r1 = 0.62, p1  = 3e-05; (ii) r2 = 0.63, p2  = 2e-05; (iii) r3 = 0.81, p4  = 9e-10; (iv) r4 = 0.80, p4  = 1e-09). The regression line is plotted to illustrate the relationship between the actual and predicted wagers.

Figure 6 with 2 supplements
Download asset Open asset
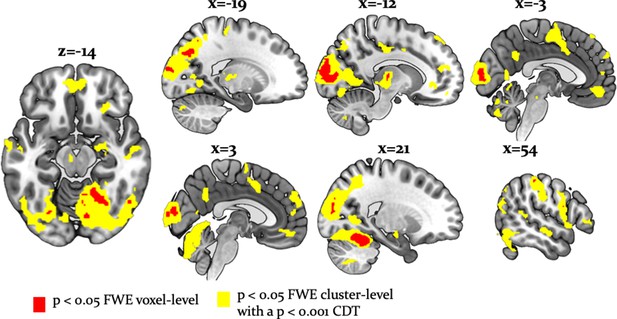
Whole-brain undirected arbitration signals.

Effects of arbitration in favor of one or the other source of information were detected in ventromedial PFC, orbitofrontal cortex, right frontopolar cortex, VLPFC, the left midbrain, bilateral fusiform gyrus, lateral occipital gyrus, lingual gyrus, anterior insula, right amygdala, left thalamus, right cerebellum, bilateral middle cingulate sulcus and SMA. The figure shows whole-brain FWE-corrected voxel (red) - and cluster-level-corrected (yellow) results of an undirected F-test, p<0.05 (CDT = cluster defining voxel-level threshold).

Figure 6—figure supplement 1
Download asset Open asset
Main effects of precision-weighted PEs about card and advice outcomes (Equations 8 and 14).

(a) Whole-brain activation by ε2: Activations by unsigned precision-weighted PE about the card probabilities (blue) were detected in the bilateral inferior/middle occipital gyri, anterior insula, bilateral inferior, medial and middle frontal gyri, and the bilateral intraparietal sulcus (whole-brain FWE peak- and cluster-level corrected, p<0.05). Activations by signed precision-weighted PE about the adviser fidelity (green) were observed in the bilateral fusiform gyrus, lingual gyrus, anterior insula, bilateral supplementary motor area, left middle temporal cortex, right posterior supior temporal sulcus, temporal-parietal junction, bilateral dorsolateral and left dorsomedial prefrontal cortex (whole-brain FWE peak- and cluster-level corrected, p<0.05). (b) Activation of the right VTA was associated with the unsigned precision-weighted PE about the card probabilities (blue) and activation of bilateral VTA/SN associated with the signed precision-weighted prediction error about the adviser fidelity (green). This activation is shown at p<0.05 FWE corrected for the volume of our anatomical mask comprising dopaminergic nuclei (yellow).

Figure 6—figure supplement 2
Download asset Open asset
Main effects of precision-weighted PEs about card and advice volatility.

(a) Whole-brain activation by ε3:  Whole-brain activations by signed precision-weighted volatility PEs about the card probabilities (blue) were detected in the right superior temporal gyrus, supramarginal gyrus, and posterior insula. Whole-brain activations by signed precision-weighted volatility PEs about the adviser fidelity (green) were detected in the right anterior SMA and anterior insula (whole-brain FWE cluster-level corrected, p<0.05). (b) Whole-brain activation by ε3. in the PPT/LDT nuclei: Activation of the right cholinergic PPT/LDT associated with the signed precision-weighted volatility prediction error about the adviser fidelity is shown at p<0.05 FWE corrected for the volume of our anatomical mask comprising cholinergic nuclei (yellow).

Figure 7 with 1 supplement
Download asset Open asset
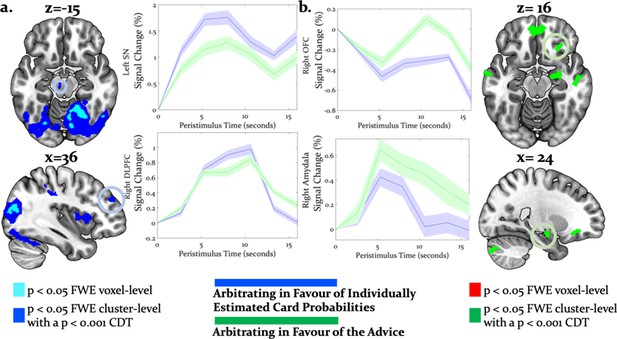
Neural arbitration directed to specific source of information.

(a) Activity in the left midbrain (substantia nigra (SN)) [−6,–18, −10] (top) and the right DLPFC [36, 46, 30] (bottom) during the prediction of card color increased more when participants arbitrated in favor of individually estimated card color probability as compared to the advisor’s suggestions (whole-brain FWE cluster-level corrected, p<0.05). (b) Activity in right (OFC [28, 26, -16] (top) and in right amygdala [18, -10, -16] (bottom) increased more when participants arbitrated in favor of the advisor’s suggestion than when they arbitrated in favor of the individually learned estimates of card probability (whole-brain FWE cluster-level corrected, p<0.05). The line plots reflect the average BOLD signal activity in the respective significantly activated cluster aligned to the onset of advice presentation relative to pre-advice baseline averaged across trials for one representative participant in midbrain and DLPFC (a) or OFC and amygdala (b). The shaded areas depict + / - standard error of this mean. In this figure, the scales reflect t-values.

Figure 7—figure supplement 1
Download asset Open asset
Social versus non-social weighting (Equation 21).

Whole-brain activations by non-social weighting (one’s individual predictions about the card color outcome) compared to social weighting were detected in bilateral cerebellum, occipital cortices (lingual gyrus, superior occipital cortex), left anterior cingulate sulcus, right supramarginal gyrus, and left postcentral gyrus (blue). Conversely, activation by social weighting was significantly larger in the subgenual ACC (green) (whole-brain FWE cluster-level corrected, p<0.05).

Figure 8 with 1 supplement
Download asset Open asset
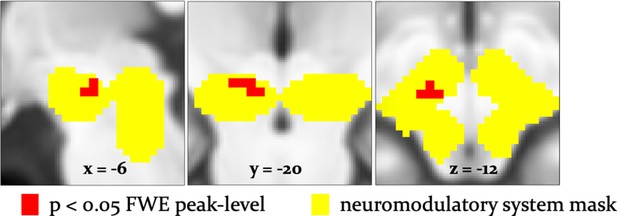
Arbitration signals in neuromodulatory ROI.

Activation of the dopaminergic midbrain was associated with arbitrating in favor of individually learned information. Activation (red) is shown at p<0.05 FWE corrected for the full anatomical ROI comprising dopaminergic, cholinergic, and noradrenergic nuclei (yellow).

Figure 8—figure supplement 1
Download asset Open asset
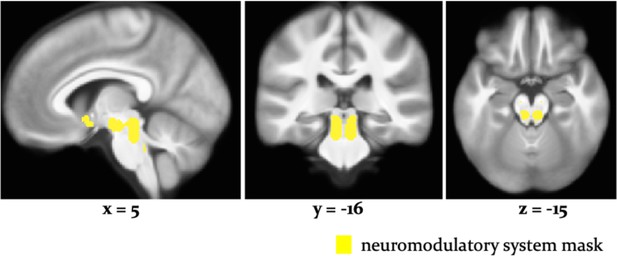
Neuromodulatory nuclei anatomical mask.

The mask for ROI analyses included (i) the dopaminergic midbrain (substantia nigra, SN, and ventral tegmental area, VTA), (ii) the cholinergic basal forebrain, (iii) cholinergic nuclei in the tegmentum of the brainstem, that is, the pedunculopontine tegmental (PPT) and laterodorsal tegmental (LDT) nuclei, and (iv) the noradrenergic locus coeruleus (LC).

Figure 9
Download asset Open asset
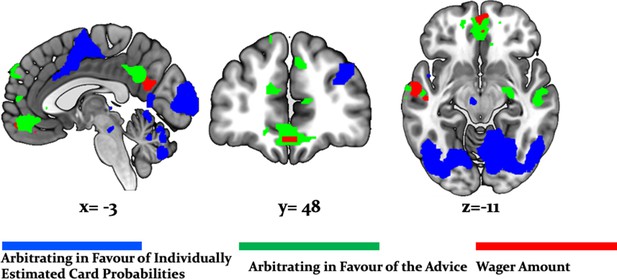
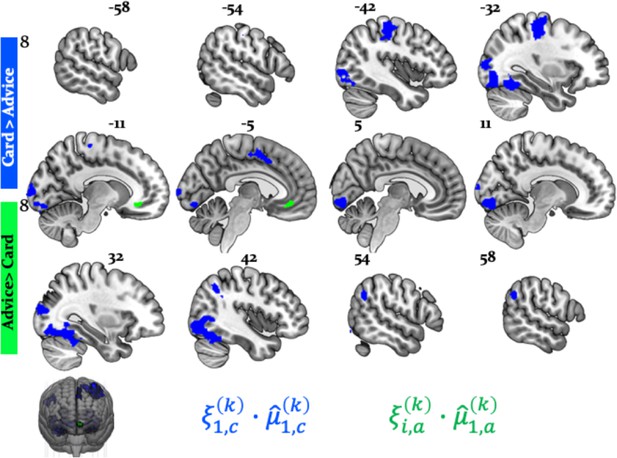
Arbitration vs. Wager Amount.

Effects of arbitration (individual) (blue) were significantly larger in cortical and subcortical brain regions when compared to wager amount. Effects of arbitration in favor of social information were also significantly larger in ventromedial PFC and amygdala when compared to wager amount (green). Activity in precuneus and ventromedial PFC regions increased with increases in wager amount (magenta) (whole-brain FWE cluster-level corrected, p<0.05).

Figure 10
Download asset Open asset
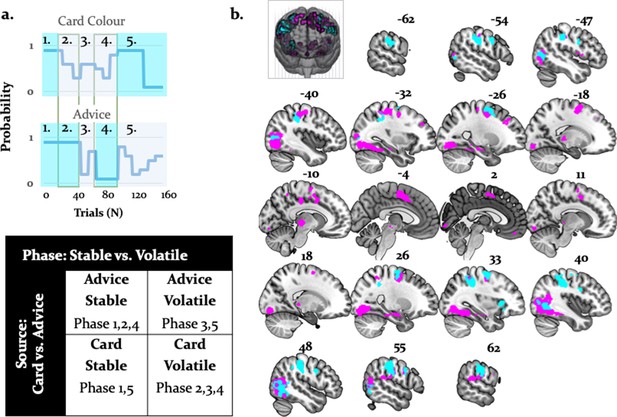
Activations related to task phase and interaction with source of information.

(a) The task mapped onto a factorial structure with four conditions: (i) stable card and stable advisor, (ii) stable card and volatile advisor, (iii) volatile card and stable advisor, and (iv) volatile card and volatile advisor, as reflected by the shaded areas: blue (stable), grey (volatile). (b) The main effect of stability irrespective of source of information activated primarily parietal regions and the anterior insula (cyan, whole-brain FWE cluster-level corrected, p<0.05). Moreover, the interaction between task phase and source of information was localized to left midbrain, occipital regions, anterior insula, thalamus, middle cingulate sulcus, SMA, OFC, and VLPFC (magenta, whole-brain FWE cluster-level corrected, p<0.05).

Figure 11
Download asset Open asset
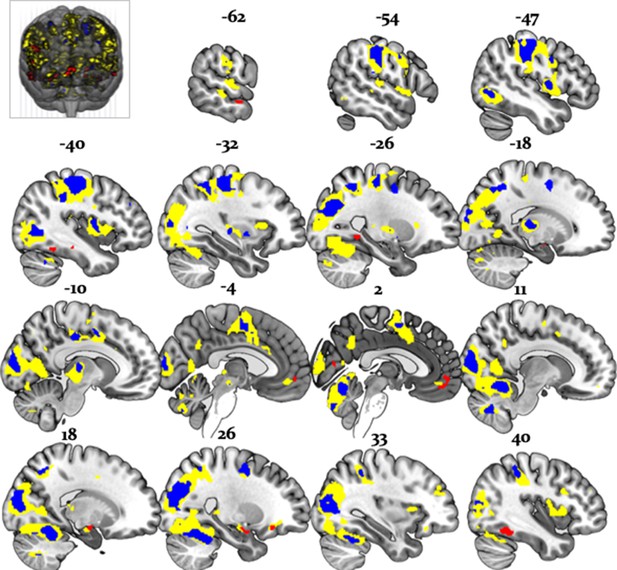
Overlap between model-dependent and model-independent results.

Arbitration signal (Equation 19) (yellow) overlapped with the regions showing an enhanced effect of stability for individual compared to social learning systems (blue) and regions showing enhanced effects of stability in the social compared to individual learning systems (red) (whole-brain FWE peak-level corrected, p<0.05).

Tables

Table 1
(a) Results of Bayesian model selection: Model probability (p(m|y)) and protected exceedance probabilities (ϕp).

Please refer to the participants’ LME and BMS results in Table 1—source datas 1 and 2, respectively. (b) Average maximum a-posteriori estimates of the learning and arbitration parameters of the winning model (Arbitrated three-level HGF). Please refer to participants’ individual posterior parameter estimates for perceptual and response model parameters in Table 1—source datas 3 and 4.

Perceptual Models:
Response models:ArbitratedAdvice OnlyCard Only
3-level HGF
p(m|y)0.630.040.02
ϕp0.994.7e-124.7e-12
Normative HGF
p(m|y)0.030.030.02
ϕp4.7e-124.7e-124.7e-12
2-level HGF
p(m|y)0.150.060.02
ϕp6.2e-054.7e-124.7e-12
Perceptual Model
Parameters		MeanSDResponse Model
Parameters		MeanSD
κc0.580.17ζ1.031.24
κa0.560.28β1−1.590.94
ϑc0.590.07β21.421.69
ϑa0.620.09β30.231.37
β40.631.24
β5−2.972.47
β6−0.511.83
βch2.250.92
Table 1—source data 1

Log model evidences for all models.

https://cdn.elifesciences.org/articles/54051/elife-54051-table1-data1-v2.mat
Table 1—source data 2

Random effects Bayesian model selection.

https://cdn.elifesciences.org/articles/54051/elife-54051-table1-data2-v2.mat
Table 1—source data 3

Maximum a posteriori estimates of the perceptual model parameters and response model parameters influencing choice along with subject IDs.

https://cdn.elifesciences.org/articles/54051/elife-54051-table1-data3-v2.mat
Table 1—source data 4

Maximum a posteriori estimates of the response model parameters influencing wagers along with subject IDs.

https://cdn.elifesciences.org/articles/54051/elife-54051-table1-data4-v2.mat
Table 2
Prior mean and variance of the perceptual and response model parameters.
ModelPrior meanPrior variance
Perceptual models:
Three-level HGFκa, κc0.51
ϑa, ϑc0.551
Normative HGFκa, κc0.50
ϑa, ϑc0.550
Two-level HGFϑa, ϑc0.000620
Response models:
β1−604
βch481
β06.214
βwager1.50100
1. Arbitratedζ025
2. Advice OnlyζInf0
3. Card Onlyζ00

  1. Note: The prior variances are given in the numeric space in which parameters are estimated. κ, ϑ, and μ3(k=0) are estimated in logit-space, while the other parameters are estimated in log-space. Although the prior variances for all parameters are set to be rather broad, we selected a shrinkage prior mean and variance for the decision noise parameter βch such that behavior is explained more by variations in the remaining parameters rather than decision noise.

Table 3
MNI coordinates and F-statistic of maxima of activations induced by either form of arbitration (Equations 19-20; p<0.05, cluster-level whole-brain FWE corrected).

Related to Figure 7.

HemisphereXYZ# VoxelsF-statistic
ξ(k)
MidbrainL-6−18−122023.49
ThalamusL−12−18849059.87
Anterior insulaL−4420174452.97
Anterior insulaR486-281331.56
Fusiform gyrusR28−78−10132775.32
Fusiform gyrusL−28−76−1022739.55
Inferior occipital gyrusR48−68−1081052.70
Inferior occipital gyrusL−42−68-4151967.56
Calcarine sulcusR12−86622285199.99
Superior temporal gyrusL−60−30-27924.02
Superior temporal sulcusR52−18-810430.35
AmygdalaR18−10−167627.01
PrecuneusR4−523023838.50
Dorsal medial PFCL−10445210823.14
Superior medial PFCR4562849339.83
Ventrolateral PFCR5036020224.28
Frontopolar cortexR4543013824.28
Orbitofrontal cortexR2634−108030.47
Ventromedial PFCL-246−1039337.43
Supramarginal gyrusR54−305046.46952
CerebellumR18−48−181919166.69
Table 4
MNI coordinates and t-statistic of maxima of activations induced by arbitration for the individually estimated card reward probability (Equation 20; p<0.05, cluster-level whole-brain corrected).

Related to Figure 8a.

HemisphereXYZ# Voxelst-statistic
ξc(k): Positive correlations
 MidbrainL-6−18−10954.94
 ThalamusL−16−1882325.10
R22−3042065.10
 Anterior insulaL−442022327.28
R361689436.23
 Supplementary motor area/anterior cingulate sulcusL-2-85216886.29
 Dorsolateral PFCR3646301365.93
 Middle occipital gyrusR12−86623711.70
L−32−82161368.26
 Superior occipital gyrusR28−783034311.00
L−26−82321438.73
 CerebellumR18−48−182155712.91
Table 5
MNI coordinates and t-statistic of maxima of activations induced by arbitration for the social advice (Equation 19; p<0.05, cluster-level whole-brain FWE corrected).

Related to Figure 8b.

HemisphereXYZ# Voxelst -statistic
ξa(k): Positive correlations
 PrecuneusR6−51322846.25
 AmygdalaR18−10−161075.20
 Anterior cingulate cortexL-244−101364.82
 Ventromedial PFCR852142315.72
 Ventrolateral PFCR503603054.93
 Frontopolar cortexR462221534.59
 Orbitofrontal cortexR2826−161265.11
 Middle frontal gyrusR3814283055.36
 Superior temporal gyrusL−60−30-21074.90
 Superior temporal sulcusR52−18-81525.51
 Anterior temporoparietal junctionR56−52241734.18
 CerebellumL−24−84−341214.11
Table 6
MNI coordinates and F-statistic for main effects of stability (p<0.05, FWE whole-brain corrected).

Related to Figure 11 (activations in cyan).

HemisphereXYZ# VoxelsF-statistic
Stability > Volatility
 Supramarginal gyrusR46−2842119938.16
 Inferior occipital gyrusR46−66058033.99
L−46−70425620.82
 Anterior insulaR342029829.30
 Postcentral gyrusL−5223410728.97
R54−22341295.59
 Precentral gyrusL−60−203251240.21
R5043212920.58
 Middle frontal gyrusL−2605811720.18
Table 7
MNI coordinates and F-statistic for interactions between task phases and stimulus type (p<0.05, FWE whole-brain corrected).

Related to Figure 11 (activations in magenta).

HemisphereXYZ# VoxelsF-statistic
Information Source × Task Phase
 MidbrainL-4−22-815448.03
 ThalamusL−12−240189116.73
R16−302154104.27
 Middle cingulate gyrusL−1016329437.10
 Anterior insulaL−34-2108826.71
 Supplementary motor area/anterior cingulate sulcusL-6-256736104.45
 Dorsolateral PFCL−3852813322.96
R3434349421.02
 Inferior occipital gyrusR44−6663600190.83
L−40−76−123300162.67
 Superior occipital gyrusR28−78308023.54
L−26−82328128.64
 Orbitofrontal cortexL048−22189100.84
R240−2418034.66
 Ventrolateral prefrontal cortexL−4648−128137.69
R5044-88023.53
 CerebellumR30−86−429525.15

Additional files

Supplementary file 1

Main effects of precision-weighted outcome prediction errors.

MNI coordinates and F-statistic of activations induced by precision-weighted prediction error about individually estimated card color probability (Equation 14). Related to Figure 6—figure supplement 1a. (B) MNI coordinates and F-statistic of activations induced by precision-weighted prediction error about advice validity (Equation 8). Related to Figure 6—figure supplement 1b.

https://cdn.elifesciences.org/articles/54051/elife-54051-supp1-v2.docx
Transparent reporting form
https://cdn.elifesciences.org/articles/54051/elife-54051-transrepform-v2.docx

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

  1. Andreea Oliviana Diaconescu
  2. Madeline Stecy
  3. Lars Kasper
  4. Christopher J Burke
  5. Zoltan Nagy
  6. Christoph Mathys
  7. Philippe N Tobler
(2020)
Neural arbitration between social and individual learning systems
eLife 9:e54051.
https://doi.org/10.7554/eLife.54051