Figures and data in Combining magnetoencephalography with magnetic resonance imaging enhances learning of surrogate-biomarkers

Figures
Tables
Additional files

5 figures, 5 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

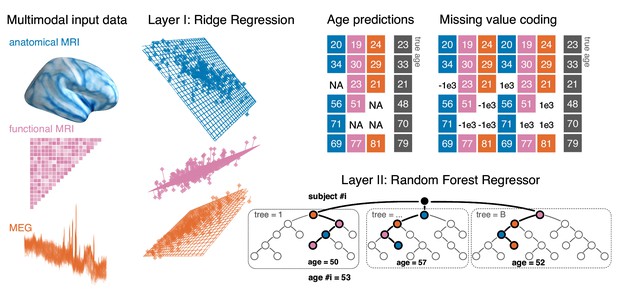
Opportunistic stacking approach.

The proposed method allows to learn from any case for which at least one modality is available. The stacking model first generates, separately for each modality, linear predictions of age for held-out data. 10-fold cross-validation with 10 repeats is used. This step, based on ridge regression, helps reduce the dimensionality of the data by generating predictions based on linear combinations of the major directions of variance within each modality. The predicted age is then used as derived set of features in the following steps. First, missing values are handled by a coding-scheme that duplicates the second-level data and substitutes missing values with arbitrary small and large numbers. A random forest model is then trained to predict the actual age with the missing-value coded age-predictions from each ridge model as input features. This potentially helps improve prediction performance by combining additive information and introducing non-linear regression on a lower-dimensional representation.

Figure 2 with 3 supplements

Download asset Open asset

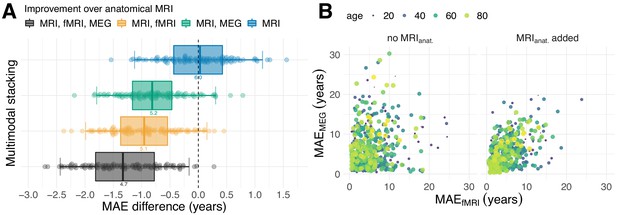
Combining MEG and fMRI with MRI enhances age-prediction.

(A) We performed age-prediction based on distinct input-modalities using anatomical MRI as baseline. Boxes and dots depict the distribution of fold-wise paired differences between stacking with anatomical MRI (blue), functional modalities, that is fMRI (yellow) and MEG (green) and complete stacking (black). Each dot shows the difference from the MRI testing-score at a given fold (10 folds × 10 repetitions). Boxplot whiskers indicate the area including 95% of the differences. fMRI and MEG show similar improvements over purely anatomical MRI around 0.8 years of error. Combining all modalities reduced the error by more than one year on average. (B) Relationship between prediction errors from fMRI and MEG. Left: unimodal models. Right: models including anatomical MRI. Here, each dot stands for one subject and depicts the error of the cross-validated prediction (10 folds) averaged across the 10 repetitions. The actual age of the subject is represented by the color and size of the dots. MEG and fMRI errors were only weakly associated. When anatomy was excluded, extreme errors occurred in different age groups. The findings suggest that fMRI and MEG conveyed non-redundant information. For additional details, please consider our supplementary findings.

Figure 2—figure supplement 1

Download asset Open asset

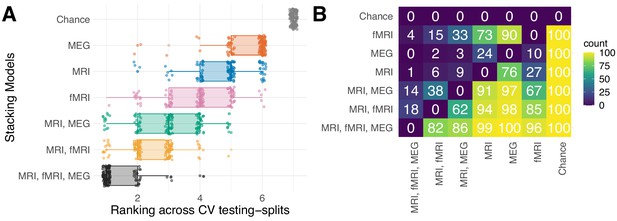
Rank statistics.

Rank statistics for multimodal stacking models. (A) depicts rankings over cross-validation testing splits for the six stacking models and the chance-level estimator. The ranking was overall stable with perfect separation from chance and top-rankings predominantly occupied by the multimodal stacking model. (B) Matrix of pairwise rank frequencies. The values indicate how many times the row-item ranked better than the column-item. For example, all models ranked 100/100 times better than chance (right-most column) and the full model ranked 82/100 times better than MRI + fMRI (row 1 from bottom, column 2 from left), 86/100 better than MRI + MEG (row 1 from bottom, column 3 from left), which in turn ranked 91/100 better than MRI (row 3 from bottom, column 4 from left).

Figure 2—figure supplement 2

Download asset Open asset

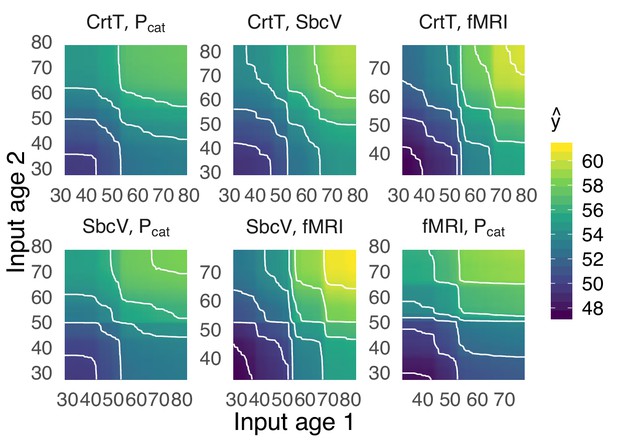
Partial dependence.

Two-dimensional partial-dependence analysis for 6 top-important stacking inputs. This analysis demonstrates, intuitively, how stacked predictions change as the input predictions from different modalities into the stacking layer change, two at a time. The x and y axes depict the empirical value range of the age inputs (CrtT = cortical thickness, SbcV = subcortical volume). The color and contours show the resulting output prediction of the stacking model. Additive patterns dominated, suggesting independent contributions of MEG and fMRI with little evidence for interaction effects. It is noteworthy that the range of output ages was somewhat wider when the age input from fMRI was manipulated, suggesting that the model trusted fMRI more than MEG.

Figure 2—figure supplement 3

Download asset Open asset

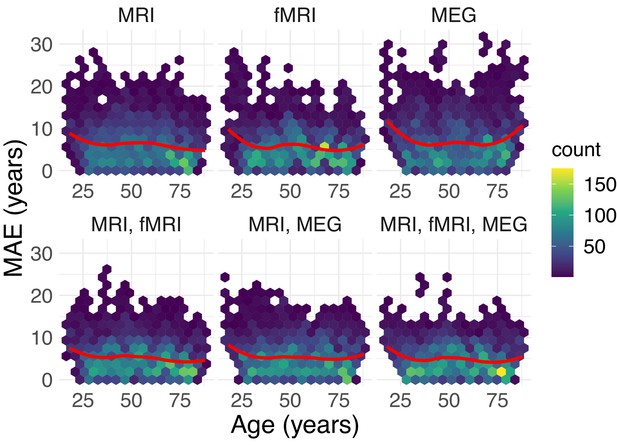
Relationship between predication performance and age.

Breakdown of prediction error across age by stacking model. It is a common characteristic of regression models for prediction of brain age to show systematically increased very old or young sub-populations (Smith et al., 2019; Le et al., 2018), hence, referred to as brain age bias. Could the enhanced performance of the full stacking model possibly go along with reduced brain age bias or is the improvement uniform across age groups? To investigate the mechanism of action of the stacking-method, we visualized the subject-wise prediction errors across age. The upper row shows unimodal models, the lower row multimodal ones. The average trend is depicted by a regression line obtained from locally estimated scatter plot smoothing (LOESS, degree 2). One can see that the overall shape of the error distributions are similar with increasing errors in young and old subjects. This tendency seemed more pronounced for the single-modality MEG models showing more extreme errors, especially in young and old sub-populations. Overall, the multimodal models (bottom-row) made visibly fewer errors beyond 15 years of MAE (y-axis), suggesting that, in this dataset, improvements of stacking were predominantly uniform across age. These impressions can be formalized with an ANOVA model of log-error by family and age group (7 approximately equally sized groups) suggesting a main-effect of age group ( $F (6, 3174) = 8.362, 5.13 \times 10^{- 09}$ ), a main effect of family ( $F (5, 3174) = 12.938, p < 1.75 \times 10^{- 12}$ ) and an interaction effect ( $F (30, 3174) = 1.740, p < 0.008$ ). However, such statistical inference has to be treated with caution as the cross-validated predictions made by the models are not necessarily statistically independent.

Figure 3 with 5 supplements

Download asset Open asset

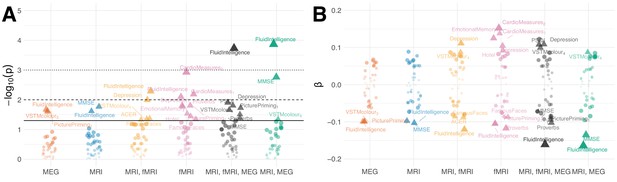
Residual correlation between brain ageΔ and neuropsycholgical assessment.

(A) Manhattan plot for linear fits of 38 neuropsychology scores against brain ageΔ from different models (see scores for Table 5). Y-axis: $- l o g_{10} (p)$ . X-axis: individual scores, grouped and colored by stacking model. Arbitrary jitter is added along the x-axis to avoid overplotting. For convenience, we labeled the top scores, arbitrarily thresholded by the uncorrected 5% significance level, indicated by pyramids. For orientation, traditional 5%, 1% and 0.1% significance levels are indicated by solid, dashed and dotted lines, respectively. (B) Corresponding standardized coefficients of each linear model (y-axis). Identical labeling as in (A). One can see that, stacking often improved effect sizes for many neuropsychological scores and that different input modalities show complementary associations. For additional details, please consider our supplementary findings.

Figure 3—figure supplement 1

Download asset Open asset

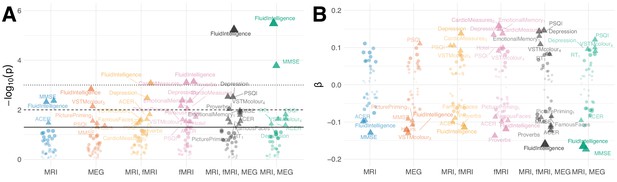
Results based on joint deconfounding.

Association between brain age Δ and neuropsychological assessments based on joint confounding for age through multiple regression.

Figure 3—figure supplement 2

Download asset Open asset

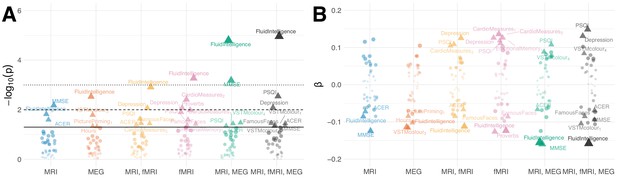
Results based on joint deconfounding with additional regressors of non-interest.

Association between brain age Δ and neuropsychological assessments based on joint confounding for age, gender, handedness and motion through multiple regression.

Figure 3—figure supplement 3

Download asset Open asset

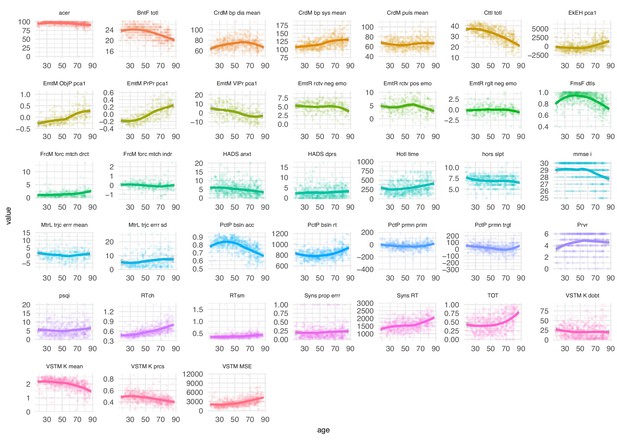
Distribution of neuropsychological scores by age.

Neuropsychological scores across lifespan.

Figure 3—figure supplement 4

Download asset Open asset

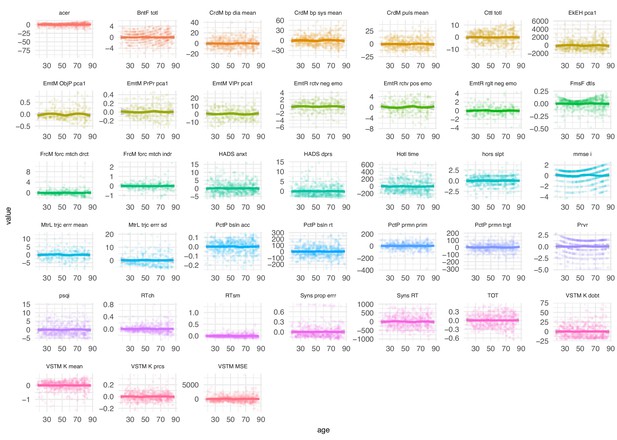
Distribution of neuropsychological scores by age after residualizing.

Neuropsychological scores across lifespan after residualizing for age with polynomial regression (third degree).

Figure 3—figure supplement 5

Download asset Open asset

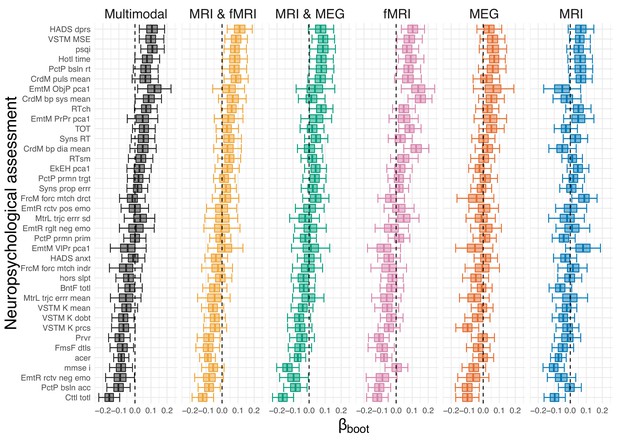
Bootstrap estimates.

Residual correlation between brain ageΔ and neuropsycholgical assessment. The x-axis depicts the coefficients from univariate regression models. Uncertainty intervals are obtained from non-parametric bootstrap estimates with 2000 iterations.

Figure 4 with 4 supplements

Download asset Open asset

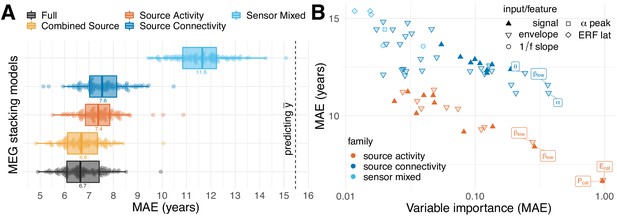
MEG performance was predominantly driven by source power.

We used the stacking-method to investigate the impact of distinct blocks of features on the performance of the full MEG model. We considered five models based on non-exhaustive combinations of features from three families. ‘Sensor Mixed’ included layer-1 predictions from auditory and visual evoked latencies, resting-state alpha-band peaks and 1/f slopes in low frequencies and the beta band (sky blue). ‘Source Activity’ included layer-1 predictions from resting-state power spectra based on signals and envelopes simultaneously or separately for all frequencies (dark orange). ‘Source Connectivity’ considered layer-1 predictions from resting-state source-level connectivity (signals or envelopes) quantified by covariance and correlation (with or without orthogonalization), separately for each frequency (blue). For an overview on features, see Table 2. Best results were obtained for the ‘Full’ model, yet, with negligible improvements compared to ‘Combined Source’. (B) Importance of linear-inputs inside the layer-II random forest. X-axis: permutation importance estimating the average drop in performance when shuffling one feature at a time. Y-axis: corresponding performance of the layer-I linear model. Model-family is indicated by color, characteristic types of inputs or features by shape. Top-performing age-predictors are labeled for convenience (p=power, E = envelope, cat = concatenated across frequencies, greek letters indicate the frequency band). It can be seen that solo-models based on source activity (red) performed consistently better than solo-models based other families of features (blue) but were not necessarily more important. Certain layer-1-inputs from the connectivity family received top-rankings, that is alpha-band and low beta-band covariances of the power envelopes. The most important and best performing layer-1 models concatenated source-power across all nine frequency bands. See Table 4 for full details on the top-10 layer-1 models. For additional details, please consider our supplementary findings.

Figure 4—figure supplement 1

Download asset Open asset

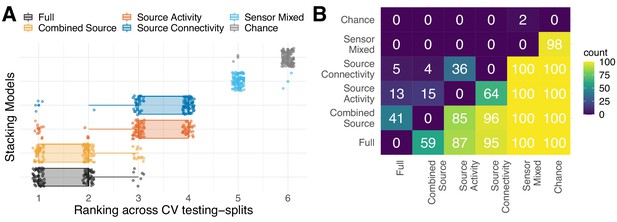
Rank statistics.

Rank statistics for MEG stacking models. (A) depicts rankings over cross-validation testing splits for the five stacking models and the chance-level estimator. The ranking was, overall, stable with perfect separation from chance for all but the ’Sensor Mixed’ models. Two blocks surfaced: models based on either source-level activity (power of signals) or source-level connectivity (covariance, correlation) and a second block with models that combined source-level activity with connectivity. In the first block, models competed for rankings higher than sensor space models but lower than combined models. At the same time, the ‘Combined Source’ and ‘Full’ higher order models predominantly competed for top-rankings. (B) Matrix of pairwise rank frequencies. The values indicate how many times the row-item ranked better than the column-item. For example, all models (except ‘Sensor Mixed’) ranked 100/100 times better than chance (right-most column). The ‘Full’ model ranked 87/100 times better than ‘Source Activity’ (row one from bottom, column three from left), 95/100 better than ‘Source Connectivity’ (row one from bottom, column four from left). Competition between models is expressed by quasi-alternation, for example, ‘Full’ was 59 times better than ‘Combined Source’, which, in turn, was better than 'Full' 41 times.

Figure 4—figure supplement 2

Download asset Open asset

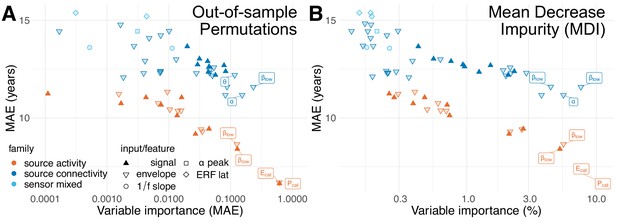
Ranking-stability across methods for variable importance.

Alternative metrics for estimation of variable importance. The permutation-based variable importance presented so far may suffer from two limitations: overfitting and insensitivity to conditional dependencies between variables. (A) Results obtained with out-of-sample permutations from the 100 cross-validation splits used for model evaluation. This analysis is less prone to overfitting than in-sample permutations but, by design, is not prepared to handle correlation between the inputs and does not capture interaction effects between variables. (B) Results from the mean decrease impurity (MDI) metric defined for the training data. MDI can capture interaction effects but increases the risk of false positives and false negatives. Compared with the main findings in Figure 4B, all three metrics strongly agreed on the subset of most important variables and yielded highly similar importance rankings. The association between these importance estimates was $r_{S p e a r m a n} = 0.95, r^{2} = 0.90, p < 2.2 \times 10^{- 16}$ for in-sample permutations and MDI, $r_{S p e a r m a n} = 0.96, r^{2} = 0.92$ for in-sample permutations and out-of-sample permutations and $r_{S p e a r m a n} = 0.94, r^{2} = 0.88, p < 2.2 \times 10^{- 16}$ for MDI and out-of-sample permutations. These supplementary findings suggest that the detection of the most important factors contributing to model performance was robust across distinct variable importance metrics.

Figure 4—figure supplement 3

Download asset Open asset

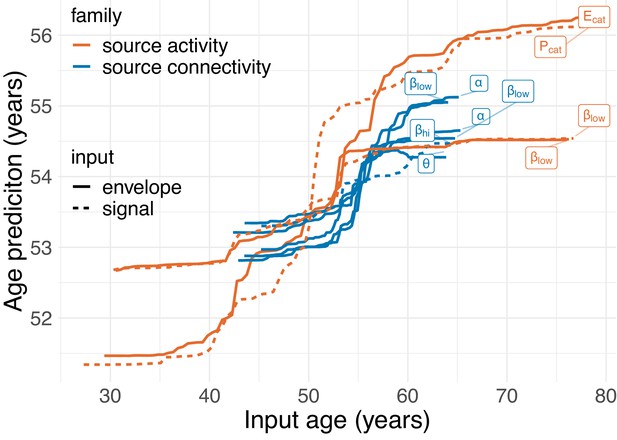
Partial dependence.

Partial dependence between top age-inputs and the final stacked age-prediction. This analysis simulates how stacked predictions change as the age predicted from layer-1 linear models increases. Results revealed a staircase pattern suggesting dominant monotonic and non-linear relationship. Moreover, the analysis revealed that more important input models had wider ranges of age predictions and were, on average, less strongly corrected by shrinkage toward the mean age. This provides some insight into one potential mechanism by which the stacking model helps improve over the linear model, that is, by pulling implausible extreme predictions towards the mean prediction by age-group-dependent amounts.

Figure 4—figure supplement 4

Download asset Open asset

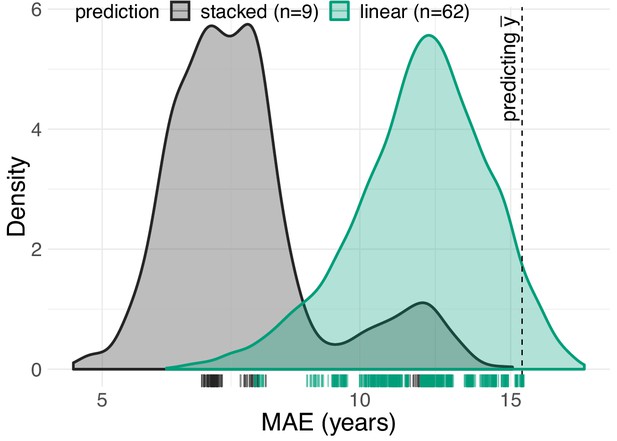
Performance of solo- versus stacking-models.

Distribution of prediction errors across 62 first-level linear models (green) and 9 second-level stacking models (black) based on random forests. One can see that stacking mitigates prediction error beyond the best performing linear model.

Figure 5

Download asset Open asset

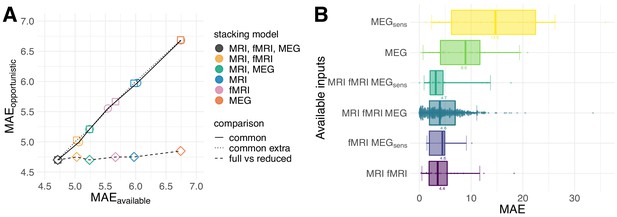
Opportunistic learning performance.

(A) Comparisons between opportunistically trained model and models restricted to common available cases. Opportunistic versus restricted model with different combinations scored on all 536 *common* cases (circles). Same analysis extended to include *extra common* cases available for sub-models (squares). Fully opportunistic stacking model (all cases, all modalities) versus reduced non-opportunistic sub-models (fewer modalities) on the cases available to the given sub-model (diamonds). One can see that multimodal stacking is generally of advantage whenever multiple modalities are available and does not impact performance compared to restricted analysis on modality-complete data. (B) Performance for opportunistically trained model for subgroups defined by different combinations of available input modalities, ordered by average error. Points depict single-case prediction errors. Boxplot-whiskers show the 5% and 95% uncertainty intervals. When performance was degraded, important modalities were absent or the number of cases was small, for example, in MEG_sens where only sensor space features were present.

Tables

Table 1

Frequency band definitions.

Name	Low	$δ$	$θ$	$α$	$β_{1}$	$β_{2}$	$γ_{1}$	$γ_{2}$	$γ_{3}$
range (Hz)	0.1 - 1.5	1.5 - 4	4 - 8	8 - 15	15 - 26	26 - 35	35 - 50	50 - 74	76 - 100

Table 2

Summary of extracted features.

#	Modality	Family	Input	Feature	Variants	Spatial selection
1	MEG	sensor mixed	ERF	latency	aud, vis, audvis	max channel
2	…	…	PSDα	peak		max channel
3	…	…	PSD	1/f slope	low, $γ$	max channel in ROI
4	…	source activity	signal	power	low, $δ$ , $θ$ , $α$ , $β_{1, 2}$ , $γ_{1, 2, 3}$	MNE, 448 ROIs
5	…	…	envelope	…	…	…
6	…	source connectivity	signal	covariance	…	…
7	…	…	envelope	…	…	…
8	…	…	env.	corr.	…	…
9	…	…	env.	corr. ortho.	…	…
10	fMRI	connectivity	time-series	correlation	…	256 ROIs
11	MRI	anatomy	volume	cortical thickness		5124 vertices
12	…	…	surface	cortical surface area		5124 vertices
13	…	…	volume	subcortical volumes		66 ROIs

Note. ERF = event related field, PSD = power spectral density, MNE = Minimum Norm-Estimates, ROI = region of interest, corr. = correlation, ortho. = orthogonalized.

Table 3

Available cases by input modality.

Modality	MEG sensor	MEG source	MRI	fMRI	Common cases
cases	589	600	621	626	536

Note. MEG sensor space cases reflect separate task-related and resting state recordings corresponding to family ‘sensor mixed’ in Table 2. MEG source space cases were exclusively based on the resting state recordings and mapped to family ‘source activity’ and ‘source connectivity’ in Table 2.

Table 4

Top-10 Layer-1 models from MEG ranked by variable importance.

ID	Family	Input	Feature	Variant	Importance	MAE
5	source activity	envelope	power	E_cat	0.97	7.65
4	source activity	signal	power	P_cat	0.96	7.62
7	source connectivity	envelope	covariance	$α$	0.37	10.99
7	source connectivity	envelope	covariance	$β_{l o w}$	0.36	11.37
4	source activity	signal	power	$β_{l o w}$	0.29	8.79
5	source activity	envelope	power	$β_{l o w}$	0.28	8.96
7	source connectivity	envelope	covariance	$θ$	0.24	11.95
8	source connectivity	envelope	correlation	$α$	0.21	10.99
8	source connectivity	envelope	correlation	$β_{l o w}$	0.19	11.38
6	source connectivity	signal	covariance	$β_{h i}$	0.19	12.13

Note. ID = mapping to rows from features. MAE = prediction performance of solo-models as in Figure 4.

Table 5

Summary of neurobehavioral scores.

#	Name	Type	Variables (38)
1	Benton faces	neuropsychology	total score (1)
2	Emotional expression recognition	…	PC1 of RT (1), EV = 0.66
3	Emotional memory	…	PC1 by memory type (3), EV = 0.48,0.66,0.85
4	Emotion regulation	…	positive and negative reactivity, regulation (3)
5	Famous faces	…	mean familiar details ratio (1)
6	Fluid intelligence	…	total score (1)
7	Force matching	…	Finger- and slider-overcompensation (2)
7	Hotel task	…	time(1)
9	Motor learning	…	M and SD of trajectory error (2)
10	Picture priming	…	baseline RT, baseline ACC (4)
…	…	…	M prime RT contrast, M target RT contrast
11	Proverb comprehension	…	score (1)
12	RT choice	…	M RT (1)
13	RT simple	…	M RT (1)
14	Sentence comprehension	…	unacceptable error, M RT (2)
15	Tip-of-the-tounge task	…	ratio (1)
16	Visual short term memory	…	K (M,precision,doubt,MSE) (4)
17	Cardio markers	physiology	pulse, systolic and diastolic pressure 3)
18	PSQI	questionnaire	total score (1)
19	Hours slept	…	total score (1)
20	HADS (Depression)	…	total score (1)
21	HADS (Anxiety)	…	total score (1)
22	ACE-R	…	total score (1)
23	MMSE	…	total score (1)

Note. M = mean, SD = standard deviation, RT = reaction time, PC = principal component, EV = explained variance ratio (between 0 and 1), ACC = accuracy, PSQI = Pittsburgh Sleep Quality Index HADS = Hospital Anxiety and epression Scale, ACE-R = Addenbrookes Cognitive Examination Revised, MMSE = Mini Mental State Examination. Numbers in parentheses indicate how many variables were extracted.