Diverse and complex muscle spindle afferent firing properties emerge from multiscale muscle mechanics
Figures

Overview of methodologies to test hypothesis that muscle spindle Ia afferent firing rates follow intrafusal muscle fiber force due to cross-bridge interactions.
Ia afferent firing rates were recorded from dorsal rootlets during stretches of the triceps surae muscle in anesthetized rats. Muscle fiber forces were estimated by subtracting noncontractile forces from measured whole musculotendon force. The exponential rise in force with stretch was assumed to arise from non-contractile tissue in parallel with the muscle-tendon unit with exponential stiffness (Blum et al., 2019). The remaining estimated muscle fiber force and yank exhibited similar temporal characteristics to the muscle spindle IFR. Intrafusal muscle fiber force and yank were then simulated using a cross-bridge based model to predict muscle spindle IFRs.
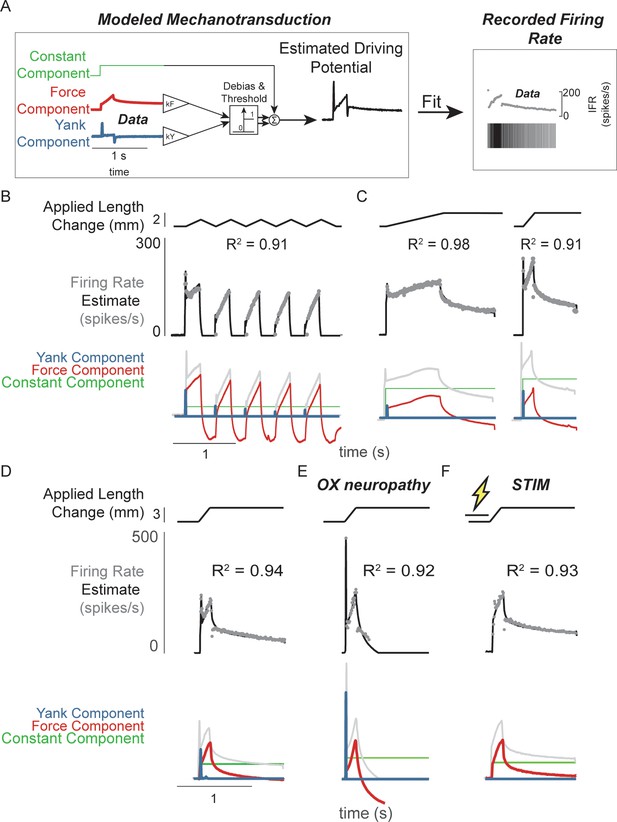
Muscle spindle driving potentials estimated from independent contributions of experimentally-derived muscle fiber force and yank.
(A) Estimated driving potentials were derived from linear combinations of muscle fiber force and yank, half-wave rectified, and compared against recorded muscle spindle Ia afferent firing rates. Weights of each component were optimized to match recorded spiking dynamics. (B) Recorded muscle spindle Ia afferent firing rates (gray dots) in history-dependent conditions, having non-unique relationships to muscle length and velocity, were reproduced using muscle fiber force and yank (black lines). Notably, the initial burst and increased firing during ramp in the first stretch were attributed to increased muscle fiber yank and to greater force during the first stretch, respectively. (C) Likewise, muscle fiber force and yank could also account for the temporal dynamics of Ia afferent firing in response to both slow and fast stretches. (D) This model permits independent manipulation of the force and yank contributions to muscle spindle firing rates. As such, we can explain the altered muscle spindle Ia afferent firing patterns in (E) oxaliplatin chemotherapy-induced sensory neuropathy as a loss of force sensitivity, and (F) after antidromic electrical stimulation of the axon as loss of yank sensitivity.
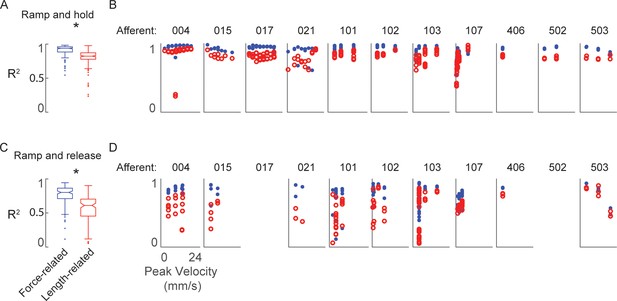
Goodness-of-fit to measured muscle spindle Ia afferent firing rates using estimated muscle fiber force and yank (blue) compared to kinematics model (red) as baseline comparison.
(A) Box and whisker plots of model goodness of fit (R2) for all ramp-and-hold trials using estimated fiber force-based (blue) versus length-based (red) models. * denotes a significant difference between the model goodness of fit based on cumulative squared errors; p<0.05, one-way ANOVA. (B) R2 values for all individual trials of ramp-and-hold and within each afferent plotted versus stretch velocity for force-based (blue dots) versus length-based (red dots) models. (C–D) Same as A-B, only for repeated ramp-release trials.
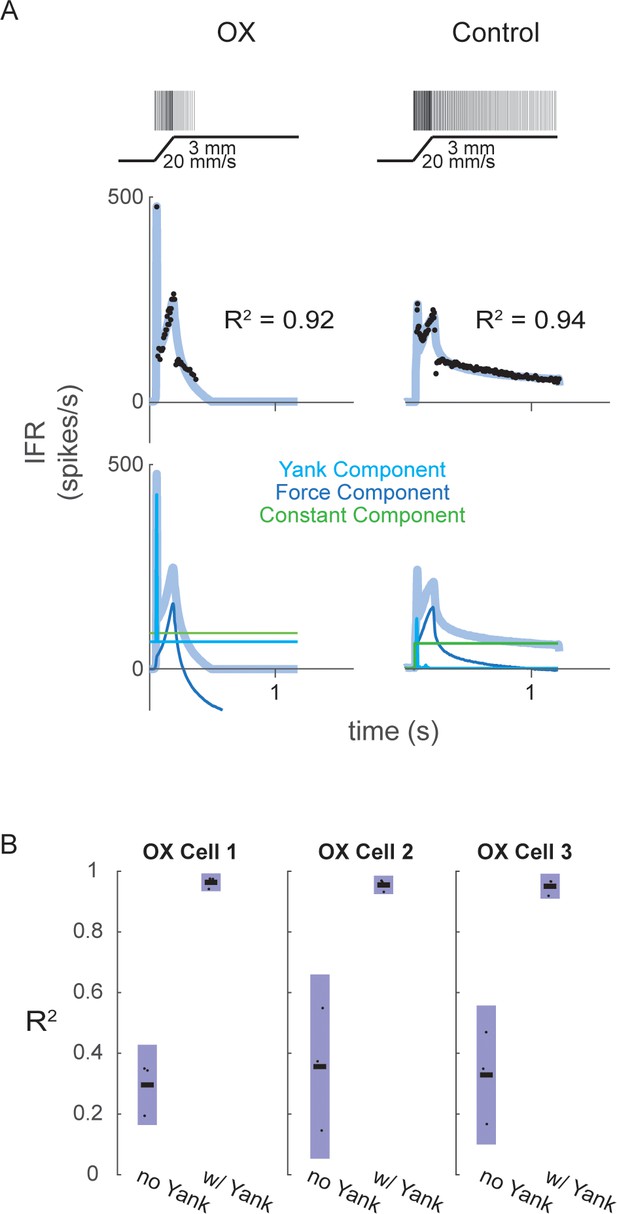
Fits of muscle spindle firing rates before and after oxaliplatin-induced neuropathy using estimated muscle fiber force and yank.
(A) Example Ia afferent responses to stretch and force-based model fits. Left column shows a typical Ia afferent response to a ramp-hold stretch applied to the triceps surae of a rat treated with oxaliplatin chemotherapy (Bullinger et al., 2011). Right column shows typical response of Ia afferent in response to same ramp-hold stretch. Raster plots indicate times at which action potentials are recorded and are shown above imposed stretches. Below are the IFR and corresponding model fits shown above the same model fits with their respective components. (B) Variance of muscle spindle Ia afferent responses accounted for by force related model with (right bar in each plot) and without (left bar in each plot) yank for three Ia afferents from three oxaliplatin-treated rats. Black horizontal bars represent the means, blue bars represent the standard deviations, and black dots represent the data points from each trial (three trials per afferent).
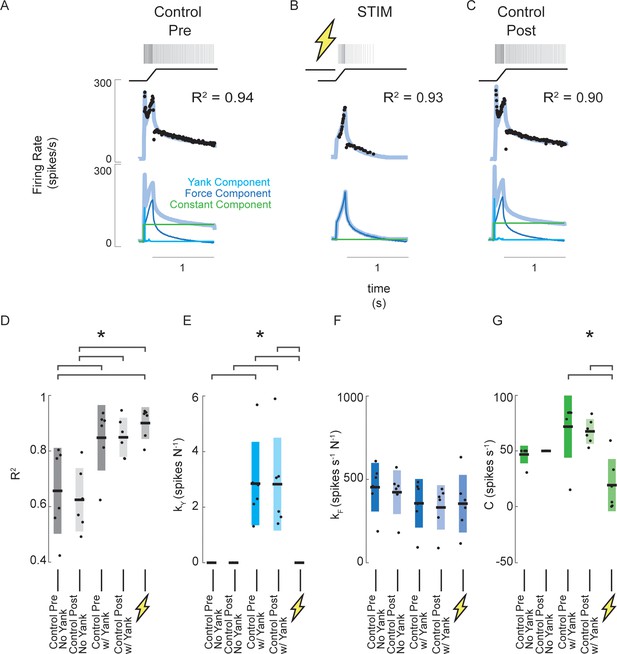
Estimated muscle fiber force-related model predicts changes in muscle spindle encoding caused by axonal stimulation.
(A) Example of pre-stimulus control trial consisting of a 3 mm ramp-hold stretch at 20 mm/s. Raster represents the times of recorded action potentials in response to the ramp-hold stimulus shown directly below it. Black dots represent the afferent IFR corresponding to the raster. The gray-blue line represents the model prediction using force, yank, and constant components. Below this are the same model prediction as above (gray-blue) and model prediction components (blue – force component; cyan – yank component; green – constant component). (B) Example of stimulus trial consisting of the same stretch applied as A, with a train of antidromic action potentials induced by suprathreshold current injection into the Ia axon prior to stretch. The model fit in this trial represents the best fit without the yank component. Notice the quality of fit does is roughly equal in this trial with that of the pre-stimulus trial in A, but no yank component was necessary. (C) Example of post-stimulus control trial. Same stretch and model components were used as in A. (D) Goodness of fit (R2) of force-related model for six afferents subjected to the same trials as shown in A-C. The first two columns show R2 values of the model fits without yank components for the pre- and post-stimulus control trials, respectively, for all six afferents. The third and fourth columns from the left show R2 values for the model fits with yank components for the pre- and post-stimulus control trials, respectively, for the same six afferents. The fifth column shows R2 values for the model fits for the stimulus trials. This model did not use a yank component. (E) Model sensitivity to yank for the same model fits and afferents as D. (F) Model sensitivity to force for the same model fits and afferents as D and E. (G) Model constant component for the same model fits and afferents as D-F. Brackets above plots indicate significant differences between the means (p<0.05).
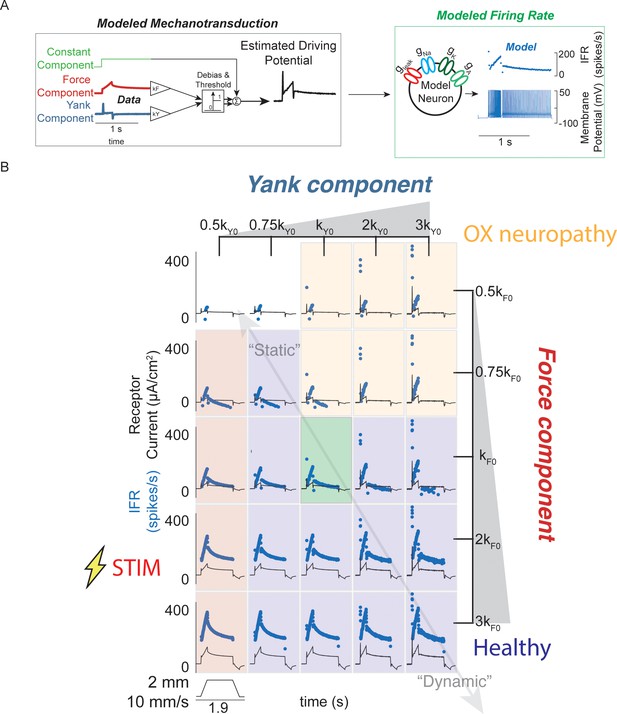
Spectrum of passive muscle spindle firing phenotypes accounted for by varying sensitivity to experimentally derived muscle fiber force and yank.
(A) Sensitivity to experimentally-derived force and yank was systematically varied for a single stretch and resultant driving potentials were input to a Connor-Stevens model neuron to generate firing patterns. (B) Nominal force and yank weights were identified to recreate experimentally-recorded muscle spindle response to a representative stretch (green box). Increasing sensitivity to yank (left to right) generated larger initial bursts and dynamic responses during the ramp, and resembled responses from oxaliplatin-treated specimens at the highest yank and lowest force sensitivities (orange boxes, compare to Figure 2E). Increasing sensitivity to force (top to bottom) generated higher firing rates during the hold period and resembled Ia afferent firing responses after axonal stimulation at the lowest yank and highest force sensitivities (red boxes, compare to Figure 2F). Varying the weights of the force and yank sensitivities could recreate the spectrum of healthy muscle spindle firing profiles reported classically (purple boxes).
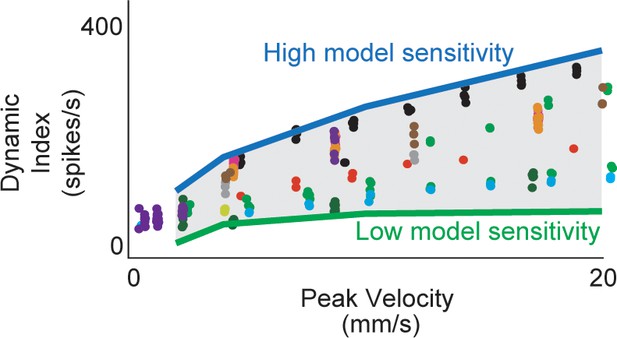
Estimated muscle fiber force model predicts inter-afferent variability of healthy afferent firing properties across perturbation velocity and acceleration.
(A) Same dynamic index data shown in Figure 3-2 (colored dots) with predicted range of dynamic indices from model (gray shaded area). Nominal simulations were performed with the same force and yank model sensitivities for four stretch trials (2, 4, 10, 20 mm/s) from the same animal. Model parameter sweeps were performed for force and yank sensitivities for each of the four trials from 0.1 to 5 times the nominal value for each parameter. Green line represents the minimum dynamic indices from each of the four parameter sweeps from trials for which there was a spiking response (usually corresponding to low force and yank sensitivities). Blue line represents maximum dynamic indices from each of the four parameter sweeps (usually corresponding to high force and yank sensitivities). Gray shaded area represents plausible space of simulated dynamic index.

Generative model of muscle spindle driving potentials based on simulated muscle cross-bridge kinetics.
(A) The muscle spindle model consists of two muscle fibers in a parallel mechanical arrangement, loosely representing intrafusal bag and chain fibers. (B) During stretch, force and yank of the ‘dynamic’ fiber is linearly combined with force of the ‘static’ fiber, with different proportions generating driving potentials consistent with ‘dynamic’ and ‘static’ muscle spindle firing response phenotypes. (C) A population of myosin cross-bridges and their relative displacement and velocity with respect to active actin binding sites was simulated during three consecutive ramp-stretch-release stretches. The distribution of cross-bridge lengths relative to actin binding sites is shown at different timepoints of imposed kinematics (numbered graphs and timepoints). The length of the dynamic and static fibers (lower trace) and the stress in the dynamic and static fibers (middle trace) is shown. Deviations between applied length and muscle fiber length occur due to muscle fiber slack.
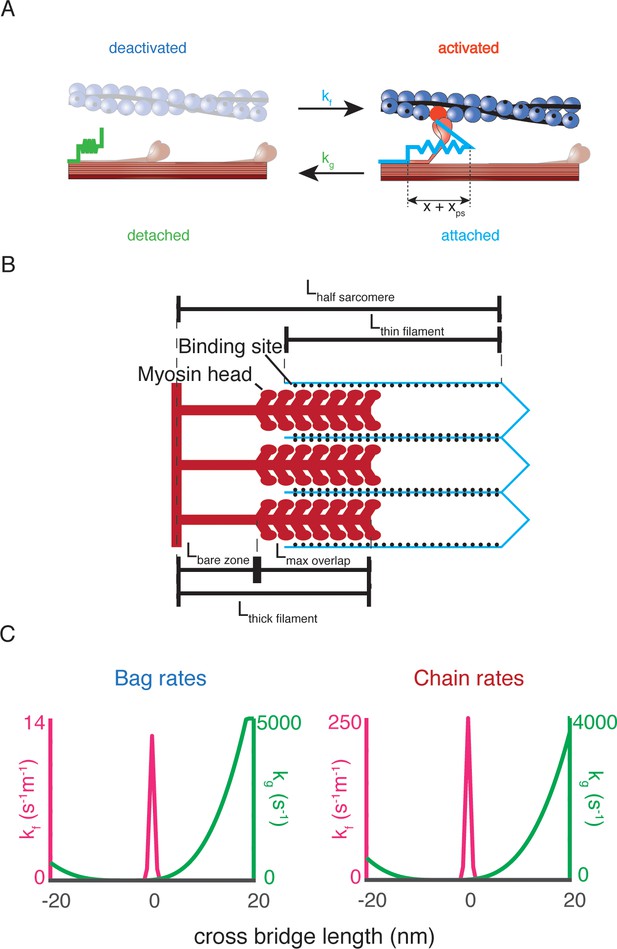
Biophysical intrafusal muscle models.
(A) Two-state dynamic system of cross-bridge cycling. A population of detached cross-bridges attaches at rate kf(x), and the population of attached cross-bridges detaches at rate kg(x). When a cross-bridge is formed at length x, an additional ‘powerstroke’ length, xps, is applied to the cross-bridge to generate a contractile force. (B) Schematic of length variables accounted for in muscle model. The amount of overlap between the myosin heads of the thick filament (red) and actin binding sites of the thin filament (blue lines, black dots) is the relevant variable for the simulations. The fraction of overlap is simply the difference between the total length of the thick and thin filaments with the length of the half sarcomere, expressed as a fraction of the maximum potential overlap. (C) Rate equations for myosin dynamics. The rate at which detached myosin heads will attach as a function of the length, kf(x) of attachment is a Gaussian function, centered around 0 nm (shown in blue). The rate at which attached cross-bridges will detach as a function of their length kg(x) is an offset polynomial function (shown in orange).

Muscle spindle firing dynamics emerge from cross-bridge mechanisms during simulated muscle stretch.
Simulations assume a low level of muscle cross-bridge cycling consistent with relaxed muscle. Length displacements were imposed on the muscle fiber. (A) Predicted driving potentials (upper traces) during ramp stretches of varying velocity and acceleration (lower traces). (B) Classical data showing Ia afferent firing modulation with different stretch velocity (Matthews, 1963). (C) Dynamic index emergent from cross-bridge mechanisms. Dynamic index is defined classically as the ratio of firing rate at the end of the ramp phase and the firing rate 0.5 s into the hold phase (upper diagram). The muscle spindle model exhibits a sublinear relationship between dynamic index and stretch velocity (middle plot – colors correspond to A), similarly to classical findings (bottom plot). (E) Linear acceleration scaling of initial burst emergent from cross-bridge mechanisms. Initial burst amplitude is defined as the difference between peak firing rate during initial burst and baseline. Muscle spindle model exhibits linear scaling with stretch acceleration at stretch onset (top plot), which is consistent with classical findings (bottom plot – Schäfer and Schäfer, 1969). Figure 5B,C (bottom panel) is reproduced from Matthews and Stein, 1969 with permission from John Wiley and Sons. These images are not covered by the CC-BY 4.0 license and further reproduction of these panels would need permission from the copyright holder. Figure 5D (bottom panel) is redrawn from Schäfer and Schäfer, 1969 with permission from Springer Nature.
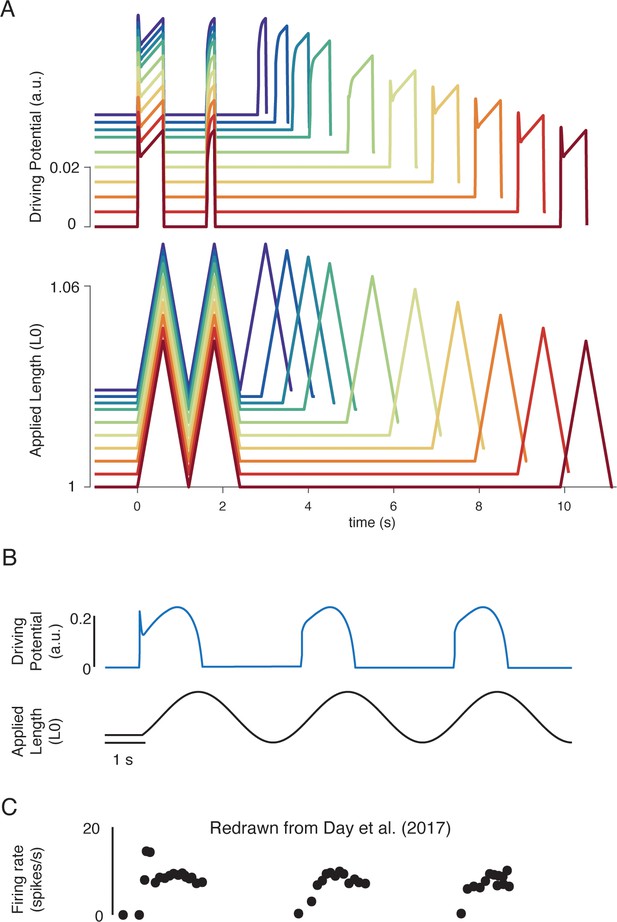
Emergent movement history-dependence of muscle spindle.
(A) When repeated stretch-shorten length cycles were applied, a larger response was predicted if the length was held constant prior to stretch (bottom plot – all traces). An abolished initial burst and reduced dynamic response were predicted in the second stretch, immediately applied after the length was returned to the initial value (top plot – all traces). In the third stretch, recovery of the initial burst was dependent on the time interval between the second and third stretch, with the effect saturating between 5 and 10 s (top plot, recovery from violet to red traces). This finding predicts the results found by Haftel et al., 2004 in rat muscle spindles. Similarly, dynamic response recovered gradually with time interval between second and third stretch (top plot, recovery from violet to red traces). This finding predicts the results found by Proske and Stuart, 1985 in toad muscle spindles. (B) Sinusoidal displacement imposed from rest elicited a history-dependent initial burst in the predicted muscle spindle driving potential at the onset of stretch, resembling data from (C) human muscle spindles recorded during the application of sinusoidal motion to the ankle in relaxed conditions (Day et al., 2017). Figure 6C is redrawn from Day et al., 2017 with permission from The American Physiological Society.
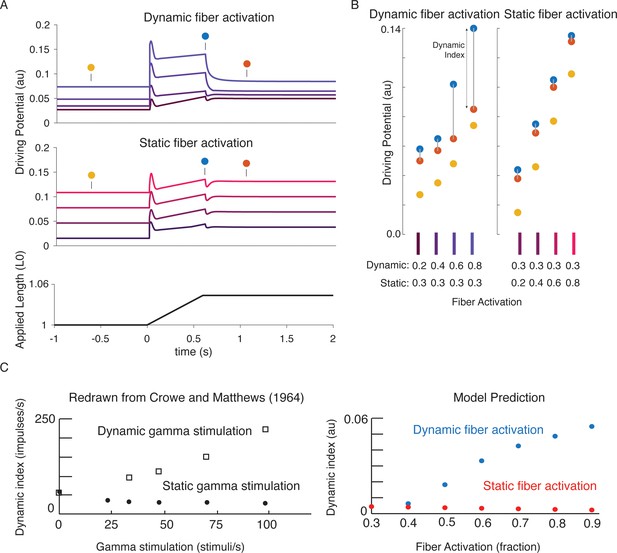
Changes in muscle spindle sensitivity caused by central drive emergent from interactions between dynamic and static fibers.
Fusimotor activity was imposed on either the dynamic or the static fiber by increasing the number of active actin binding sites in the appropriate fiber. (A) Simulated dynamic fiber activation increased the driving potential predominantly during the ramp, with smaller increases during the background and hold period (top traces). Simulated static fiber activation predominantly increases the driving potential rate during the background and hold period, with only modest increases in during the ramp. (B) Emergent scaling of the dynamic index with dynamic (increase in dynamic index) and static fiber activation (decrease in dynamic index) resembled trends reported previously in the literature with (C) dynamic index increasing with bag fiber activation, and dynamic index decreasing with chain fiber activation, respectively. Figure 7C is redrawn from Crowe and Matthews, 1964a with permission from John Wiley and Sons.
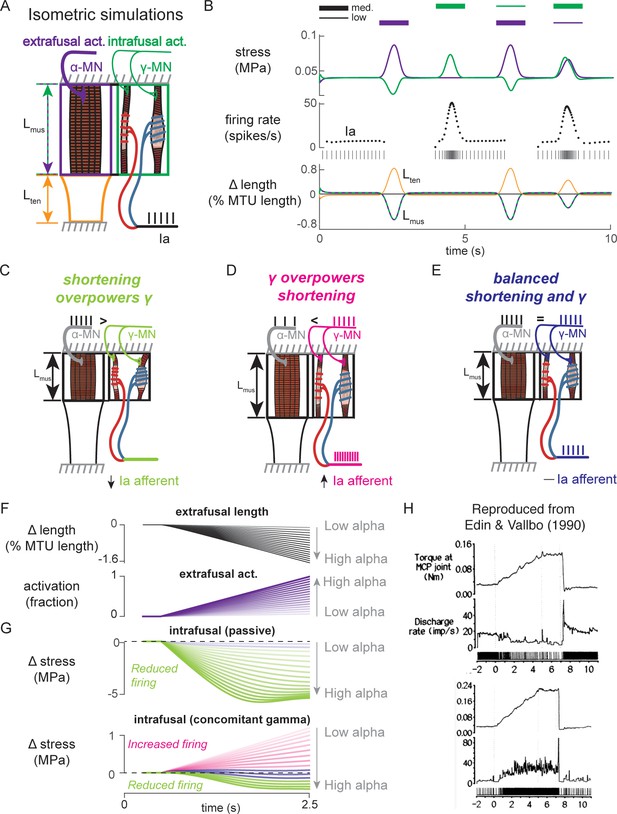
Paradoxical muscle spindle firing activity during isometric musculotendon conditions emergent from multiscale muscle mechanics.
(A) Framework of isometric musculotendon simulations. We simulated an in-series muscle-tendon with ends fixed to its initial length. The extrafusal muscle length was shared with the intrafusal muscle fibers, which were activated independently from the extrafusal muscle. (B) Decoupling of intra- and extrafusal force during short isometric contractions. Different combinations of extrafusal (purple bars) and intrafusal (green bars) activation were simulated. Top row contains intra- (green) and extrafusal (purple) stress during these conditions. Middle row is the simulated Ia afferent firing rate, generated by using our mechanistic model simulated driving potential combined with a leaky integrate-and-fire neural model. Extrafusal activation shortens the extrafusal muscle, and in the absence of sufficient intrafusal activation, silences the Ia afferent firing. Intrafusal activation by itself causes the Ia afferent to fire more. When both intra- and extrafusal muscle are activated concomitantly, the relative weighting of activity determines whether the Ia afferent will increase or decrease its firing rate. (C-E) Schematic representation of the multi-scale mechanics responsible for Ia afferent behavior in these simulations. When the effects of extrafusal shortening overpower the effect of fusimotor activity on the spindle, the Ia afferent firing rate decreases, or stops altogether (left, green). When fusimotor activity overpowers the effect of extrafusal shortening on the spindle, the Ia afferent firing rate increases (center, pink). In theory, this suggests there are combinations of fusimotor activity and shortening that will result in no net change to the Ia afferent firing, despite the dynamics of the muscle (right, blue). (F) A spectrum of musculotendon isometric conditions arising from the interplay of extrafusal shortening and intrafusal activation. We activated the musculotendon model with ramp activations and simulated the intrafusal muscle force with and without concomitant gamma activation. When increasing alpha motor neuron drive (purple traces; directionally indicated in all plots by an arrow), extrafusal muscle shortened more (top plot). (G) The passive spindle always decreased its force because of the shortening imposed by the surrounding extrafusal muscle (top plot). When the intrafusal muscle was activated with concomitant drive, similar to the largest amplitude ramp of extrafusal muscle, we observed the spectrum of responses predicted in C-E: the intrafusal force either decreased (green), stayed relatively constant (purple), or increased (pink). (H) Experimental examples of one muscle spindle decreasing its firing rate (top traces) and another increasing its firing rate (bottom traces) during an isometric task in human. Figure 8H is reproduced from Edin and Vallbo, 1990 with permission from The American Physiological Society. It is not covered by the CC-BY 4.0 license and further reproduction of these panels would need permission from the copyright holder.
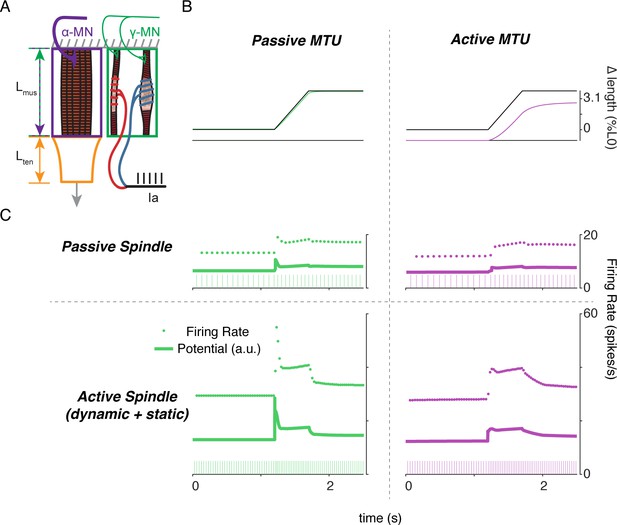
Complex interplay of movement, alpha, and fusimotor drive underlie muscle spindle Ia firing rates.
(A) Framework of free-end musculotendon simulations. We simulated an in-series muscle-tendon with one end fixed and one end free to move. The extrafusal muscle length was shared with the intrafusal muscle fibers, which were activated independently from the extrafusal muscle. (B) Passive musculotendon has a relatively compliant muscle, leading to a MTU length change being primarily applied to the muscle, not the tendon. Extrafusal activation creates a relatively stiff muscle, leading to a smaller length change for the same MTU length applied. (C) Musculotendon activation changes the coding properties of both passive and active muscle spindles. When the MTU is passive, a passive muscle spindle has an initial burst.
Additional files
-
Supplementary file 1
Constant parameters used in both dynamic and static intrafusal muscle fiber models.
These parameters did not change in any simulation presented in this study. When two values are presented, they represent the respective values for the dynamic and static fibers.
- https://cdn.elifesciences.org/articles/55177/elife-55177-supp1-v1.docx





