Ant collective cognition allows for efficient navigation through disordered environments
- Department of Physics of Complex Systems, Weizmann Institute of Science, Israel
- Department of Software Engineering, Ort Braude College, Israel
- The Research Institute on the Foundations of Computer Science (IRIF), CNRS and University of Paris, France
Figures
Figure 1 with 1 supplement
Motion within a maze.
(a) Setup for cube maze experiments. Overlaid are the measured load trajectory (blue), shortest possible path for the load (red) and shortest possible path for ants (magenta). Inset shows a close-up image of the ring-shaped load as it is carried by ants through the cube maze. A sample video of the ants’ motion is provided in Video 1. (b) Cube coverage of the maze shown in (a). Black regions are areas that are inaccessible to the load’s center, taking into account its radius. Cube coverage is defined as the fraction of inaccessible areas (Appendix 1.1, Figure 1—figure supplement 1a). The load is marked in pale green and shown at its initial location. Shortest available path for the load is plotted in red and the ants’ actual trajectory is drawn in blue, as in (a).
Figure 1—figure supplement 1
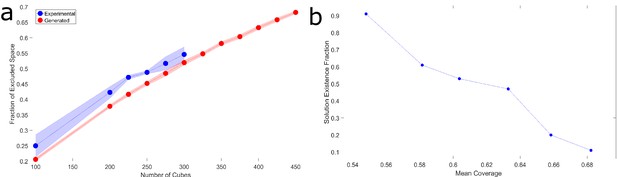
Fraction of forbidden space and dense maze solving probabilities.
(a) The fraction of space blocked by obstacles (mean coverage), as a function of number of cubes for computer-generated mazes (red) and experimental configurations (blue). Namely, the space the center of the = 1 cm ring-shaped load cannot reach. Mazes of the maximum density the ants were able to solve (300 cubes) are already at an impressive 55% coverage. Shaded regions correspond to standard error of the mean. Wherever no error is visible, the error is small enough to fit within the filled circle marker. (b) The fraction of solvable computer-generated dense cube mazes as a function of mean cube coverage is monotonically decreasing, as expected. Mazes with coverage greater than 0.62 (corresponds to 400 cubes roughly) are unsolvable more often than not, with the greatest density mazes being solvable only ∼10% of the time.
Figure 2
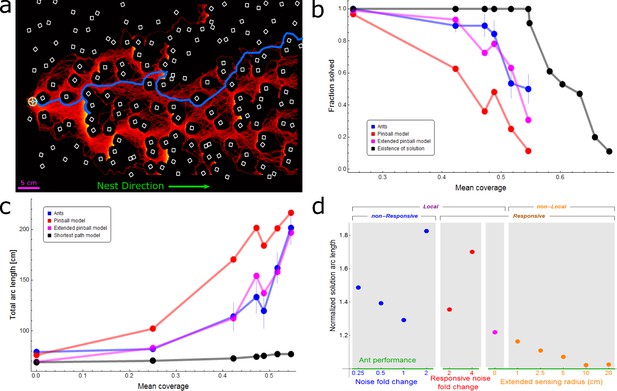
Ant vs simulation performances.
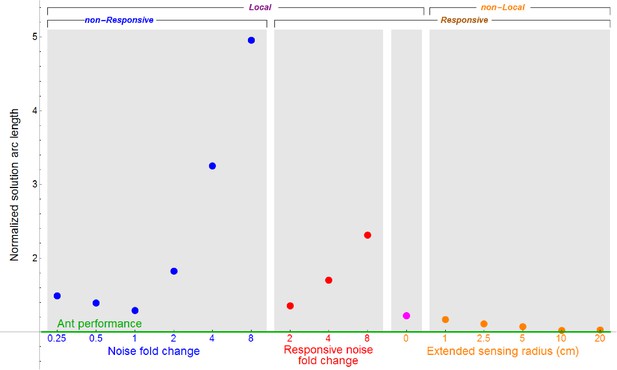
(a) Heat map of trajectories of 200 simulation iterations over an example maze (brighter colors signify more visits, cubes are drawn in white). Actual ant trajectory for this maze is overlaid in blue. Initial location for all trajectories is marked by a green cogwheel. (b) Probabilities to solve the maze as a function of mean coverage, for ants (blue), pinball model (red), and extended pinball model (magenta) simulations. The percent of solvable mazes is depicted in black (up to 0.55 coverage - experimental mazes, 0.55 coverage and above - computer generated mazes). Sample sizes (from small coverage to large): Ants - 15,57,19,19,28,30, Pinball Model - 200 iterations each over 10,14,10,8,15,11 distinct mazes, Extended Pinball Model - 500 iterations each over 10,14,10,8,15,11 distinct mazes. Existence of Solution - (experimental - up to 0.55 coverage): 10, 14, 10, 8, 15, 11 (generated- 0.55 coverage and beyond): 100 for each coverage. (c) Comparison of average total arc length of ants’ and different types of simulations’ trajectories (color scheme as in (b)). The geodesic shortest path traversing the maze is shown in black. We take into account the different success rates of the simulation and ants as shown in panel (b) by adding a penalty to each iteration/experiment which was not successful. The added penalty equals average speed multiplied by the time stuck before termination of experiment/iteration. Error margins in (b,c) are standard errors of the mean. Wherever no error is visible, the error is small enough to fit within the filled circle marker. Sample sizes (from small coverage to large): Ants - 31,10,14,10,8,15,11, Simulations - as in (b) except the first point is 200/500 iterations in the no cubes case, Shortest Path - 10,14,10,8,15,11, first point is simply the width of the board. (d) The performance of different simulated models normalized by empirical ant performance (marked by horizontal green line). We use a single inverse measure for the performance of the simulations, , where is the solution arc length (calculated as in panel (c)) averaged over all cube densities. Models are categorized by their locality and responsiveness, and separated into three differently colored x-axes; each corresponding to a different kind of simulation, wherein the numeric value is the main parameter we change in that simulation. Local non-responsive models are versions of the pinball model where noise levels were varied (Blue dots over blue axis, a noise value of 1 is the fitted value in original model. Appendix 2.1 and Appendix 2—figure 1). Local responsive models are versions of the pinball model in which noise is temporarily altered in response to the load being stuck in a trap (Red dots over red axis, Appendix 2.3 and Appendix 2—figure 3) or a new random bias direction is temporarily selected (Magenta dot over orange axis, Appendix 2.2 and Appendix 2—figure 2). The non-local responsive models are versions of the extended pinball model with different sensing radii (Orange dots over orange axis, Materials and methods, Appendix 2.4, Appendix 2—figure 4). For a full version of this panel with three additional simulations with considerably inferior performance, see Appendix 2—figure 5.
Figure 3 with 2 supplements
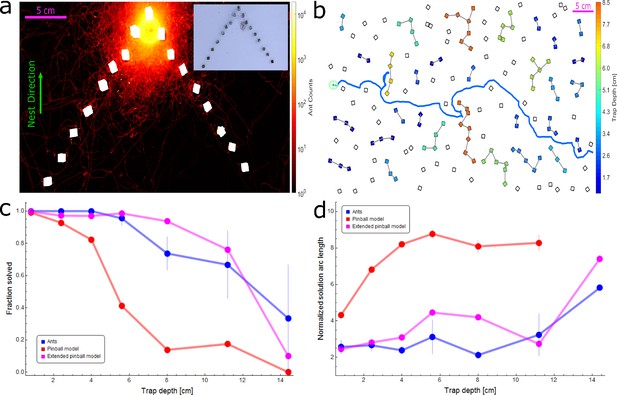
Simulation and ant performance near traps.
(a) Logarithmic heat map showing the spread of ants while the load is located near the deepest point of a triangular trap (extracted from 23 min of footage). The nest direction is towards the top. Color intensity represents the total number of ant counts within each 2D bin over the aforementioned experimental duration. A radius area centered on the load contains ∼99% of ant traffic in the vicinity of the load (see Figure 3—figure supplement 1). Inset shows an example image from the video footage of the experiment. (b) Illustration of traps on a sample maze. Each group of cubes comprising a trap are connected by gray lines and colored according to the trap depth in cm (as defined in Appendix 1.5) corresponding to the color bar. The empirical ant trajectory for this particular realization is plotted in blue (initial location marked using a pale green cogwheel). Nest direction is to the right. (C) Probability of trap solution as a function of trap depth for ants (blue), pinball model (red), and extended pinball model (magenta). Sample sizes (from shallow trap to deep): Ants - 73,70,35,22,19,6,3, Pinball Model - 2645,2886,1646,1289,982,343,105, Extended Pinball Model - 8979,8203,4637,3395,2042,815,403. (d) Average normalized arc length of the trajectory taken to solve a trap as a function of trap depth for ants and simulations (color scheme as in (c)). Trajectory lengths are normalized by trap depth (see Appendix 1.5, Materials and methods). Ant performance is approximately constant up to cm which is on the scale of (see panel (a)). Sample sizes: Ants - 73,70,35,21,14,4,1, Pinball Model - 2620,2675,1352,530,136,60,0, Extended Pinball Model - 8952,7969,4497,3347,1913,620,302. Error margins in (c,d) are standard errors of the mean. Wherever no error is visible, the error is small enough to fit within the filled circle marker.
Figure 3—figure supplement 1
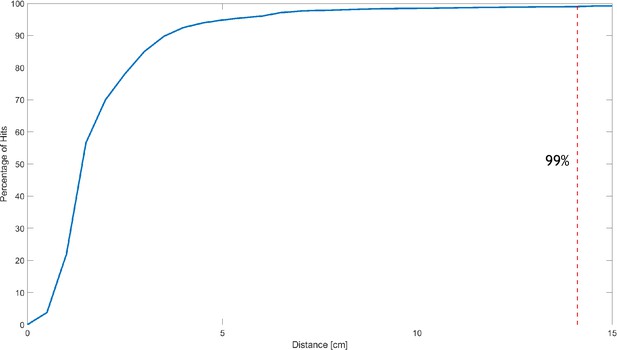
Cumulative ant spread.
Cumulative percentage of recognized ant counts as a function of distance from the center of the load (when it is located at the apex of the trap) in centimeters. The distribution reaches 99% at a distance of ∼14.1 cm (red dashed line), which is on the order of 10 cm.
Figure 3—figure supplement 2
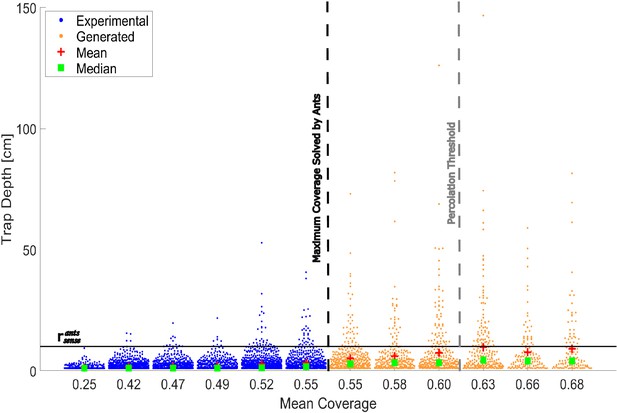
Trap depth distributions.
Bee swarm plot displaying distributions of trap sizes as a function of mean coverage. Medians and means are represented by green rectangles and red pluses, respectively. The data is taken from experiments for coverage (blue), and from computer generated mazes for coverage (orange). Solid black horizontal line represents the ants’ sensing radius . Dashed black vertical line represents the maximal maze coverage the ants solved. Dashed gray line represents the percolation threshold of the system. Note that unsolvable traps were not included in the plot. For this reason, there is less data displayed for the very high coverage distributions.
Figure 4 with 1 supplement
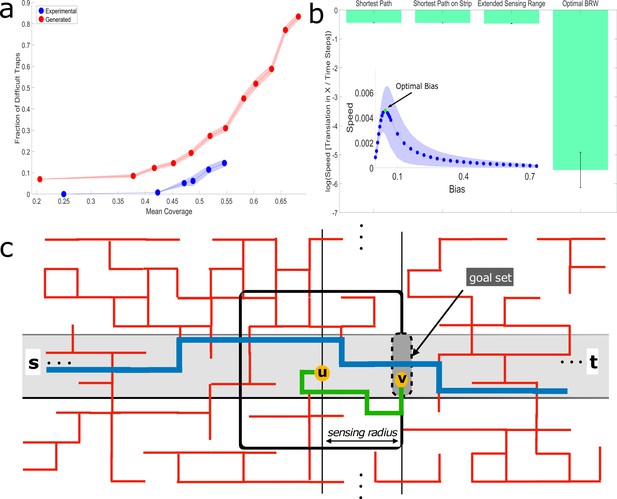
Efficiency of logarithmic range extended sensing.
(a) The fraction of cubes which belong to difficult traps, out of the total number of cubes in the system, as a function of mean coverage of the cube maze. Difficult traps are those defined by . Note the sharp increasing trend above 0.55% coverage. Error margins are standard errors of the mean. Sample Sizes (from small coverage to large): Experimental (number of cubes in the calculation) - 1017,2511,2033,1631,3380,2798, Generated - 50 different mazes for each cube number: 100,200,225,250,275,300,325,350,400,425,450. (b) Simulated performances of percolation lattice solution algorithms just above the percolation threshold (). The biased random walk model whose bias, , is optimized (Berger et al., 2003) to increase drift speed (see inset). Note that this a local-sensing algorithm with this optimized bias stillperforms significantly worse than a logarithmic extended sensing algorithm. The extended sensing algorithm is only slightly worse than the overall shortest path and the shortest path that is constrained within a logarithmic width strip crossing the maze. Error bars in the main panel and shaded regions in the inset signify standard deviation. Sample sizes: Main figure - calculation for the first 3 bars is one number per maze. The last bar is a simulation with 200 iterations over each maze. Since we used 50 different lattice configurations, the sample size is 50,50,50,10000. Inset - 200 iterations over 50 different lattices; thus, 10,000 samples per point. (c) Schematic illustration of the theoretical extended-sensing algorithm on a 2D percolation grid (see Materials and methods, Appendix 3.1, 3.2). Red lines are the open edges of the infinite cluster across which the walker moves from an initial point s to a final point t. The walker moves by executing a series of short bouts. Depicted in the image is a single bout wherein the agent, currently positioned at point u, accesses information within its sensing range (black square, of logarithmic radius) and advances along the green geodesic (fully contained within the sensing range) to some point v on the next goal set line. Such bouts allow the agent to cross the maze on a path whose distance is extremely close to that of the shortest path (blue line) between the initial point and the final point t, that is contained within a strip of logarithmic width (colored gray).
Figure 4—figure supplement 1
Carried loads stay within a confined strip.
90th percentile of perpendicular distance from mean direction of motion of the cooperatively carried load as a function of mean coverage, for all obtained load trajectories. We see that the ant group stays within a distance of ∼4–6 cm from the mean direction of motion. As expected, this distance grows slightly with mean coverage, since the path naturally must be more winding. Shaded area is the standard deviation.
Appendix 1—figure 1
Rolling upon impact.
Histograms displaying the maximal rotation of the cooperatively carried load in the first 3 s after incident with a small trap (blue) and for stretches of 3 s without any incident (red). The experimental distributions are statistically different.
Appendix 1—figure 2
Distributions of maximum backward motion.
Experimental (light blue) and simple pinball simulation (red) distributions of the maximum point reached during every backward motion bout, that is away from the nest, averaged per trap examined. Note the considerable different width of the distributions.
Appendix 1—figure 3
Example of Geodesic Measure Calculation.
A section of a ‘dilated cubes’ maze binary image. Each cube blob was dilated by 1.1 cm in all directions to create a map of regions allowed (white) and forbidden (black) for the load center. The small green square is the initial seed and the thin green line 3.2 cm ahead of it is the final destination seed. The red and blue curves together comprise the geodesic path calculated by the algorithm, corresponding to . The red section corresponds to , whereas the blue part is the 3.2 cm extra distance taken to make sure the trap is solved in the calculation. The geodesic distance of this path is used to assess the trap depth after point filtering and clustering as explained in the text of this section.
Appendix 1—figure 4
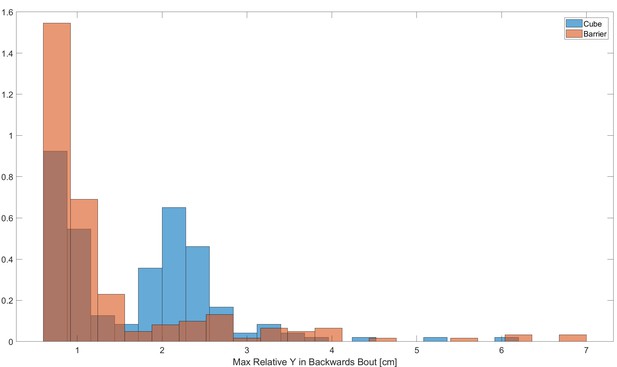
Comparison of single-entrance and composite cube traps.
Histogram portraying the probability density function of the maximum distance travelled backwards in in each backward bout for single-entrance (red) and composite (blue) trap setups.
Appendix 2—figure 1
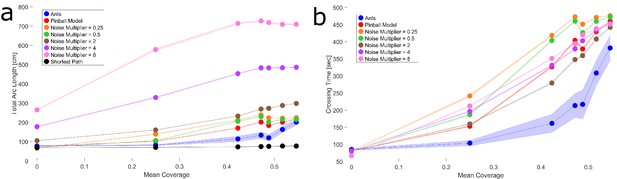
Simulations with different noise multiplier values.
Plotted are the total arc length (a) and solution time (b) as a function of mean coverage of traps in the maze for ants (blue) and simulations with different noise parameter fold-change values (as specified in the legends of the figures). The results show that there are no optimal noise parameters per cube density. Generally the original fitted noise parameter performs best for most densities. The ants always outperform the simulations. Shaded regions correspond to standard error of the mean. Wherever no error is visible, the error is small enough to fit within the filled circle marker.
Appendix 2—figure 2
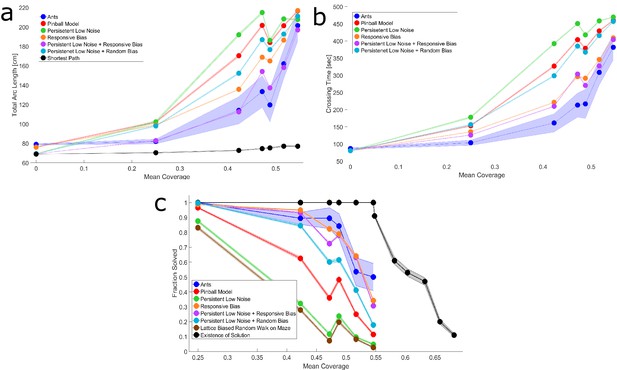
Simulation variations.
Total arc length (a), maze solution time (b) and solution probability (c) vs. mean coverage for different variations of the pinball model and extended pinball model, combining responsive bias and persistent low noise. The purple line represents the ‘extended pinball model’ referred to in the main text, and is the best performing simulation of them all. The turquoise line represents a simulation with temporary random responsive bias. Persistent low noise (green) in and of itself performs worse than the original simulation (red), but without it the responsive bias simulation (orange) does not perform as well as with it (purple). The ants outperform all simulations (blue). Black line in (a) represents the arc length of the shortest geodesic path across the maze. Black line in (c) represents the probability of a maze to be solvable (experimental mazes for coverage ≤ 0.55, computer generated mazes for coverage ≥ 0.55). Brown line in (c) represents discrete random walk on a lattice superimposed on the continuous experimental cube mazes. Shaded regions correspond to standard errors of the mean. Wherever no error is visible, the error is small enough to fit within the filled circle marker.
Appendix 2—figure 3
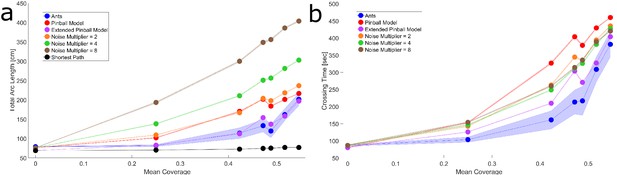
temporarily altered noise simulations.
Total arc length (a) and maze solution time (b) vs. mean coverage for simulations implementing an algorithm with temporarily altered noise when the load gets stuck within a trap, for different fold changes of the original simulation noise parameter value. These simulations perform much worse than the original simulation (red) in terms of arc length but better in terms of solution time. However, the ants (blue) and the extended pinball model (purple) perform better than these simulations in both measures. Shaded regions correspond to standard errors of the mean. Wherever no error is visible, the error is small enough to fit within the filled circle marker.
Appendix 2—figure 4
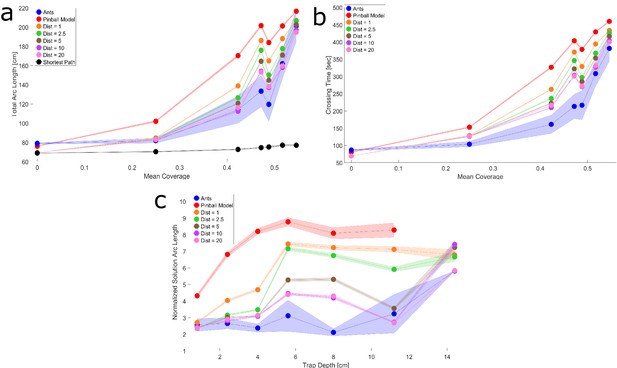
Effect of varying the spatially extended sensing parameter in the altered bias simulations.
Altered bias simulations (low persistent noise) with different spatially extended sensing parameter () used in the algorithm determining the temporarily altered bias direction at every potential point the simulation might get stuck. Plots show total arc length (a) and maze solution time (b) vs. mean coverage for different values for the extended pinball model, as well as the performance of the ants (blue), the original pinball model (red) and the shortest path (black) for comparison. The performance of these different simulations when encountering single traps, measured through arc length, as a function of trap depth is plotted in (c). Low value simulations do not perform as well as , and large simulations do not perform better. Shaded regions correspond to standard errors of the mean. Wherever no error is visible, the error is small enough to fit within the filled circle marker.
Appendix 2—figure 5
Single measure simulation comparison - full results.
A full version of Figure 2d containing three omitted points with strongly inferior performance. Here we use a single inverse measure for the performance of the simulations, , where is the average solution arc length across all cube densities.
Appendix 3—figure 1
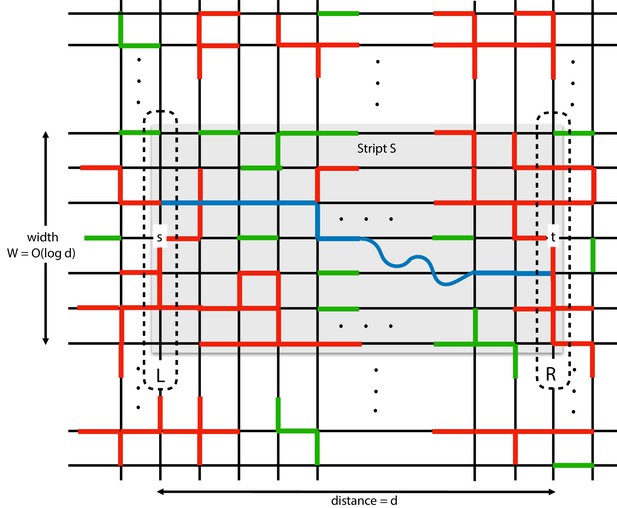
The strip is colored gray.
and are the left and right borders of the strip, respectively. Green are edges of the percolated network that are not part of the infinite component . The remaining colored edges (red or blue) are the edges of . The blue path is the shortest path connecting a node in to a node in , among those that are fully contained in . The length of this path is . As we shall see, all its edges belong to with high probability. The red edges that are the remaining edges of . The percolated strip contains the edges in the strip that are also in the infinite component. Three dots designate that the network expands in the corresponding direction.
Appendix 3—figure 2
The original grid (continuous lines) and the dual graph (dashed lines).
Appendix 3—figure 3
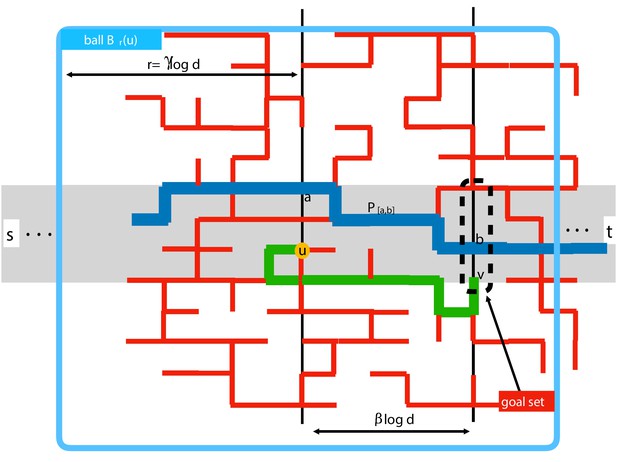
Description of a phase in Algorithm .
The colored short lines are the open edges of the infinite cluster . The strip is colored gray. The blue path is - a shortest path from to among the ones fully contained in the strip . The agent starts the phase at node (yellow circle) and finds a shortest path (colored green) in , its ball of view of radius , towards a node in the goal set . Note that this path is not necessarily fully contained in the percolated strip . The red edges that are the remaining edges of .
Appendix 3—figure 4
Comparison of simulation path lengths.
PDF histograms of percentage increase in path length comparing (a) logarithmic vision algorithm path to strip-constrained shortest path and (b) strip-constrained shortest path to overall shortest path.
Videos
Video 1
An example of cooperative transport of a 1 cm radius ring-shaped load across a 260 cubes maze.
The nest is located to the right. The video is sped up X8 of real-life speed.
Additional files
-
Source data 1
Cube locations data set caption: Coordinates of vertices of cube bases, specified in cm, relative to a known (0,0) point marked on the experimental board.
Each row in every file corresponds to the four vertices of a single cube, ordered as follows: X1, Y1, X2, Y2, X3, Y3, Y4.
- https://cdn.elifesciences.org/articles/55195/elife-55195-data1-v3.zip
-
Source data 2
Load trajectory data set caption: Experimental load trajectories, specified in cm, relative to a known (0,0) point marked on the experimental board.
Format is X,Y coordinates as a function of time. Time interval between samples is 0.04 s, except for videos 1440005 and 1440011, where the time interval is 0.02 s.
- https://cdn.elifesciences.org/articles/55195/elife-55195-data2-v3.zip
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/55195/elife-55195-transrepform-v3.pdf
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Ant collective cognition allows for efficient navigation through disordered environments
eLife 9:e55195.
https://doi.org/10.7554/eLife.55195
