Centering and symmetry breaking in confined contracting actomyosin networks
- Department of Physics, Technion- Israel Institute of Technology, Israel
- Department of Mathematics, University College London, United Kingdom
- Kennedy Institute of Rheumatology, University of Oxford, United Kingdom
- Department of Biology, Brandeis University, United States
- Courant Institute of Mathematical Sciences and Department of Biology, New York University, United States
- Network Biology Research Laboratories and Russell Berrie Nanotechnology Institute, Technion – Israel Institute of Technology, Israel
Figures
Figure 1 with 2 supplements
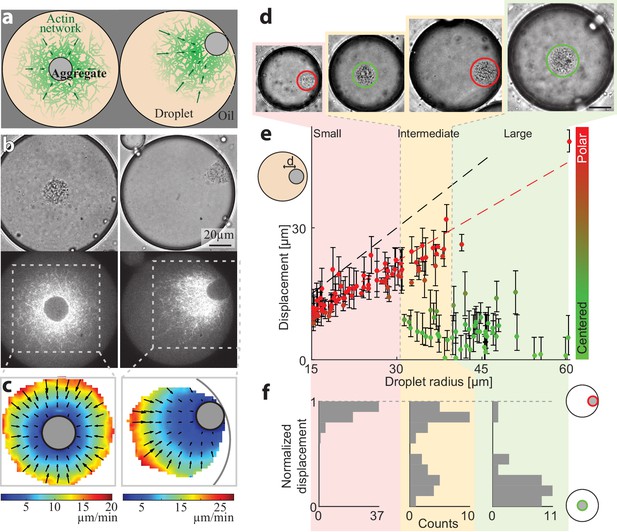
Size-dependent localization of the contraction center.
(a) Schematic illustration of the two stable configurations of the system: a symmetric state with a centered aggregate (left), and a polar state in which the aggregate is positioned near the droplet’s boundary (right). (b) Bright-field (top) and spinning disk confocal (bottom) images of the equatorial cross section of droplets in a symmetric state (left; Video 1) and a polar state (right; Video 2). The aggregate is visible both in the bright-field images, and as an exclusion zone surrounded by regions of high actin network density in the florescence images. The actin network is labeled with GFP-Lifeact. (c) The actin network velocity field as determined by correlation analysis of the time lapse movies of the symmetric and polar droplets in (b). The network exhibits contractile flows directed toward the aggregate in both cases. (d–f) The position of the aggregate surrounding the contraction center was determined for a population of droplets of different sizes, 40 min after sample preparation. (d) Bright-field images of droplets of different sizes. The aggregate position in each droplet was determined from the images, and its displacement from the droplet’s center was measured (see Materials and methods). (e) The displacement of the aggregate from the center is plotted as a function of droplet radius. The dashed black line marks the droplet radius, and the dashed red line marks the displacement where the aggregate reaches the boundary (droplet radius minus aggregate radius). (f) Histograms of the aggregates localization for droplets in different size ranges: small, intermediate and large (Materials and methods). The distance of the aggregate from the center of the droplet was normalized to be between 0 (centered) and 1 (polar). Small droplet (R < 31 µm) are polar (red; left). Intermediate droplets (31 µm < R < 40 µm) exhibit a bipolar distribution with both symmetric and polar droplets (yellow; center). Large droplet (40 µm < R) are symmetric (green; right).
Figure 1—figure supplement 1
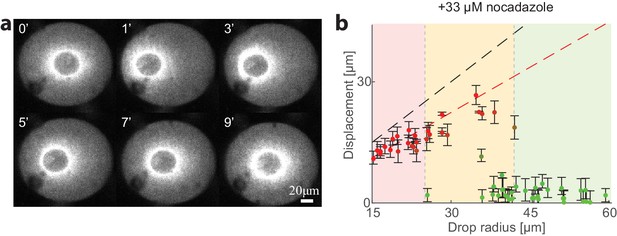
Contraction center localization and centering dynamics are not dependent on microtubules.
Aggregate positions and recentering dynamics were measured in droplets supplemented with 33 μM Nocodazole, which disrupts microtubule assembly. (a) Spinning-disk confocal images from a timelapse movie showing the recentering of the contraction center following a magnetic perturbation in a droplet with Nocodazole-treated extract. The actin network is labeled with GFP-Lifeact. (b) The position of the aggregate surrounding the contraction center was determined for a population of droplets formed with Nocodazole-treated extract. The displacement of the aggregate from the center is plotted as a function of droplet radius for unperturbed droplets. The colored regions depict the different size ranges: small droplets that are primarily polar (red), intermediate range with both polar and symmetric droplets (yellow), and large droplets which are mostly centered (green). The centering dynamics and localization distribution are similar to the untreated condition (Figures 1 and 3).
Figure 1—figure supplement 2
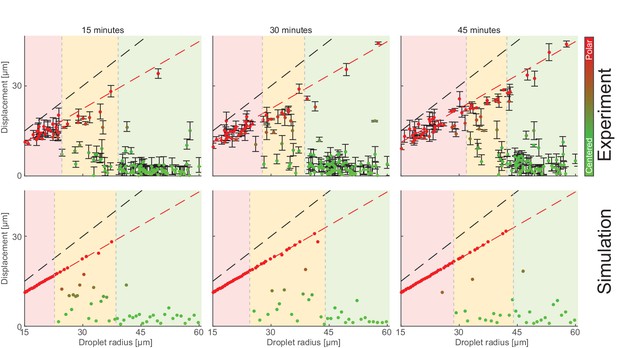
Size-dependent localization of the contraction center as a function of time.
The position of the aggregate surrounding the contraction center was determined for a population of droplets of different sizes, 15 min (left), 30 min (center) or 45 min (right) after sample preparation. The displacement of the aggregate from the center is plotted as a function of droplet radius based on the experimental data (top) and the simulation (bottom; see Appendix 2). The colored regions depict the different size ranges: small droplets that are primarily polar (red), intermediate range with both polar and symmetric droplets (yellow), and large droplets which are mostly centered (green). The dashed black line marks the droplet radius, and the dashed red line marks the displacement where the aggregate reaches the boundary (droplet radius minus aggregate radius). The centered state is metastable, with larger droplets becoming polar over time.
Figure 2 with 1 supplement
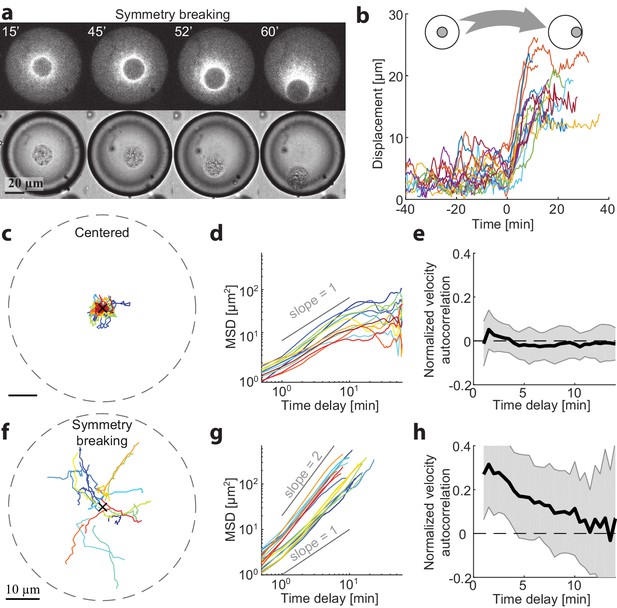
Dynamics of centering and symmetry breaking.
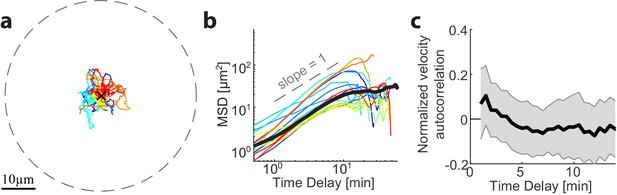
The dynamics of the contraction center were followed by imaging droplets over time for an hour.(a) Spinning disk confocal (top) and Bright-field (bottom) images from a time lapse movie (Video 3) of a droplet that starts in a centered state and breaks symmetry to become polar. (b) The symmetry breaking transition of droplets from a symmetric state to a polar state was characterized in 18 different droplets. The displacement of the aggregate from the center of the droplet is shown as a function of time for the different droplets. Time zero is defined as the onset of symmetry breaking for each droplet (see Materials and methods). (c-h) Analysis of the dynamics of aggregate position as a function of time in droplets in the centered state (c-e; N = 12) and during symmetry breaking (f-h; N = 18). (c,f) Tracks depicting the position of the aggregate in different droplets. (d,g) The mean squared displacement of aggregate positions as a function of time. The droplets in the centered state exhibit confined random fluctuations (d), whereas during symmetry breaking, the movement is directed (g). (e,h) The normalized velocity autocorrelation (mean ± STD; averaged over different droplets) is shown for the tracks on the left. The velocity autocorrelation (for t ≥ 0.5 min) is essentially zero in the centered state (e). During symmetry breaking, the aggregate velocity exhibits a positive correlation for time scales of up to ∼ 10 min (h).
Figure 2—figure supplement 1
Analysis of the dynamics of aggregate position as a function of time in droplets before symmetry breaking.
(a) The position of the aggregate in different droplets that eventually break symmetry was followed (as shown in Figure 2b). Tracks of the aggregates position are depicted during the initial period in which the aggregates remained nearly centered (i.e. for t < 0 in Figure 2b; N = 17). (b) The mean squared displacement of the aggregate position in different droplet is shown as a function of time. Thick gray line – mean MSD of droplets that remain centered for over an hour as shown in Figure 2d. The aggregates exhibit confined random fluctuations before breaking symmetry, similar to the dynamics of aggregates in centered droplets (Figure 2d). (c) The normalized velocity autocorrelation (mean ± STD; N = 17, averaged for the different droplets) is shown for the tracks on the left. The velocity is considerably less correlated over time than during the symmetry breaking phase (Figure 2h).
Figure 3 with 3 supplements
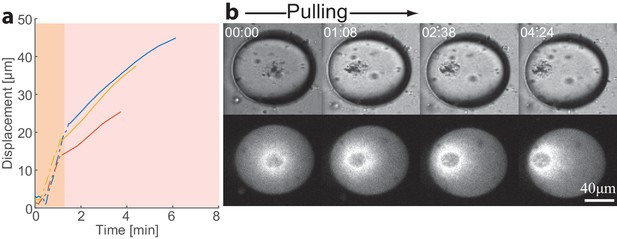
Recentering following magnetic perturbations.
The stability of the centered state was examined by introducing superparamagnetic beads that become trapped within the aggregate, and applying external magnetic fields to displace the aggregate toward the droplet’s boundary. (a) Schematic illustration of the experimental setup. A magnetic needle is introduced from the side, near a droplet placed within a glass capillary with a rectangular cross-section. The magnet exerts a pulling force on the aggregate, displacing it toward the side. The magnetic needle is then removed and the aggregate position is tracked. (b) Bright-field image of a sample, showing the tip of the magnetic needle positioned ~200 µm from a droplet in a capillary. (c) Time traces showing the displacement of the aggregate from the center (black) and its radial velocity (green) during the magnetic perturbation experiment (Video 4). During the pulling phase, the magnetic needle is held at a fixed position and the aggregate is displaced toward the side of the droplet (‘pulling phase’). After the needle is removed, the aggregate starts moving and reaches a maximal inward velocity after ~2 min (‘reorganization phase’). The recentering continues with the aggregate gradually slowing down and eventually stopping as it approaches the droplet’s center (‘recentering phase’). (d) Spinning-disk confocal images of the actin network labeled with GFP-Lifeact from a timelapse movie showing the recentering of the contraction center following a magnetic perturbation (Video 4). (e) The position of the aggregate as a function of time after removing the magnet is shown for different droplets. (f) The recentering velocity as a function of time is shown for different droplets. (g) The recentering velocity is plotted as a function of the displacement from the droplet center. (e-g) Dotted lines - reorganization phase, solid lines - recentering phase. The thick black line depicts the average over the collection of droplets (shaded region - standard deviation).
Figure 3—figure supplement 1
Magnetic pulling experimental setup.
(a) Image of the manipulator with the magnetic needle mounted on the inverted microscope. (b) Image of the magnetic needle near the sample placed in a rectangular capillary. (c) Bright field image overlaid with a spinning disk confocal image of a droplet containing fluorescent beads. Fluorescent beads were used only for demonstration; during the experiments non-fluorescent, magnetic beads were used. Inset. Zoomed confocal image of the fluorescent beads localized in the aggregate.
Figure 3—figure supplement 2
Transition to a polar state following a magnetic perturbation.
During the magnetic pulling experiments, 5 out of 31 droplets broke symmetry following the perturbation. (a) The position of the aggregates in three droplets that broke symmetry after the perturbation are plotted as a function of time. The dashed lines depict the pulling phase, while the solid lines depict the dynamics after the magnet was removed. (b) Bright-field and spinning-disk confocal images of the actin network labeled with GFP-Lifeact from a time lapse movie of a droplet which became polar after the magnetic perturbation (Video 5).
Figure 3—figure supplement 3
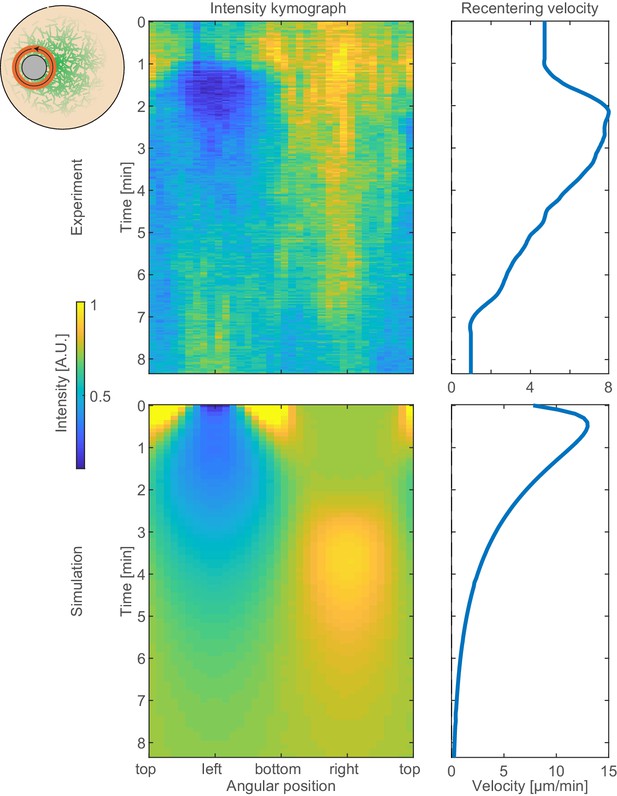
Asymmetric actin network distribution during recentering.
Left: A kymograph showing the angular distribution of the actin network density around the aggregate (x-axis; scheme on the left) as a function of time (y-axis) during the magnetic perturbation experiments (top) and their simulation (bottom). Right: Graphs depicting the recentering velocity as a function of time during the magnetic perturbation experiments (top) and their simulation (bottom). The correlation between the asymmetry in the actin network distribution around the aggregate and the recentering velocity is evident both in the experiments and in the simulations.
Figure 4 with 4 supplements
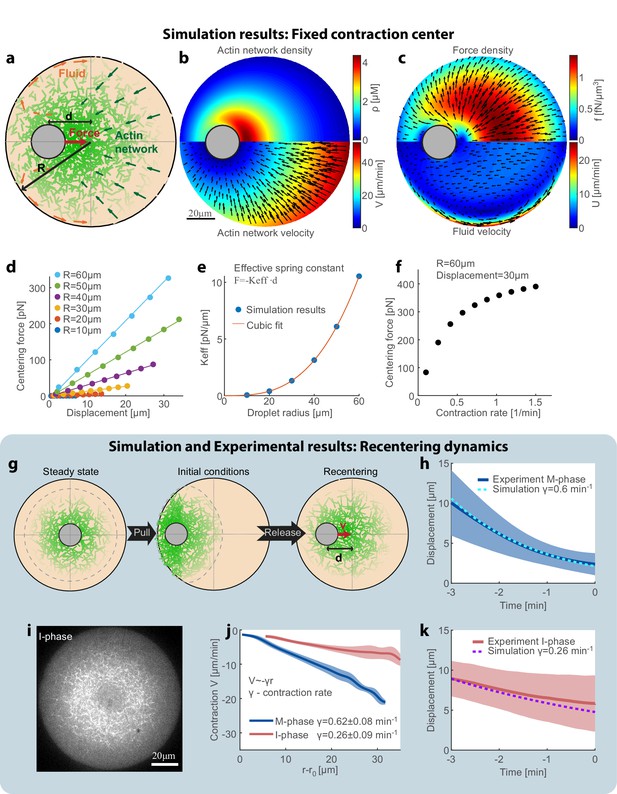
Recentering model: friction between the contracting network and the fluid cytosol generates a centering force.
(a) Schematic illustration of the model. The system is modeled as a two-phase system composed of a contracting actin network and the surrounding fluid. (b–f) Simulation results of the model when the aggregate position is held fixed (Appendix 1). The simulation results for the steady-state actin network density and flow (b) and the surrounding fluid flow and force density (c) are shown. (d) The centering force is calculated from the simulation as the net force exerted on the aggregate as a function of the displacement from the droplet center at steady-state. The net centering force is plotted as a function of the displacement for droplets of different sizes (dots- simulations results; line- linear fit). (e) The effective spring constant of the centering force, determined from the slope of the linear fit to the simulation results in (d), is plotted as a function of the droplet radius (R). The effective spring constant increases as R3. (f) The centering force is plotted as a function of the network contraction rate. The centering for was calculated for a displacement of 30 µm in a droplet with a radius of R = 60 µm. The centering force increases with network contraction. (g–k) In the dynamic model (Appendix 1), the aggregate position is part of the dynamic variables of the system and moves according to the net force acting on it. (g) Schematic illustration of the dynamic model used to model the magnetic perturbation experiments. The initial conditions are obtained by displacing a centered steady-state configuration toward the side. Subsequently, the dynamics of the system lead to recentering of the aggregate. (h) The simulation results for the displacement of the aggregate as a function of time (dashed line) are compared to the average displacement determined experimentally in M-phase extracts (standard condition) (blue line; mean ± STD; Figure 3e). (i) Spinning-disk confocal image of the equatorial cross section of an I-phase extract droplet. The actin network is labeled with GFP-Lifeact. (j) Network contraction velocity measured as a function of distance from the inner network boundary, for M-phase and I-phase extracts (mean ± STD). The contraction rate, γ, is determined from the slopes of linear fits to the data (Malik-Garbi et al., 2019). (k) The simulation prediction for the displacement of the aggregate as a function of time (dashed line) are compared to the average displacement determined experimentally in I-phase extracts (red line; mean ± STD). The observed average I-phase contraction rate is used as an input for the simulation which contains no additional fit parameters.
Figure 4—figure supplement 1
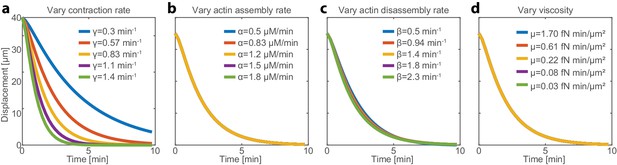
The network contraction rate is the main control parameter for the hydrodynamic centering mechanism.
The sensitivity of the hydrodynamic centering mechanism to the characteristics of the actin meshwork and the fluid cytosol was evaluated by numerical simulations of the recentering dynamics, performed using different network and fluid parameters. (a-d) The simulation results for the contraction center displacement as a function of time following a magnetic perturbation are shown. The simulations were performed with the following parameter values R = 50 μm; α = 1 μM/min; β = 1.43 min−1; γ = 0.67 min−1; μ = 1.7 fN min/μm2, except for the parameter varied in each graph as indicated. The network contraction rate is the main control parameter for the recentering mechanism. The recentering dynamics are considerably faster with higher network contraction rates (a), whereas the network assembly (c) and disassembly rates (d), and the fluid viscosity (b), have little influence on the recentering dynamics.
Figure 4—figure supplement 2
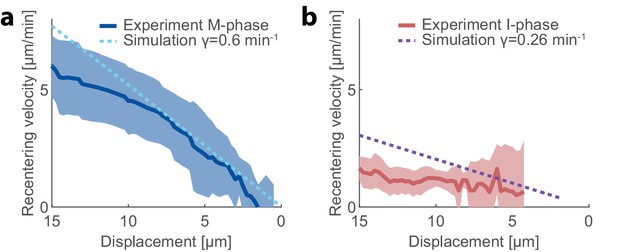
Aggregate recentering velocity in M-phase and I-phase extracts.
(a,b) The aggregate recentering velocity is depicted as a function of the displacement from the droplet center. The experimental results from magnetic pulling experiment are shown for (a) standard M-phase extracts (blue line; mean ± STD; Figures 3e and 4h) and (b) I-phase extracts (red line; mean ± STD; Figure 4k). The experimental data are compared to the results of simulations in M-phase or I-phase extracts (dashed lines), respectively. The observed contraction rates in M-phase and I-phase extracts (Figure 4j) are used as inputs for the respective simulations with no additional fit parameters.
Figure 4—figure supplement 3
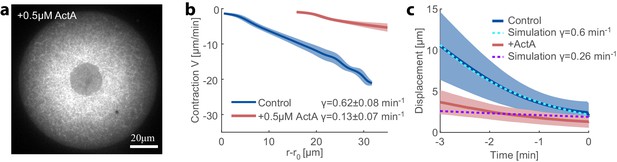
Recentering dynamics in ActA-supplemented extract.
(a) Spinning-disk confocal image of the equatorial cross section in droplets supplemented with 0.5 μM ActA. The actin network is labeled with GFP-Lifeact. (b) Network contraction velocity measured as a function of distance from the inner network boundary, for control and ActA supplemented extracts (mean ± STD). The contraction rate, γ, is determined from the slopes of linear fits to the data (c) The simulation predictions for the displacement of the aggregate as a function of time (dashed lines) are compared to the average displacement determined experimentally in control and ActA supplemented extracts (solid line; mean ± STD).
Figure 4—figure supplement 4
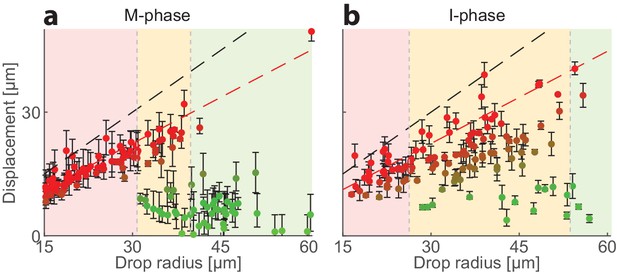
Cell-cycle dependence of the localization of the contraction center.
The localization pattern in I-phase extract, which exhibits weak contraction (Field et al., 2011), is characterized by less centered droplets and more symmetry breaking compared to M-phase extract. The position of the aggregate surrounding the contraction center was determined for a population of droplets formed with M-phase extract (left) or I-phase extract (right). The displacement of the aggregate from the center is plotted as a function of droplet radius. The colored regions depict the different size ranges: small droplets that are primarily polar (red), intermediate range with both polar and symmetric droplets (yellow), and large droplets which are mostly centered (green). The dashed black line marks the droplet radius, and the dashed red line marks the displacement where the aggregate reaches the boundary (droplet radius minus aggregate radius). I-phase droplets are more likely to be polar, even at large droplet sizes that remain centered in M-phase.
Figure 5 with 2 supplements
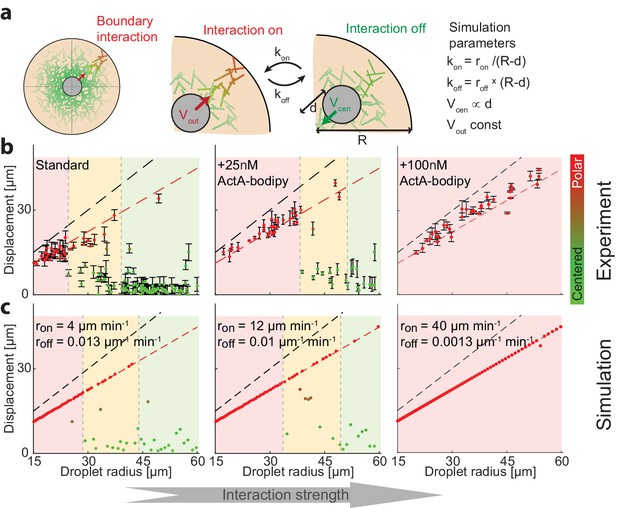
Symmetry breaking is induced by an attractive interaction with the boundary.
(a) Schematic illustration of the system which contains a bulk contracting network that has some attractive interaction with the boundary. Experimentally, the interaction with the boundary can be enhanced by adding increasing concentrations of Bodipy-conjugated ActA that localizes to the water-oil interface and nucleates actin filaments there (Abu Shah and Keren, 2014). In simulations, we introduce a clutch that can engage and disengage stochastically, connecting the contracting actin network with the boundary (Appendix 2). The competition between the recentering force that drives the aggregate to the center and the attractive interaction with the boundary, leads to size-dependent localization. (b) The aggregate displacement as a function of droplet radius is shown for standard conditions (left), and samples supplemented with 25 nM (center) or 100 nM (right) Bodipy-ActA. The colored regions depict the different size ranges: small droplets that are primarily polar (red), intermediate range with both polar and symmetric droplets (yellow), and large droplets which are mostly centered (green). The dashed black line marks the droplet radius, and the dashed red line marks the displacement where the aggregate reaches the boundary (droplet radius minus aggregate radius). As the interaction with the boundary is enhanced by increasing ActA concentrations, larger droplets are found in a polar state. (c) Simulation results for the aggregate displacement as a function of droplet radius. The interaction with the boundary is enhanced by increasing the clutch engagement rate (kon) and decreasing the disengagement rate (koff), resulting in changes in the size-dependent localization of the aggregates that resemble the changes observed experimentally in (b).
Figure 5—figure supplement 1
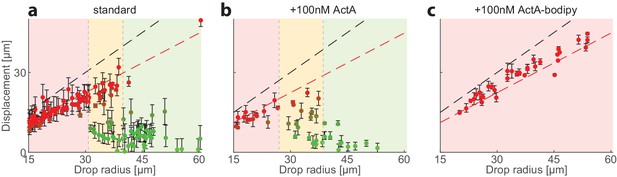
Size-dependent localization of the contraction center is not influenced by low levels of bulk ActA.
The position of the aggregate surrounding the contraction center was determined for a population of droplets formed with 80% extract (standard; left), and samples supplemented with 100 nM ActA in bulk (center) or 100 nM ActA-Bodipy which localizes at the interface. The displacement of the aggregate from the center is plotted as a function of droplet radius. The colored regions depict the different size ranges: small droplets that are primarily polar (red), intermediate range with both polar and symmetric droplets (yellow), and large droplets which are mostly centered (green). The dashed black line marks the droplet radius, and the dashed red line marks the displacement where the aggregate reaches the boundary (droplet radius minus aggregate radius). While the addition of 100 nM ActA-Bodipy at the interface leads to complete symmetry breaking (right), the same concentration of ActA in bulk does not have a significant effect on the size-dependent localization pattern (center).
Figure 5—figure supplement 2
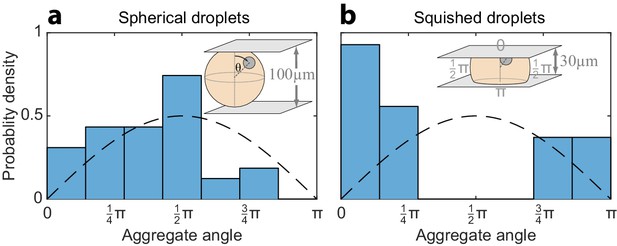
Sample geometry induces anisotropy in the localization of the aggregate in the polar state.
The angular distribution of the position of polar aggregates was determined for (a) a population of spherical droplets (100 µm chamber height), and (b) a population of pancake-shaped droplets, squished in a 30 µm-high chamber. The measured angular probability-density histograms are plotted together with the angular distribution predicted for an isotropic process (dashed line). In spherical droplets, the measured angular distribution is broad, whereas in squished droplets there is an obvious preference to break symmetry toward the top and bottom interface. Both squished and spherical droplets exhibit a slight upwards bias, (toward θ = 0), implying that the aggregate is likely buoyant relative to the surrounding fluid.
Videos
Video 1
Steady-state dynamics in a symmetric droplet.
This movie shows spinning disc confocal images of a contracting actomyosin network labeled with GFP-Lifeact in a symmetric droplet (Figure 1b,c, left). The droplet was squished in a 30µm-high chamber to improve the imaging. Images were taken at the equatorial plane.
Video 2
Steady-state dynamics in a polar droplet.
This movie shows spinning disc confocal images of a contracting actomyosin network labeled with GFP-Lifeact in a polar droplet (Figure 1b,c, right). The droplet was squished in a 30µm-high chamber to improve the imaging. Images were taken at the equatorial plane.
Video 3
Symmetry breaking in a droplet that transitions from a symmetric state into a polar state.
The dynamics of the actin network labeled with GFP-Lifeact in a spherical droplet were followed by spinning disc confocal time lapse imaging. The movie shows a symmetry breaking process, in which the aggregate moves from the center of the droplet toward the side.
Video 4
Recentering dynamics following a magnetic perturbation.
This movie shows spinning disc confocal and bright-field images of a magnetic perturbation experiment (Figure 4b–d). The aggregate was pulled from the center using a magnetic needle, and subsequently recentered after the magnet is removed.
Video 5
Transition to a polar state following a magnetic perturbation.
This movie shows spinning disc confocal and bright-field images of a magnetic perturbation experiment in which the droplet became polar following the perturbation (Figure 3—figure supplement 2). The aggregate was pulled from the center using a magnetic needle, and subsequently continued moving in the same direction until it reached the boundary.
Tables
Appendix 1—table 1
Variables.
| Variables | ||
|---|---|---|
| Name | Meaning | Computed order of magnitude |
| Fluid velocity | 10µm/min | |
| Actin network velocity | 10µm/min | |
| Actin network density | 5µM | |
| Hydrodynamic force density | fN/µm3 | |
| Distance of the aggregate to the droplet center | 10µm | |
Appendix 1—table 2
Parameters.
| Biological parameters | |||
|---|---|---|---|
| Name | Meaning | Value | Reference |
| µ | Fluid viscosity | 1.7 10-4pN min/µm2 | 10x the viscosity of water |
| Actin network permeability | see (Equation A4) | Equation (19) in Schmidt et al. (1989) and in Supp Mat of Charras et al. (2005) | |
| Contraction rate | 0.67/min (M-phase) 0.26/min (I-phase) | Measured experimentally (Malik-Garbi et al., 2019). | |
| Actin assembly rate | 1 µM/min | Estimated to give experimentally measured density | |
| Actin disassembly rate | 1.43/min | Measured experimentally (Malik-Garbi et al., 2019). | |
| Droplet radius | 20–60 µm | Measured experimentally | |
| Aggregate radius | 4–12 µm | Proportional to droplet radius, measured experimentally (Malik-Garbi et al., 2019). | |
Appendix 1—table 3
Numerical Parameters.
| Numerical parameters | ||
|---|---|---|
| Name | Meaning | Value |
| Spatial step, density simulation | 0.5–0.75 µm | |
| Temporal step, density simulation | ≈ 10-3min | |
| Temporal step | 0.5 min | |
| Maximum mesh edge length of FEM mesh | 1 µm | |
Appendix 2—table 1
Parameters.
| Parameters | |||
|---|---|---|---|
| Name | Meaning | Value | Reference |
| Symmetry breaking velocity | 2 µm min-1 | Measured experimentally (Figure 2b) | |
| Centering velocity coefficient | 0.5 min-1 | Measured experimentally (Figure 3g) and from simulation | |
| Off-rate coefficient | 0.0013- 0.0125 µm-1 min-1 | Order of magnitude estimated from experiment (Figure 2b) | |
| On-rate coefficient | 4 - 40 µm min-1 | Estimated to give reasonable results | |
| Aggregate diffusion coefficient | 0.5 µm2 min-1 | Measured experimentally | |
| Droplet radius | 15 - 100 µm | ||
| Time step | 0.1 min | ||
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Centering and symmetry breaking in confined contracting actomyosin networks
eLife 9:e55368.
https://doi.org/10.7554/eLife.55368
