Figures and data in Modelling the emergence of whisker barrels | eLife

Figures
Additional files

4 figures and 1 additional file

Figures

Figure 1 with 1 supplement

Download asset Open asset

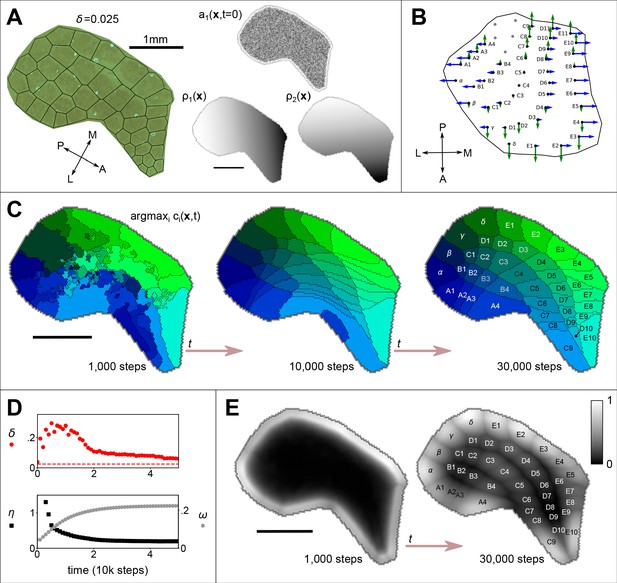
The emergence of whisker barrels.

(A) Left shows a cytochrome oxidase (CO) stain obtained from rat S1 by Zheng et al., 2001, with black lines to delineate barrels and to measure departure (Honda-δ; see Senft and Woolsey, 1991) from a perfect Voronoi tessellation. Right shows the initial distribution of axon branching density (a) for one thalamocortical projection, and two molecular guidance fields (ρ), where the domain S has been traced from the CO stain. (B) The strengths of interaction γ with fields $ρ_{1}$ and $ρ_{2}$ are indicated for each of 41 projections by the lengths of green and blue arrows respectively, assuming that similar fields aligned to the posterior-anterior and medial-lateral axes in the ventroposterior medial nucleus of the thalamus are sampled at the locations of putative barreloid centres (reconstructed from Haidarliu and Ahissar, 2001, their Figure 5b). (C) Results for the example simulation, with parameters $N = 41$ , $α = 3.6$ , $β = 16.67$ , $k = 3$ , $D = 0.5$ , $γ \in \pm 2$ , $ϵ = 1.2$ and $δ t = 0.0001$ . Colours indicate the thalamic projection for which the connection density is maximal, barrel labels are located at the centroid of each region and black lines delineate boundaries (see Figure 1—video 1). (D) Red dots show the Honda– $δ (t)$ metric obtained from the simulation approaching that obtained from the real barrels in A (dotted line); black squares show the pattern difference metric $η (t)$ , and reveal the emergence of a correspondence between the real and simulated barrel shapes (units mm³); grey hexagons show how selectively each cortical site is innervated; $ω (t) = ∯_{S} μ (x, t) d S$ , where $μ (𝐱) \equiv \max_{i} (c_{i} (𝐱, t)) / \sum_{j = 1}^{N} c_{j} (𝐱, t)$ . (E) Plotted across the cortical sheet, the selectivity develops to reveal an alignment with the emergent barrel boundary shapes. Greyscale colour indicates values of $μ (𝐱)$ . All scale bars 1 mm.

Figure 1—video 1

Download asset

posterframe for video — Video corresponding to Figure 1C in the main paper.

Simulation parameters were $N = 41$ , $α = 3.6$ , $β = 16.67$ , $k = 3$ , $D = 0.5$ , $γ \in \pm 2$ , $ϵ = 1.2$ and $δ t = 0.0001$ . Colours indicate the thalamic projection for which the connection density is maximal and black lines delineate boundaries. Barrel labels are always located at the centroid of their field(s). The final frame in the movie is step 30000 of the simulation.

Figure 2

Download asset Open asset

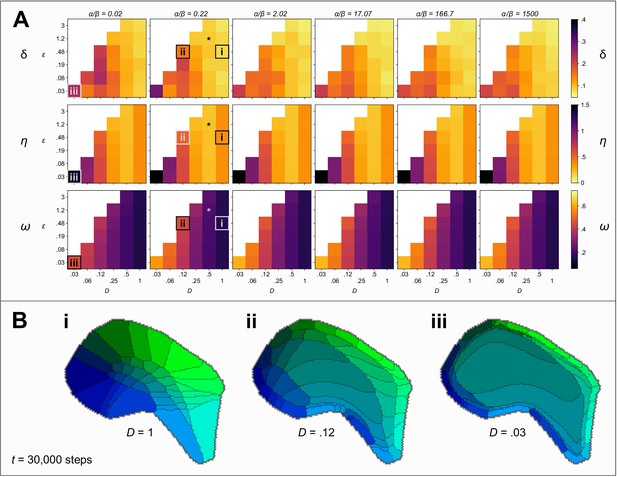
Exploring the parameter space.

(A) Colour indicates the quality of the pattern at $t = 30000$ steps, against three measures: Low values of Honda–δ (top row) suggest a Voronoi-like pattern of fields. The pattern difference, η (middle row) measures the difference in the area and arrangement of barrels in real and simulated fields. The connection selectivity, ω (bottom row), measures the specificity with which the cortical sheet is innervated. Colour maps are chosen so that lighter (orange and yellow) colours indicate higher quality patterns against each measure. White squares indicate combinations of parameters for which simulations were numerically unstable. The parameter space explored is three dimensional with the ratio $α / β$ varying between plots, and the competition parameter $ϵ$ and the diffusion constant D varying within plots. An asterisk (*) marks the parameters used in Figure 1. Boxes (i), (ii) and (iii) mark parameter sets for which corresponding patterns are shown in B (for $t = 30000$ steps). (B) Varying the diffusion constant D generates qualitatively different patterns. Higher values cause expansions of the peripheral barrels and a corresponding compression of the inner barrels (i). Lower values instead cause an expansion of the central barrels and compression of the peripheral barrels (ii). Further reducing the rate of diffusion (iii), which is equivalent to increasing the size of the domain and hence simulating development in an animal with a larger cortex, causes a large area to be occupied by projections with intermediate interaction parameters; those with strong interaction parameters are compressed around the edge of the domain, and consequently a barrel pattern fails to form.

Figure 3

Download asset Open asset

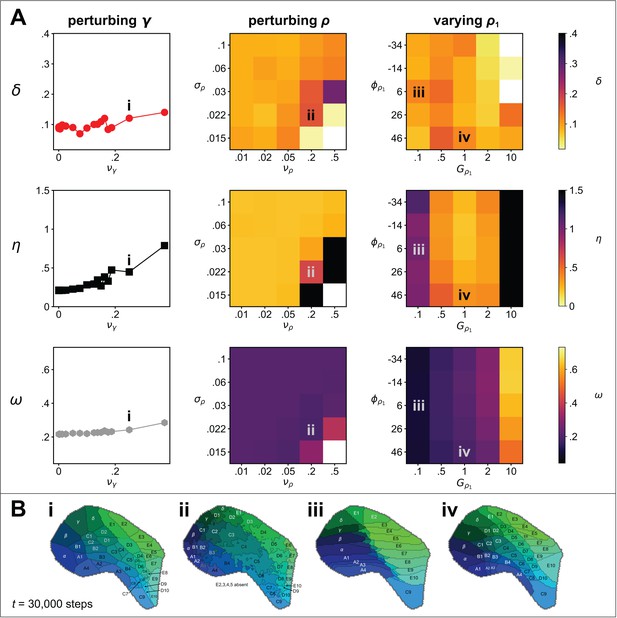
Sensitivity analysis.

(A) Metrics of map quality $δ (t)$ (top row), $ω (t)$ (middle row) and $η (t)$ (bottom row), were evaluated at $t = 30000$ steps. The y-axes and colour scales have identical ranges to the colour scales in Figure 2, for easy comparison. Left column: The effect of adding noise drawn from a uniform distribution, $(γ_{m a x} - γ_{m i n}) U (0, ν_{γ})$ , to the values of the interaction parameters, γ used in Figure 1. Middle column: The effect of changing the magnitude and the length scale of noise applied to the guidance fields. Uniform random noise $(ρ_{m a x} - ρ_{m i n}) U (0, ν_{ρ})$ was added to each (hexagonal) element of $ρ_{1} (𝐱)$ and $ρ_{2} (𝐱)$ and the result was smoothed by convolution with a symmetric 2D Gaussian kernel of width $σ_{ρ}$ . Right column: The effect of setting the rotational angle of the linearly varying guidance field, $ρ_{1} (𝐱)$ , to $ϕ_{ρ_{1}}$ , and modifying its overall gain to $G_{ρ_{1}}$ , whilst keeping the parameters of $ρ_{2} (𝐱)$ unchanged from those used in the example simulation, for which $ϕ_{ρ_{2}} = 84$ ° and $G_{ρ_{2}} = 1$ . (B) Four ways in which the perturbations in A affect the patterns. (i) The effect of significant interaction parameter noise is to introduce topological defects. (ii) High magnitude, short length scale noise in $ρ (𝐱)$ leads to non-straight edges between adjacent barrels. (iii) Reducing the slope of gradient $ρ_{1}$ (by a factor of 10) causes barrel rows B, C and D to become ‘crushed’ down the centre line, and edge barrels to dominate. (iv) Rotating $ρ_{1}$ by 20° causes a slight distortion of the pattern, resulting in an overall anticlockwise rotation of the field locations.

Figure 4

Download asset Open asset

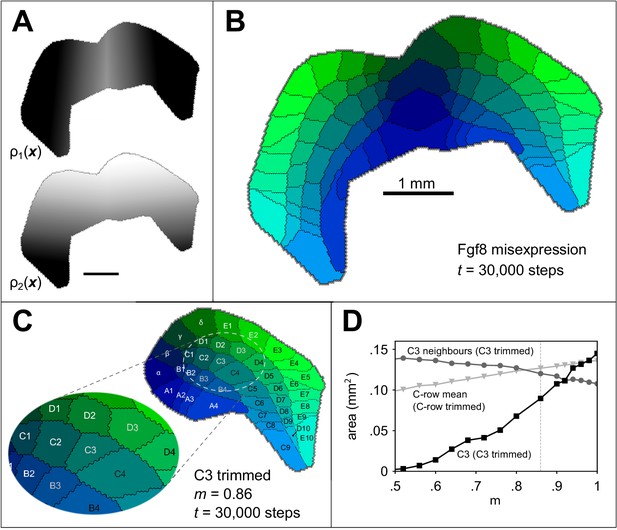
Simulating altered barrel development.

Guidance fields (A) and emergent barrel pattern (B) in a Fgf8 misexpression experiment (Assimacopoulos et al., 2012), simulated by reflecting $ρ_{1}$ from Figure 1A at the join of the original boundary with its mirror. All other model parameters match those in Figure 1C. C Simulating whisker trimming by reducing the competitiveness, $ϵ$ , of one projection. For C3 only, $ϵ$ was multiplied by $m \in (0, 1)$ . The pattern shown is that formed after 30000 steps with $m = 0.86$ , which reduces the size of the C3 field to 65% of its original size, matching the average barrel area reduction observed by Kossut, 1992. D The area of the C3 barrel (black squares) reduces as m is reduced, whereas the mean area of neighbouring barrels (B3, C2, C4, D2 and D3, grey circles) increases. The dotted grey line indicates $m = 0.86$ for comparison with panel C. If the $ϵ$ value is instead reduced for all row C projections (including the interstitial γ projection), the mean row C barrel area is only slightly reduced (light grey triangles). In this case, the mean area of a simulated row C barrel at $m = 0.86$ is 91% of that for $m = 1$ .

Additional files

Transparent reporting form: https://cdn.elifesciences.org/articles/55588/elife-55588-transrepform-v1.docx
Download elife-55588-transrepform-v1.docx

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Sebastian S James
Leah A Krubitzer
Stuart P Wilson

(2020)

Modelling the emergence of whisker barrels

eLife 9:e55588.

https://doi.org/10.7554/eLife.55588

Sign up for email alerts

Privacy notice