Stoichiometric interactions explain spindle dynamics and scaling across 100 million years of nematode evolution
- Department of Molecular and Cellular Biology and School of Engineering and Applied Sciences, Harvard University, United States
- Center for Computational Biology, Flatiron Institute, United States
- Experimental Center, Faculty of Medicine Carl Gustav Carus, Germany
- Department of Biology and Center for Genomics & Systems Biology, New York University, United States
- Courant Institute, New York University, United States
Figures
Figure 1 with 5 supplements
High-throughput microscopy and measurements of spindle variation across a panel of C. elegans recombinant inbred advanced intercross lines.
(A–E) High-throughput microscopy and image processing of C. elegans embryos across the RIAIL panel. (A) Five replicates per line, for 182 RIAILs, were imaged. (B) A sample picture from high-throughput 4D DIC microscopy (3D time-lapse) of C. elegans embryos. Scale bar 20 μm. (C) Automated analysis of ~12,000,000 microscopy images from ~10,000 C. elegans embryos using high-performance computing. (D) Segmentation of the mitotic spindle and tracking of its poles (centrosomes) during the first cell division. Scale bar 10 μm. (E) Spindle length as a function of time for the embryo shown in D (red curve, sigmoid function fit to the data). Initial and final spindle length and elongation rate are indicated. (F–N) Quantitative variation in spindle size and positioning across the RIAIL panel (F, I, and L, solid dots, mean; shaded region, standard deviation; H, K, and N, gray line, standard error): (F) Spindle length as a function of time for two RIAILs, QX18 (n = 12) and QX145 (n = 42). Inset shows sample embryos from these two lines (red arrow, distance between spindle poles). Scale bar 10 μm. (G) Measured distribution of the initial spindle length in embryos from QX18 (n = 12) and QX145 (n = 42). (H) Ranked order plot of the line-averaged initial spindle length for each of the 182 RIAILs. (I) Spindle length as a function of time for two RIAILs, QX41 (n = 34) and QX139 (n = 11). Inset shows sample embryos from these two lines (red arrow, distance between spindle poles). Scale bar 10 μm. (J) Measured distribution of the final spindle length in embryos from QX41 (n = 34) and QX139 (n = 11). (K) Ranked order plot of the line-averaged final spindle length for each of the 182 RIAILs. (L) Centrosome distance as a function of time for two RIAILs, QX18 (n = 12) and QX30 (n = 31). Inset shows sample embryos from these two lines (red arrow, distance between spindle pole and cell periphery). Scale bar 10 μm. (M) Measured distribution of the final centrosome distance in embryos from QX18 (n = 12) and QX30 (n = 31). (N) Ranked order plot of the line-averaged final centrosome distance for each of the 182 RIAILs.
Figure 1—figure supplement 1
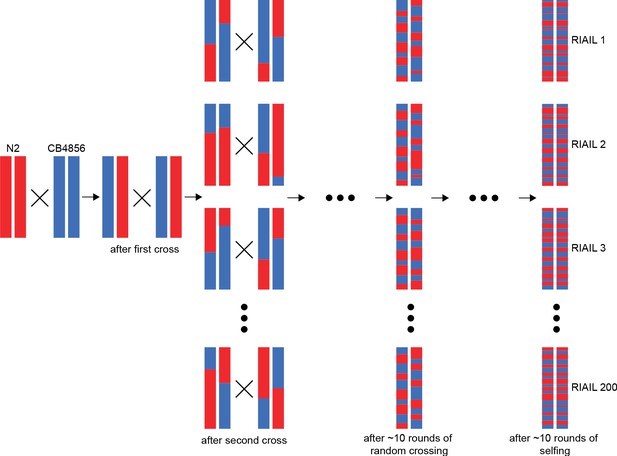
Breeding design for recombinant inbred advanced intercross lines.
The panel of 182 RIAILs was generated from ten rounds of random intercrossing, followed by ten rounds of selfing. The final lines were genotyped at 1454 markers along the genome.
Figure 1—figure supplement 2
Cell division traits.
Illustration of cell division traits (see Materials and methods).
Figure 1—figure supplement 3
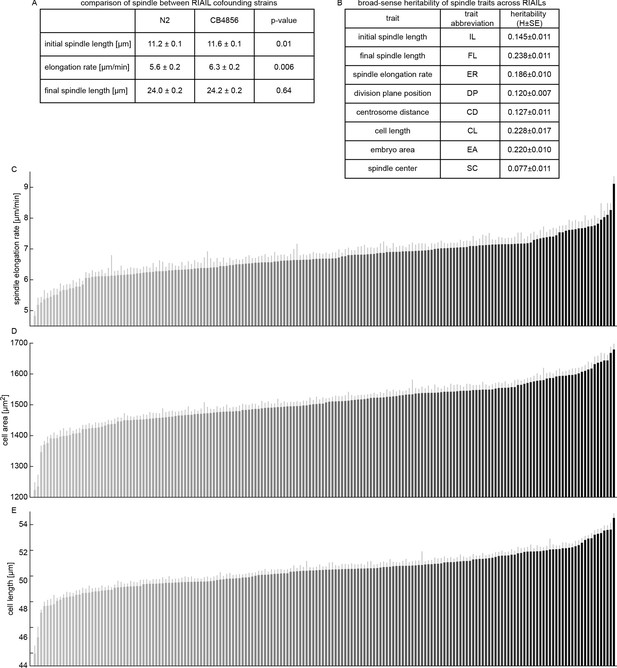
Variation of spindle traits across the RIAIL panel.
(A) Measured spindle traits for N2 and CB4856. (B) Broad-sense heritability of spindle traits (H, with standard error SE) across the RIAIL panel. (C-E) Ranked order plots of the line-averaged of spindle elongation rate, cell area, and cell length for each of the 182 RIAILs (gray line, standard error).
Figure 1—video 1
High-throughput 3D microscopy of spindle in C. elegans embryos.
A single plane from 3D time-lapse DIC microscopy of multiple C. elegans embryos. Scale bar 10 μm. This supplementary movie corresponds to Figure 1B.
Figure 1—video 2
Segmentation of the spindle in C. elegans.
Segmentation of the spindle (green) and centrosomes (red) in the first mitotic division of C. elegans. Only one plane from the 3D DIC time-lapse and segmentation is shown. This supplementary movie corresponds to Figure 1D.
Figure 2
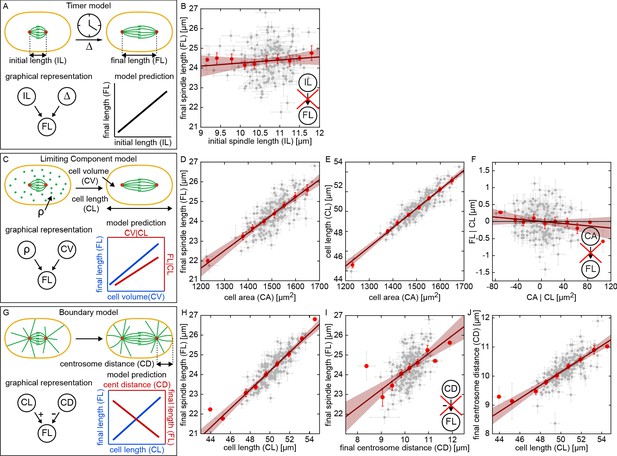
Testing models of spindle size control and coordination.
(A, C, and G) possible models of spindle size control and associate predictions. (B, D-F) and (H-J) measured correlations and partial correlations of spindle traits to test models (gray dots, mean and standard error of RIAILs; red dots, binned averages; red line, linear fit with 95% prediction bounds). (A) Overview of the Timer model. Initial spindle length (IL), spindle elongation (), and final spindle length (FL) are indicated (). (B) Final spindle length as a function of initial spindle length across the RIAIL panel. Inset indicates a lack of correlation between initial and final spindle length, in disagreement with the prediction of the Timer model. (C) Overview of the Limiting Component model. Density of the limiting component (), cell volume (CV), and cell length (CL) are indicated. (D) Final spindle length as a function of cell area across the RIAIL panel. (E) Cell length as a function of cell area across the RIAIL panel. (F) Final spindle length conditioned on cell length (FL|CL) as a function of cell area conditioned on cell length (CA|CL) across the RIAIL panel. Inset indicates a lack of correlation between cell area and final spindle length conditioned on cell length, in disagreement with the prediction of the Limiting Component model. (G) Overview of the Boundary model. Centrosome distance (CD) is indicated. (H) Final spindle length as a function of cell length across the RIAIL panel. (I) Final spindle length as a function of final centrosome distance across the RIAIL panel. Inset indicates a positive correlation between final centrosome distance and final spindle length conditioned, in disagreement with the prediction of the Boundary model. (J) Final centrosome distance as a function of cell length across the RIAIL panel.
Figure 3 with 5 supplements
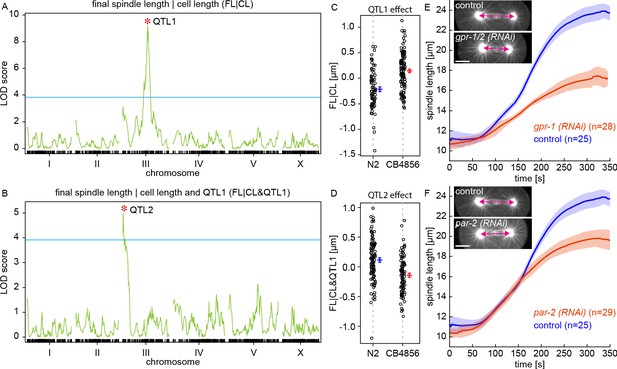
QTL mapping of final spindle length.
(A) QTL mapping of final spindle length conditioned on cell length (FL|CL) and (B) QTL mapping of final spindle length conditioned on cell length and QTL1 (FL|CL and QTL1) (green line, logarithm of the odds (LOD) score; blue line, permutation-based threshold for genome-wide significance at p=0.05; red star indicates the position of a QTL) (C) Final spindle length conditioned on cell length for RIAILs grouped by presence of QTL1 variants (blue, N2 variant, mean and standard error; red, CB4856 variant, mean and standard error). (D) Final spindle length conditioned on cell length and QTL1 for RIAILs grouped by presence of QTL2 variants (blue, N2 variant, mean and standard error; red, CB4856 variant, mean and standard error). (E) Spindle length as a function of time for control (blue) and gpr-1/2 (RNAi) (red) embryos (solid line, mean; shaded region, standard deviation). Sample embryos from control and gpr-1/2 (RNAi) are shown as insets. Scale bar 10 μm. (F) Spindle length as a function of time for control (blue) and par-2 (RNAi) (red) embryos (solid line, mean; shaded region, standard deviation). Sample embryos from control and par-2 (RNAi) are shown as insets. Scale bar 10 μm.
Figure 3—figure supplement 1
QTL mapping of final spindle length and cell length.
(A) QTL mapping of final spindle length (FL) across the RIAIL panel (green line, LOD score; blue line, permutation-based threshold for genome-wide significance at p=0.05). (B) QTL mapping of cell length (CL) across the RIAIL panel (green line, LOD score; blue line, permutation-based threshold for genome-wide significance at p=0.05). (C) QTL mapping of final spindle length conditioned on cell length, QTL1, and QTL2. No statistically significant QTLs were detected.
Figure 3—figure supplement 2
Variations of gpr-1 and par-2 between N2 and CB4856.
Single nucleotide variations for genes gpr-1 and par-2 between N2 and CB4856 (red star, missense variation; green star, synonymous variation).
Figure 3—figure supplement 3
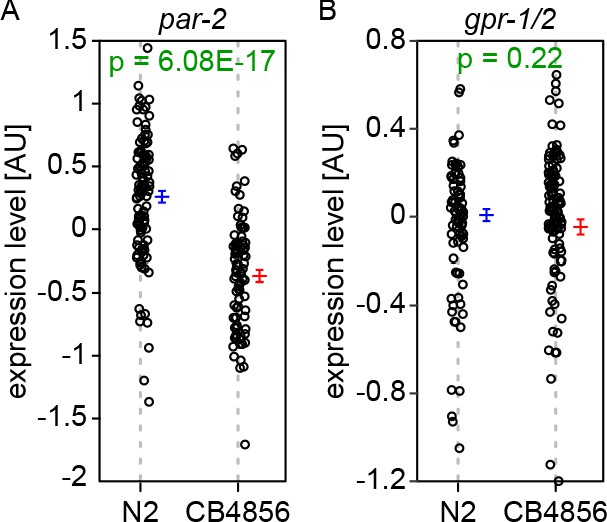
Transcript abundance of PAR-2 and GPR1/2.
(A) Transcript abundance for PAR-2 for RIAILs grouped by presence of QTL2 variants (blue, N2 variant, mean and standard error; red, CB4856 variant, mean and standard error). (B) Transcript abundance for GPR-1/2 for RIAILs grouped by presence of QTL1 variants (blue, N2 variant, mean and standard error; red, CB4856 variant, mean and standard error).
Figure 3—video 1
Spindle elongation in a gpr-1/2 (RNAi) embryo.
Time-lapse microscopy of the first mitotic spindle (β-tubulin::GFP) in a gpr-1/2 (RNAi) embryo. Scale bar 10 μm. This supplementary movie corresponds to Figure 3E.
Figure 3—video 2
Spindle elongation in a par-2 (RNAi) embryo.
Time-lapse microscopy of the first mitotic spindle (β-tubulin::GFP) in a par-2 (RNAi) embryo. Scale bar 10 μm. This supplementary movie corresponds to Figure 3F.
Figure 4 with 7 supplements
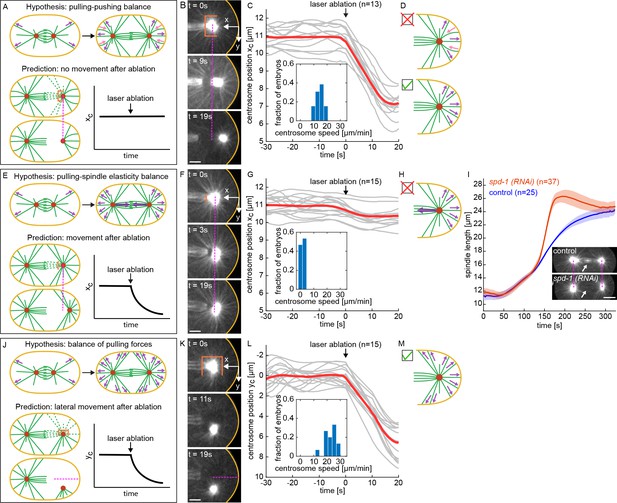
Investigating forces on spindle by laser ablation of microtubules.
(A) Overview of the hypothesis of balanced pulling and pushing (purple arrows, hypothesized pulling forces; pink arrows, hypothesized pushing forces; orange line, ablation geometry; , centrosome position in x). (B) Laser ablation of MTs in a cylindrical geometry with one open end around the centrosome, performed after spindle elongation has ceased. Scale bar 5 μm. (C) x-position of centrosomes relative to the cell periphery as a function of time for the laser ablation geometry shown in B (gray lines, individual experiments; red line, average). Inset is the histogram of centrosome’s speed after ablation. (D) Observed centrosome motion after ablation is inconsistent with predictions of balanced pulling and pushing (red cross) and suggests net pulling forces (green check). (E) Overview of the hypothesis of balanced pulling and spindle elasticity (purple arrows, hypothesized pulling forces; orange line, ablation geometry; , centrosome position). (F) Laser ablation of MTs in a planar geometry, performed after spindle elongation has ceased. Scale bar 5 μm. (G) x-position of centrosomes relative to the cell periphery as a function of time for the laser ablation geometry shown in F (gray lines, individual experiments; red line, average). Inset is the histogram of centrosomes speed after ablation. (H) Observed centrosome motion after ablation is inconsistent with predictions of balanced pulling and spindle elasticity (red cross). (I) Spindle length as a function of time (solid line, mean; shaded region, standard deviation) for control (blue) and spd-1 (RNAi) (red) embryos. Insets are examples of control and spd-1 (RNAi) embryos. Dashed lines indicate the position of centrosomes in the control embryo. Scale bar 10 μm. (J) Overview of the hypothesis of balanced pulling forces (purple arrows, hypothesized pulling forces; orange line, ablation geometry; , centrosome position). (K) Laser ablation of MTs in a cylindrical geometry with one open end around the centrosome, performed after spindle elongation has ceased. Scale bar 5 μm. (L) y-position of centrosomes relative to the cell periphery as a function of time for the laser ablation geometry shown in K (gray lines, individual experiments; red line, average). Inset is the histogram of centrosomes speed after ablation. (M) Observed centrosome motion after ablation is consistent with predictions of balanced pulling forces (green check).
Figure 4—figure supplement 1
Centrosome movement after horizontal ablation.
(A) Laser ablation of MTs in a cylindrical geometry along the spindle axis with one open end around the posterior centrosome, performed after spindle elongation has ceased. Scale bar 5 μm. (B) x-position of posterior centrosomes relative to the cell periphery as a function of time for the laser ablation geometry shown in A (gray lines, individual experiments; red line, average). (C) Laser ablation of MTs in a cylindrical geometry along the spindle axis with one open end around the anterior centrosome, performed after spindle elongation has ceased. Scale bar 5 μm. (D) x-position of anterior centrosomes relative to the cell periphery as a function of time for the laser ablation geometry shown in C (gray lines, individual experiments; red line, average).
Figure 4—figure supplement 2
Centrosome movement after planar ablation.
(A) Laser ablation of MTs in a planar geometry around the posterior centrosome, performed after spindle elongation has ceased. Scale bar 5 μm. (B) x-position of posterior centrosomes relative to the cell periphery as a function of time for the laser ablation geometry shown in A (gray lines, individual experiments; red line, average). (C) Laser ablation of MTs in a planar geometry around the anterior centrosome, performed after spindle elongation has ceased. Scale bar 5 μm. (D) x-position of posterior centrosomes relative to the cell periphery as a function of time for the laser ablation geometry shown in C (gray lines, individual experiments; red line, average).
Figure 4—figure supplement 3
Centrosome movement after lateral ablation.
(A) Laser ablation of MTs in a cylindrical geometry perpendicular to the spindle axis with one open end around the posterior centrosome, performed after spindle elongation has ceased. Scale bar 5 μm. (B) y-position of posterior centrosomes relative to the cell periphery as a function of time for the laser ablation geometry shown in A (gray lines, individual experiments; red line, average). (C) Laser ablation of MTs in a cylindrical geometry perpendicular to the spindle axis with one open end around the anterior centrosome, performed after spindle elongation has ceased. Scale bar 5 μm. (D) y-position of anterior centrosomes relative to the cell periphery as a function of time for the laser ablation geometry shown in C (gray lines, individual experiments; red line, average).
Figure 4—video 1
Longitudinal cup-cut ablation of MTs.
Laser ablation of MTs in a cylindrical geometry with one open end around the centrosome towards the embryo’s pole, performed after spindle elongation has ceased. Scale bar 10 μm. This supplementary movie corresponds to Figure 4B.
Figure 4—video 2
Plane ablation of MTs.
Laser ablation of MTs in a plane geometry after spindle elongation has ceased. Scale bar 10 μm. This supplementary movie corresponds to Figure 4F.
Figure 4—video 3
Spindle elongation in a spd-1 (RNAi) embryo.
Time-lapse microscopy of the first mitotic spindle (β-tubulin::GFP) in a spd-1 (RNAi) embryo. Scale bar 10 μm. This supplementary movie corresponds to Figure 4I.
Figure 4—video 4
Lateral cup-cut ablation of MTs.
Laser ablation of MTs in a cylindrical geometry with one open end around the centrosome oriented perpendicular to the axis of the spindle, performed after spindle elongation has ceased. Scale bar 10 μm. This supplementary movie corresponds to Figure 4K.
Figure 5 with 5 supplements
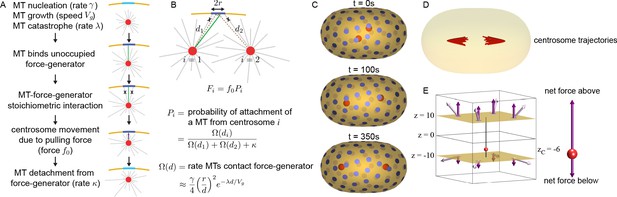
Stoichiometric Model of centrosome positioning by cortical pulling forces.
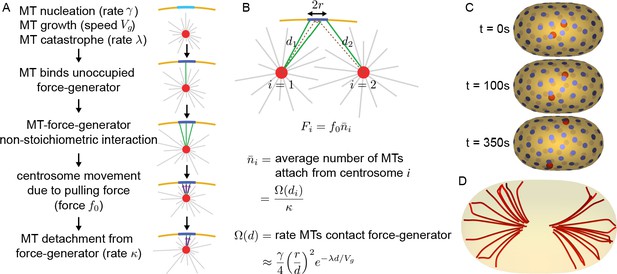
(A) From top to bottom: MTs nucleate from the centrosome with rate , grow with speed , and undergo catastrophe with rate . An MT (green) that contacts an unoccupied CFG (light blue) becomes bound. Additional MTs (crossed) that contact an occupied CFG (dark blue) do not bind because of their stoichiometric interaction. Bound MTs are pulled with force along the MT direction, causing motion of the centrosome. MTs detach from CFGs with rate . (B) An CFG, with capture radius r, in the presence of two centrosomes (i=1 and i=2) at distances and away. Because of the stoichiometric MT-CFG interactions, only one MT (green) can bind the CFG at a time, so additional MTs (crossed) do not bind the CFG if it is occupied. The average force from the CFG on each centrosome is , where is the probability of attachment of a MT from centrosome i to the CFG. The probability of attachment, , depends on the rate growing MTs impinge upon the CFG, , and the MTs detachment rate, . (C) Three-dimensional simulation of two centrosomes (red spheres) in the presence of multiple CFGs (blue disks). (D) Multiple simulations showing centrosome trajectories (red lines) from different initial starting positions close to the cell center. Centrosomes migrate to the same final position irrespective of their initial positions. (E) Simulation of centrosome positioning between two parallel planes with eight CFGs evenly positioned (four on each plane). The pulling force (light purple) and its z-projection (dark purple) for each CFG is shown. The net pulling force on centrosome is shown on the right panel.
Figure 5—figure supplement 1
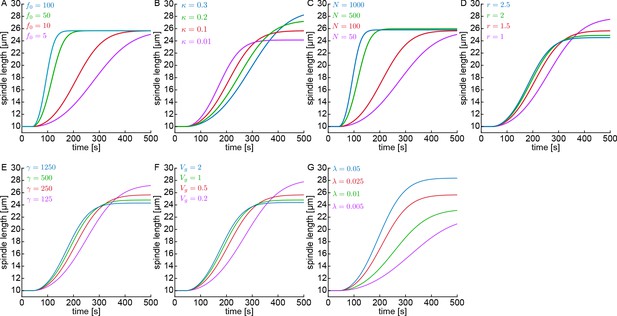
Simulations for various parameters.
Spindle length as a function of time for various parameters of the model including (A) pulling force , (B) detachment rate , (C) CFG number , (D) CFG capture radius , (E) MT nucleation rate , (F) MT growth speed , and (G) catastrophe rate .
Figure 5—figure supplement 2
Simulation of spindle elongation for simultaneous varying parameters.
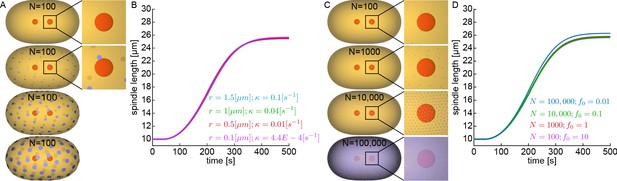
(A) One hundred uniformly distributed FGs with different capture radii , and (blue disks, CFGs; red spheres, centrosomes). (B) Simulation of spindle dynamics with 10,000 MTs for various combinations of CFG capture radii, , and detachment rates, . Spindle dynamics can remain unaffected by appropriately decreasing both and . (C) Different numbers, 100, 1000, 10,000, and 100,000, of uniformly distributed CFGs (blue disks, CFGs; red spheres, centrosomes). (D) Simulation of spindle dynamics with 10,000 MTs for various combinations of CFG number, , and pulling force, . Spindle dynamics remains unaffected when increases if decreases proportionally. Thus, in this model, the spindle remains stably positioned even when there are more FGs than MTs.
Figure 5—figure supplement 3
Non-stoichiometric model of centrosome positioning by cortical pulling forces.
(A) From top to bottom: MTs nucleate from the centrosome with rate , grow with speed , and undergo catastrophe with rate . Without stoichiometric interactions, any MT (green) that contacts an CFG becomes bound, irrespective of whether the CFG is unoccupied (light blue) or occupied (dark blue). All bound MTs are pulled with force along the MT direction, causing motion of the centrosome. MTs detach from CFGs with rate . (B) An CFG, with capture radius r, in the presence of two centrosomes (i=1 and i=2) at distances and away. The average force from the CFG on each centrosome is , where is the average number of MTs from centrosome i bound to the CFG. The average number of microtubules, , depends on the rate growing MTs impinge upon the CFG, , and the MTs detachment rate, . (C) Three-dimensional simulation of two centrosomes (red spheres) in the presence of multiple CFGs (blue disks). (D) Multiple simulations showing centrosome trajectories (red lines) from different initial starting positions close to the cell center. With non-stoichiometric interactions, centrosomes are not stably positioned and migrate to the cell periphery.
Figure 5—figure supplement 4
Probability of attachment of microtubules to force-generators.
(A) Probability of attachment of MTs to CFGs as a function of x-position along the embryo in the presence of two centrosomes. The probability of attachment for MTs from the left centrosome (green) and right centrosome (red) are shown. (B) In the absence of the left centrosome, the probabilities of attachments of MTs from the right centrosome changes (from red to purple). This change is due to the stoichiometric interaction of MTs and CFGs (i.e. they can only bind to one MT at a time), so that there is a competition of MTs for CFGs when two centrosomes are present.
Figure 5—figure supplement 5
Schematic of centrosome and force-generator geometry.
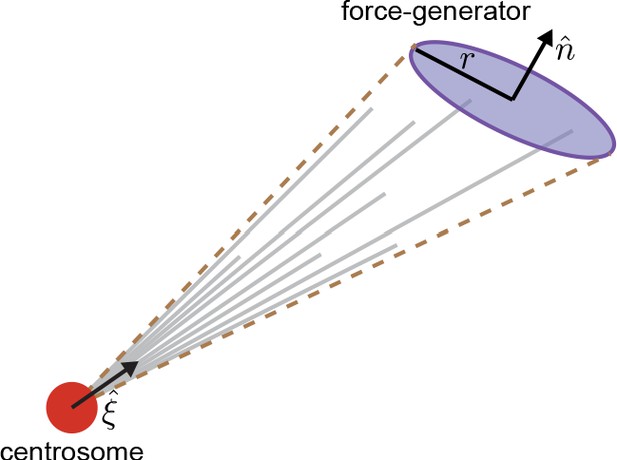
A centrosome (red ball), MTs (gray lines), and an CFG (purple disk) are shown. is the unit vector pointing from the centrosome to the center of the CFG. is the unit vector defining the orientation of the CFG. is the radius of the CFG. The dotted brown lines indicate a cone with the centrosome at its apex and the CFG at its base.
Figure 6 with 1 supplement
Stoichiometric Model explains centering of a single aster.
(A) Simulation of centrosome positioning after removing one centrosome. (B) Centrosome position from the simulation in A (red curve), after removing one centrosome, compared to a simulation with the same parameters in presence of the other centrosome (blue curve). (C) Cartoon illustrating centrosome ablation and centering. (D) After ablation of one centrosome, the other centrosome moves to the cell center. Scale bar 10 μm. (E) Centrosome position as a function of time after ablating one centrosome (solid red, mean; shaded region, standard deviation, n = 13) compared to control (solid blue, mean; shaded region, standard deviation, n = 25).
Figure 6—video 1
Centrosome ablation.
Ablation of one centrosome in an embryo (β-tubulin::GFP) leads to movement of the remaining centrosome to the cell center. Scale bar 10 μm. This supplementary movie corresponds to Figure 6D.
Figure 7 with 2 supplements
The Stoichiometric Model explains spindle elongation, positioning, and scaling with cell size.
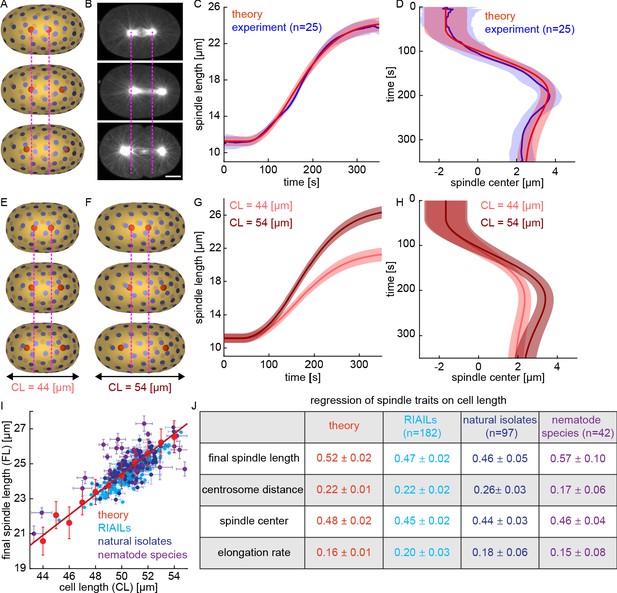
(A) Three-dimensional simulation of two centrosomes in the presence of multiple cortical CFGs with ~50% asymmetry between the right and left halves of the cell (blue disks, CFGs; red spheres, centrosomes; pink lines, position of centrosomes in the first panel). (B) Spindle elongation and centrosome movement in a C. elegans embryo (pink lines, position of centrosomes in the first panel). Scale bar 10 μm. (C) Red, spindle length as a function of time for multiple simulations with various initial centrosome positions and various arrangement of CFGs keeping their total number and asymmetry fixed (solid line, mean; shaded region, standard deviation); blue: spindle length as a function of time for multiple C. elegans embryos (solid line, mean; shaded region, standard deviation). (D) Red, spindle center as a function of time for multiple simulations with various initial centrosome positions and various arrangements of CFGs, keeping their total number and asymmetry fixed (solid line, mean; shaded region, standard deviation); blue: spindle center as a function of time for multiple C. elegans embryos (solid line, mean; shaded region, standard deviation). (E–F) Simulations with parameters as above but cell length is 44 μm in E and 54 μm in F (blue disks, CFGs; red spheres, centrosomes; pink lines, position of centrosomes in the first panel). (G–H) Spindle length (G) and spindle center (H) as a function of time for multiple simulations with various initial centrosome positions and various arrangement of CFGs, as above, but for cells of length 44 μm (light red) and 54 μm (dark red) (solid line, mean; shaded region, standard deviation). (I) In red, final spindle length as a function of cell length for multiple simulations with various cell length keeping the density and asymmetry of CFGs fixed (mean and standard error; red line, linear fit); final spindle length as a function of cell length across the RIAIL panel (light blue), C. elegans natural isolates (dark blue), and nematode species (purple) (mean and standard error). (J) Scaling of spindle traits with cell size measure by their regression on cell length for simulations (red), RIAILs (light blue), C. elegans natural isolates (dark blue), and nematode species (purple).
Figure 7—figure supplement 1
The Stoichiometric Model explains spindle elongation and positioning in par-6 (RNAi) embryos.
(A) Three-dimensional simulation of two centrosomes in the presence of multiple cortical CFGs distributed (blue disks, CFGs; red spheres, centrosomes; pink lines, position of centrosomes in the first panel). (B) Spindle elongation and centrosome movement in a par-6 (RNAi) C. elegans embryo (pink lines, position of centrosomes in the first panel). Scale bar 10 µm. (C) Red, spindle length as a function of time for multiple simulations with various initial centrosome positions and various arrangement of CFGs keeping their total number fixed (solid line, mean; shaded region, standard deviation); blue: spindle length as a function of time for multiple par-6 (RNAi) C. elegans embryos (solid line, mean; shaded region, standard deviation). (D) Red, spindle center as a function of time for multiple simulations with various initial centrosome positions and various arrangements of CFGs, keeping their total number fixed (solid line, mean; shaded region, standard deviation); blue: spindle center as a function of time for multiple par-6 (RNAi) C. elegans embryos (solid line, mean; shaded region, standard deviation).
Figure 7—video 1
Spindle elongation and positioning.
Time-lapse microscopy of the first mitotic spindle (β-tubulin::GFP). Scale bar 10 μm. This supplementary movie corresponds to Figure 7B.
Author response image 1
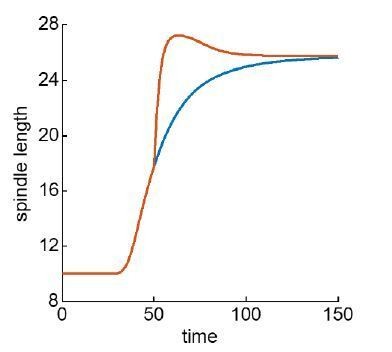
Simulation of spindle elongation using the complete theory for control spindles (blue) and when the central spindle is removed at t=50 (red), corresponding to the spd-1(RNAi) experiment.
Thus, the full Stoichiometric Model does predict an overshoot compared to controls following central spindle breakage, in which case the spindle over-elongates before going back to control length, as observed in experiments.
Additional files
-
Source code 1
Stoichiometric model.
- https://cdn.elifesciences.org/articles/55877/elife-55877-code1-v1.zip
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/55877/elife-55877-transrepform-v1.docx
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Stoichiometric interactions explain spindle dynamics and scaling across 100 million years of nematode evolution
eLife 9:e55877.
https://doi.org/10.7554/eLife.55877
