Figures and data in Slightly beneficial genes are retained by bacteria evolving DNA uptake despite selfish elements

Figures
Videos
Tables
Additional files

12 figures, 1 video, 2 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

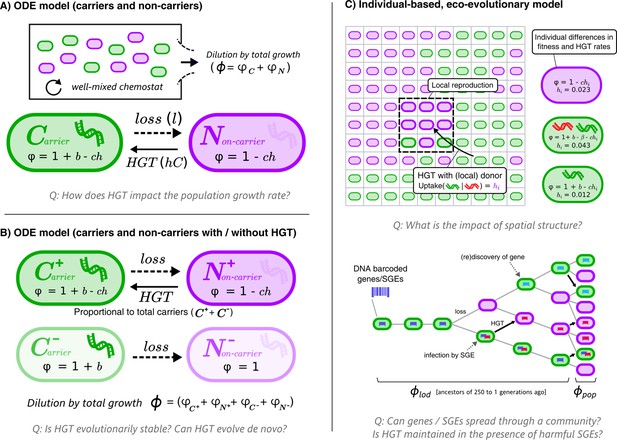
Graphical overviews of the different models: This study uses a series of models with gradually increasing complexity.

The first two models (**A+B**) are composed of Ordinary Differential Equations (ODEs), and the third model (C) is an individual-based model (IBM). The models describe a population of bacterial cells which either carry a beneficial gene (carriers, $𝑪$ ) or do not carry the genes (non-carriers, $𝑵$ ), both of which engage in costly HGT (e.g. take up DNA or enter a state of competence). The cells are competing for a limited resource, where the intrinsic growth is 1, b is the growth rate advantage (or disadvantage) for carrying the gene, l is the rate at which the gene is lost, h is the rate of HGT (*i.e.* uptake/competence), c is the cost of HGT, $𝝋$ is the growth rate of sub-populations/individual cells, and $ϕ$ represents the total growth rate. In the IBM, each cell has an individual rate of HGT (arbitrary values are shown in the cartoon), which we use to study the de novo evolution of HGT. The IBM also makes a distinction between the average growth rate of the population ( $ϕ_{𝒑 𝒐 𝒑}$ ) and the average growth rate of the line of descent ( $ϕ_{𝒍 𝒐 𝒅}$ , previous 250 generations of cells). In the IBM, both beneficial genes (with benefit $𝒃$ , green) and harmful selfish genetic elements (SGEs, red) with a fitness penalty $𝜷$ are taken into account. Genes and SGEs are tagged with a unique barcode when they flux in, which are inherited upon reproduction or transfer. Parameters $c$ , $h$ and $l$ are assumed to be positive.

Figure 2

Download asset Open asset

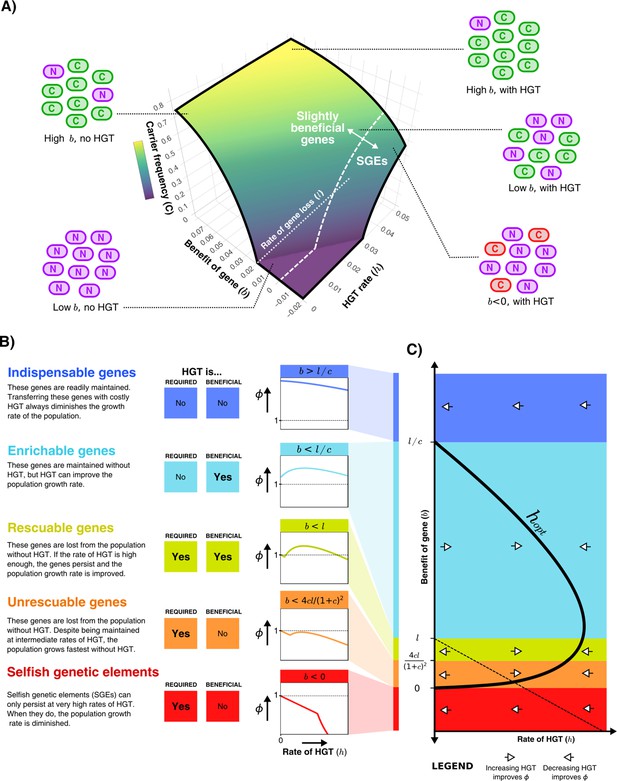
HGT can help genes persist in the population, resulting in distinct gene classes of slightly beneficial genes.

(A) For the model shown in Figure 1A, the frequency of carrier cells is shown in a 3D surface plot for different values of $b$ and $h$ . This function is derived in the Supplementary Material, and here drawn for $l = 0.02$ and $c = 0.2$ . The white dashed line ( $b = 0$ ) gives the boundary between slightly beneficial genes and selfish genetic elements (SGEs). Cartoons illustrate how, for a very beneficial gene (high $b$ ), HGT leads only to a mild increase in carrier cells, how HGT has a large impact when the gene brings a smaller fitness effect (low $b$ ), and how SGEs can also persist with high HGT rates ( $b < 0$ ). (B) Different classes of slightly beneficial genes can be distinguished based on (i) if HGT is *required* for the gene to persist within the population (when $b < l$ ) and (ii) if HGT is *beneficial* for population growth rates. The graphs on the right-hand side show, for each of these classes, how an increasing rate of HGT (x-axis) influences the population growth rate $ϕ$ (y-axis). (C) A bifurcation diagram shows how the population growth rate is either improved or diminished by HGT for different values of the rate of HGT ( $h$ , x-axis) and the benefit parameter ( $b$ , y-axis). The HGT rate that optimises population growth rates ( $h_{o p t} = \sqrt{b l / c} - b$ ) is depicted by the thick black curve. The dashed line is given by $h = l - b$ , above which the genes are able to persist in the population. Finally, white arrows depict whether $\partial ϕ / \partial h$ is positive or negative, indicating how more/less HGT changes the population growth rate.

Figure 3

Download asset Open asset

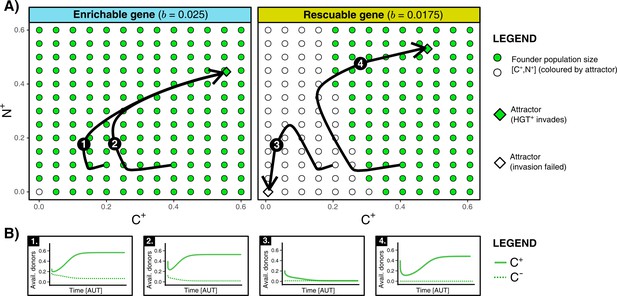
HGT is an evolutionarily stable strategy but is evolutionarily inaccessible for rescuable genes due to a lack of gene-carrying donor cells.

(A) For an enrichable and a rescuable gene ( $b = 0.025$ and $b = 0.0175$ respectively), a 2D projection of the 4D state space is shown. For various founder sizes (combinations of carriers, $C^{+}$ , and non-carriers, $N^{+}$ ), the result of invasion of $H G T^{+}$ (that has the optimal rate of HGT, $h = h_{o p t}$ ) into $H G T^{-}$ ( $h = 0$ ) is shown. $C^{+} / N^{+}$ -combination that successfully invade are annotated as green dots, while failed invasions are coloured white. $H G T^{+}$ always successfully invades for enrichable genes. For a rescuable gene, low founder populations sizes of $C^{+}$ and $N^{+}$ (white dots) fail to invade, whereas they can invade at higher population sizes (green dots). Black arrows (1-4) show the trajectories starting from two founder population sizes. (B) For the four trajectories from panel A, the graphs show the temporal dynamics of gene-carrying donor cells.

Figure 4

Download asset Open asset

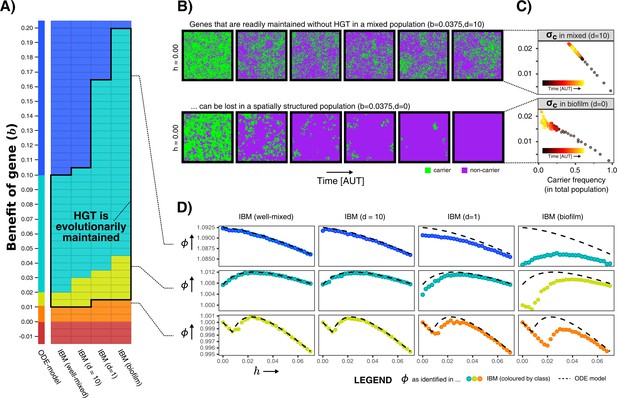
Spatial structure hinders the maintenance of slightly beneficial genes.

(A) Each tile in this table represents a series of simulations in the individual-based model (IBM), where we first test which gene class (background colour) is found when sweeping over different HGT-rates ( $h$ -values), and next test whether HGT (*i.e.* DNA uptake) is evolutionarily maintained when starting with a population consisting of only carrier cells with $h = 0.05$ (shown with black outline, see Appendix 1—table 1). This was tested for the well-mixed IBM and the IBM with different levels of mixing ( $d$ ). The continuum of gene classes from the ODE-model is presented for comparison. Colours are the same as in Figure 2 (blue = indispensable, cyan = enrichable, yellow = rescuable, orange = unrescuable, red = selfish genetic element). (B) Shown is the spatial grid of the IBM for two simulations with the same value of $b$ , and no HGT. The gene readily persists in the mixed IBM (top panel, $d = 10$ ), while the gene does not persist in the spatially structured population (bottom panel, $d = 0$ ). (C) For the simulations shown in B, we plot $σ_{c}$ (see Materials and methods) against the frequency of carrier cells. This value of $σ_{c}$ indicates how much fitter carrier cells are than their local competitors, which decreases to 0 when all local competitors are also carriers. When comparing the top and bottom panel, this shows how clumping hinders the effective benefit of carrying a gene. (D) For three rows from the table of A, it is illustrated how the effect of spatial clumping illustrated in B and C modifies the gene class found for specific $b$ -values. The dashed line indicates the growth rates predicted by the ODE model.

Figure 5

Download asset Open asset

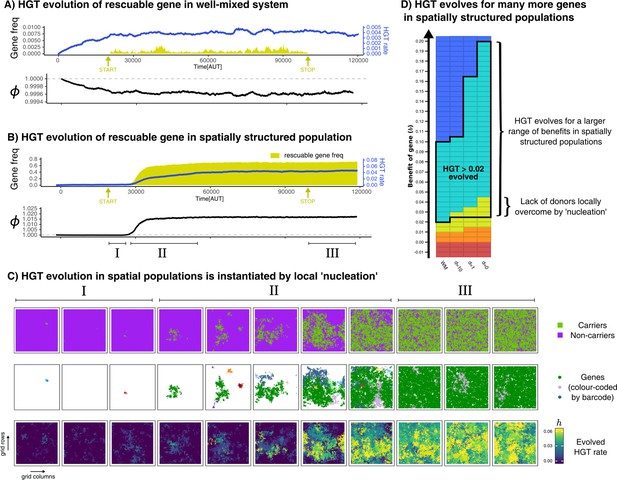
HGT of rescuable genes only evolves in spatially structured populations due to the emergence of ‘gene-sharing’ communities.

(**A-B**) Both panels show the frequency of a rescuable gene (yellow area) that is discovered with a very low probability ( $5 \cdot 10^{- 6}$ per time step), the mean evolved rate of DNA uptake within the population (blue line), and the growth rate of the population (black). Note that A and B have a different range in the y-axis for clarity. (C) Different visualisations of the grid show, in the spatially structured populations, carrier cells with a rescuable gene (colour coded by the unique barcodes) spread after a local ‘nucleation event’. A positive feedback loop follows, resulting in a ‘gene-sharing’ community which slowly overgrows the rest of the population. (D) The outcome of de novo HGT evolution for the same combinations of fitness-effects and mixing as in Figure 4A. Parameters used: $h_{i n i t} = 0.0$ , $u = 5 \cdot 10^{3}$ , $m = 0.05$ , $l = 0.02$ , $c = 0.1$ , $f = 5 \cdot 10^{- 6}$ , $f_{s t a r t} = 20, 000$ , $f_{s t o p} = 100, 000$ , $n = 400$ (*i.e.* $N = 400^{2}$ ). For the well-mixed population, we chose a rescuable gene with the highest benefit from Figure 4A ( $b = 0.0175$ ), and for the spatially structured population we used $b = 0.030$ (the average of the much broader range of rescuable genes). Both these genes require HGT to persist, and are thus rescuable within their own spatial context.

Figure 6

Download asset Open asset

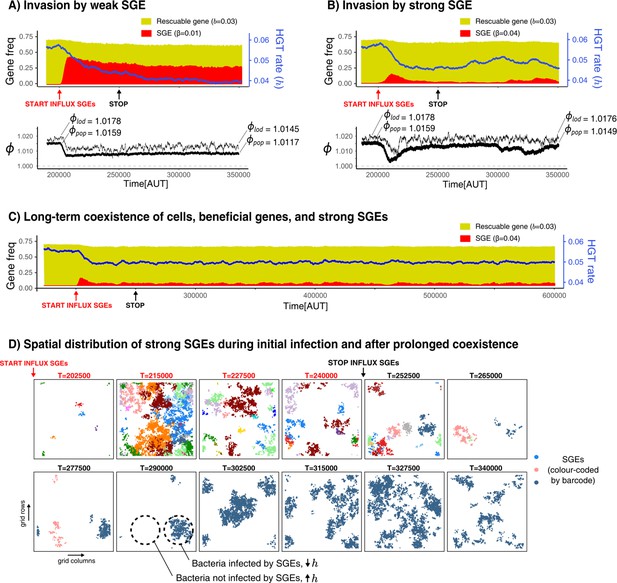
Selfish genetic elements (SGEs) can invade and stably coexist with their host cell.

(**A-B**) Temporal dynamics for a population that has evolved to rescue a slightly beneficial gene ( $b = 0.03$ ) invaded by a weak SGE (A, $β = 0.01$ ) and a strong SGE (B, $β = 0.04$ ) respectively. The blue line indicates the rate of HGT (i.e. DNA uptake) as evolved by the host cells. In the bottom graphs, the thick black line is the average growth rate of the population ( $ϕ_{p o p}$ ), and the thin black line is $ϕ_{l o d}$ , the average growth rate of individuals along the line of descent (up to 250 generations ago) . The $ϕ_{p o p}$ and $ϕ_{l o d}$ that are annotated with the dashed lines are the average of the first/final 200 generations. (C) This panel shows the long-term coexistence of cells, beneficial genes, and a strong SGEs ( $β = 0.04$ ). (D) Panels show the spatial distribution of SGEs (coloured by their unique barcodes). The top row shows this during the invasion (open ecosystem) and the bottom row shows this during prolonged coexistence (closed ecosystem). Note that the empty sites (white) only indicate the absence of SGEs, not of bacterial cells, which are instead present in every grid point. Parameters used: $h$ -parameters and frequency of carriers as evolved from Figure 5, $i = 5 \cdot 10^{- 3}$ , $m = 0.05$ , $l = 0.02$ , $c = 0.1$ , $i = 1 \cdot 10^{- 5}$ , $i_{s t a r t} = 200, 000$ , $i_{s t o p} = 250, 000$ , $n = 400$ (i.e. $N = 400^{2}$ ).

Appendix 1—figure 1

Download asset Open asset

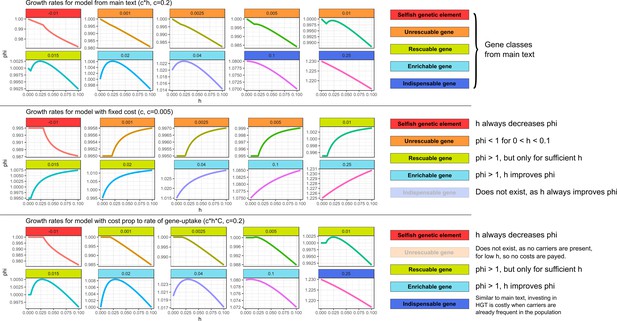
Similar gene classes exist with different assumptions for the cost of HGT In the top panel (with costs as in the main text), we can observe all the gene classes discussed in the main text.

In the middle panel (with fixed costs), HGT always improves the growth rates for genes with $b > 0$ . However, for low $b$ , the growth rate is lower than one even for very high $h$ . Therefore, it is not adaptive to invest in costly HGT (the maximal growth rate is 1.0 with $h = 0$ ). Thus, for this range of $h$ ’s, we observe a similar ‘unrescuable’ gene class as the one discussed in the main text. When growth rates *can* be improved within this range of $h$ ’s, the genes can be compared to the rescuable genes or enrichable genes, depending on whether or not HGT is required for the gene to persist. Indispensable genes do not exist under this regime, as HGT always increases growth rates when $b > 0$ . We argue, however, that a constant cost with extremely high rates of HGT is fairly unrealistic, as every HGT-event carries inherent risks, for example by chromosome disruptions, cytotoxicity, and the integration of SGEs. In the bottom panel, we investigate a scenario where costs are only present when actually taking up DNA from carrier cells (*i.e.* instead of c*h, the costs are c*h*C). Under this scenario, most gene classes from the main text exist. Unrescuable genes however do not exist, as there are no cost if no carriers are present. Similarly, the Allee effect as discussed in the main text is also not present, as this Allee effect requires costs in the absence of donor cells.

Appendix 1—figure 2

Download asset Open asset

The Allee effect for de novo evolution of HGT is also present for enrichable genes when $C^{-}$ (a carrier that cannot engage in HGT) cannot act as a donor.

Appendix 1—figure 3

Download asset Open asset

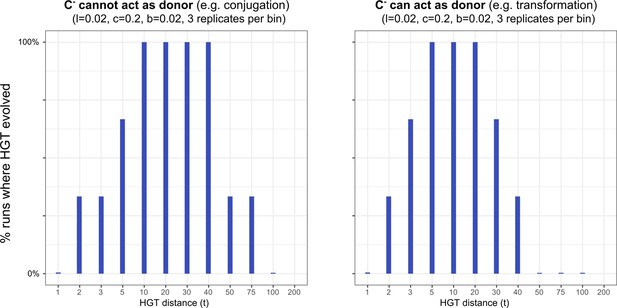
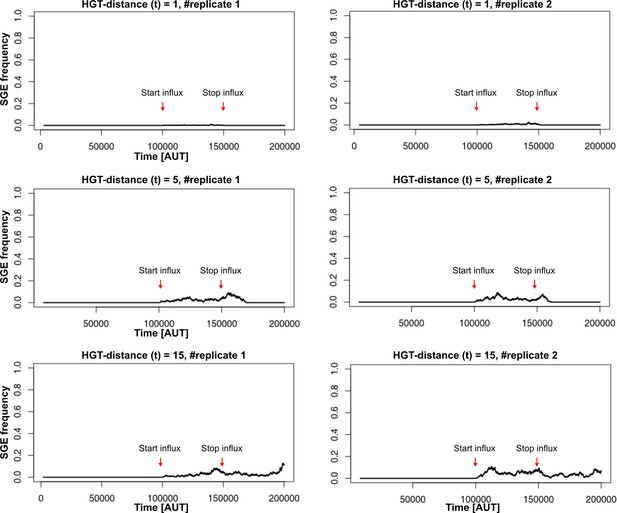
HGT evolves most readily when transfer happens between donor/recipient pairs of intermediate distances.

On the left-hand side, we consider this for a conjugation-like scenario ( $C^{-}$ , a carrier that cannot engage in HGT, cannot act as a donor), while on the right-hand side we consider this for a transformation-like scenario ( $C^{-}$ , a carrier that cannot engage in HGT, *can* act as a donor).

Appendix 1—figure 4

Download asset Open asset

Cells in the IBM can only evolve to take up ‘rescuable genes’ in a spatially structured population.

With the parameters and assumptions as used in the main text (i.e. a transformation-like HGT mechanisms with costs proportional to the rate of DNA uptake), we show how HGT for rescuable genes only evolves in a spatially structured population.

Appendix 1—figure 5

Download asset Open asset

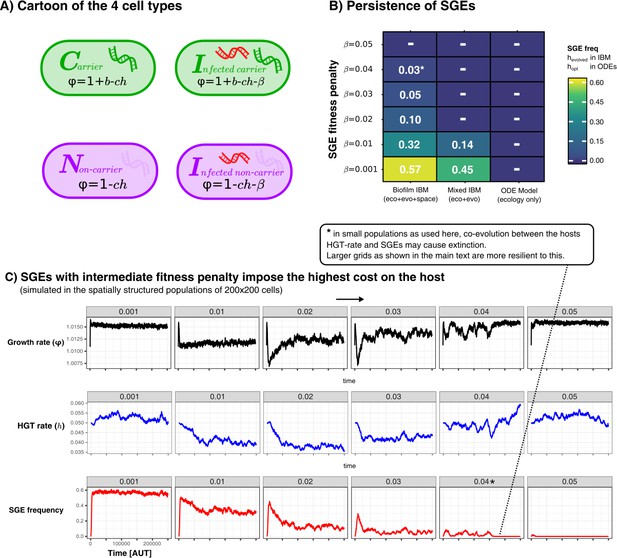
Persistence of SGEs in various implementations of our model.

A shows a cartoon of the cell types, between which competition was modelled in a various ways. In B we show for these different implementations how many SGEs persist within the populations for SGEs with different penalties. For the IBM, we simulated for 250.000 time steps and calculated the average SGE-frequency in the final 100 generations. For the ODE model, we chose the optimal rate of HGT ( $h_{o p t}$ ), and numerically integrated the equilibrium concentrations of infected cells. Finally, C shows the temporal dynamics of the growth rate ( $ϕ$ ), HGT-rate ( $h$ ), and the SGE frequency, in the spatially structured simulations. As this parameter sweep had slighly smaller populations sizes as used in the main text, the strong SGE could eventually go extinct (this is annotated with an asterisk).

Appendix 1—figure 6

Download asset Open asset

SGEs persistence can depend on the distance of HGT and on the continued influx of SGEs.(parameters used as in main text).

Videos

Video 1

Download asset

posterframe for video — Gene-sharing ‘nucleation events’ and long-term coexistence with harmful SGEs.

For the IBM-model, this Video shows how gene-sharing of rescuable genes emerges through a ‘nucleation’-event, allowing local communities to eventually overgrow all other cells. The top-left panel shows carriers/non-carriers, the top-right shows the evolved HGT-rate (i.e. DNA uptake), the bottom-left shows the barcodes of influxed genes, and the bottom-right shows the barcodes of influxed SGEs.

Tables

Table 1

Description of parameters used in the models.

Parameter (general)	Description
Gene loss ( $l$ )	Rate at which carrier cells lose the beneficial gene
HGT rate ( $h$ )	Rate at which non-carriers are transformed into carriers (when interacting with carrier cells)
Benefit of gene ( $b$ )	Growth rate benefit for carrier cells (or penalty for negative b)
Costs of HGT ( $c$ )	Growth rate penalty for the rate of HGT
Parameter (IBM only)	Description
Grid size ( $n$ )	The simulation is done on a square grid of n x n cells
Mixing rate ( $d$ )	Every time step, the grid is mixed $d$ times using the Margolus Diffusion algorithm (Toffoli and Margolus, 1987). Alternatively, the population was well-mixed by assigning new positions at random every time step.
Competition range ( $s$ )	Sub-population of s x s cells surrounding focal grid point that compete for reproduction
HGT distance ( $t$ )	Sub-population of t x t cells surrounding focal grid point from which a random potential donor is sampled for HGT
Influx genes ( $f$ )	A small probability for any cell to discover a gene de novo
Benefit of influxed gene (b*)	Growth rate benefit for carrier cells (or penalty for negative b)
Influx SGEs ( $i$ )	A small probability for any cell to be infected by an SGE de novo
Fitness penalty of SGE ( $β$ )	The fitness penalty imposed by the SGE
Mutation rate (u)	Chance of mutating the evolvable HGT-rate
Mutation step ( $m$ )	Uniform step size of mutations

Appendix 1—table 1

Values of $h_{o p t}$ that are attained when testing if HGT could be maintained.

Starting from $h = 0.05$ , we ran the model with evolving $h$ to test if HGT would be maintained. Positions in this table correspond to Figure 4A in the main text. If $h_{e v o l v e d}$ persisted at values > 0.001 after 500.000 time steps, we call HGT maintainable. Otherwise, the value in this table is 0.

(b)	IBM (well-mixed)	IBM (d = 10)	IBM (d = 1)	IBM (d = 0)
0.2025	0	0	0	0
0.1975	0	0	0	0.0035
0.1925	0	0	0	0.009
0.1875	0	0	0	0.016
0.1825	0	0	0	0.017
0.1775	0	0	0	0.022
0.1725	0	0	0	0.024
0.1675	0	0	0	0.028
0.1625	0	0	0.003	0.033
0.1575	0	0	0.003	0.033
0.1525	0	0	0.0035	0.035
0.1475	0	0	0.004	0.035
0.1425	0	0	0.004	0.035
0.1375	0	0	0.006	0.035
0.1325	0	0	0.008	0.035
0.1275	0	0	0.01	0.036
0.1225	0	0	0.011	0.036
0.1175	0	0	0.014	0.036
0.1125	0	0	0.016	0.036
0.1075	0	0	0.018	0.036
0.1025	0	0.002	0.02	0.036
0.0975	0.002	0.004	0.021	0.036
0.0925	0.004	0.006	0.022	0.037
0.0875	0.006	0.006	0.023	0.037
0.0825	0.008	0.008	0.023	0.037
0.0775	0.01	0.01	0.025	0.037
0.0725	0.012	0.012	0.026	0.037
0.0675	0.014	0.014	0.027	0.038
0.0625	0.016	0.017	0.028	0.038
0.0575	0.018	0.018	0.028	0.038
0.0525	0.02	0.021	0.028	0.038
0.0475	0.021	0.021	0.029	0.038
0.0425	0.023	0.023	0.029	0.039
0.0375	0.024	0.025	0.03	0.041
0.0325	0.025	0.025	0.03	0.041
0.0275	0.025	0.026	0.031	0.041
0.0225	0.025	0.025	0.032	0.041
0.0175	0.024	0.025	0.029	0.037
0.0125	0.023	0.024	0	0
0.0075	0	0	0	0
0.0025	0	0	0	0
−0.0025	0	0	0	0
−0.0075	0	0	0	0
−0.0125	0	0	0	0

Additional files

Transparent reporting form: https://cdn.elifesciences.org/articles/56801/elife-56801-transrepform-v3.docx
Download elife-56801-transrepform-v3.docx

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Bram van Dijk
Paulien Hogeweg
Hilje M Doekes
Nobuto Takeuchi

(2020)

Slightly beneficial genes are retained by bacteria evolving DNA uptake despite selfish elements

eLife 9:e56801.

https://doi.org/10.7554/eLife.56801

Share this article

Cite this article

Graphical overviews of the different models: This study uses a series of models with gradually increasing complexity.

HGT can help genes persist in the population, resulting in distinct gene classes of slightly beneficial genes.

HGT is an evolutionarily stable strategy but is evolutionarily inaccessible for rescuable genes due to a lack of gene-carrying donor cells.

Spatial structure hinders the maintenance of slightly beneficial genes.

HGT of rescuable genes only evolves in spatially structured populations due to the emergence of ‘gene-sharing’ communities.

Selfish genetic elements (SGEs) can invade and stably coexist with their host cell.

Similar gene classes exist with different assumptions for the cost of HGT In the top panel (with costs as in the main text), we can observe all the gene classes discussed in the main text.

The Allee effect for de novo evolution of HGT is also present for enrichable genes when C- (a carrier that cannot engage in HGT) cannot act as a donor.

HGT evolves most readily when transfer happens between donor/recipient pairs of intermediate distances.

Cells in the IBM can only evolve to take up ‘rescuable genes’ in a spatially structured population.

Persistence of SGEs in various implementations of our model.

SGEs persistence can depend on the distance of HGT and on the continued influx of SGEs.(parameters used as in main text).

Gene-sharing ‘nucleation events’ and long-term coexistence with harmful SGEs.

Description of parameters used in the models.

Values of hopt that are attained when testing if HGT could be maintained.

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

The Allee effect for de novo evolution of HGT is also present for enrichable genes when $C^{-}$ (a carrier that cannot engage in HGT) cannot act as a donor.

Values of $h_{o p t}$ that are attained when testing if HGT could be maintained.