Figures and data in How to measure and evaluate binding affinities

Figures
Tables
Additional files

13 figures, 2 tables and 3 additional files

Figures

Figure 1 with 2 supplements

Download asset Open asset

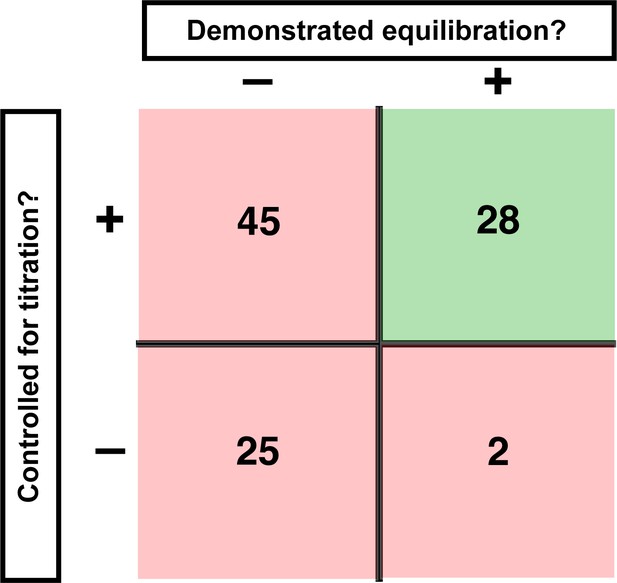
Assessment of published K_D values for RNA-binding proteins.

We analyzed 100 papers reporting K_D or ‘apparent K_D’ values of RNA/protein interactions. Measurements were evaluated based on two criteria: demonstrating equilibration (horizontal axis) and controlling for titration (vertical axis). Detailed criteria are described in Materials and methods, and the source data are provided in Supplementary file 1. The right column includes predominantly studies that used ITC and SPR, techniques that inherently record binding progress over time (24/30 in this column). The fraction of studies that varied time to demonstrate equilibration in non-ITC/SPR experiments is considerably smaller (6 of the 76 papers that did not exclusively use ITC or SPR, or <10%).

Figure 1—figure supplement 1

Download asset Open asset

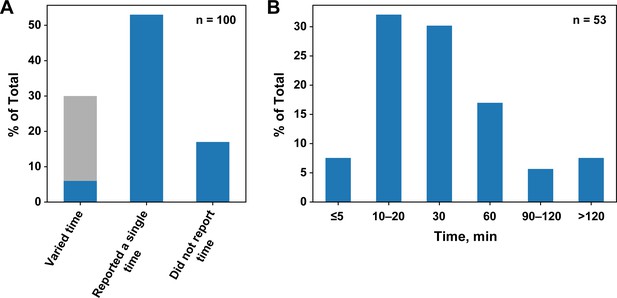
Survey of incubation times for published equilibrium dissociation constants.

(A) Percentages of publications that did or did not report and vary the incubation time. The light gray portion of the first column indicates the studies using SPR and ITC, techniques in which time is varied by default. (B) Incubation times in papers that reported a single time.

Figure 1—figure supplement 2

Download asset Open asset

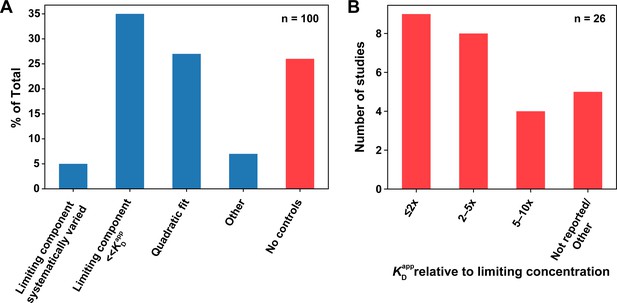
Survey of titration controls in published binding studies.

(A) Percentages of publications that did (blue) or did not (red) control for titration effects. The first category includes studies that systematically varied the limiting component concentration to rule out titration. Studies that reported using an appropriate concentration regime or analysis methods to minimize the effects of titration (second and third column, respectively) were considered titration controlled; nevertheless, we emphasize the importance of performing and reporting the control experiments described herein, instead of relying on concentrations alone (see section 'Avoid the titration regime'). The ‘Other’ category (n = 7) includes a study that reported K_D values as upper limits, recognizing possible titration (n = 1), and studies that only used SPR (n = 6), where the concentration of the immobilized species is difficult to estimate, but mass transport is typically controlled for or accounted for during analysis, as indicated in most surveyed studies. (B) Breakdown of studies that did not report controlling for titration. The first three columns denote studies that assumed negligible concentration of the limiting component in their analysis; however, the reported concentrations and K_D values were inconsistent with this assumption, with the ratio of the lowest measured K_D value to the limiting component concentration indicated. The ‘Not reported/Other’ category includes studies that did not report the limiting component concentration (n = 4), or used the quadratic equation in a titration regime (limiting component concentration in >1000-fold excess over the K_D), incompatible with reliable K_D determination (n = 1; see below).

Figure 2

Download asset Open asset

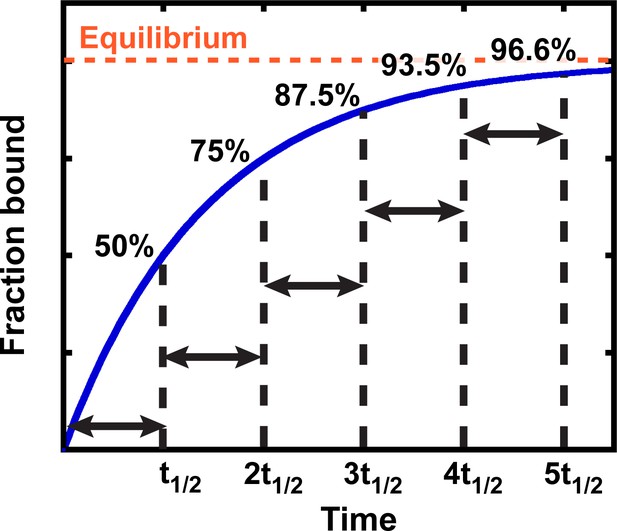
Exponential kinetics used to estimate the time needed for binding equilibration.

Arrows indicate reaction half-life t_1/2. Fraction bound is defined by the equation $1 - e^{-t \times ln2/ t_{1/2}}$ = $1 - e^{-t \times k_{equil}}$ .

Figure 3

Download asset Open asset

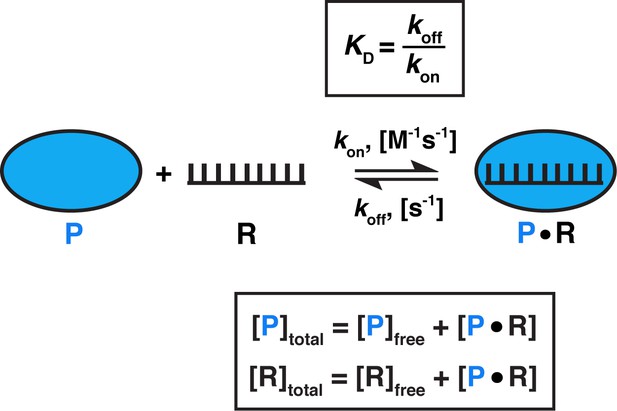
Model for one-step, non-cooperative, 1:1 binding between two molecules.

Protein (P) binding to an RNA (R) molecule is shown for illustrative purposes.

Figure 4 with 1 supplement

Download asset Open asset

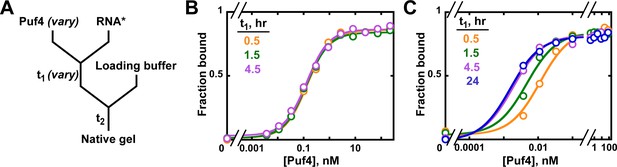
Establishing equilibration in affinity measurements.

(A) Mixing scheme. RNA*: labeled RNA (here—5´-terminally labeled with ³²P). In addition to varying equilibration time t₁ (main text), the time and conditions between adding the loading buffer and loading (t₂) are controlled (see Appendix 2—note 2). (**B, C**) Concentration dependence of Puf4 binding at 25°C (B) and at 0°C (C) after different incubation times. Data were collected at protein concentrations greater than or equal to the concentration of labeled RNA (0.002–0.016 nM, indicating the lower and upper limit of labeled RNA concentration; see section 'Avoid the titration regime' and Appendix 2—note 4).

Figure 4—figure supplement 1

Download asset Open asset

Insufficient equilibration times can lead to incorrect determination of relative affinities.

(A) Binding parameters for protein (P) interactions with two ligands, L1 and L2. The dissociation rate constant (k_off) for L1 is 100-fold lower than for L2, such that L1 requires much longer to equilibrate than L2 (Equation 2). (B) Simulated binding data for L1 and L2 with varying incubation times (t₁). The binding to each ligand is measured individually with trace amounts of L1 (blue) or L2 (red). Solid lines are fits to an equilibrium binding equation (Equation 4b), with dashed lines indicating the protein concentration at which half of the ligand is bound. Because equilibration of L1 binding is not complete until t₁ = 10 hr (while L2 equilibration only takes ~5 min), the observed relative affinity ( $K_{D}^{app}$ (rel) = $K_{D,2}^{app}$ / $K_{D,1}^{app}$ ) is time-dependent and underestimates the true specificity if the incubation time is shorter than ~10 hr. Arrows and numbers indicate $K_{D}^{app}$ (rel) values at each time point. Note the systematic deviations of the simulated data from the fit curve in cases where equilibrium has not been reached. The presence of such deviations in experimental data indicates the need for additional controls to establish equilibration and rule out titration.

Figure 5 with 5 supplements

Download asset Open asset

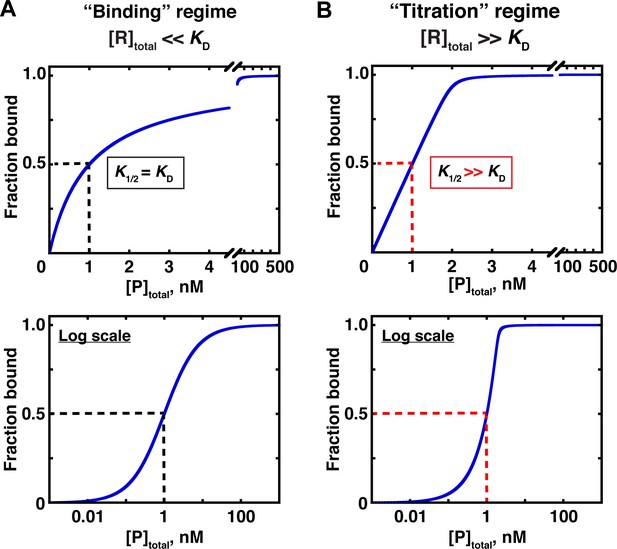
Two concentration regimes.

(A) Binding curve for the model in Figure 3 in the ‘binding’ regime—that is, the trace binding partner concentration ([R]_total) is much lower than K_D and much lower than [P]_total (Equation 4b). Here, the K_D is simply the protein concentration at which half of the RNA is bound (K_1/2, here corresponding to 1 nM). The same simulated binding curve is shown in linear (top) and log (bottom) plots, as both are useful and common in the literature. (B) Binding curve in the ‘titration’ regime, simulated for an interaction with a K_D value of 0.01 nM and an [R]_total of 2 nM. Although the K_1/2 value in this example is identical to the example in Part A, here it does not equal K_D, instead exceeding the real K_D value by 100-fold.

Figure 5—figure supplement 1

Download asset Open asset

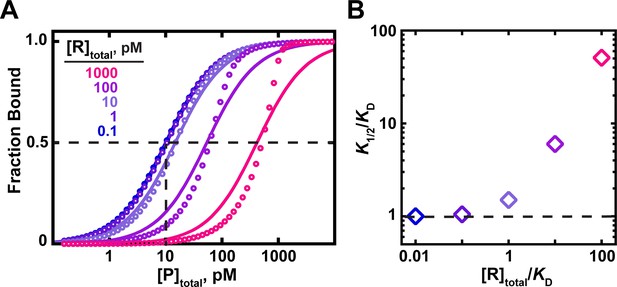
The effects of RNA (ligand) concentration on observed binding.

(A) Circles indicate simulated data for an interaction with a K_D = 10 pM in the presence of RNA concentrations ranging from 100-fold below to 100-fold above the K_D. Curves indicate fits of the simulated data to a hyperbolic equation (Equation 4b). For RNA concentrations ≤10-fold below the K_D, the data are well explained by a hyperbolic fit, and the protein concentration at which half-saturation occurs (K_1/2; indicated with dashed lines for the 0.1 pM RNA curve) is consistent with the K_D. Higher RNA concentrations lead to increasing deviations from a hyperbolic fit and have increasing K_1/2 values as the RNA concentration increases. (B). The relationship between the observed K_1/2 enhancement over the true K_D (‘K_1/2/K_D’) and the total RNA concentration relative to K_D (‘[R]_total/K_D’). K_1/2 values were derived from the simulated data in part A using Equation 4b.

Figure 5—figure supplement 2

Download asset Open asset

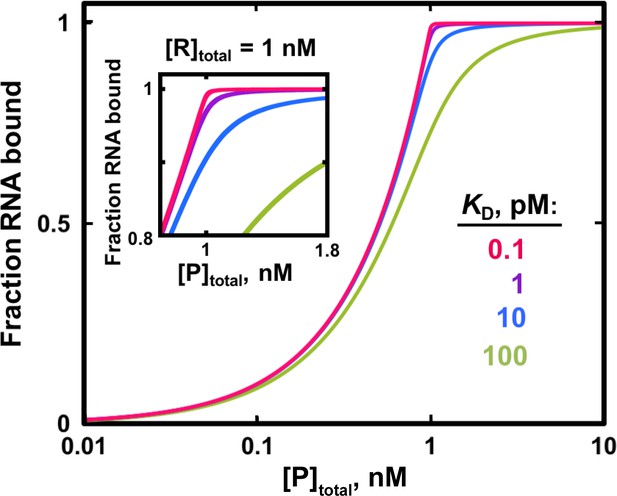
Fit to the quadratic binding equation becomes less sensitive to differences in K_D when the RNA concentration is in large excess over the K_D.

Simulated binding curves for RNA/protein interactions of varying affinities are shown in the presence of 1 nM labeled RNA. In this example, K_D = 1 pM (1000-fold lower than [R]_total) would be essentially impossible to distinguish from K_D = 0.1 pM (10,000-fold lower than [R]_total) and from even lower K_D values because of the nearly identical binding curves. To accurately measure K_D = 10 pM (100-fold lower than [RNA]) it would be critical to have a large number of data points in the narrow protein concentration range that distinguishes this curve from weaker and especially from stronger binders (inset).

Figure 5—figure supplement 3

Download asset Open asset

Application of the hyperbolic (Equation 4b) and quadratic (Equation 5) binding equations to simulated binding data with increasing noise levels.

All binding curves are for an RNA-protein interaction with a K_D of 0.1 nM, measured in the presence of different RNA concentrations (0.001–100 nM) and with increasing levels of random noise in the fraction bound (standard deviation of 0.01–0.2). Ten datasets were simulated per condition and noise level and were individually fit to Equation 4b (leftmost column) or Equation 5 (the remaining columns) to determine the K_D. The binding curves are shown as black lines, and the overlaid white circles indicate the expected fractions bound if the data were not affected by noise, with error bars indicating the standard deviation. The fit K_D values for each of the 10 simulated datasets are shown below each set of binding curves, and the error bars indicate the 95% confidence intervals (CIs) of the K_D. Gray bars indicate that the K_D could not be determined from a quadratic fit. CIs that extend beyond the axis limits indicate that the lower limit of the K_D was not defined. Note that with increasing noise and increasing RNA concentration the K_D values derived from the quadratic fits become increasingly poorly constrained, particularly the lower CIs. By contrast, using the binding regime and Equation 4b to fit the data (leftmost column) consistently yields well-defined K_D values, even with substantial noise.

Figure 5—figure supplement 4

Download asset Open asset

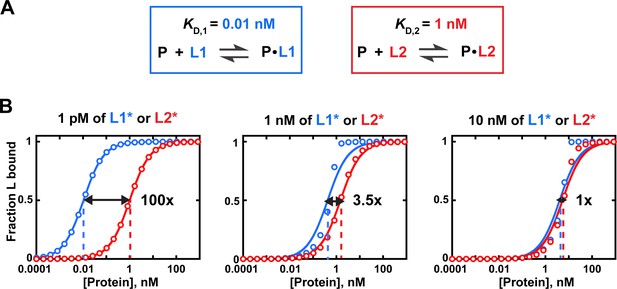
Effects of trace binding partner concentration on apparent relative affinities.

(A) Affinities of protein P for ligands L1 and L2. (B) Simulated equilibrium binding curves. Binding to each ligand is measured individually with different concentrations of labeled ligand (L1* or L2*). Solid lines are fits to Eq. 4b, with dashed lines indicating the protein concentration at which half of the ligand is bound (corresponding to K_D in Equation 4b). Arrows and numbers indicate apparent K_D(rel) values at each concentration of L ( $K_{D}^{app}$ (rel) = $K_{D,2}^{app}$ / $K_{D,1}^{app}$ ; with $K_{D,1}^{app}$ and $K_{D,2}^{app}$ derived using Equation 4b). There is a pronounced dependence of apparent relative affinity on ligand concentration if [L] is not much lower than the K_D for the most tightly bound ligand among the ligands being compared. If sufficiently low ligand concentrations are not accessible, Equation 5 should be used and results may be less reliable (see section 'Avoid the titration regime' of main text).

Figure 5—figure supplement 5

Download asset Open asset

Concentration regimes that do not (A) and do (B) affect the determination of equilibrium binding constants.

(A) Labeled RNA concentration is much lower than K_D ([R*]_total << K_D; binding regime). (B) Labeled RNA concentration is greater than K_D ([R*]_total > K_D; intermediate regime). In parts (A) and (B), concentrations are indicated schematically by the number of RNA (R*, red), protein (P, light blue) molecules and RNA-protein complexes (P●R*) shown. In each case, protein concentration is varied (6, 18, 54, 400 arbitrary units), and K_D equals 18 (in the same units). The total RNA concentration is 4 (A) and 36 (B). (C) Protein concentration dependence of binding in each of the above regimes. In the binding regime (green, [R*]_total << K_D from part A), the protein concentration at which half of the RNA is bound corresponds to the K_D. In contrast, in the intermediate regime (purple, [R*]_total > K_D from part B), a greater protein concentration is required to achieve half-saturation (40 vs. 18 arbitrary units). The discrepancy would further increase with higher RNA concentrations, as shown in Figure 5—figure supplement 1. We can understand the origin of this discrepancy as follows. In part (A), the RNA concentration (red) is below the K_D value and below the protein concentration (blue), such that the free concentration of the protein is essentially unchanged after RNA binding at both saturating (complete binding of RNA) and sub-saturating protein concentrations. Changing the RNA concentration in this regime would not change the fraction of RNA bound at a given total protein concentration, as long as the [R*]_total << K_D condition remains met. On the contrary, in part (B), the RNA concentration exceeds the dissociation constant (K_D) and is high enough that a large fraction of the total protein is bound by RNA. Thus, the *free* protein concentration, which determines the extent of binding according to Equation 4a, is depleted and can no longer be approximated by the *total* protein concentration in Equation 4b to obtain an accurate K_D value. On the molecular scale, the lowered free protein results in less binding. Consequently, for a given K_D, more protein is required to achieve half-saturation at higher RNA concentration than with a trace concentration of RNA. Intuitively, at a concentration of RNA that is greater than K_D there simply isn’t enough protein to occupy half the RNA when the total protein concentration is equal to K_D.

Figure 6

Download asset Open asset

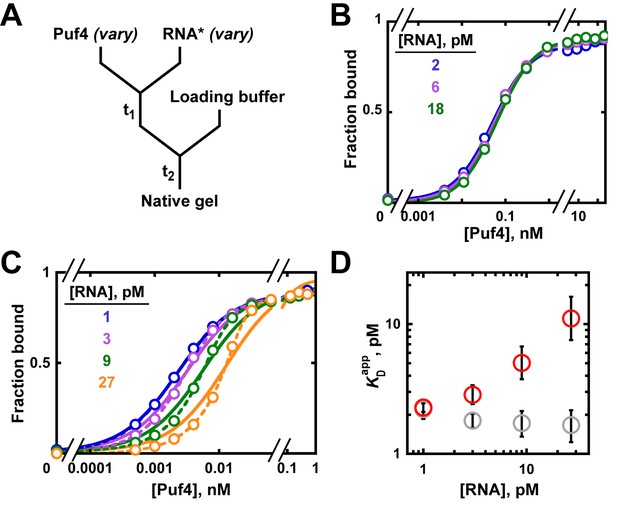
Varying the concentration of the 'trace' binding partner.

(A) Mixing scheme, as in Figure 4A but now with a series of labeled RNA concentrations. (B) Puf4 binding to different concentrations of ³²P-labeled RNA at 25°C. For simplicity, only the lower limits of RNA concentration are indicated; the corresponding upper limits were 15–140 pM RNA (see Materials and methods and Appendix 2—note 4). Incubation time t₁ was 0.5 hr, as established in Figure 4B. (C) Puf4 binding to different concentrations of ³²P-labeled RNA at 0°C. Lower limits of labeled RNA concentration are indicated. Incubation time t₁ was 40 hr. Note that these data are not fit well by Equation 4b, which assumes [R*]_total << K_D (solid lines). Quadratic fits, which do not assume negligible RNA concentration, are shown in dashed lines (Equation 5). (D) Effect of RNA concentration on apparent K_D ( $K_{D}^{app}$ ) at 0°C. Red symbols indicate $K_{D}^{app}$ values from a hyperbolic fit (Equation 4b and solid lines in C) and grey symbols indicate $K_{D}^{app}$ values from fits to the quadratic equation (Equation 5). The error bars denote 95% confidence intervals, as determined by fitting the data to the indicated equation in Prism 8.

Figure 7 with 1 supplement

Download asset Open asset

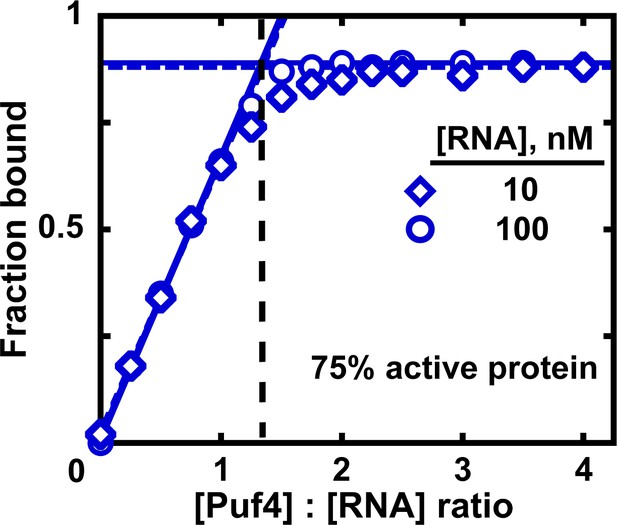
Measuring the fraction of active protein by titration.

The fraction of active protein is derived from the breakpoint, that is, the intersection of linear fits to the low and high-Puf4 concentration data. See Figure 7—figure supplement 1 for an alternative strategy using Equation 5.

Figure 7—figure supplement 1

Download asset Open asset

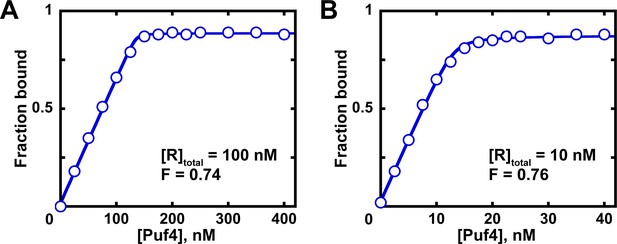
Determination of the fraction of active protein from a quadratic fit.

Fits of titration data at 100 nM (A) and 10 nM (B) RNA to the quadratic equation are shown. The quadratic equilibrium-binding equation (Equation 5) was modified to include a term for the active protein fraction.
$F r a c t i o n b o u n d = A \times \frac{({[R]}_{t o t a l} + F \times {[P]}_{t o t a l} + K_{D}) - \sqrt{({[R]}_{t o t a l} + F \times {[P]}_{t o t a l} + K_{D})^{2} - 4 \times {[R]}_{t o t a l} \times F \times {[P]}_{t o t a l}}}{2 \times {[R]}_{t o t a l}} + O$
A and O correspond to the amplitude and Y axis offset, respectively; F is the fraction of active protein; ${[R]}_{total}$ was constrained to the known RNA concentration (10 or 100 nM); here, the $K_{D}$ value was constrained to the known affinity (Table 2). The last constraint is optional, as the $K_{D}$ value contributes minimally to the fit at these high RNA concentrations and because the exact $K_{D}$ value may not yet be known at the time of measuring the active protein fraction. The fit fractions of active protein (F) are almost identical to those determined from linear fits of the same data in Figure 7 (~0.75).

Appendix 1—figure 1

Download asset Open asset

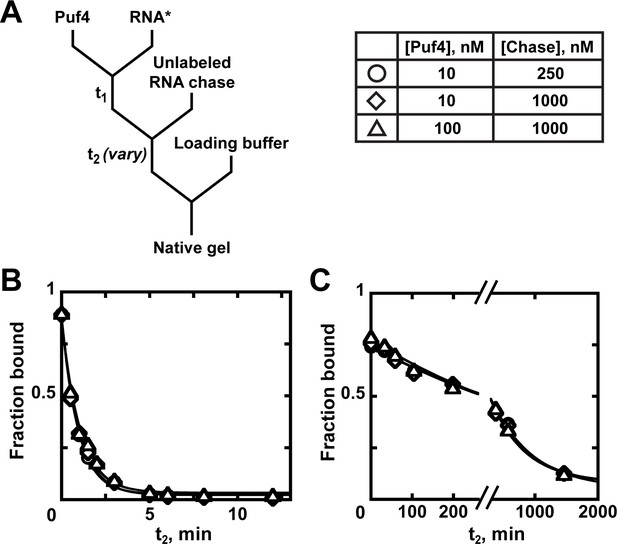
Kinetics of Puf4 dissociation.

(A) Mixing scheme for measuring the dissociation rate constant. After equilibration of a saturating or near-saturating concentration of Puf4 protein with a trace concentration of labeled RNA (t₁), a large excess of unlabeled RNA is added, with concomitant dilution of the binding reaction to prevent rebinding after dissociation. (**B–C**) Time dependence of Puf4 dissociation from its consensus RNA at 25°C (C; k_off = (0.014 ± 0.003) s⁻¹) and at 0°C (D; k_off = (2.92 ± 0.17) × 10⁻⁵ s⁻¹).

Appendix 1—figure 2

Download asset Open asset

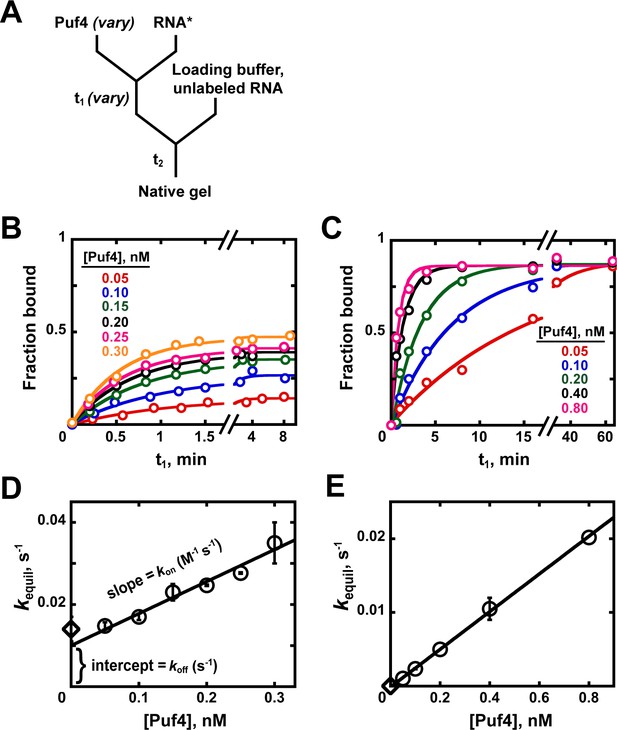
Kinetics of Puf4/RNA association.

(A) Mixing scheme for measuring association rate constants. (**B, C**) Time dependence of Puf4 association to its consensus RNA at 25°C (B) and 0°C (C). (**D, E**) Determination of k_on from the slope of the Puf4 concentration dependence of equilibration rate constants in parts B and C, respectively (circles). The k_off values from Appendix 1—figure 1 are also shown (diamonds) to illustrate the correspondence between the y-intercept and k_off (Equation 1). Panels D and E show results from two and one independent experiments, respectively (error bars in E correspond to averages from measurements at two different labeled RNA concentrations).

Appendix 3—figure 1

Download asset Open asset

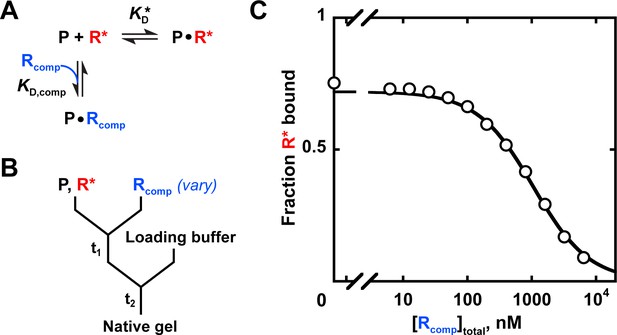
Measuring binding affinity by competition.

(A) Competitive binding reaction scheme. R*: labeled RNA ligand; R_comp: unlabeled competitor RNA; $K_{D}^{*}$ : protein affinity for R*; $K_{D,comp}$ : protein affinity for R_comp. (B) Mixing scheme for a competition measurement. (C) Competition between the U1C point mutant of the Puf4 consensus (R_comp = CGUAUAUUA) and the labeled consensus RNA (R*= ³²P-AUGUGUAUAUUAGU). The data were fit to the following equation (Lin and Riggs, 1972; Weeks and Crothers, 1992):
$F r a c t i o n b o u n d = A \times \frac{1}{2 [R^{*}]_{t o t a l}} [K_{D}^{*} + \frac{K_{D}^{*}}{K_{D, c o m p}} [R_{c o m p}]_{t o t a l} + [P]_{t o t a l} + [R^{*}]_{t o t a l} - \sqrt{{(K_{D}^{*} + \frac{K_{D}^{*}}{K_{D, c o m p}} [R_{c o m p}]_{t o t a l} + [P]_{t o t a l} + [R^{*}]_{t o t a l})}^{2} - 4 [R^{*}]_{t o t a l} [P]_{t o t a l}]} + O$
A indicates the maximum amplitude, constrained to the fit amplitude of the R* binding curve that is measured in parallel by a direct binding experiment (A = 0.89 for Puf4 binding to R*). O is the y axis offset (background). [R*]_total was constrained to the lower limit of the labeled RNA concentration. $K_{D}^{*}$ was constrained to Puf4 affinity for the labeled RNA, as determined by direct measurement in the same experiment (0.105 nM, after accounting for active protein fraction of 75%). [P]_total was 0.45 nM, after accounting for active protein fraction. The fit $K_{D,comp}$ value was 204 nM. Incubation times of 10, 30, and 110 min gave consistent $K_{D,comp}$ values (190–210 nM), as did lowering the protein concentration by three-fold (180 nM). Equation 9 is applicable only for $K_{D,comp} >> K_{D}^{*}$ . For other cases see Wang, 1995.

Appendix 4—figure 1

Download asset Open asset

Appendix 4—figure 2

Download asset Open asset

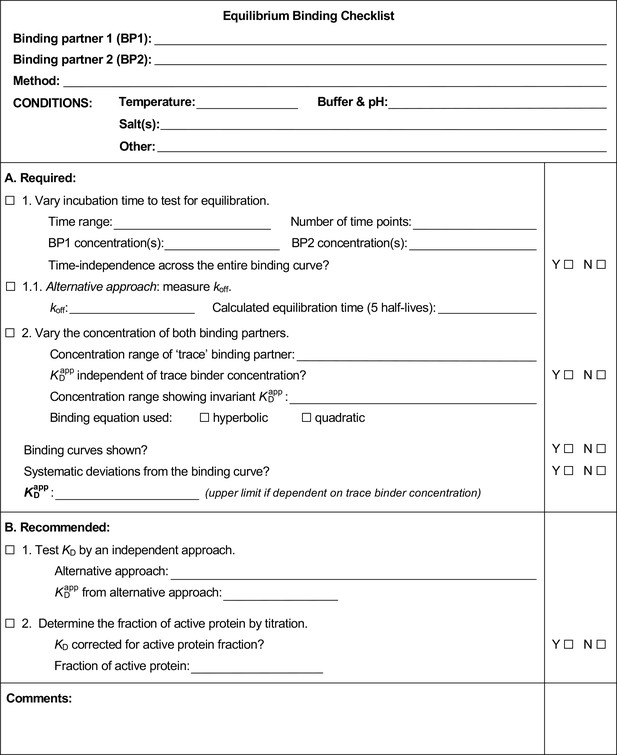
Example of a completed equilibrium binding checklist based on Puf4/RNA binding at 25°C.

Appendix 4—figure 3

Download asset Open asset

Example of a completed equilibrium binding checklist based on Puf4/RNA binding at 0°C.

Tables

Table 1

Equilibration times (t_equil) for different affinities and association rate constants.

K_D	k_on, M⁻¹ s⁻¹	t_equil*
K_D	k_on, M⁻¹ s⁻¹	sec	hr
1 µM	10⁸	0.04
	10⁶	4
	10³		1
1 nM	10⁸	40
	10⁶		1
	10³		1000
1 pM	10⁸		10
	10⁶		1000
	10³		1,000,000

*t_equil was calculated as five half-lives: t_equil = 5t_1/2 = 5 × 0.693/k_equil, where k_equil = k_off = K_D× k_on (Equation 2 and Figure 3).

Table 2

Summary of equilibrium and kinetic measurements of Puf4 affinity.

	Equilibrium*		Kinetic
Temperature,°C	K_D(hyperbolic), pM	K_D(quadratic), pM	k_on, M⁻¹s⁻¹*	k_off, s⁻¹	K_D (=k_off/k_on), pM
0	≤1.7	1.39 ± 0.09	(2.85 ± 0.14)×10⁷	(2.92 ± 0.17)×10⁻⁵	1.02 ± 0.08
25	120 ± 30	120 ± 30	(1.04 ± 0.14)×10⁸	0.014 ± 0.003	130 ± 30

*The values have been normalized by active protein fraction (75–90%). K_D(hyperbolic) and K_D(quadratic) refer to values derived from fits to Equation 4b and Equation 5, respectively. Errors are defined in Materials and methods.

Additional files

Supplementary file 1 Literature survey of 100 RNA/protein binding studies.: https://cdn.elifesciences.org/articles/57264/elife-57264-supp1-v3.xlsx
Download elife-57264-supp1-v3.xlsx
Supplementary file 2 Literature survey of CRISPR nuclease binding studies, representative of high-affinity interactions.: https://cdn.elifesciences.org/articles/57264/elife-57264-supp2-v3.xlsx
Download elife-57264-supp2-v3.xlsx
Transparent reporting form: https://cdn.elifesciences.org/articles/57264/elife-57264-transrepform-v3.docx
Download elife-57264-transrepform-v3.docx

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Inga Jarmoskaite
Ishraq AlSadhan
Pavanapuresan P Vaidyanathan
Daniel Herschlag

(2020)

How to measure and evaluate binding affinities

eLife 9:e57264.

https://doi.org/10.7554/eLife.57264

Figures

Assessment of published K_D values for RNA-binding proteins.

Survey of incubation times for published equilibrium dissociation constants.

Survey of titration controls in published binding studies.

Exponential kinetics used to estimate the time needed for binding equilibration.

Model for one-step, non-cooperative, 1:1 binding between two molecules.

Establishing equilibration in affinity measurements.

Insufficient equilibration times can lead to incorrect determination of relative affinities.

Two concentration regimes.

The effects of RNA (ligand) concentration on observed binding.

Fit to the quadratic binding equation becomes less sensitive to differences in K_D when the RNA concentration is in large excess over the K_D.

Application of the hyperbolic (Equation 4b) and quadratic (Equation 5) binding equations to simulated binding data with increasing noise levels.

Effects of trace binding partner concentration on apparent relative affinities.

Concentration regimes that do not (A) and do (B) affect the determination of equilibrium binding constants.

Varying the concentration of the 'trace' binding partner.

Measuring the fraction of active protein by titration.

Determination of the fraction of active protein from a quadratic fit.

Kinetics of Puf4 dissociation.

Kinetics of Puf4/RNA association.

Measuring binding affinity by competition.

Equilibrium binding checklist template.

Example of a completed equilibrium binding checklist based on Puf4/RNA binding at 25°C.

Example of a completed equilibrium binding checklist based on Puf4/RNA binding at 0°C.

Tables

Equilibration times (t_equil) for different affinities and association rate constants.

Summary of equilibrium and kinetic measurements of Puf4 affinity.

Additional files

Supplementary file 1

Supplementary file 2

Transparent reporting form

Download links

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Be the first to read new articles from eLife

Share this article

Cite this article

Assessment of published KD values for RNA-binding proteins.

Survey of incubation times for published equilibrium dissociation constants.

Survey of titration controls in published binding studies.

Exponential kinetics used to estimate the time needed for binding equilibration.

Model for one-step, non-cooperative, 1:1 binding between two molecules.

Establishing equilibration in affinity measurements.

Insufficient equilibration times can lead to incorrect determination of relative affinities.

Two concentration regimes.

The effects of RNA (ligand) concentration on observed binding.

Fit to the quadratic binding equation becomes less sensitive to differences in KD when the RNA concentration is in large excess over the KD.

Application of the hyperbolic (Equation 4b) and quadratic (Equation 5) binding equations to simulated binding data with increasing noise levels.

Effects of trace binding partner concentration on apparent relative affinities.

Concentration regimes that do not (A) and do (B) affect the determination of equilibrium binding constants.

Varying the concentration of the 'trace' binding partner.

Measuring the fraction of active protein by titration.

Determination of the fraction of active protein from a quadratic fit.

Kinetics of Puf4 dissociation.

Kinetics of Puf4/RNA association.

Measuring binding affinity by competition.

Equilibrium binding checklist template.

Example of a completed equilibrium binding checklist based on Puf4/RNA binding at 25°C.

Example of a completed equilibrium binding checklist based on Puf4/RNA binding at 0°C.

Equilibration times (tequil) for different affinities and association rate constants.

Summary of equilibrium and kinetic measurements of Puf4 affinity.

Supplementary file 1

Supplementary file 2

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Assessment of published K_D values for RNA-binding proteins.

Fit to the quadratic binding equation becomes less sensitive to differences in K_D when the RNA concentration is in large excess over the K_D.

Equilibration times (t_equil) for different affinities and association rate constants.