Optogenetic investigation of BMP target gene expression diversity

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: December 10, 2020 (This version)
Accepted Manuscript published: November 11, 2020 (Go to version)
Accepted: November 10, 2020
Received: May 6, 2020

1. Of interest
Cohesin-independent STAG proteins interact with RNA and R-loops and promote complex loading

Hayley Porter, Yang Li ... Suzana Hadjur

Research Article Updated Jun 2, 2023
Further reading

Article
Figures and data
Abstract
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Signaling molecules activate distinct patterns of gene expression to coordinate embryogenesis, but how spatiotemporal expression diversity is generated is an open question. In zebrafish, a BMP signaling gradient patterns the dorsal-ventral axis. We systematically identified target genes responding to BMP and found that they have diverse spatiotemporal expression patterns. Transcriptional responses to optogenetically delivered high- and low-amplitude BMP signaling pulses indicate that spatiotemporal expression is not fully defined by different BMP signaling activation thresholds. Additionally, we observed negligible correlations between spatiotemporal expression and transcription kinetics for the majority of analyzed genes in response to BMP signaling pulses. In contrast, spatial differences between BMP target genes largely collapsed when FGF and Nodal signaling were inhibited. Our results suggest that, similar to other patterning systems, combinatorial signaling is likely to be a major driver of spatial diversity in BMP-dependent gene expression in zebrafish.

Introduction

Embryogenesis is orchestrated by signaling pathways that activate spatiotemporally diverse patterns of gene expression. A prominent theory relating signaling to gene expression diversity is the gradient threshold model, in which a signaling gradient across a tissue defines unique spatial gene expression domains by activating target genes at different signaling thresholds (Figure 1A; Sharpe, 2019; Briscoe and Small, 2015; Dubrulle et al., 2015; Rogers and Schier, 2011; Barkai and Shilo, 2009; Ashe and Briscoe, 2006). Gene expression patterns can also be influenced by signaling dynamics and expression kinetics (Sagner and Briscoe, 2017) as well as interactions with other signaling pathways (Briscoe and Small, 2015). However, in many patterning systems the factors leading to diverse developmental gene expression profiles are incompletely characterized. Here, we investigate how signaling levels, target gene expression kinetics, and combinatorial signaling contribute to gene expression diversity during dorsal-ventral patterning in zebrafish.

Figure 1 with 1 supplement see all

Download asset Open asset

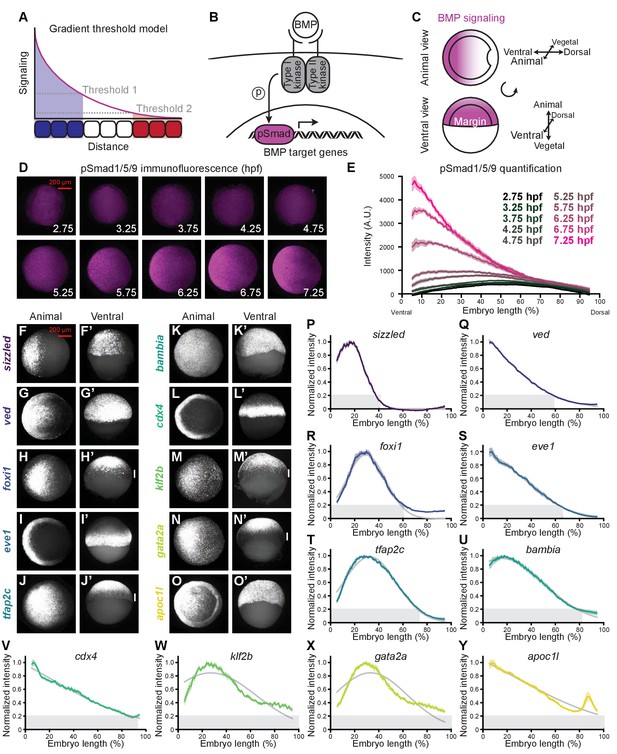
BMP target genes have diverse spatial expression patterns at shield stage.

(A) The gradient threshold model states that a signaling gradient activates genes (blue, white, red) at different thresholds (dashed gray lines). (B) BMP binding induces receptor complex formation, phosphorylation of Smad1/5/9, and activation of target genes. (C) Schematic of shield-stage zebrafish embryos with BMP signaling gradients (magenta) along the dorsal-ventral axis. (**D-E**) Representative images (D) of pSmad1/5/9 immunofluorescence in embryos at the indicated time post-fertilization and quantification (E). (**F-O’**) Fluorescence *in situ* hybridization (FISH) showing spatial expression of the indicated high-confidence BMP target genes at shield stage (~6.75 h post-fertilization (hpf)). (F,G,H,I,J,K,L,M,N,O) are animal views, dorsal to the right. (F’,G’,H’,I’,J’,K’,L’,M’,N’,O’) are ventral views. Vertical white bars indicate regions where expression is excluded from the margin. (**P-Y**) Quantification of FISH signal along the dorsal-ventral axis for the indicated BMP target genes at shield stage (ventral on the left, dorsal on the right as in (E)). Normalized intensities are shown; error bars represent standard error. The Gaussian function $A e^{- \frac{{(x - μ)}^{2}}{ς}}$ was fitted to each profile (gray lines), and gene expression range was defined as $r = μ + 2 \sqrt{ς / 2}$ (gray bars). Some BMP target genes could not be reliably quantified due to weak FISH signal (*bmp4*, *id2a*, *smad6a*, *smad7*, and *znfl2b*) or inability to reliably identify the ventral side in all assays (*crabp2b*). See the Figure 1—source data 1 file for source data.

Figure 1—source data 1 Source data for Figure 1.: https://cdn.elifesciences.org/articles/58641/elife-58641-fig1-data1-v2.xlsx
Download elife-58641-fig1-data1-v2.xlsx

We focused on patterning mediated by BMP, a TGF-β superfamily member with important developmental roles across the animal kingdom (reviewed in Zinski et al., 2018). BMP ligands bind and assemble complexes of type I and II receptor serine/threonine kinases, resulting in the phosphorylation of the signal transducers Smad1/5/9 and activation of BMP target genes (Figure 1B; Derynck and Budi, 2019). The regulation of BMP gradient formation during early development has been analyzed in a variety of organisms including Drosophila, Nematostella, and Xenopus (Genikhovich et al., 2015; Iber and Gaglia, 2007; Mizutani et al., 2005; Plouhinec et al., 2013) as well as zebrafish. During late blastula and early gastrulation stages in zebrafish embryos, graded transcription and subsequent diffusion of BMP ligands, together with dorsally secreted BMP inhibitors such as Chordin, generate a ventrally-peaking gradient of BMP signaling that patterns the dorsal-ventral axis (Figure 1C; Pomreinke et al., 2017; Zinski et al., 2017). Loss of BMP signaling results in dorsalization, whereas excess BMP signaling produces ventralized embryos (Zinski et al., 2018). The degree of dorsalization or ventralization can be modulated by mutations in BMP pathway components with different strengths (Mintzer et al., 2001; Barth et al., 1999; Nguyen et al., 1998; Mullins et al., 1996) or by injecting different amounts of mRNA encoding pathway activators or inhibitors (Schumacher et al., 2011; Dick et al., 2000; Kishimoto et al., 1997; Neave et al., 1997).

These observations have led to the suggestion that BMP functions as a morphogen to pattern the dorsal-ventral axis by activating different target genes at different signaling level thresholds (Figure 1A; Zinski et al., 2018; Tuazon and Mullins, 2015; Schumacher et al., 2011; Barth et al., 1999; Nguyen et al., 1998; Neave et al., 1997; Mullins et al., 1996). However, overexpression and genetic manipulations can affect the duration of signal exposure, dysregulate other signaling pathways, and modify earlier aspects of development such as morphogenetic movements, complicating the interpretation of these experiments. Moreover, patterning of the dorsal-ventral axis by BMP and the germ layers by FGF and Nodal occurs simultaneously in zebrafish (Zinski et al., 2018), and although these pathways are known to interact, how FGF and Nodal influence the spatiotemporal expression of BMP target genes has not been systematically assessed.

To identify the factors that contribute to differences in BMP target gene expression and rule out factors that do not contribute, we first identified BMP targets in early zebrafish embryos and quantified their diverse spatial (Figure 1) and temporal (Figure 2) expression patterns. We then used an optogenetic approach to generate acute BMP signaling pulses (Figure 3) and found that while most target genes can respond to early BMP signaling (Figure 4), differential transcription kinetics do not fully account for the observed expression differences (Figure 5). Further, target gene responses to high- and low-amplitude signaling pulses suggest that not all spatiotemporal target gene expression differences are due to different signaling activation thresholds (Figure 6). In contrast, inhibition of FGF and Nodal signaling homogenized the spatial expression patterns of BMP targets, suggesting that combinatorial regulation by BMP, FGF, and Nodal is a major driver of BMP target gene spatial diversity (Figure 7).

Figure 2

Download asset Open asset

BMP target genes have diverse temporal expression profiles.

(**A–N**) Embryos were collected every 30 min from 2.75 to 7.25 hpf, and transcript levels were quantified using NanoString technology. Error bars represent standard error. Temporal profiles were fit with the cumulative distribution function of the normal distribution (gray lines), and activation time (arrowheads) was defined as the average time point at which the curves reached about two mean average deviations (i.e., $1.5 ∙ τ$ ) from the inflection point $ν$ (excluding the maternally deposited genes *id2a* [Chong et al., 2005] and *smad6a* [White et al., 2017]). NanoString probes for two high-confidence activated BMP target genes (*apoc1l* and *znfl2b*) were not functional. (O) Average gene expression spatial range is plotted against average activation time. See the Figure 2—source data 1 file for source data.

Figure 2—source data 1 Source data for Figure 2.: https://cdn.elifesciences.org/articles/58641/elife-58641-fig2-data1-v2.xlsx
Download elife-58641-fig2-data1-v2.xlsx

Figure 3 with 1 supplement see all

Download asset Open asset

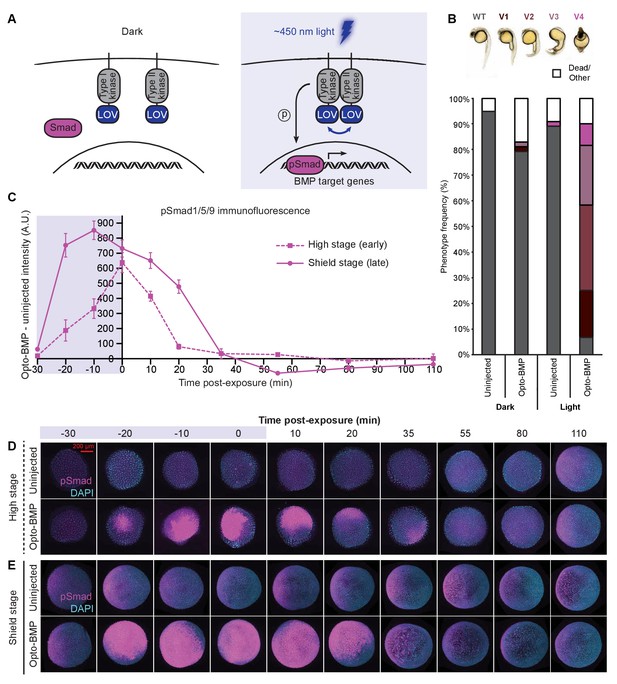
Reversible activation of BMP signaling using blue light-activated Opto-BMP.

(A) Schematic of Opto-BMP strategy. Blue light-dimerizable VfLOV domains were fused to zebrafish BMP receptor kinase domains. Blue light exposure activates BMP signaling. (B) Embryos injected with mRNA encoding Opto-BMP at the one-cell stage and their uninjected siblings were reared in the dark or exposed to blue light for 10 h starting 70–80 min post-fertilization. Ventralization phenotypes V1-V4 (indicating excess BMP signaling) were scored at 1 day post-fertilization. Number of embryos: uninjected dark = 59, Opto-BMP dark = 53, uninjected light = 55, Opto-BMP light = 60. (**C-E**) Uninjected and Opto-BMP-injected embryos were exposed to blue light (2300 lux) for 30 min starting at high stage (3.5 hpf) or shield stage (6.75 hpf) and fixed during and after exposure. pSmad1/5/9 immunofluorescence was quantified and plotted in (C) as Opto-BMP minus uninjected signal with piecewise linear interpolation between timepoints; error bars represent standard error (see Materials and methods for statistical analysis). Blue background represents light exposure. Representative embryos from the high-stage (D) and shield-stage (E) experiments quantified in (C). pSmad1/5/9 signal is shown in magenta, DAPI in cyan. See the Figure 3—source data 1 file for source data.

Figure 3—source data 1 Source data for Figure 3.: https://cdn.elifesciences.org/articles/58641/elife-58641-fig3-data1-v2.xlsx
Download elife-58641-fig3-data1-v2.xlsx

Figure 4

Download asset Open asset

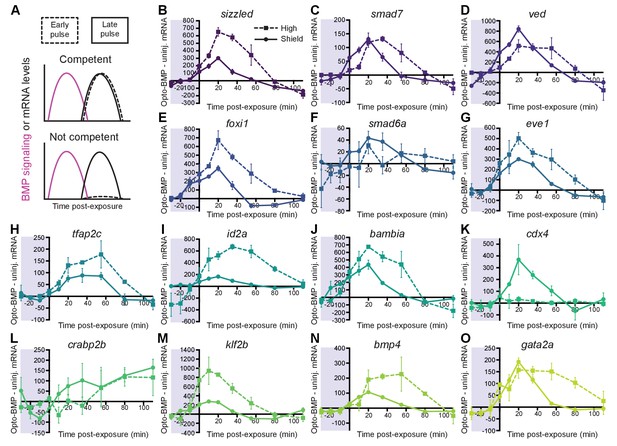
Most BMP target genes are competent to respond to an early BMP signaling pulse.

(A) Schematic of competence model: Late-activated genes should respond to a late (shield stage, solid line), but not early (high stage, dashed line) BMP signaling pulse. (**B-O**) High-confidence BMP target gene responses after an early (high stage,~3.5 hpf, dashed line) or late (shield stage,~6.75 hpf, solid line) BMP signaling pulse delivered by exposing uninjected and Opto-BMP-injected embryos to 30 min blue light (Figure 3C–E and Figure 3—figure supplement 1I,J). To assess induced transcription, NanoString transcript counts from uninjected embryos were subtracted from Opto-BMP transcript counts and are plotted here with piecewise linear interpolation between timepoints; error bars represent standard error (see Materials and methods for statistical analysis). See the Figure 4—source data 1 file for source data.

Figure 4—source data 1 Source data for Figure 4.: https://cdn.elifesciences.org/articles/58641/elife-58641-fig4-data1-v2.xlsx
Download elife-58641-fig4-data1-v2.xlsx

Figure 5 with 1 supplement see all

Download asset Open asset

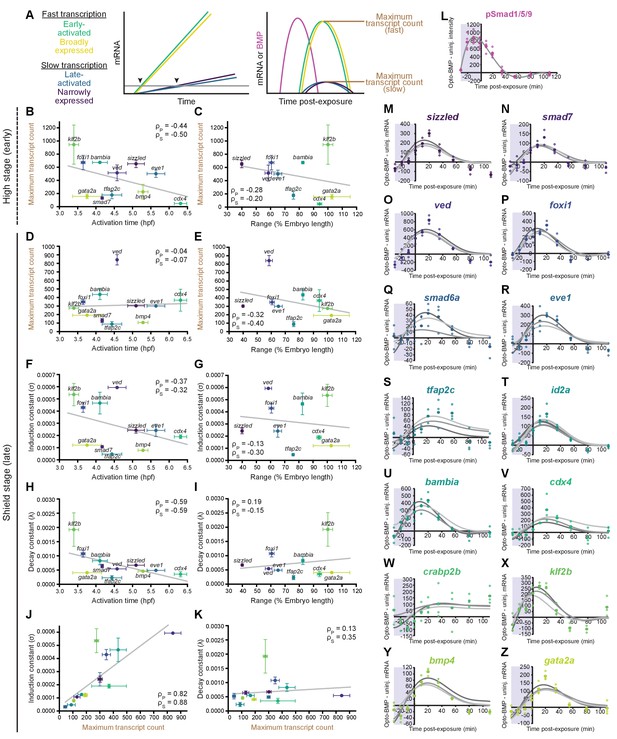
Differential expression kinetics do not fully explain BMP target gene spatiotemporal diversity.

(A) Different transcription kinetics may lead to differences in apparent activation times (arrowheads) based on assay detection thresholds (gray line). Assuming similar degradation kinetics, transcripts with faster induction rates should accumulate to higher levels in response to BMP. (**B-E**) Uninjected and Opto-BMP-injected embryos were exposed to blue light for 30 min at high (~3.5 hpf, B,C) or shield stage (~6.75 hpf, D,E), and target gene expression in response to the resulting BMP signaling pulses (Figure 3C–E and Figure 3—figure supplement 1I,J) was quantified using NanoString technology (Figure 4). Maximum average transcript counts were determined, and are plotted against activation time (B,D) (Figure 2) or spatial range (C,E). Error bars represent standard error, gray lines represent linear fits, ρ_s = Spearman correlation coefficient, ρ_p = Pearson correlation coefficient. *crabp2b* is not included due to lack of significant induction. (**F-L**) All three target gene response repeats were fitted with a model of induction and decay (Materials and methods). The average induction constant (σ) is plotted against activation time (F), spatial range (G), or maximum transcript count (J). The average decay constant (λ) is plotted against activation time (H), range (I), or maximum transcript count (K). Error bars represent standard error, ρ_s = Spearman correlation coefficient, ρ_p = Pearson correlation coefficient. *crabp2b* is not included due to lack of significant induction. pSmad1/5/9 immunofluorescence (Figure 3) was fitted with a polynomial (gray line, L) and used as signaling input. (**M-Z**) Individual fits of transcriptional responses (Figure 4); closed circles represent averages of three data points, open circles represent individual data points, and gray lines represent individual fits of each repeat. See the Figure 5—source data 1 source data file for source data.

Figure 5—source data 1 Source data for Figure 5.: https://cdn.elifesciences.org/articles/58641/elife-58641-fig5-data1-v2.xlsx
Download elife-58641-fig5-data1-v2.xlsx

Figure 6 with 1 supplement see all

Download asset Open asset

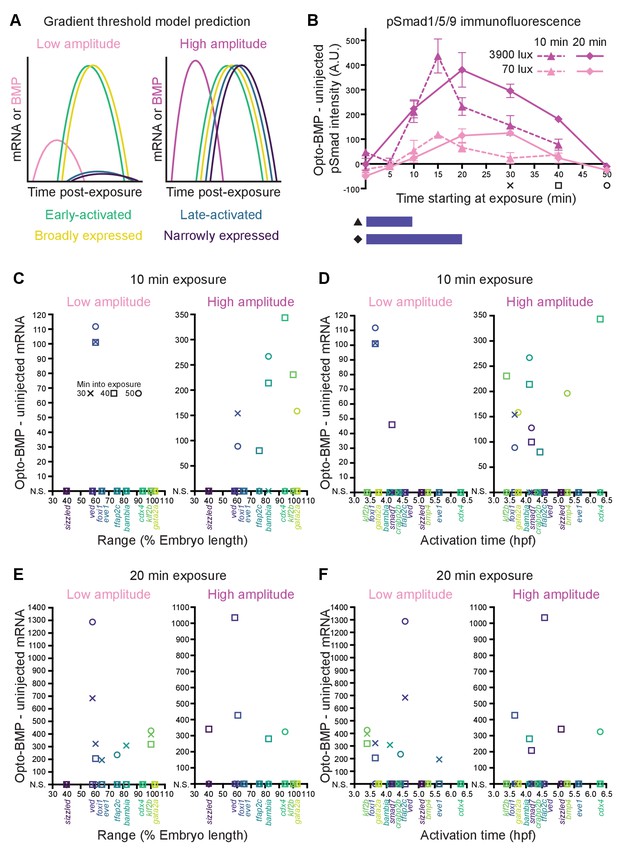
Differential sensitivity to BMP does not fully explain target gene expression diversity.

(A) The activation threshold model predicts that broadly expressed genes will be activated by lower amplitude signaling. (B) pSmad1/5/9 immunofluorescence in uninjected and Opto-BMP-injected embryos exposed to 10 (triangle, dashed line) or 20 (diamond, solid line) min of 70 (light pink) or 3900 (magenta) lux blue light starting at shield stage. Immunofluorescence was quantified and plotted as Opto-BMP signal - uninjected with piecewise linear interpolation between timepoints; error bars represent standard error (see Materials and methods for statistical analysis). Embryos for the transcriptional response experiment were collected 30 (x), 40 (square), or 50 (circle) min after the start of light exposure. (**C-F**) Transcriptional responses in Opto-BMP embryos exposed to conditions shown in (B) were quantified using NanoString technology and are plotted against spatial range (C,E) or activation time (D,F). Embryos were collected 30 (x), 40 (square), or 50 (circle) min after the start of light exposure. Responses that are not statistically significant are anchored to the x-axis (N.S.; see Materials and methods for statistical analysis). See the Figure 6—source data 1 file for source data.

Figure 6—source data 1 Source data for Figure 6.: https://cdn.elifesciences.org/articles/58641/elife-58641-fig6-data1-v2.xlsx
Download elife-58641-fig6-data1-v2.xlsx

Figure 7 with 3 supplements see all

Download asset Open asset

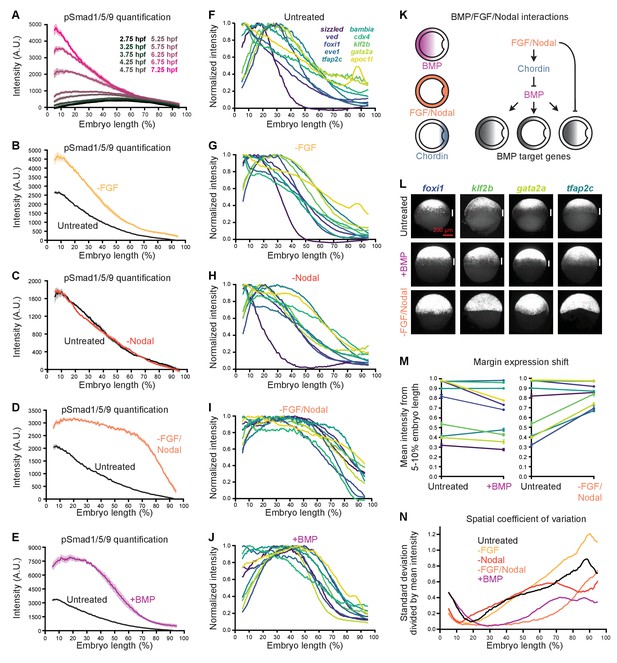
FGF and Nodal contribute to the spatial diversity of BMP target genes.

(A) pSmad1/5/9 immunofluorescence in untreated embryos at the indicated times (data also shown in Figure 1E). (**B-E**) Embryos were treated with 10 μM FGF inhibitor SU-5402 (B), 50 μM Nodal inhibitor SB-505124 (C), or both (D) starting at 2 hpf, or injected with 0.5 pg *bmp2b* mRNA at the one-cell stage (E). The BMP signaling gradient was quantified along the dorsal-ventral axis at shield stage using pSmad1/5/9 immunofluorescence; error bars represent standard error. Note that the embryos in panels B-E came from different experiments and were processed and imaged on different days, but untreated controls were always siblings of treated embryos and processed and imaged simultaneously. (**F-J**) BMP target gene expression along the dorsal-ventral axis at shield stage in untreated (F), SU-5402-treated (G), SB-505124-treated (H), SB-505124 + SU-5402-treated (I), and *bmp*-overexpressing (J) embryos quantified using fluorescence *in situ* hybridization (untreated data from Figure 1). (K) FGF and Nodal block expression of a subset of BMP target genes at the margin, and restrict BMP signaling in part by activating the BMP inhibitor Chordin. (L) Ventral views of margin-excluded BMP target gene expression at shield stage assessed by FISH in untreated embryos (top row), *bmp*-overexpressing embryos (0.5 pg *bmp2b* mRNA, middle row), and embryos treated with SU-5402 + SB-505124 (bottom row). Vertical white bars indicate regions where expression is excluded from the margin. (M) Expression levels at the margin quantified by calculating the average normalized intensity from 5–10% embryo length in untreated versus *bmp*-overexpressing embryos (left) or untreated versus SU-5402+SB-505124-treated embryos (right). Lines connect treated and untreated conditions to visualize shifts, error bars represent standard error. Lower numbers indicate less expression at the margin. (N) Spatial coefficient of variation for the 10 BMP target genes assessed here in untreated (black), SU-5402-treated (yellow), SB-505124-treated (red), SU-5402+SB-505124-treated (salmon), and *bmp*-overexpressing (magenta) embryos. Lower numbers indicate less spatial diversity. See the Figure 7—source data 1 file for source data.

Figure 7—source data 1 Source data for Figure 7.: https://cdn.elifesciences.org/articles/58641/elife-58641-fig7-data1-v2.xlsx
Download elife-58641-fig7-data1-v2.xlsx

Results

BMP target genes have diverse spatiotemporal expression patterns

We used RNA-sequencing to systematically identify genes activated by BMP during early zebrafish gastrulation, when BMP is engaged in dorsal-ventral patterning (shield stage,~6.75 h post-fertilization (hpf)) (Zinski et al., 2018). We identified 16 high-confidence target genes that are significantly upregulated in bmp-overexpressing embryos and downregulated in embryos overexpressing the BMP inhibitor chordin (Figure 1—figure supplement 1A–D and Supplementary file 1). 14 of these genes (apoc1l, bambia, bmp4, cdx4, eve1, foxi1, gata2a, id2a, klf2b, smad6a, smad7, sizzled, tfap2c, and ved) are known to be positively regulated by BMP in zebrafish (Kashiwada et al., 2015; Wang et al., 2015; Kotkamp et al., 2014; Wang et al., 2013; Das and Crump, 2012; de Pater et al., 2012; Kwon et al., 2010; Li and Cornell, 2007; Poulain et al., 2006; Chong et al., 2005; Davidson et al., 2003; Martyn and Schulte-Merker, 2003; Nissen et al., 2003; Solomon et al., 2003; Yabe et al., 2003; Pogoda and Meyer, 2002; Shimizu et al., 2002; Oates et al., 2001; Tsang et al., 2000; Chin et al., 1997; Nikaido et al., 1997; Hammerschmidt et al., 1996a; Hammerschmidt et al., 1996b; Mullins et al., 1996; Detrich et al., 1995; Joly et al., 1993; Joly et al., 1992), whereas crabp2b (Sharma et al., 2005) and znfl2b (Hogan et al., 2006) have not previously been implicated as BMP targets. Four of the 16 target genes encode repressors of BMP signaling (bambia, sizzled, smad6a, and smad7) and one encodes bmp4, consistent with roles for negative and positive feedbacks in TGF-β-mediated patterning (Zinski et al., 2018).

According to the gradient threshold model, target genes are activated by distinct signaling levels, leading to different spatial domains of target gene expression in the presence of a signaling gradient (Figure 1A). To determine whether the BMP patterning system fits this paradigm, we first sought to characterize both BMP signaling distribution and spatial target gene expression. We assessed spatial BMP signaling from 2.75 to 7.25 hpf (256-cell stage – 60% epiboly) using immunofluorescent stainings to detect the BMP signal transducer pSmad1/5/9. We imaged embryos using selective plane illumination microscopy (SPIM) and quantified fluorescence along the dorsal-ventral axis (Figure 1—figure supplement 1E, Materials and methods). Similar to previous studies (Pomreinke et al., 2017; Zinski et al., 2017; Ramel and Hill, 2013; Tucker et al., 2008), we observed a ventrally-peaking BMP signaling gradient that increases in amplitude over time (Figure 1D,E).

We then used fluorescence in situ hybridization and SPIM to quantify the spatial expression profiles of BMP target genes along the dorsal-ventral axis at shield stage (~6.75 hpf) and found that target genes have different expression profiles along this axis (Figure 1F–Y, Figure 1—figure supplement 1E, Materials and methods; some genes could not be quantified due to weak signal or inability to reliably identify the ventral side). The shape of the expression profiles can be well described by bell curves. We therefore used regression analysis with the Gaussian function

A e^{- \frac{{(x - μ)}^{2}}{ς}}

and defined the range of each target gene as

r = μ + 2 \sqrt{ς / 2}

Using this definition, spatial gene expression broadness ranges from 40–100% dorsal-ventral embryo length (Figure 1F–Y). Strikingly, pronounced differences along the orthogonal animal-vegetal axis were also evident: Genes were either uniformly expressed along this axis on the ventral side (sizzled, ved, apoc1l, and bambia), restricted to the margin (cdx4 and eve1), or excluded from the margin (foxi1, klf2b, gata2a, and tfap2c) (Figure 1C,F–O’). Margin exclusion resulted in distinct dorsal-ventral profiles in which mRNA levels peak around 30% embryo length (Figure 1R,T,W,X), compared to non-excluded genes that peaked more ventrally (Figure 1P,Q,S,U,V,Y). Therefore, some of the spatial diversity in BMP target gene expression arises from differences along the animal-vegetal axis, orthogonal to the dorsal-ventral BMP signaling gradient.

The gradient threshold paradigm (Figure 1A) implies that genes with broad ranges should be activated by lower signaling levels. Since signaling levels increase over time (Figure 1D,E; Pomreinke et al., 2017; Zinski et al., 2017; Ramel and Hill, 2013; Tucker et al., 2008), we sought to determine whether more broadly expressed targets were activated earlier. To assess temporal expression of BMP targets, we used NanoString molecular barcoding (Kulkarni, 2011) to measure transcript levels from 2.75 to 7.25 hpf (256-cell stage – 60% epiboly) (Figure 2A–N). The shape of the temporal expression profiles can be well approximated by the modified cumulative distribution function of the normal distribution

\frac{1}{2} A (1 + \erf (\frac{x - ν}{τ \sqrt{2}})) + b

We used this function for regression analysis of the temporal expression profiles and defined activation times as the average time point at which the curves reached about two mean average deviations (i.e., $1.5 ∙ τ$ ) from the inflection point $ν$ . BMP target gene activation times defined in this way ranged from 3.4 to 6.3 hpf (Figure 2).

The gradient threshold model predicts a monotonic decrease when comparing range and activation time. While this relationship is not observed for the entire dataset (Figure 2O), there is a decreasing monotonic trend when foxi1, eve1, and cdx4 are excluded (note that in contrast to the other genes, the expression of eve1 and cdx4 was only quantified in the embryonic margin [Figure 1—figure supplement 1E, Materials and methods]). This suggests the possibility that subsets of BMP target genes may behave consistently with the gradient threshold model. We therefore sought to investigate the relationship between BMP signaling and target gene expression further using an optogenetic strategy.

Reversible optogenetic activation of BMP signaling in vivo using Opto-BMP

To assess how BMP target genes respond to BMP signaling, we developed a method to optogenetically manipulate BMP signaling in vivo. We fused zebrafish BMP receptor kinase domains to an algal blue light-homodimerizable LOV domain (Rogers and Müller, 2020; Takahashi et al., 2007) and targeted the fusions to the membrane using a myristoylation motif (Figure 3A), similar to previous approaches (Ramachandran et al., 2018; Vopalensky et al., 2018; Sako et al., 2016). Blue light (~450 nm) exposure should lead to dimerization of the LOV domains and interaction of the BMP kinase domains, activating BMP signaling (Figure 3A).

Injection of mRNA encoding Opto-BMP into zebrafish embryos at the one-cell stage resulted in strong ventralization in light-reared embryos, consistent with excess BMP signaling, whereas dark-reared siblings were mostly aphenotypic (Figure 3B and Figure 3—figure supplement 1A,K,L). Spatially localized activation of BMP signaling was also possible using SPIM, further demonstrating light-dependent signaling activation (Figure 3—figure supplement 1E–H).

To facilitate optogenetic experiments, we developed a light exposure device by embedding blue LEDs into the lid of a standard six-well plate and controlling light intensity and dynamics with a single-board computer (Figure 3—figure supplement 1B–D, Materials and methods). Using the LED array, we exposed uninjected and Opto-BMP-injected embryos to blue light for 30 min during high (3.5–4 hpf) or shield (6.75–7.25 hpf) stages, fixed embryos during and after exposure, and quantified BMP signaling using pSmad1/5/9 immunofluorescence (Figure 3C–E and Figure 3—figure supplement 1I,J). At both stages, Opto-BMP embryos showed a dramatic increase in BMP signaling within 10 min of light exposure, and signaling levels returned to normal after light removal. These experiments demonstrate that Opto-BMP reversibly activates BMP signaling in zebrafish embryos in response to light.

Most BMP target genes are competent to respond to BMP at early stages

BMP target genes are activated over a range of developmental stages, from 3.4 to 6.3 hpf (Figure 2). Time-dependent differences in competence – a gene’s ability to respond to signaling – may underlie the diversity in activation timing (Figure 4A). To test this, we quantified BMP target gene expression in uninjected and Opto-BMP-injected embryos exposed to 30 min blue light during either high (3.5–4 hpf) or shield stage (6.75–7.25 hpf) (Figure 4 and Figure 5—figure supplement 1A–F).

In response to a strong BMP signaling pulse at high or shield stage (Figure 3C–E and Figure 3—figure supplement 1I,J), we observed corresponding significant pulses of BMP target gene expression for all genes except crapb2b and cdx4 (Figure 4K,L). While cdx4 is not competent to respond to an early BMP signaling pulse and crabp2b did not clearly respond to either an early or late signaling pulse, all other tested high-confidence BMP target genes responded at high stage. Therefore, differences in competence to respond to BMP signaling at early stages do not explain the majority of diversity in activation timing.

Transcription kinetics in response to BMP do not fully explain spatiotemporal expression

Target gene transcription kinetics can play important roles in defining spatial expression domains. For example, it has been suggested that Nodal target genes with faster transcript accumulation rates have broader spatial expression domains (Dubrulle et al., 2015). To investigate how the transcription kinetics of BMP target genes may influence their spatiotemporal expression patterns, we assessed the dynamics of target gene responses (Figure 4) to optogenetically generated BMP signaling pulses (Figure 3C–E and Figure 3—figure supplement 1I,J). We reasoned that the early activation timing and broad spatial range of some BMP targets might be explained by more rapid transcription in response to BMP. In this paradigm, early BMP signaling activates expression of all target genes at the same time, but transcripts of more slowly transcribed genes only accumulate to detectable levels at later stages, causing them to appear to be ‘late-activated’ (Figure 5A). Similarly, broader spatial ranges could be caused by faster accumulation of rapidly produced transcripts that would therefore be detectable farther from the ventral side than more slowly produced transcripts.

To determine whether higher transcript accumulation rates correlate with broader spatial ranges or earlier activation times, we first assessed maximum transcript counts in response to BMP signaling pulses at high or shield stage (Figure 4). Assuming similar transcript degradation kinetics, transcripts with faster production rates should accumulate to higher levels in response to a BMP signaling pulse (Figure 5A). However, we observed a weak negative correlation (Figure 5B) or no correlation (Figure 5D) between maximum transcript counts and activation time, and found similar results for range (Figure 5C,E). This suggests that differences in transcript accumulation rates in response to BMP do not fully account for differences in activation timing and spatial broadness.

We then used a second approach to assess transcript accumulation kinetics that does not require the assumption of similar transcript degradation rates (Figure 5F–Z). We fitted the transcription data from the shield-stage BMP signaling pulse with a model involving the known pSmad1/5/9 input (Figure 3C, Figure 5L, and Figure 3—figure supplement 1J) and parameters reflecting transcript induction (σ) and decay (λ) (Figure 5M–Z, Materials and methods). Each of the three experimental repeats was fitted individually, and average σ and λ values were calculated for each gene. We found a weak negative correlation between σ and activation time (Figure 5F), and no correlation between σ and range (Figure 5G). We also observed a weak negative correlation between λ and activation time (Figure 5H), and no obvious correlation between λ and spatial broadness (Figure 5I). These results are consistent with the maximum transcript count analysis (Figure 5B–E) and with an alternative fitting approach (Figure 5—figure supplement 1G–W, Materials and methods). In addition, we observed a strong positive correlation between maximum transcript count and σ (Figure 5J), and no correlation between maximum transcript count and λ (Figure 5K), suggesting that production dominates transcription kinetics, and supporting the use of maximum transcript count as a proxy for induction rate.

Together, our analyses indicate that differential transcription kinetics in response to BMP signaling play a minor role in generating the distinct spatiotemporal expression patterns of BMP target genes.

Differential activation thresholds do not fully explain spatiotemporal expression

In the gradient threshold paradigm, target genes are activated by distinct signaling thresholds that define gene expression ranges (Figure 1A). This model therefore predicts that broadly expressed genes, but not narrowly expressed genes, should be activated by low levels of signaling (Figure 6A).

To test this idea, we exposed uninjected and Opto-BMP-injected embryos to high- (3900 lux) or low-intensity (70 lux) blue light for 10 or 20 min at shield stage – resulting in high- or low-amplitude BMP signaling pulses, respectively (Figure 6B) – and then quantified BMP target gene responses using NanoString technology. As expected, target activation was generally stronger following higher amplitude, longer duration pulses (Figure 6C–F and Figure 6—figure supplement 1). However, after a 10 min low-amplitude exposure, the third most narrowly expressed gene, foxi1, was significantly activated, whereas the broader genes were not robustly induced (Figure 6C). A longer 20 min low-amplitude pulse significantly activated both narrowly and broadly expressed genes (Figure 6E). A 10 min low-amplitude pulse significantly activated two of the top 50% earliest expressed genes (foxi1 and smad7), whereas a 20 min low-amplitude pulse significantly activated both early and late-expressed genes (Figure 6D,F). High-amplitude pulses activated genes of all ranges and activation times (Figure 6C–F).

Our experiments exposing embryos to different amplitude BMP signaling pulses therefore suggest that not all spatiotemporal target gene expression differences are due to different signaling activation thresholds, although a subset may be (see Discussion).

FGF and Nodal modify BMP signaling and target gene expression

We noted that BMP target genes have unique expression patterns along the animal-vegetal axis that contribute to differences in their dorsal-ventral expression profiles (Figure 1F–Y). Specifically, 6 out of the 10 spatially quantified high-confidence BMP target genes are either restricted to (cdx4, eve1) or excluded from (foxi1, klf2b, gata2a, tfap2c) the margin. We wondered how regulation by additional signaling pathways active at the margin might contribute to these differences. We focused on the FGF and Nodal pathways, which regulate mesoderm and mesendoderm specification, respectively, and are known to influence BMP signaling (Figure 7; Rogers and Müller, 2019).

To assess the effects of FGF and Nodal signaling on BMP target gene expression, we inhibited these pathways using the small molecule inhibitors SU-5402 (Mohammadi et al., 1997) and SB-505124 (DaCosta Byfield et al., 2004), respectively (Figure 7—figure supplement 1A–J’). At shield stage, Nodal inhibition did not observably affect BMP signaling (Figure 7C and Figure 7—figure supplement 1F–G’), whereas FGF inhibition increased the amplitude of the BMP signaling gradient (Figure 7B and Figure 7—figure supplement 1D–E’). Simultaneous inhibition of both FGF and Nodal signaling increased both the amplitude and spatial broadness of the BMP signaling gradient (Figure 7D, Figure 7—figure supplement 1H–J’, and Figure 7—figure supplement 2A–K). Consistent with enhanced BMP signaling, in the absence of FGF/Nodal several BMP-activated genes were upregulated (Figure 7—figure supplement 2L–Y). Reduced levels of the secreted BMP inhibitor Chordin in embryos lacking FGF/Nodal signaling (Figure 7—figure supplement 2ZA) are likely to contribute to this BMP signaling expansion (Varga et al., 2007; Londin et al., 2005; Koshida et al., 2002). Additionally, FGF restricts the expression of bmp (Londin et al., 2005; Fürthauer et al., 2004; Fürthauer et al., 1997), and we detected increased bmp2b expression in FGF/Nodal-inhibited embryos (Figure 7—figure supplement 2Z).

Loss of FGF, Nodal, or both simultaneously affected BMP target gene dorsal-ventral spatial expression profiles differently (Figure 7F–I, Figure 7—figure supplement 1, and Figure 7—figure supplement 3). To determine whether FGF and Nodal are responsible for the margin restriction or exclusion of some BMP target genes (Figure 1F–O’), we assessed target expression along the animal-vegetal axis in inhibitor-treated embryos. In embryos lacking both FGF and Nodal signaling, margin-restricted genes were still expressed and restricted to the margin, whereas the expression of margin-excluded genes shifted into the margin (Figure 7I,L,M, and Figure 7—figure supplement 1).

We reasoned that the shift of margin-excluded genes into the margin could either be due to loss of FGF/Nodal activity, or due to enhanced BMP signaling at the margin (Figure 7D, Figure 7—figure supplement 1A–J’, and Figure 7—figure supplement 2A–K). We therefore assessed the animal-vegetal expression of margin-excluded genes in bmp-overexpressing embryos, which have dramatically elevated levels of BMP signaling at the ventral margin (Figure 7E) but intact Nodal and FGF signaling (Figure 7—figure supplement 1A–C’; Fürthauer et al., 1997). Margin-excluded genes were still clearly excluded from the margin in bmp-overexpressing embryos, suggesting that direct inhibition by FGF and Nodal normally prevents expression of these genes at the margin (Figure 7J,L,M).

To determine whether FGF and Nodal contribute to diversity in BMP target gene activation timing, we quantified the temporal expression of BMP targets in embryos lacking FGF and Nodal signaling from 2.75 to 7.25 hpf (256-cell stage – 60% epiboly) (Figure 7—figure supplement 2L–Y). Although transcript levels of several BMP targets were higher in treated compared to untreated embryos at later stages, their activation times were still diverse, suggesting that inputs other than FGF and Nodal are responsible for differences in activation times.

Finally, we noticed that much of the spatial diversity in BMP target gene expression along the dorsal-ventral axis collapsed in embryos lacking both FGF and Nodal signaling (Figure 7F,I). To quantify the decrease in spatial diversity, we calculated the spatial coefficient of variation in untreated and treated embryos (see Materials and methods). Strikingly, embryos lacking both FGF and Nodal had lower coefficients of variation at almost all positions along the dorsal-ventral axis compared to untreated embryos (Figure 7N). Together, our results identify combinatorial FGF and Nodal signaling as a major driver of spatial diversity in BMP target gene expression.

Discussion

Minor roles for differential responses to BMP in generating spatiotemporal diversity

Signaling gradients are frequently observed in developing tissues, including the embryonic axes of gastrulating zebrafish, the neural tube in mice, and the wing precursor in Drosophila (Briscoe and Small, 2015; Schier and Talbot, 2005). However, how gradients are interpreted by cells is complex to ascertain. The gradient threshold model proposes that gene-specific activation thresholds are responsible for differences in the spatial expression of target genes (Sharpe, 2019; Briscoe and Small, 2015; Dubrulle et al., 2015; Rogers and Schier, 2011; Barkai and Shilo, 2009; Ashe and Briscoe, 2006). Can gradients be reliably generated and signaling thresholds accurately interpreted with high sensitivity, or do gradients simply provide a ‘rough framework’ for patterning that is refined over time by other mechanisms such as target gene cross-talk (Briscoe and Small, 2015; Chen et al., 2012) or cell sorting (Akieda et al., 2019; Xiong et al., 2013)? In the former case, is such precision actually required for patterning?

In the context of zebrafish dorsal-ventral patterning, our data suggest minor roles for gene-specific activation thresholds in generating BMP target gene expression diversity. We did not find a clear monotonically decreasing relationship between activation time and gene expression range (Figure 2O), suggesting that more broadly expressed genes are not consistently more likely to be activated by the low levels of BMP present early (Figure 1D–E). We were also unable to detect an unambiguous correlation between range and the levels of signaling required for activation (Figure 6C,E). This suggests that not all BMP target expression boundaries are positioned by gene-specific BMP signaling thresholds (Figure 1A).

An alternative model proposes that diversity in spatiotemporal target gene expression is due to differences in expression kinetics. For example, it was shown that Nodal targets with higher transcript accumulation rates in response to Nodal signaling have broader spatial expression domains (Dubrulle et al., 2015). To determine whether the BMP patterning system might function similarly, we examined the transcriptional responses of BMP target genes (Figures 4 and 5, and Figure 5—figure supplement 1) to optogenetically generated pulses of BMP signaling (Figure 3C–D and Figure 3—figure supplement 1I,J). We did not detect a strong correlation between transcript induction rates and activation time or spatial range (Figure 5 and Figure 5—figure supplement 1G–W). Therefore, differential transcription kinetics in response to BMP are unlikely to account for spatiotemporal expression diversity.

Our results do not rule out the possibility that a different subset of BMP target genes may behave more consistently with these models. We focused on a set of high-confidence BMP targets (Figure 1—figure supplement 1), but other known targets were excluded from our analyses (Supplementary file 1). For example, the BMP target gene tp63 (Bakkers et al., 2002) is not expressed at shield stage, and was therefore excluded since it was not downregulated by chordin overexpression in our RNA-sequencing experiment (Supplementary file 1). We note that a subset of three genes (sizzled, ved, and bambia) that are neither restricted to nor excluded from the margin do show a monotonically decreasing relationship between range and activation time (Figure 2O) as well as activation dynamics that could be roughly commensurate with signaling input (Figure 6C and Figure 6—figure supplement 1), consistent with the gradient threshold model. However, it remains to be determined to what extent this subset of genes (or others) quantitatively follows the input-output relationships predicted by the gradient threshold model.

Our results also do not rule out other mechanisms of BMP signaling interpretation. For example, the graded distribution of many genes (Figure 1P–Y) could be consistent with a model in which gene expression is roughly proportional to the level of BMP signaling. In addition, BMP signaling duration may encode specific responses in vivo. Future work is needed to better define the relationship between BMP signaling levels and gene expression and to determine how BMP signaling dynamics are interpreted in embryos. Our study highlights the promise of optogenetic approaches in such investigations (Rogers and Müller, 2020). In contrast to pharmacological or genetic methods, optogenetic strategies can provide fast, tunable, and reversible spatiotemporal manipulation of signaling in vivo (Figure 3, Figure 6B, and Figure 3—figure supplement 1E–H), allowing more thorough characterization of input/output relationships.

In addition, our observations indicate that BMP signaling precision may not be required for proper patterning, or that the system is robustly buffered. For example, most embryos experiencing transient activation of BMP signaling lack gross morphological defects (Figure 3C–E, Figure 4, Figure 3—figure supplement 1A,K,L, and Figure 5—figure supplement 1). How patterning recovers from such insults will be an interesting avenue for future study. Together with previous work (reviewed in Zinski et al., 2018), several of our observations indicate that feedback is an important feature of the BMP patterning system: Five out of 16 high-confidence BMP target genes affect BMP signaling (Figure 1—figure supplement 1), and embryos can experience a dip in signaling levels after a signaling pulse (Figure 3C and Figure 3—figure supplement 1J). Cell sorting strategies that sharpen gene expression boundaries may also contribute to the observed recovery from BMP signaling manipulation (Akieda et al., 2019; Xiong et al., 2013).

Margin restriction and competence of BMP target genes

One unresolved question from our study is the restriction of the BMP target genes eve1 and cdx4 to the margin (Figure 1I,I’,L,L’ and Figure 7—figure supplement 1). Consistent with previous work (Swanhart et al., 2010; Ota et al., 2009; Bennett et al., 2007; Ho et al., 2006; Londin et al., 2005; Shimizu et al., 2005; Rentzsch et al., 2004), in the absence of FGF or Nodal, eve1 and cdx4 were still expressed at the ventral margin (Figure 7—figure supplement 1; we note, however, conflicting reports with dominant-negative FGF receptors [Ota et al., 2009; Kudoh et al., 2004; Griffin et al., 1995]). Inhibition by animal pole factors or a requirement for signaling pathways at the margin such as Wnt or retinoic acid might play a role in their margin restriction.

Both eve1 and cdx4 are also activated relatively late in development (Figure 2F,J), and cdx4 is not competent to respond to an early BMP signaling pulse (Figure 4K). FGF and Nodal have no obvious roles in regulating their activation timing or competence since their temporal expression was not significantly affected by loss of FGF/Nodal signaling (Figure 7—figure supplement 2Q,U). Understanding how the activation timing of all BMP target genes including eve1 and cdx4 is regulated is an important future goal.

FGF and Nodal are major contributors to BMP target gene spatial diversity

Inhibition of FGF, Nodal, or both together had distinct effects on BMP signaling (Figure 7B–D, Figure 7—figure supplement 1A–J’, and Figure 7—figure supplement 2A–K). The increase in BMP signaling in the absence of FGF is likely explained by several factors including the known role of FGF in activating chordin and inhibiting bmp transcription (Figure 7—figure supplement 2Z,ZA) (Varga et al., 2007; Maegawa et al., 2006; Londin et al., 2005; Fürthauer et al., 2004; Kudoh et al., 2004; Koshida et al., 2002; Fürthauer et al., 1997), as well as inactivating Smad1 (Sapkota et al., 2007; Pera et al., 2003; Kretzschmar et al., 1997). Loss of Nodal did not detectably alter BMP signaling at shield stage. This is surprising because early expression of fgf is thought to depend on Nodal (van Boxtel et al., 2015; Maegawa et al., 2006; Mathieu et al., 2004; Gritsman et al., 1999; Rodaway et al., 1999), although low levels of fgf3 appear to be present at late blastula stages in Nodal signaling mutants (Mathieu et al., 2004), and weak FGF activity is detectable in Nodal inhibitor-treated embryos (van Boxtel et al., 2015). Nodal can activate chordin expression independently of FGF (Varga et al., 2007), and chordin is detectable albeit reduced in Nodal signaling mutants (Gritsman et al., 1999), suggesting that the reduction in chordin caused by Nodal loss is not sufficient to affect BMP signaling during early gastrulation. Future work is needed to explain why FGF, but not Nodal loss enhances BMP signaling at early gastrulation, and why simultaneous loss increases not only the amplitude but the broadness of the BMP signaling gradient.

Inhibition of FGF, Nodal, or both together also had distinct effects on BMP target gene expression (Figure 7F–I, Figure 7—figure supplements 1, 2 and 3). Although Nodal loss did not detectably alter the BMP signaling gradient (Figure 7C and Figure 7—figure supplement 1F–G’), the spatial distributions of several BMP target genes were affected (Figure 7H, Figure 7—figure supplement 1N,R, and Figure 7—figure supplement 3C). Nodal is also responsible for the dorsal expression of the BMP target gene apoc1l (Figure 1O,O’,Y), which is lost in the absence of Nodal (Figure 7H, Figure 7—figure supplement 1N, and Figure 7—figure supplement 3C). Although our study defines individual target gene responses at the phenomenological level, uncovering the DNA-level mechanisms (e.g., promoter regulation and chromatin status) that lead to the observed responses to BMP, FGF, and Nodal is an important future challenge.

The margin exclusion of the BMP target genes foxi1, klf2b, gata2a, and tfap2c can be explained by FGF/Nodal-mediated inhibition (Figure 7K). Loss of either FGF or Nodal signaling shifted the expression of margin-excluded genes toward the margin, although the shifts were most dramatic in the absence of both (Figure 7F–I,L,M, Figure 7—figure supplement 1, and Figure 7—figure supplement 3), with the exception of tfap2c, which was completely margin-shifted in FGF-inhibited embryos (Figure 7G, Figure 7—figure supplement 1M,Q, and Figure 7—figure supplement 3B). Excess BMP signaling at the margin in embryos lacking FGF and Nodal (Figure 7D, Figure 7—figure supplement 1H–J’, and Figure 7—figure supplement 2A–K) does not explain the observed gene expression shifts because no shifts were evident in bmp-overexpressing embryos (Figure 7J,L,M, Figure 7—figure supplement 1L,P, and Figure 7—figure supplement 3A). The FGF/Nodal-mediated margin exclusion of a subset of BMP targets contributes to the diversity in BMP target gene expression (Figure 7F,I,K,N), creating distinct dorsal-ventral profiles for margin-excluded genes (Figure 1R,T,W,X) compared to non-excluded genes (Figure 1P,Q,S,U,V,Y).

Our results suggest that much of the spatial diversity in BMP target gene expression arises from combinatorial signaling. A similar strategy is thought to regulate Bicoid target genes during Drosophila embryogenesis: Gene expression boundary shifts in response to Bicoid manipulation are often inconsistent with the gradient threshold model (Chen et al., 2012; Ochoa-Espinosa et al., 2009), and activation thresholds do not appear to explain target gene expression profiles at the DNA level (Ochoa-Espinosa et al., 2005). Rather, Bicoid is thought to act within a system of repressive pathways that regulate Bicoid target gene expression (Chen et al., 2012). During zebrafish dorsal-ventral patterning, FGF and Nodal affect BMP target gene expression in two ways: by restricting BMP signaling (Figure 7B–D, Figure 7—figure supplement 1D–E’,H–J’, and Figure 7—figure supplement 2A–K), and by inhibiting a subset of BMP target genes at the margin (Figure 7F–I,L,M, Figure 7—figure supplement 1, and Figure 7—figure supplement 3). These interactions sculpt the spatial expression profiles of BMP target genes and contribute to the patterning of the dorsal-ventral axis.

Materials and methods

Key resources table

Reagent type (species) or resource	Designation	Source or reference	Identifiers	Additional information
Strain, strain background (E. coli)	One Shot TOP10	Life Technologies	C4040	Chemically competent
Strain, strain background (Danio rerio)	TE zebrafish	Pomreinke et al., 2017 Donovan et al., 2017		Wild type
Antibody	anti-phospho- Smad1/Smad5/Smad9 (Rabbit monoclonal)	Cell Signaling Technology	13820, RRID:AB_2493181	IF (1:100)
Antibody	anti-rabbit Alexa Fluor 488-conjugated secondary (Goat polyclonal)	Life Technologies	A11008, RRID:AB_143165	IF (1:5000)
Antibody	anti-phospho-Smad2/Smad3 (Rabbit monoclonal)	Cell Signaling Technology	8828, RRID:AB_2631089	IF (1:5000)
Antibody	anti-rabbit horseradish peroxidase (Goat polyclonal)	Jackson ImmunoResearch	111-035-003, RRID:AB_2313567	IF (1:500)
Antibody	anti-pErk (Mouse monoclonal)	Sigma	M8159, RRID:AB_477245	IF (1:5000)
Antibody	anti-mouse horseradish peroxidase (Donkey polyclonal)	Jackson ImmunoResearch	715-035-150, RRID:AB_2340770	IF (1:500)
Antibody	anti-digoxigenin horseradish peroxidase Fab fragments (Sheep polyclonal)	Roche	11207733910, RRID:AB_514500	FISH (1:150)
Recombinant DNA reagent	pCS2-Opto-Alk3	Generated in this study
Recombinant DNA reagent	pCS2-Opto-Alk8	Generated in this study
Recombinant DNA reagent	pCS2-Opto-BMPR2a	Generated in this study
Recombinant DNA reagent	pCS2-Opto-BMPR2b	Generated in this study
Chemical compound, drug	TRIzol reagent	Invitrogen	5596026
Chemical compound, drug	Co-Precipitant Pink	Bioline	BIO-37075
Chemical compound, drug	Cycloheximide	Sigma	C4859
Chemical compound, drug	Pronase	Roche	11459643001
Chemical compound, drug	DMSO	Roth	A994.2
Chemical compound, drug	FBS	Biochrom	S0415
Chemical compound, drug	DAPI	Life Technologies	D1306	1:5000
Chemical compound, drug	Blocking reagent	Roche	11096176001
Chemical compound, drug	Low melting temperature agarose	Lonza	50080
Chemical compound, drug	Nodal inhibitor SB-505124	Sigma	S4696-5MG	50 μM
Chemical compound, drug	FGF inhibitor SU-5402	Sigma	SML0443-5MG	10 μM
Commercial assay or kit	TSA plus cyanine three system	Perkin Elmer	NEL744001KT	FISH/IF (1:75)
Commercial assay or kit	RNeasy kit	QIAGEN	74104
Commercial assay or kit	Wizard SV Gel and PCR Clean-up System	Promega	A9282
Commercial assay or kit	pCR-bluntII TOPO kit	Thermo Fisher Scientific	450245
Commercial assay or kit	SP6 mMessage mMachine transcription kit	Thermo Fisher Scientific	AM1340
Commercial assay or kit	DIG RNA labeling mix	Sigma-Aldrich	11277073910
Software, algorithm	Fiji	Schindelin et al., 2012	https://fiji.sc/ RRID:SCR_002285
Software, algorithm	Prism	GraphPad Software	https://www.graphpad.com/scientific-software/prism RRID:SCR_002798
Software, algorithm	COMSOL Multiphysics 3.5a	COMSOL, Inc	https://www.comsol.com/ RRID:SCR_014767
Software, algorithm	Matlab	Mathworks	http://mathworks.com RRID:SCR_001622
Software, algorithm	edgeR 3.2.3	Robinson et al., 2010	RRID:SCR_012802
Software, algorithm	DESeq 1.12.0	Anders and Huber, 2010	RRID:SCR_000154
Software, algorithm	Cuff diff 2.1.1	Trapnell et al., 2010	https://github.com/cole-trapnell-lab/cufflinks
Software, algorithm	PWM code for controlling LED array	Generated in this study
Software, algorithm	nSolver 4.0 software	NanoString	RRID:SCR_003420
Software, algorithm	Excel	Microsoft	RRID:SCR_016137
Software, algorithm	Maple	Waterloo Maple Inc	RRID:SCR_014449
Other	RNA-sequencing data	Generated in this study	GEO: GSE135100
Other	TIP122 complementary power NPN Darlington	STMicroelectronics
Other	Regulated power supply	Disrelec Group AG	RND 320-KD3000D
Other	6-well plates	Greiner Bio-One	657160
Other	Blue LEDs	Nichia	NSPB510AS
Other	Blue LEDs	Everlight	1363-2SUBC/C470/S400-A4
Other	Temperature- controlled incubator, Heratherm IMC 18	ThermoScientific	50125882
Other	Raspberry Pi model B	Raspberry Pi Foundation
Other	LM37 luxmeter	DOSTMANN electronic GmbH
Other	White worklight	REV Ritter GmbH	90910
Other	Red color filters	Rosco	E106 Primary Red

Zebrafish husbandry

Request a detailed protocol

Zebrafish husbandry was executed in accordance with the guidelines of the State of Baden-Württemberg (Germany) and approved by the Regierungspräsidium Tübingen (35/9185.46–5, 35/9185.81–5). Wild type TE adult zebrafish were maintained under standard conditions. Embryos were incubated at 28°C in embryo medium (250 mg/l Instant Ocean salt, 1 mg/l methylene blue in reverse osmosis water adjusted to pH 7 with NaHCO₃[Müller et al., 2012]) unless otherwise noted.

mRNA in vitro synthesis

Request a detailed protocol

pCS2+-based plasmids encoding Bmp2b, Chordin (Pomreinke et al., 2017), and Opto-BMP (this work, Figure 3—figure supplement 1, see below for cloning details) were linearized with NotI-HF (NEB, R3189). Capped mRNA was generated using a mMessage mMachine SP6 kit (ThermoFisher, AM1340). mRNA was purified using an RNeasy Mini kit (Qiagen, 74104) and quantified using a NanoDrop spectrophotometer (ThermoScientific).

RNA-sequencing

Request a detailed protocol

Wild type TE zebrafish embryos were dechorionated with Pronase (Roche, 11459643001) and injected at the one-cell stage with 10 pg mRNA encoding zebrafish Bmp2b, 100 pg mRNA encoding zebrafish Chordin, or left uninjected (Pomreinke et al., 2017). When uninjected siblings reached shield stage (~6.75 hpf), embryos were snap-frozen in liquid nitrogen. 10 embryos were collected per sample, three samples per condition.

To prepare total RNA, the TRIzol reagent (Invitrogen, 15596026) manufacturer’s protocol was followed until aqueous phase recovery, then 6.25 μl Co-Precipitant Pink (Bioline, BIO-37075) was added to 250 μl aqueous phase, followed by 375 μl 100% EtOH. After vortexing briefly, samples were transferred to RNeasy Mini kit (Qiagen, 74104) spin columns and centrifuged at 13600 rpm at 4°C for 1 min. Flow-through was discarded and columns were washed twice with RPE buffer (Qiagen). RNA was eluted in 50 μl H₂O. Total RNA concentration was measured using a NanoDrop spectrophotometer (ThermoScientific). 3–5 μg total RNA per sample were provided to LCG Genomics GmbH (Berlin, Germany) for sequencing and differential expression analysis. Sequences were aligned against the reference genome Danio rerio GRCz10 with STAR 2.4.1b, and differential expression analysis was carried out with edgeR 3.2.3, DESeq 1.12.0, and Cuff diff 2.1.1. The p-value threshold for differentially expressed genes was set to 0.05.

Note that endogenous bmp2b and chordin were not distinguishable from injected mRNAs in bmp2b- or chordin-injected embryos, respectively, and were therefore excluded from consideration as BMP target genes.

Opto-BMP constructs

Request a detailed protocol

Opto-BMP constructs are based on Opto-Acvr constructs (Sako et al., 2016). These pCS2+-based Opto-Acvr constructs encode proteins that are tethered to the plasma membrane by an N-terminal myristoylation motif. Next to the membrane is a Nodal receptor kinase domain, followed by the light-oxygen-voltage (VfLOV) domain Aureochrome1 from Vaucheria frigida (Takahashi et al., 2007), and finally a C-terminal HA tag. Using splicing by overlap extension (SOE) PCR (Horton et al., 2013), Nodal receptor kinase domains in Opto-Acvr were swapped with putative kinase domains from the type I zebrafish BMP receptors Alk3 (NM_131621, bp 691–1566) (Nikaido et al., 1999) and Alk8 (NM_131345, bp 622–1497) (Mintzer et al., 2001; Yelick et al., 1998), and the type II zebrafish receptors BMPR2a (NM_001039817, bp 571–3009) and BMPR2b (NM_001039807, bp 598–1536) (Monteiro et al., 2008). In all cases except for Opto-BMPR2a, all residues after the transmembrane domain until the end of the kinase domain were included. Opto-BMPR2a contains all residues after the transmembrane domain until the end of the protein; the kinase domain-only construct was inactive.

An equimolar combination of mRNA encoding Opto-Alk3 (5.2 pg), Opto-Alk8 (5.2 pg), and Opto-BMPR2a (8.9 pg) was found to optimally induce BMP signaling in the light but not in the dark (Figure 3B, Figure 3—figure supplement 1A,K,L), and was used in all Opto-BMP experiments described here.

LED array

Request a detailed protocol

To facilitate optogenetic experiments requiring control of light intensity and exposure duration, an embedded system-based controller was developed (Figure 3—figure supplement 1B–D). To maximize the versatility of the setup for different applications, a single-board computer was deployed (Raspberry Pi 3 model B, running under a Linux kernel, version 4.9). The controller was programmed to generate signals that modulate the duration and intensity of light. The generated signal was further amplified to drive the load of the LED array. A two-stage Darlington amplifier was used (TIP122 complementary power NPN Darlington - STMicroelectronics) to raise the ceiling of the current of amplification. The Darlington pair was used in a common emitter configuration in order to achieve a large power gain. The loads were operated on a constant voltage source provided by a regulated power supply (Disrelec Group AG, RND 320-KD3000D). During initial trials, brief, weak signal spikes could be detected, and an RC filter was subsequently used across the load to dampen any sporadic light flashes. The LED array constituted the circuit load; these LEDs were glued into the plastic cover of 6-well plates (Greiner Bio-One, 657160) (Figure 3—figure supplement 1B). Blue Nichia (NSPB510AS) or Everlight (1363-2SUBC/C470/S400-A4) LEDs were used in the array. Both LEDs emitted maximal spectral intensity at 470 nm, with the Nichia LEDs having a broader radiation angle, tighter spectral distribution, and less variable performance. During experiments, the LED array was placed inside a temperature-controlled incubator (Thermo Scientific Heratherum IMC 18, 50125882) set to 28°C. Dark fabric was taped to the interior of the incubator door to prevent outside light from entering.

The circuit schematic (Figure 3—figure supplement 1D) shows how the generated square wave was used to drive the LED array. One of the Raspberry Pi’s GPIO pins was used as a pulse-width modulation (PWM) output to produce signal. The raspberry-gpio-python module (https://sourceforge.net/projects/raspberry-gpio-python) was used to interface the GPIO. A pulse program was written in Python, which allows for variable parameter settings: GPIO pin number, modulation frequency (10 kHz is the NPN Darlington amplifier linear limit), pulse duration, and duty cycle.

Light intensities were measured using an LM37 luxmeter (DOSTMANN electronic GmbH).

LED array settings used in optogenetic experiments:

Fig.	Experiment	LED	Voltage (V)	Frequency (Hz)	Intensity (lux)	Duration (min)
3, 3.1I,J	Shield stage	Everlight	24	200	2300	30
3, 3.1I,J	High stage	Everlight	25–28	2	2300	30
4, 5, 5.1 G-W	Shield stage	Everlight	24	200	2300	30
4, 5, 5.1 G-W	High stage	Everlight	25–28	2	2300	30
6, 6.1	70 lux	Nichia	15	200	70	10 or 20
6, 6.1	3900 lux	Nichia	21	200	3900	10 or 20
1.1D	bambia, klf2b, sizzled, smad6a, smad7, ved	Everlight	25–28	2	2300	30
1.1D	apoc1l, bmp4, cdx4, crabp2b, eve1, foxi1, gata2a, id2a, tfap2c, znfl2b	Nichia	21	200	3900	30
3.1K,L	Shield stage	Everlight	24	200	2300	30
3.1K,L	All except shield	Everlight	25–28	2	2300	30 or 600
5.1A-F	All	Everlight	24	200	2300	30

For all experiments above, the duty cycle was 100%, and the GPIO pin was 32.

A white worklight (REV Ritter GmbH, 90910) was used in experiments described in Figure 3—figure supplement 1A. For all exposure conditions described in this work, no phototoxicity was evident.

PWM code for controlling the LED array (sqr_pls_v01.py):

#!/usr/bin/python
import sys
import time
import getopt
import RPi.GPIO as GPIO

def usage():
  hlp_str = """Basic square pulse programme

input:
-p output BOARD pin number <int>
-f PWM frequency in Hz <int>
-d duty cycle (in percentage terms) <int>
-t length of the pulse in seconds <float>

example usage:
./sqr_pls_v01.py -p 32 -f 200 -d 100 -t 50.0
"""
  print(hlp_str)

def init_out_chan(pin_num, mod_frq):

  """###################
# initiate output #
#-----------------##################################################
# input:
# - output PWM pin number (12, 32 or 33) <int>
# - PWM frequency in Hz <int>
# output:
# - pin object
# BOARD numbering mode
# only BOARD channels 12, 32 and 33 are PWModulable
####################################################################
  """

  GPIO.setmode(GPIO.BOARD)
  GPIO.setup(pin_num, GPIO.OUT)
  pin = GPIO.PWM(pin_num, mod_frq)

  return pin

def sqr_pls(pin_num, mod_frq, dc, span):

  """###################
# generate output #
#-----------------##################################################
# input:
# - output PWM pin number (12, 32 or 33) <int>
# - PWM frequency in Hz <int>
# - duty cycle (in percentage terms) <int>
# - length of the pulse in seconds <float>
# output:
# - 0: completion; 1: interruption <int>
####################################################################
  """

  p = init_out_chan(pin_num, mod_frq)
  t_strt = time.time()
  p.start(dc)
  p.ChangeDutyCycle(dc)
  try:
    while (time.time() - t_strt) < span:
      time.sleep(1)
      print("seconds remaining: " + str(round(span - (time.time()-t_strt))))
  except KeyboardInterrupt:
    p.stop()
    GPIO.cleanup()
    return 1
  p.stop()
  GPIO.cleanup()

  return 0

def main():

  try:
    opts, args = getopt.getopt(sys.argv[1:],"p:f:d:t:")
  except getopt.GetoptError as e:
    print(str(e))
    usage()
    sys.exit(2)

  for o, a in opts:
    if o == '-p':
      pin_num=int(a)
      if pin_num not in [12, 32, 33]:
        print("--USAGE ERROR\n--PIN NUMBER UNACCEPTABLE\n")
        usage()
        sys.exit(2)
    elif o == '-f':
      mod_frq=int(a)
      if (mod_frq > 10000) or (mod_frq < 0):
        print("--USAGE ERROR\n--MODULATION FREQUENCY VALUE OUTSIDE 0-10000 RANGE\n")
        usage()
        sys.exit(2)
    elif o == '-d':
      dc=int(a)
      if (dc > 100) or (dc < 0):
        print("--USAGE ERROR\n--DUTY CYCLE VALUE OUTSIDE 0-100 RANGE\n")
        usage()
        sys.exit(2)
    elif o == '-t':
      t=float(a)
      if (t < 0):
        print("--USAGE ERROR\n--PASSING NEGATIVE TIME")
        usage()
        sys.exit(2)
  #sqr_pls(pin_num, frq, dc, t)
  try:
    print("--commencing square pulse at pin %d modulated at %d Hz at %d%% power for %.3f seconds" % (pin_num, mod_frq, dc, t))
    print("--starting at %s" % time.ctime())
  except Exception as e:
    print(str(e))
    print("--MISSING ARGUMENT(S) - REVISE USAGE")
    usage()
    sys.exit(2)

  exec_val = sqr_pls(pin_num, mod_frq, dc, t)
  if exec_val:
    print("--Terminating\n--SEQUENCE INTERRUPTED at %s" % time.ctime())
  else:
    print("--Terminating\n--sequence completed at %s" % time.ctime())
  return exec_val

if __name__ == "__main__":
  main()

To guard against inadvertent photoactivation, plates containing embryos were wrapped in aluminum foil starting from ~70 min post-injection until light exposure. Where applicable (e.g. Figure 1—figure supplement 1 and Figure 3—figure supplement 1), red color filters (Rosco, E106 Primary Red) were used to cover light sources such as dissecting microscope stages to prevent transmission of VfLOV-dimerizing wavelengths.

Cycloheximide experiment

Request a detailed protocol

For the cycloheximide (Sigma, C4859) experiment in Figure 1—figure supplement 1D, embryos from wild type TE incrosses were dechorionated using Pronase (Roche, 11459643001) and injected at the one-cell stage with 5.2 pg opto-Alk3 + 5.2 pg opto-Alk8 + 8.9 pg opto-BMPR2a mRNA (Figure 3—figure supplement 1A). Control siblings were left uninjected, and embryos were sorted into agarose-coated 6-well plates and incubated at 28°C. 70–90 min post-fertilization at the 4–16 cell stage, unfertilized and damaged embryos were removed, and plates were individually wrapped in aluminum foil to prevent light exposure and incubated at 28°C. At 6.25 h post-fertilization (hpf), embryos were transferred into new agarose-coated 6-well dishes containing either 50 μg/ml cycloheximide (Bennett et al., 2007; Poulain and Lepage, 2002) or an equivalent volume of DMSO (Roth, A994.2) diluted in embryo medium that had been incubated at 28°C prior to transfer. Red color filters (Rosco, E106 Primary Red) were used to cover the dissecting microscope light source during the transfer to prevent transmission of VfLOV-dimerizing wavelengths and minimize BMP activation, and plates were wrapped in aluminum foil after transfer. At 6.75 hpf (~shield stage, 30 min after cycloheximide exposure), plates were transferred to a small 28°C incubator containing the LED array (Figure 3—figure supplement 1B) and exposed to blue light for 30 min (6.75–7.25 hpf). 20 min after light exposure, when most BMP target genes are maximally induced (Figure 4), embryos were fixed and colorimetric in situ hybridization was carried out as described in the Fluorescence and colorimetric in situ hybridization section below.

pSmad1/5/9, pSmad2/3, and pErk immunofluorescence staining

For pSmad1/5/9, pSmad2/3, and pErk immunofluorescence staining, embryos were fixed in 4% formaldehyde in PBS at 4°C overnight, then transferred to MeOH and stored at −20°C for at least 2 h. See below and Figure 1—figure supplement 1E for imaging and quantification details.

pSmad1/5/9

Request a detailed protocol

Embryos were washed at least three times with PBST (phosphate buffered saline + 0.1% Tween-20), then blocked for at least 1 h at room temperature in blocking buffer (10% FBS (Biochrom, S0415), 1% DMSO, 0.1% Tween-20 in PBS). Embryos were incubated in 1:100 rabbit anti-phosphoSmad1/5/9 antibody (Cell Signaling Technology, 13820) in blocking buffer at 4°C overnight. One wash with blocking buffer followed by 3–5 washes with PBST were carried out at room temperature, then embryos were blocked again with blocking buffer for at least 1 h. Embryos were incubated in 1:5000 goat anti-rabbit Alexa Fluor 488-conjugated secondary antibody (Life Technologies, A11008) in blocking buffer at 4°C overnight. Embryos were then incubated in 1:5000 DAPI (Life Technologies, D1306; stock concentration: 5 mg/ml) in blocking buffer at room temperature for at least 1 h, then washed at least five times with PBST. Stained embryos were wrapped in aluminum foil and stored at 4°C overnight before SPIM imaging.

pSmad2/3

Request a detailed protocol

Embryos were incubated in ice-cold acetone (Roth, 5025.5) for 7 min, then washed at least three times with PBST, blocked for at least 1 h in 10% FBS in PBST and incubated in 1:5000 rabbit anti-pSmad2/3 (Cell Signaling Technology, 8828) in 10% FBS in PBST at 4°C overnight. Embryos were then washed at least five times in PBST, blocked again for at least 1 h in 10% FBS in PBST, and incubated in 1:500 goat anti-rabbit HRP secondary antibody (Jackson ImmunoResearch, 111-035-003) in 10% FBS in PBST at 4°C overnight. Next, embryos were washed at least five times in PBST, then once in TSA 1x amplification buffer (TSA Plus Cyanine 3 System, Perkin Elmer, NEL744001KT). For staining, embryos were incubated in 75 μl 1:75 Cy3-TSA in 1x amplification buffer in the dark at room temperature for 45 min. After washing at least six times with PBST, embryos were incubated in 1:5000 DAPI (Life Technologies, D1306; stock concentration: 5 mg/ml) in PBST at room temperature for at least 1 h, then washed at least four times with PBST. Finally, embryos were wrapped in aluminum foil and stored at 4°C overnight before SPIM imaging.

pErk

Request a detailed protocol

Embryos were washed at least three times with PBST, then transferred to ice-cold acetone for 20 min and washed at least three times with PBST. After blocking in 10% FBS in PBST for at least 1 h, embryos were incubated in 1:5000 mouse anti-pErk antibody (Sigma, M8159) in 10% FBS in PBST at 4°C overnight. Embryos were then washed at least five times in PBST, blocked again for at least 1 h in 10% FBS in PBST, and incubated in 1:500 donkey anti-mouse HRP secondary antibody (Jackson ImmunoResearch, 715-035-150) in 10% FBS in PBST at 4°C overnight. Embryos were washed at least five times with PBST, then once in TSA 1x amplification buffer. Next, embryos were incubated in 75 μl 1:75 Cy3-TSA in 1x amplification buffer in the dark at room temperature for 45 min. After washing at least six times with PBST, embryos were incubated in 1:5000 DAPI (Life Technologies, D1306; stock concentration: 5 mg/ml) in PBST at room temperature for at least 1 h, then washed at least four times with PBST. Stained embryos were wrapped in aluminum foil and stored at 4°C overnight before SPIM imaging.

Fluorescence and colorimetric in situ hybridization

Request a detailed protocol

BMP target gene probes were generated by amplifying full or partial coding sequences (CDS) from wild type TE zebrafish cDNA and cloning into pCS2+ or pCR-bluntII TOPO (ThermoFisher, 450245) vectors. Plasmids were linearized with the indicated restriction enzymes, column purified (Promega, A9282), and DIG-labeled probes were generated using the indicated polymerase (Roche, 11175025910).

High-confidence BMP target gene in situ hybridization probes:

Gene	Vector	Sequence	Enzyme	Polymerase
apoc1l	pCS2+	entire CDS	ClaI	T7
bambia	pCR-bluntII TOPO	partial CDS; bp 47–425	BamHI	T7
bmp4	pCR-bluntII TOPO	partial CDS; bp 103–558	EcoRV	SP6
cdx4	pCR-bluntII TOPO	partial CDS; bp 132–810	EcoRV	SP6
crabp2b	pCR-bluntII TOPO	partial CDS; bp 14–436	EcoRV	SP6
eve1	pCR-bluntII TOPO	partial CDS; bp 42–665	BamHI	T7
foxi1	pCS2+	entire CDS	ClaI	T7
gata2a	pCR-bluntII TOPO	partial CDS; bp 40–1141	SpeI	T7
id2a	pCR-bluntII TOPO	partial CDS; bp 6–401	BamHI	T7
klf2b	pCS2+	entire CDS	ClaI	T7
smad6a	pCR-bluntII TOPO	partial CDS; bp 8–880	BamHI	T7
smad7	pCR-bluntII TOPO	partial CDS; bp 23–1024	BamHI	T7
sizzled	pCS2+	entire CDS	ClaI	T7
tfap2c	pCS2+	entire CDS	ClaI	T7
ved	pCR-bluntII TOPO	partial CDS; bp 7–825	EcoRV	SP6
znfl2b	pCR-bluntII TOPO	partial CDS; bp 25–435	BamHI	T7

Note that the znfl2b in situ probe contained 47 SNPs compared to the reference genome (Danio rerio GRCz11).

The same DIG-labeled probes were used for both fluorescence (Figures 1F–Y and 7F–J, Figure 7—figure supplement 1K–O, and Figure 7—figure supplement 3) and colorimetric (Figure 1—figure supplement 1C–D and Figure 5—figure supplement 1A–F) in situ hybridization at a concentration of 1 ng/μl.

Whole-mount colorimetric in situ hybridization was carried out as described previously (Thisse and Thisse, 2008). Embryos were fixed in 4% formaldehyde in PBS, incubated at 4°C overnight, then transferred to MeOH and stored at −20°C for at least 2 h. Stained embryos were imaged in 2:1 benzyl benzoate:benzyl alcohol with an Axio Zoom.V16 microscope (ZEISS).

For fluorescence in situ hybridization (FISH), the same protocol was used until the blocking step, at which point embryos were blocked in FISH blocking buffer (2% blocking reagent (Roche, 11096176001) in 1x maleic acid buffer (100 mM maleic acid, 150 mM NaCl, 180 mM NaOH, 0.1% Tween)) for at least 2 h at room temperature with gentle rocking, then incubated at 4°C overnight in 1:150 anti-DIG-POD (Roche, 11207733910). The following day embryos were washed at least five times with PBST. To develop signal, embryos were incubated in 75 μl 1:75 Cy3-TSA in 1x amplification buffer (TSA Plus Cyanine 3 System, Perkin Elmer, NEL744001KT) for 30 min at room temperature in the dark. Embryos were then washed at least five times with PBST, incubated in 1:5000 DAPI (Life Technologies, D1306; stock concentration: 5 mg/ml) with agitation at room temperature for at least 1 h (or overnight at 4°C), then washed at least five times with PBST. One day after Cy3 incubation, embryos were imaged on a ZEISS Lightsheet Z.1 (see below and Figure 1—figure supplement 1E for imaging and quantification details). All FISH embryos shown in Figure 1F–Y were fertilized and fixed on the same day.

SPIM imaging of immunofluorescence staining and fluorescence in situ hybridization

Request a detailed protocol

Fixed embryos were mounted in 1% low melting temperature agarose (Lonza, 50080) using a glass capillary and imaged with a ZEISS Lightsheet Z.1 selective plane illumination microscope (SPIM). The imaging chamber was filled with water, and filters and light sheets were auto-aligned prior to imaging. For fluorescence in situ hybridization (FISH) and pSmad1/5/9 immunofluorescence (IF) experiments, embryos were positioned using the DAPI signal with the animal pole pointing toward the imaging objective to produce animal views; for ventral views, embryos in the correct orientation were rotated 90°. For animal views, 50–90 z-slices with 7 μm between each slice were acquired per embryo, covering the entire blastoderm over a distance of 350–630 μm depending on embryo size. For ventral views, ~70 z-slices with 7 μm between each slice were acquired per embryo, spanning roughly half of the embryo.

For pSmad2/3 and pErk IF, embryos were mounted in the orthogonal orientation compared to pSmad1/5/9 and FISH experiments, and three lateral images were acquired per embryo: one at the brightest region, a second rotated 120°, and a third rotated 240°.

All images were acquired with dual light sheet illumination using a W Plan-Apochromat 20x objective at 0.5x zoom and the imaging conditions described below.

SPIM imaging conditions:

Experiment	Signal	Fluorophore	Laser wave length (nm)	Laser intensity	Filter	Exposure (ms)
pErk IF	pErk	Cy3	561	1.5%	BP 575–615	100
pErk IF	Nuclei	DAPI	405	1.5%	BP 420–470	100
pSmad2/3 IF	pSmad2/3	Cy3	561	1%	BP 575–615	100
pSmad2/3 IF	Nuclei	DAPI	405	1.1%	BP 420–470	100
pSmad1/5/9 IF	pSmad 1/5/9	Alexa488	488	2%	BP 505–545	200
pSmad1/5/9 IF	Nuclei	DAPI	405	1.3%	BP 420–470	200
All FISH except SB-treated	FISH	Cy3	561	1.5%	BP 575–615	100
All FISH except SB-treated	Nuclei	DAPI	405	1.5%	BP 420–470	100
SB-treated FISH	FISH	Cy3	561	1%	BP 575–615	100
SB-treated FISH	Nuclei	DAPI	405	1.1%	BP 420–470	100

Maximum intensity projections were generated using the software ZEN (2014 SP1, black edition) and used for the analyses described below.

Mathematical modeling of target gene induction and decay kinetics

To estimate induction and decay of transcripts from the NanoString data (Figure 4), time-dependent pSmad1/5/9 and transcript changes were modeled mathematically. The change in the amount of endogenous (P_e) and optogenetically induced (P_o) pSmad1/5/9 levels can be described by the following general differential equations:

\frac{d P_{e}}{d t} = \dot{G} (t)

\frac{d P_{o}}{d t} = \dot{H} (t)

The observed pSmad1/5/9 levels in uninjected embryos correspond to G(t), whereas the observed pSmad1/5/9 levels (P_s) in light-exposed Opto-BMP embryos correspond to the sum of G(t) and H(t). Therefore, the change in the amount of P_s over time can be described by:

\frac{d P_{s}}{d t} = \dot{G} (t) + \dot{H} (t) = \dot{I} (t)

Thus, the levels of optogenetically induced pSmad1/5/9 can be calculated by subtracting the pSmad1/5/9 levels in uninjected embryos from the pSmad1/5/9 levels in light-exposed Opto-BMP embryos:

I (t) - G (t) = H (t)

Similarly, changes in the endogenous transcript levels (T_e) and optogenetically induced transcript levels (T_o) over time can be described by the following general differential equations:

\frac{d T_{e}}{d t} = \dot{K} (t)

\frac{d T_{o}}{d t} = \dot{L} (t)

The observed transcript levels in uninjected embryos correspond to K(t), whereas the observed transcript levels (T_s) in light-exposed Opto-BMP embryos correspond to the sum of K(t) and L(t). The change in the amount of T_s over time can therefore be described by:

\frac{d T_{s}}{d t} = \dot{K} (t) + \dot{L} (t) = \dot{M} (t)

Thus, the levels of optogenetically induced transcripts can be calculated by subtracting the transcript levels in uninjected embryos from the transcript levels in light-exposed Opto-BMP embryos:

M (t) - K (t) = L (t)

Modeling method 1

Request a detailed protocol

The NanoString transcription data was first analyzed using the simplest model of induction and decay (Figure 5):

\frac{d T_{o}}{d t} = σ P_{o} - λ T_{o}

where P_o represents the optogenetically induced pSmad1/5/9 input, T_o the pSmad1/5/9-dependent target gene, σ the induction rate constant, and λ the decay rate constant of the induced gene. P_o was obtained by fitting the measured pSmad1/5/9 immunofluorescence data H(t) (Figure 3C, Figure 5L, and Figure 3—figure supplement 1J) with a polynomial of degree five using the function polyfit in MATLAB 7.10.0 (R2010a). The induction-decay model was simulated in COMSOL Multiphysics 3.5a in a 10 μm domain (representing approximately one cell) with no-flux boundary conditions and an initial concentration T_o(0).

For each experiment, the combination of parameters T_o(0), σ, and λ was found that minimizes the sum of squared differences (SSD)

S S D = \sum_{n} {(L (t_{n}) - T_{o} (t_{n}))}^{2}

between the simulations of the induction-decay model T_o(t_n) and the data L(t_n) for all measured time points n.

The minimization was performed numerically using a constrained optimization algorithm (Nelder-Mead, MATLAB 7.10.0) with zero for the initial guesses of T_o(0), σ, and λ, and a maximum of 500 iterations. σ and λ were constrained between biologically plausible values of 0.00001/s and 0.1/s, and T_o(0) was bounded between −100 a.u. and 100 a.u. R² values were calculated from the minimizing SSD (SSD_min) to assess the goodness of the fits by

R^{2} = 1 - \frac{S S D_{m i n}}{\sum_{n} {(L (t_{n}) - \frac{1}{n} \sum_{n} L (t_{n}))}^{2}}

Fitted values for high-confidence BMP target genes, experimental repeat 1:

Target gene	σ (1/s)	λ (1/s)	T_o(0) (a.u.)	R²
bambia	0.000414	0.000879	−95.84	0.9125
bmp4	0.000076	0.000452	−42.71	0.7060
cdx4	0.000220	0.000434	−81.48	0.6871
crabp2b	0.000041	0.000010	10.27	0.0951
eve1	0.000233	0.000514	−20.49	0.7132
foxi1	0.000371	0.000835	−91.10	0.7821
gata2a	0.000105	0.000336	−46.01	0.6056
id2a	0.000111	0.000539	−20.54	0.7354
klf2b	0.000394	0.001262	5.369	0.6880
smad6a	0.000016	0.000670	1.606	0.1780
smad7	0.000116	0.000765	−65.54	0.8043
sizzled	0.000222	0.000605	−82.09	0.6470
tfap2c	0.000041	0.000153	−15.90	0.1922
ved	0.000590	0.000590	−100.0	0.8072

Fitted values for high-confidence BMP target genes, experimental repeat 2:

Target gene	σ (1/s)	λ (1/s)	T_o(0) (a.u.)	R²
bambia	0.000344	0.000564	90.73	0.6248
bmp4	0.000066	0.000474	−17.10	0.6114
cdx4	0.000169	0.000170	−26.84	0.2825
crabp2b	0.000056	0.000010	−43.72	0.2517
eve1	0.000158	0.000394	7.77	0.6689
foxi1	0.000413	0.001217	−14.67	0.7806
gata2a	0.000111	0.000399	−71.03	0.5647
id2a	0.000141	0.000522	−35.84	0.6967
klf2b	0.000708	0.003101	−62.70	0.6394
smad6a	0.000029	0.000340	−6.326	0.3140
smad7	0.000112	0.000613	−54.51	0.7397
sizzled	0.000217	0.000692	−99.99	0.6918
tfap2c	0.000056	0.000160	−27.15	0.4203
ved	0.000588	0.000554	−100.0	0.7354

Fitted values for high-confidence BMP target genes, experimental repeat 3:

Target gene	σ (1/s)	λ (1/s)	T_o(0) (a.u.)	R²
bambia	0.000640	0.001045	−99.99	0.9362
bmp4	0.000094	0.000455	−73.00	0.7986
cdx4	0.000181	0.000468	−99.81	0.5390
crabp2b	0.000087	0.000010	−87.63	0.4399
eve1	0.000334	0.000568	−100.0	0.7789
foxi1	0.000505	0.001174	−6.052	0.8502
gata2a	0.000148	0.000491	−65.45	0.8464
id2a	0.000126	0.000579	9.476	0.8000
klf2b	0.000505	0.001407	−100.0	0.6530
smad6a	0.000051	0.000563	−25.92	0.8935
smad7	0.000095	0.000553	−19.75	0.5364
sizzled	0.000290	0.000721	−100.0	0.7169
tfap2c	0.000045	0.000378	−38.42	0.4709
ved	0.000602	0.000489	−100.0	0.6802

Average fitted values for high-confidence BMP target genes:

Target gene	σ (1/s)		λ (1/s)		T_o(0) (a.u.)
Target gene	Mean	Stdev	Mean	Stdev	Mean	Stdev
bambia	0.00047	0.00015	0.00083	0.00024	−35.04	108.9
bmp4	0.00008	0.00001	0.00046	0.00001	−44.27	27.98
cdx4	0.00019	0.00003	0.00036	0.00016	−69.38	37.96
crabp2b	0.00006	0.00002	0.00001	0.00000	−40.36	49.04
eve1	0.00024	0.00009	0.00049	0.00009	−37.57	55.88
foxi1	0.00043	0.00007	0.00108	0.00021	−37.27	46.81
gata2a	0.00012	0.00002	0.00041	0.00008	−60.83	13.13
id2a	0.00013	0.00002	0.00055	0.00003	−15.63	23.05
klf2b	0.00054	0.00016	0.00192	0.00102	−52.44	53.43
smad6a	0.00003	0.00002	0.00052	0.00017	−10.21	14.17
smad7	0.00011	0.00001	0.00064	0.00011	−46.60	23.90
sizzled	0.00024	0.00004	0.00067	0.00006	−94.03	10.34
tfap2c	0.00005	0.00001	0.00023	0.00013	−27.15	11.26
ved	0.00059	0.00001	0.00054	0.00005	−100.0	0.000

Modeling method 2

Request a detailed protocol

In a second approach (Figure 5—figure supplement 1G–W), the NanoString transcription data was fitted with the analytical solutions to the differential equation system

\frac{d P_{e}}{d t} = k_{1} - k_{2} P_{e}

\frac{d P_{o}}{d t} = k_{3} (θ (t) - θ (t - t_{L})) - k_{2} P_{o}

\frac{d T_{e}}{d t} = k_{4} P_{e} - k_{5} T_{e}

\frac{d T_{o}}{d t} = σ P_{o} - λ T_{o}

which describes the changes in endogenous as well as optogenetically induced pSmad1/5/9 and transcript levels based on the simplest model of induction and decay after an optogenetic pulse of length t_L (i.e., 30 min = 1800 s for all experiments). k₁ represents the activation rate of endogenous pSmad1/5/9, k₂ the decay rate constant of pSmad1/5/9, and k₃ the activation rate of optogenetically induced pSmad1/5/9. Optogenetic switch-like activation was modeled with the Heaviside step function θ. k₄ and k₅ represent the activation rate and decay rate constants of endogenously induced BMP-dependent transcripts, and σ and λ are the induction rate and decay rate constants of the induced gene.

The analytical solutions to this equation system are:

P_{e} (t) = e^{- k_{2} t} δ_{P_{e}} + \frac{k_{1}}{k_{2}}

\begin{array}{ll} P_{o} (t) = \frac{1}{k_{2}} (k_{3} (θ (t_{L}) - θ (t_{L} - t)) e^{- k_{2} (t - t_{L})} + k_{3} θ (t_{L} - t) \\ + (- k_{3} θ (t) - θ (t_{L}) k_{3} + δ_{P_{o}} k_{2} + k_{3}) e^{- k_{2} t} + k_{3} (θ (t) - 1)) \end{array}

\begin{array}{ll} T_{e} = \frac{1}{k_{2} k_{5} (k_{2} - k_{5})} (k_{2} k_{5} (δ_{P_{e}} k_{4} + δ_{T_{e}} k_{2} - δ_{T_{e}} k_{5}) e^{- k_{5} t} \\ + (- k_{2} k_{5} δ_{P_{e}} e^{- k_{2} t} + k_{1} (k_{2} - k_{5})) k_{4}) \end{array}

\begin{array}{ll} T_{o} = \frac{1}{(k_{2} - λ) k_{2} λ} (- σ k_{3} λ (θ (t_{L}) - θ (t_{L} - t)) e^{- k_{2} (t - t_{L})} \\ + σ k_{2} k_{3} (θ (t_{L}) - θ (t_{L} - t)) e^{- λ (t - t_{L})} + σ k_{3} (k_{2} - λ) θ (t_{L} - t) \\ - k_{2} (θ (t_{L}) k_{3} σ + σ k_{3} θ (t) + (- δ_{P_{o}} λ - k_{3}) σ - λ δ_{T_{o}} (k_{2} - λ)) e^{- λ t} \\ + σ (λ (θ (t_{L}) k_{3} + k_{3} θ (t) - δ_{P_{o}} k_{2} - k_{3}) e^{- k_{2} t} + k_{3} (θ (t) - 1) (k_{2} - λ))) \end{array}

with

P_{e} (0) = δ_{P_{e}} + \frac{k_{1}}{k_{2}}

P_{o} (0) = δ_{P_{o}}

T_{e} (0) = δ_{T_{e}} + \frac{k_{1} k_{4}}{k_{2} k_{5}}

T_{o} (0) = δ_{T_{o}}

The pSmad1/5/9 data was fitted with the computer algebra system Maple (Waterloo Maple Inc) using the function LSSolve to minimize the difference between the pSmad1/5/9 data in uninjected embryos and P_e(t), as well as the difference between the pSmad1/5/9 data in light-exposed Opto-BMP embryos and P_e(t) + P_o(t) with the initial guesses $δ_{P_{e}} = 0 a.u.$ , $δ_{P_{o}} = 0 a.u.$ , $k_{1} = 0 / s$ , $k_{2} = 0.00167 / s$ , $k_{3} = 0 / s$ , $k_{4} = 00167 / s$ and a maximum of 20000 iterations and an optimality tolerance of 0.3981071706 × 10⁻¹⁴. The best fitting parameters $δ_{P_{e}} = - 76.19 a.u$ , $δ_{P_{o}} = 264.1 a.u.,$ $k_{1} = 0.1429 a.u./s,$ $k_{2} = 0.000900 / s,$ and $k_{3} = 0.954 a.u./s$ were then used for the simulation of the gene induction dynamics in the NanoString data.

The NanoString data was fitted in Maple using the function LSSolve to simultaneously minimize the difference between the NanoString data in uninjected embryos and T_e(t), as well as the difference between the NanoString data in light-exposed Opto-BMP embryos and T_e(t) + T_o(t) with the initial guesses $δ_{T_{e}} = 0 a.u.$ , $δ_{T_{o}} = 0 a.u.$ , $k_{4} = 0 / s$ , $k_{5} = 0.00167 / s$ , $σ = 0 / s$ , $λ = 0.00167 / s$ and a maximum of 10000 iterations and an optimality tolerance of 0.3981071706 × 10⁻¹⁴.

Fitted values for high-confidence BMP target genes:

Target gene	σ (1/s)	λ (1/s)	$δ_{T_{e}}$ (a.u.)	$δ_{T_{o}}$ (a.u.)	R²
bambia	0.000327	0.000671	520.4	16.01	0.7509
bmp4	0.000070	0.000362	171.2	−41.52	0.7912
cdx4	0.000238	0.000550	−1331	−29.22	0.8682
crabp2b	0.000048	−0.000191	−310.9	−40.27	0.8111
eve1	0.000177	0.000313	950.7	−52.74	0.8599
foxi1	0.000401	0.000094	47.34	−72.26	0.5592
gata2a	0.000144	0.000427	62.39	−77.72	0.4272
id2a	0.000143	0.000449	231.3	−21.14	0.7586
klf2b	0.000419	0.001114	9.959	−97.86	0.5082
smad6a	0.000030	0.000318	49.62	−15.67	0.3307
smad7	0.000125	0.000626	122.9	−54.50	0.7043
sizzled	0.000274	0.000758	238.9	−120.7	0.5116
tfap2c	0.000062	0.000316	44.54	−31.75	0.1597
ved	0.000732	0.000531	1200	−403.0	0.8063

Inhibition of Nodal and FGF signaling with small molecule inhibitors

Request a detailed protocol

The Nodal inhibitor SB-505124 (Sigma, S4696-5MG) (Soh et al., 2020; Almuedo-Castillo et al., 2018; Rogers et al., 2017; van Boxtel et al., 2015; Vogt et al., 2011; Fan et al., 2007; Hagos and Dougan, 2007; Hagos et al., 2007; DaCosta Byfield et al., 2004) and the FGF inhibitor SU-5402 (Sigma SML0443-5MG) (van Boxtel et al., 2015; Poulain et al., 2006; Londin et al., 2005; Fürthauer et al., 2004; Kudoh et al., 2004; Mathieu et al., 2004; Mohammadi et al., 1997) were diluted to 10 mM in DMSO (Roth, A994.2), aliquoted, and stored at −20°C. Aliquots were thawed the same day that experiments were carried out and were not re-used. 10 mM stocks of SB-505124 and SU-5402 were diluted to 50 and 10 μM, respectively, in embryo medium the day of each experiment. 5 ml diluted inhibitors were then dispensed into each well of agarose-coated (Sigma, A9539) 6-well plates (Greiner Bio-One, 657160), and plates were incubated at 28°C at least 30 min before embryos were added.

Quantification of pSmad1/5/9 immunofluorescence staining and fluorescence in situ hybridization

Request a detailed protocol

To measure spatial intensity profiles along the dorsal-ventral axis (Figure 1—figure supplement 1E) from pSmad1/5/9 immunofluorescence experiments (IF) (Figures 1D–E and 7A–E, Figure 7—figure supplement 1A–J’, and Figure 7—figure supplement 2A–K) and BMP target gene fluorescence in situ hybridization (FISH) (Figure 1P–Y, Figure 7F–J, and Figure 7—figure supplement 3), maximum intensity projections of animal views were manually rotated in Fiji (Schindelin et al., 2012) with ventral to the left (brightest signal) and dorsal to the right (dimmest signal; for the very early pSmad1/5/9 images prior to clear onset of BMP signaling, embryos were oriented with the brightest side on the left and the dimmest on the right where obvious, but correspondence with ventral-dorsal is not clear in those early cases). A polygonal region of interest (ROI) was then manually drawn around the embryo and used to create a mask in order to remove image background (for FISH experiments, the Cy3 signal was used to draw the mask; for IF experiments the DAPI signal was used). The average pixel intensity in each column of pixels from ventral to dorsal was then acquired (pixel area: 0.46 μm × 0.46 μm). For genes that are restricted to the margin (cdx4 and eve1), a second manually positioned circular ROI was used to exclude the non-margin region of the embryo (Figure 1—figure supplement 1E).

For FISH experiments, non-probe-exposed control embryos for background subtraction were imaged and intensity profiles acquired as described above. The orientation of these background subtraction embryos was random. Images for background subtraction controls were acquired in the same imaging session as experimental FISH images.

After intensity profiles were acquired, absolute distance was converted into percent embryo length to account for embryo-to-embryo variability in size, and intensity measurements were averaged into bins of 0.5% embryo length using an automated routine (0 < bin 1 < 0.5%, 0.5 < bin 2 < 1%, etc.).

For FISH experiments, the average intensity at each position in all 10 non-probe-exposed background embryos was calculated. This spatial background average was subtracted from each experimental FISH raw intensity profile, and data from the first and last 5% embryo length was excluded because the averages at the most ventral and dorsal regions are composed of relatively few pixels and are therefore less reliable.

The profiles of individual embryos were normalized following the procedure in Gregor et al., 2007 using the model

{I_{n} (x) = A}_{n} \bar{c} (x) + b_{n}

which relates the mean intensity profile $\bar{c} (x)$ of all data points for a given target gene to the intensity profile $I_{n} (x)$ for an embryo n through the embryo-specific proportionality constant $A_{n}$ and the nonspecific background $b_{n}$ . $A_{n}$ and $b_{n}$ were determined by minimizing the objective function

\sum_{i} (I_{n} (x_{i}) - (A_{n} \bar{c} (x_{i}) + b_{n}))^{2}

for the data points at all positions x_i with the Nelder-Mead algorithm using the function fminsearch in MATLAB 7.10.0, the initial guesses 1 and 0 for $A_{n}$ and $b_{n}$ , a maximum of 10000 function evaluations, and a maximum of 5000 iterations. For display, each average profile was then divided by its maximum intensity (Figure 1P-Y, Figure 7F-J, and Figure 7—figure supplement 3).

The Gaussian function $A e^{- \frac{{(x - μ)}^{2}}{ς}}$ was fitted to each profile using a constrained Nelder-Mead algorithm in MATLAB 7.10.0 with a maximum of 10000 function evaluations, a maximum of 5000 iterations, the initial guesses 300, 20, and 10000, the lower bounds 300, -50, and 100, and the upper bounds 100000, 50, and 100000 for A, µ, and ς, respectively. Gene expression range was defined as $r = μ + 2 \sqrt{ς / 2}$ . The resulting ranges from 9-10 embryos were averaged to define each gene’s mean range.

For pSmad1/5/9 IF spatial quantification experiments, the average image background intensity was determined for each image using a small ROI in the corner outside of the embryo, and subtracted from each IF raw intensity profile. Since the averages at the most ventral and dorsal regions are composed of relatively few pixels and are therefore less reliable, data from the first and last 5% embryo length was not considered. The mean of the dorsal-most 5% at 2.75 hpf was then subtracted from all profiles. These profiles were then normalized as described above for the FISH data, assuming embryo-specific constant nonspecific background and proportionality constants that relate immunofluorescent staining intensity to protein concentration.

Number of embryos assessed in spatial quantification experiments:

Experiment		Fig.	Number of embryos
FISH	All except apoc1l in bmp-overexpressing embryos	1P-Y, 7 F-J, 7.3	10
FISH	apoc1l in bmp-overexpressing embryos	7J, 7.3A	9
pSmad 1/5/9 IF	Time course in untreated and SU-5402/SB-505124-treated embryos	1E,7A, 7.2A-K	8–9
	Untreated and bmp-overexpressing embryos	7E, 7.1A-A’	10
	Untreated and SU-5420-treated embryos	7B, 7.1D-D’	10
	Untreated and SB-505124-treated embryos	7C, 7.1 F-F’	9–10
	Untreated and SU-5402/SB-505124-treated embryos	7D, 7.1 H-H’	10

To quantify total pSmad1/5/9 IF intensity (Figures 3C–E and 6B, and Figure 3—figure supplement 1I,J), an ROI was manually drawn around the embryo in Fiji based on DAPI signal and used to create a mask in order to remove image background as described above. The average intensity within the ROI was then calculated.

For experiments shown in Figure 3C–D and Figure 3—figure supplement 1I, image background intensity was measured using a small ROI in the corner of each image outside of the embryo. The average image background was then subtracted from the embryo intensity measurements to generate background-subtracted intensities.

For shield-stage experiments shown in Figure 3C,E, Figure 5L, Figure 6B, and Figure 3—figure supplement 1J, the average intensity within a small ROI on the dorsal side was measured in uninjected embryos; for each time point, these values were averaged and subtracted from the embryo intensity measurements to generate background-subtracted intensities.

Number of embryos assessed in total pSmad1/5/9 IF quantification time course experiments:

Experiment	Fig.	Number of embryos
High-stage BMP signaling pulse	3C, 3.1I	5
Shield-stage BMP signaling pulse	3C, 5L, 3.1J	5
Low- and high-amplitude BMP signaling pulse	6B	5 uninjected
Low- and high-amplitude BMP signaling pulse	6B	7 Opto-BMP

NanoString RNA quantification

Request a detailed protocol

For the NanoString time course experiment in untreated (Figure 2) and FGF/Nodal-inhibitor-treated embryos (Figure 7—figure supplement 2L-ZA), embryos from wild type TE incrosses were collected ~15 min after mating commenced. Embryos were incubated at 28°C, dechorionated using Pronase (Roche, 11459643001) at ~1.5 hpf, and sorted into 10 agarose-coated 6-well plates, one plate per time point. Each plate had one well containing embryo medium and one well containing FGF/Nodal inhibitor. To keep temperature and therefore development steady, plates were only removed from the 28°C incubator immediately prior to embryo collection. Every 30 min from 2.75 to 7.25 hpf, treated and untreated embryos were snap-frozen in liquid nitrogen.

For NanoString experiments quantifying responses to BMP signaling pulses using Opto-BMP (Figures 4, 5 and 6, Figure 5—figure supplement 1J–W, and Figure 6—figure supplement 1), embryos from TE incrosses were dechorionated using Pronase and injected at the one-cell stage with 5.2 pg opto-Alk3 + 5.2 pg opto-Alk8 + 8.9 pg opto-BMPR2a mRNA (Figure 3—figure supplement 1A). Control siblings were left uninjected, and embryos were sorted into agarose-coated 6-well plates and incubated at 28°C. 70–90 min post-fertilization at the 4–16 cell stage, unfertilized and damaged embryos were removed, and plates were individually wrapped in aluminum foil and incubated at 28°C. At the appropriate time, individual plates were transferred to a small 28°C incubator containing the LED array, exposed to light for the appropriate duration, and embryos were either snap-frozen in liquid nitrogen immediately (e.g., for the 10 min during exposure time point), or re-wrapped in aluminum foil and returned to 28°C incubation in the dark (e.g., for the 80 min post-exposure time point).

RNA was prepared as described for the RNA-sequencing experiment. 30 μl aliquots at 20 ng/μl were provided to Proteros GmbH (Planegg-Martinsried, Germany) for analysis using a custom-designed NanoString nCounter Elements TagSet with probes targeting high-confidence BMP target genes identified by RNA-sequencing, and housekeeping genes for normalization. Samples were measured using an nCounter SPRINT according to the standard protocol with a 24–30 h hybridization length.

nSolver 4.0 software (https://www.nanostring.com/products/analysis-software/nsolver) was used to subtract background and normalize the RNA count data using the geometric means of the positive spike-in controls and the housekeeping genes eef1a1l1 and act2b, respectively. Lanes that failed quality control were repeated.

Number of embryos assessed in NanoString experiments:

Experiment		Fig.	Number of embryos
Time course from 2.75 to 7.25 hpf	Untreated embryos	2, 7.2L-ZA	25
Time course from 2.75 to 7.25 hpf	SU-5402/SB-505124-treated embryos	7.2L-ZA	20–25
High-stage BMP signaling pulse		4	21–25
Shield-stage BMP signaling pulse		4, 5, 5.1I-W	19–25
Low- and high-amplitude BMP signaling pulse		6 C-F, 6.1	25

Each of the experiments described in the table above was repeated three times.

For experiments in which transcriptional responses to BMP signaling pulses are assessed (Figures 4, 5 and 6C–F, and Figure 6—figure supplement 1), it is necessary to determine changes in transcript levels compared to uninduced embryos. Because each of the three sets of Opto-BMP embryos had uninjected control siblings collected at the same time, average induction was calculated by first subtracting the uninjected transcript count from its corresponding injected sibling count, then by averaging the three subtracted counts (also see the section Mathematical modeling of target gene induction and decay kinetics above for a formal description of this procedure).

Calculation of spatial coefficients of variation

Request a detailed protocol

The spatial coefficient of variation (Figure 7N) for each condition (untreated, bmp-overexpressing, +SB-505124, + SU-5402, and +SB-505124 and SU-5402) was calculated as follows: First, at each position x, the average normalized intensity

μ (x) = \frac{1}{n} \sum_{i = 1}^{n} I_{i} (x)

and standard deviation

σ (x) = \sqrt{\frac{1}{n - 1} \sum_{i = 1}^{n} {(I_{i} (x) - μ (x))}^{2}}

for all n genes quantified by FISH were determined (Figure 7F–J). Next, the standard deviation was divided by the average normalized intensity at that position

c_{v} (x) = \frac{σ (x)}{μ (x)}

This was repeated for every position along the dorsal-ventral axis for all five conditions to calculate the spatial coefficients of variation for the 10 measured genes.

Statistical analyses

Request a detailed protocol

In the following experiments, significance was defined as a p-value≤0.05 using an unpaired two-tailed Student’s t-test assuming equal variance in Excel.

To determine how light exposure at different developmental stages affects BMP signaling in Opto-BMP embryos, total pSmad1/5/9 immunofluorescence intensity was quantified in uninjected and Opto-BMP-injected embryos exposed to light at high (3.5–4 hpf) or shield (6.75–7.25 hpf) stage (Figure 3C–D and Figure 3—figure supplement 1I,J).

Early and late light exposure, Opto-BMP versus uninjected p-values (Figure 3C–D and Figure 3—figure supplement 1I,J):

Time post- exposure (min)	High stage (early)	Shield stage (late)
−30	0.065	0.003
−20	0.029	1.422 × 10⁻⁵
−10	0.001	7.732 × 10⁻⁷
0	1.189 × 10⁻⁵	1.610 × 10⁻⁶
10	2.052 × 10⁻⁶	1.181 × 10⁻⁵
20	0.002	6.800 × 10⁻⁶
35	0.077	0.407
55	0.021	0.016
80	0.455	0.025
110	0.948	0.135

To determine how different light intensities affect BMP signaling in Opto-BMP embryos, total pSmad1/5/9 immunofluorescence intensity was quantified in uninjected and Opto-BMP-injected embryos exposed to low (70 lux) or high (3900 lux) intensity light for 10 or 20 min (Figure 6B).

Low- and high-intensity light, Opto-BMP versus uninjected p-values (Figure 6B):

Time post- exposure (min)	70 lux, 10 min	3900 lux, 10 min	70 lux, 20 min	3900 lux, 20 min
0	0.419	0.020	0.013	0.975
5	0.782	0.782	ND	ND
10	0.328	0.003	0.493	0.001
15	0.001	0.0004	ND	ND
20	0.097	0.0004	0.009	0.001
30	0.583	0.012	0.0002	0.00003
40	0.059	0.018	0.367	8.656 × 10⁻⁷
50	ND	ND	0.367	0.729

To determine whether BMP target gene expression domain boundaries differ significantly in untreated embryos, range was defined in individual embryos as described in the section Quantification of pSmad1/5/9 immunofluorescence staining and fluorescence in situ hybridization. Ranges were then averaged.

BMP target gene range comparison p-values (Figure 1P–Y):

	bambia	cdx4	eve1	foxi1	gata2a	klf2b	sizzled	tfap2c	ved
*apoc1l*	0.0122	0.136	3.27 × 10⁻⁴	9.47 × 10⁻⁵	0.682	0.371	1.06 × 10⁻⁶	0.003	6.79 × 10⁻⁵
*bambia*		4.44 × 10⁻⁶	1.06 × 10⁻⁵	1.2 × 10⁻⁹	0.129	9.95 × 10⁻⁵	1.12 × 10⁻¹⁸	2.70 × 10⁻⁵	1.58 × 10⁻⁸
*cdx4*			3.38 × 10⁻⁸	2.70 × 10⁻¹¹	0.511	0.138	3.67 × 10⁻¹⁷	5.59 × 10⁻⁹	2.15 × 10⁻¹⁰
*eve1*				0.182	0.010	2.64 × 10⁻⁷	5.40 × 10⁻⁸	0.001	0.081
*foxi1*					0.004	5.70 × 10⁻⁹	1.66 × 10⁻⁹	2.09 × 10⁻⁷	0.466
*gata2a*						0.838	1.07 × 10⁻⁴	0.049	0.003
*klf2b*							1.26 × 10⁻¹²	2.01 × 10–⁶	8.46 × 10⁻⁹
*sizzled*								7.92 × 10⁻¹⁸	5.19 × 10⁻⁷
*tfap2c*									1.33 × 10⁻⁶

The shape of the temporal BMP target gene expression profiles assessed by NanoString in untreated and SU-5402/SB-505124-treated embryos can be well approximated by the modified cumulative distribution function of the normal distribution

\frac{1}{2} A (1 + \erf (\frac{x - ν}{τ \sqrt{2}})) + b

which was used for regression analysis using a constrained Nelder-Mead algorithm in MATLAB 7.10.0 with a maximum of 10000 function evaluations, a maximum of 5000 iterations, the initial guesses 1000, 5 h, 1 h, and 100, the lower bounds 100, 3 h, 0.05 h, and 0, and the upper bounds 10000, 7 h, 3 h, and 1000 for A, $ν$ , $τ$ , and b, respectively. The activation time of each BMP target gene was defined as the average time point at which the curves reached about two mean average deviations (i.e., $1.5 ∙ τ$ ) from the inflection point $ν$ (Figure 2 and Figure 7—figure supplement 2L-Y). id2a (Chong et al., 2005) and smad6a (White et al., 2017) were excluded from this analysis because they are maternally contributed.

To determine whether FGF/Nodal loss affects the timing of gene activation, activation times in untreated versus SU-5402/SB-505124-treated samples were compared (Figure 7—figure supplement 2L–Y).

SU-5402/SB-505124-treated versus untreated activation time p-values (Figure 7—figure supplement 2L–Y):

bambia	bmp4	cdx4	crabp 2b	eve1	foxi1	gata 2a	klf2b	smad7	sizzled	tfap2c	ved
0.446	0.248	0.551	0.346	0.450	0.184	0.043	0.760	0.571	0.201	0.082	0.333

To identify differences in BMP target gene expression in the absence of FGF/Nodal signaling, transcript counts from SU-5402/SB-505124-treated embryos were compared to counts from untreated embryos (Figure 7—figure supplement 2L–Y).

SU-5402/SB-505124-treated versus untreated p-values (Figure 7—figure supplement 2L–Y):

hpf	bambia	bmp4	cdx4	crabp 2b	eve1	foxi1	gata 2a	id2a	klf2b	smad 6a	smad7	sizzled	*tfap* 2c	*ved*
2.75	0.796	0.677	0.770	0.389	0.835	0.654	0.675	0.961	0.652	0.578	0.826	0.824	0.897	0.968
3.25	0.757	0.590	0.855	0.905	0.573	0.790	0.386	0.946	0.341	0.918	0.704	0.497	0.514	0.682
3.75	0.695	0.749	0.941	0.951	0.593	0.791	0.804	0.700	0.729	0.159	0.816	0.854	0.245	0.818
4.25	0.565	0.954	0.650	0.434	0.561	0.661	0.590	0.720	0.855	0.785	0.358	0.258	0.521	0.751
4.75	0.988	0.943	0.996	0.655	0.645	0.751	0.919	0.965	0.820	0.460	0.643	0.224	0.630	0.947
5.25	0.910	0.477	0.554	0.996	0.927	0.874	0.759	0.733	0.877	0.511	0.561	0.095	0.489	0.800
5.75	0.877	0.323	0.622	0.405	0.237	0.324	0.083	0.589	0.108	0.739	0.615	0.122	0.319	0.926
6.25	0.443	0.509	0.731	0.399	0.450	0.149	0.091	0.767	0.085	0.938	0.966	0.077	0.105	0.483
6.75	0.493	0.596	0.713	0.325	0.723	0.041	0.038	0.163	0.022	0.415	0.120	0.006	0.023	0.103
7.25	0.346	0.078	0.657	0.262	0.874	0.021	0.014	0.256	0.011	0.067	0.055	0.008	0.019	0.020

For experiments in which transcriptional responses to BMP signaling pulses at high or shield stage were measured using NanoString (Figures 4 and 5M–Z), mRNA counts in Opto-BMP-injected embryos were compared to uninjected embryos.

High-stage BMP signaling pulse, Opto-BMP versus uninjected p-values (Figure 4):

Time post- exposure (min)	bambia	bmp4	cdx4	crabp2b	eve1	foxi1	gata 2a	id2a	klf2b	smad6a	smad7	sizzled	*tfap2c*	*ved*
−30	0.274	0.381	0.279	0.362	0.428	0.610	0.401	0.315	0.573	0.173	0.983	0.295	0.283	0.312
−20	0.270	0.419	0.225	0.144	0.386	0.051	0.354	0.275	0.364	0.301	0.897	0.456	0.171	0.124
−10	0.232	0.273	0.799	0.501	0.563	0.019	0.874	0.570	0.359	0.398	0.711	0.249	0.900	0.527
0	0.019	0.181	0.053	0.483	0.004	0.071	0.152	0.459	0.053	0.732	0.167	0.016	0.001	0.169
10	0.005	0.539	0.760	0.136	0.031	0.002	0.168	0.040	0.043	0.793	0.124	0.0001	0.012	0.017
20	0.002	0.034	0.190	0.902	0.002	0.083	0.021	0.001	0.067	0.156	0.007	0.001	0.019	0.060
35	0.002	0.002	0.458	0.726	0.006	0.0002	0.002	0.017	0.098	0.897	0.0003	0.0004	0.0001	0.001
55	0.113	0.139	0.912	0.566	0.033	0.242	0.043	0.004	0.182	0.214	0.097	0.083	0.043	0.138
80	0.175	0.069	0.497	0.061	0.166	0.310	0.003	0.008	0.807	0.279	0.287	0.804	0.079	0.623
110	0.056	0.449	0.793	0.356	0.209	0.440	0.463	0.402	0.226	0.760	0.084	0.006	0.357	0.214

Shield-stage BMP signaling pulse, Opto-BMP versus uninjected p-values (Figures 4 and 5M–Z, and Figure 5—figure supplement 1J–W):

Time post-exposure (min)	bambia	bmp4	cdx4	crabp2b	eve1	foxi1	gata 2a	id2a	klf2b	smad6a	smad7	sizzled	*tfap2c*	*ved*
−30	0.544	0.401	0.983	0.522	0.869	0.423	0.382	0.909	0.278	0.828	0.168	0.154	0.667	0.003
−20	0.111	0.069	0.727	0.440	0.686	0.474	0.116	0.242	0.084	0.731	0.509	0.983	0.631	0.483
−10	0.166	0.667	0.698	0.098	0.634	0.013	0.522	0.489	0.197	0.881	0.834	0.820	0.492	0.680
0	0.032	0.071	0.599	0.627	0.041	0.005	0.280	0.004	0.046	0.136	0.002	0.056	0.781	0.004
10	0.013	0.001	0.084	0.658	0.082	0.000	0.006	0.013	0.0001	0.242	0.003	0.005	0.151	0.002
20	0.003	0.002	0.020	0.201	0.001	0.000	0.0001	0.012	0.007	0.045	0.006	0.004	0.006	0.002
35	0.006	0.012	0.031	0.254	0.088	0.015	0.005	0.002	0.222	0.067	0.013	0.075	0.034	0.020
55	0.415	0.001	0.139	0.408	0.158	0.011	0.460	0.024	0.038	0.044	0.766	0.563	0.051	0.162
80	0.237	0.067	0.726	0.231	0.101	0.067	0.695	0.089	0.067	0.336	0.374	0.031	0.710	0.011
110	0.673	0.009	0.828	0.050	0.079	0.568	0.783	0.410	0.094	0.222	0.214	0.005	0.537	0.049

For experiments in which transcriptional responses to low- and high-amplitude BMP signaling pulses of different durations were measured using NanoString (Figure 6C–F and Figure 6—figure supplement 1), mRNA counts from uninjected embryos were first subtracted from Opto-BMP-injected siblings. Then the subtracted counts from light-exposed embryos were compared to subtracted counts from unexposed control embryos.

Low- and high-amplitude BMP pulses, exposed versus unexposed p-values (Figure 6C–F, Figure 6—figure supplement 1):

Exp.	Time into exposure (min)	bambia	bmp4	cdx4	crabp 2b	eve1	foxi1	gata 2a	id2a	klf 2b	smad 6a	smad 7	*szl*	*tfap* 2c	*ved*
70 lux, 10 min	30	0.083	0.597	0.390	0.967	0.487	0.021	0.856	0.703	0.271	0.894	0.071	0.405	0.816	0.603
	40	0.945	0.917	0.247	0.928	0.467	0.020	0.700	0.436	0.586	0.263	0.045	0.309	0.230	0.291
	50	0.078	0.234	0.659	0.358	0.104	0.046	0.067	0.050	0.341	0.081	0.084	0.205	0.070	0.079
3900 lux, 10 min	30	0.122	0.967	0.758	0.998	0.317	0.020	0.456	0.085	0.155	0.343	0.355	0.475	0.583	0.425
	40	0.013	0.367	0.008	0.296	0.085	0.056	0.171	0.154	0.027	0.572	0.037	0.261	0.019	0.062
	50	0.029	0.013	0.169	0.805	0.517	0.030	0.011	0.015	0.163	0.332	0.005	0.051	0.190	0.206
70 lux, 20 min	30	0.001	0.635	0.176	0.660	0.037	0.001	0.062	0.019	0.002	0.304	0.056	0.087	0.321	0.031
	40	0.120	0.348	0.217	0.126	0.479	0.011	0.172	0.104	0.031	0.270	0.181	0.136	0.102	0.250
	50	0.121	0.103	0.273	0.173	0.075	0.075	0.068	0.033	0.042	0.216	0.064	0.085	0.031	0.047
3900 lux, 20 min	30	0.178	0.448	0.201	0.233	0.061	0.160	0.061	0.035	0.154	0.491	0.166	0.232	0.122	0.189
	40	0.005	0.123	0.934	0.761	0.083	0.003	0.075	0.028	0.077	0.020	0.001	0.028	0.324	0.033
	50	0.324	0.271	0.006	0.615	0.077	0.540	0.144	0.382	0.062	0.929	0.238	0.160	0.225	0.237

Data and code availability

Request a detailed protocol

The raw images, data, and source code for custom scripts used in this work are available from the corresponding author upon request. Image quantification data and differential gene expression analyses are available in the accompanying source data files and Supplementary file 1, respectively. The RNA-sequencing data has been deposited at the GEO repository (accession number: GSE135100).

Data availability

The RNA-sequencing data has been deposited at the GEO repository (accession number: GSE135100) and can be accessed at https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE135100. Image quantification data is available in the accompanying source data files.

The following data sets were generated

1. Rogers KW
2. Müller P
(2020) NCBI Gene Expression Omnibus
ID GSE135100. Identification of BMP-regulated genes in early gastrulation stage zebrafish embryos.

http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE135100

References

1. Akieda Y
2. Ogamino S
3. Furuie H
4. Ishitani S
5. Akiyoshi R
6. Nogami J
7. Masuda T
8. Shimizu N
9. Ohkawa Y
10. Ishitani T
(2019) Cell competition corrects noisy wnt morphogen gradients to achieve robust patterning in the zebrafish embryo
Nature Communications 10:4710.
https://doi.org/10.1038/s41467-019-12609-4
- PubMed
- Google Scholar
(2018) Scale-invariant patterning by size-dependent inhibition of Nodal signalling
Nature Cell Biology 20:1032–1042.
https://doi.org/10.1038/s41556-018-0155-7
- PubMed
- Google Scholar
1. Anders S
2. Huber W
(2010) Differential expression analysis for sequence count data
Genome Biology 11:R106.
https://doi.org/10.1186/gb-2010-11-10-r106
- PubMed
- Google Scholar
1. Ashe HL
2. Briscoe J
(2006) The interpretation of morphogen gradients
Development 133:385–394.
https://doi.org/10.1242/dev.02238
- PubMed
- Google Scholar
(2002) Zebrafish DeltaNp63 is a direct target of Bmp signaling and encodes a transcriptional repressor blocking neural specification in the ventral ectoderm
Developmental Cell 2:617–627.
https://doi.org/10.1016/S1534-5807(02)00163-6
- PubMed
- Google Scholar
1. Barkai N
2. Shilo BZ
(2009) Robust generation and decoding of morphogen gradients
Cold Spring Harbor Perspectives in Biology 1:a001990.
https://doi.org/10.1101/cshperspect.a001990
- PubMed
- Google Scholar
(1999)
Bmp activity establishes a gradient of positional information throughout the entire neural plate

Development 126:4977–4987.
- PubMed
- Google Scholar
1. Bennett JT
2. Joubin K
3. Cheng S
4. Aanstad P
5. Herwig R
6. Clark M
7. Lehrach H
8. Schier AF
(2007) Nodal signaling activates differentiation genes during zebrafish gastrulation
Developmental Biology 304:525–540.
https://doi.org/10.1016/j.ydbio.2007.01.012
- PubMed
- Google Scholar
1. Briscoe J
2. Small S
(2015) Morphogen rules: design principles of gradient-mediated embryo patterning
Development 142:3996–4009.
https://doi.org/10.1242/dev.129452
- PubMed
- Google Scholar
1. Chen H
2. Xu Z
3. Mei C
4. Yu D
5. Small S
(2012) A system of repressor gradients spatially organizes the boundaries of Bicoid-dependent target genes
Cell 149:618–629.
https://doi.org/10.1016/j.cell.2012.03.018
- PubMed
- Google Scholar
(1997) Bone morphogenetic protein-4 expression characterizes inductive boundaries in organs of developing zebrafish
Development Genes and Evolution 207:107–114.
https://doi.org/10.1007/s004270050097
- PubMed
- Google Scholar
1. Chong SW
2. Nguyen TT
3. Chu LT
4. Jiang YJ
5. Korzh V
(2005) Zebrafish id2 developmental expression pattern contains evolutionary conserved and species-specific characteristics
Developmental Dynamics 234:1055–1063.
https://doi.org/10.1002/dvdy.20625
- PubMed
- Google Scholar
(2004) SB-505124 is a selective inhibitor of transforming growth factor-beta type I receptors ALK4, ALK5, and ALK7
Molecular Pharmacology 65:744–752.
https://doi.org/10.1124/mol.65.3.744
- PubMed
- Google Scholar
1. Das A
2. Crump JG
(2012) Bmps and id2a act upstream of Twist1 to restrict ectomesenchyme potential of the cranial neural crest
PLOS Genetics 8:e1002710.
https://doi.org/10.1371/journal.pgen.1002710
- PubMed
- Google Scholar
1. Davidson AJ
2. Ernst P
3. Wang Y
4. Dekens MP
5. Kingsley PD
6. Palis J
7. Korsmeyer SJ
8. Daley GQ
9. Zon LI
(2003) cdx4 mutants fail to specify blood progenitors and can be rescued by multiple hox genes
Nature 425:300–306.
https://doi.org/10.1038/nature01973
- PubMed
- Google Scholar
(2012) Bmp signaling exerts opposite effects on cardiac differentiation
Circulation Research 110:578–587.
https://doi.org/10.1161/CIRCRESAHA.111.261172
- PubMed
- Google Scholar
1. Derynck R
2. Budi EH
(2019) Specificity, versatility, and control of TGF-β family signaling
Science Signaling 12:eaav5183.
https://doi.org/10.1126/scisignal.aav5183
- PubMed
- Google Scholar
1. Detrich HW
2. Kieran MW
3. Chan FY
4. Barone LM
5. Yee K
6. Rundstadler JA
7. Pratt S
8. Ransom D
9. Zon LI
(1995) Intraembryonic hematopoietic cell migration during vertebrate development
PNAS 92:10713–10717.
https://doi.org/10.1073/pnas.92.23.10713
- PubMed
- Google Scholar
1. Dick A
2. Mayr T
3. Bauer H
4. Meier A
5. Hammerschmidt M
(2000) Cloning and characterization of zebrafish smad2, smad3 and smad4
Gene 246:69–80.
https://doi.org/10.1016/S0378-1119(00)00056-1
- PubMed
- Google Scholar
(2017) Paracrine Activin-A signaling promotes melanoma growth and metastasis through immune evasion
Journal of Investigative Dermatology 137:2578–2587.
https://doi.org/10.1016/j.jid.2017.07.845
- PubMed
- Google Scholar
(2015) Response to Nodal morphogen gradient is determined by the kinetics of target gene induction
eLife 4:e05042.
https://doi.org/10.7554/eLife.05042
- Google Scholar
1. Fan X
2. Hagos EG
3. Xu B
4. Sias C
5. Kawakami K
6. Burdine RD
7. Dougan ST
(2007) Nodal signals mediate interactions between the extra-embryonic and embryonic tissues in zebrafish
Developmental Biology 310:363–378.
https://doi.org/10.1016/j.ydbio.2007.08.008
- PubMed
- Google Scholar
(1997)
A role for FGF-8 in the dorsoventral patterning of the zebrafish gastrula

Development 124:4253–4264.
- PubMed
- Google Scholar
(2004) Fgf signalling controls the dorsoventral patterning of the zebrafish embryo
Development 131:2853–2864.
https://doi.org/10.1242/dev.01156
- PubMed
- Google Scholar
1. Genikhovich G
2. Fried P
3. Prünster MM
4. Schinko JB
5. Gilles AF
6. Fredman D
7. Meier K
8. Iber D
9. Technau U
(2015) Axis patterning by BMPs: cnidarian network reveals evolutionary constraints
Cell Reports 10:1646–1654.
https://doi.org/10.1016/j.celrep.2015.02.035
- PubMed
- Google Scholar
(2007) Probing the limits to positional information
Cell 130:153–164.
https://doi.org/10.1016/j.cell.2007.05.025
- PubMed
- Google Scholar
(1995)
Analysis of fgf function in normal and no tail zebrafish embryos reveals separate mechanisms for formation of the trunk and the tail

Development 121:2983–2994.
- PubMed
- Google Scholar
1. Gritsman K
2. Zhang J
3. Cheng S
4. Heckscher E
5. Talbot WS
6. Schier AF
(1999) The EGF-CFC protein one-eyed pinhead is essential for Nodal signaling
Cell 97:121–132.
https://doi.org/10.1016/S0092-8674(00)80720-5
- PubMed
- Google Scholar
1. Hagos EG
2. Fan X
3. Dougan ST
(2007) The role of maternal Activin-like signals in zebrafish embryos
Developmental Biology 309:245–258.
https://doi.org/10.1016/j.ydbio.2007.07.010
- PubMed
- Google Scholar
1. Hagos EG
2. Dougan ST
(2007) Time-dependent patterning of the mesoderm and endoderm by Nodal signals in zebrafish
BMC Developmental Biology 7:22.
https://doi.org/10.1186/1471-213X-7-22
- PubMed
- Google Scholar
(1996a)
Dino and mercedes, two genes regulating dorsal development in the zebrafish embryo

Development 123:95–102.
- PubMed
- Google Scholar
(1996b) Genetic analysis of dorsoventral pattern formation in the zebrafish: requirement of a BMP-like ventralizing activity and its dorsal repressor
Genes & Development 10:2452–2461.
https://doi.org/10.1101/gad.10.19.2452
- PubMed
- Google Scholar
1. Ho DM
2. Chan J
3. Bayliss P
4. Whitman M
(2006) Inhibitor-resistant type I receptors reveal specific requirements for TGF-β signaling in vivo
Developmental Biology 295:730–742.
https://doi.org/10.1016/j.ydbio.2006.03.050
- PubMed
- Google Scholar
1. Hogan BM
2. Pase L
3. Hall NE
4. Lieschke GJ
(2006) Characterisation of duplicate zinc finger like 2 erythroid precursor genes in zebrafish
Development Genes and Evolution 216:523–529.
https://doi.org/10.1007/s00427-006-0062-y
- PubMed
- Google Scholar
1. Horton RM
2. Cai Z
3. Ho SM
4. Pease LR
(2013) Gene splicing by overlap extension: tailor-made genes using the polymerase chain reaction
BioTechniques 54:129–133.
https://doi.org/10.2144/000114017
- PubMed
- Google Scholar
1. Iber D
2. Gaglia G
(2007) The mechanism of sudden stripe formation during dorso-ventral patterning in Drosophila
Journal of Mathematical Biology 54:179–198.
https://doi.org/10.1007/s00285-006-0047-5
- PubMed
- Google Scholar
1. Joly JS
2. Maury M
3. Joly C
4. Duprey P
5. Boulekbache H
6. Condamine H
(1992) Expression of a zebrafish caudal homeobox gene correlates with the establishment of posterior cell lineages at Gastrulation
Differentiation 50:75–87.
https://doi.org/10.1111/j.1432-0436.1992.tb00488.x
- PubMed
- Google Scholar
(1993)
The ventral and posterior expression of the zebrafish homeobox gene eve1 is perturbed in dorsalized and mutant embryos

Development 119:1261–1275.
- PubMed
- Google Scholar
1. Kashiwada T
2. Fukuhara S
3. Terai K
4. Tanaka T
5. Wakayama Y
6. Ando K
7. Nakajima H
8. Fukui H
9. Yuge S
10. Saito Y
11. Gemma A
12. Mochizuki N
(2015) β-Catenin-dependent transcription is central to Bmp-mediated formation of venous vessels
Development 142:497–509.
https://doi.org/10.1242/dev.115576
- PubMed
- Google Scholar
(1997)
The molecular nature of zebrafish swirl: BMP2 function is essential during early dorsoventral patterning

Development 124:4457–4466.
- PubMed
- Google Scholar
1. Koshida S
2. Shinya M
3. Nikaido M
4. Ueno N
5. Schulte-Merker S
6. Kuroiwa A
7. Takeda H
(2002) Inhibition of BMP activity by the FGF signal promotes posterior neural development in zebrafish
Developmental Biology 244:9–20.
https://doi.org/10.1006/dbio.2002.0581
- PubMed
- Google Scholar
(2014) A Pou5f1/Oct4 dependent Klf2a, Klf2b, and Klf17 regulatory sub-network contributes to EVL and ectoderm development during zebrafish embryogenesis
Developmental Biology 385:433–447.
https://doi.org/10.1016/j.ydbio.2013.10.025
- PubMed
- Google Scholar
(1997) Opposing BMP and EGF signalling pathways converge on the TGF-β family mediator Smad1
Nature 389:618–622.
https://doi.org/10.1038/39348
- PubMed
- Google Scholar
1. Kudoh T
2. Concha ML
3. Houart C
4. Dawid IB
5. Wilson SW
(2004) Combinatorial Fgf and Bmp signalling patterns the gastrula ectoderm into prospective neural and epidermal domains
Development 131:3581–3592.
https://doi.org/10.1242/dev.01227
- PubMed
- Google Scholar
1. Kulkarni MM
(2011) Digital multiplexed gene expression analysis using the NanoString nCounter system
Current Protocols in Molecular Biology Chapter 25:Unit25B 10.
https://doi.org/10.1002/0471142727.mb25b10s94
- PubMed
- Google Scholar
1. Kwon HJ
2. Bhat N
3. Sweet EM
4. Cornell RA
5. Riley BB
(2010) Identification of early requirements for preplacodal ectoderm and sensory organ development
PLOS Genetics 6:e1001133.
https://doi.org/10.1371/journal.pgen.1001133
- PubMed
- Google Scholar
1. Li W
2. Cornell RA
(2007) Redundant activities of Tfap2a and Tfap2c are required for neural crest induction and development of other non-neural ectoderm derivatives in zebrafish embryos
Developmental Biology 304:338–354.
https://doi.org/10.1016/j.ydbio.2006.12.042
- PubMed
- Google Scholar
(2005) Chordin, FGF signaling, and mesodermal factors cooperate in zebrafish neural induction
Developmental Biology 279:1–19.
https://doi.org/10.1016/j.ydbio.2004.11.016
- PubMed
- Google Scholar
(2006) FGF signaling is required for β-catenin-mediated induction of the zebrafish organizer
Development 133:3265–3276.
https://doi.org/10.1242/dev.02483
- PubMed
- Google Scholar
1. Martyn U
2. Schulte-Merker S
(2003) The ventralized ogon mutant phenotype is caused by a mutation in the zebrafish homologue of sizzled, a secreted Frizzled-related protein
Developmental Biology 260:58–67.
https://doi.org/10.1016/S0012-1606(03)00221-5
- PubMed
- Google Scholar
1. Mathieu J
2. Griffin K
3. Herbomel P
4. Dickmeis T
5. Strähle U
6. Kimelman D
7. Rosa FM
8. Peyriéras N
(2004) Nodal and Fgf pathways interact through a positive regulatory loop and synergize to maintain mesodermal cell populations
Development 131:629–641.
https://doi.org/10.1242/dev.00964
- PubMed
- Google Scholar
1. Mintzer KA
2. Lee MA
3. Runke G
4. Trout J
5. Whitman M
6. Mullins MC
(2001)
Lost-a-fin encodes a type I BMP receptor, Alk8, acting maternally and zygotically in dorsoventral pattern formation

Development 128:859–869.
- PubMed
- Google Scholar
1. Mizutani CM
2. Nie Q
3. Wan FY
4. Zhang YT
5. Vilmos P
6. Sousa-Neves R
7. Bier E
8. Marsh JL
9. Lander AD
(2005) Formation of the BMP activity gradient in the Drosophila embryo
Developmental Cell 8:915–924.
https://doi.org/10.1016/j.devcel.2005.04.009
- PubMed
- Google Scholar
1. Mohammadi M
2. McMahon G
3. Sun L
4. Tang C
5. Hirth P
6. Yeh BK
7. Hubbard SR
8. Schlessinger J
(1997) Structures of the tyrosine kinase domain of fibroblast growth factor receptor in complex with inhibitors
Science 276:955–960.
https://doi.org/10.1126/science.276.5314.955
- PubMed
- Google Scholar
(2008) Two novel type II receptors mediate BMP signalling and are required to establish left-right asymmetry in zebrafish
Developmental Biology 315:55–71.
https://doi.org/10.1016/j.ydbio.2007.11.038
- PubMed
- Google Scholar
1. Müller P
2. Rogers KW
3. Jordan BM
4. Lee JS
5. Robson D
6. Ramanathan S
7. Schier AF
(2012) Differential diffusivity of Nodal and Lefty underlies a reaction-diffusion patterning system
Science 336:721–724.
https://doi.org/10.1126/science.1221920
- PubMed
- Google Scholar
(1996)
Genes establishing dorsoventral pattern formation in the zebrafish embryo: the ventral specifying genes

Development 123:81–93.
- PubMed
- Google Scholar
(1997) A graded response to BMP-4 spatially coordinates patterning of the mesoderm and ectoderm in the zebrafish
Mechanisms of Development 62:183–195.
https://doi.org/10.1016/S0925-4773(97)00659-X
- PubMed
- Google Scholar
1. Nguyen VH
2. Schmid B
3. Trout J
4. Connors SA
5. Ekker M
6. Mullins MC
(1998) Ventral and lateral regions of the zebrafish gastrula, including the neural crest progenitors, are established by a bmp2b/swirl pathway of genes
Developmental Biology 199:93–110.
https://doi.org/10.1006/dbio.1998.8927
- PubMed
- Google Scholar
1. Nikaido M
2. Tada M
3. Saji T
4. Ueno N
(1997) Conservation of BMP signaling in zebrafish mesoderm patterning
Mechanisms of Development 61:75–88.
https://doi.org/10.1016/S0925-4773(96)00625-9
- PubMed
- Google Scholar
1. Nikaido M
2. Tada M
3. Takeda H
4. Kuroiwa A
5. Ueno N
(1999)
In vivo analysis using variants of zebrafish BMPR-IA: range of action and involvement of BMP in ectoderm patterning

Development 126:181–190.
- PubMed
- Google Scholar
1. Nissen RM
2. Yan J
3. Amsterdam A
4. Hopkins N
5. Burgess SM
(2003) Zebrafish foxi one modulates cellular responses to Fgf signaling required for the integrity of ear and jaw patterning
Development 130:2543–2554.
https://doi.org/10.1242/dev.00455
- PubMed
- Google Scholar
1. Oates AC
2. Pratt SJ
3. Vail B
4. Yan YI
5. Ho RK
6. Johnson SL
7. Postlethwait JH
8. Zon LI
(2001) The zebrafish klf gene family
Blood 98:1792–1801.
https://doi.org/10.1182/blood.V98.6.1792
- PubMed
- Google Scholar
1. Ochoa-Espinosa A
2. Yucel G
3. Kaplan L
4. Pare A
5. Pura N
6. Oberstein A
7. Papatsenko D
8. Small S
(2005) The role of binding site cluster strength in Bicoid-dependent patterning in Drosophila
PNAS 102:4960–4965.
https://doi.org/10.1073/pnas.0500373102
- PubMed
- Google Scholar
(2009) Anterior-posterior positional information in the absence of a strong Bicoid gradient
PNAS 106:3823–3828.
https://doi.org/10.1073/pnas.0807878105
- PubMed
- Google Scholar
(2009) The roles of the FGF signal in zebrafish embryos analyzed using constitutive activation and dominant-negative suppression of different FGF receptors
Mechanisms of Development 126:1–17.
https://doi.org/10.1016/j.mod.2008.10.008
- PubMed
- Google Scholar
(2003) Integration of IGF, FGF, and anti-BMP signals via Smad1 phosphorylation in neural induction
Genes & Development 17:3023–3028.
https://doi.org/10.1101/gad.1153603
- PubMed
- Google Scholar
(2013) Chordin forms a self-organizing morphogen gradient in the extracellular space between ectoderm and mesoderm in the Xenopus embryo
PNAS 110:20372–20379.
https://doi.org/10.1073/pnas.1319745110
- PubMed
- Google Scholar
1. Pogoda HM
2. Meyer D
(2002) Zebrafish Smad7 is regulated by Smad3 and BMP signals
Developmental Dynamics 224:334–349.
https://doi.org/10.1002/dvdy.10113
- PubMed
- Google Scholar
(2017) Dynamics of BMP signaling and distribution during zebrafish dorsal-ventral patterning
eLife 6:e25861.
https://doi.org/10.7554/eLife.25861
- PubMed
- Google Scholar
1. Poulain M
2. Fürthauer M
3. Thisse B
4. Thisse C
5. Lepage T
(2006) Zebrafish endoderm formation is regulated by combinatorial Nodal, FGF and BMP signalling
Development 133:2189–2200.
https://doi.org/10.1242/dev.02387
- PubMed
- Google Scholar
1. Poulain M
2. Lepage T
(2002)
Mezzo, a paired-like homeobox protein is an immediate target of Nodal signalling and regulates endoderm specification in zebrafish

Development 129:4901–4914.
- PubMed
- Google Scholar
1. Ramachandran A
2. Vizán P
3. Das D
4. Chakravarty P
5. Vogt J
6. Rogers KW
7. Müller P
8. Hinck AP
9. Sapkota GP
10. Hill CS
(2018) TGF-β uses a novel mode of receptor activation to phosphorylate SMAD1/5 and induce epithelial-to-mesenchymal transition
eLife 7:e31756.
https://doi.org/10.7554/eLife.31756
- PubMed
- Google Scholar
1. Ramel MC
2. Hill CS
(2013) The ventral to dorsal BMP activity gradient in the early zebrafish embryo is determined by graded expression of BMP ligands
Developmental Biology 378:170–182.
https://doi.org/10.1016/j.ydbio.2013.03.003
- PubMed
- Google Scholar
(2004) Fgf signaling induces posterior neuroectoderm independently of Bmp signaling inhibition
Developmental Dynamics 231:750–757.
https://doi.org/10.1002/dvdy.20244
- PubMed
- Google Scholar
(2010) edgeR: a Bioconductor package for differential expression analysis of digital gene expression data
Bioinformatics 26:139–140.
https://doi.org/10.1093/bioinformatics/btp616
- PubMed
- Google Scholar
1. Rodaway A
2. Takeda H
3. Koshida S
4. Broadbent J
5. Price B
6. Smith JC
7. Patient R
8. Holder N
(1999)
Induction of the mesendoderm in the zebrafish germ ring by yolk cell-derived TGF-β family signals and discrimination of mesoderm and endoderm by FGF

Development 126:3067–3078.
- PubMed
- Google Scholar
1. Rogers KW
2. Lord ND
3. Gagnon JA
4. Pauli A
5. Zimmerman S
6. Aksel DC
7. Reyon D
8. Tsai SQ
9. Joung JK
10. Schier AF
(2017) Nodal patterning without lefty inhibitory feedback is functional but fragile
eLife 6:e28785.
https://doi.org/10.7554/eLife.28785
- PubMed
- Google Scholar
1. Rogers KW
2. Müller P
(2019) Nodal and BMP dispersal during early zebrafish development
Developmental Biology 447:14–23.
https://doi.org/10.1016/j.ydbio.2018.04.002
- PubMed
- Google Scholar
1. Rogers KW
2. Müller P
(2020) Optogenetic approaches to investigate spatiotemporal signaling during development
Current Topics in Developmental Biology 137:37–77.
https://doi.org/10.1016/bs.ctdb.2019.11.009
- PubMed
- Google Scholar
1. Rogers KW
2. Schier AF
(2011) Morphogen gradients: from generation to interpretation
Annual Review of Cell and Developmental Biology 27:377–407.
https://doi.org/10.1146/annurev-cellbio-092910-154148
- PubMed
- Google Scholar
1. Sagner A
2. Briscoe J
(2017) Morphogen interpretation: concentration, time, competence, and signaling dynamics
Wiley Interdisciplinary Reviews: Developmental Biology 6:e271.
https://doi.org/10.1002/wdev.271
- Google Scholar
1. Sako K
2. Pradhan SJ
3. Barone V
4. Inglés-Prieto Á
5. Müller P
6. Ruprecht V
7. Čapek D
8. Galande S
9. Janovjak H
10. Heisenberg CP
(2016) Optogenetic control of Nodal signaling reveals a temporal pattern of Nodal signaling regulating cell fate specification during gastrulation
Cell Reports 16:866–877.
https://doi.org/10.1016/j.celrep.2016.06.036
- PubMed
- Google Scholar
(2007) Balancing BMP signaling through integrated inputs into the Smad1 linker
Molecular Cell 25:441–454.
https://doi.org/10.1016/j.molcel.2007.01.006
- PubMed
- Google Scholar
1. Schier AF
2. Talbot WS
(2005) Molecular genetics of axis formation in zebrafish
Annual Review of Genetics 39:561–613.
https://doi.org/10.1146/annurev.genet.37.110801.143752
- PubMed
- Google Scholar
1. Schindelin J
2. Arganda-Carreras I
3. Frise E
4. Kaynig V
5. Longair M
6. Pietzsch T
7. Preibisch S
8. Rueden C
9. Saalfeld S
10. Schmid B
11. Tinevez JY
12. White DJ
13. Hartenstein V
14. Eliceiri K
15. Tomancak P
16. Cardona A
(2012) Fiji: an open-source platform for biological-image analysis
Nature Methods 9:676–682.
https://doi.org/10.1038/nmeth.2019
- PubMed
- Google Scholar
(2011) An intermediate level of BMP signaling directly specifies cranial neural crest progenitor cells in zebrafish
PLOS ONE 6:e27403.
https://doi.org/10.1371/journal.pone.0027403
- PubMed
- Google Scholar
1. Sharma MK
2. Saxena V
3. Liu RZ
4. Thisse C
5. Thisse B
6. Denovan-Wright EM
7. Wright JM
(2005) Differential expression of the duplicated cellular retinoic acid-binding protein 2 genes (crabp2a and crabp2b) during zebrafish embryonic development
Gene Expression Patterns 5:371–379.
https://doi.org/10.1016/j.modgep.2004.09.010
- PubMed
- Google Scholar
1. Sharpe J
(2019) Wolpert's French Flag: what's the problem?
Development 146:dev185967.
https://doi.org/10.1242/dev.185967
- PubMed
- Google Scholar
1. Shimizu T
2. Yamanaka Y
3. Nojima H
4. Yabe T
5. Hibi M
6. Hirano T
(2002) A novel repressor-type homeobox gene, ved, is involved in dharma/bozozok-mediated dorsal organizer formation in zebrafish
Mechanisms of Development 118:125–138.
https://doi.org/10.1016/S0925-4773(02)00243-5
- PubMed
- Google Scholar
1. Shimizu T
2. Bae YK
3. Muraoka O
4. Hibi M
(2005) Interaction of Wnt and caudal-related genes in zebrafish posterior body formation
Developmental Biology 279:125–141.
https://doi.org/10.1016/j.ydbio.2004.12.007
- PubMed
- Google Scholar
(2020) Integration of Nodal and BMP signaling by mutual signaling effector antagonism
Cell Reports 31:107487.
https://doi.org/10.1016/j.celrep.2020.03.051
- PubMed
- Google Scholar
1. Solomon KS
2. Kudoh T
3. Dawid IB
4. Fritz A
(2003) Zebrafish foxi1 mediates otic placode formation and jaw development
Development 130:929–940.
https://doi.org/10.1242/dev.00308
- PubMed
- Google Scholar
(2010) Characterization of an lhx1a transgenic reporter in zebrafish
The International Journal of Developmental Biology 54:731–736.
https://doi.org/10.1387/ijdb.092969ls
- PubMed
- Google Scholar
1. Takahashi F
2. Yamagata D
3. Ishikawa M
4. Fukamatsu Y
5. Ogura Y
6. Kasahara M
7. Kiyosue T
8. Kikuyama M
9. Wada M
10. Kataoka H
(2007) AUREOCHROME, a photoreceptor required for photomorphogenesis in stramenopiles
PNAS 104:19625–19630.
https://doi.org/10.1073/pnas.0707692104
- PubMed
- Google Scholar
1. Thisse C
2. Thisse B
(2008) High-resolution in situ hybridization to whole-mount zebrafish embryos
Nature Protocols 3:59–69.
https://doi.org/10.1038/nprot.2007.514
- PubMed
- Google Scholar
1. Trapnell C
2. Williams BA
3. Pertea G
4. Mortazavi A
5. Kwan G
6. van Baren MJ
7. Salzberg SL
8. Wold BJ
9. Pachter L
(2010) Transcript assembly and quantification by RNA-Seq reveals unannotated transcripts and isoform switching during cell differentiation
Nature Biotechnology 28:511–515.
https://doi.org/10.1038/nbt.1621
- PubMed
- Google Scholar
1. Tsang M
2. Kim R
3. de Caestecker MP
4. Kudoh T
5. Roberts AB
6. Dawid IB
(2000) Zebrafish nma is involved in TGFβ family signaling
Genesis 28:47–57.
https://doi.org/10.1002/1526-968X(200010)28:2<47::AID-GENE20>3.0.CO;2-S
- PubMed
- Google Scholar
1. Tuazon FB
2. Mullins MC
(2015) Temporally coordinated signals progressively pattern the anteroposterior and dorsoventral body axes
Seminars in Cell & Developmental Biology 42:118–133.
https://doi.org/10.1016/j.semcdb.2015.06.003
- PubMed
- Google Scholar
(2008) The BMP signaling gradient patterns dorsoventral tissues in a temporally progressive manner along the anteroposterior axis
Developmental Cell 14:108–119.
https://doi.org/10.1016/j.devcel.2007.11.004
- PubMed
- Google Scholar
1. van Boxtel AL
2. Chesebro JE
3. Heliot C
4. Ramel MC
5. Stone RK
6. Hill CS
(2015) A temporal window for signal activation dictates the dimensions of a Nodal signaling domain
Developmental Cell 35:175–185.
https://doi.org/10.1016/j.devcel.2015.09.014
- PubMed
- Google Scholar
(2007) Chordin expression, mediated by Nodal and FGF signaling, is restricted by redundant function of two β-catenins in the zebrafish embryo
Mechanisms of Development 124:775–791.
https://doi.org/10.1016/j.mod.2007.05.005
- Google Scholar
(2011) The specificities of small molecule inhibitors of the TGFβ and BMP pathways
Cellular Signalling 23:1831–1842.
https://doi.org/10.1016/j.cellsig.2011.06.019
- PubMed
- Google Scholar
(2018) Reduced expression of the Nodal co-receptor Oep causes loss of mesendodermal competence in zebrafish
Development 145:dev158832.
https://doi.org/10.1242/dev.158832
- PubMed
- Google Scholar
1. Wang Y
2. Zhou L
3. Li Z
4. Li W
5. Gui J
(2013) Apolipoprotein C1 regulates epiboly during gastrulation in zebrafish
Science China Life Sciences 56:975–984.
https://doi.org/10.1007/s11427-013-4563-4
- PubMed
- Google Scholar
1. Wang Y
2. Li WH
3. Li Z
4. Liu W
5. Zhou L
6. Gui JF
(2015) BMP and RA signaling cooperate to regulate Apolipoprotein C1 expression during embryonic development
Gene 554:196–204.
https://doi.org/10.1016/j.gene.2014.10.047
- PubMed
- Google Scholar
1. White RJ
2. Collins JE
3. Sealy IM
4. Wali N
5. Dooley CM
6. Digby Z
7. Stemple DL
8. Murphy DN
9. Billis K
10. Hourlier T
11. Füllgrabe A
12. Davis MP
13. Enright AJ
14. Busch-Nentwich EM
(2017) A high-resolution mRNA expression time course of embryonic development in zebrafish
eLife 6:e30860.
https://doi.org/10.7554/eLife.30860
- PubMed
- Google Scholar
1. Xiong F
2. Tentner AR
3. Huang P
4. Gelas A
5. Mosaliganti KR
6. Souhait L
7. Rannou N
8. Swinburne IA
9. Obholzer ND
10. Cowgill PD
11. Schier AF
12. Megason SG
(2013) Specified neural progenitors sort to form sharp domains after noisy Shh signaling
Cell 153:550–561.
https://doi.org/10.1016/j.cell.2013.03.023
- PubMed
- Google Scholar
1. Yabe T
2. Shimizu T
3. Muraoka O
4. Bae YK
5. Hirata T
6. Nojima H
7. Kawakami A
8. Hirano T
9. Hibi M
(2003) Ogon/Secreted Frizzled functions as a negative feedback regulator of Bmp signaling
Development 130:2705–2716.
https://doi.org/10.1242/dev.00506
- PubMed
- Google Scholar
(1998) zALK-8, a novel type I serine/threonine kinase receptor, is expressed throughout early zebrafish development
Developmental Dynamics 211:352–361.
https://doi.org/10.1002/(SICI)1097-0177(199804)211:4<352::AID-AJA6>3.0.CO;2-G
- PubMed
- Google Scholar
1. Zinski J
2. Bu Y
3. Wang X
4. Dou W
5. Umulis D
6. Mullins MC
(2017) Systems biology derived source-sink mechanism of BMP gradient formation
eLife 6:e22199.
https://doi.org/10.7554/eLife.22199
- PubMed
- Google Scholar
(2018) TGF-β family signaling in early vertebrate development
Cold Spring Harbor Perspectives in Biology 10:a033274.
https://doi.org/10.1101/cshperspect.a033274
- PubMed
- Google Scholar

Decision letter

Markus Affolter

Reviewing Editor; Biozentrum der Universität Basel, Switzerland
Naama Barkai

Senior Editor; Weizmann Institute of Science, Israel

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Thank you for submitting your article "Combinatorial signaling underlies spatial diversity in BMP target gene expression" for consideration by eLife. Your article has been reviewed by three peer reviewers, one of whom is a member of our Board of Reviewing Editors, and the evaluation has been overseen by Naama Barkai as the Senior Editor. The reviewers have opted to remain anonymous.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

We would like to draw your attention to changes in our revision policy that we have made in response to COVID-19 (https://elifesciences.org/articles/57162). Specifically, when editors judge that a submitted work as a whole belongs in eLife but that some conclusions require a modest amount of additional new data, as they do with your paper, we are asking that the manuscript be revised to either limit claims to those supported by data in hand, or to explicitly state that the relevant conclusions require additional supporting data.

Our expectation is that the authors will eventually carry out the additional experiments and report on how they affect the relevant conclusions either in a preprint on bioRxiv or medRxiv, or if appropriate, as a Research Advance in eLife, either of which would be linked to the original paper.

Revisions for this paper:

1) Modify title and Abstract. The novel aspect is in the readout along the DV axis, only little data is presented for the readout along the animal-vegetative axis, and the results are confirming a model for spatial readout that has been made in numerous other model systems over the last decades

2) Please carefully respond to the points raised by reviewer 1 and 2.

Revisions expected in follow-up work:

Additional experiments are not necessarily requested, but could be later uploaded if the authors feel this adds to their work.

Reviewer #1:

The manuscript submitted by Patrick Müller and colleagues deals with the topic of morphogen signalling, in particular with the readout of different morphogen concentrations. Using optogenetic manipulation of BMP signalling in the early zebrafish embryo, the authors come to the conclusion that BMP-dependent gene regulation is not well explained or supported by a differential response to BMP doses, but instead results from combinatorial signalling. The paper is elegant and original in its experimental approaches (optogenetics, mathematical modelling, excellent assay system in vivo).

The authors look mostly at temporal regulation of genes with different expression patterns along the D/V axis, assuming that more broadly expressed genes should be activated by lower signalling levels, and since signalling levels increase, these genes should also be activated earlier. Since they do not see such a temporal behaviour, they conclude that the absence of a compelling correlation is inconsistent with the gradient threshold model. Using optogenetic approaches, they show that the differences in the competence to respond to BMP signalling at early stages cannot explain the majority of diversity in activation timing.

The major conclusion, namely that combinatorial signalling underlies the spatial diversity in BMP target gene expression, relies mostly on the gene expression patterns along the animal-vegetal axis. However, and as stated by the authors, the morphogen readout of BMP is best described and discussed in the literature with regard to the dorsal-ventral axis. I find it misleading that the major conclusions are derived from an axis along which BMP is not known to act as a morphogen. Different expression pattern in different "cell types" have long been known to arise via combinatorial signalling (Cell papers in 2000; and then many more in the last twenty years).

While the role of FGF and Nodal signaling is interesting, the description of the results obtained takes up only one page of the Results, and does not really contribute much to the overall topic of spatiotemporal expression along the DV axis. Yet, at the end, the results from this short aspect of the paper is placed into the title of the manuscript. Again, as I said, I find this misleading and the message conveyed in the title does not reflect the question addressed in the study.

So, all of the elegantly obtained data does not answer the initially posed question, and possibly leaves the reader a bit perplexed. Maybe it would be better to reformulate title and Abstract such that the experiments and the message are better aligned.

How is the different extend of expression along the gradient achieved? What is their idea?

What about different receptors and/or different ligands (homodimers versus heterodimers) and the expression pattern along the DV axis?

I am not an expert on mathematical modelling, so this part should be assessed by another reviewer who is more closely to this field.

Reviewer #2:

In this manuscript, Rogers et al. studied the read-out of the dorsal-ventral BMP gradient in zebrafish embryos. The authors first use RNA-seq to identify 16 BMP target genes and measured their spatial and temporal expression pattern in zebrafish embryos. They further induce pulses of BMP signaling and evaluate the differences in the gene expression pattern of these genes. By comparing their experimental observations with the predictions from the “gradient threshold” model, the authors conclude that their observations are inconsistent with a model based on threshold of gene activation. The authors then perturb the Nodal and/or FGF signaling pathway and show that these pathways significantly affect the expression pattern of these BMP targets, suggesting that the spatial expression of BMP targets is more dependent on the combination of BMP, Nodal and FGF signaling than on the threshold activation of BMP signal.

The question how gradients are read out is highly relevant and the experimental approach appears state-of-the art (though I am not an expert). However, the focus of this paper on a "gradient threshold" mechanism is surprising, given the large and detailed literature on how dorsal-ventral patterning, an evolutionary highly conserved process already observed in Nematostella, is controlled by a feedback-rich network architecture. The mechanism by which the BMP signaling gradient forms has been mathematically modelled, initially in Drosophila (Mizutani et al., 2005), subsequently also in Nematostella and Xenopus (Genikhovich et al., 2015), and finally in zebrafish (Zinski et al., 2017), and is rather well understood. One of its hallmarks is the sudden inversion of the BMP gradient opposite the Chordin expression domain (Iber and Gaglia 2007), which is also well visible in the here-quantified pSMAD gradient. This particular spatial dynamic makes it ever so harder to consider spatially averaged mRNA profiles (Figures 2,4,5,6) when trying to understand the regulatory logic.

This paper here focuses on the transcriptional network downstream of the pSMAD gradient (though Bmp and Smad genes themselves are transcriptional targets). Previous mathematical modelling of part of the here-considered components showed that the spatio-temporal dynamics can be captured when taking the regulatory interactions of the known transcription network into account (https://ars.els-cdn.com/content/image/1-s2.0-S2211124715001813-mmc1.pdf). In light of this, it is not unexpected that a simple threshold-based read-out mechanism cannot match the data. It is surprising that despite the rich quantitative data, no such spatio-temporal mathematical model is explored to understand how the BMP gradient is read out during dorsal-ventral patterning – and the available literature is not mentioned.

Beyond this general criticism that concerns the general approach, I have several specific concerns:

1) BMP target genes: The authors first use RNA-sequencing to systematically identify genes activated by BMP during early zebrafish gastrulation. By doing this, they ended up with a list of 16 genes. All their further analysis is highly dependent on such selection. However, it is not clear how those genes are selected, neither how robust the list is. The authors use 3 methods for the differential expression analysis (edgeR, DESeq, and Cuff diff). Why the authors have chosen those 3 methods, how their results were combined, what is the p-value threshold and whether the p-value is corrected by the number of features is not clear. Also, by changing any of those choices, how much the list of the genes would change is unclear. The resulting list of 16 BMP target genes contains 14 known BMP target genes, and the 2 newly identified target genes are not further studied or found to not show a clear BMP response. As such, it is not clear how much this unbiased approach adds over using known BMP target genes.

2) BMP read-out analysis: In order to test whether the "gradient threshold" model is sufficient to explain the expression pattern of the target genes, the authors compare the activation time and the range of expression of these genes. According to the authors, a threshold-based mechanism would implicate that broadly expressed genes are activated by lower signaling levels. Therefore, if such mechanism is the main driver of gene expression, we should observe a correlation between the activation time and the range of gene expression. The authors find a weak correlation between these variables and based on that exclude a threshold-based mechanism as the main drivers of gene expression. However, only 9 of the 16 genes are analyzed and due to such a low number of genes, the correlation is rather sensitive to the addition or removal of a gene. While the conclusion is likely correct given what is known about the feedback architecture of the BMP-dependent regulatory network (see above), the authors should test the statistical power of their conclusion using boot-strapping.

3) Optogenetics Data: It is assumed that endogenous BMP signalling is not active in high state, but the expression of several genes already jumps during high state (Figure 2) – how does this fit with this assumption? In Figure 5, the fits are shown for the dynamics of the difference between control and the induced data. As the amplitude of the difference differs between genes, the authors conclude that the induction rates must differ. However, also the uninduced control kinetics differ substantially between genes, with some expression profiles increasing and others decreasing over time. Those underlying dynamics likely also affect the extent to which the optogenetic pulse can impact, but this seems not to be considered here. Moreover, the change in amplitude reflects both increased expression and spatial expansion (Figure 5—figure supplement 1). The latter is not considered in the models. In addition, Figure 7 shows that the gradients are very different for high BMP levels, yet the comparison is made to the data in Figure 1. For lower and/or shorter pulses (Figure 6), the response is more diverse, but the presentation in Figure 6 hides the actual data. It would be important that at least a supplementary figure is provided that shows the full data as has been done in Figure 5—figure supplement 1so that one can see the temporal profile of each gene, and ideally also the ISH as in Figure 5—figure supplement 1; Figure 5—figure supplement 1itself should be expanded to show the ISH of all genes analysed in Figure 5 because the spatial data in Figure 5—figure supplement 1 nicely show that the pulses change not only the intensity, but also the range of the signal. This is expected in light of existing mathematical models, and makes it important to explicitly consider space in the analysis. In case of Figure 6, it would be important to relate the spatio-temporal kinetics to those observed in Figure 1 in a more detailed way than currently done.

4) Temporal Modelling: The authors use as a model for the transcript levels $\frac{{dT}_{o}}{dt} = σ \frac{{dP}_{o}}{dt} - λ T_{o}$ . It is an unusual assumption that the temporal change in the observed transcript levels, T_o, depends on the temporal change in the p-SMAD levels, P_o. Standard transcriptional models would assume that it depends on the p-SMAD levels, i.e. $\frac{{dT}_{0}}{dt} = σ f (P_{o}) - λ T_{0},$ where the function f is typically a Hill function. After all, their data provides them with P_o(t) as well as with T_o(t). As such, in a first simplistic approach, they could simply analyse the correlation (and transfer functions) between the two. But maybe that's what the authors mean and the above formula is just a typo?

5) Spatial Modelling: Current modelling approaches are much more powerful than what has been used in the paper (i.e. Zinski et al., 2017; Genikhovich et al., 2015). The authors should build on such work and analyse their quantitative data in the context of such more sophisticated models to understand how the different target genes are regulated. It does not help to rely on future modellers to pick up the published data as the modelling will identify missing data to arrive at a conclusion. I suspect for instance that spatial measurements of the response genes will be required at more than just a single state to understand the gradient read-out. For now, this data (Figure 1) seems not even to have been used in the analysis. The FGF/Nodal experiments will presumably only be properly interpretable when analysed in the context of the gradient-generating shuttling model from Zinski et al. as FGF appears to impact Chordin.

6) References: The authors do not comment on how the BMP gradient forms and how this depends on Chordin, even though this becomes highly relevant in the context of their FGF/Nodal experiments – and already explains why the ranges change when Chordin levels are altered, something they highlight as an open problem. They should discuss the relevant publications, i.e. Zinski et al., 2017. They should also discuss the literature on the BMP-dependent networks involved in DV patterning. Moreover, they also do not mention the paper Xiong et al., 2013 in the Discussion, which shows that in zebrafish development cells can sort to create sharp domain boundaries. Finally, they cite the neural tube as an example where a network affects the morphogen read-out, even though in the neural tube, the genes that are activated at lowest SHH levels are expressed first (PAX6 -> OLIG2 -> NKX2.2), which would actually be consistent with a threshold-based read-out.

As mentioned in my review, the authors should use boot-strapping to access the sensitivity of the estimated correlation to individual datapoints, and they should show the raw data for Figure 6.

Reviewer #3:

Rogers and co-workers used a combination of optogenetic and pharmacological approaches to test the extent to which the French Flag model of morphogen gradient interpretation can explain BMP signalling interpretation during zebrafish gastrulation. Using RNA-seq they systematically identified BMP targets during early zebrafish embryogenesis and then studied how altering BMP signalling dynamics impact on target gene expression. To do so, they developed an optogenetic approach by tagging the BMP receptor kinase domain with a LOV domain and targeted the fusion construct to the plasma membrane using a myristoylation motif. The efficacy of this optogenetic approach is demonstrated by the ventralization phenotype (normally induced upon over-expression of BMP) upon light exposure and normal development in the dark. The results presented are inconsistent with the French Flag model on three grounds. First, broader domains of target gene expression do not correlate with lower BMP concentration. Second, spatial shifts in the BMP gradient do not correlate with a corresponding shift in target gene expression. Third, they observe a lack of correlation between spatial broadness of target gene expression and levels of BMP required for activation. Together these results suggest that BMP signaling thresholds are alone insufficient to specify target gene expression. By pharmacological inhibiting Nodal and FGF signaling they show that spatial patterning of BMP targets requires the combinatorial inputs from these signaling systems.

Overall this is an interesting study addressing an important question in developmental biology, the experiments are well-controlled, clearly presented, and extensively discussed. I particularly value the development of a novel optogenetic tool to modulate BMP signalling which I think will be very useful for the community. I recommend publication of this study as it is.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

Thank you for submitting your article "Optogenetic investigation of BMP target gene expression diversity" for consideration by eLife. Your revised article has been evaluated by Naama Barkai (Senior Editor) and a Reviewing Editor.

We would like to draw your attention to changes in our revision policy that we have made in response to COVID-19 (https://elifesciences.org/articles/57162). Specifically, we are asking editors to accept without delay manuscripts, like yours, that they judge can stand as eLife papers without additional data, even if they feel that they would make the manuscript stronger. Thus the revisions requested below only address clarity and presentation.

The authors have made all requested technical corrections, but their added analysis confirms the worry that their main conclusion regarding the BMP-read-out is unsupported. Whilst we value the authors experimental approach, we worry that if the paper is published as is it will add to the confusion in the field, questioning basic principles of morphogen-related patterning without adequate experimental support. Accordingly, while no new data is required, we ask the authors to reword some of their conclusions, to further tone down their claims, by addressing the following comments.

Revisions:

1) The authors chose to analyse 9 BMP-dependent target genes. The selection is not unbiased as they say, but the result of technical limitations (as now explained much more clearly). Of these 9 target genes, two (cdx4 and eve1) are special in that they are expressed only in the margin (Figure 1). When included in the analysis, then expression range and activation time are effectively uncorrelated (Figure 2O). However, if cdx4 is removed from their analysis, the correlation increases to 65% (new analysis that was added), and if they removed also eve1, then the correlation can be expected to increase even further, thus supporting the notion that all analysed target genes, but the two margin-restricted cdx4 and eve1, are controlled in a threshold-based manner. That 2 BMP-dependent genes are constrained by further effects cannot be used to claim that the BMP read-out, in general, is not threshold-based – especially as the margin-restriction must indeed happen BMP-independently.

Also, the additional data that is now provided for Figure 6, which is most helpful, shows that the time points that were sampled are too late to reliably compare activation kinetics. Some of the genes also show transient dynamics that further confound the analysis when time points are sampled only late, especially as the variance is high and few time points could be analysed.

2) Citing Briscoe and Small, 2015, the authors use the neural tube as further support that morphogen gradients are not read out threshold-based. However, the progenitor boundaries have so far not been related to the measured SHH gradient (which was published only in 2015) – only to GBS-GFP, which is a floorplate promotor that responds only to the highest SHH concentration. The fact that the responsiveness of this promotor is limited does not mean that the progenitor boundaries are not read out threshold-based.

https://doi.org/10.7554/eLife.58641.sa1

Author response

Revisions for this paper:

1) Modify title and Abstract. The novel aspect is in the readout along the DV axis, only little data is presented for the readout along the animal-vegetative axis, and the results are confirming a model for spatial readout that has been made in numerous other model systems over the last decades

To better highlight the novel aspects of our study, we have changed the title to “Optogenetic investigation of BMP target gene expression diversity”. We have also modified the final sentence of the Abstract to point out that combinatorial signaling is a feature of other patterning systems: “Our results suggest that, similar to other patterning systems, combinatorial signaling is likely to be a major driver of spatial diversity in BMP-dependent gene expression in zebrafish, rather than activation by different BMP signaling thresholds”

Reviewer #1:

The manuscript submitted by Patrick Müller and colleagues deals with the topic of morphogen signalling, in particular with the readout of different morphogen concentrations. Using optogenetic manipulation of BMP signalling in the early zebrafish embryo, the authors come to the conclusion that BMP-dependent gene regulation is not well explained or supported by a differential response to BMP doses, but instead results from combinatorial signalling. The paper is elegant and original in its experimental approaches (optogenetics, mathematical modelling, excellent assay system in vivo).

The authors look mostly at temporal regulation of genes with different expression patterns along the D/V axis, assuming that more broadly expressed genes should be activated by lower signalling levels, and since signalling levels increase, these genes should also be activated earlier. Since they do not see such a temporal behaviour, they conclude that the absence of a compelling correlation is inconsistent with the gradient threshold model. Using optogenetic approaches, they show that the differences in the competence to respond to BMP signalling at early stages cannot explain the majority of diversity in activation timing.

The major conclusion, namely that combinatorial signalling underlies the spatial diversity in BMP target gene expression, relies mostly on the gene expression patterns along the animal-vegetal axis. However, and as stated by the authors, the morphogen readout of BMP is best described and discussed in the literature with regard to the dorsal-ventral axis. I find it misleading that the major conclusions are derived from an axis along which BMP is not known to act as a morphogen. Different expression pattern in different "cell types" have long been known to arise via combinatorial signalling (Cell papers in 2000; and then many more in the last twenty years).

While the role of FGF and Nodal signaling is interesting, the description of the results obtained takes up only one page of the Results, and does not really contribute much to the overall topic of spatiotemporal expression along the DV axis. Yet, at the end, the results from this short aspect of the paper is placed into the title of the manuscript. Again, as I said, I find this misleading and the message conveyed in the title does not reflect the question addressed in the study.

We found that combinatorial signaling contributes not only to expression differences along the animal-vegetal axis but also along the dorsal-ventral axis (Figure 7F-I, Figure 7—figure supplement 3). Nodal and FGF inhibit a subset of BMP target genes on the extreme ventral side, causing their expression to peak around 30% dorsal-ventral embryo length in contrast to other BMP targets. Thus, Nodal and FGF sculpt BMP target gene expression along both the animal-vegetal and dorsal-ventral axes.

So, all of the elegantly obtained data does not answer the initially posed question, and possibly leaves the reader a bit perplexed. Maybe it would be better to reformulate title and Abstract such that the experiments and the message are better aligned.

Our goal was “[…] to identify the factors contributing to differences in BMP target gene expression” and rule out factors that do not contribute. While our optogenetic data suggests that differential transcription kinetics in response to BMP signaling or differential BMP signaling activation thresholds do not define differences in spatiotemporal expression patterns, we do find evidence that spatial differences are predominantly due to combinatorial signaling.

As suggested, we have changed the title and Abstract to reflect that the majority of the manuscript is devoted to assessing whether BMP target gene responses to BMP signaling can explain their observed spatiotemporal expression diversity, whereas less space is dedicated to examining combinatorial signaling. We have also added further clarifications in the Introduction to avoid leaving readers perplexed.

How is the different extend of expression along the gradient achieved? What is their idea?

The major contributor to spatial differences appears to be combinatorial signaling. The more minor differences in range could be due to differential responses to other aspects of BMP signaling that we did not analyze (e.g., proportional activation by different BMP signaling levels).

What about different receptors and/or different ligands (homodimers versus heterodimers) and the expression pattern along the DV axis?

Although we are also fascinated by the regulation of BMP protein distribution (Rogers and Müller, 2019; Pomreinke et al., 2017), our current study is agnostic about how the BMP signaling gradient is formed or modified. Here, we consider the relationship between target gene expression and BMP signaling, directly measured by pSmad1/5/9 immunofluorescence. Since reviewer #2 also raised the question of how the BMP gradient forms (see below), we now elaborate more on what is known.

Reviewer #2:

In this manuscript, Rogers et al. studied the read-out of the dorsal-ventral BMP gradient in zebrafish embryos. The authors first use RNA-seq to identify 16 BMP target genes and measured their spatial and temporal expression pattern in zebrafish embryos. They further induce pulses of BMP signaling and evaluate the differences in the gene expression pattern of these genes. By comparing their experimental observations with the predictions from the “gradient threshold” model, the authors conclude that their observations are inconsistent with a model based on threshold of gene activation. The authors then perturb the Nodal and/or FGF signaling pathway and show that these pathways significantly affect the expression pattern of these BMP targets, suggesting that the spatial expression of BMP targets is more dependent on the combination of BMP, Nodal and FGF signaling than on the threshold activation of BMP signal.

The question how gradients are read out is highly relevant and the experimental approach appears state-of-the art (though I am not an expert). However, the focus of this paper on a "gradient threshold" mechanism is surprising, given the large and detailed literature on how dorsal-ventral patterning, an evolutionary highly conserved process already observed in Nematostella, is controlled by a feedback-rich network architecture.

Much of the literature suggests that BMP functions as a classical morphogen in the context of zebrafish dorsal-ventral patterning (Tuazon and Mullins, 2015; Barth et al., 1999; Nguyen et al., 1998; Neave et al., 1997; Mullins et al., 1996). Although currently there is no definitive consensus in the field, the threshold-based model remains popular. For example, Zinski, Tajer, and Mullins have recently stated that “It remains unclear how the BMP signaling gradient informs the expression of BMP target genes along the DV axis. It is postulated that cells along the BMP gradient sense the amount of signal, which determines their DV tissue fate as a morphogen. […] However, it is not known whether different BMP direct targets along the DV axis are induced by different thresholds of BMP signaling, different durations of BMP signaling, or some combination of the two.” (Zinski et al., 2018).

This motivates the use of our uniquely well-suited optogenetic approach to directly test this and other pervasive models.

The mechanism by which the BMP signaling gradient forms has been mathematically modelled, initially in Drosophila (Mizutani et al., 2005), subsequently also in Nematostella and Xenopus (Genikhovich et al., 2015), and finally in zebrafish (Zinski et al., 2017), and is rather well understood. One of its hallmarks is the sudden inversion of the BMP gradient opposite the Chordin expression domain (Iber and Gaglia, 2007), which is also well visible in the here-quantified pSMAD gradient. This particular spatial dynamic makes it ever so harder to consider spatially averaged mRNA profiles (Figures 2,4,5,6) when trying to understand the regulatory logic.

As the reviewer notes, the formation and regulation of the BMP signaling gradient is well studied, and we cite Zinski et al., 2017 as well as our own work on the subject (Pomreinke et al., 2017). In fact, our work showed that gradient formation in zebrafish does not depend on Chordin-mediated shuttling, and the mechanism is different from what had been described in Drosophila, Xenopus, and Nematostella (Pomreinke et al., 2017). Nevertheless, as mentioned in response to reviewer #1, our current study is agnostic about the mechanism of BMP signaling gradient formation since we focus on the readout by different target genes that respond to the same signaling gradient. Although we do quantify BMP signaling in our present work, we do not examine the formation or modification of the signaling gradient itself.

We now elaborate more in the Introduction on what is known about BMP gradient formation. We had previously referenced a review (Rogers and Müller, 2019) in which we discussed the Mizutani et al., 2005, Genikhovich et al., 2015, and Zinski et al., 2017 papers suggested by reviewer #2, but we now also include these primary references as well as Iber and Gaglia, 2007 directly in the current manuscript.

This paper here focuses on the transcriptional network downstream of the pSMAD gradient (though Bmp and Smad genes themselves are transcriptional targets). Previous mathematical modelling of part of the here-considered components showed that the spatio-temporal dynamics can be captured when taking the regulatory interactions of the known transcription network into account (https://ars.els-cdn.com/content/image/1-s2.0-S2211124715001813-mmc1.pdf). In light of this, it is not unexpected that a simple threshold-based read-out mechanism cannot match the data. It is surprising that despite the rich quantitative data, no such spatio-temporal mathematical model is explored to understand how the BMP gradient is read out during dorsal-ventral patterning – and the available literature is not mentioned.

As mentioned above, there is currently no consensus on whether BMP acts as a morphogen using a threshold-based strategy during zebrafish dorsal-ventral patterning, and the many factors that are known to regulate BMP gradient formation do not necessarily rule out a threshold-based readout for target genes (Zinski et al., 2018). We agree that further mathematical modeling could help clarify the relationship between BMP signaling and target gene expression. However, meaningful modeling would require significant amounts of additional data, including measurements of the dynamic changes in gene expression amplitudes and spatial profiles over time, which we cannot include in a reasonable timeline.

Beyond this general criticism that concerns the general approach, I have several specific concerns:

1) BMP target genes: The authors first use RNA-sequencing to systematically identify genes activated by BMP during early zebrafish gastrulation. By doing this, they ended up with a list of 16 genes. All their further analysis is highly dependent on such selection. However, it is not clear how those genes are selected, neither how robust the list is. The authors use 3 methods for the differential expression analysis (edgeR, DESeq, and Cuff diff). Why the authors have chosen those 3 methods, how their results were combined, what is the p-value threshold and whether the p-value is corrected by the number of features is not clear. Also, by changing any of those choices, how much the list of the genes would change is unclear. The resulting list of 16 BMP target genes contains 14 known BMP target genes, and the 2 newly identified target genes are not further studied or found to not show a clear BMP response. As such, it is not clear how much this unbiased approach adds over using known BMP target genes.

We defined high-confidence BMP target genes as those that were both significantly upregulated in BMP-overexpressing embryos and downregulated in Chordin-overexpressing embryos at shield stage (Figure 1—figure supplement 1). Significance was determined by the well-established and widely used differential expression analysis tools edgeR, DESeq, and Cuff diff (Seyednasrollah et al., 2015), and the resulting p-values can be found in the Supplementary file 1. High-confidence genes consist only of those that were deemed significantly differentially expressed by all three programs. We now also state in the Materials and methods section that the p-value threshold for differentially expressed genes was set to 0.05.

While we identified the vast majority of known direct BMP targets (Zinski et al., 2018) in at least one condition (Supplementary file 1), we note that our strict definition excludes known target genes such as tp63 (which is not expressed at shield stage and therefore not downregulated in Chordin-overexpressing embryos). However, we wanted to focus on an unbiased set of high-confidence BMP targets as representatives of the patterning system, selected based on clear and logical rules. We believe our definition achieves this aim, and we favor this approach over manually picking a subset of genes. Our approach is further validated by the corroboration of the RNA-seq data by in situ hybridization (Figure 1—figure supplement 1C) and by the fact that 14/16 high-confidence target genes have previously been described to be regulated by BMP in zebrafish.

We have published the raw data in the GEO repository, and we also now provide the complete differential expression analysis in the Supplementary file 1.

2) BMP read-out analysis: In order to test whether the "gradient threshold" model is sufficient to explain the expression pattern of the target genes, the authors compare the activation time and the range of expression of these genes. According to the authors, a threshold-based mechanism would implicate that broadly expressed genes are activated by lower signaling levels. Therefore, if such mechanism is the main driver of gene expression, we should observe a correlation between the activation time and the range of gene expression. The authors find a weak correlation between these variables and based on that exclude a threshold-based mechanism as the main drivers of gene expression. However, only 9 of the 16 genes are analyzed and due to such a low number of genes, the correlation is rather sensitive to the addition or removal of a gene. While the conclusion is likely correct given what is known about the feedback architecture of the BMP-dependent regulatory network (see above), the authors should test the statistical power of their conclusion using boot-strapping.

As described in the legends for Figure 1 and Figure 2 and in the Materials and methods section, unfortunately not all 16 high-confidence target genes provided robust FISH signal and some of the NanoString probes failed; thus, some genes could not be spatially or temporally assessed, respectively. We were therefore only able to include 9 genes in this analysis, which we now point out more explicitly in the main text.

We carried out the suggested bootstrapping analysis (Author response table 1) as well as jackknife resampling as its linear approximation (Author response table 2). The Pearson correlation coefficient for the data shown in Figure 2O is -0.23, compared to -0.24 – 0.20 for the bootstrapping analysis and an average of -0.24 – 0.18 for the jackknife estimator. We determined that the weak correlation is relatively insensitive to all data points except for cdx4, removal of which results in a more negative correlation (-0.65). However, there is no obvious reason to exclude cdx4 from the analysis.

Author response table 1

Bootstrapping analysis for Figure 2O.

100 random bootstrapped Pearson correlation coefficients
-0.55	0.04	-0.22	-0.16	-0.13	-0.33	-0.11	-0.39	-0.35	-0.02
-0.29	-0.38	-0.13	-0.38	-0.09	-0.16	-0.24	-0.10	-0.38	-0.02
-0.26	-0.13	-0.45	0.11	-0.08	-0.38	-0.26	-0.13	-0.17	-0.22
0.02	-0.08	-0.21	-0.33	-0.43	0.03	-0.62	-0.36	-0.24	-0.26
-0.71	-0.20	-0.01	-0.66	-0.05	-0.26	0.11	-0.25	0.15	-0.02
-0.13	-0.31	0.11	-0.35	0.03	-0.21	-0.16	-0.31	-0.66	-0.31
-0.33	-0.36	-0.08	-0.33	-0.66	-0.25	-0.14	-0.39	-0.33	-0.04
-0.62	-0.39	-0.13	-0.11	-0.55	-0.39	-0.03	-0.20	-0.08	-0.30
-0.22	-0.24	-0.04	-0.25	0.15	-0.14	-0.13	-0.68	-0.13	-0.20
-0.16	0.11	-0.22	-0.21	-0.24	-0.68	-0.31	-0.66	-0.28	-0.22

Author response table 2

Jackknife analysis for Figure 2O.

Pearson correlation coefficients with the indicated gene removed
bambia	cdx4	eve1	foxi1	gata2a	klf2b	sizzled	tfap2c	ved
-0.21	-0.65	-0.17	-0.35	-0.10	-0.04	-0.13	-0.23	-0.24

We have also extended our discussion to point out a subset of genes that shows behaviors consistent with the gradient threshold model: “We note that a subset of three genes (sizzled, ved, and bambia) that are neither restricted to nor excluded from the margin do show a strong negative correlation between range and activation time _(ρp = -0.99, although this correlation based on only three data points might be spurious) (Figure 2O) as well as activation dynamics that could be roughly commensurate with signaling input (Figure 6C and Figure 6—figure supplement 1), consistent with the gradient threshold model. However, it remains to be determined to what extent this subset of genes (or others) quantitatively follows the input-output relationships predicted by the gradient threshold model”.

3) Optogenetics Data: It is assumed that endogenous BMP signalling is not active in high state, but the expression of several genes already jumps during high state (Figure 2) – how does this fit with this assumption?

Genes with high levels of transcripts at 2.75 hpf (id2a and smad6a) are maternally provided (White et al., 2017; Chong et al., 2005), making it difficult to determine their activation times (Figure 2E,H). These genes were therefore excluded from our activation time analyses. However, some genes that are not maternally provided are expressed around high stage (~3.5 hpf, e.g., Figure 2D,L). We based the lack of BMP signaling at high stage on our spatiotemporal analysis of pSmad1/5/9 levels, which indicate undetectable pSmad at high stage (Figure 1D-E and Figure 7—figure supplement 2B-K). It therefore seems possible that other factors are responsible for the early activation of these genes.

In Figure 5, the fits are shown for the dynamics of the difference between control and the induced data. As the amplitude of the difference differs between genes, the authors conclude that the induction rates must differ. However, also the uninduced control kinetics differ substantially between genes, with some expression profiles increasing and others decreasing over time. Those underlying dynamics likely also affect the extent to which the optogenetic pulse can impact, but this seems not to be considered here.

The optogenetic experiments in Figure 5 included uninjected controls collected at the same time points as Opto-BMP-expressing siblings. We were therefore able to subtract the endogenous transcripts from the induced transcripts at all time points. The fact that the endogenous transcript levels have different temporal dynamics is therefore controlled for, both in our data and in the mathematical modeling (Figure 5—figure supplement 1).

Moreover, the change in amplitude reflects both increased expression and spatial expansion (Figure 5—figure supplement 1). The latter is not considered in the models.

We observe that all cells in the embryo can respond to the roughly uniform optogenetically delivered signaling pulse (Figure 3D,E), accounting for the expected spatial expansion in gene expression (the optogenetic constructs act downstream of many of the endogenous extracellular inhibitory factors on the dorsal side). The NanoString data includes all transcripts, regardless of whether they are expressed in the endogenous spatial domain. Because we subtract the uninjected transcripts from the transcripts in Opto-BMP-expressing siblings, spatial changes are accounted for in the data and modeling.

In addition, Figure 7 shows that the gradients are very different for high BMP levels, yet the comparison is made to the data in Figure 1.

Figure 7J quantifies spatial changes in BMP target gene expression when BMP mRNA is injected at the one-cell stage, but it does not provide information about target gene activation kinetics. In contrast, in Figure 5M-Z we quantify target gene activation kinetics by optogenetically introducing an acute BMP signaling pulse at shield stage (~6.75 hpf). This allowed us to address the following question: Can the differences in the endogenous spatial expression ranges be explained by differences in activation kinetics? To answer this question, we compared activation kinetics (Figure 5M-Z) to endogenous spatial expression ranges (Figure 1P-Y).

For lower and/or shorter pulses (Figure 6), the response is more diverse, but the presentation in Figure 6 hides the actual data. It would be important that at least a supplementary figure is provided that shows the full data as has been done in Figure 5—figure supplement 1 so that one can see the temporal profile of each gene, and ideally also the ISH as in Figure 5—figure supplement 1; Figure 5—figure supplement 1itself should be expanded to show the ISH of all genes analysed in Figure 5 because the spatial data in Figure 5—figure supplement 1nicely show that the pulses change not only the intensity, but also the range of the signal. This is expected in light of existing mathematical models, and makes it important to explicitly consider space in the analysis. In case of Figure 6, it would be important to relate the spatio-temporal kinetics to those observed in Figure 1 in a more detailed way than currently done.

With the data in Figure 6 we argue that different activation thresholds are unlikely to explain the differences in the endogenous spatial expression ranges (Figure 1 P-Y). According to the gradient threshold model, genes with narrow expression ranges should require high levels of BMP signaling to be activated. However, we observed that both broadly and narrowly expressed genes were activated by low levels of signaling (Figure 6C,E), indicating that differential activation thresholds do not explain the differential spatial ranges observed in Figure 1P-Y.

As suggested, we have re-plotted the data from Figure 6 C-F to show the temporal profile of each gene (Figure 6—figure supplement 1), and the raw data is also available in the Source Data file. Note that, in contrast to Figure 4, Figure 5, and Figure 5—figure supplement 1 in which 10 time points during and after exposure were collected, in Figure 6 we only collected 3 time points (30, 40, and 50 min into exposure). Collecting more time points would have been logistically challenging due to the greater number of conditions and sample numbers, and temporal data was not required to answer the question meant to be addressed by these experiments (in contrast to Figure 4, Figure 5, and Figure 5—figure supplement 1).

The question we sought to address in Figure 6 is whether more broadly expressed genes, such as klf2b and gata2a, are more likely to be activated by lower signaling levels than more narrowly expressed genes, such as foxi1 (Figure 1). The new Figure 6—figure supplement 1 shows that at a low-amplitude and short duration of BMP signaling (70 lux, 10 min), foxi1 is significantly activated, whereas klf2b and gata2a are not (see Figure 6 and Materials and methods for statistical analyses). This is inconsistent with the gradient threshold model, complementing the results shown in Figure 6.

Although we do not have additional in situ hybridization data for the 30 min pulse shown in Figure 5—figure supplement 1, in Author response image 1 we show the requested in situ hybridization of four BMP target genes responding to the different amplitudes and durations of BMP signaling applied in Figure 6. This data shows that the activation sensitivity of these genes does not correspond to the extent of the spatial expression domain. For example, the endogenous expression range of foxi1 and eve1 is comparable (Figure 1R,S), foxi1 is much more sensitive to a short and low-intensity Opto-BMP pulse than eve1 (Author response image 1B, Figure 6—figure supplement 1D,F).

Author response image 1

Download asset Open asset

BMP target gene responses to different amplitudes and durations of BMP signalling.

Embryos injected with Opto-BMP and uninjected siblings were either left in the dark (A) or exposed to 70 or 3900 lux blue light for 10 (B) or 20 (C) min starting at shield stage (~6.75 hpf), and fixed 20 min post-exposure. BMP target gene expression in response to the resulting low- and high-amplitude BMP signaling pulses (Figure 6B) was assessed using colorimetric *in situ* hybridization.

Since all cells can respond to optogenetically delivered BMP signaling pulses, the expansion of BMP target gene spatial expression ranges is expected and accounted for in our modelling by subtracting the uninjected transcript counts at each time point, as described above.

4) Temporal Modelling: The authors use as a model for the transcript levels $\frac{{dT}_{o}}{dt} = σ \frac{{dP}_{o}}{dt} - λ T_{o}$ . It is an unusual assumption that the temporal change in the observed transcript levels, T_o, depends on the temporal change in the p-SMAD levels, P_o. Standard transcriptional models would assume that it depends on the p-SMAD levels, i.e. $\frac{{dT}_{0}}{dt} = σ f (P_{o}) - λ T_{0},$ where the function f is typically a Hill function. After all, their data provides them with P_o(t) as well as with T_o(t). As such, in a first simplistic approach, they could simply analyse the correlation (and transfer functions) between the two. But maybe that's what the authors mean and the above formula is just a typo?

We thank the reviewer for pointing out this typographical error, and we apologize for any resulting confusion. We have now corrected the equations with dot notation to correctly point out the derivatives. As mentioned in the Materials and methods section, we wished to apply the simplest model of induction and decay and therefore did not use a Hill function for σ.

5) Spatial Modelling: Current modelling approaches are much more powerful than what has been used in the paper (i.e. Zinski et al., 2017; Genikhovich et al., 2015). The authors should build on such work and analyse their quantitative data in the context of such more sophisticated models to understand how the different target genes are regulated. It does not help to rely on future modellers to pick up the published data as the modelling will identify missing data to arrive at a conclusion. I suspect for instance that spatial measurements of the response genes will be required at more than just a single state to understand the gradient read-out. For now, this data (Figure 1) seems not even to have been used in the analysis.

Our modeling approach with the data in Figure 5 was designed to answer a specific and important question: Can differences in gene activation kinetics explain different spatial expression ranges? This approach suggested that activation kinetics have little explanatory power for the expression ranges of BMP-dependent genes. We agree that further modeling could complete our understanding of feedback interactions in BMP gradient formation and interpretation, but these modeling efforts will require significant amounts of new data to arrive at meaningful conclusions, such as spatiotemporal measurements of gene expression and further information on the role of Nodal and FGF. We therefore anticipate carrying out these analyses in future studies when new data can be obtained to avoid underdetermined models.

The FGF/Nodal experiments will presumably only be properly interpretable when analysed in the context of the gradient-generating shuttling model from Zinski et al. as FGF appears to impact Chordin.

Although our own previous work as well as the paper by Zinski et al., 2017 shows that Chordin does not play a role as a shuttling molecule in the formation of the BMP protein gradient in early zebrafish embryos (Pomreinke et al., 2017; Zinski et al., 2017), Chordin clearly impacts the BMP signaling gradient as an inhibitor and sink of BMP activity (Rogers and Müller, 2019). We mention the known role of Chordin in regulating BMP and the known role of Nodal and FGF in regulating chordin expression (Figure 7K). While the specific mechanisms that mediate these interactions are known in part but still merit further investigation (see below), we have precisely quantified the effects of Nodal and FGF loss on the BMP signaling gradient at shield stage, and shown that the effects on target genes are not solely due to changes in BMP signaling (Figure 7L,M).

6) References: The authors do not comment on how the BMP gradient forms and how this depends on Chordin, even though this becomes highly relevant in the context of their FGF/Nodal experiments – and already explains why the ranges change when Chordin levels are altered, something they highlight as an open problem. They should discuss the relevant publications, i.e. Zinski et al., 2017. They should also discuss the literature on the BMP-dependent networks involved in DV patterning.

In the Introduction we provided only a brief explanation of BMP gradient formation, because in this work we are interested in target gene responses, not how the gradient forms. However, as mentioned above, we now expand this discussion of how the BMP gradient forms and the role of Chordin, and discuss in more detail our previous findings (Pomreinke et al., 2017) and those of Zinski et al., 2017. We also describe the multiple ways in which FGF and Nodal are known to affect BMP signaling in zebrafish and cite the relevant literature, including a description of how Nodal and FGF affect Chordin expression (Figure 7K, Figure 7—figure supplement 2ZA), (Rogers and Müller, 2019; Sapkota et al., 2007; Varga et al., 2007; Maegawa et al., 2006; Londin et al., 2005; Fürthauer et al., 2004; Kudoh et al., 2004; Koshida et al., 2002; Gritsman et al., 1999; Fürthauer et al., 1997).

We do not claim that it is an open problem why ranges change when Chordin levels are altered. Rather, in the original manuscript refers to two unexplained observations: First, that FGF loss but not Nodal loss causes an increase in BMP signaling, and second, that inhibition of both FGF and Nodal has different effects than inhibition of either alone. These observations are surprising because Nodal is thought to be required for FGF expression, meaning that the effect of losing both Nodal and FGF should be equivalent to losing Nodal alone. In addition, we note that Nodal mutants have reduced Chordin expression (Gritsman et al., 1999), further highlighting that future work is needed to explain why the BMP signaling gradient is not altered in shield-stage embryos lacking Nodal signaling, even though presumably they produce less Chordin protein. It does not appear to be the case that changes in Chordin alone can explain these results.

Moreover, they also do not mention the paper Xiong et al., 2013 in the Discussion, which shows that in zebrafish development cells can sort to create sharp domain boundaries.

Thank you for this suggestion. We now cite (Xiong et al., 2013) as well as (Akieda et al., 2019) and mention cell sorting-based boundary sharpening mechanisms as a method to refine responses to noisy signaling gradients, and as a possible explanation for how the embryo robustly compensates for excess BMP signaling.

Finally, they cite the neural tube as an example where a network affects the morphogen read-out, even though in the neural tube, the genes that are activated at lowest SHH levels are expressed first (PAX6 -> OLIG2 -> NKX2.2), which would actually be consistent with a threshold-based read-out.

As mentioned in my review, the authors should use boot-strapping to access the sensitivity of the estimated correlation to individual datapoints, and they should show the raw data for Figure 6.

The literature we cited demonstrates that combinatorial signaling from BMP, Wnt, and Shh signaling gradients together with cross-talk between target genes patterns the well-characterized neural tube (Briscoe and Small, 2015). Even though the gene expression progression described by the reviewer superficially appears to be consistent with the threshold model, Briscoe and Small stated that “[…] signaling gradients establish initial conditions that polarize the tissue, but there is no strict correspondence between specific morphogen thresholds and boundary positions” (Briscoe and Small, 2015) since “[…] the induction of Nkx2.2 and Olig2 does not appear to be determined simply by a fixed threshold of Gli activity” (Balaskas et al., 2012), and boundaries are rather set by a Shh-driven AC-DC circuit (Perez-Carrasco et al., 2018; Panovska-Griffiths et al., 2013). This highlights the importance of testing models using multiple approaches.

[Editors' note: further revisions were suggested prior to acceptance, as described below.]

The authors have made all requested technical corrections, but their added analysis confirms the worry that their main conclusion regarding the BMP-read-out is unsupported. Whilst we value the authors experimental approach, we worry that if the paper is published as is it will add to the confusion in the field, questioning basic principles of morphogen-related patterning without adequate experimental support. Accordingly, while no new data is required, we ask the authors to reword some of their conclusions, to further tone down their claims, by addressing the following comments.

Revisions:

1) The authors chose to analyse 9 BMP-dependent target genes. The selection is not unbiased as they say, but the result of technical limitations (as now explained much more clearly).

The 16 genes classified as “high-confidence” were defined as those that were both significantly upregulated in the BMP-overexpression condition and downregulated in the Chordin-overexpression condition in our RNA-sequencing experiment. Because FISH and NanoString probes failed in some cases, we were able to analyze the spatial expression of 10/16 genes and the temporal expression of 14/16. Although we do not think that these technical limitations resulted in a selection bias, we have removed the single instance in the Discussion where the 16 high-confidence target genes were referred to as “an unbiased set”.

Of these 9 target genes, two (cdx4 and eve1) are special in that they are expressed only in the margin (Figure 1). When included in the analysis, then expression range and activation time are effectively uncorrelated (Figure 2O). However, if cdx4 is removed from their analysis, the correlation increases to 65% (new analysis that was added), and if they removed also eve1, then the correlation can be expected to increase even further, thus supporting the notion that all analysed target genes, but the two margin-restricted cdx4 and eve1, are controlled in a threshold-based manner. That 2 BMP-dependent genes are constrained by further effects cannot be used to claim that the BMP read-out, in general, is not threshold-based – especially as the margin-restriction must indeed happen BMP-independently.

As noted above, the expression of 2/10 spatially assessed BMP target genes was margin-restricted (cdx4 and eve1). In addition, the expression of a further 4/10 genes was excluded from the margin (foxi1, klf2b, gata2a, and tfap2c). Importantly, when selecting which genes to spatially assess as representative BMP targets, we chose genes based only on 2 criteria: 1) significant up/downregulation in BMP/Chordin-overexpressing embryos, respectively, and 2) functional FISH probes. It is therefore striking that, when selected without regard for spatial expression profiles, the majority of the high-confidence BMP target genes exhibit special expression profiles (6/10). We argue that the most dramatic differences in spatial expression probably arise from these characteristic profiles likely resulting from combinatorial signaling. However, as described in the Discussion section, if all of the special genes are excluded from the analysis in Figure 2O (6/9, the majority), the remaining 3 do show a negative correlation between range and activation time. We note that this subset of genes (or others) could behave consistently with the gradient threshold model, although given that only 3 genes qualified it is difficult to state this conclusively.

To clarify the expectations of the gradient threshold model, we have carried out an additional analysis taking our measured spatiotemporal BMP signaling profiles into account. Author response image 2 shows the spatial expression ranges and calculated activation times for hypothetical BMP target genes with different activation thresholds, based on the pSmad1/5/9 data shown in Figure 1E. We postulated 180 BMP target genes with different linearly spaced expression ranges along the dorsal-ventral axis, and linked each range with the corresponding pSmad1/5/9 level at 7.25 hpf. We then queried the pSmad1/5/9 time course data and determined the time at which each pSmad level first occurred (Author response image 2). We defined these time points as the activation times of the postulated BMP target genes. As expected, genes activated by low levels of signaling (“low-threshold genes”) should be expressed early and at a long range, whereas genes requiring higher levels of signaling (“high-threshold genes”) should be expressed later and at a short range (Author response image 2). Additionally, this analysis shows the expected monotonically decreasing relationship between expression range and activation time. However, it is also evident that the relationship between range and activation time isn’t necessarily linear, depending on where the relevant threshold range lies. We have therefore removed the linear fit from Figure 2O.

Author response image 2

Download asset Open asset

The activation timing and expression ranges for hypothetical genes with different activation thresholds were calculated based on quantified pSmad1/5/9/ activation kinetics (Figure 1E).

In addition, as suggested, we have now also updated the Results section to describe what happens when only the margin-restricted genes are excluded from the analysis in Figure 2O: “The gradient threshold model predicts a monotonic decrease when comparing range and activation time. While this relationship is not observed for the entire dataset (Figure 2O), there is a decreasing monotonic trend when foxi1, eve1, and cdx4 are excluded (note that in contrast to the other genes, the expression of eve1 and cdx4 was only quantified in the embryonic margin (Figure 1—figure supplement 1E, Materials and methods)). This suggests the possibility that subsets of BMP target genes may behave consistently with the gradient threshold model. We therefore sought to investigate the relationship between BMP signaling and target gene expression further using an optogenetic strategy.”

As stated in the Discussion, we agree that “[…] it remains to be determined to what extent this subset of genes (or others) quantitatively follows the input-output relationships predicted by the gradient threshold model.”. To make this caveat clearer throughout the manuscript, we have further altered the indicated text:

Abstract: “Transcriptional responses to optogenetically delivered high- and low-amplitude BMP signaling pulses indicate that spatiotemporal expression is not fully defined by different BMP signaling activation thresholds. Additionally, we observed negligible correlations between spatiotemporal expression and transcription kinetics for the majority of analyzed genes in response to BMP signaling pulses. […] Our results suggest that, similar to other patterning systems, combinatorial signaling is likely to be a major driver of spatial diversity in BMP-dependent gene expression in zebrafish.”

Introduction: “Further, target gene responses to high- and low-amplitude signaling pulses suggest that not all spatiotemporal target gene expression differences are due to different signaling activation thresholds (Figure 6).”

Results: “As expected, target activation was generally stronger following higher amplitude, longer duration pulses (Figure 6C-F and Figure 6—figure supplement 1). However, after a 10 min low-amplitude exposure, the third most narrowly expressed gene, foxi1, was significantly activated, whereas the broader genes were not robustly induced (Figure 6C). A longer 20 min low-amplitude pulse significantly activated both narrowly and broadly expressed genes (Figure 6E). A 10 min low-amplitude pulse significantly activated two of the top 50% earliest expressed genes (foxi1 and smad7), whereas a 20 min low-amplitude pulse significantly activated both early and late-expressed genes (Figure 6D,F). High-amplitude pulses activated genes of all ranges and activation times (Figure 6C-F).

Our experiments exposing embryos to different amplitude BMP signaling pulses suggest that not all spatiotemporal target gene expression differences are due to different signaling activation thresholds, although a subset may be (see Discussion).”

Discussion: “In the context of zebrafish dorsal-ventral patterning, our data suggest minor roles for gene-specific activation thresholds in generating BMP target gene expression diversity. We did not find a clear monotonically decreasing relationship between activation time and gene expression range (Figure 2O), suggesting that more broadly expressed genes are not consistently more likely to be activated by the low levels of BMP present early (Figure 1D-E). We were also unable to detect an unambiguous correlation between range and the levels of signaling required for activation (Figure 6C,E). This suggests that not all BMP target expression boundaries are positioned by gene-specific BMP signaling thresholds (Figure 1A).”

Discussion: “Our results do not rule out the possibility that a different subset of BMP target genes may behave more consistently with these models. We focused on a set of high-confidence BMP targets (Figure 1—figure supplement 1), but other known targets were excluded from our analyses (Supplementary file 1). For example, the BMP target gene tp63 (Bakkers et al., 2002) is not expressed at shield stage, and was therefore excluded since it was not downregulated by chordin overexpression in our RNA-sequencing experiment (Supplementary file 1). We note that a subset of three genes (sizzled, ved, and bambia) that are neither restricted to nor excluded from the margin do show a monotonically decreasing relationship between range and activation time (Figure 2O) as well as activation dynamics that could be roughly commensurate with signaling input (Figure 6C and Figure 6—figure supplement 1), consistent with the gradient threshold model. However, it remains to be determined to what extent this subset of genes (or others) quantitatively follows the input-output relationships predicted by the gradient threshold model.”

Discussion: “Our results suggest that much of the spatial diversity in BMP target gene expression arises from combinatorial signaling.”

Also, the additional data that is now provided for Figure 6, which is most helpful, shows that the time points that were sampled are too late to reliably compare activation kinetics. Some of the genes also show transient dynamics that further confound the analysis when time points are sampled only late, especially as the variance is high and few time points could be analysed.

We agree that in Figure 6 activation kinetics cannot be reliably established. As such, we do not base any conclusions on activation kinetics derived from the data shown in Figure 6. The experiment in Figure 6 was only designed to determine which genes are robustly induced by different levels of signaling. Technical limitations prevented us from collecting the large numbers of samples that would have been necessary to assess induction kinetics in these different scenarios. We therefore chose to focus on time points near the maximum induction level found in other experiments (Figure 4), in which more time points were assessed (and kinetics could be established).

2) Citing Briscoe and Small, 2015, the authors use the neural tube as further support that morphogen gradients are not read out threshold-based. However, the progenitor boundaries have so far not been related to the measured SHH gradient (which was published only in 2015) – only to GBS-GFP, which is a floorplate promotor that responds only to the highest SHH concentration. The fact that the responsiveness of this promotor is limited does not mean that the progenitor boundaries are not read out threshold-based.

We have now cut the following sentence from the Discussion that may have been misleading: “In vertebrates, Wnt, Shh, and BMP pattern the neural tube using a similar combinatorial mechanism together with target gene cross-regulation (Briscoe and Small, 2015).” The remainder of the references to Briscoe and Small 2015 use it either to demonstrate the ubiquity of signaling gradients in development or to emphasize the importance of combinatorial interactions in patterning.

References

Balaskas, N., Ribeiro, A., Panovska, J., Dessaud, E., Sasai, N., Page, K.M., Briscoe, J., and Ribes, V. (2012). Gene regulatory logic for reading the Sonic Hedgehog signaling gradient in the vertebrate neural tube. Cell 148, 273-84.

Panovska-Griffiths, J., Page, K.M., and Briscoe, J. (2013). A gene regulatory motif that generates oscillatory or multiway switch outputs. J R Soc Interface 10, 20120826.

Perez-Carrasco, R., Barnes, C.P., Schaerli, Y., Isalan, M., Briscoe, J., and Page, K.M. (2018). Combining a toggle switch and a repressilator within the AC-DC circuit generates distinct dynamical behaviors. Cell Syst 6, 521-530 e3.

Seyednasrollah, F., Laiho, A., and Elo, L.L. (2015). Comparison of software packages for detecting differential expression in RNA-seq studies. Brief Bioinform 16, 59-70.

https://doi.org/10.7554/eLife.58641.sa2

Article and author information

Author details

Katherine W Rogers

Systems Biology of Development Group, Friedrich Miescher Laboratory of the Max Planck Society, Tübingen, Germany

Contribution
Conceptualization, Resources, Data curation, Formal analysis, Validation, Investigation, Visualization, Methodology, Writing - original draft, Project administration, Writing - review and editing

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0001-5700-2662
Mohammad ElGamacy
1. Systems Biology of Development Group, Friedrich Miescher Laboratory of the Max Planck Society, Tübingen, Germany
2. Modeling Tumorigenesis Group, Translational Oncology Division, Eberhard Karls University Tübingen, Tübingen, Germany
3. Heliopolis Biotechnology Ltd, London, United Kingdom
Contribution
Resources, Software, Visualization, Methodology, Writing - review and editing

Contributed equally with
Benjamin M Jordan

Competing interests
is an employee of Heliopolis Biotechnology Ltd.
Benjamin M Jordan

Department of Organismic and Evolutionary Biology, Harvard University, Cambridge, United States

Contribution
Resources, Software, Formal analysis, Methodology, Writing - review and editing

Contributed equally with
Mohammad ElGamacy

Competing interests
No competing interests declared
Patrick Müller
1. Systems Biology of Development Group, Friedrich Miescher Laboratory of the Max Planck Society, Tübingen, Germany
2. Modeling Tumorigenesis Group, Translational Oncology Division, Eberhard Karls University Tübingen, Tübingen, Germany
Contribution
Conceptualization, Resources, Data curation, Software, Formal analysis, Supervision, Funding acquisition, Validation, Visualization, Methodology, Project administration, Writing - review and editing

For correspondence
pmueller@tuebingen.mpg.de

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0002-0702-6209

Funding

Max Planck Society

Patrick Müller

Human Frontier Science Program (CDA-00031/2013-C)

Patrick Müller

European Research Council (637840 (QUANTPATTERN))

Patrick Müller

European Research Council (863952 (ACE-OF-SPACE))

Patrick Müller

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We are grateful to Keisuke Sako, Harald Janovjak, and Carl-Philipp Heisenberg for kindly sharing Opto-Acvr constructs before publication and for advice on optogenetic experiments. We thank Luis Antoniotti for help constructing the LED array, Jörg Abendroth for providing the photograph of the LED array in Figure 3—figure supplement 1B, Jennifer Bergmann for the sizzled in situ hybridization probe, and Daniel Čapek, Amit Landge, David Mörsdorf, Autumn Pomreinke, and Hannes Preiß for helpful discussions. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 637840 (QUANTPATTERN) and grant agreement No 863952 (ACE-OF-SPACE)). This work was also funded by the Max Planck Society and an HFSP Career Development Award (CDA-00031/2013 C).

Senior Editor

Naama Barkai, Weizmann Institute of Science, Israel

Reviewing Editor

Markus Affolter, Biozentrum der Universität Basel, Switzerland

Publication history

Received: May 6, 2020
Accepted: November 10, 2020
Accepted Manuscript published: November 11, 2020 (version 1)
Version of Record published: December 10, 2020 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.