Fitness variation across subtle environmental perturbations reveals local modularity and global pleiotropy of adaptation
- Department of Biology, Stanford University, United States
- Center for Mechanisms of Evolution, School of Life Sciences, Arizona State University, United States
Figures
Figure 1
Adaptive mutations can be locally modular and globally pleiotropic.
(A) In the ‘strict modularity’ model, a collection of adaptive mutations may affect a small number of phenotypes (four black squares). If these adaptive mutations only affect these phenotypes then fitness in both the environment they evolved in (local environment) and other environments (distant environment) is determined solely by these phenotypes. (B) Alternatively, in the ‘fitness-relevant modularity’ model, these mutations may collectively (and individually) affect many phenotypes, but only a small number of phenotypes may matter to fitness in the local environment (those indicated by black squares with thick arrows pointing to fitness), whereas other phenotypes may make very small contributions to fitness (those indicated by the gray squares and thin, dashed lines leading to fitness). Under this model, the contribution of each phenotype to fitness can change depending on the environment. Thus, fitness differences between mutants that behave similarly in the local environment can be revealed by measuring fitness in more distant environments. Such fitness differences reveal the presence of phenotypic differences between mutants.
Figure 2 with 2 supplements
Measuring fitness for a collection of adaptive mutants across many environments reveals gene-by-environment interactions.
(A) Schematic of fitness measurement procedure. Adaptive mutants tagged with DNA barcodes are pooled at a 1:9 ratio with an ancestral reference strain. The pool is then propagated for several growth cycles, where the population is diluted into fresh media at fixed time intervals. DNA is extracted from each time-point, and the barcode region is PCR amplified and then sequenced. A mutant’s relative fitness is calculated based on the rate of change of its barcode’s frequency, corrected for the mean fitness of the population (see Materials and methods). Relative fitness is calculated in units of ‘per cycle’, representing the improvement of each barcode relative to the reference over the course of the time between transfers. (B) Fitness advantage of each mutant in the evolution condition relative to the ancestor. This fitness advantage is measured per transfer cycle and calculated as the average across all nine Evolution Condition (EC) batches. (C) (top) Environments are ordered from left to right depending on the degree to which they perturb mutant fitness from the average fitness observed across all EC batches. Environments in which average mutant fitness is within two standard deviations of average mutant fitness across EC batches are denoted in black and make up the subtle perturbation set. Environments in which aggregate mutant behavior exceeds two standard deviations are shown in red and make up the strong perturbations set. (bottom) This plot displays, for the four most common types of adaptive mutation observed in response to glucose limitation (Venkataram et al., 2016a), the average fitness in each of the 45 environments we study. Brackets on the right represent the amount of variation in fitness observed for each type of mutation across the EC batches, with the notch representing the mean and the arms representing two standard deviations on either side of the mean. For visualization purposes, we represent relative fitness values below −1.25 as arrows. Specifically, PDE2 mutants (orange arrows) have on average fitness −3.3 and −3.4 in 0.5 M KCl and 0.5 M NaCl, respectively. IRA1 nonsense mutants (blue arrows) have an average fitness −3.0 and −4.2 in 0.5 M KCl and 0.5 M NaCl, respectively.
-
Figure 2—source data 1
Fitness measurement data.
This table shows the fitness measurement data of each barcoded mutant in all the 45 environments. This includes the final fitness estimate for each environment (a weighted average of the replicates) as well as the fitness estimate in each replicate (e.g. denoted by ‘-R1’ to indicate replicate 1). The error for each fitness estimate is also included, in units of standard deviations. Mutants are classified by their putative causal mutation (see ‘Classifying mutations by mutation type’ in methods). Any additional mutations identified in Venkataram et al., 2016a are also listed.
- https://cdn.elifesciences.org/articles/61271/elife-61271-fig2-data1-v2.csv
Figure 2—figure supplement 1
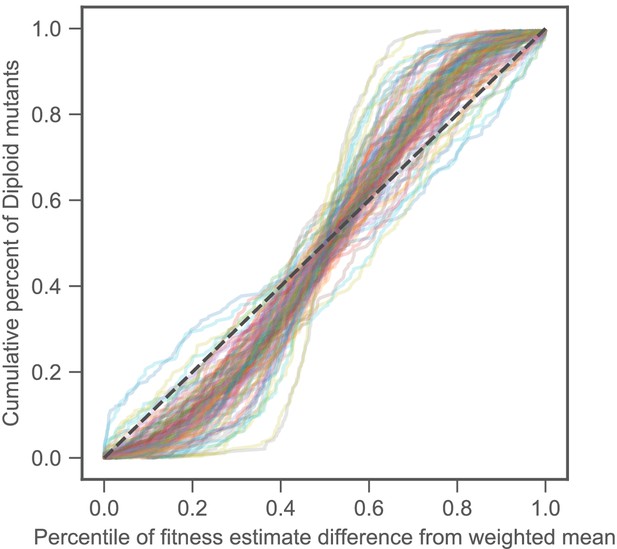
Noise model is a conservative measure of uncertainty.
Fitness differences among strains that are genetically identical and have very similar fitness effects tell us about the amount of measurement noise. Our strain collection includes 188 diploids that have similar fitnesses and possess no mutations other than diploidy. For each diploid fitness estimate, we calculated the percentile of deviation from the weighted average of all diploid fitness estimates in a particular environment. This is shown on the horizontal axis. The vertical axis shows the cumulative percent of diploids with deviations listed on the horizontal axis. If the noise model perfectly captures the uncertainty of each measurement, then it should be represented by the black dashed line, as, for instance, 20% of the diploids should have a difference from the mean in the 20th percentile. Each line represents a single experiment (we have 45 environments each with several replicates for a total of 109 experiments, see Materials and methods). For the vast majority of experiments, the diploids are closer to the mean than predicted by our noise model, as indicated by each line’s sigmoidal shape. This indicates that the noise model is conservative.
Figure 2—figure supplement 2
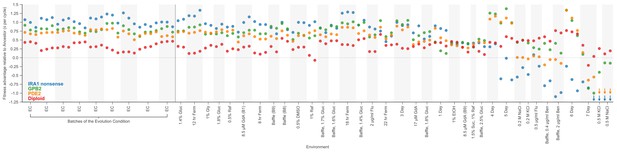
Replicates show consistent estimates of fitness.
This plot is similar to Figure 2C except that it displays all replicate experiments separately. The four most common types of adaptive mutations observed in response to glucose limitation are indicated by color. The vertical axis displays the average fitness advantage of each mutation type relative to the ancestor. Replicates of the same environment are grouped by shading. For visualization purposes, we represent relative fitness values below −1.25 as arrows.
Figure 3 with 4 supplements
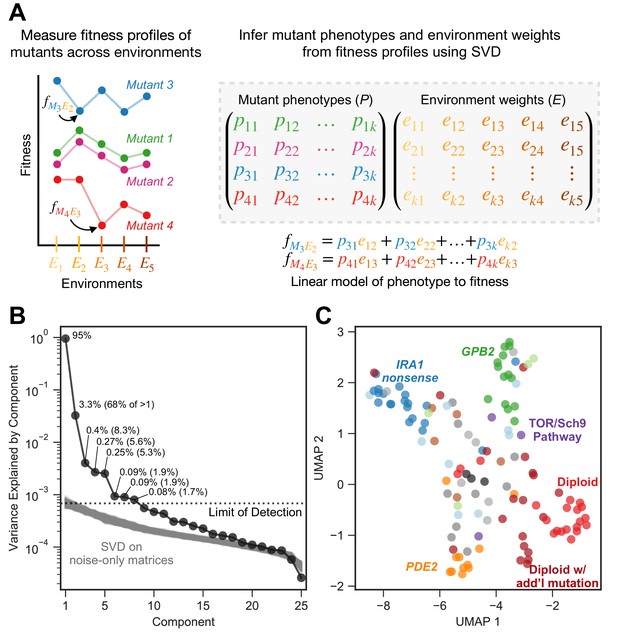
Subtle environmental perturbations reveal an eight-component phenotypic model that reflects known biological features.
(A) To infer fitness-relevant phenotypes, we measure the fitness of mutants in a collection of environments and compare their fitness profiles. Mutants with similar fitness profiles (mutants 1 and 2) are inferred to have similar effects on phenotypes. Mutants with dissimilar fitness profiles (mutants 3 and 4) are inferred to have dissimilar phenotypic effects. We use SVD to decompose these fitness profiles into a model consisting of two abstract spaces: one that represents the fitness-relevant phenotypes affected by mutants (P) and another which represents the degree to which each phenotype impacts fitness in each environment (E). Here, we represent the model with k fitness-relevant phenotypes. The model’s estimate for fitness for a particular mutant in a particular environment is a linear combination of each mutant phenotype (mutant one is represented by the vector ()) scaled by the degree to which that phenotype affects fitness in the relevant environment (environment one is represented by the vector ). We show two examples of the equation used to estimate fitness for the mutants and environments highlighted in the left panel. Note that, for presentation purposes, we show SVD as inferring two matrices. It in fact infers three, but is consistent with our presentation if you fold the third matrix, which represents the singular values, into E (see Materials and methods). (B) Decomposing the fitness profiles of 292 adaptive mutants across 25 subtle environmental perturbations reveals eight fitness-relevant phenotypic components. The variance explained by each component is indicated as a percentage of the total variance. The percentages in parentheses indicate the relative amount of variation explained by each component when excluding the first component. Each of these components explain more variation in fitness than do components that capture variation across a simulated dataset in which fitness varies due to measurement noise. These simulations were repeated 1000 times (gray lines) and used to define the limit of detection (dotted line). (C) An abstract space containing eight fitness-relevant phenotypic components reflects known biological features. This plot shows the relationships of the mutants in a seven-dimensional phenotypic space that excludes the first component, visualized using Uniform Manifold Approximation and Projection (UMAP). Mutants that are close together have similar fitness profiles and are inferred to have similar effects on fitness-relevant phenotypes. Mutants with mutations in the same gene tend to be closer together than random, in particular IRA1 nonsense mutants in dark blue, GPB2 mutants in dark green, PDE2 mutants in dark orange, and diploid mutants in red. Six diploid mutants that had higher than average diploid EC fitness (and thus are likely to harbor additional mutation(s) so are categorized as ‘diploid with additional mutation’) also form a cluster. Colors are as in Figure 2B; IRA1 missense mutants shown in light blue, IRA2 in dark gray, GPB1 in light green, other Ras/PKA pathway mutants in brown, TOR/Sch9 pathway mutants in purple, other adaptive mutants in light gray, and known neutral lineages in black.
Figure 3—figure supplement 1
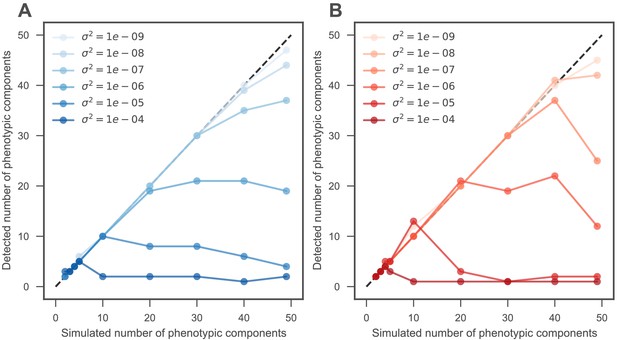
Accurate predictions of the number of phenotypic components in simulated data.
(A) The horizontal axis represents the number of phenotypic components in simulated data consisting of 100 mutants and 50 environments. The vertical axis indicates the number of components we detected when we only count components that explain more variation than does our noise model (see Materials and methods). For low levels of measurement noise (light blue), our method accurately detects the number of simulated components. As measurement noise increases (darker blue dots), the noise begins to swamp signal and the number of detected components decreases. (B) Same as (A), but here we set the threshold for detecting components using bi-cross validation rather than our noise model. Bi-cross validation is performed by holding out each environment and half of the mutants. Darker color indicates more measurement noise.
Figure 3—figure supplement 2
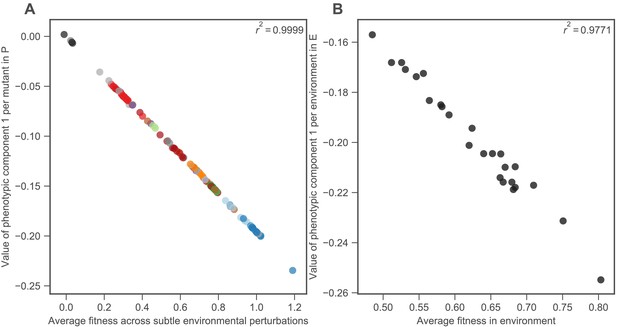
The first component represents the mean fitness of each mutant in the 25 subtle perturbations, as well as the mean impact of each perturbation on fitness.
(A) The horizontal axis shows the average fitness of each mutant across all 25 environments that represent subtle perturbations. The vertical axis shows the value of the first phenotypic component for each mutant. Mutants are colored as in Figure 2B. (B) The horizontal axis shows the average fitness of all 292 mutants in each environment, thus there are 45 points, one per environment. The vertical axis shows the value of the first phenotypic component in the environment weight space E.
Figure 3—figure supplement 3
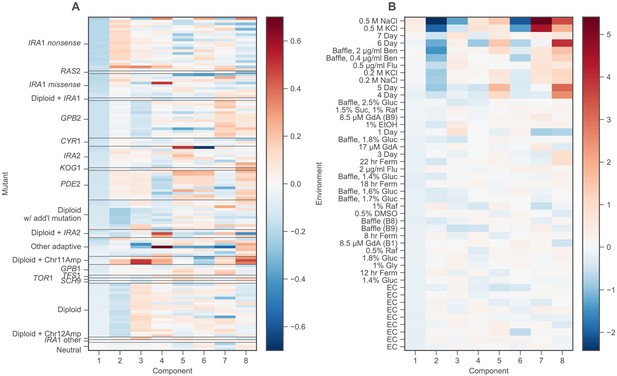
Locations of mutants and environments in phenotype space.
(A) The loadings of each mutant on each component, grouped by mutation type. Mutations types are ordered from bottom to top by their average fitness across nine EC batches. (B) The loadings of each environment on each component. Environments ordered from bottom to top as in Figure 2C.
Figure 3—figure supplement 4
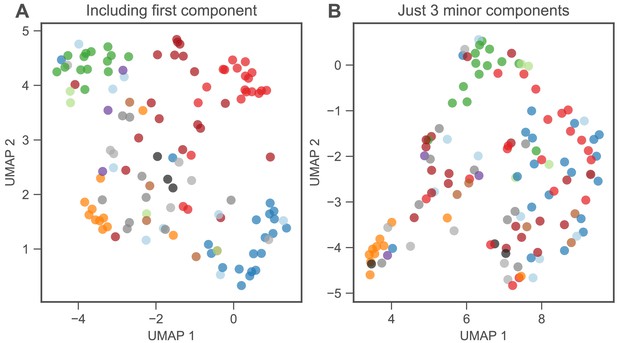
Low-dimensional phenotypic models, and subsets of such models, cluster mutants by gene and mutation type.
(A) UMAP clusters mutants visually by gene when using the full eight-component phenotype space. (B) UMAP also shows some clustering when using only the three components that explain the least variation in mutant fitness in the EC. Although the clustering is clear for PDE2 and GPB2, it less clearly delineates IRA1 nonsense and diploid mutants. This suggests these mutants do not have substantial effects on these three phenotypic components in the EC.
Figure 4 with 4 supplements
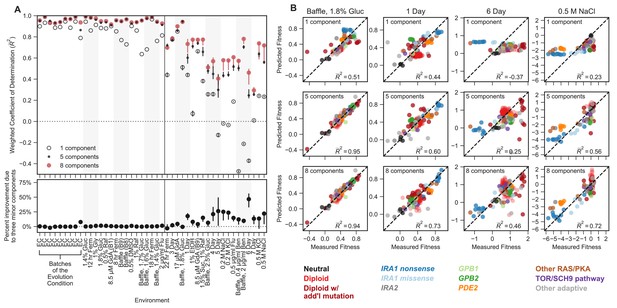
Mutant fitness variation across subtly different environments predicts mutant fitness in novel and substantially different environments.
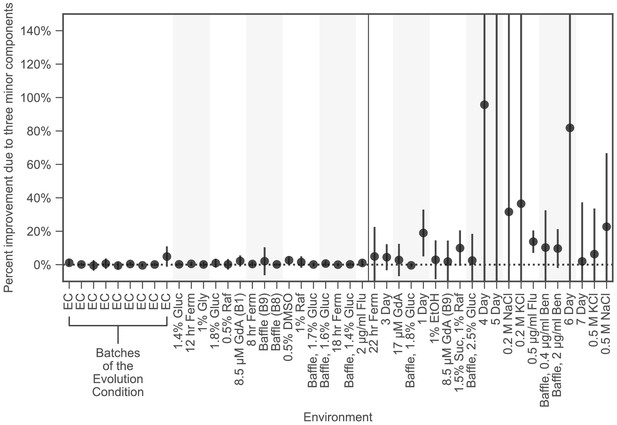
(A) Top panel vertical axis shows the accuracy of fitness predictions in each of 45 environments on the horizontal axis. The accuracy is calculated as the coefficient of determination, weighted such that each mutation type contributes equally. The left side of this plot represents predictions of mutant fitness in subtle environmental perturbations. These predictions are generated by holding out data from that environment when building the phenotypic model. The right side of the plot displays predictions of mutant fitness in strong environmental perturbations. These predictions are generated using a phenotypic model inferred from fitness variation across all 25 subtle different environments (denoted by each of the points or open circles) and for each of the 25 leave-one-out models (range of predictions is depicted with the error bars surrounding each point or open circle). Predictions from the eight-component model (red point) are typically better than the one-component model (open circle) and sometimes better than the five-component model (black point). Bottom panel vertical axis shows the percent of the eight-component model’s improvement due to the three minor components (calculated by the percent difference between the five- and eight-component models). The left side shows the improvement of the prediction in subtle environmental perturbations when that subtle perturbation was held out. The right side shows the improvement of the prediction in strong environmental perturbations when using the full model (dots) or the 25 leave-one-out models (the error bars represent the range of improvement). (B) For each subplot, the horizontal axis shows the measured fitness value. The vertical axis shows the predicted fitness value when predictions are made using the one-component (top row), five-component (middle row), or eight-component (bottom row) models. Columns represent different environments. Points are colored by the mutation type. Note that less than zero indicates that the prediction is worse than predictions using the mean fitness in that condition (see Materials and methods).
Figure 4—figure supplement 1
Number of detected components and predictive power increase with the number of training environments.
(A) The vertical axis shows the number of detected phenotypic components in various subsamples of the 25 environments that comprise our training set. The number of environments included in each subsample is shown on the horizontal axis. To select these environments, we randomly subsample from the full set of 25 training environments 25 times. Points are colored in accordance with the number of components detected from that subsample. The black dot represents the median number of components detected for each number of environments used. (B) The vertical axis shows the proportion of weighted variance explained for the fitness of the test mutants in the strong perturbation environments. The horizontal axis shows the number of subtle environments used to build the phenotypic model. For each number of environments used, the blue dots on the left show the proportion of weighted variance explained by a four-component model (solid blue dot with error bars shows mean and standard deviation). There are 25 blue dots because we subsampled the subtle environments 25 times. The multicolored dots on the right show the proportion of weighted variation explained by the full model picked for that subsample (solid red dot with error bars shows mean and standard deviation). The colors represent the number of components detected in the full model for each subsample and match the colors in panel (A).
Figure 4—figure supplement 2
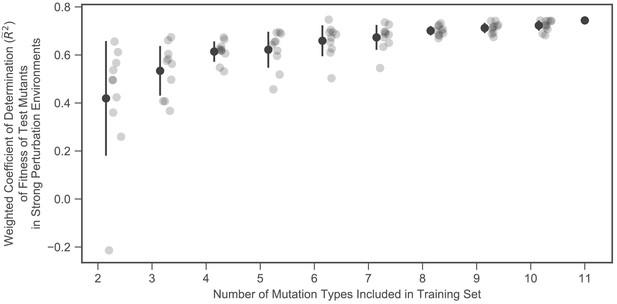
Predictive power increases with the number of mutation types included.
The vertical axis shows the proportion of weighted variance explained for the fitness of the test mutants in the strong perturbation environments. The horizontal axis shows the number of mutation types included in the training set. Ten sets of each size were chosen. The solid black dot with error bars shows the mean and standard deviation across the 10 sets of each size.
Figure 4—figure supplement 3
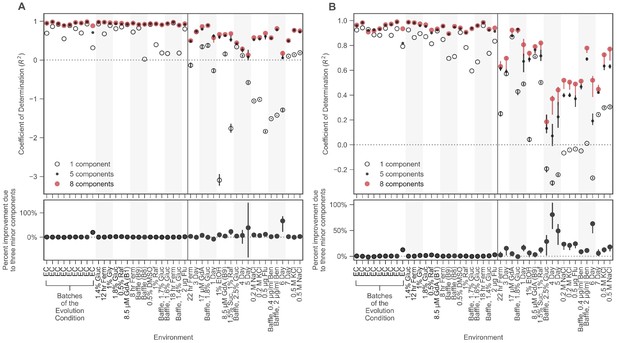
Improved fitness predictions when including the three smallest phenotypic components is not specific to choice of training mutants.
This plot is similar to the lower panel of Figure 4A, except here, black dots indicate the average improvement across 100 choices of the training and test sets, each with the same mutant type composition as the training and test set used in the main text. Error bars indicate two standard deviations from the mean.
Figure 4—figure supplement 4
Prediction ability using unweighted coefficient of determination.
These plots are similar to Figure 4A except here the vertical axis displays prediction power using a standard, rather than a weighted, coefficient of determination measure. Because diploids dominate the number of mutants in the collection, there are large differences between panel A (which shows all mutants) and panel B (which omits diploids).
Figure 5
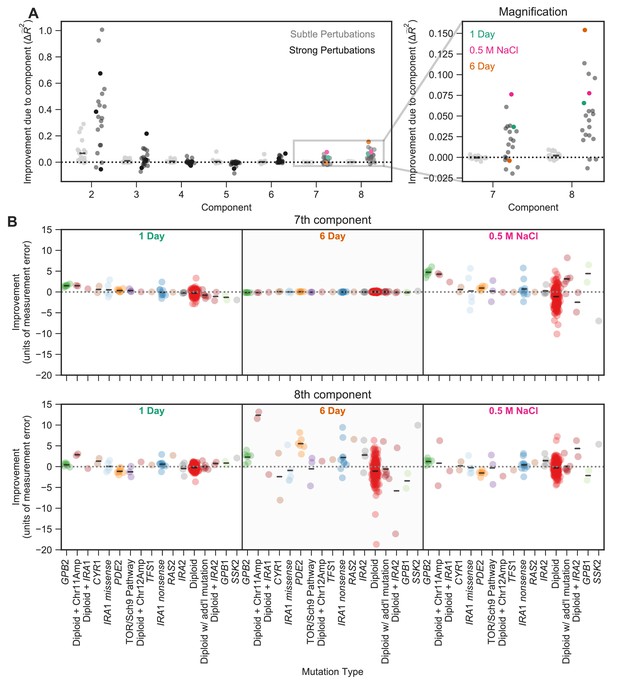
The contribution of a phenotypic component to fitness changes across environments and differs for different types of mutants.
(A) Some phenotypic components improve fitness predictions in some environments substantially more than they do in others. The vertical axis shows the improvement in the predictive power of our eight-component phenotypic model due to the inclusion of each component. For example, the improvement due to component seven is calculated by the difference between the seven-component model and the six-component model. The improvement of predictive power for each of the subtle environmental perturbations is shown as a gray point and for each of the strong perturbations in black. Magnification shows improvement upon including each of the two smallest components, with three strong perturbations highlighted. (B) Some phenotypic components improve fitness predictions for some mutants substantially more than they do for others. For example, the 7th component explains little variation in the 6-Day environment, but the 8th component explains a lot of variation in fitness in the 6-Day environment and is particularly helpful in predicting the fitness of Diploid + Chromosome 11 Amplification mutations in this environment. Vertical axis shows the improvement in predictive power (in units of standard deviation of measurement error) for each type of mutant (denoted on the horizontal axis) in one of three environments (1 Day, 6 Day, and 0.5 M NaCl) when adding either the 7th (top panel) or the 8th (bottom panel) component. Mutants are ordered by the improvement due to the 7th component in the 1-Day environment. Since some types of mutants are more common, for example diploids, there are more data points in that category.
Tables
Key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Commercial assay or kit | OneTaq Hot Start 2X Master Mix with Standard Buffer | New England Biolabs | Cat#M0484L | |
| Commercial assay or kit | Q5 DNA Polymerase | New England Biolabs | Cat#M0491L | |
| Commercial assay or kit | ApaLI restriction enzyme | New England Biolabs | Cat#R0507L | |
| Commercial assay or kit | MasterPure Yeast DNA Purification Kit | Lucigen | Cat#MPY80200 | |
| Strain, strain background (Saccharomyces cerevisiae) | S. cerevisiae constructed reference strain | Venkataram et al., 2016a | GSY 6704 | |
| Commercial assay or kit | Nextera XT Index Kit v2 | Illumina | Cat#FC-131–2004 | |
| Sequence-based reagent | Primers F201-F212 and R301-R308 | This paper | Step 1 PCR primers | See Materials and methods section ‘PCR Amplification of the Barcode Locus’ |
| Software, algorithm | Pipeline to determine the number of barcode reads | Venkataram et al., 2016a | ||
| Software, algorithm | Pipeline to calculate fitness from barcode counts | Venkataram et al., 2016a |
Additional files
-
Supplementary file 1
List of all mutants included in this study.
- https://cdn.elifesciences.org/articles/61271/elife-61271-supp1-v2.xlsx
-
Supplementary file 2
List of all conditions used in this study, ordered by deviation from the EC batch as in the main text figures.
- https://cdn.elifesciences.org/articles/61271/elife-61271-supp2-v2.xlsx
-
Transparent reporting form
- https://cdn.elifesciences.org/articles/61271/elife-61271-transrepform-v2.docx
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Fitness variation across subtle environmental perturbations reveals local modularity and global pleiotropy of adaptation
eLife 9:e61271.
https://doi.org/10.7554/eLife.61271
