Optimal evolutionary decision-making to store immune memory
Figures
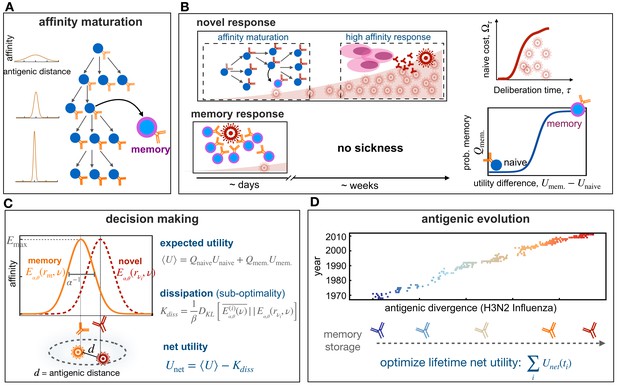
Immune memory or naive response upon infection.
(A) Schematic shows affinity maturation in germinal centers(right), where B-cell receptors acquire mutations and undergo selection, resulting in an increase in their affinity to an antigen (from light to dark receptors), indicated by the sharpening of receptors’ affinity profiles (on left). (B) Upon infection, the immune system can initiate a novel response (top) or a memory response (bottom). A novel B-cell response could involve affinity maturation to generate memory or high-affinity plasma cells (pink) that can secrete antibodies to battle the pathogen. A novel response can take 1–2 weeks, during which pathogen can replicate within a host and a patient can show symptoms from the disease (top, left). During this time, the proliferation of pathogens within a host incurs a cost associated with a naive response , which is a monotonic function of the deliberation time τ (top, right). If the host carries memory from a previous infection or vaccination (bottom), the immune system can robustly and rapidly activate a memory response to battle the infection. The probability to mount such memory response depends non-linearly on the relative utilities of memory versus naïve responses against a given infection (bottom, right). (C) Affinity profile of a memory receptor rm is shown in orange as a function of the distance in the antigenic shape space, between the receptor’s cognate antigen (orange) and an evolved novel target (red). The affinity of a receptor decays with increasing distance between targets and its cognate antigen. The antigenic range over which a receptor is reactive inversely depends on its specificity α. The shape of the binding profile is tuned by the factor θ, here shown for . The expected binding profile and the expected utility for an immune response are weighted averages of these quantities over memory and naïve responses. The Kullback-Leibler distance between the expected profile and the profile centered around the infecting antigen , in units of the deliberation factor β, defines the sub-optimality of a response, that is,, dissipation (Equation 1). The net utility measures the goodness of a decision to mount a memory vs. naive response against an infection (Equation 2). (D) Antigenic evolution of the H3N2 influenza virus is shown over 40 years along its first (most variable) antigenic dimension (data from Bedford et al., 2014). The decision of an immune system to utilize memory or to mount a novel response (B,C) is determined by the specificity α of receptors and the deliberation factor β. We characterize the optimal immune strategies () by maximizing the total net utility of immune responses against pathogens with different antigenic divergences, experienced over the lifetime of an organisms (Equation 3).

Optimal memory strategies against evolving pathogens.
(A) and (B) show the optimal specificity and deliberation factor , scaled by their respective upper bounds, as a function of the antigenic divergence per infection, scaled by the cross-reactive range (or inverse of maximum specificity) . Colors/markers indicate different naïve cost functions for deliberation, including no-cost , linear cost , and quadratic cost , with varying amplitudes . (C) The heat map shows the expected rescaled net utility (Equation 2) per round of infection for an immune system with an optimal specificity , as a function of rescaled antigenic divergence and deliberation factor . Rescaling by sets the magnitude of net utility to one, for a response to conserved antigens (with ) and in the limit of zero deliberation cost . Boundaries indicate different levels of dissipation, with orange and blue encompassing regions of and of the maximum dissipation , respectively. The three modes of immune response are indicate based on the magnitude of dissipation and net utility in each reagion: (i) equilibrium memory, (ii) non-equilibrium memory, and (iii) equilibrium naive. Simulation parameters, (A–C): , , and , (C): linear deliberation cost function with . Results for other shape parameters θ and specificity thresholds are shown in Figure 2—figure supplement 2, Figure 2—figure supplement 3, respectively.
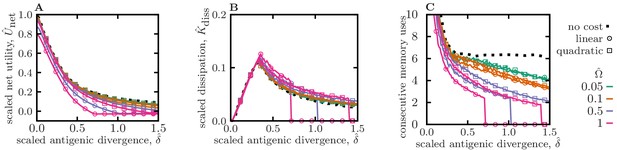
Utility, dissipation, and usage of optimal memory.
Utility, dissipation, and usage of optimal memory. (A) and (B) show the scaled net utility (Equation 2) and dissipation (Equation 1) per round of infection as a function of the antigenic divergence . Rescaling by sets the magnitude of net utility for a response to conserved antigens (with ), and in the limit of zero deliberation cost , to 1; see Figure 2 in the main text for comparison. (C) The expected number of rounds that a memory receptor is utilized prior to a novel response in an optimal system is shown to decay as the antigenic divergence increases. The results are evaluated for immune systems with optimized strategies (, ) against pathogens with a given scaled antigenic divergence ; the corresponding strategies are shown in Figure 2. Colors/markers indicate different naïve cost functions for deliberation, including no-cost , linear cost , and quadratic cost , with varying amplitudes . Simulation parameters: , , and .
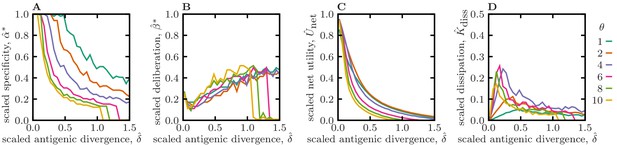
Optimal memory strategies for different specificity shape factors θ.
Optimal memory strategies for different specificity shape factors θ. (A) Scaled specificity , (B) scaled deliberation factor , (C) scaled net utility , and (D) scaled dissipation are shown as a function of the scaled antigenic divergence per infection (similar to Figure 2). Colors indicate different shape factors θ of the specificity function, ranging from a double-sided exponential (), to Gaussian for (as in Figure 2), and top-hat functions . The dependence of memory strategies on antigenic divergence is qualitatively insensitive to the shape factor of the specificity function. Simulation parameters: linear deliberation cost function with , , and .

Optimal memory strategies for different specificity thresholds .
Optimal memory strategies for different specificity thresholds . (A) Scaled specificity , (B) scaled deliberation factor , (C) scaled net utility , and (D) scaled dissipation are shown as a function of the scaled antigenic divergence per infection (similar to Figure 2). Colors indicate different specificity thresholds . Memory strategies are qualitatively insensitive to the specificity threshold. Simulation parameters: linear deliberation cost function with and .
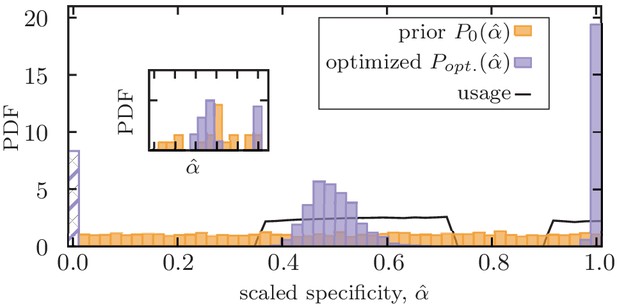
Mixed memory strategy against a mixture of pathogens with a broad range of evolutionary rates.
Distribution of scaled optimized specificities for functional memory (purple) is shown for an immune system with a fixed deliberation factor . A mixture strategy with a bimodal distribution of specificities is established to counter pathogens with a broad range of antigenic divergences. The dashed bar indicates stored memory with specificity , which is not further used in response to infections. The solid line indicates the probability that a stored memory with a given specificity is utilized in future infections (Materials and methods). Optimization is done by maximizing the net utility of immune response averaged over encounters with 1000 independently evolving antigens with (scaled) antigenic divergences drawn uniformly from a range (Materials and methods). The distribution shows the ensemble statistics of functional memory accumulated from 200 independent optimizations, each starting from a flat prior for specificities (orange). The insert shows the optimized mixture strategy for one optimization with 3000 steps. Simulation parameters: , , and .
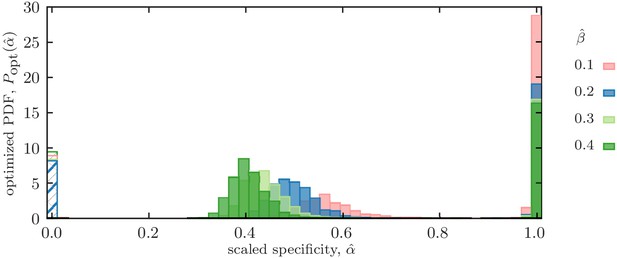
Mixed memory strategy against pathogens for different deliberation factors .
Mixed memory strategy against pathogens for different deliberation factors . Distribution of scaled optimized specificities of functional memories is shown for an immune system with a fixed deliberation factor , in which a mixture strategy with a bimodal distribution of specificities is established to counter pathogens with a broad range of antigenic divergences, drawn uniformly from a range (similar to Figure 3). The dashed bars indicate stored memory with specificity , which is not further used in response to infections. Colors indicate different deliberation factors. Simulation parameters: , and .

Life expectancy influences the specificity of optimal memory.
(A,B) Memory strategies, that is, optimal rescaled specificity (green) and deliberation factor (orange) are shown as a function of the organism’s life expectancy (bottom axis) and the corresponding expected antigenic divergence over the organism’s life-time (top axis). Antigenic divergence (per encounter) of the infecting pathogen is in (A) and in (B). Memory is highly specific in organisms with very short lifetimes, during which re-infections with evolved forms of a pathogen are unlikely (i.e. when life-expected antigenic divergence is smaller than 1, indicated by a dotted pink line). Memory becomes more cross-reactive with a smaller deliberation in organisms with (realistic) short lifetimes, up to a transition point (indicated by dotted purple line), after which specificity increases again. (C) Scaled net utility is shown as a function of organism’s life span, whose immune strategies (, ) are optimized for a specified life expectancy (colors as indicated in the legend). Net utility for memory optimized against pathogens with antigenic divergence (panel A) and (panel B) are shown by full and dashed lines, respectively. Life span and life expectancy are measured in units of the number of pathogenic encounters during lifetime. Simulation parameters: linear deliberation cost function with an amplitude , , , and .
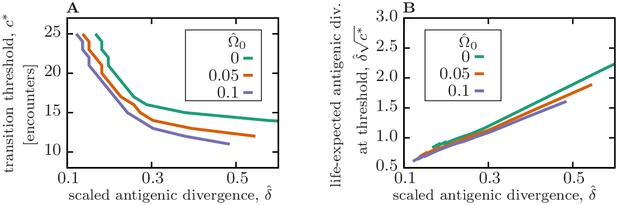
Pathogen encounter threshold to transition between cross-reactive and specific memory.
Pathogen encounter threshold to transition between cross-reactive and specific memory. (A) The encounter threshold , shown in Figure 4A,B, decays as a function of the antigenic divergence (per encounter) and the amplitude of the naive cost (colors). (B) The expected antigenic divergence for the duration of (threshold) encounters is shown as a function of antigenic divergence (per encounter) . Simulation parameters: linear deliberation cost function , , , and .





