Figures and data in Dynamics of diffusive cell signaling relays

Figures
Tables
Additional files

13 figures, 1 table and 1 additional file

Figures

Figure 1

Download asset Open asset

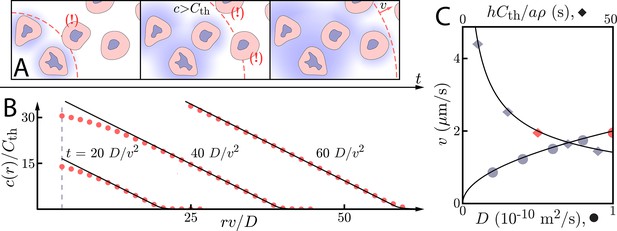
Asymptotic relay dynamics of cells in 2D with diffusion in 2D.

(A) Schematic illustrating the diffusive relay motif. Cells (pink with purple nucleus) release a signaling molecule that diffuses (blue clouds). They do so when the local concentration exceeds a threshold, $C_{th}$ . This gives rise to a diffusive wave with wave speed v. (B) Snapshot concentration profiles. Asymptotic theory (Equation (6), black lines) and numerical simulation of Equation (2) (red dots, details of the numerical methods can be found in Materials and methods) are in good agreement and show outward-propagating waves. Here, $D = 10^{- 10}$ m²/s, $v = 2$ µm/s, and $h C_{th} / a ρ = D / v^{2}$ . Numerical simulations assume that a cell colony of size $r_{i} = 4 D / v$ (dashed vertical line) centered at the origin starts signaling $t = 0$ . (C) Numerical wave speed as measured at $t = 100 D / v^{2}$ (markers) agrees well with theory (Equation (5), black line) as we independently vary D (circles) and $h C_{th} / a ρ$ (diamonds) relative to the panel B values (red circle and diamond).

Figure 2

Download asset Open asset

Asymptotic relay dynamics with cells in 2D and diffusion in 3D.

(A) Schematic of cells (pink with purple nucleus) performing a diffusive relay in which signaling molecules (blue clouds) can diffuse out-of-plane. Here, such relays give rise to a diffusion-constant-independent wave speed, v. (B) Snapshot concentration profiles of the signaling molecule show good agreement between numerical simulation of Equation (2) (blue dots, details of numerical methods can be found in Materials and methods) and asymptotic theory (Equation (9), black lines). Here, $D = 10^{- 10}$ m²/s and $v = 2$ µm/s with $C_{th} / a ρ = 2 / π v$ . The initial signaling colony is of size $r_{i} = 4 D / v$ (dashed vertical line). (C) Numerical wave speed as measured at $t = 100 D / v^{2}$ (markers) agrees well with theory (Equation (8), black line) as we independently vary D (circles) and $C_{th} / a ρ$ (diamonds) relative to the panel B values (blue circle and diamond). As predicted, v is indeed D-independent in this system.

Figure 3

Download asset Open asset

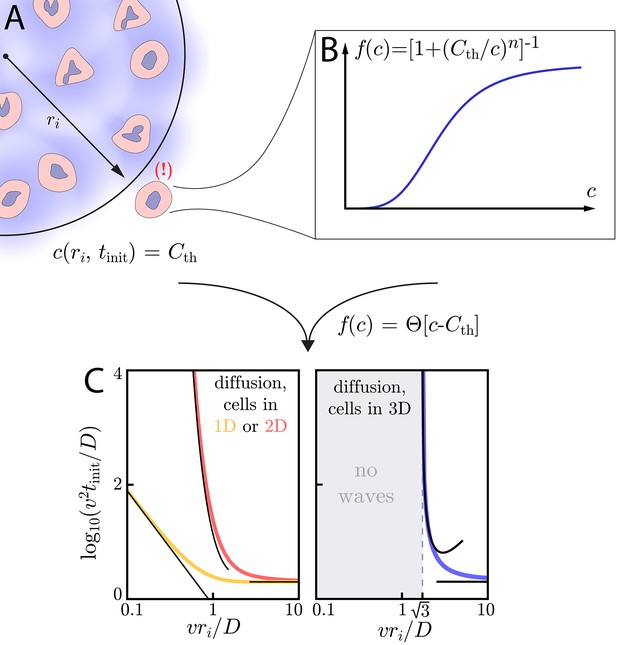
Wave initiation dynamics.

(A) Schematic demonstrating wave initiation. Cells within some initial signaling volume of radius r_i begin signaling at some rate a. The signaling wave is initiated when the concentration at nearby cells exceeds the threshold concentration, $C_{th}$ . (B) Cells near the initial signaling volume participate in the emission according an activation function, $f (c)$ . For instance, in the case of Hill function activation, $f (c) = {[1 + {(C_{th} / c)}^{n}]}^{- 1}$ . C: Initiation times for Heaviside activation, in which $f (c) = Θ [c - C_{th}]$ . Numerics (thick colored lines) and approximate asymptotic theory (Equations (10) and (11), thin black lines) of the initiation time’s dependence on r_i for cells and diffusion in 1D or 2D (left) or cells in 2D with diffusion in 3D (right). For cells and diffusion in 1D, Equation (10) provides a good approximation in the limits $v r_{i} / D ≪ 1$ and $v r_{i} / D ≫ 1$ . Similarly, for cells and diffusion in 2D, Equation (11) governs the large and small $v r_{i} / D$ limits. In both of these cases, the wave always initiates, but the initiation time can be orders of magnitude larger than $D / v^{2}$ if $r_{i} ≪ D / v$ . For cells and diffusion in 3D (right), signaling waves do not initiate for $v r_{i} / D < \sqrt{3}$ . Here again, the asymptotic theory Equation (12) is in good agreement with numerics.

Figure 4

Download asset Open asset

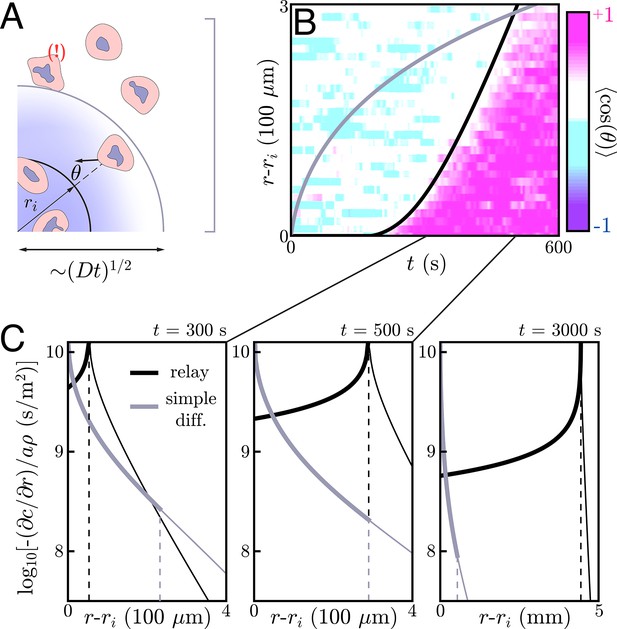
Application to neutrophil swarming.

(A) Schematic of the simple diffusion model. Here, cells on the target (within r_i) signal distant neighbors by continuously emitting a single signaling molecule. If the neighboring cells have a chemotactic response, they migrate toward the target with some noise – that is, some non-zero angle $θ$ with respect to the target. Otherwise, they move around with no sustained directionality. (B) Experimental data (color plot) reproduced from Reátegui et al., 2017 showing the information wave front in neutrophil swarming experiments. By tracking the neutrophils in space and time, they observe highly directed motion of the neutrophils towards the target (pink) starting around $t = 200$ s. There is a clear boundary in space and time – the information wave front – between the regions where cells migrate toward the target (pink) and jostle around with no particular direction (white and light blue). While a relay theory (black line) is consistent with the convex shape of the information wave front, simple diffusive signaling by only the cells on the target (gray line) is not. The diffusion constants for both models is $D = 1.25 \times 10^{- 10}$ m²/s. The threshold concentrations for the relay and simple diffusion models are $C_{th} / a ρ \approx 3.66 \times 10^{5}$ s/m and $2.91 \times 10^{4}$ s/m, respectively. The parameters for the relay model are chosen to fit the wave front by eye while the simple diffusion model parameters are chosen to give the same signaling distance at $t = 500$ s. (C) Gradients created by signaling relays (black) and simple diffusion (gray) models in panel B. The dashed vertical lines indicate the location of the information wave front. As time increases from left to right, the relay signaling motif gives an information wave that signals cells faster than simple diffusion in the long time limit. Cells within the wave front (to the left of the dashed lines that indicate the wave fronts) experience significantly larger gradients when the cells utilize a relay, which may facilitate efficient chemotaxis.

Appendix 3—figure 1

Download asset Open asset

Relay concentration profiles.

(A) Signaling molecule concentration profiles for cells in 2D and diffusion in 2D. Here, we assume continuous emission and no signaling molecule decay (left panel), continuous emission and signaling molecule decay (middle panel), or pulsed emission with no signaling molecule decay (right panel). The decay constant for the middle panel is $γ = v^{2} / 4 D$ while the pulse width is $τ = 2 D / v$ in the right panel. For the left, center, and right panels, the threshold concentration is calculated according to Equations (24), (41), and (38), respectively. As discussed in the main text, the concentration profiles flatten (with respect to the profile generated by continuous emission without decay) inside the wave front once decay or pulsed emission is accounted for. (B) Signaling molecule concentration profiles for the same cases as in A, but with diffusion in 3D. Compared to the case of continuous emission without decay, the concentration profiles flatten (when accounting for decay) or have a local maximum (in the case of pulsed emission).

Appendix 3—figure 2

Download asset Open asset

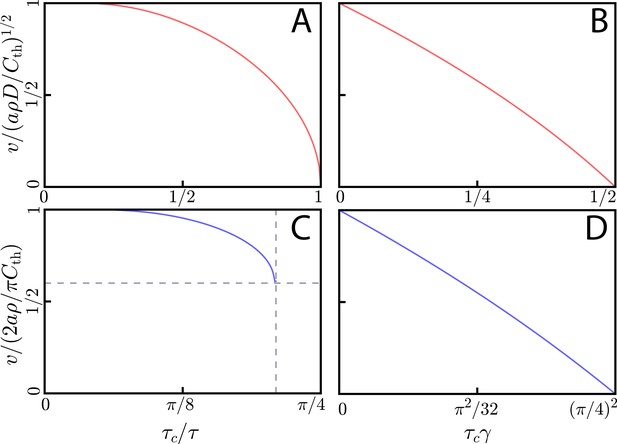
Wave speed with pulsed emission or decay.

(A) Wave speed v for square pulse emission by cells in 2D with diffusion in 2D as a function of pulse width $τ$ . We normalize v by the $τ \to \infty$ wave speed of ${(a ρ D / C_{th})}^{1 / 2}$ . At $τ = τ_{c} = h C_{th} / a ρ$ , the wave speed goes to zero, and for shorter pulses there is no wave-like solution. (B) Wave speed for continuous emission by cells in 2D with diffusion in 2D, accounting for signaling molecule decay at rate $γ$ . For $γ = t_{min, 2D} = 1 / 2 τ_{c}$ , with $τ_{c}$ as in panel A, the wave speed goes to zero and there are no wave-like solutions for larger decay rates. (C) Wave speed v as a function of pulse width $τ$ for square pulse emission of a signaling molecule by cells in 2D with a 3D diffusive environment. At $τ \approx 1.53 τ_{c} = 1.53 D {(2 C_{th} / π a ρ)}^{2}$ (vertical dashed line), there is a minimum wave speed of $v \approx 0.6 \times (2 a ρ / π C_{th})$ (horizontal dashed line), unlike with 2D diffusion. Importantly, $τ \approx 1.53 τ_{c}$ is longer than the minimum initiation time of $4 τ_{c} / π$ . Thus, for values of $τ$ between these two, cells can reach the threshold concentration but cannot propagate a traveling information wave. (D) Wave speed v as a function of decay rate $γ$ for cells in 2D with diffusion in 3D. At $γ = {(π / 4)}^{2} / τ_{c}$ , with $τ_{c}$ as in C, the wave speed goes to zero.

Appendix 4—figure 1

Download asset Open asset

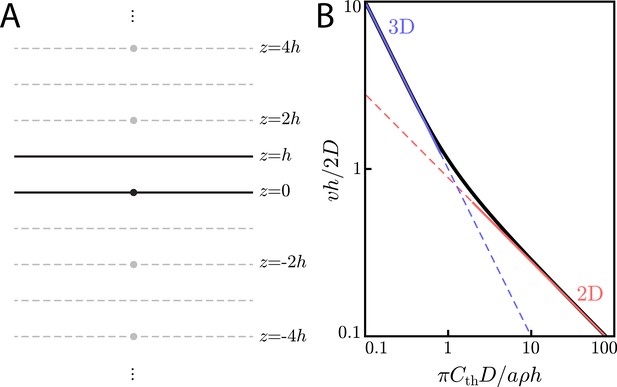
Wave speed in a finite extracellular medium.

(A) Method of images configuration for solving for concentrations in a finite-sized extracellular medium of thickness h. A point-like source (a cell) at $z = 0$ is placed in an extracellular medium of thickness h. In order to calculate the concentration with the appropriate boundary conditions of $\partial c / \partial z$ at $z = 0, h$ , one need only add the contributions from ‘image cells’ at $z = \pm 2 j h$ for $j = 1, 2, \dots$ . (B) Universal curve (black line) showing non-dimensionalized wave speed ( $v h / 2 D$ ) versus non-dimensionalized threshold concentration ( $π C_{th} D / a ρ h$ ). In the limit of $v h / 2 D ≫ 1$ , we recover the familiar 3D scaling law of Equation (29) (blue line). In the limit of $v h / 2 D ≪ 1$ , we get the 2D scaling law of Equation (24) (red line).

Appendix 5—figure 1

Download asset Open asset

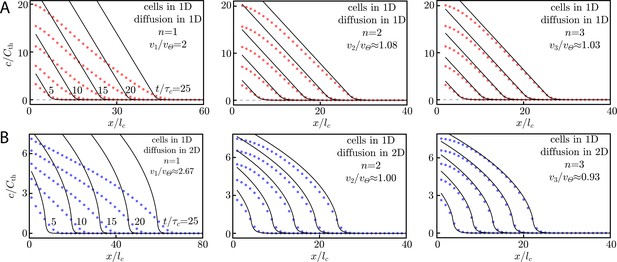
Wave speeds and profiles with Hill function activation.

(A) Numerical simulation of cells in 1D with diffusion in 1D and Hill function activation. The details of the simulation are described in Appendix 5: Asymptotic wave dynamics with Hill function activation. For $n \geq 2$ , we see good agreement between the Heaviside theory (black lines) and the Hill function numerics (red dots). Snapshots are shown at $t / τ_{c} = 5, 10, 15, 20, 25$ where $τ_{c} = h^{2} C_{th} / a ρ$ equals $D / v_{Θ}^{2}$ , the characteristic time scale for Heaviside activation. Note that the x-axis is scaled by the characteristic length $l_{c} = h {(D C_{th} / a ρ)}^{1 / 2}$ , which is the length scale for Heaviside activation with a delta function source, $D / v_{Θ}$ . In the insets, we display the wave speed for the order-n Hill function, v_n, compared to the Heaviside activation wave speed, $v_{Θ} = {(a ρ D / h^{2} C_{th})}^{1 / 2}$ . Our fit to the $n = 1$ data gives $v_{n = 1} \approx 1.93 v_{Θ}$ , but we have shown in Appendix 5: Asymptotic wave dynamics with Hill function activation that $v_{n = 1} = 2 v_{Θ}$ , meaning that the wave speeds in the insets are slight underestimates. (B) Numerical simulation of cells in 1D and diffusion in 2D with Hill function activation. For $n \geq 2$ , the wave speed and concentration profiles (blue dots) agree well with the Heaviside theory (black lines). The theory plotted here assumes a delta-function-like source with respect to the extra diffusive dimension, as in Equation (25). The numerics, however, use a very narrow ( $H = l_{c} / 10$ ) Gaussian source. Here, the characteristic length $l_{c} = π h D C_{th} / 2 a ρ$ equals $D / v_{Θ}$ , the length scale for Heaviside activation. The x-axis is scaled by the same quantity. Snapshots are shown at $t / τ_{c} = 5, 10, 15, 20, 25$ with the characteristic time $τ_{c} = D {(π h C_{th} / 2 a ρ)}^{2}$ equal to $D / v_{Θ}^{2}$ , the time scale for Heaviside activation. In the insets, we display the wave speed for the order-n Hill function, v_n, compared to the Heaviside activation wave speed, $v_{Θ} = 2 a ρ / π C_{th}$ .

Appendix 6—figure 1

Download asset Open asset

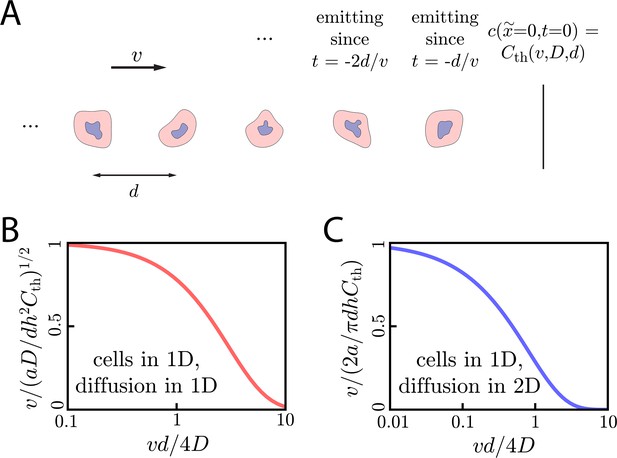
Wave dynamics with discrete sources.

(A) Cartoon showing the discrete lattice model of cell signaling relays for cells in 1D. Here, a concentration wave propagates rightward at speed v through a group of cells spaced by a constant distance d. The concentration at $\tilde{x} = t = 0$ defines the threshold concentration in this discrete system and is a function of $v, D,$ and d: $C_{th} = C_{th} (v, D, d)$ . (B) Wave speed v compared to the continuous theory value of ${(a D / d h^{2} C_{th})}^{1 / 2}$ as a function of $v d / 4 D$ for cells in 1D with diffusion in 1D. We can see that the wave speed approaches the continuous theory value for $v d / 4 D ≪ 1$ . (C) Same as B but for cells in 1D and diffusion in 2D.

Appendix 8—figure 1

Download asset Open asset

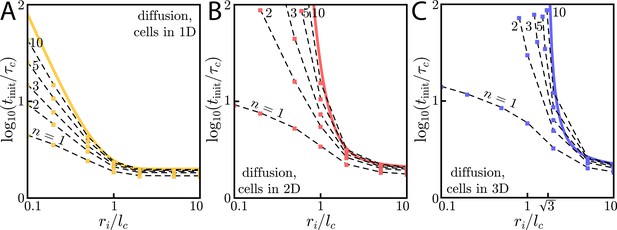
Diffusive wave initiation with Hill function activation.

(A) Wave initiation for cells in 1D with diffusion in 1D. Here, the initiation time $t_{init}$ is normalized by the characteristic time scale $τ_{c} = h^{2} C_{th} / a ρ$ and the initial signaling colony size r_i is normalized by the characteristic length scale $l_{c} = {(h^{2} C_{th} D / a ρ)}^{1 / 2}$ . Yellow data points are individual simulations with dashed black guides to the eye connecting the yellow points. The solid yellow line corresponds to Heaviside-like activation and is reproduced from the main text. (B) Same as A, but for cells in 2D and diffusion in 2D. Here, $τ_{c} = h C_{th} / a ρ$ and $l_{c} = {(h C_{th} D / a ρ)}^{1 / 2}$ . (C) Same as A, but for cells in 3D and diffusion in 3D. Here, $τ_{c} = C_{th} / a ρ$ and $l_{c} = {(C_{th} D / a ρ)}^{1 / 2}$ . We note the value of $r_{i} = \sqrt{3} l_{c}$ , the value below which waves fail to initiate for Heaviside-like activation.

Appendix 9—figure 1

Download asset Open asset

Wavefront fitting of the simple diffusion and relay models.

(A) Plot showing the information waves for various choices of diffusion constant (black) overlaid on the experimental chemotactic index data from Reátegui et al., 2017 (color plot). Here, we take $r_{i} = 100$ µm, although the target in the experiment is a smaller, oblong object. The size of the target has no effect on the convex shape of the information wave front. The black line is reproduced from the main text and has $D = 1.25 \times 10^{- 10}$ m²/s and asymptotic wave speed $v \approx 1.7$ µm/s (the threshold concentration is $C_{th} / a ρ = 2 / π v$ ). This diffusion constant is consistent with a small molecule like LTB4, and the resulting information wave dynamics can be made to fit the information wave front – both the initiation time of $\approx 200$ s and the transient dynamics. Other choices of parameters (green: $D = 1.8 \times 10^{- 10}$ m²/s, $v \approx 2.3$ µm/s, navy: $D = 0.8 \times 10^{- 10}$ m²/s, $v \approx 1.3$ µm/s) give information wave fronts that are also roughly consistent with the experimental data. (B) However, with a much larger ( $D = 10^{- 9}$ m²/s, red) or smaller ( $D = 10^{- 11}$ m²/s, dashed) diffusion constant, an information wave with the correct initiation time does not have the correct transient dynamics. The wave speeds for these larger and smaller diffusion constants are, respectively, $v \approx 11$ µm/s and $v \approx 0.3$ µm/s. (C) Simple diffusion models of various diffusion constants overlaid atop data from Reategui et al. in which the the same swarming assay as in A/B (but with a slightly smaller 80 µm target) was utilized but with neutrophils whose LTB4 receptors (BLT1/2) had been blocked. Here, we see a 250 s offset before the propagation of a slow-moving diffusive front. A simple diffusive model does not capture this offset well, but does accurately capture the concave shape of the front (which contrasts with the convex shape of the front propagated by a relay). (D) Same as in C but with a 250 s offset in the theoretical curves. These curves fit the observed chemotactic index dynamics fairly well.

Appendix 10—figure 1

Download asset Open asset

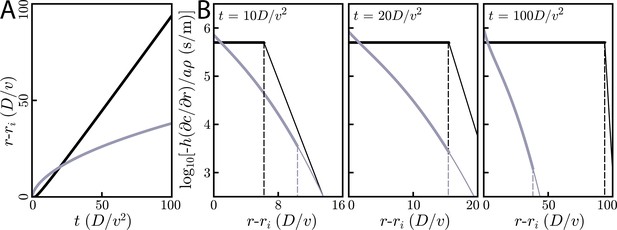
Comparison of relay and simple diffusion for cells and diffusion in 2D.

All plots are for $D = 10^{- 10}$ m²/s, $v = 2$ µm/s, and $r_{i} = 4 D / v$ . (A) Information fronts for relay (black) and simple diffusion (gray) models. The information wave travels like $\sqrt{t}$ for simple diffusion and $v t$ for the relay. The threshold concentration for the simple diffusion model is chosen such that the its information front intersects the relay model at $t = 20 D / v^{2}$ . Thus, $h C_{th,relay} / a ρ = 25 s$ while $h C_{th,diff.} / a ρ \approx 0.25$ s. (B) Snapshots of radial gradients at various times for both the relay (black) and simple diffusion (gray) models. The dashed vertical lines indicate the location of the wave fronts. For short times (left) the relay’s information wave front lags behind the simple diffusion model’s information front, though it later catches up (middle) and passes it (right). At all times, for cells just inside the wave front, the relay model creates gradients that are orders of magnitude larger than does simple diffusion.

Appendix 11—figure 1

Download asset Open asset

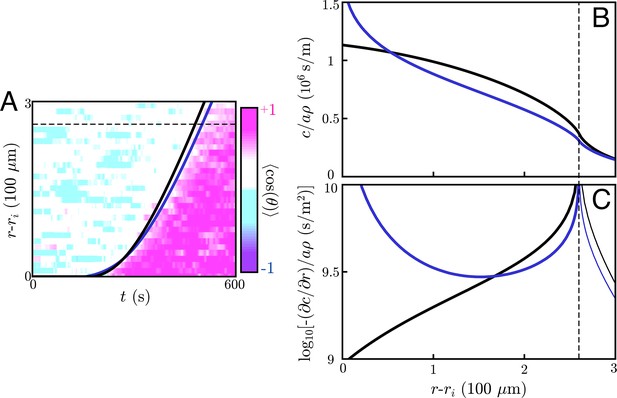
Effects of chemotaxis on wavefront location and concentration profiles.

(A) Information wave fronts for cell signaling relays with (navy) and without (black) chemotaxis. The information wave fronts are overlaid on the experimental chemotactic index data from (color plot) (Reátegui et al., 2017). The black curve is reproduced from the main text. Both models can account for the observed information wave fronts by fitting two parameters: the signaling molecule diffusivity, D and the threshold concentration, $C_{th}$ . (**B/C**) Concentration profiles (B) and gradients (C) generated by the signaling relay models in A. The wave front is indicated in all panels by the dashed line, and the concentration profiles and gradients are plotted at the times such that the threshold concentration is equal to the concentration at the wave front. When one accounts for chemotaxis, the concentration profiles near the target steepen relative to models without chemotaxis.

Tables

Table 1

Summary of asymptotic and initiation dynamics with Heaviside activation.

For different system dimensionalities, we summarize the asymptotic wave speed, v; the initiation time for small initial signaling colony size, $t_{init}, \frac{v r_{i}}{D} ≪ 1$ ; and the initiation time for large initial signaling colony size, $t_{init}, \frac{v r_{i}}{D} ≫ 1$ . One-dimensional diffusive environments are assumed to be narrow channels of width h in each direction perpendicular to the channel length. The cell density $ρ$ has units 1/m for cells in 1D, 1/m² for cells in 2D, and 1/m³ for cells in 3D. When the diffusive and cell dimensions do not match, the environment is assumed to be semi-infinite.

		$t_{init},$	$t_{init},$
	v	$\frac{v r_{i}}{D} ≪ 1$	$\frac{v r_{i}}{D} ≫ 1$
Cells in 1D, diff. in 1D	${(\frac{a ρ D}{h^{2} C_{th}})}^{1 / 2}$	$\sim {(\frac{D}{v r_{i}})}^{2}$	$2 D / v^{2}$
Cells in 1D, diff. in 2D	$\frac{2 a ρ}{π h C_{th}}$	$\sim \exp {(\frac{2 D}{v r_{i}})}^{2}$	$4 D / π v^{2}$
Cells in 2D, diff. in 2D	${(\frac{a ρ D}{h C_{th}})}^{1 / 2}$	$\sim \exp {(\frac{2 D}{v r_{i}})}^{2}$	$2 D / v^{2}$
Cells in 2D, diff. in 3D	$\frac{2 a ρ}{π v}$	no waves	$4 D / π v^{2}$
Cells in 3D, diff. in 3D	${(\frac{a ρ D}{C_{th}})}^{1 / 2}$	no waves	$2 D / v^{2}$

Additional files

Transparent reporting form: https://cdn.elifesciences.org/articles/61771/elife-61771-transrepform-v2.pdf
Download elife-61771-transrepform-v2.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Paul B Dieterle
Jiseon Min
Daniel Irimia
Ariel Amir

(2020)

Dynamics of diffusive cell signaling relays

eLife 9:e61771.

https://doi.org/10.7554/eLife.61771

Share this article

Cite this article

Asymptotic relay dynamics of cells in 2D with diffusion in 2D.

Asymptotic relay dynamics with cells in 2D and diffusion in 3D.

Wave initiation dynamics.

Application to neutrophil swarming.

Relay concentration profiles.

Wave speed with pulsed emission or decay.

Wave speed in a finite extracellular medium.

Wave speeds and profiles with Hill function activation.

Wave dynamics with discrete sources.

Diffusive wave initiation with Hill function activation.

Wavefront fitting of the simple diffusion and relay models.

Comparison of relay and simple diffusion for cells and diffusion in 2D.

Effects of chemotaxis on wavefront location and concentration profiles.

Summary of asymptotic and initiation dynamics with Heaviside activation.

Transparent reporting form

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)