De novo learning versus adaptation of continuous control in a manual tracking task
- Department of Neuroscience, Johns Hopkins University, United States
- Department of Mechanical Engineering, Laboratory for Computational Sensing and Robotics, Johns Hopkins University, United States
- Department of Neurology, Johns Hopkins University, United States
Figures
Figure 1
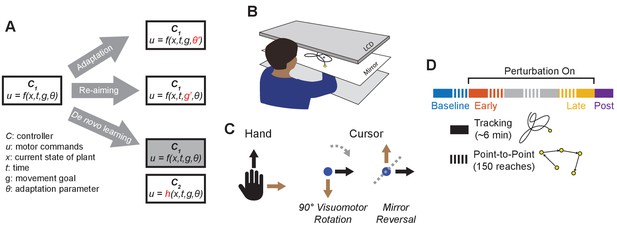
Conceptual overview and experimental design.
(A) We conceptualize adaptation as a parametric change to an existing controller (changing to ), re-aiming as feeding surrogate movement goals to an existing controller (changing to ), and de novo learning as building a new controller () to replace the baseline controller (). (B) Participants performed planar movements with their right hand while a target (yellow) and cursor (blue) were presented to them on an LCD display. Participants were asked to either move the cursor to a static target (point-to-point task) or track a moving target with the cursor (tracking task). (C) Twenty participants learned to control the cursor under one of two visuomotor perturbations: a 90° clockwise visuomotor rotation (), or a mirror reversal (). (D) Participants alternated between point-to-point reaching (one block = 150 reaches) and tracking (one block = 8 trials lasting 46 s each) in a single testing session in one day. We first measured baseline performance in both tasks under veridical visual feedback (blue), followed by interleaved tracking and point-to-point blocks with perturbed visual feedback from early learning (orange) to late learning (yellow). Blocks between early and late learning are indicated in grey. At the end of the experiment, we assessed aftereffects in the tracking task by removing the perturbation (purple).
Figure 2 with 1 supplement
Task performance improved in the point-to-point and tracking tasks.
(A) Performance in the point-to-point task, as quantified by initial reach direction error, is plotted as heat maps for the rotation group (top) and mirror-reversal groups (bottom). Each column shows the distribution of initial reach direction errors, pooled across all participants, over a horizontal bin of 15 trials. The intensity of color represents the number of trials in each 10° vertical bin where the maximum possible value of each bin is 150 (15 trials for 10 participants for each group). (B) Example tracking trajectories from a representative participant in each group. Target trajectories are shown in black while cursor trajectories are shown in brown. Each trajectory displays approximately 5 s of movement. (C) Performance in the tracking task as quantified by average mean-squared positional error between the cursor and target during each 40 s trial. Individual participants are shown in thin lines and group mean is shown in thick lines.
Figure 2—video 1
Video of tracking behavior at different time points during learning.
Figure 3
The rotation group exhibited reach-direction aftereffects while the mirror-reversal group did not.
(A) Alignment matrices relating target and hand movement established by trajectory alignment. The top row illustrates the ideal alignment matrices at baseline or to successfully compensate for each perturbation (blue represents positive values, red represents negative values). Alignment matrices (calculated from one trial averaged across participants) from the rotation (middle row) and mirror-reversal (bottom row) groups are depicted at different points during learning. Below each matrix, we visualized how the unit and vectors (black lines) would be transformed by the columns of the matrices (transformed = green, transformed = purple). Shaded areas are 95% confidence ellipses across participants. (B) The average of the two off-diagonal elements of the estimated alignment matrices across all blocks of the experiment in the tracking task (for the rotation group, the negative of the element in row 1, column 2 was used for averaging). Grey boxes indicate when the rotation or mirror reversal were applied. Thin black lines indicate individual participants and thick lines indicate the mean across participants. (C) (Left: rotation group) Angular compensation for the rotation, computed by approximating each alignment matrix with a pure rotation matrix. (Right: mirror-reversal group) Scaling factor orthogonal to the mirror axis. In each plot, dashed lines depict ideal performance when the perturbation is (green) or is not (black) applied. Thin black lines indicate individual participants and thick lines indicate the mean across participants.
-
Figure 3—source data 1
This file contains the results of all statistical analyses performed on the data in Figure 3B.
- https://cdn.elifesciences.org/articles/62578/elife-62578-fig3-data1-v2.xlsx
Figure 4 with 2 supplements
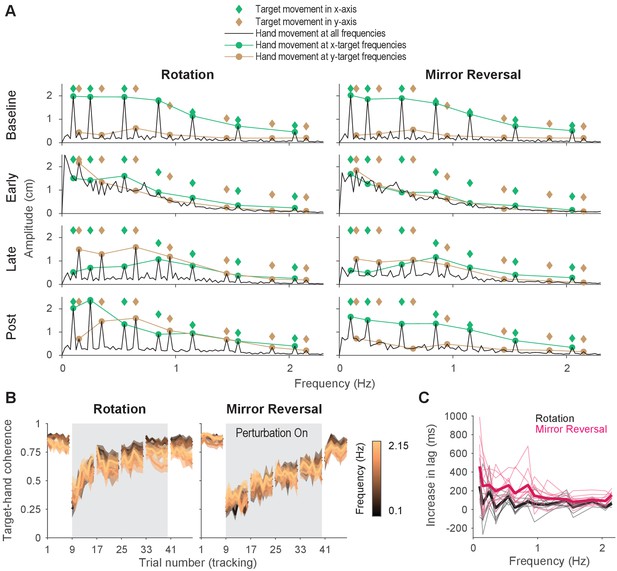
Tracking behavior was approximately linear, indicating that the hand tracked the target continuously.
(A) Amplitude spectra of -axis hand trajectories (black line) averaged across participants from one trial in each listed block. In each plot, the amplitudes and frequencies of target motion are indicated by diamonds (green: -axis target frequencies; brown: -axis target frequencies). Hand responses at - and -axis target frequencies are highlighted as green and brown circles, respectively, and are connected by lines for ease of visualization. (B) Spectral coherence between target movement in the -axis and hand movement in both axes. This measure is proportional to the linear component of the hand’s response to the target. Darker colors represent lower frequencies and lighter colors represent higher frequencies. Error bars are SEM across participants. (C) Difference in phase lag between movements at late learning and baseline. Data from individual participants are shown as thin lines and averages for the rotation (black) and mirror-reversal (pink) groups are shown as thick lines.
Figure 4—figure supplement 1
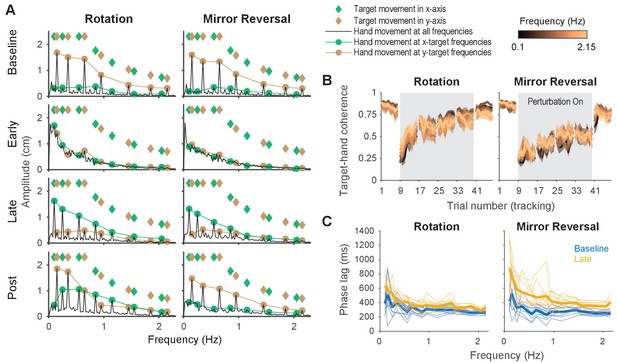
Amplitude spectra (-axis), spectral coherence, and phase lag plots.
(A) Amplitude spectra of -axis hand movements (black) averaged across participants from one trial in each listed block. The amplitudes and frequencies of target movement are indicated by green (-axis) and brown (-axis) diamonds. Hand responses at the - (green circles) and -axis (brown circles) target frequencies are connected by lines, respectively, for ease of visualization. (B) Spectral coherence between target movement in the -axis and hand movement in both axes. Darker colors represent lower frequencies and lighter colors represent higher frequencies. Error bars are SEM across participants. (C) Phase lag of movements at baseline (blue) and late learning (yellow), the difference of which was used to generate Figure 4B. Data from individual participants are shown as thin lines and group averages are shown as thick lines.
Figure 4—figure supplement 2
Amplitude spectra of -axis hand movements from single subjects.
Amplitude spectra of -axis hand movements from single subjects. The amplitudes and frequencies of target movement are indicated by green (-axis) and brown (-axis) diamonds. Hand responses at the - (green circles) and -axis (brown circles) target frequencies are connected by lines, respectively, for ease of visualization.
Figure 5 with 2 supplements
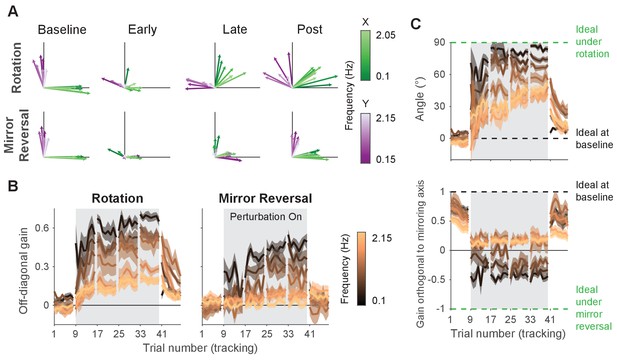
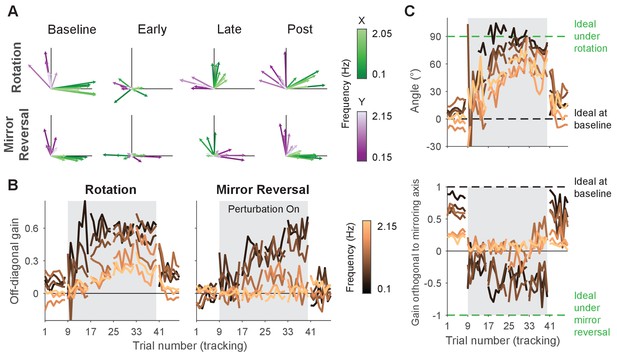
Adaptation and de novo learning exhibit distinct frequency-dependent signatures.
We estimated how participants transformed target motion into hand movement across different frequencies (i.e., gain matrix analysis). (A) Visualizations of the gain matrices relating target motion to hand motion across frequencies (associated gain matrices can be found in Figure 5—figure supplement 1). These visualizations were generated by plotting the column vectors of the gain matrices from one trial of each listed block, averaged across participants. Green and purple arrows depict hand responses to - and -axis target frequencies, respectively. Darker and lighter colors represent lower and higher frequencies, respectively. (B) Average of the two off-diagonal values of the gain matrices at different points during learning. Grey boxes indicate when the rotation or mirror reversal were applied. (C) (Top) Compensation angle as a function of frequency for the rotation group. (Bottom) Gain of movement orthogonal to the mirror axis for the mirror-reversal group. Green and black dashed lines show ideal compensation when the perturbation is or is not applied, respectively. All error bars in this figure are SEM across participants.
-
Figure 5—source data 1
This file contains the results of all statistical analyses performed on the data in Figure 5B.
- https://cdn.elifesciences.org/articles/62578/elife-62578-fig5-data1-v2.xlsx
Figure 5—figure supplement 1
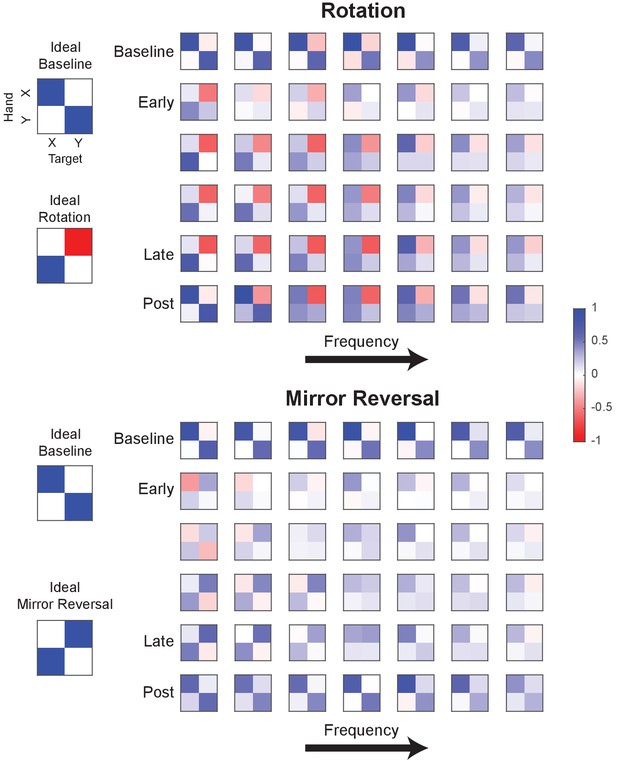
Example gain matrices for each block and frequency.
Gain matrices fitted for different frequencies (0.1–2.15 Hz) of hand movement. Each element within a matrix is the gain estimated between hand and target movement at a particular frequency. Each row of matrices displays the data from one trial of a tracking block (averaged across participants) and each column is a frequency (frequencies increase from left to right). Although only one trial of each block is depicted, other trials within each block were qualitatively similar. Figure 5A was created by plotting the left column vector of each matrix as a green arrow and the right column vector as a purple arrow.
Figure 5—figure supplement 2
Gain matrix analysis performed on single-subject data.
Gain matrix analysis, identical to the one performed in Figure 5 except performed on a single subject from each group. (A) Visualizations of gain matrices from a single trial in each listed block. (B) Average of the off-diagonal values of the gain matrix. (C) Compensation angle for the rotation group and gain orthogonal to the mirror axis for the mirror-reversal group. Note that compensation angles could not be computed for every trial using our singular value decomposition approach, so several data points are missing in the figure (see ‘Trajectory-alignment analysis’ for details on this approach).
Figure 6 with 1 supplement
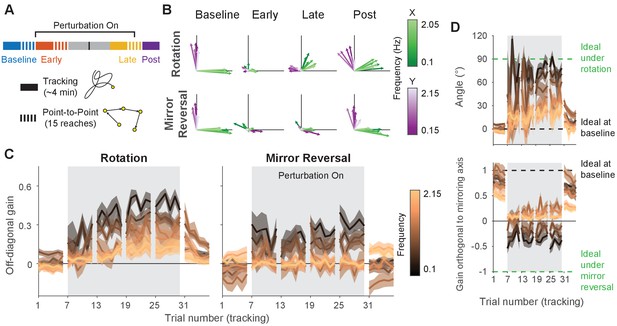
Making point-to-point reaches improves tracking performance, especially under mirror reversal.
(A) Participants learned to counter either a visuomotor rotation () or mirror-reversal (). The experimental design was similar to the main experiment except point-to-point reaching practice was almost entirely eliminated; between the early- and late-learning tracking blocks, participants only performed 15 point-to-point reaches. The purpose of these reaches was not for training but simply to assess learning in the point-to-point task. (B–D) Gain matrix analysis, identical to that in Figure 5, performed on data from the follow-up experiment. (B) Visualization of the gain matrix from one trial of each listed block, averaged across participants. (C) Off-diagonal elements of the gain matrices, averaged across participants. (D) Computed rotation angle for the rotation group’s gain matrices (upper) and gain orthogonal to mirroring axis for the mirror-reversal group (lower), averaged across participants. All error bars in this figure are SEM across participants.
-
Figure 6—source data 1
This file contains the results of all statistical analyses performed on the data in Figure 6C.
- https://cdn.elifesciences.org/articles/62578/elife-62578-fig6-data1-v2.xlsx
Figure 6—figure supplement 1
Gain matrix analysis performed on single-subject data for the follow-up experiment.
Gain matrix analysis, identical to the one performed in Figure 6 except performed on a single subject from each group. (A) Visualizations of gain matrices from a single trial in each listed block. (B) Average of the off-diagonal values of the gain matrix. (C) Compensation angle for the rotation group and gain orthogonal to the mirror axis for the mirror-reversal group. Note that compensation angles could not be computed for every trial using our singular value decomposition approach, so several data points are missing in the figure (see ‘Trajectory-alignment analysis’ for details on this approach).
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
De novo learning versus adaptation of continuous control in a manual tracking task
eLife 10:e62578.
https://doi.org/10.7554/eLife.62578
