Figures and data in Response-based outcome predictions and confidence regulate feedback processing and learning

Figures
Tables
Additional files

5 figures, 7 tables and 11 additional files

Figures

Figure 1

Download asset Open asset

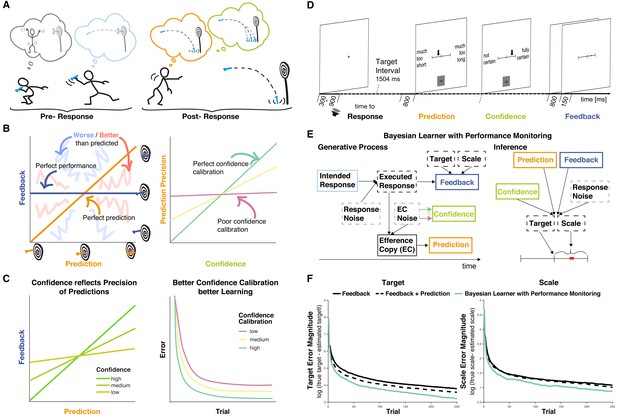
Interactions between performance monitoring and feedback processing.

(A) Illustration of dynamic updating of predicted outcomes based on response information. Pre-response the agent aims to hit the bullseye and selects the action he believes achieves this goal. Post-response the agent realizes that he made a mistake and predicts to miss the target entirely, being reasonably confident in his prediction. In line with his prediction and thus unsurprisingly the darts hits the floor. (B) Illustration of key concepts. Left: The feedback received is plotted against the prediction. Performance and prediction can vary in their accuracy independently. Perfect performance (zero deviation from the target, dark blue line) can occur for accurate or inaccurate predictions and any performance, including errors, can be predicted perfectly (predicted error is identical to performance, orange line). When predictions and feedback diverge, outcomes (feedback) can be better (closer to the target, area highlighted with coarse light red shading) or worse (farther from the target, area highlighted with coarse light blue shading) than predicted. The more they diverge the less precise the predictions are. Right: The precision of the prediction is plotted against confidence in that prediction. If confidence closely tracks the precision of the predictions, that is if agents know when their predictions are probably right and when they’re not, confidence calibration is high (green). If confidence is independent of the precision of the predictions, then confidence calibration is low. (C) Illustration of theoretical hypotheses. Left: We expect the correspondence between predictions and Feedback to be stronger when confidence is high and to be weaker when confidence is low. Right: We expect that agents with better confidence calibration learn better. (D) Trial schema. Participants learned to produce a time interval by pressing a button following a tone with their left index finger. Following each response, they indicated on a visual analog scale in sequence the estimate of their accuracy (anchors: ‘much too short’ = ‘viel zu kurz’ to ‘much too long’ = ‘viel zu lang’) and their confidence in that estimate (anchors: ‘not certain’ = ‘nicht sicher’ to ‘fully certain’ = ‘völlig sicher’) by moving an arrow slider. Finally, feedback was provided on a visual analog scale for 150 ms. The current error was displayed as a red square on the feedback scale relative to the target interval indicated by a tick mark at the center (Target, t) with undershoots shown to the left of the center and overshoots to the right, and scaled relative to the feedback anchors of -/+1 s (Scale, s; cf. E). Participants are told neither Target nor Scale and instead need to learn them based on the feedback. (E) Bayesian Learner with Performance Monitoring. The learner selects an intended response (i) based on the current estimate of the Target. The Intended Response and independent Response Noise produce the Executed Response (r). The Efference Copy (c) of this response varies in its precision as a function of Efference Copy Noise. It is used to generate a Prediction as the deviation from the estimate of Target scaled by the estimate of Scale. The Efference Copy Noise is estimated and expressed as Confidence (co), approximating the precision of the Prediction. Learners vary in their Confidence Calibration (cc), that is, the precision of their predictions, and higher Confidence Calibration (arrows: green >yellow > magenta) leads to more reliable translation from Efference Copy precision to Confidence. Feedback is provided according to the Executed Response and depends on the Target and Scale, which are unknown to the learner. Target and Scale are inferred based on Feedback (f), Response Noise, Prediction, and Confidence. Variables that are observable to the learner are displayed in solid boxes, whereas variables that are only partially observable are displayed in dashed boxes. (F) Target and scale error (absolute deviation of the current estimates from the true values) for the Bayesian learner with Performance monitoring (green, optimal calibration), a Feedback-only Bayesian Learner (solid black), and a Bayesian Learner with Outcome Prediction (dashed black).

Figure 2 with 3 supplements

Download asset Open asset

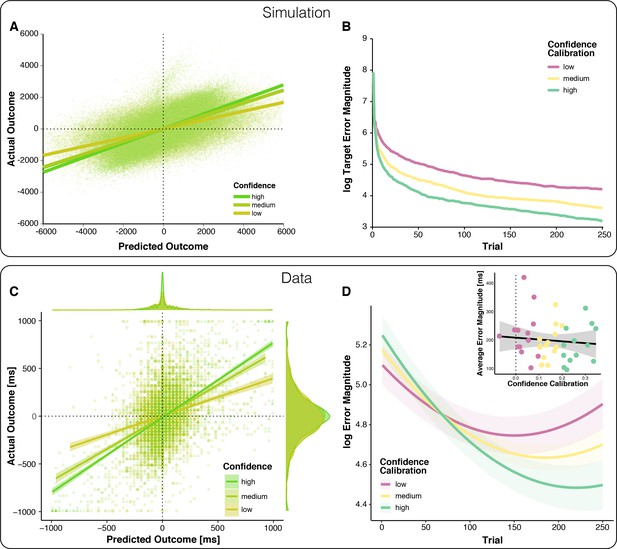
Relationships between outcome predictions and actual outcomes in the model and observed data (top vs.bottom).

(A) Model prediction for the relationship between Prediction and actual outcome (Feedback) as a function of Confidence. The relationship between predicted and actual outcomes is stronger for higher confidence. Note that systematic errors in the model’s initial estimates of target (overestimated) and scale (underestimated) give rise to systematically late responses, as well as underestimation of predicted outcomes in early trials, visible as a plume of datapoints extending above the main cloud of simulated data. (B) The model-predicted effect of Confidence Calibration on learning. Better Confidence Calibration leads to better learning. (C) Observed relationship between predicted and actual outcomes. Each data point corresponds to one trial of one participant; all trials of all participants are plotted together. Regression lines are local linear models visualizing the relationship between predicted and actual error separately for high, medium, and low confidence. At the edges of the plot, the marginal distributions of actual and predicted errors are depicted by confidence levels. (D) Change in error magnitude across trials as a function of confidence calibration. Lines represent LMM-predicted error magnitude for low, medium and high confidence calibrations, respectively. Shaded error bars represent corresponding SEMs. Note that the combination of linear and quadratic effects approximates the shape of the learning curves, better than a linear effect alone, but predicts an exaggerated uptick in errors toward the end, Figure 2—figure supplement 3. Inset: Average Error Magnitude for every participant plotted as a function of Confidence Calibration level. The vast majority of participants show positive confidence calibration. The regression line represents a local linear model fit and the error bar represents the standard error of the mean.

Figure 2—figure supplement 1

Download asset Open asset

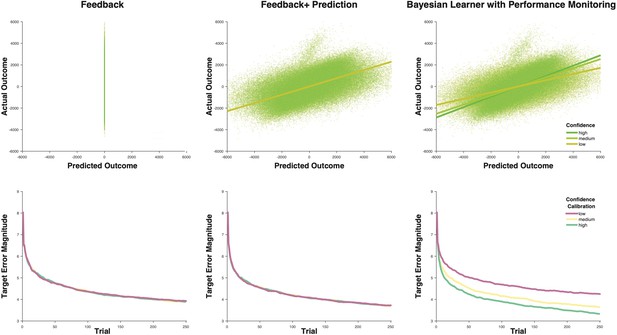
Model comparison.

Shown are the relationship between predicted and actual outcomes as a function of Confidence (top) and the Target Error Magnitude as a function of Confidence Calibration for the model that learns from feedback only (left), the model that learns from feedback and outcome predictions (center) and our Bayesian Learner with Performance Monitoring. While the Feedback only model learns the target adequately, it is not able to predict outcomes of its actions. The Feedback and Prediction model learns faster and is able to predict outcomes; however, it cannot distinguish between accurate and inaccurate predictions. Finally, the Bayesian Learner with performance monitoring predicts outcomes and distinguishes between accurate and inaccurate predictions. Whether these are advantageous depends on the fidelity of confidence as a read-out of the precision of the predictions, that is confidence calibration. The well-calibrated Bayesian Learner with Performance Monitoring outperforms both alternative models.

Figure 2—figure supplement 2

Download asset Open asset

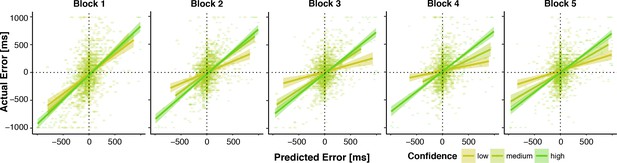
Predictions and Confidence improve as learning progresses.

Plotted are actual errors as a function of predicted errors and confidence terciles. Regression lines represent local linear models. In block 1, many large actual errors are inaccurately predicted to be zero or small. These prediction errors decrease over time. Across blocks, Confidence further dissociates increasingly well between accurate and inaccurate predictions.

Figure 2—figure supplement 3

Download asset Open asset

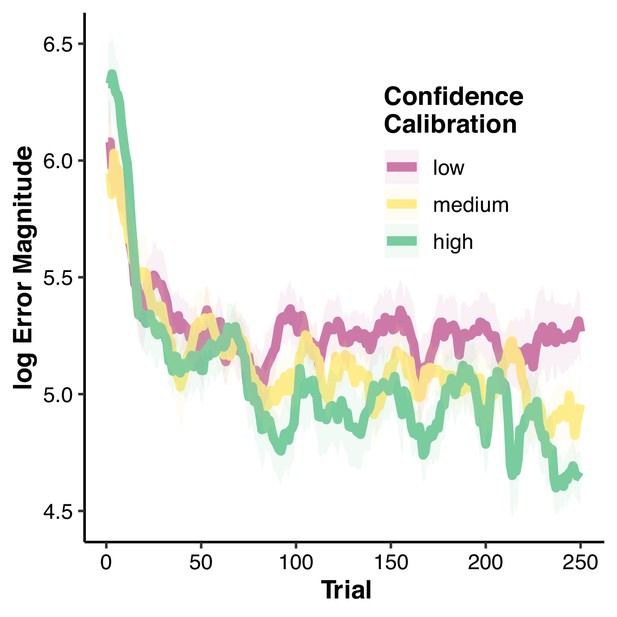
Running average log error magnitude across trials.

Running average performance averaged across participants within terciles of Confidence calibration. Shaded error bars represent standard error of the mean.

Figure 3

Download asset Open asset

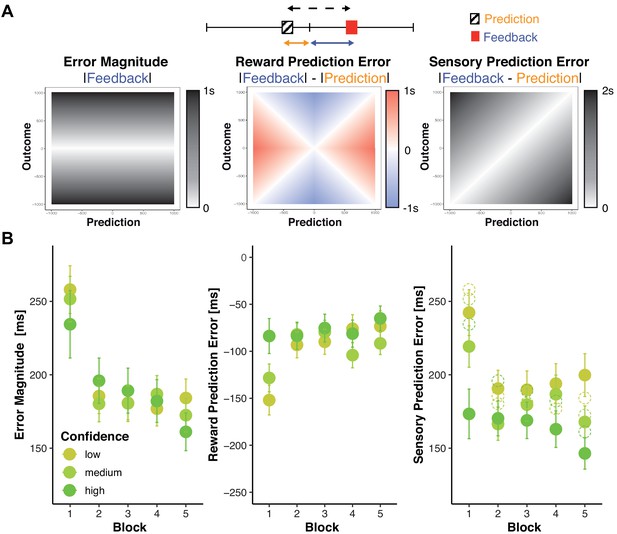
Changes in objective and subjective feedback.

(A) Dissociable information provided by feedback. An example for a prediction (hatched box) and a subsequent feedback (red box) are shown overlaid on a rating/feedback scale. We derived three error signals that make dissociable predictions across combinations of predicted and actual outcomes. The solid blue line indicates Error Magnitude (distance from outcome to goal). As smaller errors reflect greater rewards, we computed Reward Prediction Error (RPE) as the signed difference between negative Error Magnitude and the negative predicted error magnitude (solid orange line, distance from prediction to goal). Sensory Prediction Error (SPE, dashed line) was quantified as the absolute discrepancy between feedback and prediction. Values of Error Magnitude (left), RPE (middle), and SPE (right) are plotted for all combinations of prediction (x-axis) and outcome (y-axis) location. (B) Predictions and confidence associate with reduced error signals. Average error magnitude (left), Reward Prediction Error (center), and Sensory Prediction Error (right) are shown for each block and confidence tercile. Average prediction errors are smaller than average error magnitudes (dashed circles), particularly for higher confidence.

Figure 4

Download asset Open asset

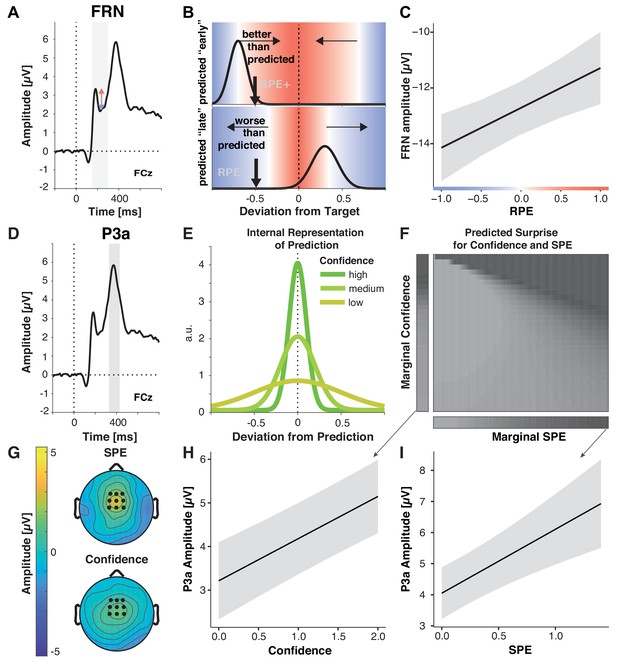
Multiple prediction errors in feedback processing.

(**A-C**) FRN amplitude is sensitive to predicted error magnitude. (A) FRN, grand mean, the shaded area marks the time interval for peak-to-peak detection of FRN. Negative peaks between 200 and 300 ms post feedback were quantified relative to positive peaks in the preceding 100 ms time window. (B) Expected change in FRN amplitude as a function of RPE (color) for two predictions (black curves represent schematized predictive distributions around the reported prediction for a given confidence), one too early (top: high confidence in a low reward prediction) and one too late (bottom: low confidence in a higher reward prediction). Vertical black arrows mark a sample outcome (deviation from the target; abscissa) resulting in different RPE/expected changes in FRN amplitude for the two predictions, indicated by shades. Blue shades indicate negative RPEs/larger FRN, red shades indicate positive RPEs/smaller FRN and gray denotes zero. Note that these are mirrored at the goal for any predictions, and that the likelihood of the actual outcome given the prediction (y-axis) does not affect RPE. In the absence of a prediction or a predicted error of zero, FRN amplitude should increase with the deviation from the target (abscissa). (C) LMM-estimated effects of RPE on peak-to-peak FRN amplitude visualized with the effects package; shaded error bars represent 95% confidence intervals. (**D– I**) P3a amplitude is sensitive to SPE and Confidence. (D) Grand mean ERP with the time-window for quantification of P3a, 330–430 ms, highlighted. (E) Hypothetical internal representation of predictions. Curves represent schematized predictive distributions around the reported prediction (zero on abscissa). Confidence is represented by the width of the distributions. (F) Predictions for SPE (x-axis) and Confidence (y-axis) effects on surprise as estimated with Shannon information (darker shades signify larger surprise) for varying Confidence and SPE (center). The margins visualize the predicted main effects for Confidence (left) and SPE (bottom). (G) P3a LMM fixed effect topographies for SPE, and Confidence. (**H–I**) LMM-estimated effects on P3a amplitude visualized with the effects package; shaded areas in (H) (SPE) and (I) (confidence) represent 95% confidence intervals.

Figure 5 with 1 supplement

Download asset Open asset

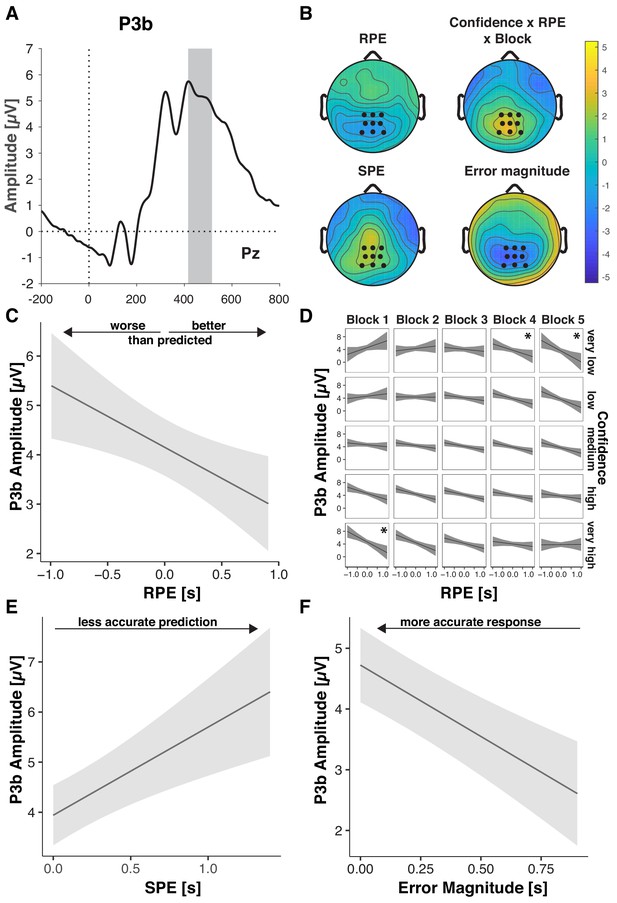
Performance-relevant information converges in the P3b.

(A) Grand average ERP waveform at Pz with the time window for quantification, 416–516 ms, highlighted. (B) Effect topographies as predicted by LMMs for RPE, error magnitude, SPE and the RPE by Confidence by Block interaction. (**C–F**) LMM-estimated effects on P3b amplitude visualized with the effects package in R; shaded areas represent 95% confidence intervals. (C.) RPE. Note the interaction effects with Block and Confidence (D), that modulate the main effect (D) Three-way interaction of RPE, Confidence and Block. Asterisks denote significant RPE slopes within cells. (E) P3b amplitude as a function of SPE. (F) P3b amplitude as a function of Error Magnitude.

Figure 5—figure supplement 1

Download asset Open asset

P3b to feedback modulates error-related adjustments on the subsequent trial.

Top: y-hats illustrating the interaction of previous error magnitude and P3b on improvement on the current trial for each block. Bottom: Distribution of errors in each block.

Tables

Table 1

Relations between actual performance outcome (signed error magnitude), predicted outcome, confidence in predictions and their modulations due to learning across blocks of trials.

	Signed error magnitude
Predictors	Estimates	SE	CI	t	p
Intercept	4.63	9.99	−14.94–24.20	0..46	6.427e-01
Predicted Outcome	523.99	29.66	465..86–582.12	17.67	7.438e-70
Block	29.47	8.12	13..56–45.37	3..63	2.832e-04
Confidence	−27.07	11.05	−48.73 – −5.42	−2..45	1.428e-02
Predicted Outcome: Block	−149.70	21.90	−192.62 – −106.78	−6..84	8.145e-12
Predicted Outcome: Confidence	322.56	27.31	269.03–376.09	11.81	3.477e-32
Block: Confidence	−25.52	9..15	−43.46 – −7.58	−2..79	5.297e-03
Predicted Outcome: Block: Confidence	90.68	33.65	24.73–156.64	2..69	7.043e-03
Random effects			Model Parameters
Residuals	54478.69		N	40
Intercept	3539.21		Observations	9996
Confidence	2813.79		log-Likelihood	−68816.092
Predicted Outcome	22357.33		Deviance	137632.185

Formula: Signed error magnitude ~Predicted Outcome*Block*Confidence+(Confidence +Predicted Outcome+Block|participant); Note: ‘:” indicates interactions between predictors.

Table 2

Relations of confidence with the precision of prediction and the precision of performance and changes across blocks.

	Confidence
Predictors	Estimates	SE	CI	t	p
(Intercept)	0.26	0.04	0.18–0.33	6.35	2.187e-10
Block	0.05	0.02	0.02–0.08	3.05	2.257e-03
Sensory Prediction Error (SPE)	−0.44	0.04	−0.52 – −0.36	−10.84	2.289e-27
Error Magnitude (EM)	0.17	0.05	0.08–0.27	3.73	1.910e-04
Block: SPE	−0.08	0.04	−0.15 – −0.00	−1.99	4.642e-02
Block: EM	0.15	0.05	0.05–0.25	3.07	2.167e-03
Random effects			Model Parameters
Residuals	0.12		N	40
Intercept	0.06		Observations	9996
SPE	0.03		log-Likelihood	−3640.142
Error Magnitude	0.06		Deviance	7280.284
Block	0.01
Error Magnitude: Block	0.04

Formula: Confidence ~ (SPE +Error Magnitude)*Block+(SPE +Error Magnitude *Block|participant); Note: ‘:” indicates interactions between predictors.

Table 3

Confidence calibration modulation of learning effects on performance.

	log Error Magnitude
Predictors	Estimates	SE	CI	t	p
(Intercept)	5.17	0.06	5.05–5.30	80.74	0.000e + 00
Confidence Calibration	0.58	0.58	−0.57–1.72	0.99	3.228e-01
Trial (linear)	−0.59	0.07	−0.72 – −0.45	−8..82	1.197e-18
Trial (quadratic)	0.16	0.02	0.11–0.20	6.80	1.018e-11
Trial (linear): Confidence Calibration	−0.86	0.32	−1.48 – −0.24	−2.72	6.467e-03
Random effects			Model Parameters
Residuals	1.18		N	40
Intercept	0..12		Observations	9996
Trial (linear)	0..03		log-Likelihood	−15106.705
			Deviance	30213.411

Formula: log Error Magnitude ~ (Confidence Calibration* Trial(linear)+Trial(quadratic) + (Trial(linear)|participant)); Note: ‘:' indicates interactions between predictors.

Table 4

LMM statistics of learning effects on FRN.

	Peak-to-Peak FRN amplitude
Predictors	Estimates	SE	CI	t	p
Intercept	−12.67	0.49	−13.62 – −11.71	−26.03	2.322e-149
Confidence	−0.19	0.15	−0.49–0.11	−1.25	2.126e-01
Reward prediction error	1.43	0.41	0.62–2.24	3.47	5.302e-04
Sensory prediction error	−0.67	0.42	−1.49–0.15	−1.61	1.078e-01
Error magnitude	0.51	0.55	−0.57–1.58	0.92	3.553e-01
Block	−0.15	0.11	−0.36–0.06	−1.43	1.513e-01
Random effects			Model Parameters
Residuals	27.69		N _vpn	40
Intercept	9.23		Observations	9678
Error magnitude	2.24		log-Likelihood	−29908.910
Block	0.22		Deviance	59817.821

Formula: FRN ~ Confidence + RPE+SPE + EM+Block + (EM +Block|participant).

Table 5

LMM statistics of learning effects on P3a.

	P3a Amplitude
Predictors	Estimates	SE	CI	t	p
Intercept	4.10	0.42	3.28–4.93	9.79	1.293e-22
Confidence	0.97	0.14	0.70–1.24	6.96	3.338e-12
Block	−0.91	0.07	−1.05 – −0.77	−12.93	3.201e-38
Sensory prediction error	2.06	0..48	1.11–3.00	4..27	1.969e-05
Reward prediction error	−0.75	0.38	−1.49 – −0..01	−1.98	4.794e-02
Error magnitude	−1..95	0..44	−2.81 – −1..09	−4.43	9.512e-06
Random effects			Model Parameters
Residuals	22.98		N	40
Intercept	6.83		Observations	9678
SPE	3.02		log-Likelihood	−28997.990
			Deviance	57995.981

Formula: P3a ~ Confidence + Block +SPE + RPE+EM + (SPE|participant).

Table 6

LMM statistics of learning effects on P3b.

	P3b Amplitude
Predictors	Estimates	SE	CI	t	p
Intercept	4.12	0.29	3.55–4.70	14.12	2.937e-45
Block	−0.48	0.09	−0.66 – −0.30	−5.20	2.037e-07
Confidence	0.08	0.20	−0.31–0.48	0.42	6.740e-01
Reward prediction error	−1.12	0.46	−2.03 – −0.22	−2.43	1.493e-02
Sensory prediction error	1.75	0.47	0.84–2.66	3.76	1.691e-04
Error magnitude	−2.35	0.46	−3.24 – −1.45	−5.14	2.743e-07
Confidence: Reward prediction error	−0.51	0.55	−1.60–0.57	−0.92	3.556e-01
Block: Confidence	0.07	0.18	−0.28–0.43	0.41	6.823e-01
Block: Reward prediction error	−0.52	0.44	−1.39–0.34	−1.19	2.359e-01
Block: Sensory prediction error	−0.98	0.46	−1.88 – −0.07	−2.12	3.405e-02
Block: Confidence: Reward prediction error	2.22	0.72	0.81–3.64	3.08	2.057e-03
Random effects
Residuals	23.95		N	40
Intercept	3.17		Observations	9678
Sensory Prediction Error	2.16		log-Likelihood	−29197.980
Reward prediction error	1.67		Deviance	58395.960
Confidence	0.63

Formula: P3b ~ Block*(Confidence*RPE +SPE)+Error Magnitude + (SPE +RPE + Confidence|participant); Note: ‘:” indicates interactions.

Table 7

LMM statistics of confidence weighted predicted error discounting on P3b.

	P3b Amplitude
Predictors	Estimates	SE	CI	t	p
Intercept	4.26	0.30	3.68–4.85	14.22	7.239e-46
Confidence	0.31	0.22	−0.12–0.75	1.41	1.595e-01
Predicted error magnitude	−0.83	0.46	−1.74–0.07	−1.80	7.133e-02
Block	−0.32	0.11	−0.52 – −0.11	−2.98	2.860e-03
Error magnitude	−1.06	0.49	−2.03 – −0.09	−2.13	3.277e-02
Sensory prediction error	1.49	0.40	0.71–2.28	3.72	1.992e-04
Confidence: Predicted error magnitude	−0.98	0.69	−2.34–0.38	−1.41	1.582e-01
Confidence: Block	−0.50	0.20	−0.90 – −0.11	−2.50	1.249e-02
Predicted Error magnitude: Block	−1.12	0.56	−2.22 – −0.02	−2.00	4.540e-02
Confidence: Predicted error magnitude: Block	3.12	0.84	1.47–4.78	3.70	2.141e-04
Random effects			Model Parameters
Residuals	23.98		N	40
Intercept	3.30		Observations	9678
Error magnitude	3.43		log-Likelihood	−29201.951
Confidence	0.72		Deviance	58403.902

Formula: P3b ~ Block*(Confidence*Predicted Error Magnitude +SPE)+Error Magnitude + (Error Magnitude +Confidence|participant); Note: ‘:” indicates interactions.