Optimal plasticity for memory maintenance during ongoing synaptic change
- Department of Engineering, University of Cambridge, United Kingdom
Figures
Figure 1
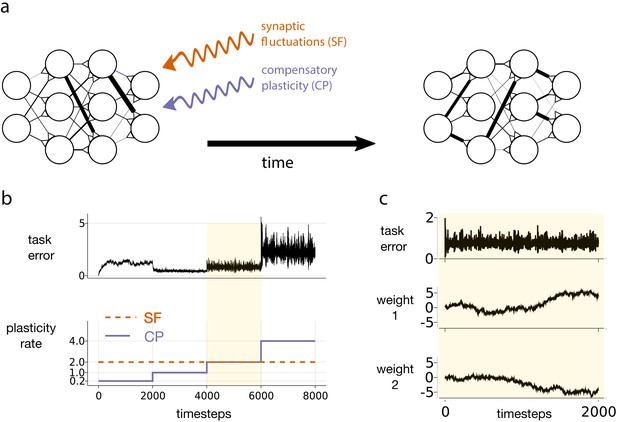
Motivating simulation results.
(a) We consider a network attempting to retain previously learned information that is subject to ongoing synaptic changes due to synaptic fluctuations and compensatory plasticity. (b) Simulations performed in this study use an abstract, rate based neural network (described in section Motivating example). The rate of synaptic fluctuations is constant over time. By iteratively increasing the compensatory plasticity rate in steps we observe a ‘sweet-spot’ compensatory plasticity rate, which is lower than that of the synaptic fluctuations, and which best controls task error. (c) A snapshot of the simulation described in b, at the point where the rates of synaptic fluctuations and compensatory plasticity are matched. Even as task error fluctuates around a mean value, individual weights experience systematic changes.
Figure 2
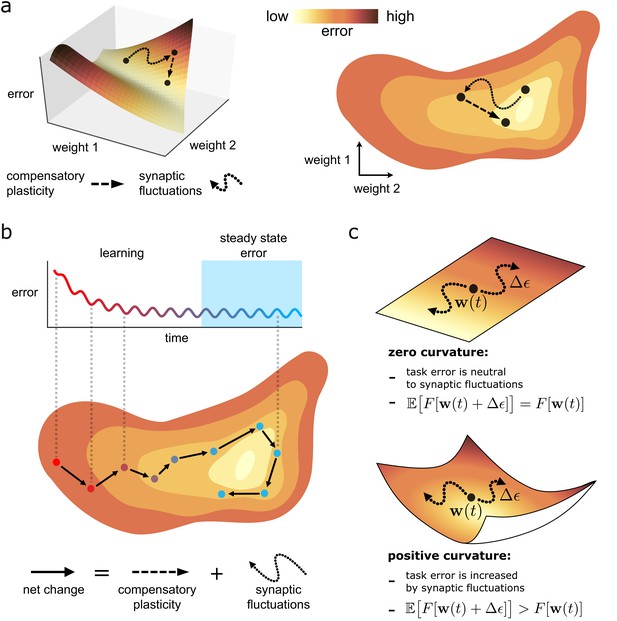
Task error landscape and synaptic weight trajectories.
(a) Task error is visualised as the height of a ‘landscape’. Lateral co-ordinates represent the values of different synaptic strengths (only two are visualisable in 3D). Any point on the landscape defines a network state, and the height of the point is the associated task error. Both compensatory plasticity and synaptic fluctuations alter network state, and thus task error, by changing synaptic strengths. Compensatory plasticity reduces task error by moving ‘downwards’ on the landscape. (b) Eventually, an approximate steady state is reached where the effect of the two competing plasticity sources on task error cancel out. The synaptic weights wander over a rough level set of the landscape. (c) The effect of synaptic fluctuations on task error depends on local curvature in the landscape. Top: a flat landscape without curvature. Even though the landscape is sloped, synaptic fluctuations have no effect on task error in expectation: up/downhill directions are equally likely. Bottom: Although up/downhill synaptic fluctuations are still equally likely, most directions are upwardly curved. Thus, uphill directions increase task error more, and downhill directions decrease task error less. So in expectation, synaptic fluctuations wander uphill.
Figure 3
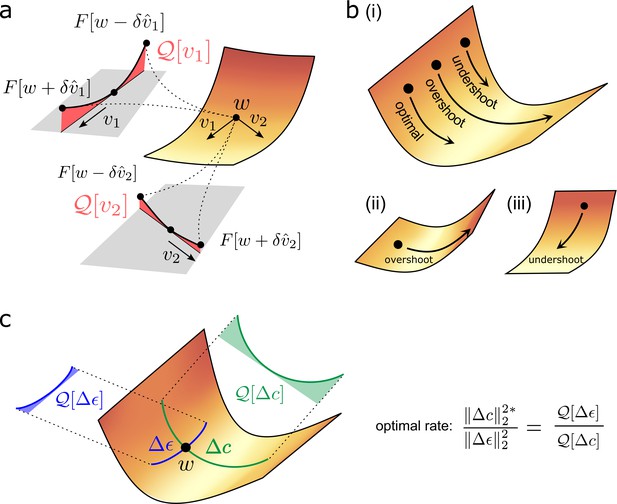
Quantifying effect of task error lanscape curvature on compensatory plasticity.
(a) Geometrical intuition behind the operator . The operator charts the degree to which a (normalised) direction is upwardly curved (i.e. lifts off the tangent plane depicted in grey). The red, shaded areas filling the region between the tangent plane and the upwardly curved directions are proportional to , and , respectively. (b) Compensatory plasticity points in a direction of locally decreasing task-error. Excessive plasticity in this direction can be detrimental, due to upward curvature (‘overshoot’). The optimal magnitude for a given direction is smaller if upward curvature (i.e. the -value) is large, as for cases (i) and (ii), and if the initial slope is shallow, as for case (ii). It is greater if the initial slope is steep, as for case (iii). This intuition underlies Equation (6) for the optimal magnitude of a given compensatory plasticity direction, which includes as a coefficient the ratio of slope to curvature. (c) Equation (11) depends upon the ratio of the upward curvatures in the two plasticity directions, , and . As illustrated, steep downhill directions often exhibit more upward curvature than arbitrary directions. In such cases, the optimal magnitude of compensatory plasticity should be outcompeted by synaptic fluctuations.
Figure 4
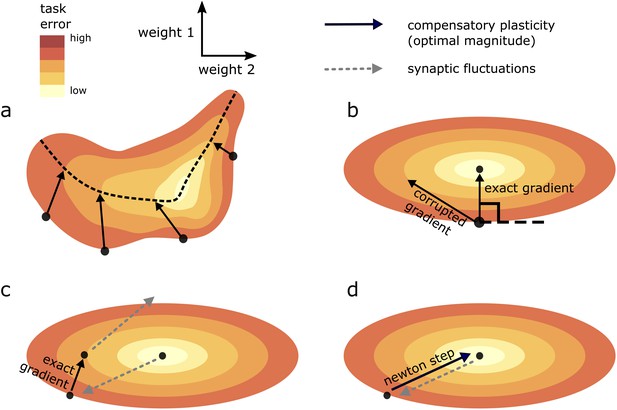
Geometric intuition for the optimal magnitude of different compensatory plasticity directions.
Colours depict level sets of the loss landscape. Elliptical level sets correspond to a quadratic loss function (which approximates any loss function in the neighbourhood of a local minimum). In c and d, we depict compensatory plasticity and synaptic fluctuations as sequential, alternating processes for illustrative purposes, although they are modelled as concurrent throughout the paper. (a) Compensatory plasticity directions locally decrease task error, so point from darker to lighter colours. Optimal magnitude is reached when the vectors ‘kiss’ a smaller level set, that is, intersect that level set while running parallel to its border. Increasing magnitude past this past this point increases task error, by moving network state to a higher-error level set. (b) If compensatory plasticity is parallel to the gradient (i.e. it enacts gradient descent), then it runs perpendicular to the border of the level set on which it lies (i.e. the tangent plane). This is shown explicitly for the ‘exact gradient’ direction of plasticity. The optimal magnitude of plasticity in this direction is smaller than that of a corrupted gradient descent direction, even though the former is more effective in reducing task error, because the exact gradient points in a more highly curved direction. (c) Synaptic fluctuations of a certain magnitude perturb the network state. The optimal magnitude of compensatory plasticity (in the exact gradient descent direction, for this example) is significantly smaller than that of the synaptic fluctuations, using the geometric heuristic explained in (a). If the magnitude of compensation increased to match the synaptic fluctuation magnitude there would be overshoot, and task error would converge to a higher steady state. (d) If compensatory plasticity mechanisms can perfectly calculate both the local gradient and hessian (curvature) of the loss landscape, then network state will move in the direction of the ‘Newton step’. In the quadratic case (elliptical level sets), this will directly ‘backtrack’ the synaptic fluctuations. Thus, the optimal magnitude of compensatory plasticity will be equal to that of the synaptic fluctuations. However, time delays in the sensing of synaptic fluctuations and limited precision of the compensatory plasticity mechanism will preclude this.
Figure 5 with 1 supplement
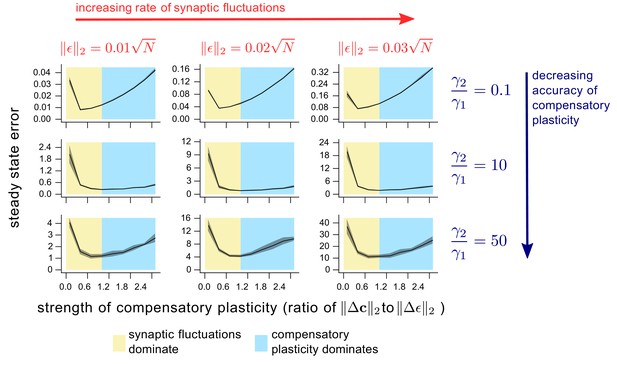
The dependence of steady state task performance in a nonlinear network on the magnitudes of compensatory plasticity and synaptic fluctuations, and on the learning rule quality.
Each value on a given graph corresponds to an 8000 timepoint nonlinear neural network simulation (see ‘Methods’ for details). The value gives the steady-state task error (average task error of the last 500 timepoints) of the simulation, while the value gives the ratio of the magnitudes of the compensatory plasticity and synaptic fluctuations terms. Steady state error is averaged across 8 simulation repeats; shading depicts one standard deviation. Between graphs, we change simulation parameters. Down rows, we increase the proportionate noise corruption of the compensatory plasticity term (see Materials and methods section for details). Across columns, we increase the magnitude of synaptic fluctuations.
Figure 5—figure supplement 1
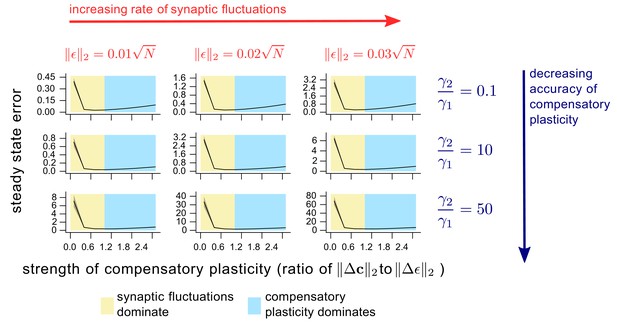
The dependence of steady state task performance in a linear network on the magnitudes of compensatory plasticity and synaptic fluctuations, and on the learning rule quality.
The description of this figure is identical to that of Figure 5. The only difference is the choice of network. Here, we use the linear networks as described in Methods.
Tables
Table 1
Synaptic plasticity rates across experimental models, and the effect of activity suppression.
| Reference | Experimental system | Total baseline synaptic change | % synaptic change that is activity / learning-independent |
|---|---|---|---|
| Pfeiffer et al., 2018 | Adult mouse hippocampus | 40% turnover over 4 days | NA |
| Loewenstein et al., 2011 | Adult mouse auditory cortex | >70% of spines changed size by >50% over 20 days | NA |
| Zuo et al., 2005 | Adult mouse (barrel, primary motor, frontal) cortex | 3–5% turnover over 2 weeks for all regions. 73.9 ± 2.8% of spines stable over 18 months (barrel cortex) | NA |
| Nagaoka et al., 2016 | Adult mouse visual cortex | 8% turnover per 2 days in visually deprived environment. 15% in visually enriched environment. 7–8% in both environments under pharmacological suppression of spiking. | (turnover) |
| Quinn et al., 2019 | Glutamatergic synapses, dissociated rat hippocampal culture | 28 ± 3.7% of synapses formed over 24 hr period. 28.6 ± 2.3% eliminated. Activity suppression through tetanus neurotoxin -light chain. Plasticity rate unmeasured. | (turnover) |
| Yasumatsu et al., 2008 | CA1 pyramidal neurons, primary culture, rat hippocampus | Measured rates of synaptic turnover and spine-head volume change. Baseline conditions vs activity suppression (NMDAR inhibitors). Turnover rates: 32.8 ± 3.7% generation/elimination per day (control) vs 22.0 ± 3.6% (NMDAR inhibitor). Rate of spine-head volume change: | (turnover). Size-dependent, but consistently >50% (spine-head volume) |
| Dvorkin and Ziv, 2016 | Glutamatergic synapses in cultured networks of mouse cortical neurons | Partitioned commonly innervated (CI) synapses sharing same axon and dendrite, and non-CI synapses. Quantified covariance in fluorescence change for CI vs non-CI synapses to estimate relative contribution of activity histories to synaptic remodelling | 62–64% (plasticity) |
| Minerbi et al., 2009 | Rat cortical neurons in primary culture | Created ‘relative synaptic remodeling measure’ (RRM) based on frequency of changes in the rank ordering of synapses by fluorescence. Compared baseline RRM to when neural activity was suppressed by tetrodotoxin (TTX). RRM: 0.4 (control) vs 0.3 (TTX) after 30 hr. | (plasticity) |
| Kasthuri et al., 2015 | Adult mouse neocortex (Three-dimensional post mortem reconstruction using electron microscopy). | Data on 124 pairs of ‘redundant’ synapses sharing a pre/post-synaptic neuron was analysed in Dvorkin and Ziv, 2016. They calculated the correlation coefficient of spine volumes and post-synaptic density sizes between redundant pairs. This should be one if pre/post-synaptic activity history perfectly explains these variables. | 77% (post-synaptic density, ). 66% (spine volume, ) |
| Ziv and Brenner, 2018 | Literature review across multiple systems | ‘Collectively these findings suggest that the contributions of spontaneous processes and specific activity histories to synaptic remodeling are of similar magnitudes’ |
Table 2
Table elements highlighted in teal correspond to scenarios in which our main claim holds, as Equation (11) is satisfied.
| Quadratic | Nonlinear , low steady-state error | Nonlinear , high steady-state error | |
|---|---|---|---|
| 0th order algorithm | |||
| 0st order algorithm | |||
| 0nd order algorithm |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Optimal plasticity for memory maintenance during ongoing synaptic change
eLife 10:e62912.
https://doi.org/10.7554/eLife.62912
