Learning precise spatiotemporal sequences via biophysically realistic learning rules in a modular, spiking network

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record updated: March 13, 2023 (This version)
Version of Record published: March 18, 2021 (Go to version)
Accepted: February 16, 2021
Received: October 6, 2020

1. Of interest
ACC neural ensemble dynamics are structured by strategy prevalence

Mikhail Proskurin, Maxim Manakov, Alla Karpova

Research Article Dec 7, 2023
Further reading

Abstract
Introduction
Results
Discussion
Materials and methods
Data availability
References
Decision letter
Author response
Article and author information
Metrics

Abstract

Multiple brain regions are able to learn and express temporal sequences, and this functionality is an essential component of learning and memory. We propose a substrate for such representations via a network model that learns and recalls discrete sequences of variable order and duration. The model consists of a network of spiking neurons placed in a modular microcolumn based architecture. Learning is performed via a biophysically realistic learning rule that depends on synaptic ‘eligibility traces’. Before training, the network contains no memory of any particular sequence. After training, presentation of only the first element in that sequence is sufficient for the network to recall an entire learned representation of the sequence. An extended version of the model also demonstrates the ability to successfully learn and recall non-Markovian sequences. This model provides a possible framework for biologically plausible sequence learning and memory, in agreement with recent experimental results.

Introduction

So long as time flows in one direction, nature itself is fundamentally sequential. To operate in this reality, the brain needs to think, plan, and take action in a temporally ordered fashion. When you sing a song, hit a baseball, or even utter a word, you are engaging in sequential activity. More accurately, you are engaging in sequential recall of a learned activity – your actions not only have 'a' temporal order and duration but 'the' temporal order and duration which you learned. Hence, the question of how sequence representations are learned, stored, and recalled is of fundamental importance to neuroscience. Recent evidence has shown that such learned representations can exist in cortical circuits (Gavornik and Bear, 2014; Xu et al., 2012; Cooke et al., 2015; Eagleman and Dragoi, 2012; Yin et al., 2008), begging the question: through what sort of circuits and learning paradigms can these representations arise?

To address these questions, we introduce a modular spiking network that can robustly learn and recall both the order and duration of elements in a sequence, via a local and biophysically realistic eligibility trace-based learning rule. Although the parts of the model’s construction are based upon recent experimental observations in visual cortex (Gavornik and Bear, 2014; Xu et al., 2012; Cooke et al., 2015), utilizing observed cell types (Shuler and Bear, 2006; Liu et al., 2015; Chubykin et al., 2013) and laminar structure (Potjans and Diesmann, 2014; Binzegger et al., 2009), many of its key aspects (modularity, heterogenous representations) are illustrative of general principles of sequence learning. The ability of the network to internally learn and recall both duration and order, along with its use of a local learning rule that bypasses the need for constant and explicit targets, differs from most historical and contemporary models of sequence learning (Fiete et al., 2010; Pereira and Brunel, 2019; Klos et al., 2018; Jun and Jin, 2007; Liu and Buonomano, 2009; Maes et al., 2020; Murray and Escola, 2017; Martinez et al., 2019; Rajan et al., 2016; DePasquale et al., 2018; Laje and Buonomano, 2013; Sussillo and Abbott, 2009; Nicola and Clopath, 2017). We also present an extended formulation of the model, which is capable of learning and recalling sequences with non-Markovian (i.e. history-dependent) transitions.

A variety of different models have been proposed to account for the representation and learning of sequences. Most of these models fall into one of two classes: chain structures or recurrent neural networks (RNNs). Chain structure models of neural sequence learning operate in a method akin to synfire chains (Abeles, 1991) – that is, representations of different individual stimuli are linked together, in order, via feed-forward synaptic connections (Fiete et al., 2010; Pereira and Brunel, 2019; Klos et al., 2018; Jun and Jin, 2007; Liu and Buonomano, 2009). These models can be formulated either via an explicit neuron to neuron chain or via an implicit embedding in a random network. While such a chain-like structure can readily encode order, there is nothing internally encoding start times, stop times, or durations of the individual elements of the sequence. Some models use the resulting activity chain as a temporal basis or ‘clock’, upon which elements and their durations can be learned at the level of the output, but the fragility of the chain itself can make such output representations very sensitive to noise (Liu and Buonomano, 2009). Other models have attempted to address these issues via ad hoc solutions such as variable adaptation time constants (Martinez et al., 2019), but these typically require the network to have a priori information about the sequence it will be representing.

RNNs are another common class of sequence learning models (DePasquale et al., 2018; Laje and Buonomano, 2013; Sussillo and Abbott, 2009; Nicola and Clopath, 2017). Unlike explicit feed-forward chain models, RNNs learn complex sequences by leveraging rich, dynamical representations to approximate target outputs. RNNs are fully capable of encoding duration and order, and can embed multiple sequences at once. However, common learning rules for these models, such as backpropagation through time (BPTT) or FORCE, are biologically unrealistic, as they require some combination of non-local information, precise and symmetrical feedback structures, and/or explicit feedback about the targets at every time point (Whittington and Bogacz, 2019). Interestingly, recent work has shown that networks can under some conditions learn inputs via random feedback connections rather than backpropagation (Lillicrap et al., 2016), but this random feedback is less effective than BPTT for learning sequences with long time scales (Murray, 2019).

Experimentally, the expression of sequences in the brain often follows a compressed encoding, in which order is represented but duration is not, and sequences are replayed with a time scale dictated by the intrinsic time scales of the circuit (Foster and Wilson, 2006; Skaggs and McNaughton, 1996; Davidson et al., 2009; Ji and Wilson, 2007). Such results can be accounted for by chain-like models. However, there are also many cases where neural sequences are learned and replayed at or near their behavioral time scale (Gavornik and Bear, 2014; Louie and Wilson, 2001; Eichenlaub et al., 2020; Dave and Margoliash, 2000), for which a simple ordered chain is insufficient. To account for this latter phenomenon, our model takes elements from both chain and recurrent models in order to establish a new, hybrid framework for sequence learning. Our model’s chain-like, modular structure enables it learn the order of elements, while the recurrent structure within that chain allows it to internally and flexibly learn those elements’ duration. The structure of our network allows us to use a local, biophysically realistic learning rule to adjust the synaptic weights. A transient sequential input is presented during training, and over the course of training, our learning rule causes the weights to reach fixed points. After training, the network can then recall the uncompressed transient activity of the sequential input, complete with both duration and order, upon only partial reactivation (e.g. stimulating only the first element in the sequence).

Results

A model for sequence learning based on modular architecture and eligibility trace learning

Any model that can account for learning of behavioral temporal sequences must provide answers to a simple set of questions: what measures the timing of each event in a sequence? How is that information passed to the next, or the same computational unit? What mechanism provides the appropriate delay? How are all of these elements, the order, duration, and specific timing, learned from experience? In a traditional ‘chain-like’ network with Hebbian learning, order of presented stimuli can be readily encoded by learning directional feed-forward connections between populations. However, this simple architecture proves insufficient for internally representing the duration of presented stimuli and their specific start and end times, as intrinsic time constants determine the speed at which the signal travels through the network (Murray and Escola, 2017; Martinez et al., 2019).

This issue is illustrated in Figure 1. In this schematic model, each module responds to a specific external stimulus. An external sequence activates these different modules in a given order and with externally determined durations for each element (Figure 1a). Learning can change the feed-forward synaptic efficacies between modules to reflect the order of the presented stimuli. Upon recall, triggered by activating the first stimulus, each of the encoded stimuli are activated at the correct order. However, the duration of activation within the module, as well as the timing of the activation of the subsequent module, is determined by the intrinsic time constants of the network (Figure 1b), causing a temporal compression of the recalled sequence. While certain time constants, asymmetrical inhibition, or adaptation with slow time constants could be manually placed in the network to facilitate recall of the particular sequence in Figure 1a, there does not yet exist a realistic, robust, and general solution to this problem.

Figure 1

Download asset Open asset

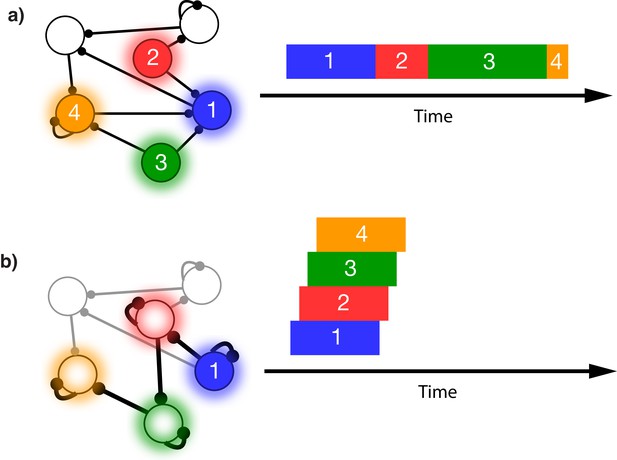
Sequence representation in networks.

(a) A network composed of different populations of cells, each population is activated by a specific stimulus, and there are plastic connections between and within these populations. Initially these connections are random and weak. Upon presentation of a sequence of stimuli (filled circles, left), the populations will become activated for the duration and in the order in which they are stimulated (right). (b) After many presentations of a particular sequence, successful asymmetric Hebbian learning encodes the order of the stimuli into the synaptic weights of the network. After training, upon presentation of the first element of the sequence (filled circle, left), the network can recall (right) the order of presentation, but the timing and duration of each element is lost. In a generic network such as this, the timing of recall is determined by intrinsic time constants of the system and not the duration in the sequence that was presented.

In this work we present a network of spiking neurons that can learn the order, duration, and specific timing of sequence elements. This model uses local and biophysically realistic learning rules, in contrast to most RNN models (DePasquale et al., 2018; Laje and Buonomano, 2013; Sussillo and Abbott, 2009; Nicola and Clopath, 2017). As in the ‘chain-like’ models, the order is learned by modifying the feed-forward synaptic efficacies between modules. Unlike those models, the duration of each element is learned via modification of the recurrent connections within each module (Fiete et al., 2010; Pereira and Brunel, 2019; Klos et al., 2018). However, these two components are still not sufficient in order to avoid sequence compression during recall. In order to solve this problem, we assume additional structure within each module and in the allowed connections between modules. This additional structure allows us to avoid compression during recall while using relatively simple local learning rules. Consequently, the cellular response types generated by this network are consistent with experimental observation (Shuler and Bear, 2006; Liu et al., 2015), as described below.

Our network is composed of different modules that are selectively activated via feed-forward connections by different external stimuli. Within each module, there are two populations of excitatory cells as well as inhibitory cells (Figure 2a). The excitatory cells in both populations are identical in their intrinsic properties but differ in their learned and fixed connections with other cells within the module and in different modules. We name these two excitatory populations ‘Timers’ and ‘Messengers’ – the reason for these terms will become clear below as we describe their roles within the network. The ‘Timer’ cells learn strong recurrent connections with other Timer cells within the module. This strong recurrent connectivity results in long-lasting transient activity, which is used to represent the duration of a given stimuli. Previous studies have analyzed in detail the relationship between recurrent connectivity and duration of resulting transient activity following a stimulus (Gavornik et al., 2009; Gavornik and Shouval, 2011). Timers also excite the inhibitory cells and the ‘Messenger’ cells. Since the inhibitory cells receive input from the Timers, they have roughly the same temporal profile. However, inhibitory cells in the module decay slightly more quickly than their Timer counterparts, thanks to a combination of shorter time constants for synaptic activation (80 ms for excitatory, 10 ms for inhibitory), and small Timer to inhibitory weights (there are a number of degenerate sets of parameters which can facilitate quickly decaying inhibitory cells) (Huertas et al., 2015) (see 'Materials and methods' and Supplementary materials for more details). Owing to this temporal offset, Messenger cells selectively fire at the end of the Timers’ transient activity, since they receive input from both the Timer cells and the (faster decaying) inhibitory cells. The temporally specific profile of the Messenger cells enables them to convey a temporally specific transition between elements, via learned feed-forward connections to Timer cells in other modules. The Timer/inhibitory/Messenger modular architecture can be constructed in a number of redundant ways, including simply via random distributions of connections (see previous work (Huertas et al., 2015) for a more detailed analysis).

Figure 2

Download asset Open asset

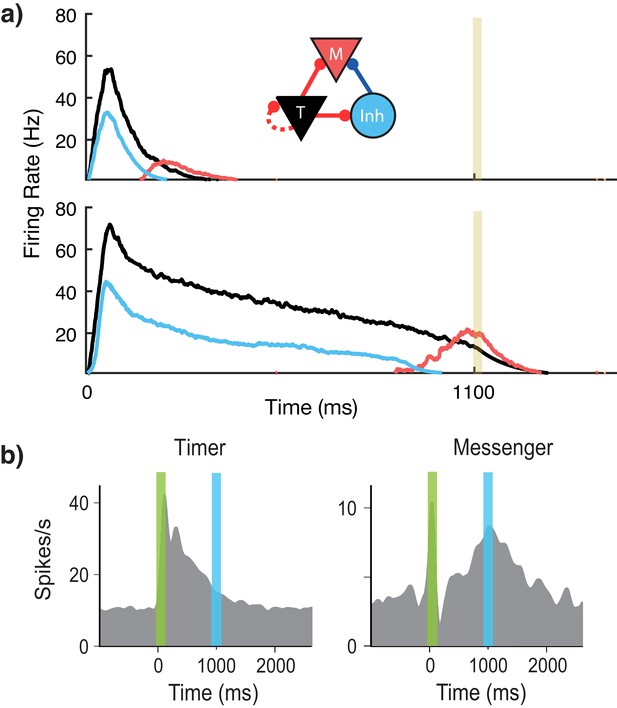
Microcircuit learns time intervals.

(a) Mean firing rates of Timer (black), Messenger (red), and inhibitory populations (light blue) in a microcircuit before learning (top) and after learning (bottom) to represent an 1100 ms interval. Inset: Core neural architecture (CNA) microcircuit. Solid lines indicate fixed connections, while dotted lines indicate learned connections. (b) Timer and Messenger cell type responses to delayed reward task in V1. Green bar represents stimulus and blue bar represents reward. Schematic representation of data from Liu et al. (2015).

For learning, we use a previously described reinforcement learning rule based on two competing, synapse-specific, Hebbian-activated eligibility traces (Huertas et al., 2016; He et al., 2015): one for long-term potentiation (LTP) and one for long-term depression (LTD) (see 'Materials and methods'). The presence of Hebbian activity at a given synapse activates the two traces at different rates (and to different saturation levels), and the absence of Hebbian activity causes the traces to decay at different rates. The change in synaptic weight is determined simply by the difference in these traces upon presentation of a reinforcement signal. We have assumed that on every transition between external stimuli, a ‘novelty’ signal causes a global release of a neuromodulator, which acts as a reinforcement signal (see 'Materials and methods'). The assumption of a temporally precise but spatially widespread neuromodulatory signal might seem at odds with common notions of temporally broad neuromodulator release, but they are indeed consistent with recent recordings in several neruomodulatory systems (Howe and Dombeck, 2016; Hangya et al., 2015). Eligibility traces for LTP have been found in multiple brain regions (Yagishita et al., 2014; Bittner et al., 2017; Brzosko et al., 2017), and eligibility traces for both LTP and LTD have been found in both visual and prefrontal cortex (He et al., 2015). We have used this rule because it can solve the temporal credit assignment problem, allowing the network to associate events distal in time, and because it reaches fixed points in both recurrent and feed-forward learning tasks (Huertas et al., 2016).

Using this rule and the described architecture within a single module, we find (Figure 2a) that the network naturally generates cells that learn to be active for the duration of the stimulus (Timers), and other cells that activate toward the end of the stimulus duration (Messengers). The Timer cells learn the duration of the stimulus via changes in the excitatory synaptic efficacies within the Timer population. The Messenger cells evolve their specific temporal profile due to the temporal profiles of their fixed excitatory and inhibitory inputs from the Timer cells and the inhibitory cells. These results are consistent with experimental observations in V1 circuits that learn the duration between a stimulus and a reward (Shuler and Bear, 2006; Liu et al., 2015; Chubykin et al., 2013), as shown in Figure 2b. These results replicate our previous results (Huertas et al., 2015) which used a learning rule with a single trace (Gavornik et al., 2009).

This modular microcircuit, in which both Timer and Messenger cells emerge from learning, acts as a ‘core neural architecture’ (CNA) (Huertas et al., 2015), an elemental package of basic temporal neural responses which can then be used within the larger network to create more complicated representations. This CNA functions as the basic microcircuit for our sequence model, and each ‘element’ of an input sequence is represented by one of these CNA circuits. One must note that the individual CNAs are plastic, as their temporal properties are not fixed but adapt to the environment, through recurrent learning in the Timer population. In a structure akin to the microcircuits found in cortical columns (Potjans and Diesmann, 2014), this model places distinct CNAs sensitive to particular visual stimuli in a columnar structure, as shown in Figure 3a. To prevent spurious excitation in our noisy, spiking network, there is soft winner-take-all (WTA) inhibition between the columns (see 'Materials and methods' and 'Discussion' for more details). When presenting a sequence of visual stimuli, different CNAs in turn become activated in sequence. Timer cells within those CNAs learn the duration of their particular stimuli via recurrent connections, while order is learned via feed-forward connections from Messengers in one column to Timers in a subsequently presented column. We will show that this modular architecture can overcome the problem of sequence compression encountered by ‘chain-like’ models.

Figure 3 with 6 supplements see all

Download asset Open asset

Sequence learning and recall.

(a) Network of 12 columns, each containing a core neural architecture (CNA) microcircuit selective for a different stimulus. Columns containing microcircuits responding to blue, red, green, and orange stimuli are indicated. (**b–e**) Mean firing rates for Timer cells (light colors) and Messenger cells (dark colors) of four different columns during different stages of learning. Stimuli presented are shown as color bars in the top of plots. During learning, columns are stimulated in the sequence indicated by the color bars (500, 1000, 700, and 1800 ms for blue, red, green, and orange, respectively). (b) Before learning, the stimulation of a particular column only causes that column to be transiently active. (c) During the first trial of learning, all columns in the sequence become activated by the stimuli but have not yet learned to represent duration (through recurrent learning of Timer cells) or order (through feed-forward learning of the Messenger cells). (d) After many trials, the network learns to match the duration and order of presented stimuli. (e) After learning, presenting the first element in the sequence is sufficient for recall of the entire sequence. Figure 3—figure supplements 1–6 provide additional information on the network’s construction, accuracy, robustness, spiking statistics, dynamics, and limits.

Learning and recalling the order and variable duration of presented sequences

Using the above described architecture and learning rule (see 'Materials and methods' for more details), the network is capable of robustly learning sequences of temporal intervals. Figure 3 shows the network learning a sequence of four different elements, of duration 500, 1000, 700, and 1800 ms. The different stimuli here are labeled by color (blue, green, red, orange), and there are four corresponding columns in the network (out of 12) which are sensitive to these stimuli. In this example, the inputs are modeled after lateral geniculate nucleus (LGN) responses to spot stimuli (Ruksenas et al., 2007; Mastronarde, 1987, see Figure 3—figure supplement 1), but more generally one may consider these stimuli to be oriented gratings, specific natural images in a movie, or non-visual stimuli such as pitches of sounds in a song.

Before learning, presentation of the blue stimulus only produces a transient response in the CNA microcircuit housed in the blue-sensitive column (Figure 3b). During learning (Figure 3c,d), a sequence of stimuli is presented, and microcircuits in their respective columns learn to represent the duration of the stimulus which activates them. The different microcircuits also learn to ‘chain’ together in the order in which they were stimulated. After learning, presentation of the blue stimulus triggers a ‘recall’ of the entire sequence (Figure 3e): blue for 500 ms, red for 1000 ms, green for 700 ms, and orange for 1800 ms. The network is capable of learning sequences of temporal intervals where the individual elements can be anywhere from ~300 to ~1800 ms (see Figure 3—figure supplement 2) in duration, which agrees with the observed ranges used for training V1 circuits (Gavornik and Bear, 2014; Shuler and Bear, 2006). Additional examples of learned sequences are shown in Figure 3—figure supplement 3.

The network itself shows realistic spiking statistics, with interspike interval coefficients (ISIs) of variation near 1. Figure 3—figure supplement 4 shows both spike rasters and ISIs for a single recall trial. The resulting firing rates are also roughly consistent with the experimentally observed Timers and Messengers (Figure 2).

In simulations we have been able to learn a sequence of up to eight elements (Figure 3—figure supplement 5). The upper limit on the number of elements which can be learned in a sequence has not been fully explored due to the computational time required. For this work, sequences of four elements were chosen to match experimental results (Gavornik and Bear, 2014). The model presented here is a high dimensional spiking model, but similar results are obtained with a low dimensional rate model in which the activity of each population is presented by a single dynamical variable (for details, see 'Materials and methods' and Figure 3—figure supplement 6).

To gain an understanding of why learning succeeds in this model, we focus on the learning occurring between and within two selected modules in a sequence (Figure 4). Before training, presentation of an isolated stimulus only evokes a transient response of the CNA sensitive to that specific stimulus, since the Timer cells have yet to learn any recurrent connections, and the Messenger cells have yet to establish any feed-forward connections to the Timer cells in other columns (Figure 4a). During training, a particular sequence of inputs is presented and then repeated over many trials. Hebbian activity in the network triggers activation of synapse-specific LTP and LTD associated eligibility traces, which are then converted into changes in synaptic connections upon neuromodulator release (purple arrows in Figure 4), occurring here closely after a change in stimuli (see Equations 8, 9, and 14 in 'Materials and methods'). Each trial pushes the weights in the network toward their fixed points (Equations 17 and 18 in 'Materials and methods'). Hebbian activity within the Timer population causes activation of their respective eligibility traces, and subsequently an increase in their recurrent connections (Figure 4—figure supplement 1). As these lateral connections grow, Timer cells sustain their activity for longer, ‘extending’ their firing profile out in time toward the neuromodulator signal associated with the start of the subsequent stimulus. As this occurs, Messenger cells get ‘dragged’ along by the Timer cells, eventually coactivating with Timer cells of the column which is stimulated next (Figure 4b). This Hebbian coactivation triggers the eligibility traces of these feed-forward synaptic connections, before they too are converted into synaptic weight changes by the neuromodulator ‘novelty’ signal (Figure 4—figure supplement 2). After many trials (50–100 for the examples in this paper), weights in the network reach their steady-state values (see 'Materials and methods', Figure 3—figure supplement 2) and learning is complete. As the result of successful learning, a physical synaptic pathway has been traced out which encodes both the duration and order of the input. After learning, the encoded sequence can be recalled by stimulation of only the first element (Figure 4c). Importantly, recall does not demonstrate sequence compression, as the Messenger cells’ activation (and thereby the activation of the next element) is appropriately temporally delayed.

Figure 4 with 2 supplements see all

Download asset Open asset

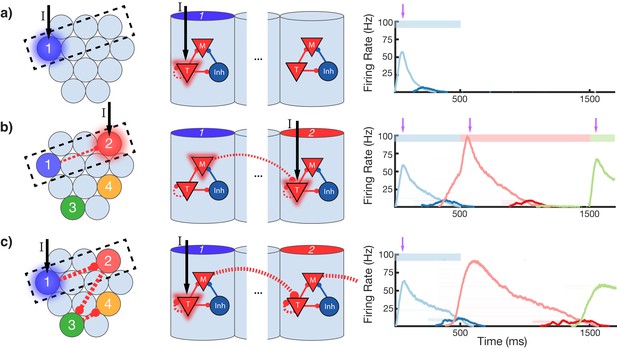
Change in connectivity patterns resulting from learning.

(a) Before, (b) during, and (c) after learning a sequence. Left, view of columnar structure and learned intercolumnar connections. Dotted box indicates region shown in side view, middle. Middle, the detailed view of two columns and their core neural architectures (CNAs) and learned intracolumnar connectivity. Dotted lines indicate learned connections, continuous lines indicate fixed connections. Right, illustration of mean firing rates for color coded columns. Light colors indicate Timer cells, dark colors indicate Messenger cells. Color bars indicate stimulated columns. Purple arrows indicate global neuromodulator release. (a) Before learning, stimulus of a column's Timer (T) cells only causes that column to be transiently active. (b) If another column is stimulated shortly after the first, the Messenger (M) cells of the previous column will be coactive with the Timer cells of the stimulated column, thereby increasing the feed-forward synaptic weights between these two populations. (c) After learning, a physical synaptic pathway has been traced out which links columns in the temporal order in which they were stimulated during training. Figure 4—figure supplements 1 and 2 demonstrate the dynamics of trace learning in the recurrent and feed-forward cases, respectively.

Properly encoded durations and orders are the result of the fixed points in the learning rule, as described in the 'Materials and methods' section and in previous publications (Gavornik and Shouval, 2011; Huertas et al., 2016). Recurrent learning ends in a fixed point which sets the time D between the end of firing in one column and the start of firing in the next (see Equation 17, Figure 4—figure supplement 1). Feed-forward learning results in a fixed point which determines the connection strength between Messenger and Timer cells in subsequent columns (see Equation 18, Figure 4—figure supplement 2). Formally, the fixed point sets the value of the Hebbian term, $H_{i j}$ = $r_{i} \cdot r_{j}$ , between the Messenger cells and the Timer cells in the next column at the time of reward, and implicitly this results in setting the connection strengths $W_{i j}$ . Both these fixed points depend on the parameters of the learning rule, which can be chosen such that these terms achieve desired values (D arbitrarily small, $H_{i j}$ to a fixed value at time of reward). Such learning can then correctly encode any presented sequence. Earlier work examines in detail the dependence of D on network parameters (Gavornik and Shouval, 2011; Huertas et al., 2016; He et al., 2015).

Empirically, temporal accuracy of recall depends on many non-trivial factors (i.e. length of individual elements, length of entire sequence, placement of short elements near long elements, etc.), owing to the many non-trivial effects of stochasticity of the spiking network (spike rasters are shown in Figure 3—figure supplement 4). In addition to fluctuations in recall accuracy, there can also be fluctuations in learning accuracy, as randomness in spiking can happen to accumulate such that the traces (and therefore the fixed points) are also sufficiently modified over the course of training. Over the whole network, over the course of many trials, and over the course of learning instances, these effects tend to wash out. Reported times in the recalled sequence generally match the times of the input sequence to within 10% (see Figure 3—figure supplement 2). This model does not observe any intrinsic bias toward over- or under-predicting, as this can be modulated by network parameters and can change stochastically from trial to trial or from element to element.

Our model also exhibits robustness to changes in its parameters. In Figure 5, we demonstrate the network successfully recalling a learned four element sequence, in which the fixed connections that establish the Timer and Messenger cells are modified by +/- 20%. Furthermore, the mean reported time in a two-column network is conserved after application of random fluctuations to the learning parameters (Figure 5—figure supplement 1). In addition, the network can also function if the synaptic time constant for excitatory connection is shortened from 80 to 20 ms (Figure 5—figure supplement 2). A long time constant of excitatory connections is often used in models of working memory (Lisman et al., 1998) and models of long-lasting but transient recurrent networks (Gavornik et al., 2009; Gavornik and Shouval, 2011). Such long time constants make the network mode robust, able to learn longer transient durations and to operate in a more physiological range (Wang, 2001), and there is evidence for such time constants in some brain regions (Wang et al., 2013). Nevertheless, our network can operate with faster excitatory time constants (Figure 5—figure supplement 2), but shorter synaptic time constants limit the duration of elements that can be learned.

Figure 5 with 2 supplements see all

Download asset Open asset

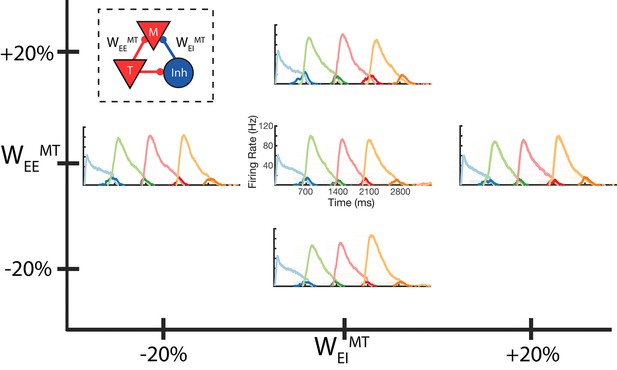
Robustness to core neural architecture (CNA) weight changes.

Firing rates of four columns, after learning a four element sequence, each of 700 ms duration. Only the first element is stimulated for recall. Before learning, static CNA weights W_EE^MT and W_EI^MT are either set as in Supplementary file 1 (center plot), or independently adjusted +/– 20% from their values in Supplementary file 1. In each of the four ‘modified’ cases, sequence learning is still successful and retains the correct timing. The most noticeable difference is along the W_EE^MT axis, where the amplitude of the Messenger cells can be seen to increase as W_EE^MT increases. Inset: CNA microcircuit with labeled connections. Figure 5—figure supplement 1 demonstrates a two-column network’s robustness to random variations in the learning parameters. Figure 5—figure supplement 2 shows the success and failure cases for a network with a 20 ms excitatory time constant.

While the results shown in this work were obtained using a two-trace learning (TTL) rule, the network can also be trained with a learning rule based on a single trace (Gavornik et al., 2009; Gavornik and Shouval, 2011), and the results are similar to those demonstrated here (one-trace results not shown).

Learning and recalling non-Markovian sequences

In the modular network described above, the transitions from each module to the next depend only on the identity of the current module that is active; such a model is formally called a Markovian model (Gillespie, 1991). While the Markov property is typically discussed in the context of probabilistic models, here we apply it to deterministic sequences as well. A Markovian model can only reproduce specific types of sequences and is unable to reproduce a sequence in which the same element is repeated more than once and is followed each time by a different element, for example, the sequence ABAC. The columnar network described above is essentially Markovian since activation of a neural population will necessarily feed forward to all other populations it is connected to, no matter the history or context. Behaviorally, learning of non-Markovian sequences is ubiquitous, and cells responsible for producing and learning non-Markovian sequences exhibit non-Markovian activation (Cohen et al., 2020).

To learn non-Markovian sequences, we modify the network structure while maintaining local learning rules. Ideally, the network should be able to learn sequences which are in themselves non-Markovian (ABACAD), as well as simultaneous combinations of sequences which are non-Markovian when learned together (ACE and BCD). We will demonstrate both cases here.

For the network to learn and recall non-Markovian sequences, it must somehow keep track of its history and use this history to inform transitions during sequence learning and recall. To this end, we include two additional stages to the network (Figure 6). The first is a fixed (non-learning) recurrent network, sometimes called a ‘reservoir’ (as in reservoir computing) or a ‘liquid’ (as in a liquid state machine) ( Maass et al., 2002; Maass et al., 2004), which receives inputs from the Messenger cells in the main columnar network. Owing to these inputs and due to its strong recurrent connectivity, the current state of the reservoir network is highly dependent on the history of network activity. Therefore, it acts as a long-term memory of the state of the columnar network. The second additional stage is a high dimensional, sparse, non-linear network which receives input from the reservoir, serving to project the reservoir states into a space where they are highly separated and non-overlapping. The result is that a given pattern in this sparse network at time t uniquely identifies the history of the main network up to and including time t. Since these patterns are highly non-overlapping (due to the sparsity and non-linearity), a particular pattern at time t can use simple, local, and biophysically realistic Hebbian learning to connect to Timer cells firing at time t + Δ $∆$ t in the main network (direct Messenger to Timer feed-forward learning is removed in this non-Markovian example).

Figure 6

Download asset Open asset

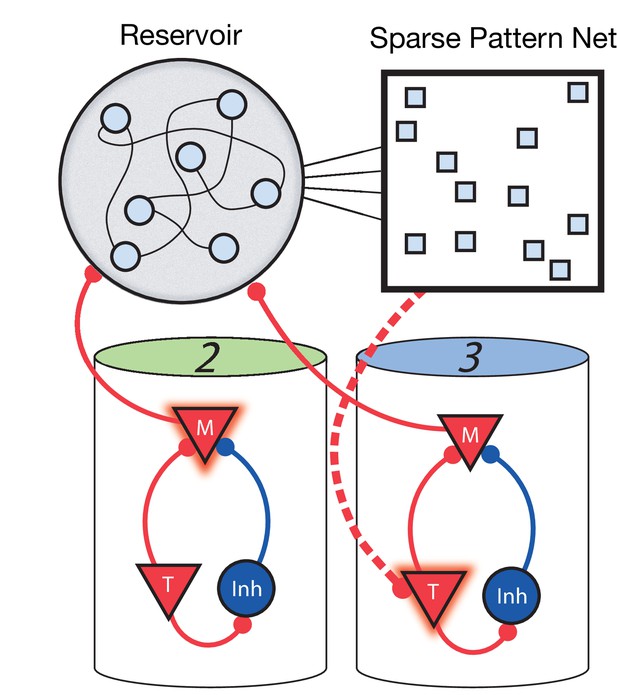
Non-Markovian sequence learning and recall.

Three-stage network. Two sequentially activated columns (2–3) learn to connect to each other through a reservoir and sparse pattern net. At time t, Messenger cells from column 2 are active and act as inputs into the reservoir (earlier, Messenger cells from column 1 also fed into the reservoir). The sparse pattern net receives input from the reservoir, so as to be a unique representation of the history of the network up to and including time t. Timer cells active at t + Δt (column 3) connect to the sparse pattern via Hebbian learning.

We test the ability of this three-stage network to learn long, non-Markovian sequences with repeated elements by presenting a sequence blue-green-blue-red-blue-orange (BGBRBO) during training (Figure 7). A simplified, rate-based version of the columnar network is used to reduce computation time (see 'Materials and methods). The presented sequence is such that there are three different transitions from blue to another element, and each stimulus is also presented for a different duration, making this a non-trivial problem. Before learning (Figure 7a), the blue stimulus does not evoke any recall, only triggering a transient response of the blue-responsive column. During learning (Figure 7b,c), Timer cells learn the duration of their stimulus, as before, but now it is the sparse pattern net which is using Hebbian learning to feed forward to Timers in subsequently stimulated columns. After learning (Figure 7d), external input to the blue stimulus is sufficient to trigger recall of the entire trained non-Markovian sequence. In this case, each blue element in the sequence has the same duration; this is owing to the fact that our TTL rule currently only supports one dynamic attractor per population. In order for repeated elements to have different durations during recall, an appropriate learning rule must be capable of creating multiple attractors within that element’s Timer population, with each attractor triggering a different duration of activity.

Figure 7

Download asset Open asset

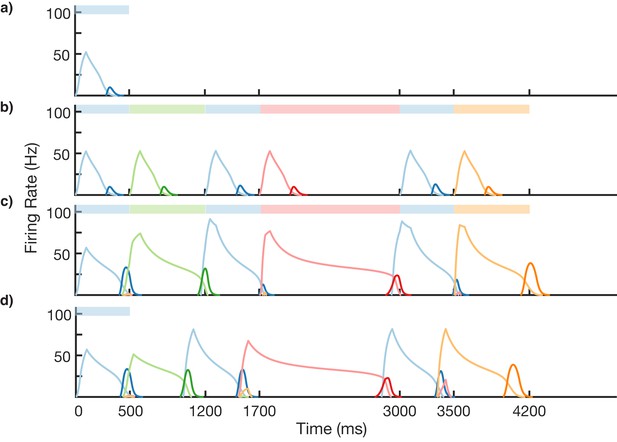
Non-Markovian sequence learning and recall.

Mean firing rates for Timer cells (light colors) and Messenger cells (dark colors) of four different columns during different stages of learning (before, first trial of learning, last trial of learning, after learning). Stimuli presented are shown in color bars inset in top of plots (500, 700, 500, 1300, 500, and 700 ms for blue, green, blue, red, blue, and orange, respectively).

We also demonstrate an example of simultaneous learning of two sequences with a shared element (Figure 8). First, a sequence blue-red-orange (BRO) is trained, and then a sequence green-red-purple (GRP) is also learned. Each of the elements in these sequences has a duration of 500 ms. With both these sequences learned and stored simultaneously in the same network, transitions from red are non-Markovian – red should transition to orange if it was preceded by blue and should transition to purple if it was preceded by green. Figure 8a shows recall upon stimulation of blue, while Figure 8b shows recall upon stimulation of green. In both cases, the sequence makes the correct transition from red to the appropriate third element. Recall of both sequences is also robust to perturbations in the initial state of the reservoir, as shown in (Figure 8—figure supplement 1.)

Figure 8 with 1 supplement see all

Download asset Open asset

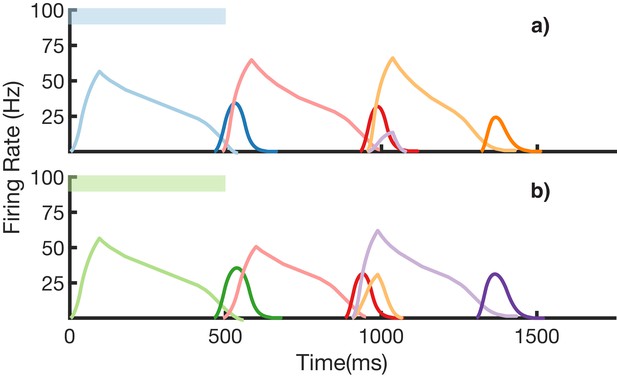
Recall of two overlapping sequences.

Mean firing rates for Timer cells (light colors) and Messenger cells (dark colors) during recall of two sequences. Both blue-red-orange (BRO) and green-red-purple (GRP) have been stored in the network via learning. (a) Recall of BRO, following presentation of a blue stimulus. (b) Recall of GRP, following presentation of a green stimulus. Note that R transitions to a different element in the two sequences. Figure 8—figure supplement 1 demonstrates the network’s robustness to perturbations of the reservoir’s initial state.

Of note in these two simulations is that the ‘incorrect’ transitions do get slightly activated, as the sparse patterns responsible for these transitions are not completely non-overlapping. There is an interplay here between the robustness and uniqueness of these patterns – the sparser they are, the more non-overlapping they are, but also the more sensitive they are to noise. Other parameters in the model, such as the level of recurrence in the reservoir, or the projection strengths from the reservoir to the sparse net, also affect the robustness/uniqueness of the patterns. For the simulations shown, a set of parameters (Supplementary file 2) was empirically chosen so that a handful of non-Markovian transitions could be reliably encoded. Though we have not optimized the network parameters, or fully characterized its properties, these results demonstrate that such an architecture can overcome the problem of non-Markovian sequences.

The addition of the reservoir and sparse network is essential for the ability to encode and replay non-Markovian sequences, but they alone are not sufficient for sequence learning and recall in our model. One must note that the reservoir receives its input from the modular network, not from the environment, and therefore if the modular network does not learn, the inputs to the reservoir would not be generated appropriately. In this formulation, during learning, the entire sequence is presented as inputs, but to trigger recall after learning, only the first element of the learned sequence is presented. In short, the input during learning and recall is different. Typical reservoir computing models can learn an output, given a specific input signal, but if that input signal changes, then so would the resulting output. This means that typically the reservoir alone cannot learn to recall with only the first element of the sequence as input, given that it was presented the whole sequence during training.

We use rate-based versions of all three stages for simplicity and computational efficiency, but a spiking based model is likely to have similar results. In our Markovian modular model described above, we use a fully spiking model. The rate-based approximation, which we use here in the non-Markovian case, is shown to produce similar results (Figure 3—figure supplement 6). The reservoir itself does not learn and needs only to be highly recurrent to recapture the demonstrated functionality. Therefore, a spiking implementation is likely to work, albeit using many more neurons and at a much higher computational cost. The sparse network as used here is binary (see 'Materials and methods'), but non-binary sparse representations are likely to produce similar results. Transitioning all three stages to using actual spiking neurons would require much time, computational power, and parameter adjustments, but there are no clear fundamental roadblocks to doing so.

We have chosen this simple sparse representation of this three-stage network, not because it is a biophysically realistic implementation but in order to demonstrate the concept that such an addition is sufficient for learning and expressing non-Markovian sequences, while still using local learning rules. The viability of this relatively simple, compartmentalized structure demonstrates two things: first, that our original columnar network can be used as a building block in more complicated tasks, and second, that even a complex task such as learning non-Markovian sequences does not require non-local learning rules to perform. There are, in general, likely a large number of architectures which would effectively achieve a similar aim – take a very complex problem like non-Markovian sequence learning and constrain the possible solution space, allowing for a local learning rule to ‘finish the job’. Other groups have approached non-Markovian sequences by including additional hierarchy or long synaptic time constants (Hawkins and Ahmad, 2016; Tully et al., 2016), and solutions like RNNs handle such sequences natively (albeit with non-local learning rules) since they are continuous systems with a dependence on a relatively long history when compared to the intrinsic time constants. We combine these two methods, using highly recurrent networks in the context of a larger architecture, and this combination allows us to maintain local and biophysically realistic learning rules.

Discussion

In this work, we demonstrate the ability of a modular, spiking network to use local, biophysically realistic learning rules to learn and recall sequences, correctly reporting the duration and order of the individual elements. In combining modular, heterogenous structure with a learning rule based on eligibility traces, the model can accurately learn and recall sequences of up to at least eight elements, with each element anywhere from ~300 to ~1800 ms in duration. We have also shown a modified architecture that is capable of learning and recalling non-Markovian sequences with multiple history-dependent transitions.

The capabilities, construction, and rules of our model are significantly different from most contemporary and historical models of sequence learning, such as synfire chains and RNNs. In particular, we are not aware of another model that uses spiking networks and local, biophysically realistic learning rules, along with experimentally observed cell responses, to robustly learn both the order and duration of presented sequences of stimuli. Previous approaches which have attempted to internally learn both duration and order of elements (Veliz-Cuba et al., 2015) have been highly sensitive to changes in parameters and/or were not based on experimentally observed cell responses. Other types of hybrid models combine chain structures with additional hierarchy/functionality (Murray and Escola, 2017; Martinez et al., 2019), but either requires manually set adaptation time constants that are specific for a set duration to represent the duration of elements or do not treat the duration of elements as variable at all. Recently another model has been proposed, based on a periodic and essentially deterministic timing network, which also uses biologically plausible learning rules to learn to represent single non-Markovian sequences (Maes et al., 2020). However, it cannot learn arbitrarily long (and self-terminating) sequences, such as those presented in (Figure 7), nor can it learn several different sequences and replay them separately, such as those presented in (Figure 8)

The modified three-stage model is capable of learning non-Markovian sequences because of inclusion of a non-learning recurrent network that stores memory over longer durations than the modular network. However, the model’s ability to generate learned sequences depends crucially on the backbone of the modular network – because of this, we can use a non-plastic, highly recurrent reservoir and maintain biophysically realistic learning rules in the network. This modified model also differs in functionality from traditional RNNs, as in our model, the stimulus presented during training (the entire sequence) is different from the stimulus presented after learning in order to trigger recall (usually the first element is sufficient). In general, the number of elements necessary to trigger recall is the same as the number of elements needed to disambiguate the sequence (i.e. ‘A’ would be sufficient to trigger ABCD in a network embedded with learned sequences ABCD and EFGH, but ‘AB’ would be required to trigger ABCD in a network embedded with learned sequences ABCD and AFGH). In a way, our network acts as an autoencoder, both learning a reduced encoding (e.g. ‘A’ instead of ‘ABCD’) and reconstructing the original external input from this reduced encoding.

The reservoir and sparse network components of our three-stage model could be thought to arise from a projection from other cortical or subcortical areas. Functionally similar networks (ones that take complex, multimodal, and dynamic context and repackage it into sparse, separated patterns) have been observed in the dentate gyrus (Leutgeb et al., 2007; van Dijk and Fenton, 2018) and the cerebellum (Chadderton et al., 2004; Billings et al., 2014). However, these model components could also be thought of as part of the same cortical network, partially segregated in function but not necessarily by location. Pattern separation is likely a common neural computation that might occur in many brain areas, so we make no particular predictions about the locations of these network components.

Our model suggests that the types of single cell responses in V1 observed in delayed reward tasks (Timers and Messengers) (Shuler and Bear, 2006; Liu et al., 2015; Chubykin et al., 2013) will also be present when learning a visual sequence. Furthermore, we predict that distinct populations of these cells are sensitive to and can learn the dynamics of distinct stimuli. This functional modularity could be physically implemented as physically compartmentalized in columns and layers, though this is not strictly required. We present here two equivalent possible configurations of the network. The first, Figure 9a, shows an architecture that more directly implements the CNA, where inhibitory neurons are physically located next to their associated excitation for clarity, and long-range inhibitory connections exist. Figure 9b displays a more realistic structure by restricting inhibitory connections to be local. Both architectures are functionally identical, and there are a number of other redundant constructions which recapture the behavior described in this work.

Figure 9

Download asset Open asset

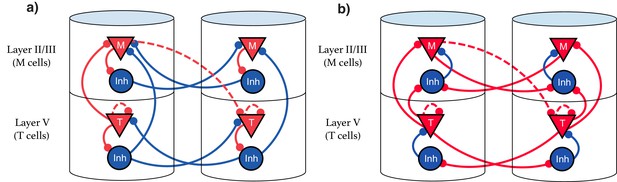
Explicit microcircuit structure.

(**a,b**) Two examples of complete microcircuit structure displayed in laminar architecture of cortical columns. Dashed lines represented learned connections, while continuous lines represent fixed connections. (a) Intercolumn inhibition produces soft winner-take-all dynamics between columns, interlaminar inhibition generates core neural architecture (CNA). (b) Same functionality as (a) but rearranged so as to only have local inhibition.

Recent results showing sequence learning and recall in visual cortex support the idea that these cell types are implicated in sequence learning (Gavornik and Bear, 2014). When multiple visual stimuli are presented sequentially, Local Field Potential (LFP) recordings indicate Timer-like responses (long, sustained potentiation) in layer V, with Messenger-like responses (short bursts centered around the transition between elements) arising in layer II/III (see Figure 4 from Gavornik and Bear, 2014). These results are consistent with the hypothesis that Timers and Messengers are indeed compartmentalized into different cortical layers.

Our model makes several testable predictions. It predicts that: (1) After learning a sequence, Messenger cells will more strongly functionally connect to Timer cells that represent subsequent stimuli, than to Timers which represent previous stimuli, or to other Messengers. (2) Learning sequences with long duration elements will increase lateral connection efficacies between Timers within the same modules. However, learning sequences with short duration elements may actually weaken those same lateral connections, depending on initial conditions. (3) There will be a population of inhibitory cells within each module that have firing properties similar to Timers but that decay more quickly (Figure 2a).

From a theoretical perspective, the main takeaway is that the architecture of our model enables it to accurately learn and recall sequences while maintaining local learning rules. If we were to start with a homogenous, randomly connected pool of neurons, sequence learning would require precise credit assignment, which is very difficult or impossible to calculate locally. Instead, the modular structure and the functionally heterogeneous cell types of the CNA perform some of this credit assignment implicitly, by breaking down a complex, difficult to learn task into a hierarchy of well-defined and easy to learn tasks. The Timers learn the duration, and the Messengers learn the order (components in the non-Markovian formulation have similarly simple and segregated tasks). While these restrictions end up limiting the types of outputs our network can represent, they enable the use of local learning rules.

Materials and methods

Network architecture

Request a detailed protocol

In a totally unstructured network, the learning rule described below would be insufficient for the task of sequence learning and memory. In exchange for the freedom of online, biophysically realistic reinforcement learning, we must presuppose some restrictions on the macro structure of the network. The structure imposed on the network has two components: a modular columnar structure with restricted connections and the weight distribution of the non-plastic synaptic efficacies. The weight distribution results in the emergence of distinct Timer and Messenger cell types, and the columnar structure places populations of these cells into stimulus-specific modules.

The network consists of 12 different ‘columns’, each containing 100 excitatory Timer cells, 100 inhibitory Timer cells, 100 excitatory Messenger cells, and 100 inhibitory Messenger cells, all assembled in a CNA microcircuit. Neither the particular number nor the ratio of the cell types is a strict requirement. These populations can be represented by many spiking neurons, few spiking neurons, or a single mean field neuron, and the populations can emerge even from distributions of random connections (Huertas et al., 2015). Each column is tuned to be selective for a particular stimulus from the input layer, such that a sequence of external stimuli (e.g. ABCD or ‘red-green-orange-blue’) will trigger a corresponding sequence of input-selective columns.

To simulate presentation of visual cues, the network is stimulated by an input layer designed to mimic spiking inputs from the LGN. Each stimulus is represented in the input layer by a Poisson spike train with a 50 ms pulsed peak, in accordance with the observed cellular responses in LGN (Ruksenas et al., 2007; Mastronarde, 1987). In general, this spike train can also include a decaying exponential tail, but short pulses were chosen both for analytical simplicity and to match experimental data (Ruksenas et al., 2007; Mastronarde, 1987), as shown in Figure 3—figure supplement 1. The cells of the input layer feed directly into the respective Timer cells of the columnar network.

Intercolumnar inhibition exists between Timer populations and between Messenger populations in the different columns, for the purposes of soft WTA dynamics between the columns of the network. This WTA inhibition can be thought of functionally as long-range inhibitory connections (Figure 8a), but in reality, is much more likely to be long-range excitatory connections synapsing onto local inhibition (Figure 8b). Such inhibition is generally not necessary in the low-noise case (or in a rate-based model), but the stochastic, spiking nature of the network makes it a desirable practical inclusion to guard against spurious runaway excitatory chains.

For the purposes of this paper, Timer cells can only learn to connect to other Timer cells within their column, and Messenger cells can only learn to connect to (any) Timer cells outside of their column. In case of the extended network that can learn non-Markov sequences, Messenger cells connect to the reservoir and not directly to Timer cells in other columns, as described above. While we include these restrictions for practical purposes, previous publications have shown all possible intracolumnar excitatory connections to be learnable with the use of a single trace eligibility rule (Huertas et al., 2015). The strengths of non-plastic connections within columns are modeled after those learned in previous publications (Huertas et al., 2015). These fixed connections serve to establish the Timer and Messenger cells used in the network. In Figure 5, we demonstrate that successful sequence learning is robust to +/– 20% changes in these connections. By only learning task relevant connections, we simplify the computation and analysis while maintaining the complete general functionality of variable sequence learning and recall.

Spiking and rate-based dynamics

Request a detailed protocol

The network comprises microcircuits of both excitatory and inhibitory spiking leaky-integrate-and-fire neurons placed in a modular architecture akin to that observed in cortical columns. The following equations describe the membrane dynamics for each model neuron i:

C \frac{d v_{i}}{d t} = g_{L} (E_{L} - v_{i}) g_{E, i} (E_{E} - v_{i}) g_{I, i} (E_{I} - v_{i}) σ

\frac{d s_{i}}{d t} = - \frac{s_{i}}{τ_{s}} ρ (1 - s_{i}) \sum_{k} δ (t - t_{k}^{i})

Here, subscripts L, E, and I refer to leak, excitatory, and inhibitory, respectively. g refers to the corresponding conductance, and E to the corresponding reversal potentials. $v_{i}$ and $s_{i}$ are the membrane potential and synaptic activation, respectively, of neuron i. $σ$ is a random noise term. Once the membrane potential reaches a threshold $v_{t h}$ , the neuron spikes and enters a refractory period $t_{r e f}$ . Each spike (at time $t_{k}^{i}$ ) updates the synaptic activation $s_{i}$ by an amount $ρ (1 - s_{i})$ , and in the absence of spikes, synaptic activation decays exponentially. Conductance $g$ is the product of the synaptic weight matrix with the synaptic activation, summed over all presynaptic neurons:

g_{α, i} = \sum_{j} W_{i j}^{α} s_{j}

Here, $α$ can be either $E$ (excitatory) or $I$ (inhibitory), and $W_{i j}^{α}$ are the connection strengths from neuron j to neuron i. A firing rate estimate for each neuron $r_{i}$ is calculated by an exponential filter of the spikes at times $t_{k}^{i}$ , with a time constant $τ_{r}$ .

τ_{r} \frac{d r_{i}}{d t} = - r_{i} \sum_{k} δ (t - t_{k}^{i})

Our excitatory time constant is notably long (80 ms), but this is not strictly required for our model. This is shown in Figure 5—figure supplement 2, in which we set the excitatory time constant to 20 ms and demonstrate successful learning of a sequence with elements 500 ms long each. However, the ability of the Timers to learn long times via their recurrent connections (without prohibitively small learning rates) depends on such large time constants, which are common in working memory literature (Gavornik and Shouval, 2011; Lisman et al., 1998; Wang et al., 2013). Figure 5—figure supplement 2b shows that the Timer cells reach bistability when trying to learn 1000 ms with a 20 ms time constant, causing failure in learning. The relationship between reported time, recurrent weights, and time constants in Timer-like cells is analyzed in detail in previous work (Gavornik et al., 2009; Gavornik and Shouval, 2011; Huertas et al., 2016). Although there is some evidence for a slow time constant in preforntal cortex (PFC) (Wang et al., 2013), this might not be so in sensory cortex. There are alternative ways to acquire a slow time constant that can facilitate learning of long interval times, such as derivative feedback (Lim and Goldman, 2013) or active intrinsic conductance (Gavornik and Shouval, 2011; Fransén et al., 2006).

For the rate-based version of these dynamics (used in the three-stage network model), each population of spiking neurons is represented by a single rate-based unit, which is governed by the following equations:

τ_{u} \frac{d u_{i}}{d t} = - u_{i} + \sum_{j, α} W_{i j}^{α} ξ (u_{j})

r_{i} = ξ (u_{i})

where $τ_{u}$ is the characteristic time constant and $r_{i}$ is the resulting firing rate for neuron i. $ξ$ is a piecewise non-linear transfer function used in previous sequential activation models (Brunel, 2003):

ξ (u) = {\begin{cases} 0 i f u \leq θ \\ v \frac{u - θ}{{(u_{c} - θ)}^{2}} i f θ < u < u_{c} \\ 2 v \sqrt{\frac{u - θ}{u_{c} - θ} - \frac{3}{4}} i f u_{c} < u \end{cases}

where $u_{c}$ is the critical activity level, $θ$ is a lower threshold, and $v$ a scaling parameter.

TTL rule

Request a detailed protocol

In place of a pair-based spike timing-dependent rule or rate-based Hebbian rule, which fails to solve the temporal credit assignment problem, the network learns based on ‘eligibility traces’ for both LTP and LTD (Huertas et al., 2015; Frémaux and Gerstner, 2015). These eligibility traces are synapse-specific markers that are activated via a Hebbian coincidence of activity between the pre- and postsynaptic cells. At a maximally allowed activation level, these traces saturate, and in the absence of Hebbian activity, these traces decay. LTP and LTD traces are distinct in that they activate, decay, and saturate at different rates/levels. These dynamics are described in the following equations:

τ^{p} \frac{d T_{i j}^{p}}{d t} = - T_{i j}^{p} + η^{p} H_{i j} (T_{m a x}^{p} - T_{i j}^{p})

τ^{d} \frac{d T_{i j}^{d}}{d t} = - T_{i j}^{d} + η^{d} H_{i j} (T_{m a x}^{d} - T_{i j}^{d})

The superscripts $p$ and $d$ indicate LTP or LTD synaptic eligibility traces, respectively. Here, $T_{i j}^{a}$ (where $a \in (p, d)$ ) is the eligibility trace located at the synapse between the $j$ th presynaptic cell and the $i$ th postsynaptic cell. The Hebbian activity, $H_{i j}$ , is a simple multiplication $r_{i} \cdot r_{j}$ in this rule, where $r_{j}$ and $r_{i}$ are the time averaged firing rates at the pre- and postsynaptic cells. Here, we use a simple case where $H_{i j}$ for LTP and LTD are identical, this is the simplest option and it is sufficient here, but experimentally the Hebbian terms are more complex and are different for LTP and LTD traces (He et al., 2015). Our Hebbian term is also subject to rate thresholds $r_{t h}$ and $r_{_{t h, F F}}$ in the recurrent and feed-forward cases, which we further discuss at the end of this section.. The parameter $T_{m a x}^{a}$ refers to the saturation level, $τ^{a}$ to the characteristic decay time constant of the trace, and $η^{a}$ to the Hebbian activation constant. If we assume steady-state activity such that $< H_{i j} >$ is constant (a first-order approximation), we can derive effective saturation levels and effective time constants ${\tilde{T}}^{a}$ and ${\tilde{τ}}^{a}$ , which vary as a function of the Hebbian term:

{\tilde{T}}^{a} = \frac{T_{m a x}^{a} ⟨ H_{i j} ⟩}{T_{m a x}^{a} + ⟨ H_{i j} ⟩}

{\tilde{τ}}^{a} = \frac{T_{m a x}^{a} τ^{a}}{T_{m a x}^{a} + ⟨ H_{i j} ⟩}

where $⟨H_{i j}⟩$ is the mean of Hebbian activity during trace saturation, in cases of prolonged and steady pre- and postsynaptic activation (Huertas et al., 2016). For increasing $⟨ H_{i j} ⟩ / T_{m a x}^{a}$ , ${\tilde{T}}^{a}$ asymptotically approaches $T_{m a x}^{a}$ . In our model this ratio is large for appreciable $⟨H_{i j}⟩$ , so practically speaking the traces saturate very close to $T_{m a x}^{a}$ (see Figure 4—figure supplement 1). Equations 8 and 9, using parameters as in Supplementary file 1, create traces with a fast, quickly saturating rising phase in the presence of constant activity, and a long, slow falling phase in the absence of activity. The trace dynamics in the rising and falling phases can be approximated using these effective terms to have the simple exponential forms:

T_{F}^{a} (t) = {\tilde{T}}^{a} e^{(t - t_{s t i m}) / τ^{a}}

T_{R}^{a} (t) = {\tilde{T}}^{a} (1 - e^{- t / {\tilde{τ}}^{a}})

where $T_{F}^{a} (t)$ is the trace dynamics in the falling phase and $T_{R}^{a} (t)$ represents the trace dynamics in the rising phase.

In this rule, synaptic weights are updated upon presentation of a global neuromodulatory signal $R (t)$ . In general, this signal can be either a traditional reward signal or a ‘novelty’ signal that accompanies the beginning or end of an external stimulus. This neuromodulatory signal then converts eligibility traces into synaptic efficacies, consuming them in the process, via a simple subtraction of the LTD trace from the LTP trace:

\frac{d W_{i j}}{d t} = η R (t) (T_{i j}^{p} - T_{i j}^{d})

Here, $W_{i j}$ is the synaptic efficacy between pre- and postsynaptic cells $j$ and $i$ , $R (t)$ is the neuromodulatory signal, and $η$ is the learning rate. Following presentation of the neuromodulatory signal, the eligibility traces are ‘consumed’ and reset to zero, and their activation is set into a short refractory period (25 ms). Synaptic efficacies reach a steady state under the following condition:

\int_{0}^{t_{t r i a l}} R (t) (T_{i j}^{p} - T_{i j}^{d}) d t = 0

where $t_{t r i a l}$ is the time at the end of the trial. In our model, each time a stimulus (whether a novel or familiar) starts or ends, a global novelty neuromodulator is released, and this acts as the ‘reward’ in the learning rule. As a result, synaptic efficacies update every time a stimulus is changed, according to the learning rule in Equation 14, until they reach the fixed point of Equation 15. Under the simplifying assumption that the reward function $R (t)$ is a delta function $δ (t - t_{r e w a r d})$ , this fixed point becomes:

T_{i j}^{p} (t_{r e w a r d}) = T_{i j}^{d} (t_{r e w a r d})

In our model there are two classes of synaptic plasticity, plasticity of recurrent connections to learn duration, and of feed-forward connections between modules to learn order. When feed-forward projections or external input activate a group of neurons, they cause an increase in the firing rates of those neurons, this we call the rising phase. Once input ceases, the activity in these neurons starts decaying, this decaying activity is the falling phase, and its dynamics are determined by recurrent connections. Synaptic eligibility traces follow the activity profiles, they rise or saturate during the rising phase, and decay during the falling phase. Since the traces saturate, the information relating to the feed-forward activity is contained exclusively in the rising phase of the traces, and during the falling phase, such information has been lost due to saturation. On the other hand, the information relating to the recurrent activity is contained in the falling phase, precisely because the input has ceased and the feed-forward information has been lost via saturation, so all that remains is the recurrent information. As such, learning the appropriate order via feed-forward connections needs to happen during the rising phase, and learning appropriate decay times via recurrent connections needs to happen during the falling phase. The differing activation, decay, and saturation rates/levels of the LTP and LTD traces have been chosen such that a fixed point can be reached either during the rising phase or falling phase of the traces (see Figure 4—figure supplements 1 and 2).

We show the fixed points obtained in simulations of sequence learning in Figure 3—figure supplement 2 and demonstrate how learning occurs in Figure 4—figure supplements 1 and 2. To gain intuition of when these fixed points are obtained and how they depend on the learning parameters, we make several simplifying approximations. To solve for the falling phase fixed point, we first assume that the traces are saturated when the underlying Hebbian activity is above a certain threshold, $H_{t h}$ . We call the time when Hebbian activity crosses below that threshold $t_{t h}$ . Then, combining Equations 12 and 16 (substituting $t_{r e w a r d}$ in for $t$ and $t_{t h}$ in for $t_{s t i m}$ ), we can solve for $D = t_{r e w a r d} - t_{t h}$ at the fixed point:

D = \frac{l n (\frac{{\tilde{T}}^{d}}{{\tilde{T}}^{p}})}{(\frac{1}{τ^{p}} - \frac{1}{τ^{d}})}

The objective of learning, then, is to move $D$ from its starting value to the value in Equation 17, which is determined by the parameters in the network. The parameters can be chosen such that the fixed-point value of $D$ is arbitrarily small. As shown in Figure 4—figure supplement 1, this recaptures the behavior of the Timer cells.

The rising phase fixed point can be determined by combining Equations 13 and 16 to give us an implicit function of $H$ :

{\tilde{T}}_{i j}^{p} (1 - e^{t_{r e w a r d} / {\tilde{τ}}_{i j}^{p}}) = {\tilde{T}}_{i j}^{d} (1 - e^{t_{r e w a r d} / {\tilde{τ}}_{i j}^{d}})

Since ${\tilde{T}}_{i j}^{a}$ and ${\tilde{τ}}_{i j}^{a}$ both depend on $H$ (Equations 8 and 9), given $t_{r e w a r d}$ , $T_{m a x}^{a}$ , and $τ^{a}$ , $H$ at the time of reward is uniquely determined by this fixed point. Practically, this means feed-forward learning increases synaptic efficacies $W_{i j}$ in order to increase postsynaptic firing $r_{i}$ , until $H_{i j}$ = $r_{i} \cdot r_{j}$ = a fixed value at t = $t_{r e w a r d}$ , as determined by Equation 18 (Figure 4—figure supplement 2). Qualitatively, successful feed-forward learning in our model uses traces with dominant LTP in the rising phase ( $η^{p} > η^{d}$ ) and dominant LTD in the falling phase ( $τ^{d} > τ^{p}$ ) ( see Supplementary file 1).

Through these learning dynamics, the Timer cells learn to represent the duration of their particular element in the sequence (by decreasing $D$ to its fixed-point value), while Messengers learn to feed forward to the Timer cells in the next stimulated column (by increasing $W_{i j}$ until $H_{i j} (t_{r e w a r d})$ reaches its fixed-point value). Note that for modules that do not have overlapping activation, the Hebbian term $H_{i j}$ is zero, and therefore the associated weights $W_{i j}$ do not change. However, in the presence of noise, modules can have spurious activity overlaps which cause non-zero $H_{i j}$ and therefore potentiation of weights $W_{i j}$ which are non-sequential. This can lead to network instability and a failure to encode the presented sequence. To account for this, rate thresholds $r_{t h}$ and $r_{_{t h, F F}}$ are included in the Hebbian term $H_{i j}$ . By setting these thresholds above the effective noise level (see Supplementary file 1), the Hebbian overlap $H_{i j}$ used to activate traces ignores the random, noise-driven overlaps. Crucially, as $r_{_{t h, F F}}$ dictates the sensitivity to inter-columnar overlaps, it is a critical and necessary parameter to enable the all-to-all connectivity of the model. Figure 3—figure supplement 2c shows these weights approaching their fixed-point values over the course of learning. Earlier work derives these equations in more detail (Huertas et al., 2016).

The parameters chosen for the traces are displayed in Supplementary file 1. For the recurrent traces, the parameters follow the restrictions derived from analysis in an earlier publication (Huertas et al., 2016). The corresponding analysis for the feed-forward traces, however, is not necessarily applicable in the context of sequence learning, since multiple neuromodulator signals are active during each learning epoch. As a result, the parameters for the feed-forward traces are empirically derived. Multiple different sets were found to work, but the set in Supplementary file 1 was the one used for all simulations included in this paper. Figure 5—figure supplement 1 shows that the mean reported times are robust to random perturbations (ranging from +/– 20%) of the learning parameters. The perturbations are added via independently drawing each parameter randomly from a uniform distribution with bounds of 80–120% of each parameter’s initial value. Note that the standard deviation increases, as expected, but is of the same order of magnitude. One hundred different random sets are used, and the resulting learned times compare favorably to trials with no parameter randomization.

The above eligibility trace learning rules are referred to as TTL. As described in a previous publication (Huertas et al., 2016), and demonstrated throughout this work, TTL allows for both feed-forward and recurrent learning, and as such can robustly encode temporally dependent input patterns. TTL is supported by recent experiments which have found evidence for eligibility traces existing in cortex (He et al., 2015), striatum (Yagishita et al., 2014), and hippocampus (Bittner et al., 2017; Brzosko et al., 2017). Other eligibility trace rules, such as the one-trace rule demonstrated in earlier work (Gavornik et al., 2009; Gavornik and Shouval, 2011), can also replicate the results of this paper. In general, any rule which can associate distal events/rewards, thereby solving the temporal credit assignment problem, would be likely to work with this network model. TTL was chosen for its biological realism, but the novel capabilities of this model (its ability to learn and recall both the duration and order of elements in a sequence) primarily result from the network architecture, combined with a history-dependent learning rule.

Non-Markovian network dynamics

Request a detailed protocol

The three-stage network used to learn and recall non-Markovian sequences comprises the main columnar network, a highly recurrent network (reservoir), and a sparse pattern net. The dynamics of the rate-based columnar network are described above. The dynamics of the units $u_{i}$ in the reservoir are described by the equation:

τ_{n e t} \frac{d u_{i}}{d t} = - u_{i} + \sum_{j} J_{i j} ψ (r_{j} - θ_{m}) + \sum_{k} \begin{matrix} W_{i k} ϕ (u_{k}) \end{matrix}

where $u_{i}$ are the firing rates of the units in the reservoir and $r_{j}$ are the firing rates of the Messenger cells in the main network. $J_{i j}$ is a K × n binary matrix of projections from the columnar network to the reservoir, where K is the number of units in the reservoir and n is the number of columns in the network. $J_{i j}$ is structured such that the first K/n units in the reservoir receive direct input from the Messengers in the first column, the second K/n units receive direct input from the Messengers in the second column, and so on. $W_{i k}$ are the recurrent weights of the reservoir, each of which is drawn from a normal distribution $N (0, \frac{g}{\sqrt{K}})$ , where g is the ‘gain’ of the network (Rajan et al., 2010).

$ψ$ is a piecewise linear activation function:

ψ (x) = {\begin{cases} 0 i f x \leq 0 \\ x i f x > 0 \end{cases}

so $θ_{m}$ is the firing threshold. $ϕ$ is a sigmoidal activation function:

ϕ (x) = \tanh (x) (21)

The reservoir projects to a high-dimensional sparse pattern network. Each unit in the sparse pattern net receives input from the reservoir, fed through a sparse matrix $O_{m i}$ , with fraction $ρ = . 04$ of entries non-zero and drawn from a normal distribution $N (0, \frac{g}{M})$ , where M is the number of units in the sparse pattern net and g is the gain, as described above. The activation of each unit $ν_{m}$ of the sparse network is determined by the following:

ν_{m} = Θ (r_{j} - θ_{m}) Θ (\sum_{i} O_{m i} ϕ (u_{i}) - θ_{o})

where $Θ$ is the Heaviside function. The sparse pattern network is binary in our implementation but this is not essential, as long as its non-linear and sparse. The sparse network feeds back into the main network via weights $Q_{j m}$ , which are learned via a simple Hebbian rule:

\frac{d Q_{j m}}{d t} = H_{j m} = r_{j} \cdot ν_{m}

with the additional restriction ${0 \leq Q}_{j m} \leq Q_{m a x}$ . Here, $j$ indexes units in the main network and $m$ indexes units in the sparse pattern net.

Data availability

All software used for simulations will be available on ModelDb. http://modeldb.yale.edu/266774.

The following data sets were generated

1. Cone I
2. Shouval HZ
(2021) ModelDb
ID 266774. Markovian and non-Markovian learning via biophysically realistic learning rules.

http://modeldb.yale.edu/266774

References

Book
1. Abeles M
(1991)
Corticonics: Neural Circuits of the Cerebral Cortex

Cambridge University Press.
- Google Scholar
(2014) Network structure within the cerebellar input layer enables lossless sparse encoding
Neuron 83:960–974.
https://doi.org/10.1016/j.neuron.2014.07.020
- PubMed
- Google Scholar
(2009) Topology and dynamics of the canonical circuit of cat V1
Neural Networks 22:1071–1078.
https://doi.org/10.1016/j.neunet.2009.07.011
- PubMed
- Google Scholar
(2017) Behavioral time scale synaptic plasticity underlies CA1 place fields
Science 357:1033–1036.
https://doi.org/10.1126/science.aan3846
- PubMed
- Google Scholar
1. Brunel N
(2003) Dynamics and plasticity of stimulus-selective persistent activity in cortical network models
Cerebral Cortex 13:1151–1161.
https://doi.org/10.1093/cercor/bhg096
- PubMed
- Google Scholar
1. Brzosko Z
2. Zannone S
3. Schultz W
4. Clopath C
5. Paulsen O
(2017) Sequential neuromodulation of hebbian plasticity offers mechanism for effective reward-based navigation
eLife 6:e27756.
https://doi.org/10.7554/eLife.27756
- PubMed
- Google Scholar
(2004) Integration of quanta in cerebellar granule cells during sensory processing
Nature 428:856–860.
https://doi.org/10.1038/nature02442
- PubMed
- Google Scholar
(2013) A cholinergic mechanism for reward timing within primary visual cortex
Neuron 77:723–735.
https://doi.org/10.1016/j.neuron.2012.12.039
- PubMed
- Google Scholar
1. Cohen Y
2. Shen J
3. Semu D
4. Leman DP
5. Liberti WA
6. Perkins LN
7. Liberti DC
8. Kotton DN
9. Gardner TJ
(2020) Hidden neural states underlie canary song syntax
Nature 582:539–544.
https://doi.org/10.1038/s41586-020-2397-3
- PubMed
- Google Scholar
(2015) Visual recognition memory, manifested as long-term habituation, requires synaptic plasticity in V1
Nature Neuroscience 18:262–271.
https://doi.org/10.1038/nn.3920
- PubMed
- Google Scholar
1. Dave AS
2. Margoliash D
(2000) Song replay during sleep and computational rules for sensorimotor vocal learning
Science 290:812–816.
https://doi.org/10.1126/science.290.5492.812
- PubMed
- Google Scholar
(2009) Hippocampal replay of extended experience
Neuron 63:497–507.
https://doi.org/10.1016/j.neuron.2009.07.027
- PubMed
- Google Scholar
1. DePasquale B
2. Cueva CJ
3. Rajan K
4. Escola GS
5. Abbott LF
(2018) Full-force: a target-based method for training recurrent networks
PLOS ONE 13:e0191527.
https://doi.org/10.1371/journal.pone.0191527
- PubMed
- Google Scholar
1. Eagleman SL
2. Dragoi V
(2012) Image sequence reactivation in awake V4 networks
PNAS 109:19450–19455.
https://doi.org/10.1073/pnas.1212059109
- PubMed
- Google Scholar
1. Eichenlaub JB
2. Jarosiewicz B
3. Saab J
4. Franco B
5. Kelemen J
6. Halgren E
7. Hochberg LR
8. Cash SS
(2020) Replay of learned neural firing sequences during rest in human motor cortex
Cell Reports 31:107581.
https://doi.org/10.1016/j.celrep.2020.107581
- PubMed
- Google Scholar
1. Fiete IR
2. Senn W
3. Wang CZ
4. Hahnloser RH
(2010) Spike-time-dependent plasticity and heterosynaptic competition organize networks to produce long scale-free sequences of neural activity
Neuron 65:563–576.
https://doi.org/10.1016/j.neuron.2010.02.003
- PubMed
- Google Scholar
1. Foster DJ
2. Wilson MA
(2006) Reverse replay of behavioural sequences in hippocampal place cells during the awake state
Nature 440:680–683.
https://doi.org/10.1038/nature04587
- PubMed
- Google Scholar
(2006) Mechanism of graded persistent cellular activity of entorhinal cortex layer v neurons
Neuron 49:735–746.
https://doi.org/10.1016/j.neuron.2006.01.036
- PubMed
- Google Scholar
1. Frémaux N
2. Gerstner W
(2015) Neuromodulated Spike-Timing-Dependent plasticity, and theory of Three-Factor learning rules
Frontiers in Neural Circuits 9:85.
https://doi.org/10.3389/fncir.2015.00085
- PubMed
- Google Scholar
(2009) Learning reward timing in cortex through reward dependent expression of synaptic plasticity
PNAS 106:6826–6831.
https://doi.org/10.1073/pnas.0901835106
- PubMed
- Google Scholar
1. Gavornik JP
2. Bear MF
(2014) Learned spatiotemporal sequence recognition and prediction in primary visual cortex
Nature Neuroscience 17:732–737.
https://doi.org/10.1038/nn.3683
- PubMed
- Google Scholar
1. Gavornik JP
2. Shouval HZ
(2011) A network of spiking neurons that can represent interval timing: mean field analysis
Journal of Computational Neuroscience 30:501–513.
https://doi.org/10.1007/s10827-010-0275-y
- PubMed
- Google Scholar
Book
1. Gillespie DT
(1991)
Markov Processes: An Introduction for Physical Scientists

Elsevier.
- Google Scholar
1. Hangya B
2. Ranade SP
3. Lorenc M
4. Kepecs A
(2015) Central cholinergic neurons are rapidly recruited by reinforcement feedback
Cell 162:1155–1168.
https://doi.org/10.1016/j.cell.2015.07.057
- PubMed
- Google Scholar
1. Hawkins J
2. Ahmad S
(2016) Why neurons have thousands of synapses, a theory of sequence memory in neocortex
Frontiers in Neural Circuits 10:23.
https://doi.org/10.3389/fncir.2016.00023
- PubMed
- Google Scholar
1. He K
2. Huertas M
3. Hong SZ
4. Tie X
5. Hell JW
6. Shouval H
7. Kirkwood A
(2015) Distinct eligibility traces for LTP and LTD in cortical synapses
Neuron 88:528–538.
https://doi.org/10.1016/j.neuron.2015.09.037
- PubMed
- Google Scholar
1. Howe MW
2. Dombeck DA
(2016) Rapid signalling in distinct dopaminergic axons during locomotion and reward
Nature 535:505–510.
https://doi.org/10.1038/nature18942
- PubMed
- Google Scholar
(2015) A simple network architecture accounts for diverse reward time responses in primary visual cortex
Journal of Neuroscience 35:12659–12672.
https://doi.org/10.1523/JNEUROSCI.0871-15.2015
- PubMed
- Google Scholar
(2016) The role of multiple neuromodulators in reinforcement learning that is based on competition between eligibility traces
Frontiers in Synaptic Neuroscience 8:37.
https://doi.org/10.3389/fnsyn.2016.00037
- PubMed
- Google Scholar
1. Ji D
2. Wilson MA
(2007) Coordinated memory replay in the visual cortex and Hippocampus during sleep
Nature Neuroscience 10:100–107.
https://doi.org/10.1038/nn1825
- PubMed
- Google Scholar
1. Jun JK
2. Jin DZ
(2007) Development of neural circuitry for precise temporal sequences through spontaneous activity, axon remodeling, and synaptic plasticity
PLOS ONE 2:e723.
https://doi.org/10.1371/journal.pone.0000723
- PubMed
- Google Scholar
1. Klos C
2. Miner D
3. Triesch J
(2018) Bridging structure and function: a model of sequence learning and prediction in primary visual cortex
PLOS Computational Biology 14:e1006187.
https://doi.org/10.1371/journal.pcbi.1006187
- PubMed
- Google Scholar
1. Laje R
2. Buonomano DV
(2013) Robust timing and motor patterns by taming Chaos in recurrent neural networks
Nature Neuroscience 16:925–933.
https://doi.org/10.1038/nn.3405
- PubMed
- Google Scholar
(2007) Pattern separation in the dentate gyrus and CA3 of the Hippocampus
Science 315:961–966.
https://doi.org/10.1126/science.1135801
- PubMed
- Google Scholar
(2016) Random synaptic feedback weights support error backpropagation for deep learning
Nature Communications 7:13276.
https://doi.org/10.1038/ncomms13276
- PubMed
- Google Scholar
1. Lim S
2. Goldman MS
(2013) Balanced cortical microcircuitry for maintaining information in working memory
Nature Neuroscience 16:1306–1314.
https://doi.org/10.1038/nn.3492
- PubMed
- Google Scholar
(1998) A role for NMDA-receptor channels in working memory
Nature Neuroscience 1:273–275.
https://doi.org/10.1038/1086
- PubMed
- Google Scholar
(2015) Selective activation of a putative reinforcement signal conditions cued interval timing in primary visual cortex
Current Biology 25:1551–1561.
https://doi.org/10.1016/j.cub.2015.04.028
- PubMed
- Google Scholar
1. Liu JK
2. Buonomano DV
(2009) Embedding multiple trajectories in simulated recurrent neural networks in a self-organizing manner
Journal of Neuroscience 29:13172–13181.
https://doi.org/10.1523/JNEUROSCI.2358-09.2009
- PubMed
- Google Scholar
1. Louie K
2. Wilson MA
(2001) Temporally structured replay of awake hippocampal ensemble activity during rapid eye movement sleep
Neuron 29:145–156.
https://doi.org/10.1016/S0896-6273(01)00186-6
- PubMed
- Google Scholar
(2002) Real-time computing without stable states: a new framework for neural computation based on perturbations
Neural Computation 14:2531–2560.
https://doi.org/10.1162/089976602760407955
- PubMed
- Google Scholar
(2004) Fading memory and kernel properties of generic cortical microcircuit models
Journal of Physiology-Paris 98:315–330.
https://doi.org/10.1016/j.jphysparis.2005.09.020
- PubMed
- Google Scholar
(2020) Learning spatiotemporal signals using a recurrent spiking network that discretizes time
PLOS Computational Biology 16:e1007606.
https://doi.org/10.1371/journal.pcbi.1007606
- PubMed
- Google Scholar
(2019) Probabilistic associative learning suffices for learning the temporal structure of multiple sequences
PLOS ONE 14:e0220161.
https://doi.org/10.1371/journal.pone.0220161
- PubMed
- Google Scholar
1. Mastronarde DN
(1987) Two classes of single-input X-cells in cat lateral geniculate nucleus. II. retinal inputs and the generation of receptive-field properties
Journal of Neurophysiology 57:381–413.
https://doi.org/10.1152/jn.1987.57.2.381
- PubMed
- Google Scholar
1. Murray JM
(2019) Local online learning in recurrent networks with random feedback
eLife 8:e43299.
https://doi.org/10.7554/eLife.43299
- PubMed
- Google Scholar
1. Murray JM
2. Escola GS
(2017) Learning multiple variable-speed sequences in striatum via cortical tutoring
eLife 6:e26084.
https://doi.org/10.7554/eLife.26084
- PubMed
- Google Scholar
1. Nicola W
2. Clopath C
(2017) Supervised learning in spiking neural networks with FORCE training
Nature Communications 8:2208.
https://doi.org/10.1038/s41467-017-01827-3
- PubMed
- Google Scholar
1. Pereira U
2. Brunel N
(2019) Unsupervised learning of persistent and sequential activity
Frontiers in Computational Neuroscience 13:97.
https://doi.org/10.3389/fncom.2019.00097
- PubMed
- Google Scholar
1. Potjans TC
2. Diesmann M
(2014) The cell-type specific cortical microcircuit: relating structure and activity in a full-scale spiking network model
Cerebral Cortex 24:785–806.
https://doi.org/10.1093/cercor/bhs358
- PubMed
- Google Scholar
(2010) Stimulus-dependent suppression of Chaos in recurrent neural networks
Physical Review E 82:011903.
https://doi.org/10.1103/PhysRevE.82.011903
- Google Scholar
(2016) Recurrent network models of sequence generation and memory
Neuron 90:128–142.
https://doi.org/10.1016/j.neuron.2016.02.009
- PubMed
- Google Scholar
(2007) Dynamics of spatial resolution of single units in the lateral geniculate nucleus of cat during brief visual stimulation
Journal of Neurophysiology 97:1445–1456.
https://doi.org/10.1152/jn.01338.2005
- PubMed
- Google Scholar
1. Shuler MG
2. Bear MF
(2006) Reward timing in the primary visual cortex
Science 311:1606–1609.
https://doi.org/10.1126/science.1123513
- PubMed
- Google Scholar
1. Skaggs WE
2. McNaughton BL
(1996) Replay of neuronal firing sequences in rat Hippocampus during sleep following spatial experience
Science 271:1870–1873.
https://doi.org/10.1126/science.271.5257.1870
- PubMed
- Google Scholar
1. Sussillo D
2. Abbott LF
(2009) Generating coherent patterns of activity from chaotic neural networks
Neuron 63:544–557.
https://doi.org/10.1016/j.neuron.2009.07.018
- PubMed
- Google Scholar
(2016) Spike-Based Bayesian-Hebbian learning of temporal sequences
PLOS Computational Biology 12:e1004954.
https://doi.org/10.1371/journal.pcbi.1004954
- PubMed
- Google Scholar
1. van Dijk MT
2. Fenton AA
(2018) On how the dentate gyrus contributes to memory discrimination
Neuron 98:832–845.
https://doi.org/10.1016/j.neuron.2018.04.018
- PubMed
- Google Scholar
(2015) Networks that learn the precise timing of event sequences
Journal of Computational Neuroscience 39:235–254.
https://doi.org/10.1007/s10827-015-0574-4
- PubMed
- Google Scholar
1. Wang XJ
(2001) Synaptic reverberation underlying mnemonic persistent activity
Trends in Neurosciences 24:455–463.
https://doi.org/10.1016/S0166-2236(00)01868-3
- PubMed
- Google Scholar
1. Wang M
2. Yang Y
3. Wang CJ
4. Gamo NJ
5. Jin LE
6. Mazer JA
7. Morrison JH
8. Wang XJ
9. Arnsten AF
(2013) NMDA receptors subserve persistent neuronal firing during working memory in dorsolateral prefrontal cortex
Neuron 77:736–749.
https://doi.org/10.1016/j.neuron.2012.12.032
- PubMed
- Google Scholar
1. Whittington JCR
2. Bogacz R
(2019) Theories of error Back-Propagation in the brain
Trends in Cognitive Sciences 23:235–250.
https://doi.org/10.1016/j.tics.2018.12.005
- PubMed
- Google Scholar
1. Xu S
2. Jiang W
3. Poo MM
4. Dan Y
(2012) Activity recall in a visual cortical ensemble
Nature Neuroscience 15:449–455.
https://doi.org/10.1038/nn.3036
- PubMed
- Google Scholar
(2014) A critical time window for dopamine actions on the structural plasticity of dendritic spines
Science 345:1616–1620.
https://doi.org/10.1126/science.1255514
- PubMed
- Google Scholar
1. Yin P
2. Mishkin M
3. Sutter M
4. Fritz JB
(2008) Early stages of melody processing: stimulus-sequence and task-dependent neuronal activity in monkey auditory cortical fields A1 and R
Journal of Neurophysiology 100:3009–3029.
https://doi.org/10.1152/jn.00828.2007
- PubMed
- Google Scholar

Decision letter

Tatyana O Sharpee

Reviewing Editor; Salk Institute for Biological Studies, United States
Ronald L Calabrese

Senior Editor; Emory University, United States

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

This paper describes how spiking neurons can learn spatio-temporal sequences with flexible duration of intermediate states. Available methods only allowed learning of sequences where duration could not be varied broadly. The proposition put forward in this work solves this long-standing problem in a convincing and in a biologically plausible way.

Decision letter after peer review:

[Editors’ note: the authors submitted for reconsideration following the decision after peer review. What follows is the decision letter after the first round of review.]

Thank you for submitting your work entitled "Learning precise spatiotemporal sequences via biophysically realistic learning rules in a modular, spiking network" for consideration by eLife. Your article has been reviewed by a Senior Editor, a Reviewing Editor, and two reviewers. The reviewers have opted to remain anonymous.

Our decision has been reached after consultation between the reviewers. The consensus was that the manuscript raises an interesting problem and provides an interesting but partial solution to it. The reviewers described many analyses that needed to be completed prior to publication. The reviewers thought that once all of that work was completed, the manuscript would be so substantially different that it would qualify as a new submission. Therefore, the consensus decision at this stage is not to consider further this manuscript for publication in eLife.

Reviewer #1:

In this study authors note that many models of sequential activity in the brain only account for the order in which neurons spike and fail to take into account the duration for which each neuron responds. This is indeed an interesting problem. Authors provide a network architecture that can solve part of the problem.

They assume that a neural activity sequence is consisted of many events. Neuron groups are tuned to these events and spike in order as these events occur. Each neuron group (Core Neural Architecture or CNA) consists of Timer, Messenger (both excitatory) and inhibitory neurons subgroups. The recurrent connections within Timer neurons encode the duration. The Messenger neurons project to the next CNA and encode the order.

An important part of the circuit is the inhibitory neurons which stop firing before the timer neurons (even though they are driven by timer neurons) and thereby release the Messenger neurons from inhibition at the end of the duration of the event. Thus, messenger neurons firing maximizes and signals the end of the “duration”.

Authors then expand the network to have a “reservoir” network and show that their scheme can also generate non-markovian sequences in which a particular neuron group is activated multiple times in the sequence.

I think the authors have raised an interesting problem and provide a solution that at least partly solves the problem. However, there are a number of shortcomings of the work which reduce the significance of the work.

1) Here authors are assuming sequences of distinct events. But to facilitate learning it is crucial that the animal is rewarded after each event. I am not convinced that every component of a sequential behavior is rewarded.

2) The key to indicate the end of duration of a sequence component, is that the inhibitory neurons stop firing before the Timer neurons. Why should this be? Since inhibitory neurons are driven by time neurons and that typically inhibitory neurons have low spike threshold one would expect the inhibitory neurons to remain active as long as Timer neurons are active. This must require fine tuning of the circuit which is beyond synaptic changes. This particular component of the model makes it appear contrived. Authors have not provided biological motivation or evidence of robustness of the mechanism. Authors finally predict that "There will be a population of inhibitory cells within each module that have firing properties similar to Timers but that decay more quickly (Figure 2A)." But is this enough? There will also be other inhibitory neuron type which will not have this exact dynamics -- will that be a problem?

3) While it is possible to have non-Markovian sequences but still each Timer can show only a single duration. Authors only make passing remark on how this could be amended but the solution is very ad-hoc and very likely will not scale.

4) The main motivation of the work is to come up with a biologically plausible model of sequence (order and durations). But the addition of reservoir and a sparse readout makes it non-biological. Moreover, authors have not specified the properties of the reservoir, specifically how does it keeps the memory of sequence of different messengers. And if the long-term memory of the messenger sequence is already in the reservoir, then why the sparse-net readout stage is needed.

5) The whole work is presented as demonstrations of key results, there is no systematic analysis of robustness of the results. I disagree that it is beyond the scope of the current work - I think that is exactly what should have been done, after all this is a computational study.

Author response

[Editors’ note: the authors resubmitted a revised version of the paper for consideration. What follows is the authors’ response to the first round of review.]

Reviewer #1:

[…]

I think the authors have raised an interesting problem and provide a solution that at least partly solves the problem. However, there are a number of shortcomings of the work which reduce the significance of the work.

1) Here authors are assuming sequences of distinct events. But to facilitate learning it is crucial that the animal is rewarded after each event. I am not convinced that every component of a sequential behavior is rewarded.

We do not claim that the animal is rewarded after every event, simply that there is some neuromodulator released during any change in the input (not “after each event”, what is an event?). This is how it was stated in the Results: “We have assumed that on every transition between external stimuli, a “novelty” signal causes a global release of a neuromodulator, which acts as a reinforcement signal (see Methods). The assumption of a temporally precise but spatially widespread neuromodulatory signal might seem at odds with common notions of temporally broad neuromodulator release, but they are indeed consistent with recent recordings in several neruomodulatory systems^40,41.” Still, this is an assumption, which can be tested, and might be wrong. Our view is that we need to state our assumptions clearly, as we have done, we also think that this is a reasonable, though not a proven, assumption.

2) The key to indicate the end of duration of a sequence component, is that the inhibitory neurons stop firing before the Timer neurons. Why should this be? Since inhibitory neurons are driven by time neurons and that typically inhibitory neurons have low spike threshold one would expect the inhibitory neurons to remain active as long as Timer neurons are active.

This is addressed directly in the Results: “However, inhibitory cells in the module decay slightly more quickly than their Timer counterparts, thanks to shorter time constants for synaptic activation (80ms for excitatory, 10ms for inhibitory), and small Timer to Inhibitory weights (there are a number of degenerate sets of parameters which can facilitate quickly decaying Inhibitory cells³⁷).” In modeling studies, it is indeed easy to generate this form of activity in the inhibitory population, and we have previously shown that such activity profiles can arise in a subpopulation of cells when the weights are chosen from a broad random distribution (Huertas et al., 2015). However, it is true that this is a putative mechanism which has not yet been validated experimentally.

This must require fine tuning of the circuit which is beyond synaptic changes. This particular component of the model makes it appear contrived. Authors have not provided biological motivation or evidence of robustness of the mechanism.

In our previous cited study (Huertas et al., 2015) we have shown that such sub-populations can arise in a network with efficacies chosen randomly from a broad distribution. It therefore does not depend on fine tuning. Further, such subpopulations have been observed experimentally in interval timing experiments, though there is not sufficient data in sequence learning experiments to determine if they arise there as well. We have provided a putative mechanism for how these different sub-populations may arise. The mechanism does not require fine tuning as suggested. However, it is true that it has not yet been validated experimentally.

Authors finally predict that "There will be a population of inhibitory cells within each module that have firing properties similar to Timers but that decay more quickly (Figure 2A)." But is this enough? There will also be other inhibitory neuron type which will not have this exact dynamics - will that be a problem?

In trying to interpret the question we find several options as to what they mean, we will therefore answer all options we can think of:

a) The ability to experimentally detect this sub-population. Of course, when any experimentalist looks for particular types of neurons (take place cells, or really any functionally specific cell type as an example), there will be plenty of other neurons the experimenter records which do not have the desired dynamics. This problem of detection is a universal problem in neuroscience, and is not unique to our prediction of this particular type of inhibitory neuron existing in visual cortex.

b) Will the exitance of other inhibitory cell types eliminate the ability of the model to perform. In Huertas et al., (2015) we showed that a wide distribution of inhibitory cell types results in a heterogeneity of excitatory cell types, some of these will be of the “Messenger” cell type. So, this heterogeneity of inhibitory cell types does not eliminate the ability to generate “Messenger” cell types. The harder problem in the context of the sequence learning model, is that only these “Messenger” type cells should have plasticity in their synaptic connections to the “Timers” of the subsequent column. For this we assume actually that there is some structure in the micro-column, so that the “Messenger” cells don’t arise in simply due to the distribution, but to some structure in the microcircuit column, or in other words, they are predestined to become “Messenger”. In that case it will be easier to mark them, and assume they have plastic synapses to Timers.

3) While it is possible to have non-Markovian sequences but still each Timer can show only a single duration. Authors only make passing remark on how this could be amended but the solution is very ad-hoc and very likely will not scale.

The ability to learn several target times within a single recurrent population is indeed currently a general problem with local learning rules. We have changed our language referring to this in the new version to: “In order for repeated elements to have different durations during recall, an appropriate learning rule must be capable of creating multiple attractors within that element’s Timer population, with each attractor triggering a different duration of activity.” Since this issue is not yet resolved for local learning rules, this challenge must still be overcome, and our lab is currently working on this.

4) The main motivation of the work is to come up with a biologically plausible model of sequence (order and durations). But the addition of reservoir and a sparse readout makes it non-biological.

Yes, our ultimate aim is to generate a biologically plausible model for sequence learning. More than that we want to identify the correct model. However, in this paper we do not make the claim that the reservoir structure itself is biologically realistic, nor is that the “main motivation of the work”. Our main focus it to identify architectural constraints that allow for local, biophysically plausible learning rules. From the Results: “To learn non-Markovian sequences, we modify the network structure while maintaining local learning rules.” and the Discussion: “We combine these two methods, using highly recurrent networks in the context of a larger architecture, and this combination allows us to maintain local and biophysically realistic learning rules.” From the very beginning of the Discussion: “In this work, we demonstrate the ability of a modular, spiking network to use biophysically realistic learning rules to learn and recall sequences, correctly reporting the duration and order of the individual elements.”

The rate-based implementation used here for the reservoir machine is indeed not biophysical. Additionally, the reviewer might still wonder if there is any biophysical realism to reservoir machines. This is indeed debatable and is a current focus of research in many labs. There have been various publications that have tried to implement RNN type architectures with spiking neurons (Abbott et al., 2016, Nicola and Clopath 2016, etc.) Whether this attempt has been successful is beyond the scope of this paper, and this might take years to resolve. However, some network with extended memory dependence is necessary for the formulation outlined here to work for non-Markovian sequences. We have chosen a simple sparse implementation of such a network to demonstrate its utility in solving this problem, not in order to show that this specific implementation is used in the brain. We have tried to clarify this in the current version of the paper.

Moreover, authors have not specified the properties of the reservoir, specifically how does it keeps the memory of sequence of different messengers.

We are not quite sure what the reviewer means by “properties of the reservoir”. However, the key property of the reservoir used here is that its current state depends on a long-term history of its activity. This is the property of reservoir machines explored extensively in the literature. In the paper we state: “For the network to learn and recall non-Markovian sequences, it must somehow keep track of its history, and use this history to inform transitions during sequence learning and recall. To this end, we include two additional “stages” to the network (Figure 5). The first is a fixed (non-learning) recurrent network, sometimes called a “reservoir” (as in reservoir computing) or a “liquid” (as in a liquid state machine)^49,50, which receives inputs from the Messenger cells in the main columnar network. Owing to these inputs and due to its strong recurrent connectivity, the current state of the reservoir network is highly dependent on the history of network activity. Therefore, it acts as a long-term memory of the state of the columnar network.” Moreover, in the Materials and methods section all implementation details of the reservoir machine are given.

And if the long-term memory of the messenger sequence is already in the reservoir, then why the sparse-net readout stage is needed.

This is directly addressed in the Results: “The second additional stage is a high dimensional, sparse, non-linear network which receives input from the reservoir, serving to project the reservoir states into a space where they are highly separated and non-overlapping. The result is that a given “pattern” in this sparse network at time t uniquely identifies the history of the main network up to and including time t. Since these patterns are highly non-overlapping (due to the sparsity and non-linearity), a particular pattern at time t can use simple, local, and biophysically realistic Hebbian learning to connect to Timer cells firing at time t + ∆t in the main network (Direct Messenger to Timer feed forward learning is removed in this non-Markovian example).”

5) The whole work is presented as demonstrations of key results, there is no systematic analysis of robustness of the results. I disagree that it is beyond the scope of the current work -- I think that is exactly what should have been done, after all this is a computational study.

We have already addressed many aspects of the robustness in the original paper, even though we did not specifically call these results robustness. This might have caused the reviewer to disregard these results. Robustness to stochasticity is addressed directly in Figure 3—figure supplement 2. Robustness to input deviations is addressed directly in Figure 8—figure supplement 1. Many other aspects of the robustness of the learning rule, and of the CNA have been previously addressed in previous papers that are cited here (He et al. 2015, Huertas et al., 2015, 2016). However, we have further extended our robustness analysis and these results are currently shown in Figure 5—figure supplement 1 and cited in the main text. We have also changed our wording in several places to make to clearer to the readers that this model is robust to many parameter variations. We must note however, that the model has 35 parameters, we did not modify all of these in our computational study as this is not feasible

Other questions:

- If the Timer neurons are recurrently connected with excitatory neurons, how come their activity dies out and what determines the decay time constant in a timer circuit. Recurrently connected population of only excitatory neurons (timer cells) has only two fixed points: one at maximum value (and then the activity will sustain for ever) and the zero activity fixed point. So it would require fine tuning to get to the right duration. This again goes back to the issue of the robustness of the results.

The activity of the Timer neurons is clearly transient. We are not at an activity fixed point, nor do we ever claim to be. Our weights reach fixed points, but these fixed points are not in the bi-stable regime of the network. An activity fixed point is a completely different thing. Our network is given a transient stimulus and produces a transient response. The timer cell network was previously comprehensively analyzed in Gavornik and Shouval, 2011, using mean field theory methods; these previous results are cited in this paper.

- In a computational study like this it is very important to show the parameter ranges in which the demonstrated phenomenon is observed. Here it is also important to show under what conditions we can get a wide range of timings. Authors have chosen equal number of timer, messenger and inhibitory neurons -- how crucial is this? Could we still get the same results if we assume 80-20 ratio of excitatory/inhibitory neurons?

We hope that our modified language, previous cited work, and additional work regarding robustness provide an answer to some of these questions as well. A different ratio of E/I cells would not fundamentally alter these results, neither would a different ratio of T and M cells.

- What is the min. and maximum duration for each event in the sequence that can be learned and recalled? (This goes back to the issue of the parameter ranges).

This is addressed directly in the Discussion of the original paper: “In combining modular, heterogenous structure with a learning rule based on eligibility traces, the model can accurately learn and recall sequences of up to at least 8 elements, with each element anywhere from ~300ms to ~1800ms in duration.” From the Results: “The network is capable of learning sequences of temporal intervals where the individual elements can be anywhere from ~300ms to ~1800ms (see Supplementary Figure 2) in duration, which agrees with the observed ranges used for training V1 circuits^1,6.” With different sets of parameters, these ranges will likely differ, though we have good reason to believe that ranges beyond ~2000ms cannot be implemented in a stochastic spiking network, without additional mechanisms.

- What happens when the sequence parts overlap?

We are not sure exactly by what they mean by overlap, however we address overlaps directly in subsection “Learning and recalling non-markovian sequences”. In particular Figure 7 is titled: “Recall of Two Overlapping Sequences”.

- Does the learning automatically stop or it has to be manually stopped.

The phrase “fixed point” appears many times in the manuscript in relation to our learning rule. Here are a few examples: “We have used this rule because it can solve the temporal credit assignment problem, allowing the network to associate events distal in time, and because it reaches fixed points in both recurrent and feedforward learning tasks³⁵” “Properly encoded durations and orders are the result of the fixed points in the learning rule, as described in the Materials and methods section and in previous publications^35,46.” “Recurrent learning ends in a fixed point which sets the time D between the end of firing in one column and the start of firing in the next.” “Feed forward learning results in a fixed point which determines the connection strength between Messenger and Timer cells in subsequent columns.” Moreover, Supplementary Figure 2C shows the convergence to these fixed points, and in the Materials and methods section Equations 15-17 define these fixed points, and show analytical results regarding their convergence in a simple case, which has been previously analyzed and is cited here.

- Since the three-stage model is more general, I guess that should be the one implemented in the brain.

Yes, indeed the three-stage model, as the reviewer notes, is more general and can learn and reproduce more types of sequences. Indeed, behaviorally these are problems we can solve, so they must be embedded somewhere in the brain.

So I think authors should make predictions at that level? Where are reservoir and sparse net located and how would be the activity in these two modules.

For the modular network, there is some physiological data suggesting that this network resides already in primary sensory cortex. For the three-stage network, we have almost no physiological information, and therefore cannot meaningfully make specific predictions. However, some brain structures have circuit elements and connectivity that suggest they could be used for these purposes. In the original paper we state: “The reservoir and sparse network components of our three-stage model could be thought to arise from a projection from other cortical or subcortical areas. Functionally similar networks (ones that take complex, multimodal, and dynamic context and repackage it into sparse, separated patterns) have been observed in the dentate gyrus^54,55 and the cerebellum^56,57. However, these model components could also be thought of as part of the same cortical network, partially segregated in function but not necessarily by location.” The modular network is also a component of the three-stage network. For that network we make very clear predictions about the identity of the modular network, and its properties. The specific predictions we make about this modular network go significantly beyond the typically generic predictions made in most previous models (see Figure 8).

Reviewer #2:

In the manuscript "Learning precise spatiotemporal sequences via biophysically realistic learning rules in a modular, spiking network," the authors propose a plastic spiking network model that learns selective temporal sequences with variable timing.

The authors propose a novel and tractable plasticity model with separate eligibility traces for LTD and LTP. The normative fixed point approach the authors employ to solve the temporal learning problem is elegant. Further, the writing is clear, the question well-motivated, and relevant literature cited correctly. However, the manuscript lacks a closer comparison to existing experimental data, and several open questions remain related to the network’s temporal dynamics and the robustness of the proposed learning mechanism.

1) From where do the long time scales in the network model come?

The long time-scales arise from the strong recurrent weights in the network, and is explicitly stated as such in the paper. From the Results:” The “Timer” cells learn strong recurrent connections with other Timer cells within the module. This strong recurrent connectivity results in long lasting transient activity, which is used to represent the duration of a given stimuli. Previous studies have analyzed in detail the relationship between recurrent connectivity and duration of resulting transient activity following a stimulus^35,36.” We have previously extensively analyzed the dynamics of such recurrent networks, and this analysis is cited in the paper. We have tried to make this even more clear in this rewritten version of the paper.

A crucial property of the timer cells is their slowly decaying firing rate which is the basis of the adjustable decays, presumably linked to the learning of the recurrent connections. It was not entirely clear what causes these slowly decaying rates in the model.

As the reviewer implies, and as is stated in the model, the slowly decaying activity arises from recurrent connections. The ability of recurrent connections to represent the correct times arises from the learning rule. We have analyzed these aspects of the model previously in our publications (Gavornik and Shouval, 2011, Huertas et al., 2016), and try to make this even more clear in the current version of this paper.

The question arises because slow working memory like dynamics are non-trivial to get, especially, in spiking neural networks with physiological time constants. A body of literature tackled this issue with, for instance, attractor models (Amit and Brunel, 1997; Yakovlev et al., 1998), non-normal network dynamics (Goldman, 2009; Hennequin et al., 2012), or negative derivative feedback (Lim and Goldman, 2013). However, the present model does not seem to contain any intrinsically slow time constants. Perhaps the unusual combination of slow excitation ~80ms vs. fast inhibition (~10ms) results in some form of negative derivative feedback? This choice is opposite to the usual fast AMPA vs. slower GABA dynamics. While several potential mechanisms could underlie such slow ramping activity, it is essential to clarify this point and, perhaps, illustrate that the proposed learning scheme is robust to other slow timescale mechanisms.

The slow dynamics here are a property of a recurrent excitatory network. We have previously shown and mathematically analyzed such a network (Gavornik, Shouval, 2011). In order to carry out this analysis we indeed use the MFT methods developed by Brunel and Amit. Formally, this is the same type of network as a working memory network, only operating slightly below the bifurcation at which the network becomes bi-stable. The slow dynamics are a reflection of the “ghost” of this bifurcation. Synaptic plasticity acts to bring the “source” and “sink” terms to the appropriate distance such that the network decays with the appropriate time. Given the time constants used here, the stochastic spiking network can represent decays of close to 2000ms. For decays within this range we do not need additional mechanisms such as negative derivative feedback. The slow decay of the network can be achieved with normal weight matrixes, and this does not require non-normal dynamics. Additional mechanisms might extend the time ranges that the network can reproduce.

2) How plausible is the delay activity state in the network model?

Although the authors used spiking neural network models for part of the study, the spiking network activity is neither shown nor characterized. How does the spiking activity look like in the present model?

The reviewer failed to notice Figure 3—figure supplement 4, which shows a spike raster of the entire network for a trial before learning, and a trial after learning. It is referenced in the Results: “Empirically, temporal accuracy of recall depends on many non-trivial factors (i.e. length of individual elements, length of entire sequence, placement of short elements near long elements, etc.), owing to the many non-trivial effects of stochasticity of the spiking network (spike rasters are shown in Figure 3—figure supplement 4).”

The firing rates seems rather high, which raises the question of how compatible the network activity is with cortical networks. For instance, the firing rates during the onset phase of the timer cell do look relatively high (>80Hz). Whereas, in many sensory areas spiking activity is relatively low and asynchronous irregular, possibly linked to a balanced state.

The cell types in our model are based off of findings of interval timing-based cells in visual cortex, such as from Liu et al., (2015). Figure 2 compares our model to these experimentally observed cell types, which also have very high firing rates (~40 Hz) for the Timers.

How does the activity in the present model compare to such balanced models? Would balance and the associated activity pose a problem? The manuscript would benefit if the mechanism proves robust to such presumably more realistic activity regimes.

The model was not set up to be in the balanced regime, however its spike statistics are quire realistic. This can be seen in the additional subplot showing the ISI distributions of Timer and Messenger cells (Figure 3—figure supplement 4). It’s actually quite intriguing and surprising that despite not being in the balanced regime, the model results in reasonable spike statistics. Partially this is due to injected noise into neurons in order to generate spontaneous activity. We primarily included this additional variability in order to make sure that our learning mechanisms are robust enough to handle such noise. We are currently analyzing the source of these surprisingly realistic spike statistics, as part of a different project.

3) Comparison to experimental data

One misses a more detailed treatment of how the proposed learning algorithm can be further verified with experimental data. Although inspired by experiments (Gavornik and Bear, 2014), a closer and perhaps more quantitative comparison to experimentally observable network activity in sensory cortices is desirable. Such verification may be challenging to accomplish solely based on LFP recordings. Maybe there are specific salient dynamical signatures that the present model predicts? One of the strong assumptions of the model is that there are two functionally different excitatory populations (timers and messengers) with a stereotypical interplay in time. How easily can such populations be recovered from (simulated) data?

Indeed, our model predicts that in sequence learning networks would develop “Timer” and “Messenger” type populations of cells. These cells are indeed found in single unit recording in interval-timing paradigms, but not yet in sequence learning paradigms as most of the data there is based on LFPs. In our simulated data it is easy to distinguished from the data alone these two different populations, even without knowing a priori which cell belong to which group. The statistical properties of these cells even at the single cell level, such as duration of higher firing rate, and the firing rates themselves, are clearly significantly different. Indeed, we make a strong prediction that these two population will exist, and testing experimentally this is essential for experimentally validating, rejecting, or modifying the model.

[Editors’ note: what follows is the authors” response to the second round of review.]

This manuscript addresses the problem of learning sequences of events with variable durations. This is an important problem. The revised manuscript was reviewed by two new reviewers and one previous reviewer. The consensus was that the manuscript will be suitable for publication after the following two points are addressed:

1) Time constants of inhibitory neurons:

The choice of synaptic time constants (80ms for exc. and 10ms for inhibition) is very odd. There is no justification provided for these values.

The solution that was proposed by the reviewers is that to solve this issue by redifining the time scale by, say division by 5. So that what now is 80 milliseconds becomes 16 milliseconds. This has to be done consistently throughout the paper, but new simulations are not absolutely necessary. The point can be addressed by careful re-definition of time scales throughout the manuscript, if this is what the authors prefer.

Our excitatory time constant is notably long (80 ms), but this is not strictly required for our model. We have included a new figure (Figure 5—figure supplement 2) where we set the excitatory time constant to 20ms and demonstrate successful learning of a sequence with elements 500ms long each. However, the ability of the Timers to learn long times via their recurrent connections (without prohibitively small learning rates) depends on such large time constants, which are common in working memory literature (Wang et al., 2013, Lisman et al., 1998, Gavornik and Shouval, 2011). Figure 5—figure supplement 2B shows that the Timer cells reach bistability when trying to learn 1000ms with a 20ms time constant, causing failure in learning. The relationship between reported time, recurrent weights and time constants in Timer-like cells is analyzed in detail in previous work (Gavornik and Shouval, 2011 in particular). Although there is some evidence for a slow time constant in PFC (Wang et al., 2013), this might not be so in sensory cortex. There are alternative ways to acquire a slow time constant that can facilitate learning of long interval times. Such options include derivative feedback (Lim and Goldman, 2013), and active intrinsic conductance (Fransen et al.,. 2006, Gavornik and Shouval, 2011). Such work is beyond the scope of the current paper.

2) The emergence of CNA and fine tuning of the model:

Another crucial parameter is the connections from timer-->messenger and inhibitory neurons--> messenger neurons. These have to be tuned such that messengers only fire when inhibition has gone down. These synapses do not appear to have been learned using the TTL in this model. This point can be addressed by testing robustness with respect to changes in the synaptic weights: what happens if connection weights are change by +/- 29 percent. New simulations are necessary here.

These synapses were not learned using TTL in this model, but were learned using single trace learning in Huertas et al., 2015. We demonstrate that sequence learning is robust to +/- 20% changes in these synaptic weights in a new Figure (5). There is very little difference between any of the cases. The most notable is the +20% Timer to Messenger weight case, where the Messengers have a noticeably higher firing rate, but other than that, changes to the network are negligible. These weights do not have to be particularly finely tuned in order to achieve successful sequence learning.

Reviewer 1:

One of the main points raised in the previous review was that of the fine tuning of the parameters. In this revision authors have not done much to address that concern (see below for my comments on their reply). So for now, I maintain that the model is contrived and rests on very strong assumptions for which there is little experimental evidence.

We hope that our responses to (1) and (2) above help assuage your concerns.

1) The issue of rewards:

Authors write: We have assumed that on every transition between external stimuli, a “novelty” signal causes a global release of a neuromodulator, which acts as a reinforcement signal (see Materials and methods).

This is a big assumption. Clearly, we don’t just make sequences of novel events. Familiar events are also added in sequences with novel events.

The neuromodulatory “novelty” signal acts on “every transition between external stimuli”, not just novel external stimuli (as can be seen in the non-Markovian section, where stimuli are repeated).

2) Time constants of inhibitory neurons:

The choice of synaptic time constants (80ms for exc. and 10ms for inh) is very odd as also noted by the second reviewer -- but this is also crucial to the model. But there is no justification provided for these values.

See response to “Time constants of inhibitory neurons”.

3) The emergence of CNA and fine tuning of the model:

Another crucial parameter is the connections from timer-->messenger and inh neurons--> messenger neurons. These have to be tuned such that messenger only fire when inhibition has gone down - I do not think these synapses have been learned using the TTL in this model.

Authors argue that these synaptic weights can be learned as they have shown in Huerta et al. But CNA architecture is different from the model studied in Huerta et al. Three types of cells in Huerta et al. are all excitatory and there is a global inhibitory population. But for the CNA here we need two excitatory populations and one inhibitory. Moreover, the third inhibitory population cannot serve the function of global inhibition that may give rise to the timer/messenger cells (e.g. following Huerta et al.,). Furthermore, in the Huerta paper number of messenger cells are way too low but here authors have assumed that there are equal number of timer and messenger cells. Therefore, authors” claim that they have provided a putative mechanism for the emergence of the CNA structure is not correct.

The CNA we use here is the same as in Huertas et al., see Figure 7 inset from that paper. The “sustained decrease” (SD) cells in Figure 4D from that paper are omitted because they are not necessary for sequence learning. Huertas starts from a global excitatory and inhibitory population, but the main connections that result from trace learning (hence “core” neural architecture) results in a CNA identical to the one we show in Figure 2. It is true that we have assumed an equal number of Timers and Messengers, while Heurtas (and experimental evidence) suggest a smaller number of Messengers than Timers. Our model can still function with a smaller number of Messengers, we simply chose an equal number here for simplicity. Functionally the Messengers will operate the same as long as there are enough neurons to produce a mean response of the population with a high SNR (from some quick simulations this seems to be around 20 or so rather than 100).

Since authors argue that "there are a number of degenerate sets of parameters" they should show some of those. In addition, since the choice of synaptic time constants is so odd, they should show that the model works when exc. synaptic time constant is smaller than inh time constant - or how close these two time constants can be. When a model has so many parameters it is important to question the robustness of the model.

See responses to “Time constants of inhibitory neurons” and “The emergence of CNA and fine tuning of the model”.

Authors have shown the robustness of the learning algorithm (supp 9) but there are other parameters in the model that are not associated with plastic synapses. How crucial are they? At the outset it is obvious that the synaptic time constant are crucial and for some reason exc. syn time constant has to be longer than inhibitory time constant. Similarly, the connectivity from timer-->messenger and inh-neurons-->messenger needs to be tuned very carefully.

See responses to “Time constants of inhibitory neurons” and “The emergence of CNA and fine tuning of the model”. Those weights do not in fact need to be tuned especially carefully.

4) The issue of other inhibitory neurons:

My question was not about the detectability. My concern is that besides the inh neurons in the CNA there will be other inhibitory neurons in the network e.g. those needed for the emergence of time/messenger populations. Would their activity cause problems?

I do not understand this question. Within each CNA there is only a single class of inhibitory interneurons. The inhibitory neurons in the CNA are the ones responsible for the emergence of the timer/messenger population.

5) Biological realism:

I agree with the authors that they have a local learning rule and the rule is biologically plausible. My concern was about using reservoir network (which is fine) and still calling the model (Figure 5) biologically realistic.

We explicitly do not use the terms “biologically realistic” or “biophysically realistic” to describe the non-Markovian part of the model (nor do we use them wholesale to describe the Markovian part of the model, either). We only claim that it maintains a local learning rule. From the Results: “We have chosen this simple sparse representation of this three-stage network, not because it is a biophysically realistic implementation but in order to demonstrate the concept that such an addition is sufficient for learning and expressing non-Markovian sequences, while still using local learning rules.”

I also do not understand the use of the term “reservoir”. To me it seems like an attractor network. As the authors know, in reservoir computing we need to train the readout of the “reservoir” to get a specific pattern in response to an input.

Reservoir (or “liquid”) are general terms for the recurrent network used in reservoir computing or in a liquid state machine. We are not performing reservoir computing, but we are using a reservoir (or liquid, or RNN) in our model. From the Results: “The first is a fixed (non-learning) recurrent network, sometimes called a “reservoir” (as in reservoir computing) or a “liquid” (as in a liquid state machine)^49,50, which receives inputs from the Messenger cells in the main columnar network.” I would not consider it an attractor network since the only fixed points are 0 and saturation (in the limit of large N and large t, but we operate far away from this regime, and therefore far away from the fixed points).

Reviewer 4:

The paper addresses the problem of learning sequences composed of events of variable duration. This is an important problem and solution using messenger and timer cells is interesting and novel. I am less convinced of the utility of relying on reservoir computing to solve non-Markovian sequences. I wonder whether this can be done using connections between different CAN.

The reviewer offers an interesting alternative approach to learning non-Markovian sequences. We indeed tried approaches similar to the ones he proposes, and have not been able to get them to work. Of course, it might still be possible with different details than the ones we have tried, so this is still an interesting direction for future work. One interesting model of hierarchical non-Markovian sequence processing is Hawkins and Ahmad, 2016.

It is not clear whether the primary visual cortex (or a primary sensory area) is the best brain area to draw parallels with the proposed framework. Perhaps hippocampus would be more appropriate. In any case, layer 4 and 5 of primary sensory areas have very different properties and assigning them the same properties detracts from biological plausibility. There is some sequence learning in the visual cortex, but this is not the main effect in primary sensory processing.

The direct experimental evidence that inspires our model (the results of Gavornik and Bear, the evidence for Timer and Messenger cells) all occurs in visual cortex, hence why we draw parallels there. Hippocampus is certainly more traditionally associated with sequences, but they are often compressed, i.e. during place cell replay. Layer 4/5 were grouped here together because the deep layers appear to be functionally similar for sequence learning in Gavornik and Bear (see Figure 8D). There is some unpublished data that suggests Layer 5 as a more likely candidate for the Timer cells, so we will revise to simply layer 5. Our notation Layer 4/5 was more an indication of our uncertainty on which it was rather than implying that Timers were occurring in both.

There is also emerging evidence of Timer/Messenger type responses in other brain areas, including PFC (J. Cohen lab, unpublished), and we are currently working on related models in these brain areas.

https://doi.org/10.7554/eLife.63751.sa2

Article and author information

Author details

Ian Cone
1. Neurobiology and Anatomy, University of Texas Medical School at Houston, Houston, TX, United States
2. Applied Physics, Rice University, Houston, TX, United States
Contribution
Conceptualization, Software, Investigation, Writing - original draft

Competing interests
No competing interests declared
Harel Z Shouval

Neurobiology and Anatomy, University of Texas Medical School at Houston, Houston, TX, United States

Contribution
Conceptualization, Software, Formal analysis, Writing - review and editing

For correspondence
harel.shouval@uth.tmc.edu

Competing interests
No competing interests declared

"This ORCID iD identifies the author of this article:" 0000-0003-2799-1337

Funding

National Institute of Biomedical Imaging and Bioengineering (1R01EB022891-01)

Harel Z Shouval

Office of Naval Research (N00014-16-R-BA01)

Harel Z Shouval

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Acknowledgements

We would like to acknowledge conversations with Marshall Hussain Shuler and Nicolas Brunel.

Senior Editor

Ronald L Calabrese, Emory University, United States

Reviewing Editor

Tatyana O Sharpee, Salk Institute for Biological Studies, United States

Version history

Received: October 6, 2020
Accepted: February 16, 2021
Version of Record published: March 18, 2021 (version 1)
Version of Record updated: March 13, 2023 (version 2)

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.