Predicting bacterial promoter function and evolution from random sequences
- School of Biological Sciences, Faculty of Biology, Medicine and Health, University of Manchester, United Kingdom
- Institute of Science and Technology Austria, Austria
- Center for Physiology and Pharmacology, Medical University of Vienna, Austria
- Institute of Integrative Biology, Functional and Comparative Genomics, University of Liverpool, United Kingdom
Figures
Figure 1 with 2 supplements
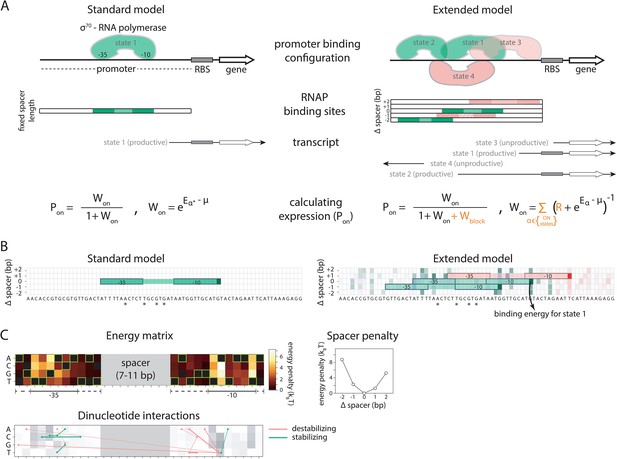
Standard and Extended models.
(A) The standard thermodynamic model assumes only one (strongest) σ70-RNAP binding configuration at the promoter, which generates a productive transcript. We refer to ‘promoter’ as the entire cis-regulatory element, while ‘binding site’ refers to the RNA polymerase (RNAP) contact residues of a specific binding configuration (colored area in ‘RNAP binding sites’). The Extended model incorporates structural features of bacterial promoters into the thermodynamic framework: (i) cumulative binding, permitting σ70-RNAP to bind multiple binding sites independently on the same promoter (binding configurations 1–4); (ii) spacer length flexibility (difference between configurations 1 and 2); (iii) occlusive unproductive binding (configuration 3); (iv) occlusive binding on the reverse complement (RC) (configuration 4). To predict gene expression levels, we calculate the probability of productive σ70-RNAP binding (Pon), where μ is the chemical potential related to RNAP concentration, Eα the energy of binding for binding state α, R the clearance rate relative to σ70-RNAP recruitment rate, and Wblock the binding free energy of unproductive states, which is calculated in the same way as Won but for unproductive as opposed to productive (on) states. The Standard model does not allow for any unproductive binding, and it considers only the single strongest binding site (α*). How the structural features are incorporated into the Extended model is shown in orange. (B) Example model output for a selected PR mutant (stars mark mutated positions) for the Standard and the Extended model, showing binding configuration on the forward strand. Pixels forming the background grid indicate –10 end-points of binding sites, with the intensity of color corresponding to the strength of binding in that configuration (green productive, red unproductive binding). States that are bound strongly enough to independently lead to measurable expression are framed (one for the Standard model, three for the Extended model – two productive, one unproductive). For illustration purposes, the pixel corresponding to the binding energy of State 1 in panel A is marked with an arrow. (C) Main biophysical parameters of the Extended model, fitted from sort-seq data. Energy matrix shows the effect of every possible binding site residue on the binding energy between σ70-RNAP and DNA (strongest binding indicated by green squares). The optimal energy matrix consists of the –10 and –35 elements (underlined), positions outside the canonical elements that significantly affect quantitative predictions of gene expression levels (dotted underline), and spacer of optimal length 9 bp (corresponding to the canonical 17 bp between –10 and –35 elements). Strongest stabilizing (green) and destabilizing (red) interactions between dinucleotides are shown, with line thickness indicating the deviation from independent energy contribution to binding (range 0.15–0.38kBT). For other model parameters and all significant dinucleotide interactions, see Figure 1—source data 1. Figure 1—figure supplement 1 describes the experimental system and protocol; Figure 1—figure supplement 2 shows the comparison between our and previously obtained energy matrix for σ70-RNAP.
-
Figure 1—source data 1
Inferred values for model parameters.
For each position in the energy matrix, the energy penalty is normalized to the lowest energy (strongest binding) residue in that position, which is set to zero. Same applies for the spacer variation penalty, where the optimal spacer length is set to zero. Orange background marks the canonical –10 and –35 binding sites of σ70-RNAP. For pairwise interaction, ‘identity’ refers to the two positions and specific residues that have a significant positive (destabilizing) or negative (stabilizing) interaction, with numbers indicating the position of the residue in the matrix shown in Figure 1C. Shaded cells indicate the strongest interactions, which are shown in Figure 1C. The numbers indicate the position in the energy matrix, starting from the most upstream to the most downstream (left to right in the energy matrix shown in Figure 1C).
- https://cdn.elifesciences.org/articles/64543/elife-64543-fig1-data1-v1.zip
Figure 1—figure supplement 1
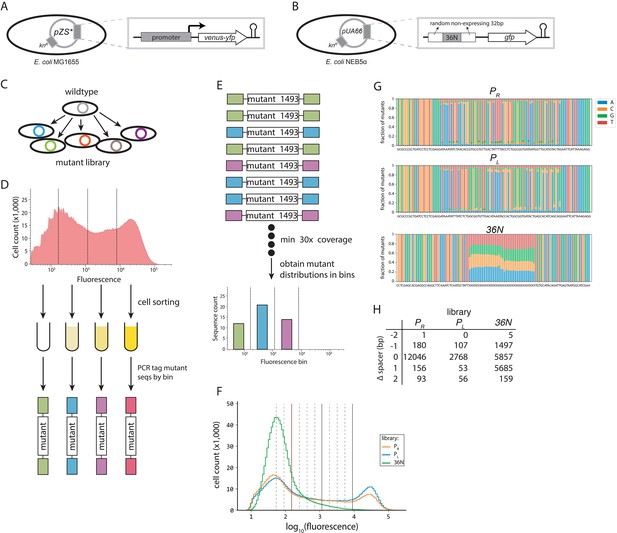
Experimental plasmid systems and protocol.
(A) For the PR and PL libraries, the synthetic construct used to detect the effects of promoter mutations consisted of a yellow fluorescent marker (venus-yfp), preceded by a ribosomal binding site (RBS), and under the control of either the PR or PL promoter (or a PR or PL promoter mutant). The system was isolated from the rest of the plasmid by a T1 terminator (hairpin). This construct was placed on a small copy number pZS* plasmid (SC101* origin) with kanamycin resistance, with Escherichia coli MG1655 as host. (B) The expression of a green fluorescence protein (gfp) was under the control of a random 100 bp sequence consisting of: two 32-bp-long random, non-expressing flanking sequences that were not mutated; and a 36-bp-long sequence that was mutated randomly, with each nucleotide having 25% chance of being found at each position. This construct was placed on a pUA66 plasmid (SC101 origin), with E. coli NEB5α as a host. (C) Promoter mutants were cloned into the plasmid system using restriction/modification. The mutations were introduced at random, using pre-synthesized oligonucleotides with a fixed mutation rate (12% for the PR, 9% for the PL, and fully random for the 36N mutant library). The plasmids carrying mutant promoters were cloned either into MG1655 (PR and PL libraries) or NEB5α (36N library). (D) Each random mutant library was sorted through fluorescence activated cell sorting (FACS) based on the fluorescence intensity detected at the single cell level. Mutants in PR and PL libraries were sorted into four, while the 36N library was sorted into 12 equidistant bins. 150-bp-long fragments containing the promoter region of each sorted sub-library were PCR-tagged, and each library sequenced in bulk with 5 million total reads per library. (E) We screened each sequence library for only those mutants that had at least 30× coverage, and obtained fluorescence distributions of each mutant across the bins. (F) Flow cytometry measurements of 1 million mutants from each library showing distributions of fluorescence (as proxy for gene expression levels). The vertical red dotted line separates the mutants with no measurable expression (corresponding to Figure 4A). The red dotted line and the solid lines separate the four bins used to sort the PR and PL libraries (no, low, intermediate, and high expression, from left to right). The dotted lines mark the boundaries of the additional bins used to sort the 36N library. (G) Mutation frequencies in the three experimental libraries are shown as fraction of mutants with a given nucleotide at each position for PR, PL, and 36N libraries. We did not observe any bias in the mutagenesis of libraries. The consensus sequence for each library is provided underneath each plot. (H) Number of sequences in each library containing a spacer of specific length. The reported counts are based only on the spacer length of the strongest binding site identified in each sequence. Note that the Extended model accounts for cumulative binding between all possible σ70-RNAP configurations binding to a given sequence, meaning that our libraries contained a much greater number of sequences with each spacer length than shown here. In fact, because here we considered only the single strongest binding site, the counts over-represent the optimal spacer length because it has the lowest energy and, hence, binding configurations with that spacer length are more likely to be most strongly bound.
Figure 1—figure supplement 2
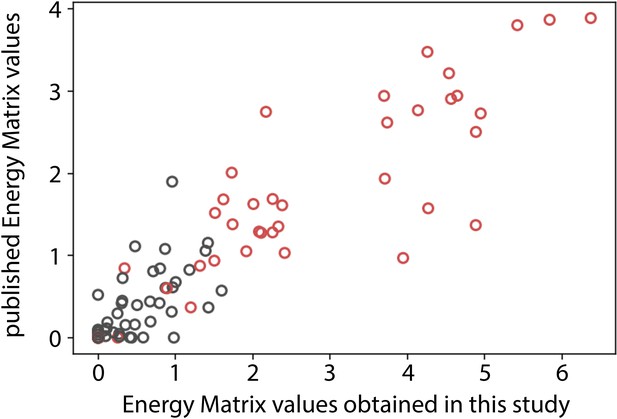
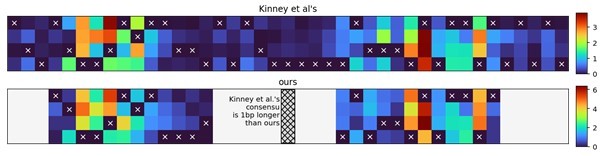
Comparison of σ70-RNAP (RNA polymerase) energy matrix values.
Correlation between corresponding energy matrix values in the matrix obtained in this study (Figure 1C) to that obtained by Kinney et al., 2010. Points shown in red correspond to the canonical –10 and –35 sites, while the points in black represent other entries in the matrix.
Figure 2 with 2 supplements
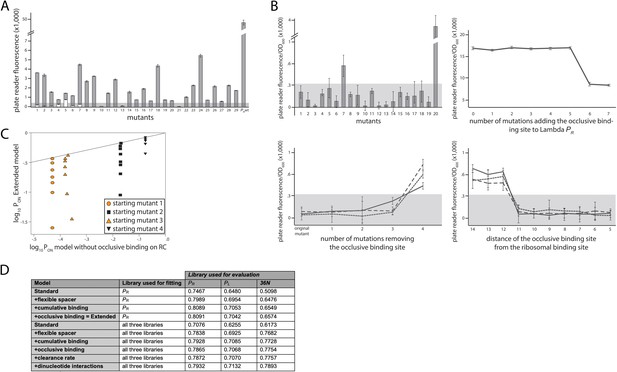
Experimental validation of structural promoter features.
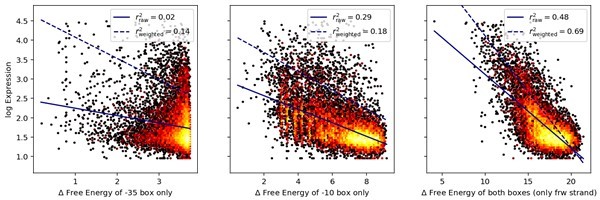
(A) Cumulative binding affects expression in most tested sequences. We experimentally created 29 promoters with the following property: the Standard model predicts no measurable expression from these promoters, while the Extended model predicts measurable expression due to the existence of multiple σ70-RNAP (RNA polymerase) binding sites. Fluorescence measurements are shown in gray bars, with error bars indicating standard error of the mean from three replicate biological measurements. The gray horizontal bar indicates the detectability (‘no measurable expression’) threshold, determined for plate reader measurements as the mean fluorescence/OD600 value across all replicates of the population carrying the plasmid without any fluorescence markers. All promoters but 10, 13, and 21 exhibited significant measurable expression. We introduced additional mutations into promoters 1–7, in order to remove the secondary binding site(s) without affecting the strongest binding site. White bars show the expression levels of these additional mutants. Only the mutated promoter 5 exhibited significant measurable expression. (B) Characterizing sequence determinants of occlusive unproductive binding. (Top left panel) We created 20 promoter sequences for which the Extended model that accounts for occlusive unproductive binding predicted no measurable expression, while the model which did not account for occlusive unproductive binding predicted measurable expression. Bars are mean fluorescence measured from three biological replicates, and error bars are standard error of the mean. The gray shaded area indicates the detectability (‘no measurable expression’) threshold. Only mutants 7 and 20 exhibited significant measurable expression. (Top right panel) We inserted mutations into the wildtype PR promoter to gradually introduce an additional binding site that was predicted to bind in an occlusive unproductive manner. These mutations were not predicted to significantly alter σ70-RNAP binding to the existing dominant PR binding site. As mutations are introduced into the promoter, they generate stronger binding to the new site, which lowers gene expression levels. (Bottom left panel) We mutated three promoters (originally found in the PR mutant library) to gradually remove their existing, predicted occlusive unproductive binding sites. As the predicted occlusive unproductive sites were removed, we measured a significant increase in gene expression levels. (Bottom right panel) In order to experimentally verify the occlusive unproductive binding cutoff distance from the –10 end of the binding site to the beginning of the ribosomal binding site (RBS), we started with the same three promoters as in bottom left panel. We used the Extended model to identify the predicted occlusive unproductive binding site, and then we moved the site upstream and downstream to increase or decrease the distance from the RBS, respectively. We identified that a binding site that is 11 or fewer base pairs away from the RBS acts as an unproductive site, while those that are 12 or more base pairs away productively and cumulatively contributed to gene expression levels. (C) Mixed support for the role of unproductive binding on the reverse complement in driving expression. We identified four promoter sequences for which we introduced up to eight mutations that would not alter predicted gene expression levels if the model did not account for unproductive binding on the reverse complement, but would if the Extended model was used. In other words, the eight introduced mutations would gradually increase the strength of binding on the reverse complement while having a minimal effect on the strength of binding on the productive strand. Colored points indicate mutants whose measured expression changes in line with Extended model predictions, while black points are mutants whose expression doesn’t change compared to the original promoter. Individual responses of each mutant are shown in Figure 2 – Extended Figure 1. (D) Improvement to predictability based on each promoter feature. Each structural promoter feature was added to the simpler iteration of the model, starting from the Standard model and building progressively toward the Extended. The clearance rate and dinucleotide interactions were included only in the model fitted on all three libraries. The ‘unproductive binding’ term includes the combined contribution of the occlusive unproductive binding and the unproductive binding on the reverse complement, both of which individually provided a small but significant improvement to model predictions. The values are the fraction of variance explained on the evaluation dataset. Figure 2 – Extended Figure 2 contains additional verifications of model predictions.
Figure 2—figure supplement 1
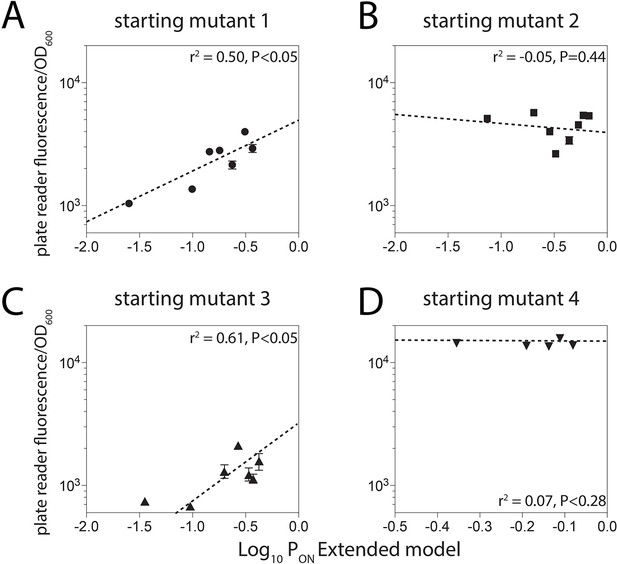
Unproductive binding on the reverse complement.
We identified four promoter sequences for which we could introduce up to eight mutations that would not alter predicted gene expression levels if the model did not account for unproductive binding on the reverse complement, but would if the Extended model was used (Figure 2C). Introduction of these mutations reduced the measured gene expression levels for two promoters (1 and 3) but had no effect on the expression levels from promoters 2 and 4.
Figure 2—figure supplement 2
Validation of model predictions.
(A) Verifying model predictions on 115-bp-long sequences. In order to verify the ability of the Extended model to predict expression levels from 115-bp-long promoters, and in particular to verify the model prediction of the ease of generating promoters from random non-expressing sequences, we generated 20 pairs of promoters. These pairs consisted of a randomly generated non-expressing sequence, and a sequence exactly one point mutation away that was predicted to have measurable expression. White bars are mean expression levels of three biological replicate measurements of non-expressing promoters; gray bars are the promoters with a single point mutation. Error bars are standard error of the mean. The gray horizontal bar indicates the detectability (‘no measurable expression’) threshold. (B) Model determination of occlusive unproductive binding sites. We evaluated the Extended model fitted on the PR training dataset, with varying thresholds between productive and occlusive unproductive bindings. Shown is the change in the negative log likelihood on the dataset indicated in the legend. Red arrow indicates the actual threshold ultimately used in the model. Because this modeling only provided a range for the productive/unproductive cutoff distance between the RNA polymerase (RNAP) binding site and the ribosomal binding site (RBS), we carried out dedicated experiments to systematically validate and probe occlusive unproductive binding (Figure 2B). (C) Optimal value of the clearance rate. We scanned through the possible values of the relative clearance rate of the σ70-RNAP complex from the promoter, using the Extended model fitted on the training subsets of all mutant libraries. For each value, we refit chemical potential and hyperparameters of logistic regression using the training dataset. Shown is the change in negative log likelihood on the training data. The optimal value is indicated with the red arrow, though a wider range of values is compatible with the data. For the majority of values in the compatible range including the optimal value, the model performance improves also on the validation dataset.
Figure 3 with 3 supplements
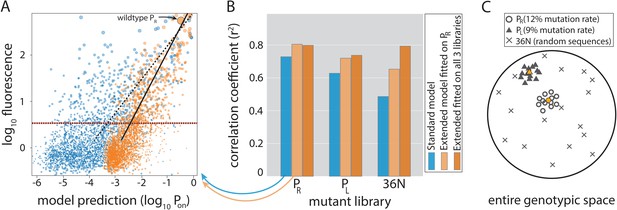
Model performance.
(A) Model-to-data correlation for the Standard (blue) and the Extended model (orange) trained on PR only, shown for the evaluation subset (20%) of the PR mutant library. The experimentally measured fluorescence of each mutant is the mean bin (out of four) across all sequenced reads of that mutant (we only consider mutants with at least 30× coverage). Best-fit line (dashed for the Standard model, solid black for Extended) and the instrument detectability threshold, which we refer to as the ‘measurable expression’ and which marks the 99th percentile of plasmid-free strain (red dashed line), are shown. Marker sizes indicate data-point weights used in fits. We assume that the model predictions are independent of the instrumentally determined measurable expression threshold. (B) Model performance on mutant libraries (PR, PL, 36N), shown as fraction of variance explained on evaluation data. Arrows indicate which bars correspond to the correlation plot shown in (A). (C) Cartoon of the three mutant libraries: PR and PL sample locally around a wildtype, with each position having a 12% or 9% chance, respectively, of containing the non-wildtype residue; 36N library contains random 36-bp-long sequences, meaning that it uniformly samples the full 36-bp-long genotypic space (see Figure 3—figure supplement 2G). Colored circle and triangle represent the wildtype PR and PL sequences, respectively. Figure 3—source data 1, Figure 3—source data 2 provide additional details on the processing of mutant libraries, as does the Figure 3—figure supplement 2. Figure 3—figure supplement 1 shows the performance of the two models on previously published datasets of promoter mutants. Figure 3—figure supplement 3 shows the plate reader validation of 36N library data processing.
-
Figure 3—source data 1
Processing of the mutant libraries and sizes of datasets after splits.
The table shows the number of reads remaining in the datasets following each step of data processing, from original sequenced library down to the final library used for model fitting and evaluation.
- https://cdn.elifesciences.org/articles/64543/elife-64543-fig3-data1-v1.zip
-
Figure 3—source data 2
Number of mutants per expression bin for each split of the PR, PL, and 36N dataset.
Bins are no (‘0’), low (‘1’), intermediate (‘2’), and high (‘3’) for the PR and PL libraries, and are ordered from lowest (‘0’) to highest (‘11’) for the 36N library.
- https://cdn.elifesciences.org/articles/64543/elife-64543-fig3-data2-v1.zip
Figure 3—figure supplement 1
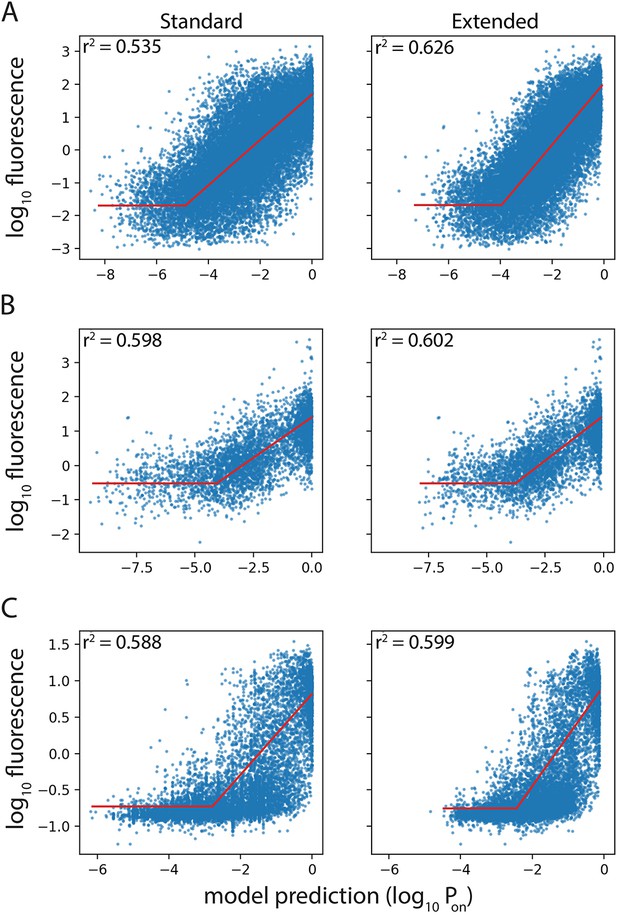
Performance of Standard and Extended model on previously published datasets.
Expression level predictions from the Standard and the Extended model were correlated to measured expression levels, in the promoter mutant libraries published by (A) Johns et al., 2018; (B) Hossain et al., 2020; (C) Urtecho et al., 2019. Red line shows the line of best fit, resulting in the reported correlation coefficient, r2.
Figure 3—figure supplement 2
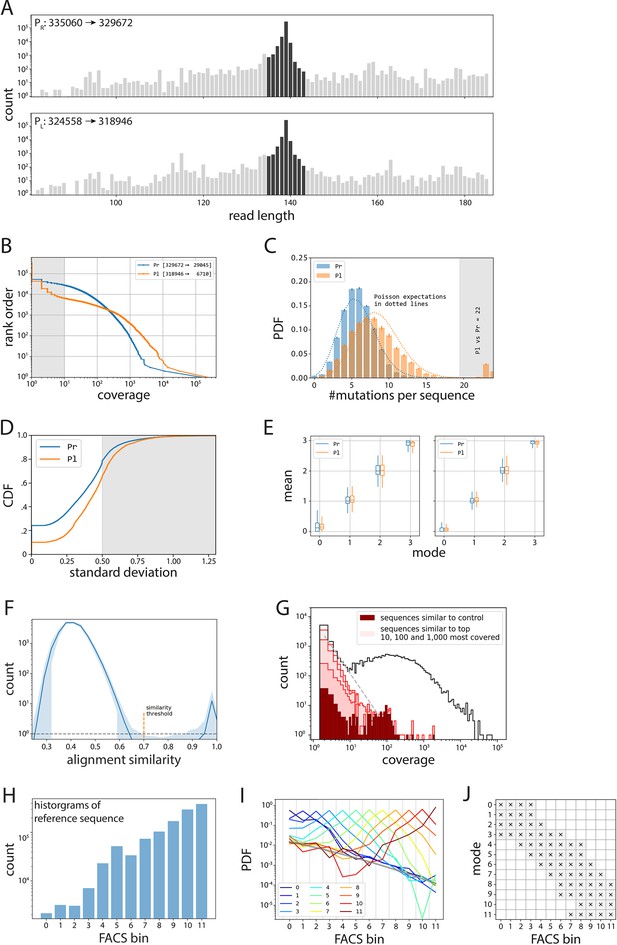
Processing of mutant libraries.
(A–E) Processing of PR and PL libraries. (A) All reads in the PR and PL libraries (gray), from which we take only those reads that are ±4 bp away in length from the wildtype sequence (dark gray). (B) Inverse cumulative distribution function (normalized to the total number of sequences), with shaded indicating the sequences we removed due to having less than 10× coverage. (C) We removed sequences that had 20 or more single point mutations compared to their respective wildtype sequence. Note that this mainly affected the PL library (orange), as the original plasmid from which the libraries were cloned contained the wildtype PR sequence. (D) Cumulative distribution function (CDF) of standard deviation of expression bin numbers, with shaded sequences the ones we removed from subsequent analyses. (E) Box plots indicating the distributions of mean values (in bin units) for a given mode (in bin units), before (left) and after (right) selecting for only those where mean, mode, and median are within 0.5. (F–J) Processing of the 36N library. (F) Average histogram of alignment similarity for the 1000 most covered sequences (shaded area indicates 95% confidence interval). We used the similarity threshold of 0.7 between low- and high-scoring modes to select for unique sequences and eliminate sequencing errors. (G) Histogram of coverage (black line), with highlighted contributions of the noise cloud around the reference sequence (dark red), and the clouds around the 10, 100, and 1,000 most abundant sequences (from darkest to lightest shade of red, respectively). (H) Histogram of counts for the reference sequence per bin, used to debias all other distributions. (I) Template probability distribution functions (PDFs) obtained as averages of PDFs that have the same mode (indicated by color). The inferred fluorescence activated cell sorting (FACS) noise background is shown as a thick gray line. Given a distribution, we only accepted values in the bins in which the appropriate reference was three times above the inferred background. Such filter is shown in (J).
Figure 3—figure supplement 3
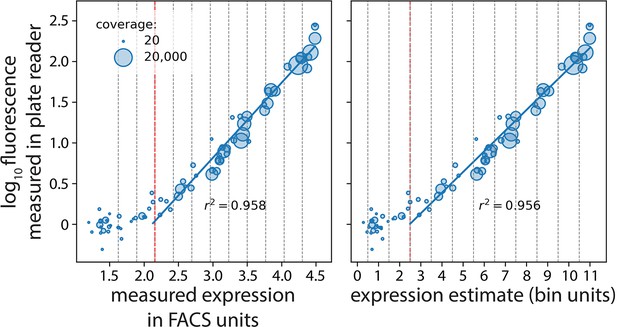
Plate reader validation of 36N data processing.
Seventy-seven mutants (with an approximately equal number of mutants selected from each of the 12 bins) were selected randomly and their expression levels measured in a plate reader. We correlated their expression measured in the plate reader with our estimates in fluorescence activated cell sorting (FACS) units (left) and bin units (right). The vertical red dotted line marks the measurable expression threshold in the flow cytometer. Measured expression in FACS units and expression estimate are shown in log scale.
Figure 4 with 3 supplements
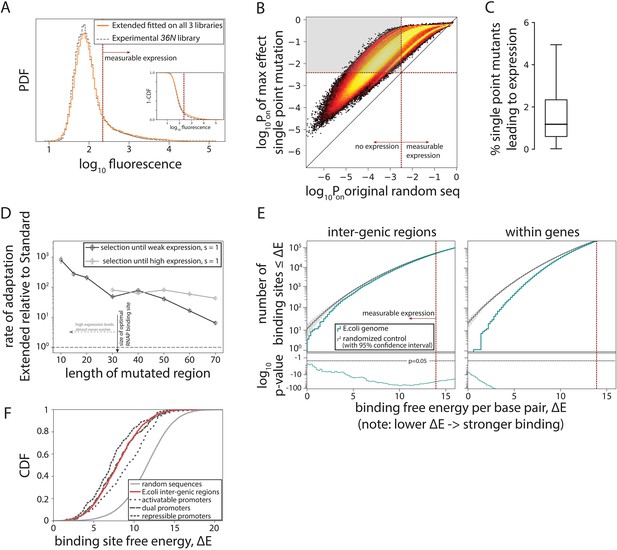
Evolution of promoters.
(A) Probability density function (PDF) for the flow cytometry measurement of the 36N library (gray dashed line) compared to the flow cytometry fluorescence intensities simulated from 106 randomly generated 115-bp-long sequences using the Extended model fitted on all three libraries. Red dotted line marks the cutoff for ‘measurable expression’, estimated from experimental data. Measurable expression is defined to correspond to the 99th percentile of fluorescence measurements of the experimental strain carrying no plasmid and, hence, no fluorescence. Inset: cumulative distribution function (CDF) for the same comparison. (B) Density heat map (brighter color represents higher density), showing, for every simulated random sequence (expression on x-axis), the expression of a single point mutant with the largest positive effect on predicted expression (Pon) (y-axis). For 82% of non-expressing random sequences (sequences left from the dotted line on the x-axis), that mutation led to measurable expression (gray area). (C) Box plot showing the percentage of all possible point mutations predicted to convert a given random non-expressing sequence into one with measurable expression (obtained from 105 random sequences). (D) Increase in rates of adaptive evolution of the Extended relative to the Standard model. Evolution to either weakest measurable expression, or high (PR) expression levels was modeled through single point mutations. Evolution was simulated 100 independent times for each of the 100 random 115-bp-long starting sequences, by mutating the central contiguous part of the indicated length. Evolving promoters would almost never reach high expression levels when only a region smaller than the RNA polymerase (RNAP) binding site (30 bp) was allowed to mutate. (E) For evidence of selection against σ70-RNAP binding sites, we compared the free energy per bp between either the inter-genic (typically, promoter containing) or the within-genic regions of the Escherichia coli genome, and that of a random sequence with the GC% of the corresponding region (note that higher energy means weaker binding and hence lower expression). At lower binding energies (corresponding to stronger binding), the actual number of binding sites in the E. coli genome (teal) is lower than expected based on random sequences (gray). Associated p-values are also shown. The total number of binding sites increases with binding energy (i.e. there are a lot more weaker than stronger binding sites), explaining the variability in p-values. (F) CDFs for predicted binding strengths of different E. coli promoters, obtained from RegulonDB. Figure 4—figure supplement 1 shows further details on how promoter evolution was modeled. Figure 4—figure supplement 2 contains the information about the contribution of cumulative binding to expression. Figure 4—figure supplement 3 shows additional tests for selection against σ70-RNAP binding sites.
Figure 4—figure supplement 1
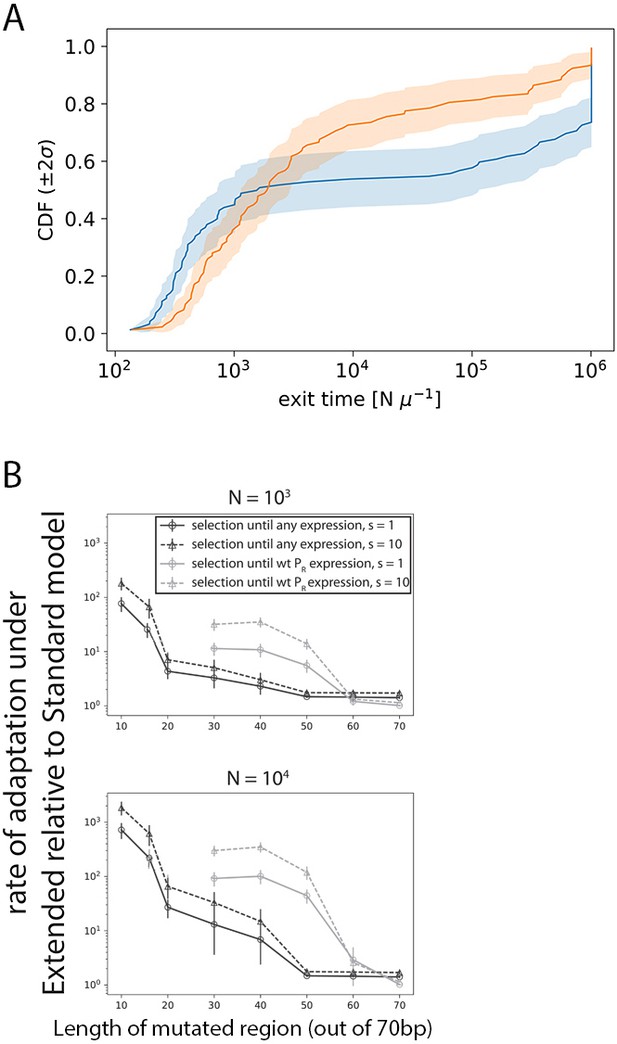
Modeling evolution.
(A) Cumulative distribution function (CDF) of the median times for promoter evolution under the Extended (orange) and Standard (blue) models for s = 1, N = 104, length of central mutagenized region of 70 bp and high target expression level (that of wildtype PR). Evolution was simulated 100 independent times for each of the 100 starting random sequences. We present this specific set of parameters as this is the case where the largest fraction of simulations stopped at 10 N iterations (our simulation limit), before reaching the target expression. For all parameter combinations, including the one shown here, more Standard model simulations terminate at 10 N iterations compared to Extended model simulations. Taking a ratio of the mean time under this CDF for the Extended model over that for the Standard model therefore represents a conservative lower bound for the speedup in promoter evolution. (B) Selection at two different population sizes (top panel: N = 103; bottom panel: N = 104) using the Strong-Selection-Weak-Mutation model at two selection strengths (s) and selecting to either PR-levels of expression or any measurable expression. Selection was simulated through 100 independent runs for each of the 100 random starting sequences, with different lengths of the sequence allowed to mutate. Errors bars are standard errors of the mean across all replicates and starting sequences. Indicated selection refers to the selection on the phenotype difference (Δlog10Pon).
Figure 4—figure supplement 2
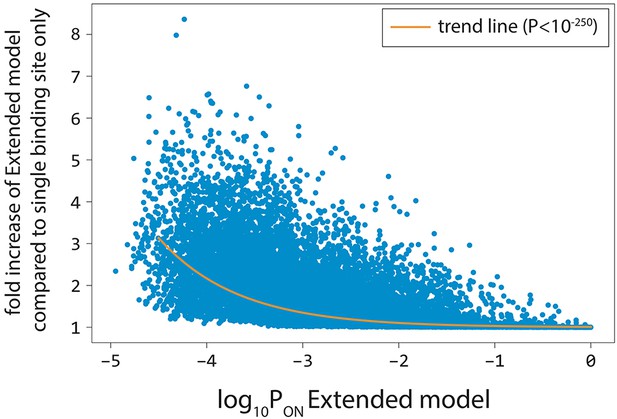
Cumulative binding contributes more to expression at weak promoters.
For 100,000 random 100-bp-long sequences, we calculated the fold increase in predicted gene expression levels of the Extended model compared to the model that is constrained to only the single strongest σ70-RNAP binding site. Predicted expression levels from stronger promoters (higher log10Pon) were determined primarily by binding to the strongest σ70-RNAP binding site. In contrast, predicted gene expression levels at weak promoters were more likely to be determined by σ70-RNAP binding at multiple sites. The orange line is the trend line obtained through non-linear regression.
Figure 4—figure supplement 3
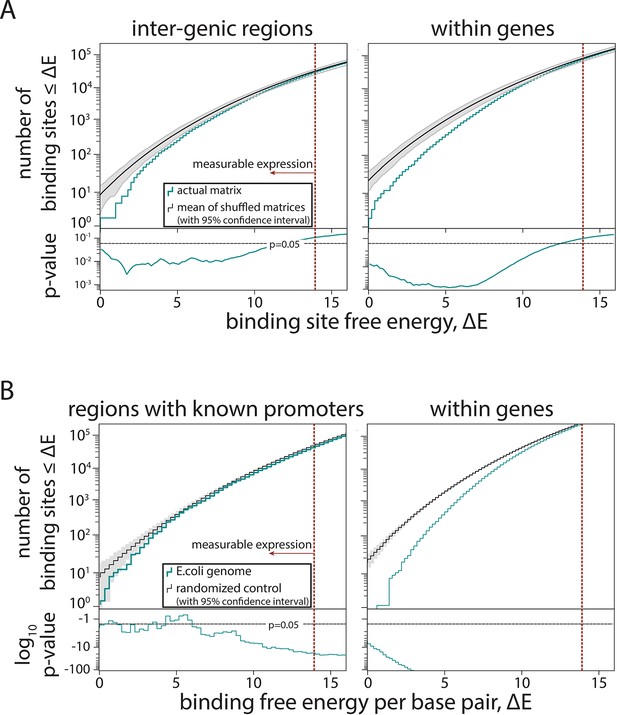
Further tests of selection against σ70-RNAP (RNA polymerase) binding sites.
(A) To provide an alternative measure to that presented in Figure 4E, instead of creating a random sequence and comparing the number of predicted σ70-RNAP binding sites in it and in the Escherichia coli genome, here we created 100 shuffled σ70-RNAP energy matrices and used each of them to predict the expression from every single position in the E. coli genome. For each shuffle, we constructed cumulative histograms of free energy for inter-genic and within-genes regions. For each bin, we then calculated the p-value of the Extended model that used the actual σ70-RNAP energy matrix, assuming a normal distribution with mean and standard deviation given by the set of models with shuffled matrices. This is a conservative estimate, as for energies ΔE < 1, the assumption of Gaussian distribution leads to overestimates of standard deviation. The matrices were shuffled per position, that is, an energy matrix of dimension 4× L, with L being the length of the binding site, is shuffled by randomly reordering the L columns while leaving the energy entries in each column unchanged in order and magnitude. Gray lines represent 95% confidence intervals. (B) For evidence of selection against σ70-RNAP binding sites only in the inter-genic regions that contain experimentally confirmed promoters (based on RegulonDB), we compared model-predicted binding energy across the region to the expected binding for a 108 bp random sequence with the GC% of the corresponding region. Also shown is the selection against binding sites within genes (same as in Figure 4E). Gray shaded areas are 95% confidence intervals.
Scheme 1
Modelling RNA polymerase binding.
Author response image 1
Author response image 2
Author response image 3
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Predicting bacterial promoter function and evolution from random sequences
eLife 11:e64543.
https://doi.org/10.7554/eLife.64543
